디퓨저 베인에 기인한 공진조건에서의 임펠러 강제진동 및 구조응답 예측

2.1 임펠러의 진동 특성

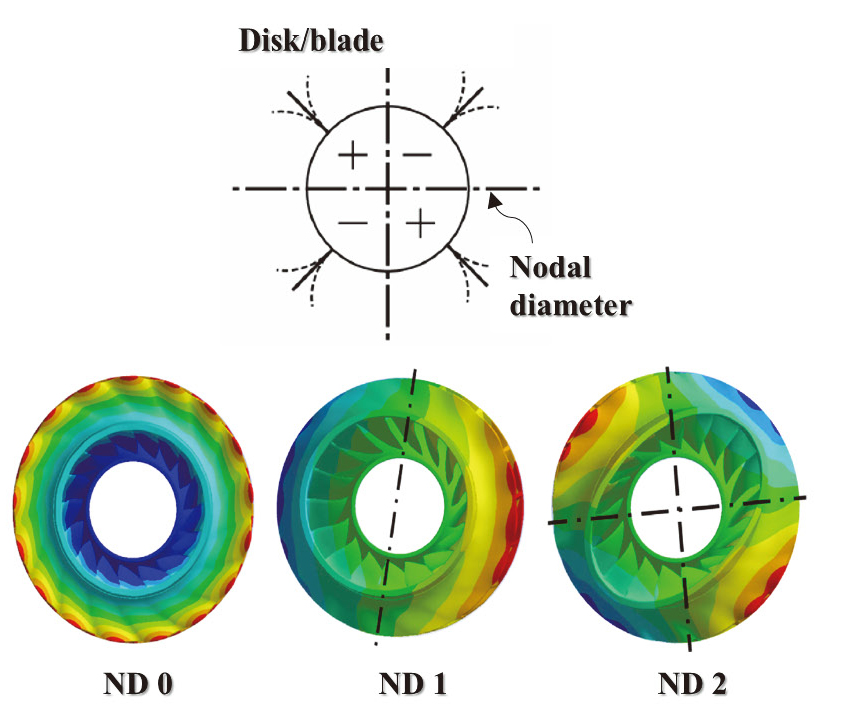
디스크 형상을 가진 진동모드에서는 Fig. 2와 같이 면외(out-of-plane) 방향으로 변위가 발생하지 않는 선 형태가 발생하는데 이를 노달 직경(nodal diameter, ND)라고 한다. 임펠러와 같이 디스크가 유연도(flexibility)를 가지고 블레이드가 일체화 된 구조물(bladed-disk)의 고유 모드형상(mode shape)은 디스크 진동모드로 인해 노달 직경 값을 기준으로 변형이 발생하며, 유사한 고유진동수 값을 가진 모드일지라도 서로 다른 모드형상을 가지게 된다. 임펠러의 블레이드가 N_b개로 짝수일 경우, 노달 직경 값은 0부터 N_b/2의 값을 가질 수 있으며 N_b이 홀수일 경우, 0부터 (N_b−1)/2의 값을 가지게 된다. 또한, 임펠러의 블레이드는 노달 직경의 값에 따라 블레이드 간 위상각(inter-blade phase angle, IBPA) 값이 변화하게 되는데 N_b의 값이 짝수일 경우 IBPA β와 노달 직경 k의 관계는 Eq. 1, 2와 같다[6].

Fig. 2

Nodal diameter of the bladed-disk structure.

따라서, 노달 직경 k의 값이 0일 경우 모든 블레이드는 같은 위상각을 가지고 가진 시 거동을 하게 되며, 노달 직경 k의 값이 N_b/2일 경우 블레이드 간 최대 크기의 서로 다른 위상각을 가지고 가진 시 거동을 한다. 그리고 Eq. 1의 경우 forward traveling wave mode를 가지며, Eq. 2는 backward traveling wave mode를 가지게 된다.

2.2 디퓨저 베인에 기인한 가진력 특성

주기적으로 회전하는 임펠러와 임펠러 토출 유동의 불균일성(non-uniformity)으로 인해 디퓨저 베인의 입구 유동 조건은 주기적으로 변화한다. 마찬가지로 임펠러 내부 유동장 역시 디퓨저 베인의 잠재 영향(potential effect)에 의해 주기적으로 변화한다. 이러한 영향으로 인해 임펠러와 디퓨저 베인에 형성되는 압력장이 주기적으로 변화하며, 이것이 임펠러에 공력가진력으로 작용하게 된다. 이러한 디퓨저 베인에 기인한 가진주파수는 VPF(vane passing frequency)로서 Eq. 3과 같이 나타낼 수 있다. 디퓨저 베인 개수가 N_v개 일 때, 임펠러 회전수의 N_v배에 해당하는 가진주파수는 임펠러 팁 근방 N_v등분 위치에 가해진다.

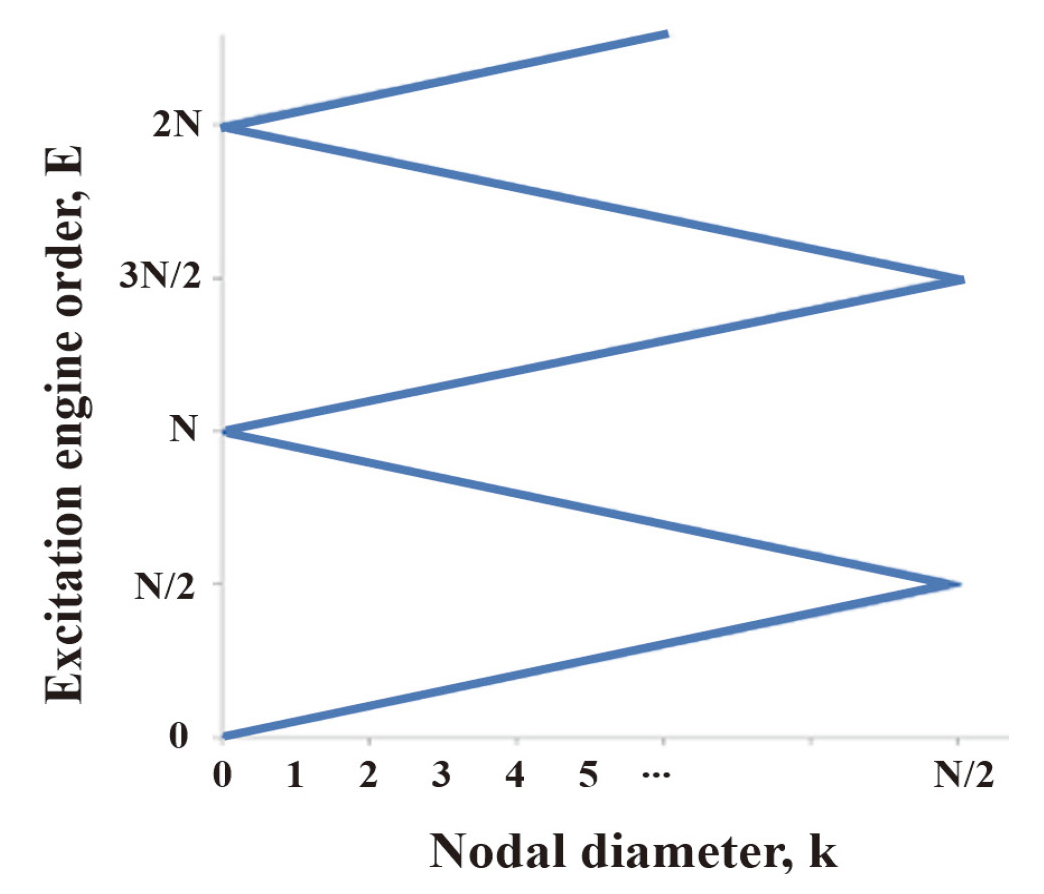
이 때, 디퓨저 베인 개수는 노달 직경으로 표현되는 가진력의 형상을 나타내고, 가진력은 디퓨저 베인 개수에 따라 임펠러 원주 방향으로 주기적인 분포를 가지게 된다. N_b개의 블레이드를 가진 임펠러의 경우 디퓨저 베인과 같은 가진원으로부터 가진력을 받을 때, 가진되는 노달 직경의 관계는 Table 1과 같으며, 이를 도시화한 그래프는 Fig. 3과 같다[6].

Table 1.

Relation between number of excitation sources and nodal diameters.

Fig. 3

Diagram of the relationship between engine order and nodal diameter.

2.3 SAFE 선도

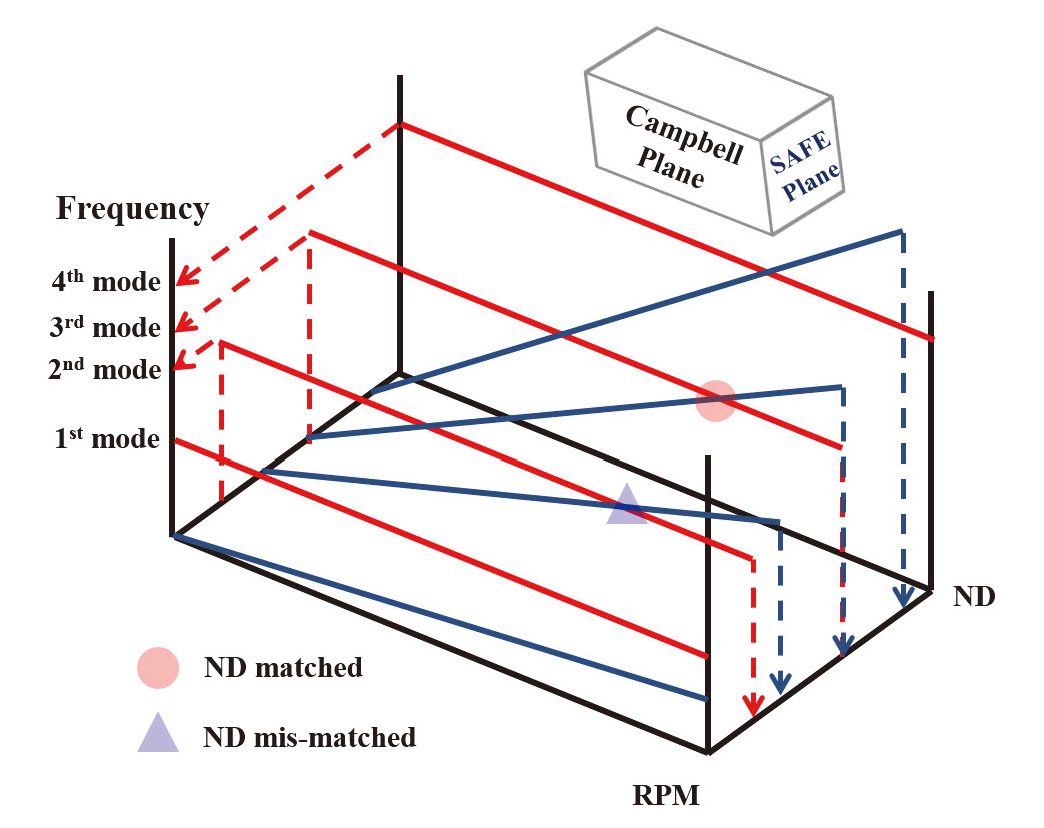
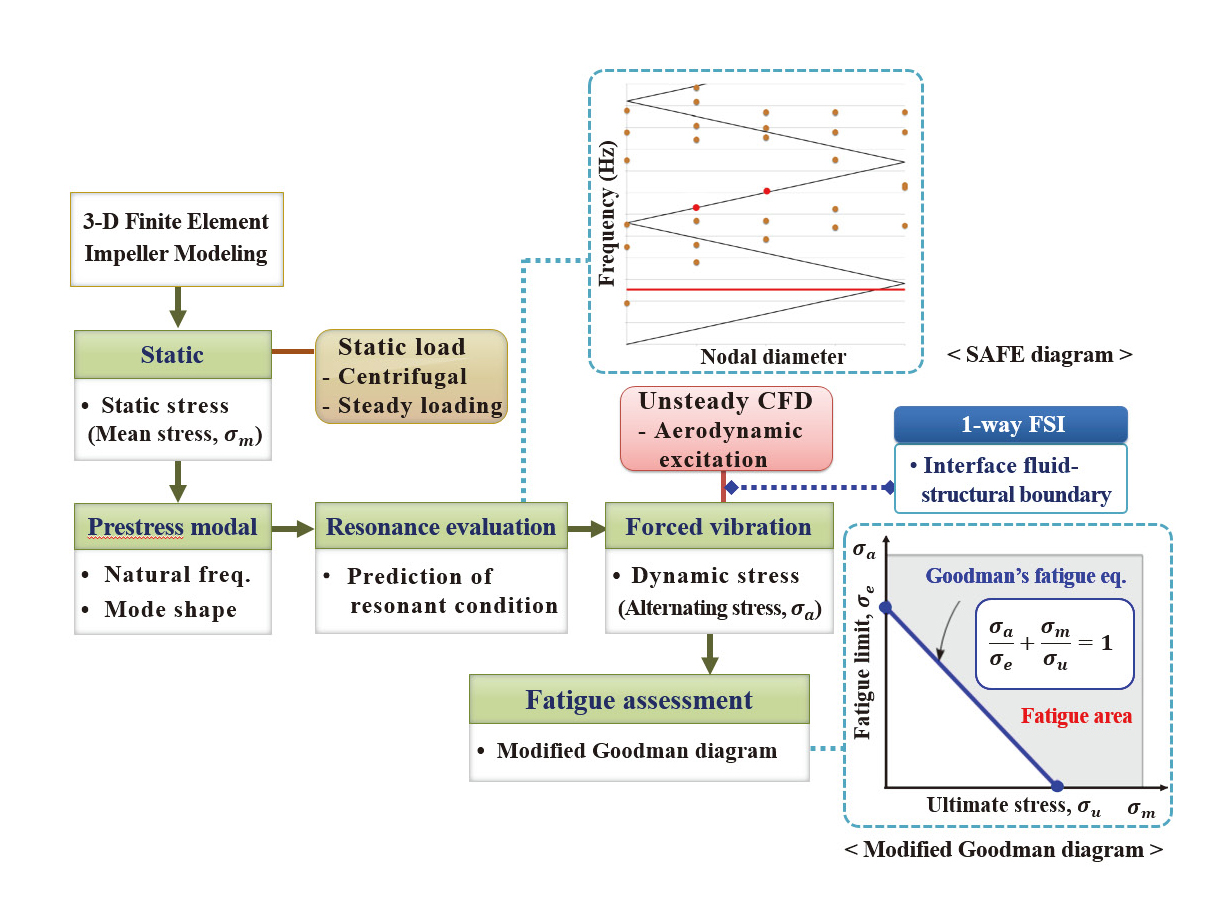
공진은 외부 가진력의 주파수와 구조물의 고유진동수가 유사할 때 발생하며, 이는 구조물에 대해 과도한 응력을 발생시켜 피로 파손을 야기한다. 이에 많은 산업체에서는 구조 신뢰성을 확보하기 위해 외부 가진력이 공진을 야기할 때 설계단계에서부터 이를 시각적으로 확인할 수 있는 Campbell 선도를 사용해 왔다. 반면, 임펠러와 같이 블레이드와 유연도를 가진 디스크가 일체화 된 구조물은 SAFE(Singh’s advanced frequency evaluation) 선도를 적용하여 공진 조건을 도출하게 된다. 이 SAFE 선도에서의 공진 발생 조건은 가진력의 주파수와 구조물의 고유진동수의 일치뿐 아니라 가진력의 형상과 구조물의 모드 형상까지 일치해야 한다[7]. 즉, 디퓨저 베인에 기인한 가진력이 가지는 노달 직경과 임펠러 모드형상의 노달 직경이 일치해야 실제 공진이 발생한다. 이러한 공진 발생 조건을 Campbell 평면과 SAFE 평면으로 구성된 3차원 그래프로 도시화하면, Fig. 4와 같다.

Fig. 4

Concept of SAFE diagram.

3.1 유체-구조 연성해석

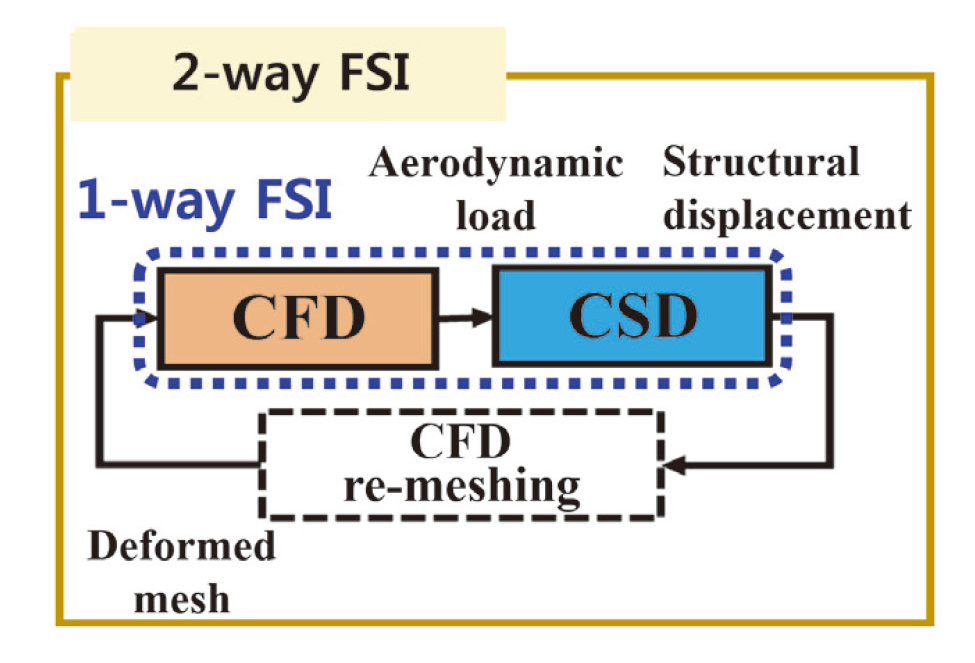
디퓨저 베인에 기인한 공력가진력에 대한 임펠러 강제진동 및 구조응답 예측을 위해서는 수치적으로 안정적이고 정확도가 높은 유체-구조 연성기반의 해석이 필요하다. Fig. 5는 유체-구조 연성 해석 시 유체와 구조간의 정보교환 방법에 대해 도시화하여 나타낸 것이다. 양방향의 유체-구조 연성(2-way FSI) 해석은 각 시간 증분(time step)에서 공력하중과 변위 값을 교환하여 비선형 효과를 반영할 수 있으나, 많은 계산 시간이 소요되어 산업 현장에 적용하는데 무리가 있다. 반면, 가스터빈 또는 산업용 압축기에 장착되는 임펠러의 재질은 큰 밀도와 강성을 가지고 있고, 상대적으로 작은 변위로 유동 속에서 진동하게 된다. 이는 블레이드의 고유진동수, 모드형상이 유동하중에 영향을 주지 않아 선형해석으로 가정할 수 있기 때문에 단방향의 유체-구조 연성(1-way FSI) 해석 적용이 유효하다. 이러한 1-way FSI 방법은 유동해석과 구조해석을 각기 수행하기 때문에 계산 자원의 부담을 줄여주고, 높은 계산 효율성을 가진다.

Fig. 5

Fluid-structure interaction algorithm.

Fig. 6는 1-way FSI 방법을 토대로 구성한 임펠러 구조 건전성 평가 절차이다. 먼저 정적해석을 수행하기 위한 3차원 유한요소 모델을 구성하고, 정적 해석 시 원심력과 함께 정상 유동해석으로부터 얻은 정상하중을 입력하중으로 적용하여 구조영향성 예측과 평균응력을 도출한다. 다음으로 전 하중(prestress) 모드해석을 수행하고 예측된 고유진동수, 모드형상과 디퓨저 베인에 기인한 가진주파수, 가진되는 노달 직경을 고려하여 SAFE 선도를 구성함으로서 임펠러의 운용 중에 발생 가능한 주요 공진 조건(공진 여유 10% 이내)을 도출한다. 이 후, 비정상 유동 해석으로부터 얻은 공력가진력을 입력하중으로 적용하고, 주요 공진 조건에서의 고유진동수로 강제진동 해석을 수행하여 교번응력을 도출한다. 최종적으로 정적 해석을 통해 도출한 평균응력과 강제진동 해석을 통해 도출한 교번응력을 토대로 안전(safe)―파괴(fail) 기반의 보수적인 피로평가 방법인 modified Goodman 선도를 구성함으로써 고주기 피로에 대한 구조 건전성을 평가한다.

Fig. 6

Structural safety evaluation procedure for an impeller.

3.2 유동해석

ANSYS Turbogrid 17.0을 사용하여 임펠러와 디퓨저 베인의 모든 계산 영역에 대해 육면체 격자를 생성하고, 격자 의존도 평가를 위해 격자 개수 변화에 따른 임펠러-디퓨저 베인 전압력비의 변화를 조사한다. 일정 개수 이상의 격자에서 전압력비의 변화가 없을 경우, 해당 격자 개수를 기반으로 해석을 수행한다.

ANSYS CFX 17.0을 사용하여 3차원 Reynolds-averaged Navier-stokes(RANS) 정상 및 비정상 유동해석을 수행한다. 정상 유동해석을 위해 입구 경계조건으로 전압력(total pressure), 전온도(total temperature)를 부과하고 출구 경계조건으로 질량유량(mass flow rate)을 부과하였다. 난류모델은 SST 모델을 사용하였는데, 이는 역압력 구배에 의한 유동 박리(separation)가 발생하는 것을 보다 정확히 예측하기 위해 만들어진 난류(turbulence) 모델로서 본 연구와 같이 유동 박리가 광범위하게 발생하는 유동 문제를 해석하는데 적합한 모델이다. 정상 유동해석 시에는 임펠러, 디퓨저 베인 각 1개의 유로에 대해서 해석을 수행한다. 원주 방향 경계면에는 회전 주기성을 부과하고, 회전부(임펠러)와 정지부(디퓨저) 사이의 경계면은 mixing plane 방법으로 모델링한다. 비정상 유동해석 시에는 정상 유동 해석결과를 초기조건으로 사용하며, 효율적인 계산을 위해 Fourier transformation 기법을 적용하여 임펠러, 디퓨저 베인 각 2개의 유로에 대하여 비정상 유동 해석을 수행한다[8].

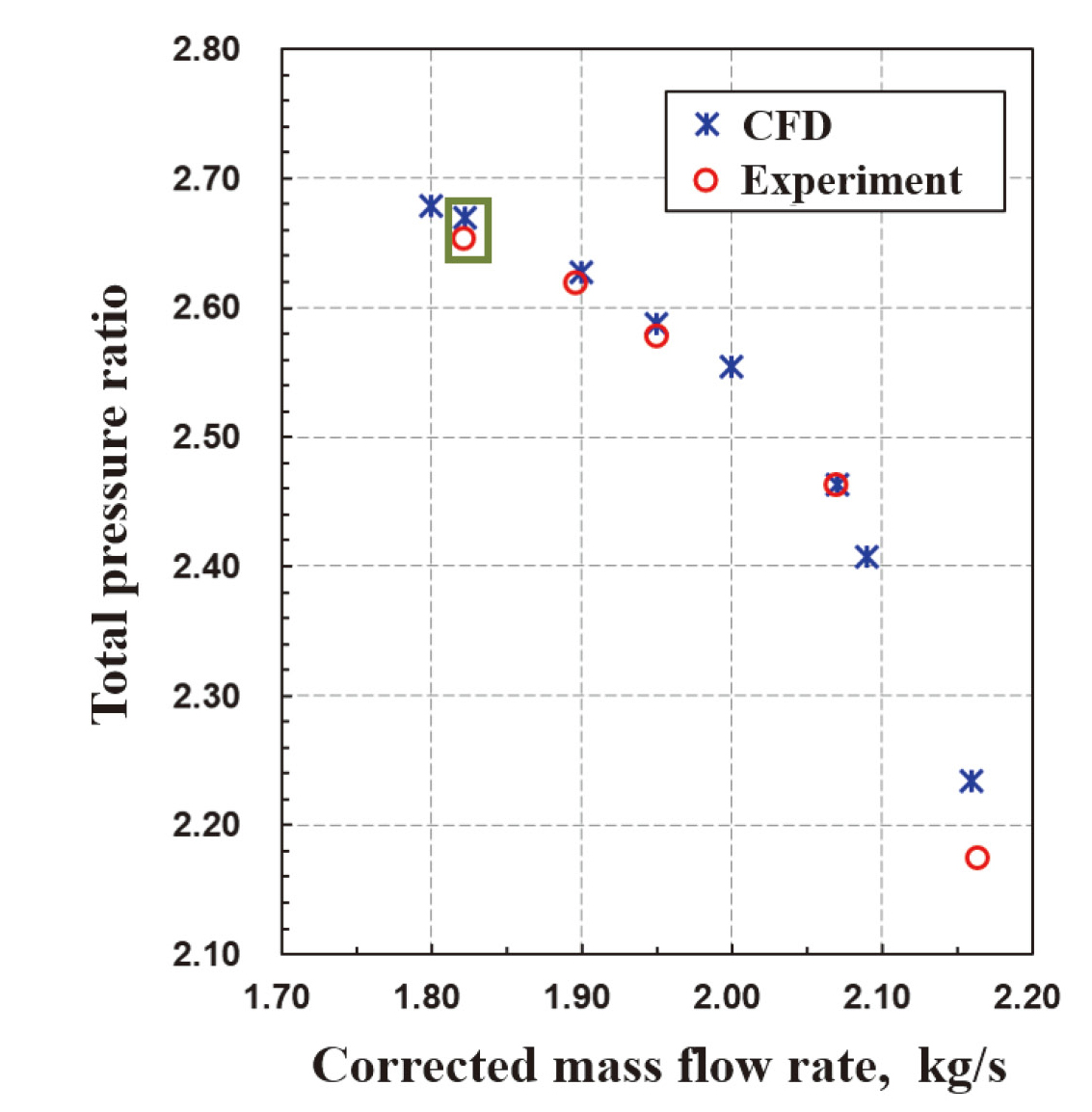
정상 및 비정상 유동해석의 검증을 위하여 아헨공과대학교(RWTH Aachen, Germany)로부터 형상 및 실험 결과[9,10]를 제공받아 해석 방법의 타당성을 검증하였다. Fig. 7는 정상 유동해석과 실험을 비교한 결과이다. 유량 변화에 따른 압축기 입구와 출구의 전압력비를 비교한 결과, 정상 유동해석 결과가 실험결과 대비 최대 오차 1.5%이내로 잘 일치함을 확인하였다.

Fig. 7에서 사각형으로 표시된 작동점에서 비정상 유동해석을 수행하고 실험 결과와 비교하였다.

Fig. 7

Comparison of total pressure ratio with mass flow rate.

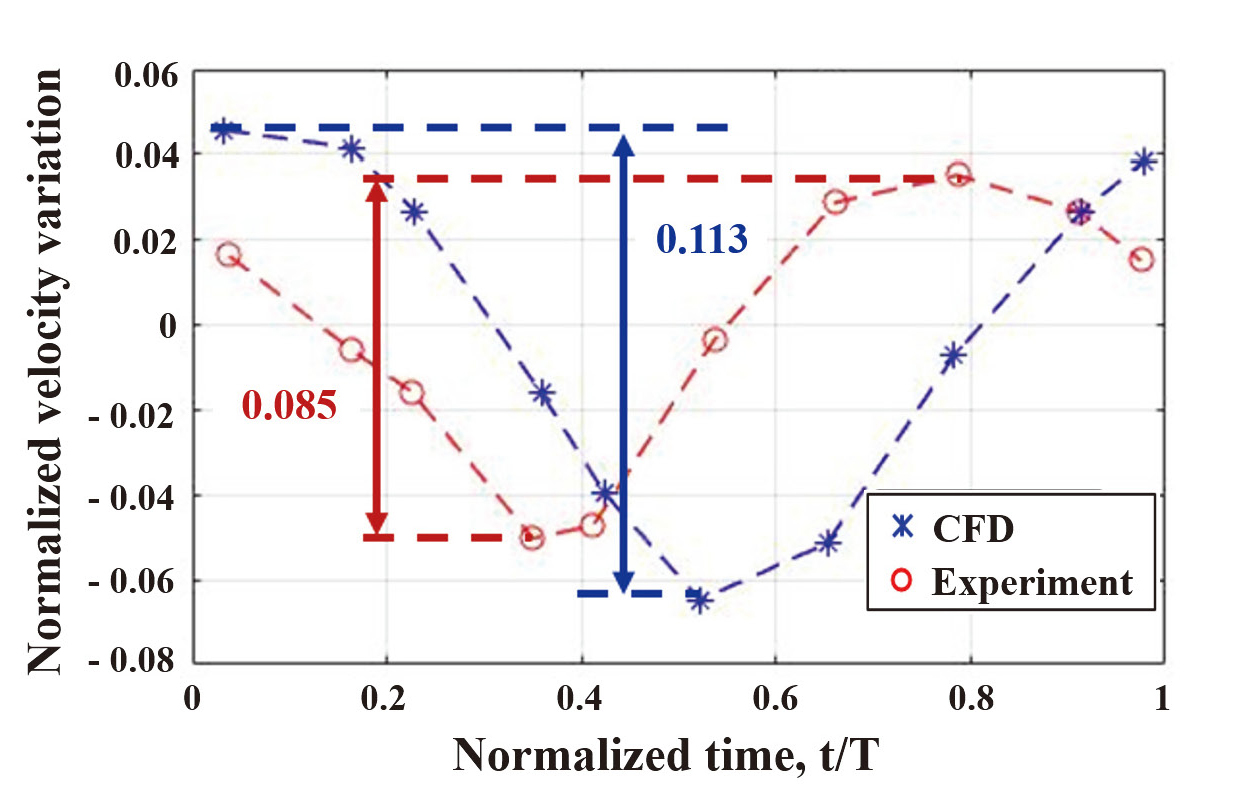
Fig. 8은 디퓨저 베인 입구의 한 측정점에서의 시간에 따른 속도 변화를 비교한 결과로서 x축은 블레이드 passing period로 무차원화한 시간이며, y축은 무차원화한 속도 변화로서 Eq. 4와 같다.

Fig. 8

Comparison of velocity change of inlet of diffuser vane with time.

여기서 C(x,y,t)는 특정 공간에서 시간에 따라 변화하는 속도이고 $$ \overline{C} (x,y)$$는 특정 공간에서의 시간 평균 속도이다.

비정상 유동해석이 실험보다 속도 변화를 약 30% 크게 예측하였고, 위상은 t/T = 0.2 뒤처지게 예측하였다. 이와 같이 전반적인 비정상 유동 형태를 잘 예측함을 확인하여 유동해석 방법에 대한 검증을 수행하였으며, 이렇게 정립한 유동해석 방법론을 본 연구의 대상 원심압축기에 대해서 동일하게 적용하였다.

3.3 구조해석

ANSYS Mechanical 17.0을 사용하여 유한요소기법을 기반으로 정적-모드-강제진동과 같은 일련의 구조해석을 수행한다. 임펠러 블레이드의 구조 모델링 시 곡면 격자 생성에 적합한 사면체 10절점 요소를 적용한다. 유동해석과 마찬가지로 격자 의존도 평가를 통해 유한요소 격자의 개수를 선정하고, 임펠러 운용 중 파손사례가 많고 응력 집중이 예상되는 블레이드 표면, 앞전(leading edge), 블레이드-디스크 접합(fillet) 부위에 디스크 대비 요소 크기를 더욱 조밀하게 생성한다.

정적 구조해석 시에는 정상 유동해석에 따른 압력 값과 임펠러 회전속도를 입력하중으로 적용하여 평균응력을 예측하고, 재료의 항복응력 대비 안전 여유(safety margin) 확인을 통해 구조영향성을 예측한다. 모드 해석 시에는 회전에 의한 관성효과로 강성이 변화함에 따라 고유진동수가 변화하는 응력 강화(stress stiffening)와 회전 연성(spin softening) 효과를 고려하는 전하중(prestress) 모드해석을 수행하여 고유진동수와 모드형상을 예측한다. 이와 관련된 식은 Eq. 5와 같다. 여기서 [S]는 응력 강화, Ω²[M]은 회전 연성 효과를 각각 나타낸다.

이러한 모드해석 방법의 신뢰성 검증을 위해동일한 해석 조건하에 Fig. 9과 같이 레이저 스캐닝 진동측정장비(laser scanning vibrometer)를 이용하여 모드시험을 수행하였고, 고유진동수와 모드형상을 비교한 결과 평균 오차 2% 범위 내에서 잘 일치함을 확인하였다.

Fig. 9

Modal test using laser scanning vibrometer.

이 후, SAFE 선도를 이용한 공진평가를 통해 임펠러 운용 중, 디퓨저 베인에 의해 공진이 발생 가능한 주요 공진조건을 도출한다.

강제진동 해석 시에는 비정상 유동해석에 따른 공력가진력을 입력하중으로 적용하며, 이와 관련한 구조 동역학 식은 Eq. 6과 같다.

여기서 P(t)항은 비정상 유동해석에 따른 공력가진력으로서 시간에 따른 압력 값이며, 이는 임펠러 표면에서의 각 위치마다 크기(amplitude)나 위상각(phase angle)이 다르지만 주기적인(periodic) 형태를 가지게 된다. 따라서 임펠러 절점(node) 좌표에 저장된 시간에 따른 압력 값을 Fourier 변환을 통해 Eq. 7과 같이 나타낼 수 있다.

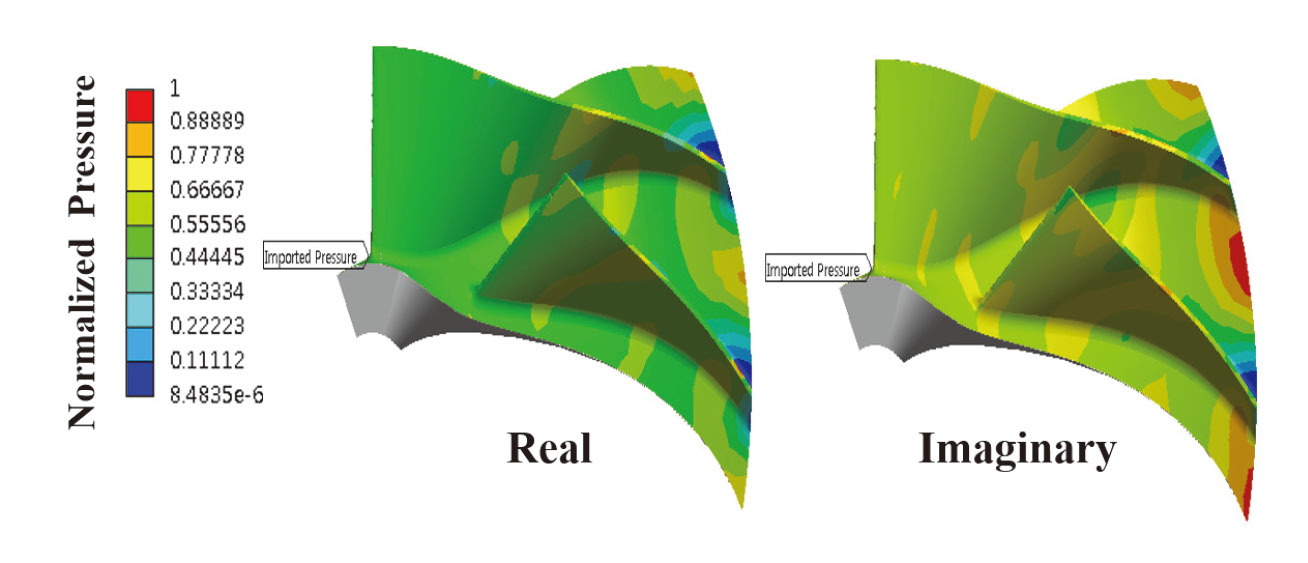
여기서 A_n, B_n는 각 절점 좌표에 대한 Fourier 계수로서 이는 각 유한체적 중심점에서의 실수부(real)와 허수부(imaginary)로 구성된 복소형태의 압력분포이다. 이 후, 강제진동 해석을 수행하기 위해 Eq. 8과 같이 임펠러 구조물의 유한요소 격자에서의 압력하중으로 변환하여 반복응력의 진폭인 교번응력을 예측한다[11].

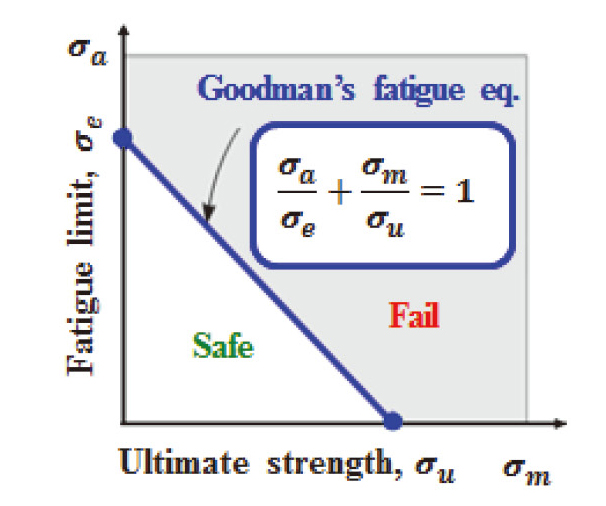
최종적으로 고주기 피로수명 평가를 위해 구조 응답 예측 결과를 이용하여 modified Goodman 선도를 구성한다. Goodman의 피로 수명평가 방법은 설계 하중조건에서 피로 파손이 발생하지 않는 무한수명설계를 하는 것으로 보수적인 결과를 주기 때문에 가스터빈 구조물에서 많이 사용되고 있다. Fig. 10는 Goodman의 피로 방정식을 도시화한 것으로서 σ_a는 강제진동해석으로부터 얻은 교번응력, σ_e는 재질의 피로한도, σ_m는 정적해석으로부터 얻은 평균응력, σ_u는 실험에서 얻은 재질의 인장강도를 각각 나타낸다. 응력 해석의 결과가 safe 영역에 존재하면 임펠러는 무한수명이나, fail 영역에 존재하면 고주기 피로 파손의 가능성이 있으므로 구조적 개선 등을 통해 safe 영역에 존재하도록 해야 한다.

Fig. 10

Modified Goodman diagram.

4.1 정적 구조해석

정상 유동해석에 따른 압력 값과 임펠러 회전속도에 따른 원심력을 하중 조건으로 적용 후 임펠러의 정적 구조해석을 수행하였다. 격자 의존도 평가를 통해 158,800개 요소로 모델링 하였고, 임펠러의 장착 상태를 고려하여 허브(hub) 앞면은 회전방향 구속, 뒷면은 회전방향과 축방향을 구속하였다.

Fig. 12은 Von Mises 기준 평균응력 해석결과로서 각 절점의 응력 값은 최대 응력 값으로 나누어 무차원화하여 나타내었다. 여기서 임펠러는 동일한 구역(sector) 모델이 원주방향으로 반복되어 있는 원형대칭(circular symmetric)의 구조물이므로 1개 구역(sector) 모델의 해석결과만 나타내었다.

Fig. 12

Mean stress distribution results.

최대 평균응력은 블레이드-디스크 접합 부위에 발생하였으며, 이는 재료의 항복응력(yield stress) 대비 약 75%로 충분한 안전 여유(safety margin)을 가지고 있음을 확인하였다.

4.2 모드 해석 및 주요 공진조건 도출

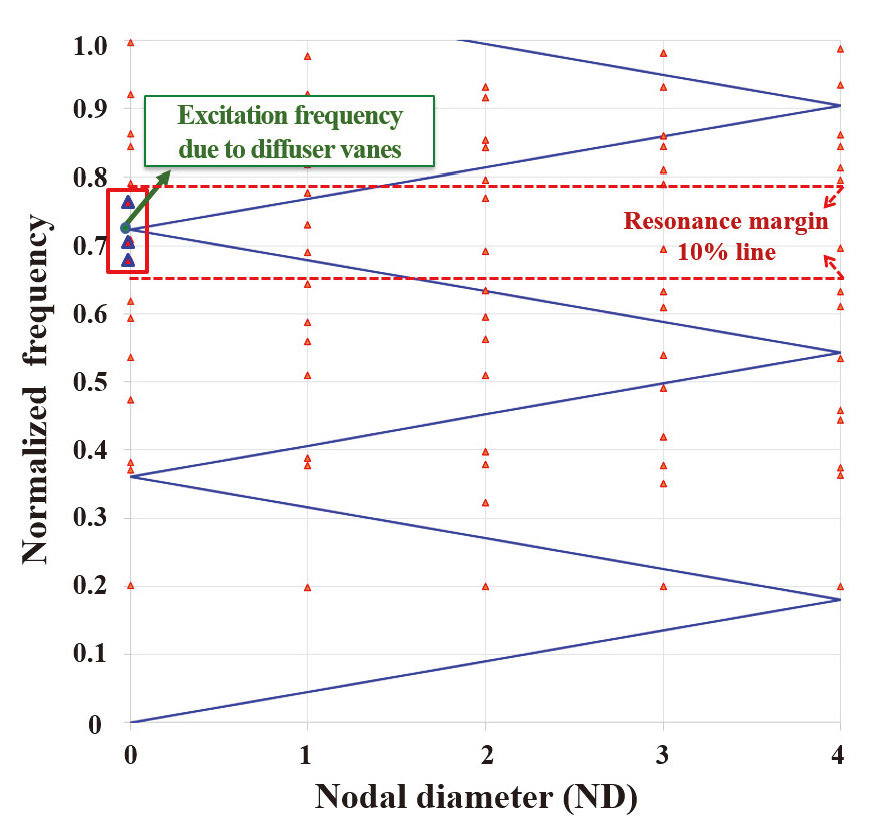
정적하중에 의한 초기응력을 적용하여 모드해석을 수행하였다. 해석 대상의 블레이드가 8개이므로 노달 직경 값이 0부터 4까지에 대하여 각각의 고유모드가 도출되었고, 도출된 고유모드 결과와 디퓨저 베인에 기인한 가진주파수를 토대로 구성한 SAFE 선도는 Fig. 13와 같다.

Fig. 13

SAFE diagram.

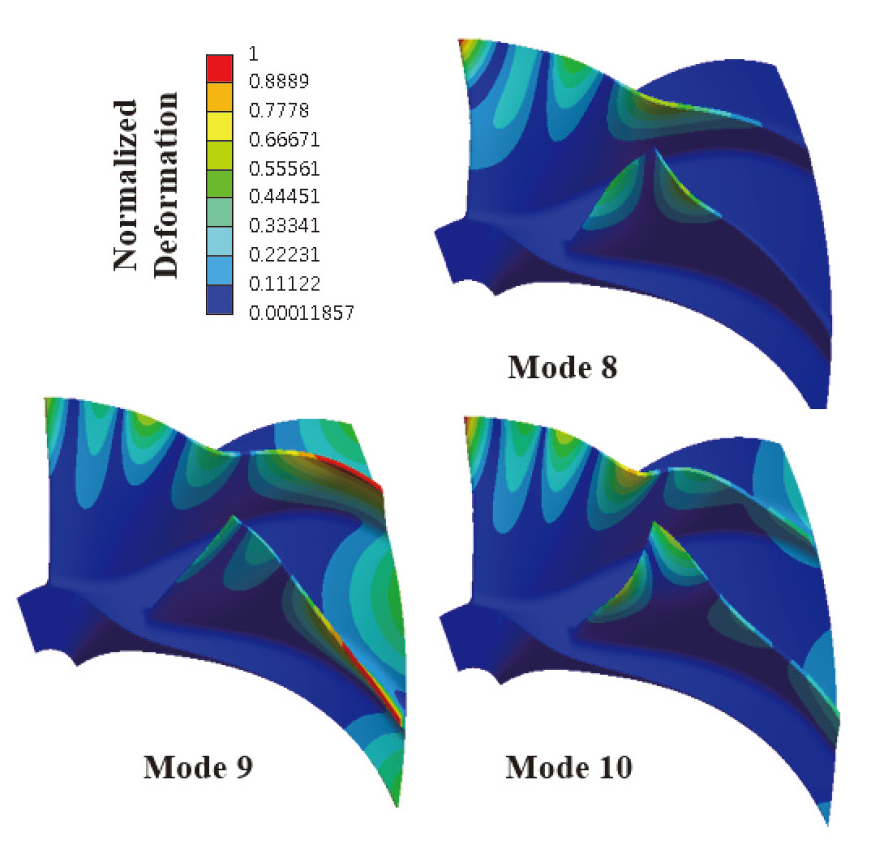
빨간색 삼각형의 점은 모드해석 결과로 얻어진 각 노달 직경에 따른 고유진동수 값으로서 최대 고유진동수 값으로 나누어 무차원화하여 나타내었다. 파란색 지그재그 선은 디퓨저 베인에 기인한 가진주파수와 가진력의 노달 직경을 나타내며, 이는 Eq. 3과 Table 1의 관계식을 통해 도시화 할 수 있다. SAFE 선도 분석 결과, 디퓨저 베인에 기인하여 임펠러를 가진하는 노달 직경 값은 0이며, 가진주파수와 교차하여 공진이 발생 가능한 고유 모드들이 존재한다. Table 3은 노달 직경 값 0에서의 주요 고유모드의 형상과 공진 여유를 나타낸 것으로 다른 고유모드 대비 공진 여유가 10% 이내인 3개의 고유모드(Mode 8, 9, 10)를 주요 공진조건으로 도출하였다. 도출된 주요 공진조건의 모드형상은 Fig. 14와 같다.

Table 3.

Mode shape and resonance margin at nodal diameter 0.

Fig. 14

Mode shape of major resonant conditions.

4.3 디퓨저 베인에 기인한 공력가진력 도출

격자 의존도 평가를 통해 임펠러와 디퓨저 베인 각 1개 유로에 대해 총 3,000,000개 격자 기반으로 해석을 수행하였고, 임펠러 1개 유로는 약 2,300,000개, 디퓨저 1개의 유로는 약 700,000개의 격자로 모델링 하였다.

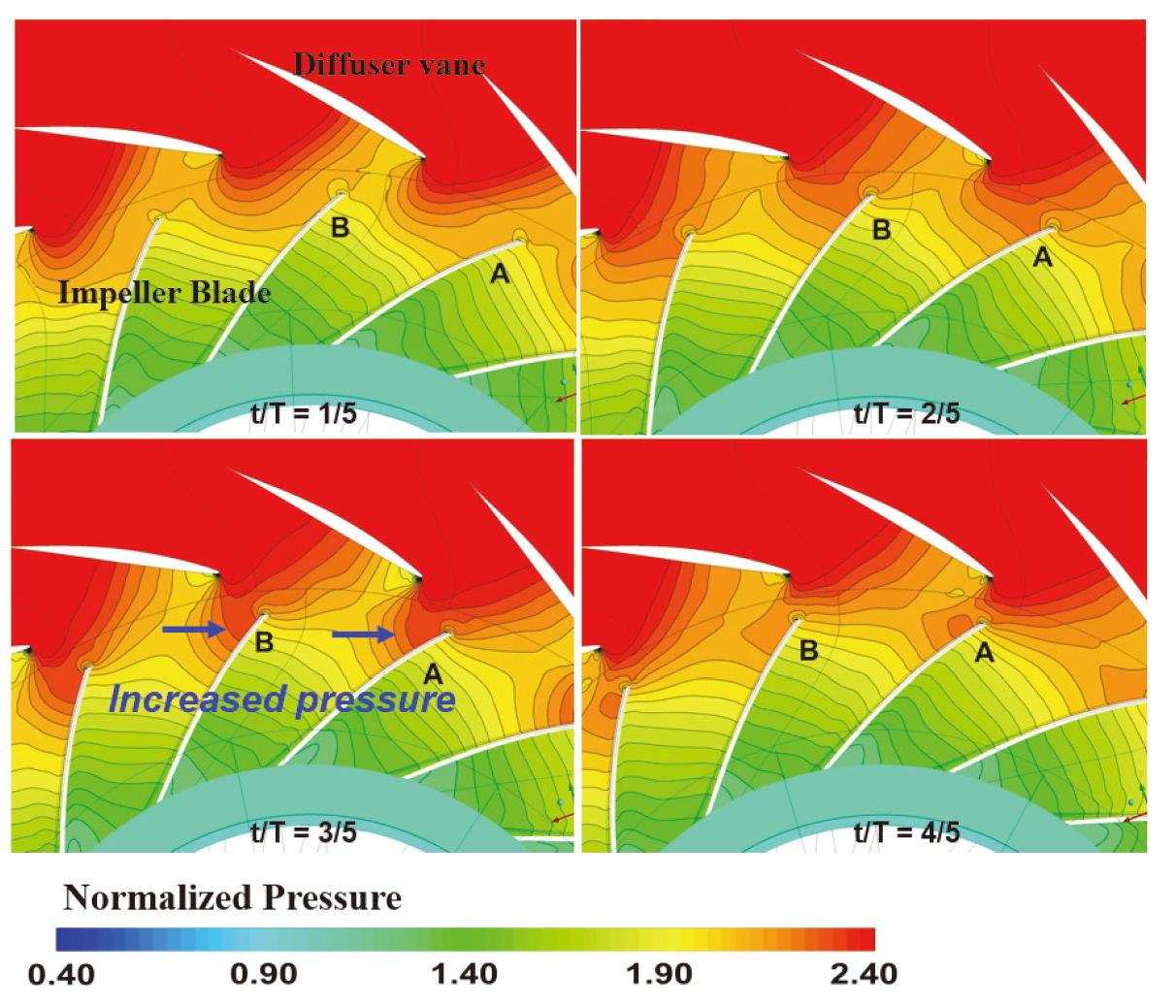
디퓨저 베인에 기인한 공력가진력을 정량화하기 위해 운용 조건에서의 비정상 유동 해석을 수행하였다. 이 때, 비정상 해석을 위한 시간 간격은 디퓨저 베인 피치의 1/20에 해당하며, 이는 1.125도 회전과 동일하다. Fig. 15은 시간에 따른 임펠러와 디퓨저 베인 사이의 정압 분포 변화이다. 50% span 위치에서의 정압 분포이며, 임펠러 팁 회전 속도에 근거한 동압으로 무차원화 하였다. Fig. 15에서 보이는 바와 같이 임펠러와 디퓨저 베인 사이의 vaneless 공간에서 잠재 효과(potential effect)로 인한 불균일한 정압이 분포하며, 이는 디퓨저 베인에 기인한 공력가진력의 근원이 된다.

Fig. 15

Static pressure distribution variation between impeller and DV with time.

또한, 임펠러가 시계 반대방향으로 회전함에 따라 디퓨저 베인의 앞전에 가까워지면서 임펠러의 압력면(pressure side)에서 높은 정압이 형성되는 반면 흡입면(suction side)의 경우 정압 변화가 작음을 확인할 수 있다.

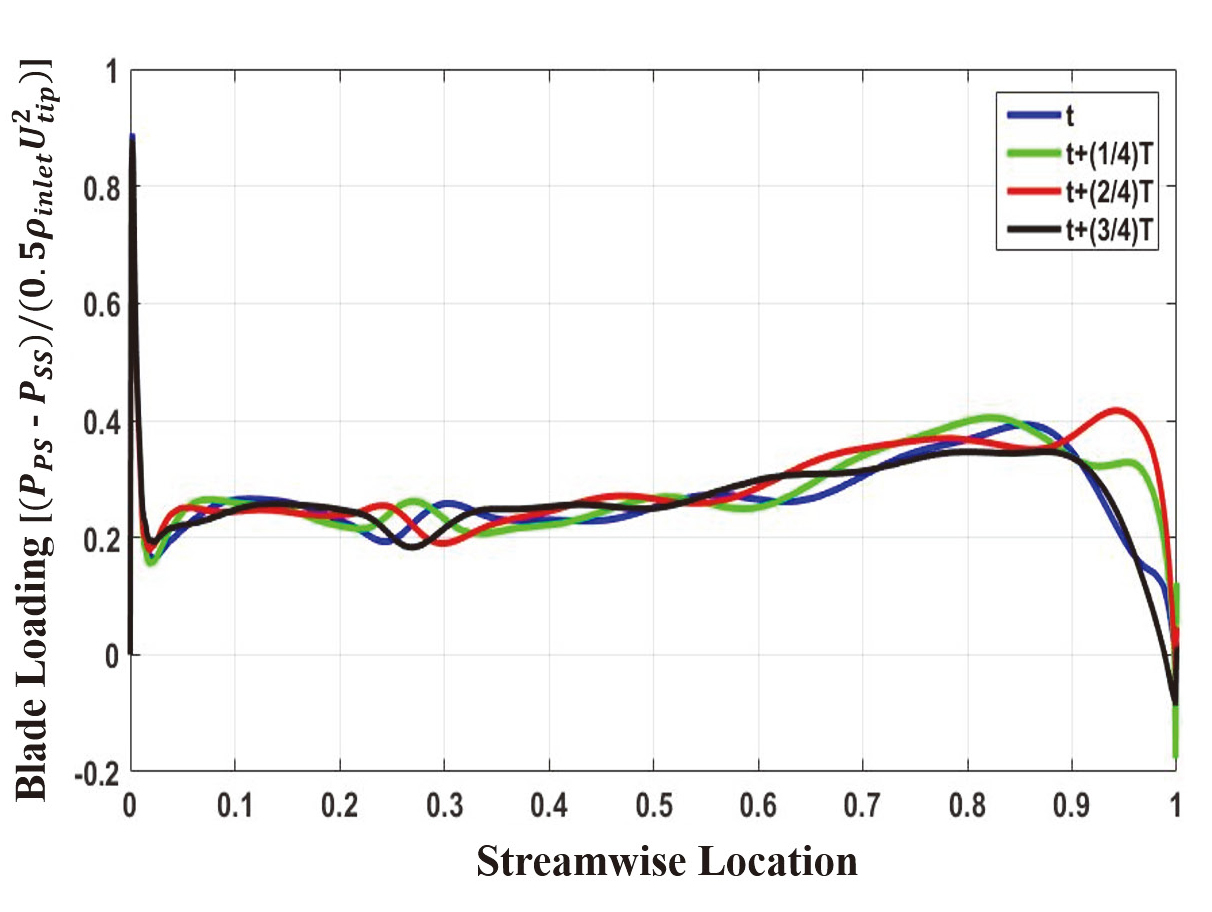
Fig. 16은 시간에 따른 임펠러 메인 블레이드 하중의 변화로서 x축은 무차원화된 유선 방향 위치이며, 0은 블레이드 앞전을, 1은 블레이드 뒷전을 각각 나타내며, y축은 압력면과 흡입면에서의 정압차이를 임펠러 팁 속도에 근거한 동압으로 무차원화하여 나타내었다. Fig. 16에서 보이는 바와 같이 디퓨저 베인에 기인한 공력가진력은 임펠러 뒷전에 집중되어 있음을 확인할 수 있다.

Fig. 16

Main blade load variation with time.

4.4 강제진동 및 고주기피로 평가

강제진동 해석을 수행하기 위해 비정상 유동해석에 따른 복소형태의 압력분포인 공력가진력을 Fig. 17와 같이 유한요소 격자에서의 압력하중으로 적용하고, SAFE 선도를 통해 도출한 주요 공진조건 3개의 고유진동수로 강제진동 해석을 수행하였다.

Fig. 17

Aerodynamic excitation mapping on structural nodes.

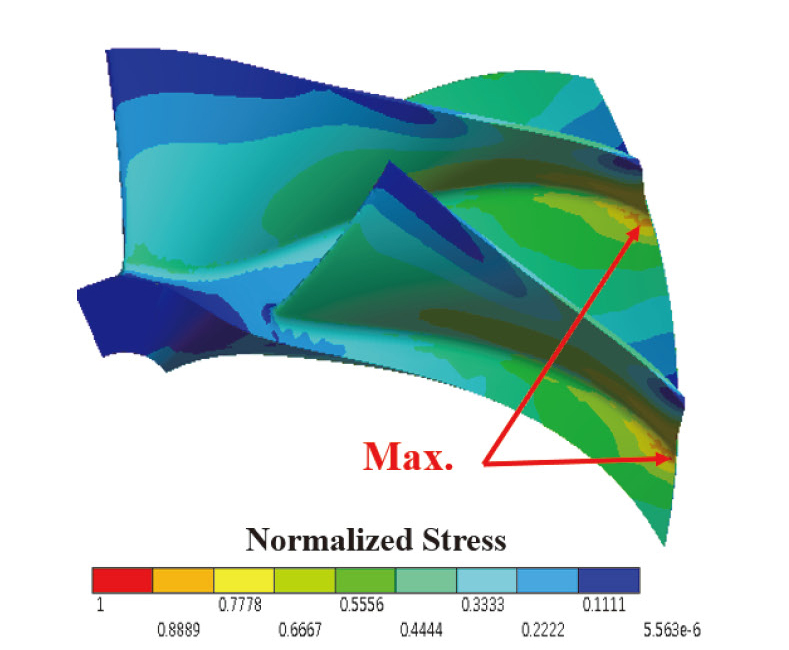
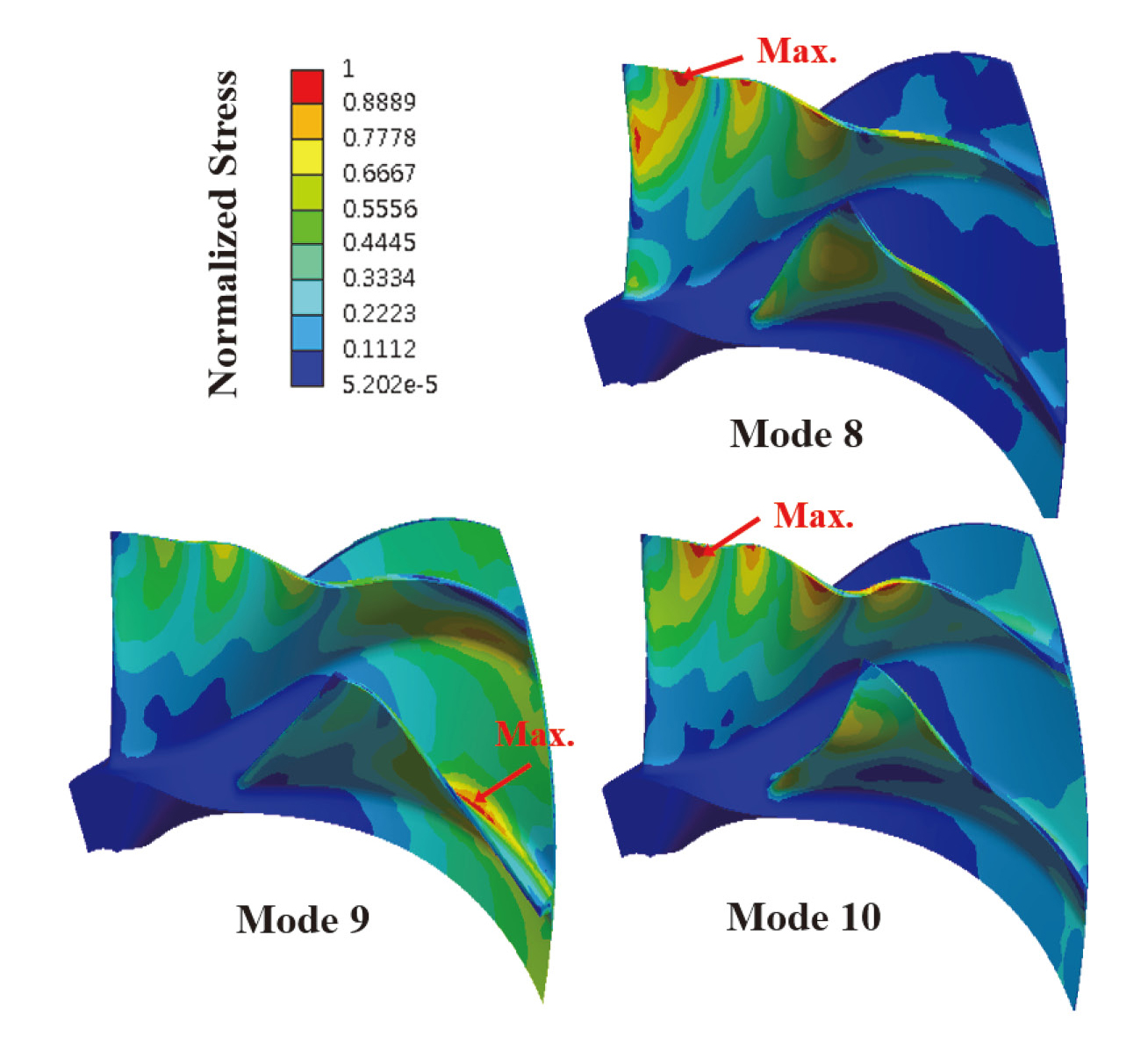
Fig. 18은 교번응력 분포 결과로서 각 절점의 응력 값은 최대 응력 값으로 나누어 무차원화하여 나타내었다. Mode 8과 Mode 10의 고유진동수로 강제진동 해석한 결과, 최대 교번응력이 블레이드 앞전에서 발생하였으며, Mode 9의 경우에는 최대 교번응력이 블레이드 뒷전 접합부위에서 발생함을 확인할 수 있다.

Fig. 18

Alternating stress distribution results.

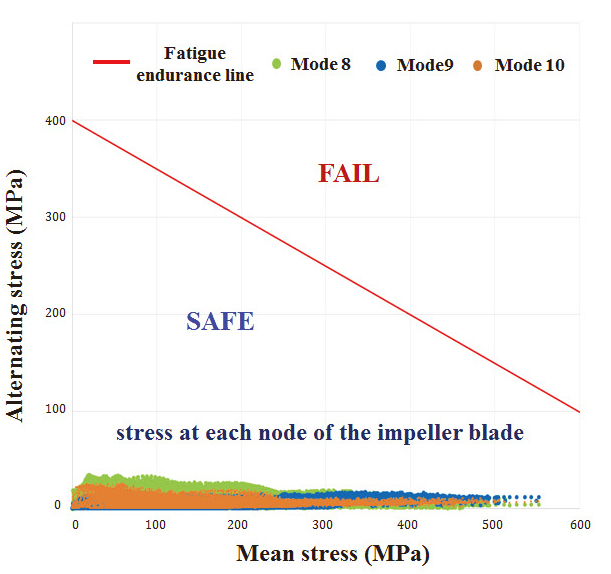
정적 구조해석을 통해 도출한 평균응력과 강제진동 해석을 통해 도출한 교번응력을 기반으로 Fig. 19와 같이 modified Goodman 선도를 구성하였다. 빨간색 대각선은 고주기피로에 대한 허용응력 한도를 나타낸 선으로서 재료의 S-N 선도에서의 파단되풀이 10⁷이상 피로한도 값(0, y축)이며, x축은 인장강도 값(x축, 0)을 기준으로 도시하였으며, 분포된 점들은 각 임펠러 블레이드 절점에서의 평균응력과 교번응력 값의 분포를 나타낸다. 해석 대상의 교번응력이 낮은 관계로 아래쪽에 점들이 결집되어 있어 고주기피로에 대해 안전한 상태인 것을 알 수 있다.

Fig. 19

Modified Goodman diagram results.

하지만, 원심압축기의 성능 향상을 위해 임펠러와 디퓨저 베인 간 간격(radial gap)이 작아지거나, 입구 유량속도 등이 증가한다면, 구조응답 수준도 함께 증가하여 보다 위쪽으로 점들이 상승할 것으로 예상된다.