고체 추진제 장시간 물성거동 반응 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
고체 추진기관이 노즐마개에 의해 외기와의 교환이 완벽히 차단된다면, 구조적 안정성은 제작초기 조건인 내부조성간의 잔류반응(Post Cure, Migration etc.), 그리고 자유공간 내의 산소(또는 산화방지제)와 습기(제습제)와의 반응에 종속된다. 이로부터 발생하는 혼합형 고체추진제의 기계적 특성은 매우 복잡하며, 추진기관은 발사직전까지 일교차/년교차의 끊임없는 열하중을 받게 된다. 본 연구에서는 고체 추진기관의 제조공정인 성형오븐에서 출고 후 저장안정화까지의 거동을 고체추진제의 열유변학적 단순특성을 적용하여 신속하게 산출할 수 있는 방법을 제시하였다. 이를 위해 온도제어 가능한 Endurance Test 장치를 고안 제작하였으며, 추가적으로 점진적 응력과 변형율 증가에 따른 비선형 특성도 검토한다.
Abstract
Structural integrity of solid rocket depends on the residual reactions between constituents of its composition(post cure, migration etc.), the oxygen(or anti-oxydent) in the free volume and humidity (desiccant) under the perfect sealed condition. Mechanical Properties of composite solid propellant arising from those factors are very complex. Moreover the propulsion are faced with thermal loads from diurnal & seasonal cycle till firing. In this study, the fast evaluation method of long term mechanical properties is suggested based on Thermo-Rheological Simplicity from curing oven to cool-down stage in view point of thermal stabilization. For this subject, endurance tester having temperature control capability are devised. From the results from incremental load and strain, non-linear characteristics are discussed.
Keywords:
Solid Composite Propellant, Thermo-Rheological Simplicity, Long Term Response, Endurance Test키워드:
고체 혼합형 추진제, 열-유변학적 단순성, 장시간 반응, 내구성 시험1. 서 론
HTPB(Hydroxy-terminated polybutadiene) 계열의 혼합형 추진제는 가격과 제조 및 습기 저항 등의 장점으로 전 세계적으로 고체 로켓에 적용되고 있다. 최근 국내에서도 구조-유동 통합기술의 개발을 목표로 고압에서의 크랙 발생과 진전에 대한 연구까지도 수행하고 있을 정도로 발전하고 있는 분야이다. 크랙 인성은 –60℃ 이상의 온도범위에서는 순차적으로 비례하다가 그 이후 급격히 변하는 것으로 발표되었다[1]. 이는 결과적으로 로켓모타의 일반적 저장운용조건인 +60 ~ -40℃에서 추진제 구조적 안전성을 지배하는 것은 응력완화에 의한 점탄성(Visco-elastic) 기계강도 특성이라고 할 수 있다. 크립(Creep)이나 응력이완(Relaxation) 특성과 관련하여, 폴리머 공학과 과학 분야에서는 단시간의 시험으로부터 장기간의 거동을 예측하는 것이 매우 중요한 영역이다. 응력피로나 온도피로 현상을 제외하고, 금속과 세라믹 등의 물성은 시간에 독립 거동을 한다는 가정이 널리 사용되고 있으나, 폴리머는 완전히 다른 현상이며, 비선형 점탄성 거동을 한다고 알려져 있다[2].
본 논문에서는 추진제 구조 물성의 기본뿐만 아니라 점탄성 물체의 시간과 온도에 따른 상응 원리와 현상에 대하여 분석한다. 이 원리가 비록 한계는 있으나, 본 연구에서는 HTPB 바인더 추진제의 기계물성에 대하여 논하고, 실험적으로 분석함으로서 크립과 응력이완에 대한 상관관계를 근거로 좀 더 빠른 실험방법을 찾는 시도를 하였다.
2. 이론적 배경
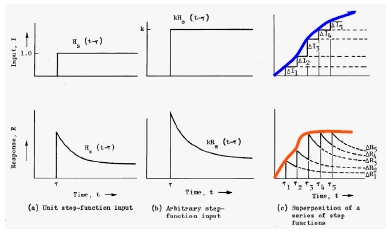
고체 추진제의 구조해석 점탄성 지배방정식은 1874년 Boltzmann이 제안한 중첩원리에 의한 Convolution Integral에 기인되며[3], 추진제 일축시편의 시간 종속 응력σ(t)과 변형률ϵ(t)은 다음과 같이 표현된다[4].
| (1) |
| (2) |
여기서 Erel은 응력이완 탄성계수, Dcrp은 크립 Compliance이다. 만약 체적 탄성계수(K)가 일정하고 온도에 독립적이라면, 평균 응력(또는 압력, Θ/3)과 체적팽창률(e)간의 관계식은 Θ/3=Ke이며, 여기서 팽창인자(Dilatationanl Components) Θ=σii, e=ϵii이다. 형상변화(Deviatoric) 응력(sij)과 변형률(eij)와의 관계식은 다음과 같다.
| (3) |
| (4) |
따라서 점탄성재료의 3차원 응력-변형률 법칙은 다음과 같다.
| (5) |
온도변화 ∆T에 대하여, 재료가 유변학적 단순성을 갖는다면, Θ/3=K(e-3α∆T).
| (6) |
여기서 α는 열팽창 계수이며, ζ와 ζ′는 Convolution 개념의 유도 시간으로 다음과 같이 정의된다.
| (7) |
aT는 온도-시간 변환 함수로서 Williams-Landel- Ferry(WLF) model의 시간-온도 중첩원리에 의거하여 시간과 온도에 함수인 점탄성 재료의 물성을 Master화 할 수 있었다.
3. 실 험
3.1 Inert 추진제 조성
본 실험에 적용된 혼합형 Inert 추진제 조성은 HTPB 활성 추진제 특성을 확인하기 위해 HTPB 바인더를 사용하여 가소제(DOA, Dioctyl Adipate), 경화제(IPDI, Isoporon Disocyanate), 촉매제(TPB; Tetraphenylborate, MA; Maleic Acid)와 함께 산화제 대신 KCl, CaCO3를 첨가하였으며, 본 논제에 벗어나지 않는 범위에서 Non-Scale화 하였다.
3.2 Inert 추진제 제조
추진제의 제조는 온습도 환경조건 조절이 가능한 공실에서 Fig. 1의 300갤런 Mixer를 통해 Size 230x165x40(mm) 크기로 수량 8개의 개별 Box형태로 제조되어 경화 room에서 10일간 경화되었다. 혼화효율(Mixing Efficiency)은 서로 다른 물질들을 가장 빠른 시간에 균질 분포(Packing Ratio)하는데 있다. 혼화공정은, 우선 비반응/안정화 물질들을 혼화하는 Pre-Mixing과정을 거쳐 AP 및 경화제를 투입한다.
300 Gal Mixer in LIGNex1.
여기서 조성 비율 1% 미만의 기계특성 개선 결합제, 노화특성 향상을 위한 산화방지제, 연소속도 조절을 위한 연소촉매 및 경화제 & 경화촉매제의 균등 분포는 매우 중요하다. 특히 최종적으로 투입되는 경화제와 경화촉매제는 점도상승의 함수이므로 가장 짧은 시간에 균일하게 분포되도록 하는 것이 제일 중요하다. 연소촉매는 내탄도 특성을 지배하는 연소속도에 영향을 주지만 근본적으로는 AP 입자크기에 종속된다.
상기에서 언급한 미세량의 조성들 중 연소촉매제를 제외한 모든 첨가제들이 기계 물성을 형성하는 지배인자로 작용을 하므로 혼화효율은 매우 중요하다. 혼화상태의 효율성을 확인하기 위하여, 300갤런 전체량을 시편 Box로 받기에는 너무 많으므로, 상, 중, 하로 구분하여 순차적으로 시편Box를 준비하였다.
3.3 실험 방법
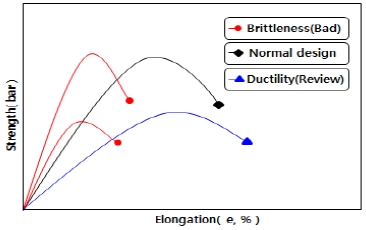
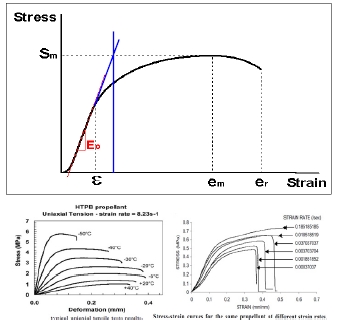
혼합형 고체 추진제는 Fig. 2와 같이 온도와 변형 속도에 따라 물성거동이 변화되지만, 또한 화학적 변화에 의해 시간이 경과됨에 따라 노화가 진행되어 취성화 또는 연성화 되기도 한다. HTPB 계열 추진제는 일반적으로 경화되는 노화특성을 보이는 것으로 알려져 있다. 이는 추진제 그레인의 취성화로 이어져 균열 및 접착성 저하와 같은 문제를 발생시키므로, 추진제의 기계적 특성을 파악하는 것은 매우 중요하다.
Stress-Strain Curve of Typical Propellent.
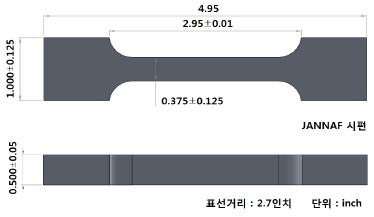
Inert 추진제 Box 시료별, 물성, 온도, 속도와의 상관관계를 알아보기 위해 우선 크로스헤드 속도를 50 mm/min, 20℃ 조건에서 1~7번 Box No.를 부여하여 Fig. 3과 같은 아령형 JANNAF 일축인장시편을 채취하고 INSTRON社 UTM MODEL 5967을 이용하여 일축인장 시험을 진행하였다. Box No.별 기계물성 차이는 크게 없었으나, 추진제 물성편차의 상/하 영역을 고려하여 모듈러스값의 내림차순에 따라 취성(B: Brittle)과 연성(D: Ductile)으로 Table 1과 같이 분류 하였다.
JANNAF Specimen Type.
Classification due to the Modulus of Boxs(*Reference value).
상기결과에 의하면, Box 간 모듈러스 편차는 ±9%이내이었고, 제작 일련순서와는 상관관계가 없는 것으로 나타났다.
시간변화에 따른 추진제의 모듈러스를 예측하기 위한 시험으로 +60℃ ~ -40℃ 범위의 조건에서 추진제에 Pre-strain 신율 2%를 부가하여 점탄성 영역에 대한 일정시험 시간에서의 모듈러스 변화량을 측정하여 온도별 모듈러스 Data를 기준온도 20℃에 맞춰 이동 및 중첩시켜 응력완화 시간에 대한 추진제의 응력 탄성률 Master 곡선을 그려 완화시간 후의 모듈러스를 예측 및 분석하는 시험이다.
본 시험에서는 일축인장시험 결과로 Table 1과 같이 분류된 취성(B: Brittle)과 연성(D: Ductile)을 근거로, Table 2와 같은 조건의 시험을 실시 하였다. 기본 크로스헤드 속도는 50 mm/min이나 속도에 따른 변화여부를 확인하기 위해 특별히 20℃에 대하여 500(1500), 0.5(10.5) mm/min 조건을 적용하였다. 또한 초기 2% 응력이완 Data값을 측정하고 시험이 끝난 시험편을 5%, 9%, 14% 응력이완 시켜 파괴시험을 수행하였다.
Plan of Relaxation Modulus Test.
추진제의 경우 저장 및 운용조건에서 외부 환경변화에 따라 온도별 응력과 변형률, 탄성률 등 인장 성질이 다르게 나타난다. 이러한 특성을 일정한 온도 및 변형 속도에 따른 인장시험을 통해 Master 곡선을 얻기 위하여 Table 3과 같은 조건으로 시험을 실시하였다.
Plan of Tensile Test under Various Condition.
내구성 시험은 추진기관 내부의 환경조건에서 장시간에 걸친 추진제의 내부의 응력 및 변형상태를 모사하는 시험으로 추진제 내부 그레인의 응력과 변형에 대한 파단시간과의 관계를 확인하는 시험이다.
본 시험에서는 Fig. 4와 같이 자체 제작 내구성 시험 장비를 사용하여, 20℃ 온도 조건에서 하중 및 변형을 부가하여 시간변화에 따른 응력 및 변형 상태를 확인하고, 60℃ 온도 조건에서 하중을 부가하여 시간에 따른 변형상태를 확인하였다.
Strain & Load Endurance Tester in LIGNex1.
장비의 검증을 위하여 별도로 준비된 Box No. 8로부터 채취한 JANNAF 시편을 Fig. 5와 같이 시험하였으며, INSTRON UTM장비와 비교하여 만족할 만한 결과를 얻었다. 따라서 계획된 Table 3에 의거하여 응력이완 시험과 온도 속도 시험을 통한 Master 곡선을 구하고 이를 확장하여, 장시간 물성거동 반응 고찰을 위해 Table 4와 같이 계획하였다. 즉 기존 시험방법은 Go-NoGo 방식의 60일 이상 유지하는 추진제 강도와 신장력(Elongation Capability)을 찾고 있으나, 본 연구에 적용된 내구성시험장비는 하중과 변위 측정이 가능하므로 점진적 시험방법인 6구간(2, 5, 12, 30, 45, 60일)으로 시험을 기획하고 파단까지의 거동을 분석하였다.
Verification Test of Endurance Tester.
Time Schedule for Endurance Load & Strain.
4. 실험 결과 및 고찰
4.1 응력완화 시험 분석
선형 점탄성재료 특성을 표현하는 다양한 수식이 있으나, Prony series가 널리 사용되고 있다.
| (8) |
| (9) |
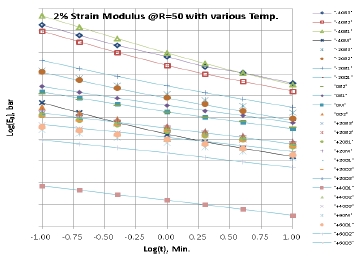
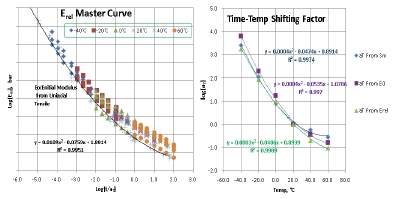
여기서 Ee는 탄성 모듈러스, Eg는 유리화 모듈러스 및 n은 Log-Log 좌표상의 기울기이며, D는 Compliance이다. 이를 측정하는 기법 중의 하나가 일축 응력완화 시험으로서 2% Pre-strain에 따른 결과는 Fig. 6과 같다.
Modulus Curves of Various Temp. & Rate.
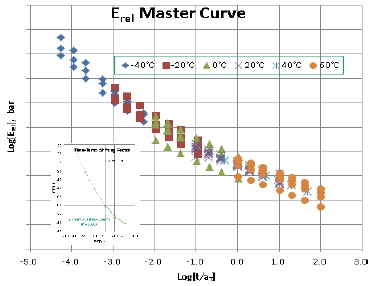
이를 Time-Temp. Shaft Factor로 보정하여 일치 선으로 만들면, Fig. 7과 같은 Master Curve가 된다.
Relaxation Modulus Master Curve.
4.2 일축인장시험 분석
고체 추진제의 점탄성 특성은 Fig. 8과 같이 외부하중이 부가되면 모듈러스에 의해 인장과 이완을 동시에 한다. 이를 취급하기 편리하게 사용하기 위하여 Eq. 8, 9를 수정된 멱급수로 표현하면 다음과 같다.
Graphical representation of the concept of convolution[4].
| (10) |
| (11) |
다양한 온도하에서 일정변형률 속도의 추진제 인장은 Fig. 9와 같은 기계적 거동을 나타낸다. 고체 추진제 일축인장 거동은 온도와 변형속도에 종속되는 점탄성 특성에 의해 인장강도와 변형률이 다르게 나타난다.
Typical Behavior of Strain-Stress.
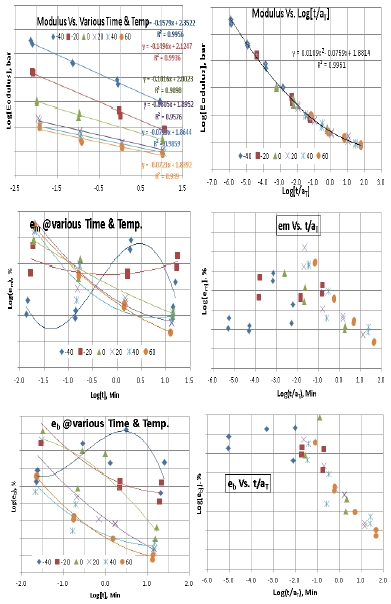
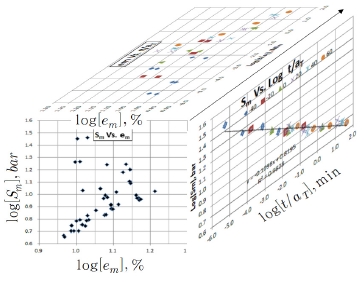
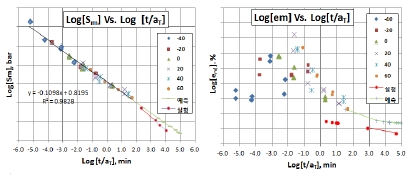
Fig. 10은 기계물성 중 최대인장강도, Sm을 Master화 한 것이다. Fig. 10-a)와 같이 혼돈된 값들이 Log-Log 과정을 거치면서 일직선화 되는 것을 알 수 있다. 특이사항은 Fig. 10-d)에서 Normal [t/aT] -Normal 좌표를 통해 모든 물성치가 매우 짧은 시간에 몰려 있는 현상을 볼 수 있다.
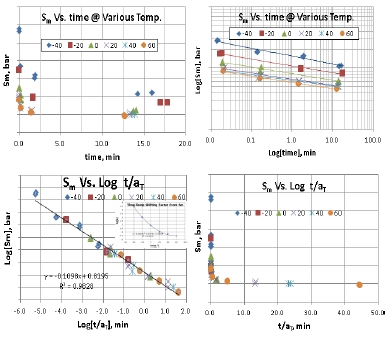
Maximum Strength with Various Time Scale, a) Normal-Normal, b) Log-Log, c) Log[t/aT]-Log, d) Normal[t/aT]-Normal.
물론 Log 좌표계의 특징이긴 하지만, 실제로 추진기관은 Curing 직후 급속 냉각 이외에는 짧은 시간의 환경에 경험하는 일은 거의 없다. 단, 공중발사 추진기관인 경우 급격한 고도 상승에 따른 저온 온도충격 반복하중이 발생될 수도 있을 것이다. 동일한 방법으로 Initial 모듈러스와 em(Elongation at Sm)의 Master Curve를 구하면 Fig. 11과 같다. 여기서의 문제는 em과 eb(Break Elongation)에 대하여 온도-시간 이송 계수를 응력이나 탄성계수로부터 구한 것을 적용한다는 것이다. Fig. 11에서 변형률은 온도에 대하여 랜덤하게 나타내는 특성이 있음을 알 수 있다.
Master Curves of Uniaxial Tensile Test.
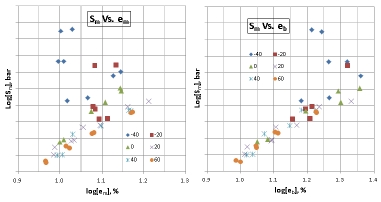
Fig. 12는 고체 추진제 시험분야에서 자주 표현하는 Failure Envelop이다.
Two Dimensional Failure Envelop(Sm-em, Sm-eb).
Fig. 12에 나타낸 Failure Envelop을 이해하기 위하여 시간 축을 갖는 3차원으로 표현하면 Fig. 13과 같다. 흥미로운 것은 Log-Log 좌표 상에서 시간에 따라 최대강도, Sm은 선형적, E0는 2차 곡선, em은 랜덤한 특성을 나타내며, 그 이유는 인장 후 내부 손상 및 파괴과정에서 나타나는 폴리머 AP와의 Dewetting, Vacuole 및 체인 절단 등의 형성에 따른 비선형특성에 기인된다고 알려져 있다.
Three Dimensional Space of Failure Envelope.
4.3 물성비교
2% 응력이완 모듈러스에 일축인장 초기 모듈러스 선분을 중첩하면 Fig. 14와 같이 거의 일치한다. 또한 각각의 Time-Temperature Shift Factor를 중첩하면 Fig. 15와 같이 유사하다. 순서로는 20℃를 기준으로 저온은 E0 > Sm > Erel, 고온은 Sm > E0 > Erel이다. 이는 변위률 순서로 판단되며, 점탄성 특성상 변형이 작거나 저온인 경우 건전하게 스프링 강성만 남는 것으로 설명가능하다.
Comparison between Relaxation & Initial Modulus, and T-t Shifting Factor from Sm, E0, Erel.
Extension to Long Time Storage of Sm - σF and em - εrr.
4.4 내구성 시험(Endurance Test)
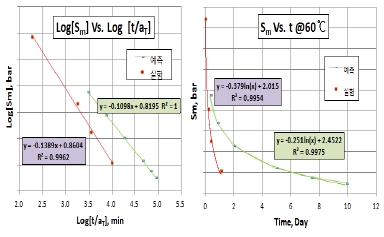
20℃에서 60일 이상 견디는 응력(σ∞)과 변형률(ε∞)을 산출하였으며, 이를 Master Curve에 적용 후 내삽하여 3.3.3 절에서 계획된 6개의 시간에 해당되는 상온(20℃) 응력과 변형률을 Table 5와 같이 계산하고 고온(60℃)에서 실험하였다. 이는 aT를 적용하여 60℃에서 시간이 단축되는가를 파악하는 시험으로서 Fig. 15에 중첩하였다. 여기서 적용한 aT는 Fig. 14의 Shifting-Factor Sm @ 60℃ 값인 –0,784를 사용하였다.
Time Conversion of Load & Strain under High Temperature.
실험 결과를 검토하면, Relaxation(σ∞) 시험의 경우, 상온 20℃하에서 60일은 고온 60℃에서 9.8일로 예측되었으나, 실제로는 1.8일 만에 파단 되었고, Creep(ε∞)시험에서는 예측된 Strain에서 모두 파단 되어 더 낮은 값에 대하여 실험하여 60일 유지 Strain 값을 기준으로 백분율 4%가 작은 Strain 값에서 30일을 유지하였다.
Fig. 15의 Master 선도와 중첩하면 큰 차이가 없어 보이나, Fig. 16과 같이 장시간 영역부위에서 비교하면 무시하지 못하는 현상이 발생됨을 알 수 있다.
Comparison of Long Time Sm Properties.
추진제의 기계적 물성은 파괴역학이나 반복하중 선도(S-N 곡선)와 같이 Log-Log 좌표로 정리하여야 하는 특성이 있어 규명하기가 쉽지 않다.
이런 현상이 고유 특성에서 비롯된 것인지, 또는 Inert 추진제에 따른 특성인지, 아니면 열유변학적 단순성(Thermo-Rheological Simplicity)이 장시간의 크립이나 응력이완 현상에는 적용되지 않는 것인지는 계속 연구할 필요가 있다.
5. 결 론
본 연구에서는 추진제의 점탄성 특성을 이해하고, 특성산출을 위해 적용되고 있는 다양한 시편형상, 속도, 온도에 따른 특성들을 통합하는 시도를 하였다. 기존 추진제 구조해석에 2% 응력이완 모듈러스를 Master Curve화하여 적용하고 있는 것은 Case Bonded Grain 접착부위의 변형률이 양 끝단(직경의 2배정도 되는 길이, 소위 Parr End Correction Factor 적용 영역)[5]를 제외한 대부분의 영역이 대략 2%로 형성되어 있기 때문이다. 여기서 구한 온도-시간 이송계수를 단순 일축인장시편시험 결과분석에도 적용하고 있으나, 일축인장시험으로부터 획득된 자료를 분석하면, 유사한 온도-시간 이송계수를 찾을 수 있다. 이런 이론들은 Log-Log 좌표계에서 표현되므로 실제 정상좌표 상에서는 매우 넓은 폭을 나타낸다. 실제 정상 좌표계의 예로서 Fig. 10-d)를 보면, 대부분시험들이 매우 짧은 시간 영역 대에서 실험을 하고 있지만, 실제 이런 온도하중 환경은 경화 후 냉각이외에는 없다. 아마 경화 후 냉각도 고무의 열전도 계수가 너무 낮아서 이것도 해당되지 않을 것이다. 다만 발사 시 급격한 연소실 압력 상승에서만 활용 가능할 것이다. 따라서 장기저장성에 좀 더 관심을 가져야 하며, 이를 위해 실제 활성 추진제를 대상으로 고온에서의 크립과 응력이완 시험을 많이 하여 t/aT가 큰 영역에서의 정교한 실험을 하고 현상을 이해할 필요가 있다.
Acknowledgments
[이 논문은 한국추진공학회 2015년도 추계학술대회(2015. 11. 25-27, 경주 현대호텔) 발표논문을 심사하여 수정・보완한 것임.]
References
-
Ha, J.S., Kim, J.H., Jung, G.D., Park, J.B., Yang, H.Y., and Seo, B.H., “Farcture Toughness Evaluation of a Solid Propellant Considering Viscoelasticity”, Journal of the Korean Society of Propulsion Engineers, Vol. 17(No. 2), p57-62, (2013).
[https://doi.org/10.6108/kspe.2013.17.2.057]
- Junga, G.D., Younb, S.K., and Kimb, B.K., “A three-dimensional nonlinear viscoelastic constitutive model of solid propellant”, International Journal of Solids and Structures, Vol. 37(Issue 34), Aug.), (2000.
-
Brostow, W., D’Souza, N.A., Kuba, ´t, J., and Maksimov, R., “Creep and stress relaxation in a longitudinal polymer liquid crystal: Prediction of the temperature shift factor”, Journal of Chemical Physics, Vol. 110(No. 19), p9706-9712, (1999).
[https://doi.org/10.1063/1.478935]
- Douglass, H.W., Collins, J.H., Noel, J.S., Keller, R.B., and Webb, L.D., “Solid propellant grain structural integrity analysis”, NASA Space Vehicle Design Criteria, NASA-SP 8073, Jun.), (1973.
- Edmund Fitzgerald, J., Handbook for the Engineering Structural Analysis of Solid Propellant, CPIA, Laurel, M.D., U.S.A., (1971).