액체 메탄을 이용한 우주 발사체 추진제 탱크의 공통 격벽 구조의 좌굴 Knockdown Factor 도출

1. 서 론

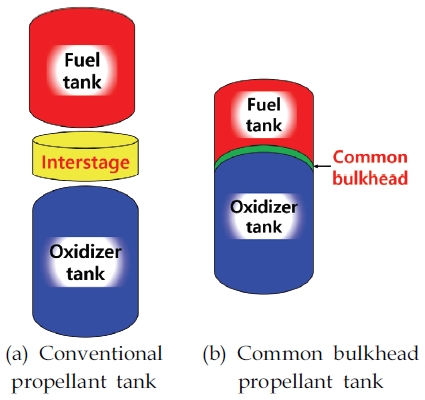
뉴 스페이스 시대(new space era)가 도래하며 민간 주도의 우주 산업이 급격히 발전하고 있다. 이에 따라 저비용 및 고효율의 우주 발사체의 개발 요구가 증가하고 있으며, 따라서 발사체의 경량 구조 설계가 더욱 중요해지고 있다[1]. 우주 발사체의 추진제 탱크 구조는 추진제를 제외한 발사체 구조 대부분의 중량을 차지하므로, 추진제 탱크 구조를 경량화한다면 발사체 구조의 중량을 낮출 수 있다[2]. Fig. 1에서 보이듯, 일반적인 발사체 추진제 탱크 구조는, 산화제 탱크와 연료 탱크가 별도로 설계 및 제작되어 이를 체결하기 위한 연결 동체(inter-stage)가 필요하다. 그러나 공통 격벽(common bulkhead) 추진제 탱크는 하나의 탱크 구조를 격벽을 이용하여 산화제 영역과 연료 영역으로 나누는 구조이므로, 연결 동체가 필요하지 않다[3]. 따라서 공통 격벽을 추진제 탱크 구조에 이용할 시, 추진제 탱크 구조의 경량 설계가 가능하다. 이러한 장점으로 인하여 공통 격벽 구조는 미국의 Saturn V, 유럽우주국(ESA)의 Ariane 5, 인도 우주연구 기구(ISRO)의 GSLV Ⅲ, 및 Space X의 Falcon 9에 사용되었다[4-7].

Fig. 1

Launch vehicle propellant tank structures.

공통 격벽은 단열성과 비강도가 우수한 폼 코어 샌드위치(foam core sandwich) 구조로 설계되며[8], 반구형 및 타원형 등 돔(dome) 형상의 얇은 쉘(shell) 구조 형식을 이용한다. 우주 발사체 구조에 사용되는 얇은 쉘 구조는 발사 및 비행 시 극심한 압축 하중에 노출되며, 이로 인하여 얇은 쉘 구조의 좌굴(buckling)이 발생할 수 있다. 얇은 쉘 구조의 전역 좌굴 하중(global buckling load)은 제작 및 운용 중 발생할 수 있는 다양한 결함(imperfection)으로 인하여 결함이 없는 완벽 구조의 선형 좌굴 하중에 비하여 감소된다[9]. 찍힘 및 비틀림 등으로 인하여 국소적인 구조 변형이 발생하는 기하학적 초기 결함(geometric initial imperfection, Imperfection_SDIA)은 대표적인 초기 결함이다. 결함으로 인하여 감소되는 좌굴 하중을 고려하기 위한 좌굴 설계 기준인 좌굴 Knockdown Factor(KDF)는 Eq. 1과 같이 결함이 없는 완벽 구조의 전역 좌굴 하중((N_cr)_perfect)에 대한 결함이 있는 구조의 전역 좌굴 하중((N_cr)_imperfect)의 비율로 정의된다. 좌굴 KDF가 낮을수록 얇은 쉘 구조는 무겁고 보수적으로 설계되므로, 좌굴 KDF는 경량 구조 설계와 직결된다.

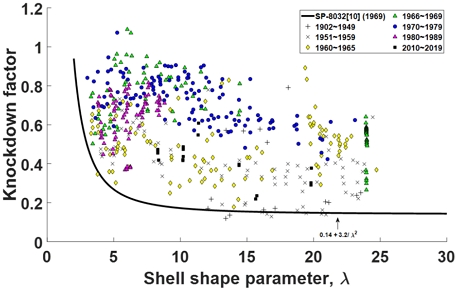
실제 쉘 구조에 존재하는 다양한 결함을 측정하여 정량화하는 것은 매우 어려우며 많은 비용이 요구되나, 좌굴 KDF는 실제 구조가 제작되기 이전인 초기 설계 단계에서 적용되어야 한다. 이를 위해 NASA는 1930~60년대까지 수행된 다수의 좌굴 시험 결과를 이용하여, 돔 형상의 쉘 구조에 대한 좌굴 설계 기준을 정립하였다(NASA SP-8032, Fig. 2, [10]). 이는 다양한 형상 변수(shell shape parameter, λ)를 갖는 돔 구조에 대하여, 측정된 좌굴 하중의 하한값을 이용하여 도출되었기 때문에, 구조 안정성을 만족시키는 좌굴 설계 기준을 제공할 수 있다. 그러나 NASA의 좌굴 설계 기준[10]은 오래전에 수행된 좌굴 시험 결과를 이용하므로, 현대의 발전된 재료 및 제작 기술을 반영하지 못한다. 또한 금속 재료 및 복합 재료 등의 다양한 재료에 대한 구분이 명확히 제시되지 않았다. 따라서, NASA의 좌굴 설계 기준[10]을 얇은 쉘 구조인 현대의 공통 격벽 구조 설계에 이용할 시, 지나치게 보수적인 설계로 이어질 수 있다. 따라서 다양한 결함을 고려한 공통 격벽 구조에 대한 좌굴 KDF를 도출하는 과정이 필요하다.

Fig. 2

Buckling Knockdown Factors and NASA SP-8032[10].

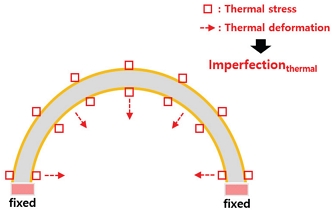
액체 메탄(Liquid methane, LCH4)은 비추력, 연소 효율, 및 열적 안전성 등이 우수하여 우주 발사체 추진제 탱크의 연료로 선호된다[11]. 그러나 연료인 액체 메탄과 산화제 사이의 온도 차이로 인한 열 전달 현상은 공통 격벽 구조의 열 응력 및 열 변형을 발생시킨다. 이러한 열적 결함(thermal imperfection, Imperfection_thermal)은 기하학적 초기 결함과 더불어 공통 격벽 구조의 결함으로 간주될 수 있다. 따라서 공통 격벽 구조의 기하학적 초기 결함 및 열적 결함을 함께 고려한 좌굴 설계 기준 도출이 필요하다.

최근 발전된 수치 해석 기법을 이용한 시뮬레이션 연구 결과와 좌굴 시험 결과를 상호 비교하여, 돔 형상의 얇은 쉘 구조에 대한 시뮬레이션 연구가 좌굴 시험을 적절히 대체할 수 있음이 입증되었다[12-18]. 수치 해석을 이용하여 초기 결함이 모델링된 금속재 돔 구조에 대하여 좌굴 설계 기준을 새롭게 도출하고 NASA의 좌굴 설계 기준 [10] 및 시험값과 상호 비교하는 연구가 수행되었다[12-16]. 수치적 초기 결함은 각각 Single Perturbation Cutout Approach(SPCA, [12-14]), Local Reduced Stiffness Method(LRSM, [12-14]), Linear Buckling Mode-shaped Imperfection(LBMI, [15]), 및 Dimplelike defect 기법[16]을 이용하여 구현되었다. 금속재가 아닌 폼 코어 샌드위치 돔 구조에 대하여, 시뮬레이션 연구를 통하여 온도에 따른 압축 거동의 차이를 확인하고, 이를 시험 결과와 비교하는 연구가 수행된 바 있다[17,18]. 또한, 공통 격벽 구조의 열 전달 현상을 확인하기 위한 과도 열 전달 해석 연구 결과와 시험 결과를 비교하였다[19,20]. 본 저자들의 선행 연구[21]에서 반구형 폼 코어 샌드위치 쉘 구조에 대한 해석 결과와 시험 결과를 상호 비교하여, 반구형 폼 코어 샌드위치 쉘 구조의 비선형 압축 거동 모델링 및 해석 기법을 정립하였다[21]. 이를 통하여, 수치 해석을 이용한 폼 코어 샌드위치 돔 형태의 공통 격벽 구조 모델링 및 해석 기법에 대한 타당성이 입증되었다. 전술한 선행 연구들은 공통 격벽 구조로 이용되는 반구형 폼 코어 샌드위치 구조의 열적 결함 및 기하학적 초기 결함을 독립적으로 고려하여 수행되었으나, 최근 본 저자들에 의하여 수치 해석 기법을 이용하여 케로신을 연료로 사용하는 추진제 탱크의 공통 격벽 구조의 좌굴 KDF가 도출되었다[22]. 그러나 전술한 장점을 갖는 액체 메탄을 연료로 사용한 추진제 탱크의 공통 격벽 구조에 대하여 기하학적 초기 결함과 열적 결함을 함께 고려한 좌굴 KDF를 도출하는 연구는 수행된 바 없다.

따라서 본 연구에서는 선행 연구[22]을 기반으로 액체 메탄을 이용한 추진제 탱크의 반구형 폼 코어 샌드위치 공통 격벽 구조에 대하여, 기하학적 초기 결함 및 열적 결함을 함께 고려한 좌굴 KDF를 수치 해석 기법을 이용하여 도출한다. 공통 격벽 구조의 유한요소 모델링 및 수치 해석을 위하여 상용 유한요소 해석 프로그램인 ABAQUS를 이용한다. 공통 격벽 모델의 기하학적 초기 결함은 공통 격벽의 상단 중심부 (Pole)에 Single Dimple Imperfection Approach (SDIA)를 적용하여 구현하며 [22], 열적 결함은 과도 열-구조 연성 해석을 통하여 모델링한다. 기하학적 초기 결함 및 열적 결함을 함께 고려한 공통 격벽 구조의 좌굴 거동을 조사하고, 이후 좌굴 KDF를 도출한다. 이 때, 공통 격벽 구조에 대하여 기하학적 초기 결함만을 고려한 모델, 열적 결함만을 고려한 모델, 및 기하학적 초기 결함 및 열적 결함을 함께 고려한 좌굴 KDF를 각각 도출한다. 이후, 얻어진 좌굴 KDF를 NASA SP-8032[10] 및 케로신을 연료로 사용한 추진제 탱크의 공통 격벽 구조의 좌굴 KDF[22]와 비교한다. 이를 통하여 액체 메탄을 연료로 이용하였을 때, 공통 격벽 구조의 좌굴 KDF를 이용한 우주 발사체 구조 경량화 가능성에 대하여 제시한다.

2. 본 론

2.1 연구 방법

본 절의 모델링 및 해석 기법은 액체 메탄의 사용을 제외하고 본 저자들의 선행 연구[22]의 내용과 동일하나 주요 내용을 다시 한번 정리 및 작성한다.

2.1.1 반구형 공통 격벽 구조 모델링

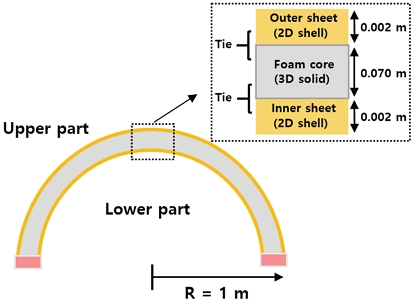
반구형 공통 격벽 구조(Fig. 3)에 대한 유한요소 모델링은 상용 유한요소 해석 프로그램인 ABAQUS를 이용한다. 공통 격벽 구조는 단열재인 폼 코어(foam core)의 내부 및 외부를 얇은 금속재 박판(surface sheet)이 감싸는 3차원 반구형 폼 코어 샌드위치 쉘 구조이며[22], 이때 폼 코어 및 금속재 박판의 재료는 공통 격벽 구조의 열-구조 거동에 대한 선행 연구[5,20]를 참고하여 각각 AIREX R82.80[5] 및 AA2219-T87[20]을 이용한다. 두 구조 재료의 자세한 물성치를 Table 1에 나타내었다. 폼 코어는 폼 재료의 큰 체적 변화를 고려하기 위한 3차원 고체 요소를 사용하며, 금속재 박판은 2차원 쉘 요소를 사용한다. 이때, 두 요소는 Tie constraint를 이용하여 서로 연결된다. 기하학적 초기 결함 모델링 및 비선형 후좌굴 해석을 위한 유한 요소로 C3D8R(폼 코어) 및 S4R(금속재 박판)을 각각 사용하며, 열-구조 연성 해석을 위한 요소로는 C3D8RT(폼 코어) 및 S4RT(금속재 박판)를 이용한다. 공통 격벽 추진제 탱크의 실제 구조 없이, 원통 구조와 결합된 공통 격벽 구조의 경계 조건을 구현하기 어렵다. 따라서, 본 연구에서는 반구형 공통 격벽 구조의 하단의 경계 조건을 완전 지지로 가정한다. 이러한 경계 조건의 가정은 다른 좌굴 설계 기준의 도출에 대한 선행 연구[12-14]에서도 확인할 수 있다.

Fig. 3

Hemispherical common bulkhead structure[22].

Table 1.

Properties for common bulkhead structures.

2.1.2 재료 비선형성 모델링

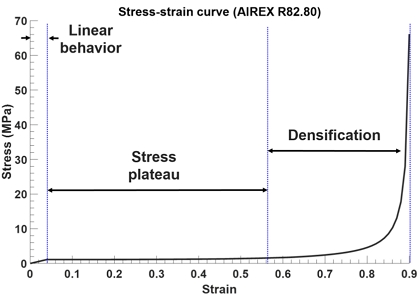
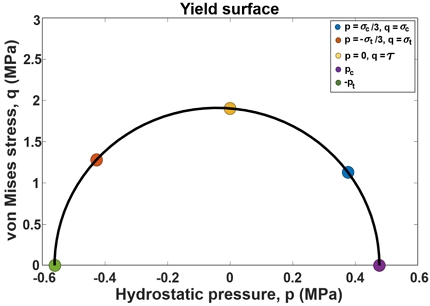
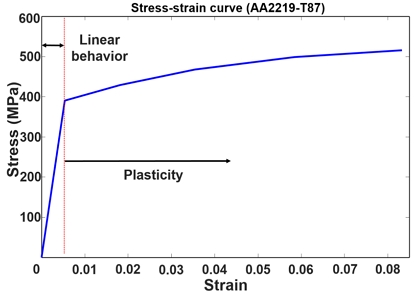
본 연구에서는 공통 격벽 모델을 나타내는 폼 코어 샌드위치 쉘 구조의 압축 거동을 적절히 구현하기 위하여, 폼 코어 및 금속재 박판에 사용된 재료의 비선형성을 고려한다. 다공성 재료인 폼 재료는 내부의 기공들로 인하여 외부 압축 하중 작용 시 매우 큰 비선형 거동이 발생한다. 이를 모사하기 위하여 폼 구조의 재료 비선형성과 더불어 변형률의 증가와 함께 응력이 급격히 증가하는 치밀화(densification)를 고려하여야 한다. Fig. 4는 압축 시험으로부터 얻어진 폼 재료인 AIREX R82.80의 응력-변형률 곡선을 보여주며[23], 본 연구에서는 ABAQUS의 Crushable foam 모델링 기법을 이용하여 폼 재료의 비선형 압축 거동을 모사한다. Crushable foam 모델링을 위하여 폼 재료의 항복 곡면(yield surface)으로부터 도출되는 압축 항복 응력 비율(compression yield stress ratio, K) 및 정수 항복 응력 비율(hydrostatic yield stress ratio, K_t)이 필요하다. 이를 위하여, AIREX R82.80의 압축, 인장, 및 전단 시험에서의 항복 강도를 이용하여, 정수압(p) 및 von Mises 응력(q)으로 표현되는 항복 곡면의 세 좌표의 값을 Eq. 2를 이용하여 계산한다. 이후 p 및 q를 Eq. 3에 대입하여 항복 곡면을 Fig. 5와 같이 정의하며, Eq. 4를 이용하여 Crushable foam 모델링을 위한 K=2.367 및 K_t=1.174를 얻는다. 보다 자세한 유도 과정은 선행 연구[22,24]에 더욱 상세히 서술되어 있다. 금속재 박판의 재료인 AA2219-T87[25]의 경우, Fig. 6의 응력-변형률 곡선을 이용하여 소성(plasticity)을 고려하여 재료 비선형성을 모델링한다.

$\[ \begin{array}{c}\mathrm{p}=-{\text{σ}}_{\mathrm{c}}/3, \mathrm{q}={\text{σ}}_{\mathrm{c}}\left(\text{uniaxial compression test}\right)\hfill \\ \mathrm{p}=-{\text{σ}}_{\mathrm{t}}/3, \mathrm{q}={\text{σ}}_{\mathrm{t}}\left(\text{uniaxial tension test}\right)\hfill \\ \mathrm{p}=0, \mathrm{q}=\sqrt{3}\text{τ }\left(\text{shear test}\right)\hfill \end{array} \]$

(2)

$\[ \begin{array}{c}\frac{{\left(\text{p}-\left({\text{p}}_{\text{c}}-{\text{p}}_{\text{t}}\right)/2\right)}^2}{{\left(\left({\text{p}}_{\text{c}}+{\text{p}}_{\text{t}}\right)/2\right)}^2}\hfill \\ +\frac{{\text{q}}^{\text{2}}}{{\left(\left(3\text{K}/\sqrt{\left(3{\text{K}}_{\text{t}}+\text{K}\right)(3-\text{K})}\right)\left(\left({\text{p}}_{\text{c}}+{\text{p}}_{\text{t}}\right)/2\right)\right)}^2}=1\hfill \end{array} \]$

(3)

$\[ \text{where }\mathrm{K}={\sigma }_{\mathrm{c}}/{\mathrm{p}}_{\mathrm{c}}, {\mathrm{K}}_{\mathrm{t}}={\mathrm{p}}_{\mathrm{t}}/{\mathrm{p}}_{\mathrm{c}} \]$

(4)

Fig. 4

True stress-strain curve of AIREX R82.80 for the foam core[23].

Fig. 5

AIREX R82.80 yield surface for the crushable foam modeling.

Fig. 6

True stress-strain curve of AA2219-T87 for the surface sheet[25].

2.1.3 공통 격벽 구조 기하학적 초기 결함 모델링

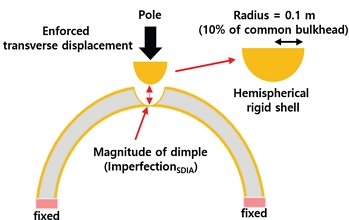
본 연구에서는 반구형 강체 쉘(hemispherical rigid shell)을 사용하는 Single Dimple Imperfection Approach(SDIA, Fig. 7, [22])을 이용하여 공통 격벽 구조의 Pole에 기하학적 초기 결함을 구현한다. 공통 격벽 반지름의 10%[26] 크기를 갖는 반구형 강체 쉘에 공통 격벽의 중심 방향으로 강제 변위를 가한다. 반구형 강체 쉘과 공통 격벽 구조 간 접촉은 Surface-to-surface 기법을 이용하여 모델링되며, ABAQUS/Implicit의 준정적(quasi-static) 해석 기법을 사용하여 얻어진 공통 격벽의 변형으로부터 기하학적 초기 결함(Imperfection_SDIA)을 구현한다.

Fig. 7

Schematic diagram of the Single Dimple Imperfection Approach(SDIA)[22].

2.1.4 공통 격벽 구조의 열적 결함 모델링

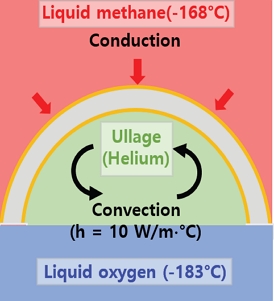
전술한 바와 같이, 액체 메탄은 우주 발사체 추진제 탱크의 연료로 선호되지만, 산화제인 액체 산소와의 온도 차이는 공통 격벽 구조의 열 응력 및 열 변형을 발생시킨다. 본 연구에서는 이러한 열적 결함을, 결함이 없는 완벽 구조 및 SDIA를 이용한 기하학적 초기 결함을 고려한 모델에 각각 적용하여 좌굴 KDF를 조사한다. 열적 결함을 구현하기 위하여 ABAQUS의 Coupled temperature-displacement 기법을 이용하며, 한국형 발사체(KSLV-Ⅱ) 1단 추진제 탱크의 연소 시간(150초)을 기준으로 과도 열-구조 연성 해석을 수행한다[22]. Fig. 8은 공통 격벽 구조의 열 전달 메커니즘을 보여주며, 공통 격벽 구조의 상단 및 하단 영역에서 각각 액체 메탄의 열 전도 및 액체 산소와 Ullage 간 열 대류가 발생한다고 가정한다. 본 연구는 반구 형상의 공통 격벽 구조에 대한 거동을 조사하므로, 외부의 열원은 없다고 가정하여 공통 격벽의 열 전달만을 고려하며, 부식 등에 의한 부가적인 효과는 고려하지 않는다[27]. 공통 격벽의 초기 온도는 15℃를 사용한다. 이를 통하여 후술할 비선형 후좌굴 해석에 사용되는 공통 격벽 구조의 열적 결함(Imperfection_thermal)을 구현한다(Fig. 9).

Fig. 8

Schematic diagram of the heat transfer for the common bulkhead.

Fig. 9

Thermal stresses and thermal deformations of the common bulkhead structure.

2.1.5 비선형 후좌굴 해석

결함이 없는 완벽 구조 및 결함을 고려한 공통 격벽 구조에 대하여 외부 압력 작용 시의 전역 좌굴 압력 (좌굴 하중) 및 후좌굴 거동을 조사하기 위하여, ABAQUS/Implicit의 준정적 해석 기법[22]을 이용한 비선형 후좌굴 해석을 수행한다. 본 연구에서는 기하학적 초기 결함 및 액체 메탄과 액체 산소 사이의 열 전달로부터의 열적 결함을 각각 고려한 모델과 더불어, 두 가지 결함을 함께 포함한 모델에 대하여 외부 압력을 가하여 비선형 후좌굴 해석을 수행한다.

2.1.5.1 기하학적 초기 결함만을 고려한 모델

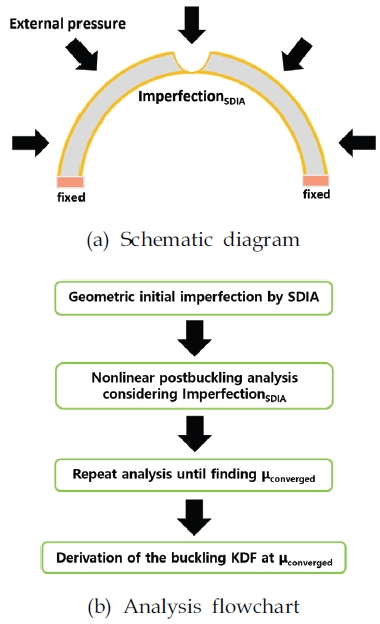
기하학적 최 결함의 크기를 무차원화한 μ (Eq. 5)의 증가에 따른 공통 격벽 구조의 비선형 후좌굴 거동을 확인한다. μ가 증가함에 따라 전역 좌굴 압력은 감소하며, 이때 특정 크기의 μ(μ_converged)에서 수렴된 전역 좌굴 압력((N_cr)_imperfect)을 얻는다. Fig. 10(a)는 SDIA를 통해 구현된 기하학적 초기 결함만을 고려한 공통 격벽 구조의 비선형 후좌굴 해석에 대한 개념도를 보여주며, 해석 절차는 Fig. 10(b)에 나타내었다[22].

$\[ \text{μ}=\frac{\mathrm{M}\mathrm{a}\mathrm{g}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{ }\left({\mathrm{I}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{\mathrm{S}\mathrm{D}\mathrm{I}\mathrm{A}\mathrm{ }}\right)}{\mathrm{T}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}} \]$

(5)

Fig. 10

Postbuckling analysis considering only ImperfectionSDIA[22].

2.1.5.2 열적 결함만을 고려한 모델

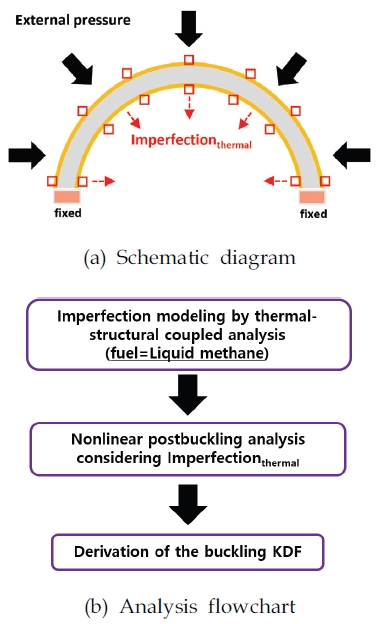
앞서 2.1.4절에서 모델링된 열 전달 현상으로 인하여 열적 변형(열적 결함)된 공통 격벽 모델에 외부 압력을 가하여 비선형 후좌굴 해석을 수행하여 전역 좌굴 압력 및 후좌굴 거동을 확인한다. 본 절에서는 기하학적 초기 결함이 아닌, 연료인 액체 메탄과 산화제인 액체 산소 간 온도 차이로 인한 열 전달 효과로부터의 열적 결함만을 고려한 결과가 얻어진다. 비선형 후좌굴 해석을 통하여 전역 좌굴 압력((N_cr)_imperfect)을 계산한다. 열적 결함만을 고려한 비선형 후좌굴 해석의 개념도 및 절차를 Fig. 11에 나타내었다.

Fig. 11

Postbuckling analysis considering only Imperfectionthermal.

2.1.5.3 기하학적 초기 결함 및 열적 결함을 함께 고려한 모델

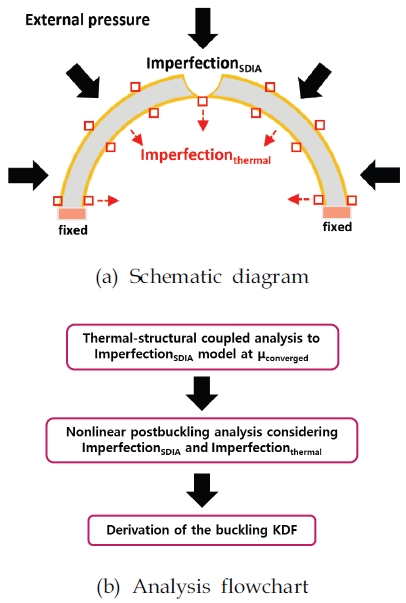
먼저 SDIA로 인한 기하학적 초기 결함의 크기(μ) 중, μ_converged에서의 변형된 공통 격벽 구조에 대하여 과도 열-구조 연성 해석을 수행한다. 이로부터 공통 격벽 구조의 기하학적 초기 결함 및 열적 결함을 함께 구현한다. 이후, 해당 모델에 외부 압력을 가하여 비선형 후좌굴 해석을 수행한다(Fig. 12).

Fig. 12

Postbuckling analysis considering both ImperfectionSDIA and Imperfectionthermal.

2.2 연구 결과

2.2.1 기하학적 초기 결함만을 고려한 공통 격벽 구조

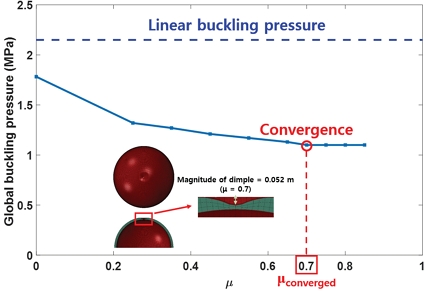
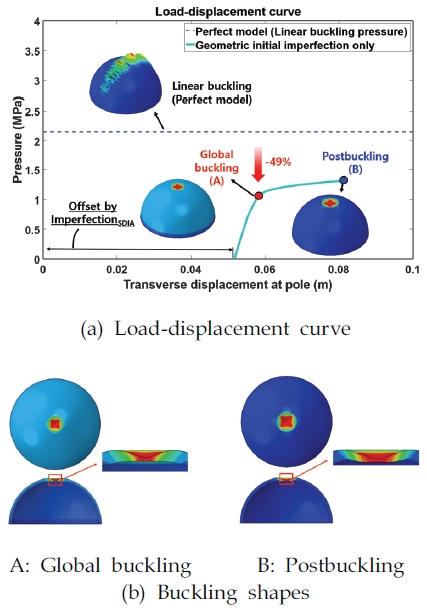
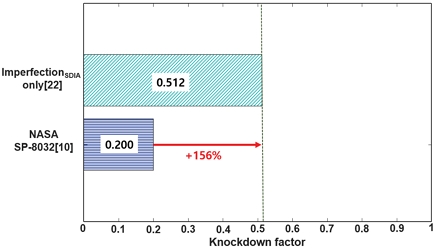
본 절의 SDIA를 이용하여 구현된 기하학적 초기 결함만을 고려한 공통 격벽 구조의 좌굴 거동은 사용된 연료의 종류(케로신 혹은 액체 메탄)와 상관없이 선행 연구[22]의 결과와 동일하다. 결함이 없는 완벽 구조의 공통 격벽 구조의 선형 좌굴 압력((N_cr)_perfect)은 2.152 MPa로 계산되었다. Fig. 13에서 보이듯, μ=0.7(μ_converged)일 때 기하학적 초기 결함만을 고려한 전역 좌굴 압력((N_cr)_imperfect)이 수렴되며, 그 크기는 1.101 MPa로 계산되었다[22]. Fig. 14는 μ_converged =0.7에서의 공통 격벽 구조의 비선형 후좌굴 해석 결과를 보여준다. 이때, 하중-변위 그래프의 횡방향 변위는 공통 격벽 구조의 Pole 위치에서 아래(downward)를 양(positive)의 방향으로 정의하였으므로, 그래프의 초기 변위는 구현된 기하학적 초기 결함의 크기(μ_converged)인 0.052 m만큼 양의 방향으로 평행 이동되었다. 전역 좌굴(A)은 SDIA를 이용한 기하학적 초기 결함이 구현된 Pole 부근에서 발생하였다. 이후, 외부 압력이 증가하며 보조개(dimple) 모양의 좌굴 형상이 Pole을 중심으로 모든 방향으로 확산되며 후좌굴(B)이 관찰되었다. 기하학적 초기 결함만을 고려한 공통 격벽 구조의 좌굴 KDF는 NASA의 좌굴 설계 기준(0.200)에 비하여 약 156% 높은 0.512로 도출되었다(Fig. 15).

Fig. 13

Convergence for the global buckling pressure in terms of μ[22].

Fig. 14

Postbuckling analysis results for the common bulkhead model with ImperfectionSDIA only[22].

Fig. 15

Comparison the buckling KDFs considering ImperfectionSDIA only and NASA’s buckling design criteria[22].

2.2.2 열적 결함만을 고려한 공통 격벽 구조

Fig. 16은 액체 메탄을 연료로 사용하는 추진제 탱크의 결함이 없는 완벽 구조에 대한 과도 열-구조 연성 해석으로부터 얻은 온도, 변위, 및 응력에 대한 결과를 보여준다. Ullage와 액체 산소 간 열 대류 및 극저온의 액체 메탄의 열 전도로 인하여 공통 격벽의 하단 및 상단 영역의 온도(15℃)가 각각 –37℃ 및 –168℃로 감소하였다. 이로 인하여 공통 격벽 구조에는 Fig. 16과 같이 열 전달로 인한 수축 변형이 발생하였다. 이때 변형된 형상 및 열 응력이 공통 격벽 구조의 열적 결함으로 고려된다.

Fig. 16

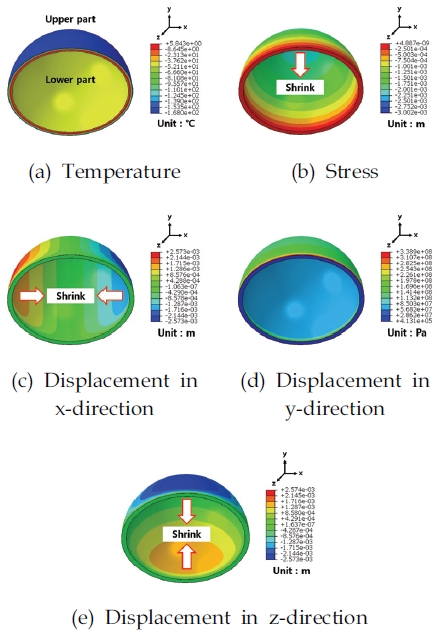
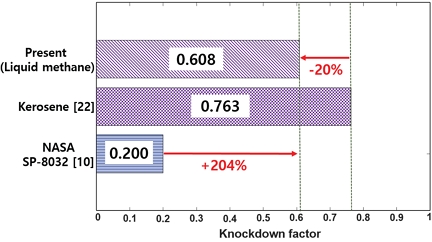
Thermal-structural coupled analysis results for the common bulkhead structure without imperfections.

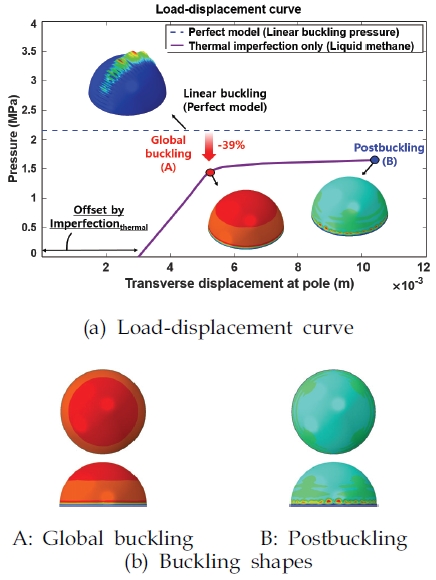
Fig. 17은 열적 결함만을 고려한 공통 격벽 구조의 비선형 후좌굴 해석 결과를 보여준다. Fig. 17(a)의 Pole 위치에서 얻어진 하중-변위 곡선에서 확인할 수 있듯이, 열적 결함으로 인하여 그래프의 초기 변위는 0.003 m만큼 양의 방향으로 평행 이동되었다. 이로부터 Pole에서의 열적 변형의 크기가, 기하학적 초기 결함(0.052 m)에 비하여 작다는 것을 알 수 있다. 또한 케로신을 연료로 사용한 모델의 열적 결함만을 고려한 초기 변위는 0.158×10^-3 m[22]이며, 본 연구의 액체 메탄을 연료로 사용한 결과(0.003 m)의 약 6%이다. 이는 극저온의 액체 메탄으로 인해 공통 격벽의 수축 변형이 더욱 크게 발생한 것에서 기인된 것으로 사료된다. 열적 결함만을 고려한 공통 격벽 구조의 전역 좌굴 압력((N_cr)_imperfect)은 1.308 MPa로 계산되며, 이는 (N_cr)_perfect=2.152 MPa에 비하여 약 39% 낮다. Fig. 17(b)는 전역 좌굴 및 후좌굴 형상을 보여준다. 전역 좌굴 파형(A)은 공통 격벽 구조 끝단의 경계 조건 부근에서 발생하고, 전역 좌굴 이후의 후좌굴 파형(B)은 원주 방향으로 확산된다. Fig. 18에서 보이듯, 액체 메탄을 연료로 사용한 공통 격벽 구조의 열적 결함만을 고려한 좌굴 KDF는 케로신을 연료로 사용한 KDF(0.763, [22])에 비하여 약 20% 낮은 0.608로 도출되었다. 이는 전술하였듯, 액체 메탄을 연료로 이용하였을 때의 열적 결함이, 케로신을 연료로 사용한 모델에 비하여 크기 때문인 것으로 판단된다. 그러나 액체 메탄을 연료로 사용하였을 때의 열적 결함만을 고려한 좌굴 KDF(0.608)는 NASA의 좌굴 설계 기준(0.200)에 비하여 약 204% 높게 도출되었다.

Fig. 17

Postbuckling analysis results for the common bulkhead model with Imperfectionthermal only.

Fig. 18

Comparison the buckling KDFs considering Imperfectionthermal only(Liquid methane and Kerosene[22]) and NASA’s buckling design criteria[10].

2.2.3 기하학적 초기 결함 및 열적 결함을 함께 고려한 공통 격벽 구조

본 절에서는 SDIA를 이용한 기하학적 초기 결함 및 열-구조 연성 해석을 통한 열적 결함을 함께 고려한 공통 격벽 구조에 외부 압력을 가하여 비선형 후좌굴 해석을 수행하였다. 2.2.1절의 μ_converged=0.7의 기하학적 초기 결함을 가진 공통 격벽 구조에 과도 열-구조 연성 해석을 수행하여, 액체 메탄이 연료로 사용되었을 때의 열적 결함을 추가로 구현하였다. Fig. 19에 보이듯, 열적 결함만을 고려한 공통 격벽 구조의 변형 결과(Fig. 16)와 유사하게 열 대류 및 극저온의 액체 메탄으로 인하여, 공통 격벽 구조의 상단 및 하단 영역에서 수축 변형이 발생하였다.

Fig. 19

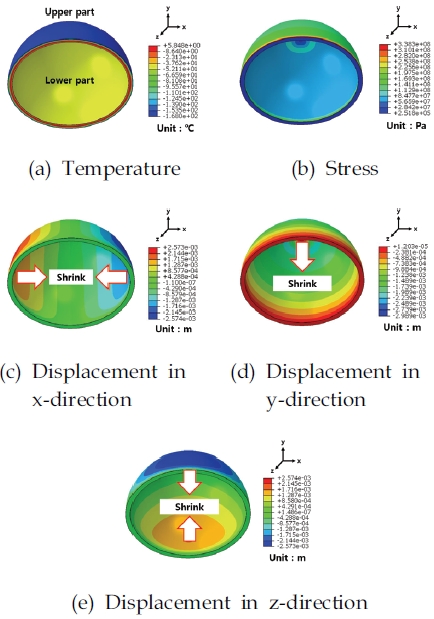
Thermal-structural coupled analysis results for the common bulkhead structure with ImperfectionSDIA.

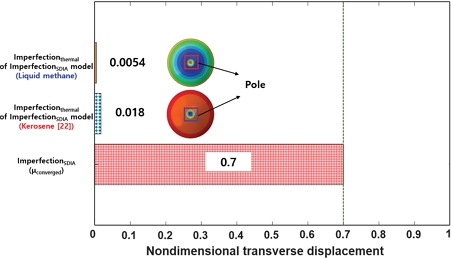
Fig. 20은 기하학적 초기 결함 및 열적 결함을 함께 고려한 공통 격벽 구조의 비선형 후좌굴 해석 결과를 나타낸다. Fig. 20(a)에서 보이듯, Pole에서의 기하학적 초기 결함 (0.052 m) 및 열적 결함의 크기 (0.0004 m)의 합만큼 하중-변위 곡선의 초기 변위가 0.0524 m만큼 양의 방향으로 평행 이동되었다. 전역 좌굴 및 후좌굴로 인하여 변형된 형상을 Fig. 20(b)에 나타내었다. 전역 좌굴(A)은 SDIA가 적용된 Pole 부근에서 보조개 형상으로 관찰되었다. 이후 Pole을 중심으로 좌굴 파형이 모든 방향으로 확산되며 후좌굴(B)이 발생하였다. 기하학적 초기 결함 및 열적 결함을 함께 고려한 전역 좌굴 압력은 (N_cr)_perfect=2.152 MPa에 비하여 약 51% 낮은 1.051 MPa((N_cr)_imperfect)로 계산되었다. 이를 통해 도출된 액체 메탄을 적용한 공통 격벽 구조의 기하학적 초기 결함 및 열적 결함을 함께 고려한 좌굴 KDF(0.488)는 NASA의 좌굴 설계 기준(0.200)에 비하여 약 144% 높다(Fig. 21). Fig. 22는 Pole에서의 횡방향 변위를 공통 격벽의 두께로 나누어 무차원화하여, 기하학적 초기 결함이 구현된 모델에서의 연료의 종류에 따른 Pole에서의 열적 변형 크기 및 기하학적 초기 결함의 크기를 비교한다. 그림에서 보이듯 기하학적 초기 결함 및 열적 결함이 함께 구현된 모델에서, Pole에서의 기하학적 초기 결함의 크기가 열적 결함의 크기에 비하여 매우 크기 때문에, 기하학적 초기 결함으로 인한 Pole의 변형이 공통 격벽 구조의 좌굴 KDF에 큰 영향을 미친다. 이때 기하학적 초기 결함이 구현된 Pole에서, 액체 메탄을 사용할 때의 열적 결함의 크기는 케로신을 사용하였을 때에 비하여 약 69% 낮다. 따라서 본 절에서 액체 메탄을 연료로 사용할 경우, 케로신을 사용한 좌굴 KDF(0.465, [22])에 비하여 약 5% 높은 결과로 도출되었다(Fig. 21).

Fig. 20

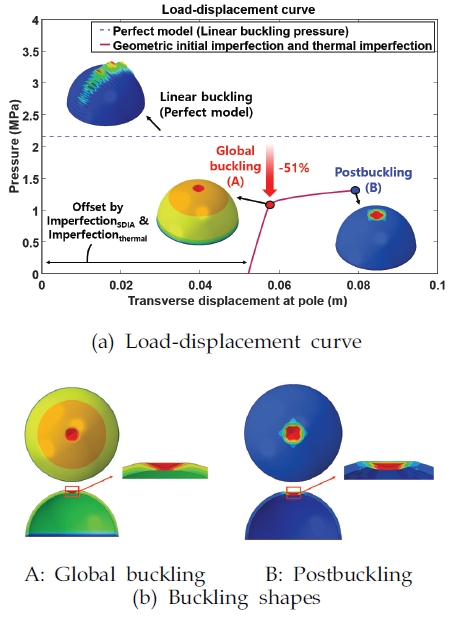
Postbuckling analysis results for the common bulkhead model with ImperfectionSDIA and Imperfectionthermal.

Fig. 21

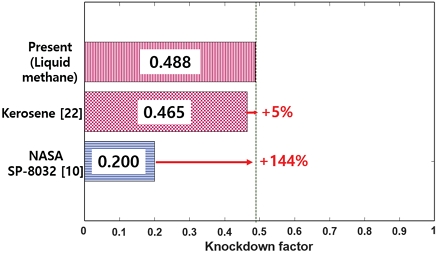
Comparison the buckling KDFs considering ImperfectionSDIA and Imperfectionthermal only(Liquid methane and Kerosene[22]) and NASA’s buckling design criteria[10].

Fig. 22

Imperfection magnitude at the Pole of the common bulkhead structures.

2.2.4 좌굴 Knockdown factor의 비교

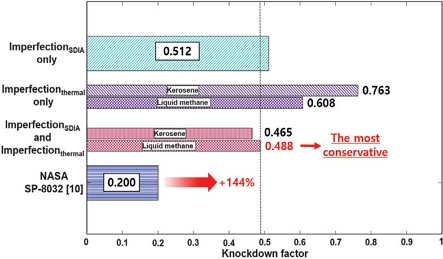
Fig. 23은 본 연구에서 얻어진 좌굴 KDF와 NASA의 좌굴 설계 기준[10]을 비교한 결과를 보여준다. 기하학적 초기 결함은 공통 격벽 구조의 좌굴 KDF(0.512, [22])를 크게 감소시키지만, 본 연구의 가장 보수적인 결과는 아니다. 액체 메탄을 사용한 모델의 열적 결함만을 고려한 좌굴 KDF(0.608)는 케로신을 연료로 사용하였을 때의 열적 결함만을 고려한 좌굴 KDF(0.763, [22])에 비하여 낮지만, 본 연구의 좌굴 KDF 중 가장 높은 값을 갖는다. 기하학적 초기 결함 및 열적 결함을 함께 고려할 경우, 본 연구에서 가장 보수적인 좌굴 KDF(0.488)가 얻어지며, 이는 NASA의 좌굴 설계 기준 (0.200, [10])에 비하여 약 144% 높은 결과이다. 또한 2.2.3절에서 전술하였듯, 이는 케로신을 연료로 사용한 좌굴 KDF(0.465, [22])에 비하여서도 5% 높은 결과이다. 따라서 우주 발사체 공통 격벽 구조 설계 시, 본 연구에서 얻어진 좌굴 KDF를 이용한 발사체 구조 경량 설계가 가능하며, 액체 메탄이 케로신에 비하여 공통 격벽 구조의 경량 구조 설계에 적절한 연료임을 확인하였다.

Fig. 23

Comparison the buckling KDFs when using liquid methane and kerosene[22], and NASA’s buckling design criteria[10].

3. 결 론

본 연구에서는 액체 메탄을 연료로 사용하는 우주 발사체 추진제 탱크 내부의 공통 격벽 구조에 대하여 ABAQUS를 이용하여 좌굴 KDF를 도출하였다. 기하학적 초기 결함은 SDIA 기법을 이용하여 공통 격벽 구조의 Pole에서 보조개 형상으로 구현하였다. 연료인 액체 메탄과 산화제인 액체 산소 간 열 전달로 인한 열적 결함은 과도 열-구조 연성 해석을 통하여 얻었다. 외부 압력이 가해진 공통 격벽 구조의 다양한 결함을 고려하여 비선형 후좌굴 해석을 수행한 결과, 기하학적 초기 결함만을 고려한 좌굴 KDF(0.512) 및 열적 결함만을 고려한 좌굴 KDF(0.608)은 NASA의 좌굴 설계 기준에 비하여 각각 156% 및 204% 높은 결과로 얻어졌다. 이때 본 연구의 액체 메탄을 연료로 사용하였을 때의 열적 결함만을 고려한 좌굴 KDF(0.608)는, 극저온의 액체 메탄으로 인한 공통 격벽의 수축 변형이 비교적 크게 발생하여 케로신을 연료로 사용한 결과(0.763)에 비하여 20% 낮게 도출되었다. 기하학적 초기 결함 및 열적 결함을 함께 고려한 좌굴 KDF(0.488)는 본 연구에서 얻어진 가장 보수적인 좌굴 설계 기준으로서, NASA의 좌굴 설계 기준에 비하여 144% 높게 얻어졌다. 이는 케로신을 연료로 사용한 공통 격벽 구조의 기존의 좌굴 KDF(0.465)에 비하여서도 약 5% 높은 결과이다. 따라서 향후 공통 격벽 구조의 초기 설계 단계에서, 본 연구에서 얻어진 공통 격벽 구조의 좌굴 KDF를 이용한 발사체 구조 경량화가 가능할 것으로 사료되며, 액체 메탄이 케로신에 비하여 공통 격벽 구조의 경량 구조 설계에 적절한 연료임을 확인하였다.

본 연구에서는 연료와 산화제 간 열 전달로 인한 공통 격벽 구조의 열적 결함을 고려하였으나, 향후 온도 변화로 인한 공통 격벽 구조 재료의 물성치 변화를 추가적으로 고려하여 열적 결함을 구현할 경우, 보다 의미있는 결과를 얻을 수 있을 것이다. 더불어 공통 격벽 구조에 대한 열 전달 시험 및 좌굴 시험이 향후 수행되고 이에 대한 상호 비교 검증 연구를 수행할 경우, 보다 신뢰성 있는 결과를 제시할 수 있을 것으로 판단된다.

Acknowledgments

본 연구는 공통 격벽 추진제 탱크 발사체 체계 활용을 위한 설계 및 평가(스페이스 파이오니어 사업, NRF-2021M1A3B9096762)의 지원을 받았습니다. 본 논문의 일부는 2023년도 한국항공우주학회 추계학술대회에서 발표되었습니다.

References

• Salt, D.J., “Space Operations for a Newspace Era,” SpaceOps 2010 Conference Delivering on The Dream Hosted by NASA Marshall Space Flight Center and Organized by AIAA, Alabama, U.S.A., April 2010. [https://doi.org/10.2514/6.2010-1972]
• Regab, M.M., Cheatwood, F.M., Hughes, S.J. and Lowry, A., “Launch Vehicle Recovery and Reuse,” AIAA SPACE 2015 Conference and Exposition, California, U.S.A., August 2015. [https://doi.org/10.2514/6.2015-4490]
• Mirshams, M., Naseh, H. and Fazeley, H.R., “Multi-objective Multidisciplinary Design of Space Launch System Using Holistic Concurrent Design,” Aerospace Science and Technology, Vol. 33, Issue 1, pp. 40-54, 2014. [https://doi.org/10.1016/j.ast.2013.12.015]
• Anonymous, Space Launch Report: SpaceX Falcon Data Sheet, Updated May 01, 2017.
• Szelinski, B., Lange, H., Rottger, C., Sacher, H., Weiland, S. and Zell, D., “Development of an Innovative Sandwich Common Bulkhead for Cryogenic Upper Stage Propellant Tank,” Acta Astronautica, Vol. 81, Issue 1, pp. 200-213, 2012. [https://doi.org/10.1016/j.actaastro.2012.06.025]
• Logsdon, T., Orbital Mechanics : Theory and Applications, 1st ed., John Wiley & Sons Inc., New York, N.Y., U.S.A., 1997.
• Singh, Y. P., Singh, H., Sahu, P. K. and Muthukumar, R., “Common Bulkhead Tank Design for Cryogenic Stage of an Indian Launch Vehicle,” Defence Science Journal, Vol. 72, No. 1, pp. 3-9, 2022. [https://doi.org/10.14429/dsj.72.17239]
• Wang, P., Lei, Y. and Yue, Z., “Experimental and Numerical Evaluation of the Flexural Properties of Stitched Foam Core Sandwich Structure,” Composite Structures, Vol. 100, pp. 243-248, 2013. [https://doi.org/10.1016/j.compstruct.2012.12.040]
• Zhang, J., Zhang, M., Tang, W., Wang, W. and Wang, M., “Buckling of Spherical Shells Subjected to External Pressure: A Comparison of Experimental and Theoretical Data,” Thin-Walled Structures, Vol. 111, pp. 58-64, 2017. [https://doi.org/10.1016/j.tws.2016.11.012]
• Weingarten, V.I. and Seide, P., “Buckling of Thin-walled Doubly Curved Shells,” NASA SP-8032, 1969.
• Kim, C.W., Lim, B.J., Lee, K.J. and Park, J.S., “A Study on Fuel Selection for Next-Generation Launch Vehicles,” Journal of the Korean Society of Propulsion Engineers, Vol. 25, No. 3, pp. 62-80, 2021. [https://doi.org/10.6108/KSPE.2021.25.3.062]
• Wagner, H.N.R., Hühne, C. and Niemann, S., “Robust Knockdown Factors for the Design of Spherical Shells Under External Pressure: Development and Validation,” International Journal of Mechanical Sciences, Vol. 141, pp. 58-77, 2018. [https://doi.org/10.1016/j.ijmecsci.2018.03.029]
• Wagner, H.N.R., Hühne, C., Zhang, J., Tang, W. and Khakimova, R., “Geometric Imperfection and Lower-bound Analysis of Spherical Shells Under External Pressure,” Thin-Walled Structures, Vol. 143, 106195, 2019. [https://doi.org/10.1016/j.tws.2019.106195]
• Wagner, H.N.R., Hühne, C., Zhang, J. and Tang, W., “On the Imperfection Sensitivity and Design of Spherical Domes Under External Pressure,” International Journal of Pressure Vessels and Piping, Vol. 179, 104015, 2020. [https://doi.org/10.1016/j.ijpvp.2019.104015]
• Wang, Y., Tang, W., Zhang, J., Zhang, S. and Chen, Y., “Buckling of Imperfect Spherical Caps with Fixed Boundary Under Uniform External Pressure,” Marine Structures, Vol. 65, pp. 1-11, 2019. [https://doi.org/10.1016/j.marstruc.2019.01.004]
• Lee, A., López Jiménez, F., Marthelot, J., Hutchinson, J.W. and Reis, P.M., “The Geometric Role of Precisely Engineered Imperfections on the Critical Buckling Load of Spherical Elastic Shells,” Journal of Applied Mechanics, Vol. 83, No. 11, 111005, 2016. [https://doi.org/10.1115/1.4034431]
• Wang, S., Li, S. and He, J., “Buckling Behavior of Sandwich Hemispherical Structure Considering Deformation Modes Under Axial Compression,” Composite Structures, Vol. 163, pp. 312-324, 2017. [https://doi.org/10.1016/j.compstruct.2016.12.050]
• He, J., Li, S. and Wang, S., “Deformation Behavior of Sandwich Hemispherical Structure Under Axial Compression at Low Temperature,” Composite Structures, Vol. 203, pp. 267-277, 2018. [https://doi.org/10.1016/j.compstruct.2018.05.046]
• Lee, C.M., Sim, C.H., and Park, J.S., “Thermal Insulation Performance Comparison Using Boil-off Mass and Boil-off Rate for Common Bulkhead Structures of Space Launch Vehicles,” Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 51, pp. 227-234, 2023. [https://doi.org/10.5139/JKSAS.2023.51.4.227]
• Sumith S. and Kumar, R.R., “Thermo-structural Analysis of Cryogenic Tanks with Common Bulkhead Configuration,” Proceedings of The Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 236, Issue 5, pp. 900-909, 2021. [https://doi.org/10.1177/09544100211024789]
• Sim, C. H., Lee, C.M., Kim, G.S., and Park, J.S., “Derivation of Buckling Knockdown Factors for Hemispherical Foam Core Shells,” Proceeding of The Aerospace Europe Conference 2023 – 10th EUCASS – 9th CEAS, 2023.
• Lee, C.M., Sim, C.H., Kim, G.S., Park, J.S., and Lee, J.S., “Derivation of Knockdown Factors for Common Bulkhead Structures Considering Geometric Initial Imperfection and Heat Transfer Effects,” International Journal of Aeronautical and Space Sciences, 2023 (Online First). [https://doi.org/10.1007/s42405-023-00692-3]
• Flores-Johnson E.A. and Li, Q.M., “Indentation into Polymeric Foams,” International Journal of Solids and Structures, Vol. 47, Issue 16, pp. 1987-1995, 2010. [https://doi.org/10.1016/j.ijsolstr.2010.03.025]
• Carranza, I., Crocombe,A.D, Mohagheghian, I., Smith, P.A., Sordon, A., Meeks, G. and Santoni, C. “Characterising and Modeling the Mechanical Behaviour of Polymeric Foams Under Complex Loading,” Journal of Material Science, Vol. 54, pp. 11328-11344, 2019. [https://doi.org/10.1007/s10853-019-03673-8]
• Dewan, M.W., Huggett, D.J., Liao, T.W., Wahab, M.A. and Okeil, A.M., “Prediction of Tensile Strength of Friction Stir Weld Joints with Adaptive Neuro-Fuzzy Inference System (ANFIS) and Neural Network,” Materials and Design, Vol. 92, pp. 288-299, 2016. [https://doi.org/10.1016/j.matdes.2015.12.005]
• Sim, C.H., Lee, C. M., Kim, G. S., Park, J.S, and Lee, J. S., “Derivation of Buckling Knockdown Factors for Hemispherical Foam Core Sandwich Shells with Single Dimple Imperfection Approach,” International Journal of Aerospace Engineering (under review).
• Choi. D.K. and Lee. S.Y., “A Study on a Modeling Method for Thermal-Structural Coupled Analysis of Cryogenic Common Bulkhead Propellant Tanks,” Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 51, pp. 761-767, 2023. [https://doi.org/10.5139/JKSAS.2023.51.11.761]