PIC-DSMC를 활용한 이온 추력기 그리드의 전산해석
bSatellite Research Directorate, Korea Aerospace Research Institute, Korea
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
이온 추력기의 성능에 큰 영향을 끼치는 이온 광학 시스템을 연구하는 것은 필수적이나, 실험 등을 통한 연구는 여러 한계점이 있어 전산해석이 필요하다. 따라서 본 연구에서는 이온 광학 시스템에서의 PIC-DSMC 코드의 타당성을 검토하고, 여러 물리적 현상을 분석하였다. 본 연구의 해석 결과는 기존 논문에서 측정한 전위 및 이온 수밀도와 높은 일치도를 보였다. 더불어, 가속 그리드의 전압이 클수록 시스가 스크린 그리드에서 멀어지고, 곡률이 증가함을 확인하였으며 이로 인해 이온의 반경 방향 속도가 증가하였다. 특히 가속 그리드 전압이 충분치 않은 경우, 가속 그리드 상류 표면에 이온이 직접 충돌함을 확인하였다.
Abstract
Studying the ion optical system is crucial due to its significant impact on ion thruster performance. Due to the numerous limitations of experimental studies, numerical simulation is indispensable. In this study, the validity of the PIC-DSMC code for ion optical systems is examined, and various physical phenomena are analyzed. The simulation results of this study show good agreement with the electric potential and ion number density measurements reported in previous studies. It was found that the larger the voltage of the acceleration grid, the farther the sheath is from the screen grid and the greater the curvature, which increases the radial velocity of the ions. Additionally, with insufficient acceleration grid voltage, ions directly collided with the surface upstream of the acceleration grid.
Keywords:
Ion Thruster, Ion Optical System, PIC-DSMC(Particle In Cell - Direct simulation Monte Carlo)키워드:
이온 추력기, 이온 광학 시스템1. 서 론
우주비행체의 운용에 있어 가장 큰 장애물은 연료 공급과 유지보수의 제한이다. 이에 따라 안정적이고 장기간 운용이 가능한 추진시스템이 요구되었으며, 자세 제어, 궤도 유지, 심우주 탐사 등 높은 수준의 미션 수행을 위해 세밀한 추력 조절 능력이 요구되었다. 기존의 화학식 추력기(Chemical Thruster)는 수명이 짧고, 세밀한 추력 조절이 어렵다는 점에서 우주 추진 시스템으로서의 한계가 있다. 이에 따라 전기에너지로 연료를 가속하는 전기추력기(Electric Thruster)에 대한 연구가 급속도로 증가하고 있다[1,2]. 그 중, 전기장을 사용하여 추진제를 가속하는 이온 추력기는 1960년대에 개발이 시작된 이후 매우 높은 비추력[2,3]의 장점으로 인해 상업용 인공위성(Boeing702, Boeing601HP 등) 및 과학 탐사선(Deep Space 1, Dawn 등)에 다수 채택되었다[1].
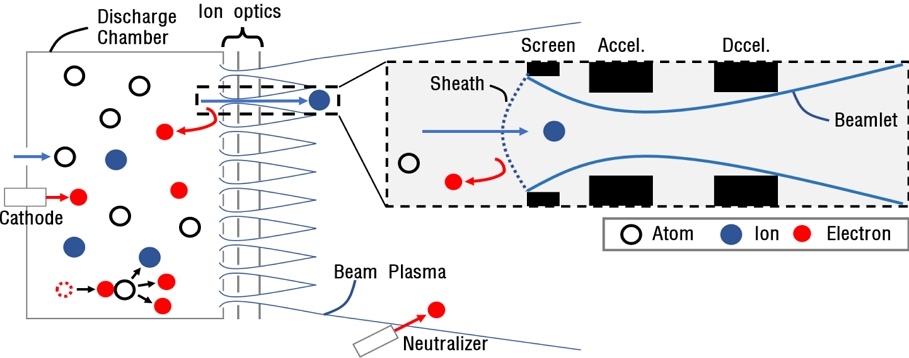
이온 추력기는 방전 챔버(Discharge Chamber)에서의 이온화 과정과, 이온 광학 시스템(Ion Optical System)에서의 이온 가속 과정이 분리되어 있다(Fig. 1). 먼저 추진제(일반적으로 기체 형태의 제논)와 전자가 이온 추력기 방전 챔버로 공급된다. 이때 전자는 중공 음극(Hollow Cathode)을 이용하여 주입된다. 이 전자는 챔버 내부의 중성 추진제 기체 원자와의 충돌을 통해 원자에서 전자를 분리하여 이온화를 일으키고, 중성 기체 원자, 전자 및 이온의 집합인 방전 챔버 플라즈마(Discharge Chamber Plasma)가 형성된다. 이렇게 형성된 이온은 각기 다른 전압을 가진 그리드들로 이루어진 이온 광학 시스템을 거쳐 가속되어 추력을 생성한다. 그리드는 이온이 통과할 수 있도록 수백에서 수천개의 구멍이 뚫려있으며 일반적으로 2개에서 3개의 그리드를 사용하여 가속한다. 방전 챔버에 가장 가까운 그리드를 스크린(Screen) 그리드, 다음 그리드를 가속(Acceleration) 그리드라고 하며 3개의 그리드를 사용한다면 마지막 그리드를 감속(Deceleraion) 그리드라고 한다.
이온 가속 과정에서 여러 입자들(추진제 이온, 전하 교환 이온, 그리드 재료의 원자 등)이 이온 광학 시스템에 충돌하게 되고, 그로 인한 이온 광학 시스템의 침식은 추력기의 수명을 제한[4-7]하는 주요 메커니즘이다. Sengupta 등[4]은 이온 추력기의 성능테스트, 수명 결정, 침식(Erosion)에 의한 스퍼터링(Sputtering) 등을 분석하기 위해 총 30,352시간 동안 추력기를 작동하였다. 장시간의 실험은 금전적, 시간적 비용이 막대하고, 동시에 여러 case를 실험할 수 없기에 이온 광학 시뮬레이션은 필수적이다. 또한 이온 광학 시뮬레이션은 이온 빔(Ion Beam)을 시각화하여 이온 광학 시스템의 이해에 큰 도움이 되며 비교적 저렴한 비용으로 수많은 설계 분석을 통해 이온 추력기의 성능 최적화에 기여한다[8,9]. 하지만 국내엔 이온 광학 시뮬레이션에 관한 논문은 찾아보기 힘들다. 이러한 이유로 본 논문에서는 PIC-DSMC 방법을 이용한 이온 광학 시뮬레이션 코드를 검증하고, 나아가 코드를 활용하여 이온 광학 시스템의 물리적 특성을 분석하고자 한다.
2. 전산해석 방법
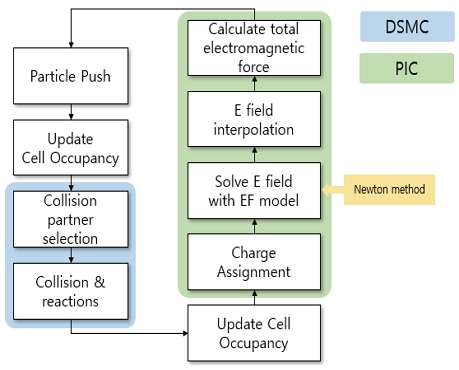
본 연구에서는 OpenFOAM 기반의 PIC-DSMC 코드인 pdFoam을 활용하였다. PIC(Particle-In–Cell)은 볼츠만 방정식에서 충돌 항을 무시하고, 전자기력을 고려한 경우인 Vlasov-Maxwell 방정식 시스템의 해를 제공하여 모사입자가 받는 전자기력을 계산하는 입자 추적기법이다. PIC 방법이 충돌 항을 무시하였기에, 별도의 모사입자 간 충돌을 반영하기 위하여 DSMC(Direct Simulation Monte Carlo)모델을 포함하였다. DSMC 방법은 볼츠만 방정식의 해를 구해 모사입자 간의 충돌을 반영한다[10,11]. Fig. 2은 pdFoam의 계산 사이클을 나타낸다.
pdFoam은 기존의 openFOAM코드들을 자유롭게 접목하고 활용할 수 있어 프로그램의 개선이 용이하다. 이러한 점을 활용하여 Kang 등[11]이 개선한 코드를 통합하였다.
Kang 등[11]은 원자-이온 간 전하 교환 모델을 추가하였으며 이를 본 연구에 적용하였다. 전하 교환(Charge Exchange, CEX) 과정에서 빠른 이온은 전자를 얻어 빠른 중성원자가 되고, 전자를 빼앗긴 느린 중성원자는 느린 이온이 된다. 여기서 생성된 느린 이온은 이온 광학 시스템의 침식에 큰 영향을 미친다[12].
이온 광학 시스템의 시뮬레이션에서 전자의 속도분포에 제한을 두지 않는 Fully Kinetic 방법은 전자를 입자로 계산하므로 전자의 움직임을 파악할 수 있다는 점에서 장점이 있지만 상당한 계산 시간이 발생한다. 따라서 본 연구에선 등온, 정전기(Electrostatic), 비자성, 관성 무시의 가정을 통해 전자를 볼츠만 전자 유체 모델을 활용한 Hybrid 방법을 이용하여 계산한다[10]. 전자 유체 모델은 볼츠만 관계식(Eq. 1)으로 전자의 밀도를 구할 수 있다. 이것을 전위(Electric Potential)와 전하 밀도(Charge Density)의 관계를 나타내는 포아송 방정식(Eq. 2)에 대입하면 전위에 대한 비선형 함수(Eq. 3)가 나온다.
| ϕ-ϕref=kBTeqeln(ne/ne,ref) | (1) |
| ∇2ϕ=ρcϵ0 | (2) |
| ϵ0∇2ϕ-qene,refexp[qe(ϕ-ϕref)kBTe]=-qini | (3) |
여기서 ϕ는 전위, kB는 볼츠만 상수, Te는 전자온도, q는 입자의 전하량, n은 수밀도, ρc는 전하 밀도, ϵ0는 유전율이다. 하첨자 i, e, ref는 각각 이온, 전자, 기준값을 의미한다.
Eq. 3의 해는 Newton method를 이용하여 근사해로 구하였다. 이러한 방법은 비선형 포아송 방정식 계산에 시간이 더 소요되지만, 경우에 따라 Fully Kinetic 방법에 비해 102 ~ 106배 큰 time step을 사용할 수 있어 총 계산 시간의 감소를 가져온다[10].
PIC방법에서 해석격자의 크기는 디바이 길이(Debye Length)와 관련있다. 디바이 길이는 전자가 외부 전기장을 차단할 수 있는 거리인데, 해석격자의 크기가 디바이 길이보다 큰 경우 개별적 쿨롱힘이 차폐되어 플라즈마의 움직임을 정확히 파악할 수 없으므로 해석격자의 크기는 디바이 길이보다 작아야한다[13]. 또한, 해석 영역 내에선 플라즈마 입자 간 충돌이 발생한다. 이를 모사하기 위해선 플라즈마 주파수보다 작은 time step을 채택[13]하여야 하며 이보다 큰 time step을 채택할 경우 개별 입자 간 충돌을 모사하지 못하고 거시적 움직임만 파악이 가능하다. 본 연구에선 위의 내용과 선행연구의 내용들을 참고하여 해석격자의 크기와 time step을 채택하였다.
3. 해석코드 타당성 검토
본 논문에선 개선코드의 타당성을 검증하기 위해 Han 등[14]의 논문을 참고하여 전산해석을 수행하였다. Han 등[14]의 연구에는 시뮬레이션에 필요한 입력 값들(경계조건, 플라즈마 상태 조건, 격자 모양, 개수, 모사입자 수, 다중 하전 이온 고려 여부)이 상당 부분 공개되어있고, 수치해석 방법 또한 본 연구에서 활용하는 PIC-DSMC와 유사한 PIC-MCC(Particle-In-Cell Monte Carlo Collisions)를 사용하고 있어, 결과의 비교 분석이 용이할 것으로 판단되었다. Han 등[13]은 3차원 PIC–MCC 방법을 이용하여, 이온 광학 시스템의 특성에 대해 분석하였다. 이때, 연구 대상이 되는 이온 광학 시스템으로 스크린 그리드와 가속 그리드 사이에 추출(Extraction) 그리드를 추가하여 비추력을 향상시키고자 하였으며, 그리드들의 형상(Geometry)과 추출 그리드의 전압에 따른 이온 추력기의 성능과 여러 물리량들의 변화를 분석하였다. 이때 이온은 Xe+만 고려하였다.
3.1 해석 조건
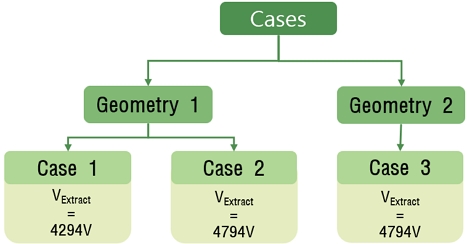
Han 등[14]는 다양한 case에 대한 연구결과를 보고하고 있으나, 그리드 내부의 플라즈마 전위 분포 및 이온의 수밀도는 일부 case에 한정하여 데이터를 제공하고 있다. 본 연구에서 산출한 플라즈마 전위 분포, 이온의 수밀도를 Han 등[14]의 결과와 비교를 위해, 해당 데이터를 제공하고 있는 case만 발췌하여 전산해석을 진행하였다. Fig. 3은 본 연구에서 채택한 case의 해석 조건을 나타낸다.
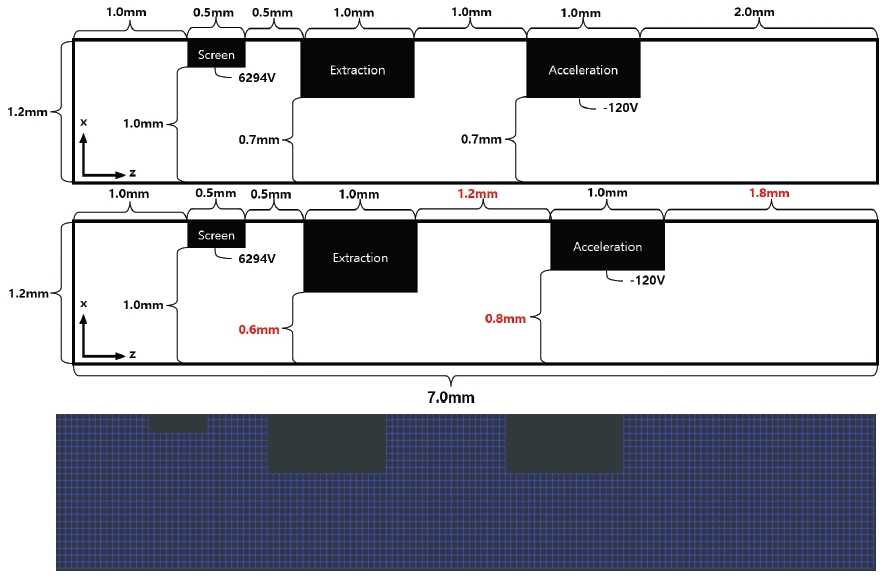
Fig. 4는 전산해석에 사용한 그리드 형상 1, 그리드 형상 2, 그리드 형상 1의 격자계를 보여준다. 형상 1에 비해 형상 2는 추출 그리드의 반경은 감소 (0.7 mm → 0.6 mm) 하고 가속 그리드의 반경은 증가 (0.7 mm → 0.8 mm) 하였으며 추출 – 가속 그리드 간 간격은 증가 (1 mm → 1.2 mm) 하였다. 전산해석을 위한 격자계는 한변의 길이가 0.05 mm인 정사각형 형태의 정렬 격자계를 사용하였으며, 24x142개를 배치했다. Time step은 5x10-10 s이며 해석은 0.1 ms까지 수행하였다.
Table 1은 설정한 경계조건과 플라즈마 상태 조건을 보여준다. case 1은 추출 그리드의 전압을 4294 V로 설정하였으며, case 2, case 3의 경우엔 4794 V로 설정하였다. 방전 챔버 영역인 Upstream과 가속 그리드 하류 영역인 Outlet은 입자가 경계면 외부로 이동할 경우 삭제 처리되는 Deletion Patch를 사용하였으며 상류와 하류의 전위는 6324 V와 0 V로 고정되어 있다. 그리드 표면 또한 Deletion Patch를 사용하여 표면에 충돌하는 입자를 삭제하였다. 스크린 그리드는 6294 V, 가속 그리드는 –120 V로 모든 case에서 동일하며 추출 그리드의 경우에만 case에 따라 다르게 설정하였다. 상단 경계면은 Specular Reflection으로 입자가 정반사되도록 하였으며 Neumann 경계로 설정하였다.
플라즈마 상태 조건은 Table 1과 같으며 전자밀도는 위에서 언급한 대로 볼츠만 관계식을 따른다고 가정한다. 또한 추진제는 제논이며, 각 time step에서 중성 제논은 제논 이온에 대해 9:1 비율로 상류에서 주입되며, 제논 이온이 상류에서 봄 속도(Bohm Velocity, vBohm)로 주입된다. 봄 속도(Eq. 4)란 이온이 시스(Sheath)를 통과하기 위해 프리 시스(Pre-Sheath) 영역을 이동하는 동안 달성하는 속도이다.
| vBohm=√kBTeMi | (4) |
여기서 Mi는 이온의 질량이다.
계산 시간의 절감을 위해 2차원 축대칭을 활용하였으며 모사입자 1개는 2,500개의 실제입자를 나타낸다.
3.2 해석 결과 비교
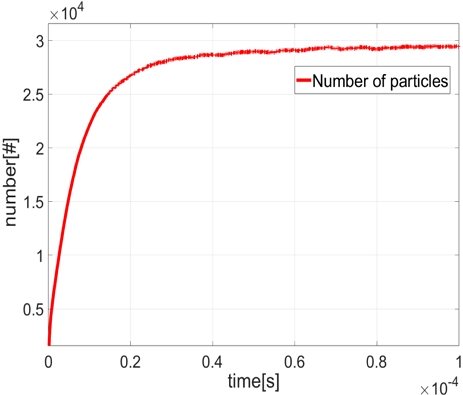
해석 시간은 전체 모사입자의 수가 일정해지는 시간보다 약 3배인 0.1 ms까지 수행하여 정상상태의 데이터를 획득했다. Fig. 5는 시뮬레이션 시간에 따른 전체 모사입자의 개수를 보여준다.
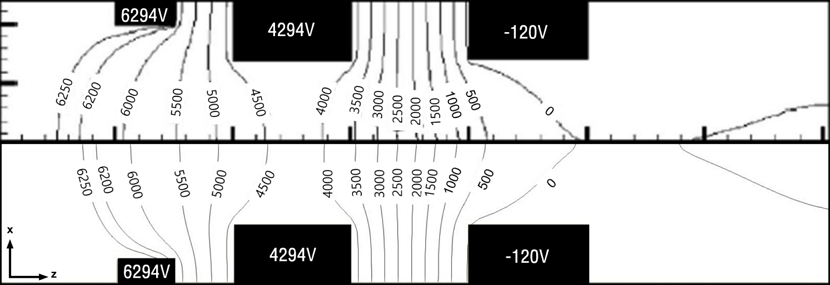
Fig. 6은 case 1에서의 이온 광학 시스템의 등전위선을 보여준다. Han 등[14]의 결과(up)와 비교하여 본 연구의 해석 결과(down)가 매우 유사함을 보인다.
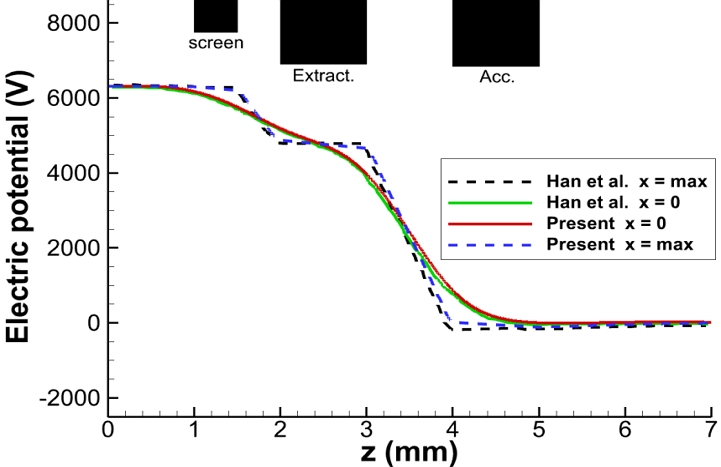
Fig. 7은 case 2에서 바깥쪽(x = xmax)과 중심축(x = 0) 에서 축 방향 거리에 따른 전위의 분포를 보여준다. Han 등[14]의 결과와 본 연구의 해석 결과는 높은 일치도를 보여주고 있다. 이를 통해, 각기 다른 전압을 가진 그리드들이 만들어내는 전위값이 타당하게 계산되고 있음을 알 수 있다. 바깥쪽의 경우엔 그리드와 밀접하여 있기에 각 그리드가 가지는 전압의 영향을 강하게 받지만, 중심축의 경우 각 그리드 전극에서 멀리 떨어져 있기에 전압에 의한 영향이 약하다. 그로 인해 바깥쪽의 전위 분포와 중심축의 전위 분포에 차이가 생긴다. Han 등[14]의 결과와 본 연구의 해석 결과 모두 상류에서 하류로 가며 급격하게 전위가 감소하는데, 이 과정에서 축 방향 전기장이 형성되어 이온이 가속된다. 이러한 전기장의 영향으로 계산 영역 내에서 이온의 밀도가 불균형하게 분포한다.
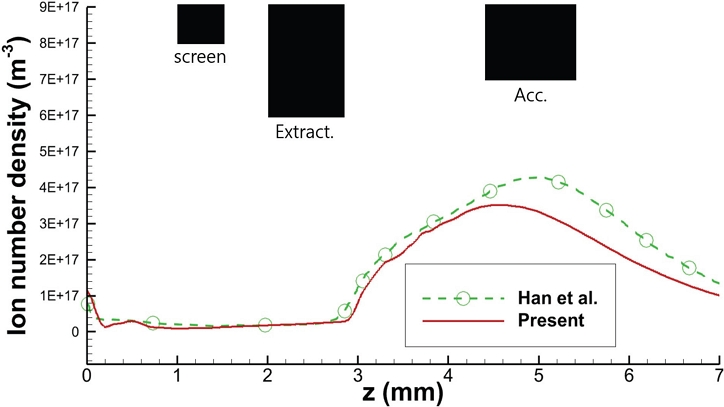
Fig. 8은 case 3에서 중심축에서 이온 수밀도를 보여준다. 이 경우에서도 Han 등[14]의 결과와 본 연구의 해석 결과의 일치도가 높음을 알 수 있었다. 이를 통해, 그리드들이 만들어내는 전기장에 의해 이온이 받는 영향이 타당하게 계산되었음을 알 수 있다. 축 방향 거리가 4.5 mm이상부터 Han 등[14]의 결과와 약간의 오차가 발생함을 보이는데 이는 3차원 계산을 수행한 Han 등[14]과는 다르게 본 연구는 2차원 축대칭 계산을 하였고, 2차원 축대칭 계산의 특징인 축 근처 모사입자 수의 부족과 본 연구의 해석코드에서는 가속 그리드 하류 영역의 전자온도(1.5eV)을 반영하지 못한다는 점이 원인으로 파악되며 추후 연구를 통해 개선할 계획이다. Han 등[14]의 결과와 본 연구의 결과 모두 이온 수밀도가 추출 그리드를 지나며 급격히 증가하게 되고(z = 3 mm), 가속 그리드를 지나며 감소하였다. 이를 통해, 빔렛(Beamlet)은 이온 광학 시스템을 거치며 축소(Shrink)와 확장(Expand)을 모두 경험하며, 빔렛의 직경이 가속 그리드 근처에서 최소가 될 것임을 알 수 있다.
위와 같은 결과 비교(Electric potential contour & distribution, Ion number density)를 통해 본 연구의 해석코드의 타당성을 검증하였다.
4. 이중 그리드 (2-grid) 시스템 전산해석
검증된 코드를 활용하여 좀 더 일반적인 이온 광학 시스템을 분석하기 위해 Lingwei 등[15]의 그리드 형상과 플라즈마 상태 조건을 활용하였다. 이온은 Xe+만 고려하였다.
4.1 해석 조건
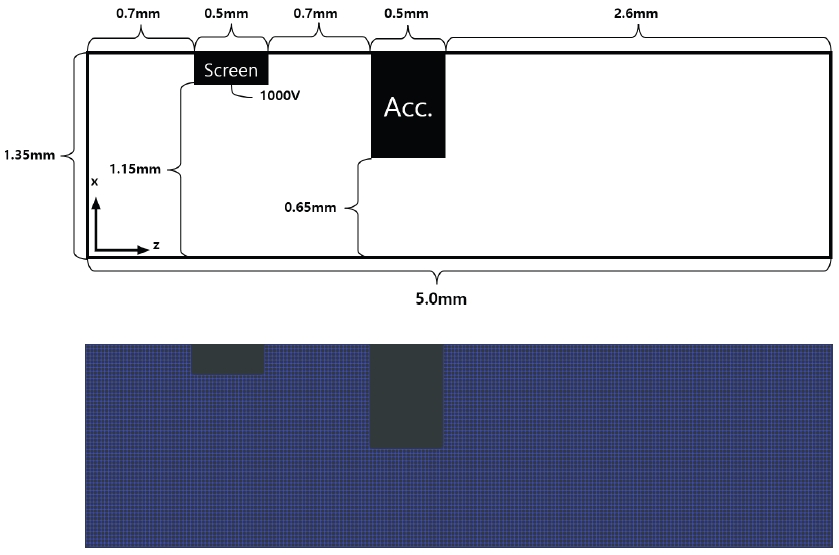
Fig. 9는 전산해석에 사용한 스크린 그리드와 가속 그리드로 이루어진 이중 그리드의 형상과 격자계이다. 스크린 그리드의 반경은 1.15 mm, 가속 그리드의 반경은 0.65 mm이다.
Table 2는 설정한 경계조건과 플라즈마 상태 조건을 보여준다. Upstream과 Outlet, 그리드 표면은 Deletion Patch를 사용하였으며 Upstream과 Outlet의 전위는 1030 V와 0 V로 고정되어 있다. 가속 그리드의 전압은 case에 따라 다르게 설정하였다. 상단 경계면은 Specular Reflection과 Neumann 경계로 설정하였다. 중성과 이온은 상류에서 9:1의 비율로 주입된다. 계산 시간의 절감을 위해 2차원 축대칭을 활용하였으며 모사 입자 1개는 10,000개의 실제입자를 나타낸다. 전산해석을 위한 격자계는 한변의 길이가 0.025 mm인 정사각형 정렬 격자계를 사용했으며, 54x200개를 배치했다. Time step은 1.5x10-10 s 이며 해석은 0.1 ms까지 수행하였다.
4.2 해석 결과 분석
플라즈마와 스크린 그리드는 전위차가 있어 시스가 형성되는데 시스 이전의 영역인 프리시스 영역에선 이온의 속도와 시스의 면이 수직한 경향이 있다. 이때 시스를 통과하는 이온의 속도는 플라즈마 전자온도에 비례하는 봄 속도이다. 봄 속도를 가지고 시스를 통과하는 이온과는 반대로 전자는 시스를 통과하지 못하고 튕겨 나가는데, 이는 디바이 길이와 연관이 있다. 플라즈마와는 다른 전위를 가지는 스크린 그리드의 표면에 디바이 길이보다 더 가까워진 전자는 스크린 그리드의 영향을 받아 플라즈마로 튕겨져 나가는 것이다.
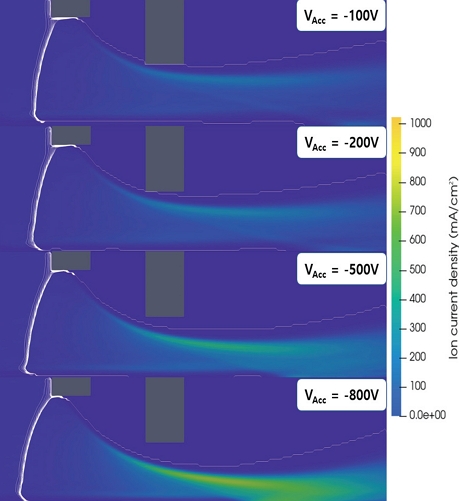
Fig. 10은 가속 그리드 전압에 따른 시스의 형태 및 이온 전류 밀도이다. 시스의 위치를 정확히 파악하는 것이 어렵기 때문에 본 연구에서는 Xe+와 전자의 수밀도 비를 10~100까지 10의 간격으로 흰색 선들을 표시하고, 이 선들이 뭉쳐져 있는 영역을 시스 위치로 간주하였다. 이를 통해 시스 전후로 이온과 전자 간의 수밀도비가 급격히 차이가 나는 특징을 표현할 수 있다. 또한 빔렛의 전류를 이온의 전류밀도를 통해 나타내었다.
가속 그리드 전압이 0에 가까울수록 시스가 스크린 그리드에 가까워지고 곡률이 작아지는 것을 볼 수 있다. 이온은 시스의 표면에 수직하게 나오므로 시스의 곡률이 작아진다는 것은 이온의 반경 방향 속도 성분이 줄어든다는 것을 의미하며, 빔렛은 직경이 충분히 축소되지 않은 채로 추출된다. 이는 가속 그리드의 전압이 0에 가까울수록 중심축 부근의 빔렛의 전류가 감소하는 것을 통해서도 알 수 있다.
스크린 그리드의 전압은 고정된 상태로 가속 그리드의 전압이 음으로 커지면 총 가속전압이 커진다. 이 경우 추출 가능한 최대 빔렛 전류가 커져 퍼비언스 분율(Perveance Fraction, fp)은 낮아지는데, 퍼비언스 분율이란 추출가능한 최대 빔렛 전류 대비 실제 빔렛 추출 전류(Eq. 5)로, 전위가 다른 두 표면 사이를 통과할 수 있는 이온의 최대 전류밀도의 개념인 차일드-랭뮤어 법칙(Child-Langmuir Law)과 관련이 있다.
| fp=j1Pmaxl2eV32T | (5) |
여기서 j는 이온의 전류밀도, le는 유효 이온 가속 길이, VT는 총 가속 전압, Pmax는 최대 퍼비언스이다.
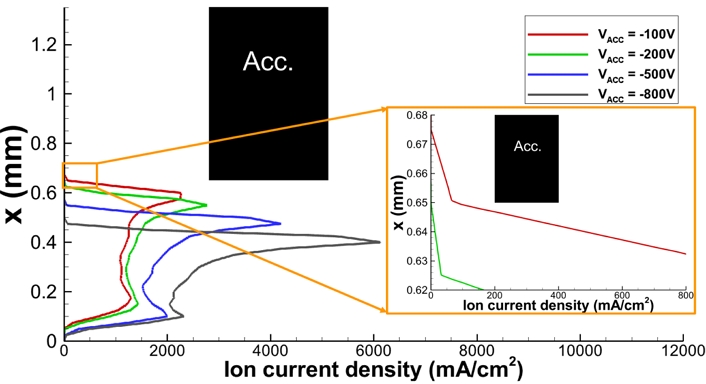
Fig. 11은 가속 그리드 상류 표면의 위치(z = 1.9 mm)에서 반경 방향 거리에 따른 빔렛의 전류밀도이다. 가속 그리드의 반경이 0.65 mm이므로 반경 방향 거리가 0.65 mm 이상의 위치에서 측정된 전류는 가속 그리드의 표면에 충돌함을 알 수 있다. 가속 그리드의 전압의 절대값이 작아지게 되면 이온은 반경 방향 힘을 점점 적게 받아 빔렛은 더 넓은 직경을 가지게 되고, -100 V의 전압에서는 미량의 전류가 가속 그리드의 상류 표면에 직접 충돌한다. 이온 광학 시스템이 주어진 인가전압에 대해 초점을 맞추어 빔으로 추출할 수 있는 최대의 전류의 양인 퍼비언스 한계(Perveance Limit)를 넘으면 case 1 (VAcc = -100 V)과 같이 가속 그리드 상류에 이온이 직접 충돌하여 가속 그리드를 마모시키게 되고 이온 추력기의 수명을 단축시킨다. 따라서 이온 추력기의 수명 유지를 위한 VAcc의 최소전압은 -100 V이다.
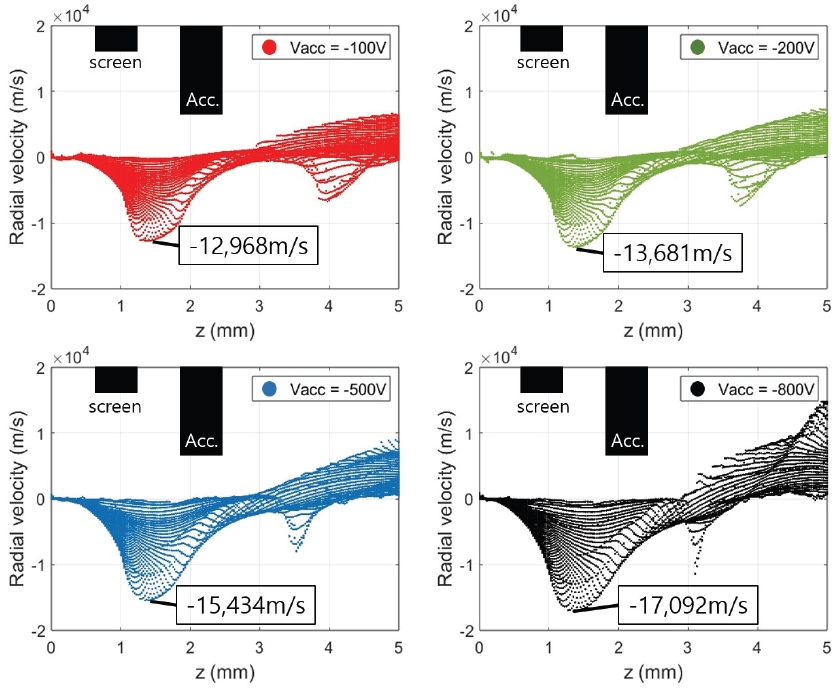
Fig. 12는 개별 이온입자의 축 방향 거리와 반경 방향 속도를 위상공간에 표시한 그림이다. 그림에 나타난 바와 같이, 낮은 전위값을 갖는 가속 그리드로 인하여, 이온의 반경 방향 속력이 음의 값을 가지며 축 중심부로 집중되는 현상을 확인할 수 있다. 이러한 경향은 가속 그리드의 전압이 낮아질수록 (절대값 기준으로 커질수록) 더 크게 나타나, VAcc = -100 V일 때에는 최저속도가 –12,698 m/s이나, VAcc = -800 V일 때에는 최저속도가 –17,092 m/s까지 떨어지는 것을 알 수 있다. 이러한 이유로, Fig. 10에 나타난 빔렛 또한 가속 그리드 전압이 낮을수록 중심부로 모이는 오목한 모양을 갖는 것을 알 수 있다. 가속 그리드를 지난 이온은 반경 방향 전기장에 의해 반경 방향 속력이 양의 값을 가지게 되며 Fig. 10에서 빔렛이 반경 방향으로 퍼진다.
가속 그리드의 하류에서의 이온 빔을 중화하기 위해 중공 음극에서 전자가 방출된다. 전자는 이온보다 훨씬 높은 이동성을 가지고 있기에 전위 장벽이 존재하지 않으면 전자의 역류(Electron Backstreaming)가 발생하고, 방전 챔버 등의 부품의 손상을 일으킬 수 있다[15-17]. 이를 막기 위해 가속 그리드는 가속 그리드 근처 전위를 음(Negative)으로 떨어뜨려 전자 역류를 방지하기 위한 장벽을 제공한다. 중심축(가속 그리드 홀의 중심부)은 가속 그리드의 전극으로부터 가장 멀리 떨어진 곳이고, 일반적으로 중심축에서의 이온밀도가 다른 곳에 비해 높기에 상대적으로 가장 양(Positive)의 전위를 가진다. 그렇기에 중심축을 따라 0 이하의 음의 값(Negative Value)인 구간이 존재한다는 것은 해당 구간의 모든 반경 방향 영역에서 전위가 음의 값을 가짐을 의미한다. 또한, 이때의 전위를 안장점 전위(Saddle Point Potential)라고 부른다.
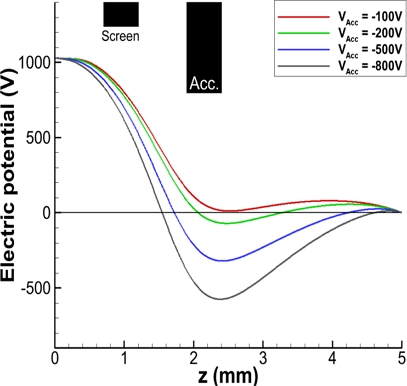
Fig. 13은 중심축에서 축 방향 거리에 따른 전위 그래프이다. VAcc = -800 V ~ -200 V의 안장점 전위는 음의 값을 가져 전자 역류 방지를 위한 장벽을 제공하지만, VAcc = -100 V의 경우 동일 위치에서의 전위값이 11.38 V로 장벽을 제공하지 못한다. 따라서 전자 역류 방지를 위해선 가속 그리드 전압을 -100 V 이상으로 주는 것이 합당하다.
5. 결 론
openFOAM의 PIC-DSMC 코드인 pdFoam을 활용하여 이온 광학 시스템해석에서 코드의 타당성을 검토하고, 여러 물리적 특성들을 시뮬레이션하였다. 이때 계산 시간의 단축을 위해 2차원 축대칭, 전자 유체모델을 사용하였으며 포아송 방정식을 풀기 위해 Newton method를 사용하였다.
본 연구는 이온의 추출에 큰 영향을 미치는 전위의 분포 결과와 그로 인해 생기는 이온의 축 방향 분포변화가 기존의 전산해석 결과와 잘 일치함을 확인하였다.
이온 광학 시스템의 물리적 특성 분석을 통해 총 가속전압이 작아질수록 시스가 스크린 그리드 상류에 가까워지고 곡률이 작아졌으며, 이온들의 반경 방향 속력이 약해졌다. 그로 인해 빔렛 직경이 충분히 축소되지 않은 조건(VAcc = -100 V)에서는 이온이 가속 그리드 상류 표면에 직접적으로 충돌하였다.
가속 그리드 하류 전자의 역류를 방지하기 위해 고려해야 하는 안장점 전위의 분석을 통해 가속 그리드 전압이 –100 V인 조건에서는 전위 방벽을 제공하지 못해 전자의 역류가 발생할 수 있음을 확인했다.
위의 결과들을 통해 해당 그리드 형상과 플라즈마 상태 조건에서 가속 그리드의 인가전압이 –100 V보다 작아질 경우 이온 추력기의 수명을 단축시키고, 고장 등을 유발할 수 있음을 확인하였다. 이온 추력기의 작동시간에 따른 성능 변화와 최대 작동 수명을 확인하기 위해선 그리드 형상의 시간에 따른 변화를 파악하여야 한다. 따라서 그리드 침식모델을 추가하는 후속 연구를 진행할 예정이다.
Acknowledgments
본 연구는 한국항공우주연구원 주관의 기본사업 ‘심우주탐사용 고효율 이온 추진 핵심기술 연구’ 의 일환으로 수행되었습니다.
References
-
Lev, D., Myers, R. M., Lemmer, K. M., Kolbeck, J., Koizumi, H. and Polzin, K., “The technological and commercial expansion of electric propulsion,“ Acta Astronautica, 159, pp. 213-227, 2019.
[https://doi.org/10.1016/j.actaastro.2019.03.058]

-
Kim, H., Kim, S. K. and Won, S. H., “Current Status and Trends of Research and Development on Electric Thruster, Part I: Overseas,“ Journal of the Korean Society of Propulsion Engineers, 23(6), pp. 95-108, 2019.
[https://doi.org/10.6108/KSPE.2019.23.6.095]

-
Goebel, D. M., Katz, I. and Mikellides, I. G., “Fundamentals of electric propulsion, vol. 1,“ John Wiley & Sons, 2008.
[https://doi.org/10.1002/9780470436448]

-
Sengupta, A., Brophy, J. and Goodfellow, K., “Status of the extended life test of the deep space 1 flight spare ion engine after 30,000 hours of operation,“ In 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, pp. 4558, 2003.
[https://doi.org/10.2514/6.2003-4558]

-
Polk, J., Anderson, J., Brophy, J., Rawlin, V., Patterson, M., Sovey, J. and Hamley, J., “An overview of the results from an 8200 hour wear test of the NSTAR ion thruster,“ In 35th Joint Propulsion Conference and Exhibit, pp. 99-2446, 1999.
[https://doi.org/10.2514/6.1999-2446]

-
Anderson, J., Katz, I. and Goebel, D., “Numerical simulation of two-grid ion optics using a 3D code,“ In 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, pp. 2004-3782, 2004.
[https://doi.org/10.2514/6.2004-3782]

-
Herman, D. A., Soulas, G. C., Van Noord, J. L. and Patterson, M. J., “NASA's evolutionary xenon thruster (NEXT) long-duration test results,” Journal of Propulsion and Power, Vol. 28, No. 3, pp. 625-635, 2012.
[https://doi.org/10.2514/1.58442]

-
Smith, P., Bond, R., Latham, P. abd Fearn, D., “Grid design improvements and test philosophy for a cost-effective approach to ion thruster qualification,” In 31st Joint Propulsion Conference and Exhibit, p. 2922, 1995.
[https://doi.org/10.2514/6.1995-2922]

-
Yang, X., Wei, L., Jiang, W., Wang, S., He, Y., Li, H. and Ding, Y., “Start-up process of ion optics in ion thrusters,” Vacuum, 210, 111875, 2023.
[https://doi.org/10.1016/j.vacuum.2023.111875]

-
Capon, C. J., Brown, M., White, C., Scanlon, T. and Boyce, R. R., “pdFOAM: A PIC-DSMC code for near-Earth plasma-body interactions,” Computers & Fluids, 149, pp. 160-171, 2017.
[https://doi.org/10.1016/j.compfluid.2017.03.020]

-
Kang, S. H, “PIC-DSMC Simulation of a Hall Thruster Plume with Charge Exchange Effects Using pdFOAM,” Aerospace, 10(1), 44, 2023.
[https://doi.org/10.3390/aerospace10010044]

-
Cao, H., Chu, Y., Wang, E., Cao, Y., Xia, G. and Zhang, Z., “Numerical simulation study on barrel erosion of ion thruster accelerator grid,” Journal of Propulsion and Power, 31(6), pp. 1785-1792, 2015.
[https://doi.org/10.2514/1.B35717]

- Hastings, Daniel E., David Oh, and MASSACHUSETTS INST OF TECH CAMBRIDGE DEPT OF AERONAUTICS AND ASTRONAUTICS, “Computational Modeling of Expanding Plasma Plume in Space Using PIC–DSMC Algorithm,”. Final Technical Report for F49620-95-1-0319, 1997.
-
Han. Y. J., Guangqing, X. I. A., Bin, S. U. N., Chang, L. U., ZhanG, J. and SAETCHNIKOV, V. A., “Plasma transport simulation under different conditions and optimization analysis of dual-stage grid ion thruster,” Chinese Journal of Aeronautics, 2023.
[https://doi.org/10.1016/j.cja.2023.03.011]

-
Lingwei, Z., Yu, L., Zheng, W. and Junxue, R., “Numerical simulation of ion extraction through ion thruster optics,” Plasma Science and Technology, 12(1), 103, 2010.
[https://doi.org/10.1088/1009-0630/12/1/22]

- Farnell, C. C., “Performance and lifetime simulation of ion thruster optics,” PhD Thesis Colorado State University, Fort Collins, Colorado, 2007.
-
Williams, J., Goebel, D. and Wilbur, P., “Analytical model of electron backstreaming for ion thrusters,” In 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, p. 4560, 2003.
[https://doi.org/10.2514/6.2003-4560]