상변화가 있는 가변추력 액체로켓엔진의 재생냉각채널에 대한 수치해법 개발
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
상변화가 있는 가변추력 액체메탄엔진의 재생냉각채널을 해석하기 위해 Stefan문제의 엄밀해를 이용한 ANSYS UDF 프로그램이 개발되었다. 계산영역으로 NASA의 팽창식사이클 메탄엔진이 선택되었다. 연소실 압력은 5.86 MPa에서 상변화가 발생할 수 있는 1.172 MPa로 감소된다. 상변화모델과 Nu상관식들에 대해 비등열전달 결과가 검토되고 관련 문제점이 제시되었다.
Abstract
In order to analyze regenerative cooling channels of a variable thrust liquid methane engine with phase change, an ANSYS UDF(User-defined function) program was developed using the exact solution of the Stefan problem. The NASA CEV(Crew Exploration Vehicle) methane engine with the expander cycle was selected for the computational domain. The combustion chamber pressure is reduced from 5.86 MPa to 1.172 MPa where phase change can occur. The results of boiling heat transfer for phase change models and Nu correlations were investigated and the related problems were presented.
Keywords:
Throttleable Rocket Engine, Subcritical Pressure, Boiling Heat Transfer, Phase-Change Model, Two-Phase Flow키워드:
가변추력엔진, 아임계 압력, 비등 열전달, 상변화 모델, 2상유동1. 서 론
가변추력 액체로켓엔진은 행성착륙선, 우주랑데부에 사용하기 위해 1930년대 후반부터 연구되어져 왔는데, 최근 SpaceX의 Falcon 엔진에 의해 추력제어를 통해 재사용 로켓시스템에 활용될 수 있다는 것이 확인되었다[1]. 재사용 발사체는 1회용 시스템보다 시스템구성이 본질적으로 복잡해지지만 우주수송비용을 획기적으로 줄일 수 있어 로켓개발의 패러다임을 바꾼 것으로 평가받고 있어 많은 연구가 진행되고 있다. 이러한 로켓시스템에서 가변추력이 가능한 액체로켓엔진의 효율적인 설계기술은 매우 중요한 역할을 한다.
문헌조사에 의하면 가변추력 로켓엔진에 대해 몇몇 기초적인 연구가 수행되었다. Lee 등[2]은 달착륙선에 적용하기 위해서 200 N급의 하이브리드 로켓모터의 산화제 유량제어를 통해 연착륙 실험을 성공적으로 검증하였다. 그들은 약 40%의 산화제 유량조건에서 1 m/s의 착륙속도가 얻어지는 것을 확인하였다. Lee 등[3]은 와류형 분사기에서 정상조건의 10%와 20%로 연료유량이 낮아질 경우 화염형성이 불안정한 분무특성이 얻어지는 것을 보여 주었다. 또한, Kim 등[4]은 핀틀 분사기가 장착된 GCH4/LOx 연소기에서 연료의 유량이 100%, 60%, 20%로 변할 때, 저유량 즉 저추력 조건에서 연소특성이 현저하게 감소하는 것을 보여주었다. 이러한 결과들로부터 가변추력 로켓엔진을 개발하기 위해 연료유량변화에 따른 연소특성에 대한 많은 이해가 필요하다는 것을 알 수 있다. 또한, 로켓연소기에 재생냉각이 사용될 경우 위와 같은 연소환경 변화에 따른 냉각채널의 열유동특징을 자세히 이해할 필요가 있다.
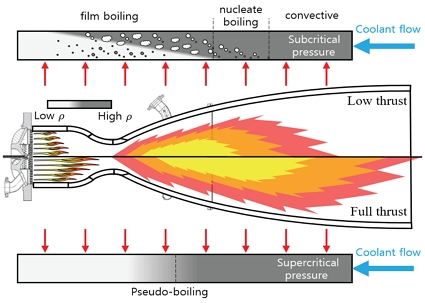
Fig. 1은 가변추력 메탄엔진의 추력단계에 따른 냉각채널의 작동압력변화와 이에 따른 채널의 유동특징을 보여준다. 메탄은 임계온도가 약 190 K으로 낮은 조건이다. 따라서 대부분의 로켓엔진 냉각채널에서 임계온도 이상으로 가열되기 때문에 열역학적 물성치가 매우 급격하게 변화하게 된다. 기존의 최대 추력단계에서는 냉각채널이 메탄의 임계압력인 약 4.6 MPa보다 높은 초임계 압력조건에서 작동된다. 물성치의 불연속적인 변화가 나타나지 않고 표면장력이 없기 때문에 단상의 대류 열전달로 가정할 수 있다. 그러나 임계온도 근처에서 비열이 급증하는 가성비등(Pseudo boiling)이 발생하여 열전달의 크기를 변화시킬 수 있다. 이런 열전달조건에 대해서는 보편적인 Dittus-Boelter 상관식[5]을 활용하기 어렵다. 최근 Pizzarelli[6]는 급격한 물성치변화가 냉각채널 단면에 2차유동을 초래함을 보여주고 가성비등 현상을 고려하는 열전달 상관식을 개발하였다.
로켓엔진의 추력을 조절하기 위해 연료유량 및 연소실 압력을 감소시키면 재생냉각채널의 작동압력 또한 아임계 압력으로 낮아질 수 있다. 이때 냉각채널 내부는 2상유동이 될 수 있다. 냉각제의 상변화 즉 비등이 발생할 때 핵비등(Nucleate boiling)의 형태는 열전달을 향상시키지만, 기화된 냉각제(메탄)가 연소실 쪽 채널벽면을 film형태로 채우는 막비등(Film boiling)이 발생하면 기체의 단열효과로 인해 열전달 저하가 발생된다[7]. 문헌조사에 의하면 Song 등[8]과 Liang 등[9]이 비등열전달을 고려한 냉각채널해석 연구를 수행하였지만 물리적인 상황의 복잡성으로 인해 많은 보완이 필요한 상태이다.
본 연구에서는 재생냉각을 이용하는 가변추력 액체로켓엔진의 추력성능 및 냉각설계를 위한 해석코드를 개발하기 위한 기초연구가 수행되었다. 설계관점에서 3차원 복합열전달 해석은 비효율적이기 때문에 2차원 축대칭 연소해석을 수행하고 채널은 열전달 및 마찰저항 상관식을 이용하여 열유동의 변화를 고려한다. 냉각채널과 연소실의 연결은 열저항법을 이용하고, 추가연구가 필요하지만 냉각채널과 연소실은 로켓엔진의 팽창식사이클을 고려하여 열적으로 연결된다. 또한, Stefan문제의 엄밀해를 이용한 아임계 냉각채널의 열해석 방법이 제안된다. 이러한 해석법에 기반하여 열전달 상관식들의 예측성과 문제점을 검토하고자 한다. 해석코드는 다양한 활용성을 위해 상용코드인 ANSYS Fluent를 활용하고 UDF(User-defined function)를 통해 새로운 냉각채널 해석법이 구현된다.
2. 수치해석 방법
2.1 해석영역
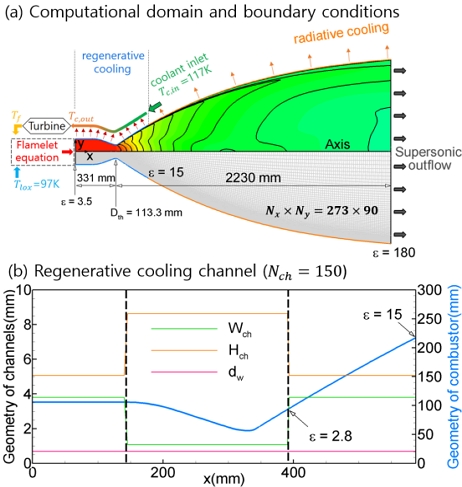
해석영역으로 25,000 lbf급인 NASA의 팽창식사이클 메탄엔진(CEV)[10]이 선택되었다. Fig. 2에 추력실 형상과 재생냉각 채널 형상을 나타내었다. 냉각채널 수는 150개로 고정되고 노즐목 부분을 효과적으로 냉각하기 위해 노즐팽창비 ϵ = 15까지 Fig. 2(b)와 같이 채널단면 형상비가 변경된다. 여기서 채널 폭 Wch, 높이 Hch, 내벽두께 dw를 나타낸다. 추력조건의 변화는 연소실 압력경계조건 변화를 이용하였다. 분사기들의 혼합/연소가 종료된 화학평형의 결과에 따른 온도와 생성물의 조성이 연소실 입구조건으로 설정되었다. 100% 추력단계의 전압력(Total pressure) 5.86 MPa과 연료-산화제 혼합비 3.5에서 연소가스온도 3601.6 K이 적용되었다. 노즐 출구는 supersonic outlet 경계조건, 모든 벽에는 no-slip 조건이 적용되었다. 냉각채널은 117 K의 메탄이 유입되는 조건이다.
면적비가 큰 로켓엔진은 노즐부가 크기 때문에 여러 종류의 냉각방법이 복합적으로 사용될 수 있다. CEV엔진은 Fig. 2와 같이 재생냉각과 노즐면적비 15 이상에서 복사냉각이 사용되었다. 복사냉각을 위한 경계조건은 이 적용되었다. 노즐벽면 재질은 Niobium합금으로 가정하여 ϵr = 0.87이고 Stefan Boltzmann 상수 이다.
2.2 노즐유동 해석을 위한 지배방정식
2차원 축대칭의 압축성 난류유동과 에너지에 대한 지배방정식은 다음과 같다.
| (1) |
| (2) |
| (3) |
여기서 ρ, ui, p, μ, h, λ, cp, T, , μt, Pr t은 각각 밀도, 속도 성분, 압력, 점성계수, 엔탈피, 열전도계수, 정압비열, 온도, 레이놀즈응력, 와점성계수와 난류 프란틀 수 Pr t = 0.85이다.
액체로켓엔진 노즐해석에는 벽면 마찰손실과 열전달이 벽 근처 난류유동에 큰 영향을 받기 때문에 점성저층 해석이 가능한 Low-Reynolds Shear Stress Transport(SST) k - ω 모델이 선택되었다. 난류 운동에너지 k와 난류에너지 소산율 ω의 수송 방정식들은 다음과 같다.
| (4) |
| (5) |
여기서 Γ, P, Y, D는 유효확산계수(Effective diffusivity), 생성항, 소산항, 교차확산항을 나타낸다. 모델의 상세한 설명은 참고문헌[11]에서 확인할 수 있다.
2.3 연소모델
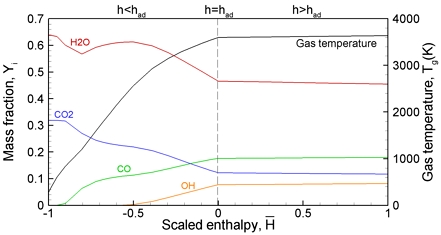
액체로켓엔진은 수 백 개의 분사기에 의한 유동혼합이 이루어지고 연소반응이 발생하지만 상세한 유동구조기반의 설계해석은 비효율적이다. 연소실 내부는 일정한 혼합비 O/F=3.5인 조건에서 혼합분율의 섭동 과 스칼라소산율 인 조건에 대해 화염편모델 (Flamelet model)이 적용된다. 설계목적을 위해 화염편모델의 방정식들은 단열조건에서 본 해석에 앞서 별도로 해석되고 얻어진 화학종, 온도와 밀도 등이 lookup table로 저장된다. 혼합비가 고정되어 혼합분율 은 일정하고 혼합분율과 스칼라소산율이 0이기 때문에 본 해석에서는 연소반응의 결과는 엔탈피값을 변수로 lookup table로부터 보간되어 얻어진다. 일반적인 로켓노즐에서는 연료온도 증가에 의해 연소가스의 엔탈피가 증가하고 노즐냉각에 의해 벽면 근처의 엔탈피가 감소한다. 이러한 상황을 고려하기 위해 엔탈피의 최대값과 최소값을 선택하여 scaled 엔탈피 를 lookup table에 반영하였다. 여기서 단열엔탈피는 , hox는 산화제 엔탈피, hf는 연료엔탈피이다. hm은 h ≧ had일 때 0.01had, h < had일 때 0.95had이다. 범위를 25등분하여 lookup table을 생성하였다. Fig. 3은 CEV엔진 조건에 대한 lookup table을 나타낸다. 연소가스온도 범위는 최소 196.7 K에서 최대 3607.6 K까지로 로켓연소기에서 벽면냉각, 노즐팽창 및 연소반응에 의해서 얻어질 수 있는 온도범위를 충분히 포함해서 생성된 것이 확인된다.
2.4 액체메탄 물성치 계산
냉각채널을 흐르는 추진제의 열역학적 물성치는 저탄화수소의 메탄과 고탄화수소의 항공유에서 모두 적용 가능한 3차 상태방정식인 Redlich-Kwong-Peng-Robinson EoS가 사용되었다[12].
| (6) |
| (7) |
| (8) |
| (9) |
여기서 A = aα(T)p/(R2T2)이고 B = bp/(RT)이다. 본 연구에서는 정확성이 개선된 Zhu 등[12]의 을 사용하였다. 실제유체 상태방정식을 통해서 밀도, 정압비열, 엔탈피가 얻어지고 점성계수 및 열전도계수는 Chung의 모델[13]으로 얻어졌다. 열역학적 물성치들의 자세한 식은 참고문헌을 통해서 확인할 수 있다[12,14]. Eq. 6의 해는 초임계 압력조건에서 하나의 실근, 임계 압력조건에서는 3개의 실근을 가진다. 이들 중 가장 큰 Zmax는 기체의 압축인자 Zv로 사용되고 가장 작은 Zmin은 액체의 압축인자 Zl로 사용된다. 중간 값은 물리적 의미가 없다. 아임계 압력의 냉각채널에서 2상유동 상태의 기체-액체 판단은 Gibbs 자유에너지의 부호를 통해 결정된다[14].
| (10) |
여기서 dg > 0이면 액체이고 ρl = p/ZlRT로 밀도가 계산되고 dg < 0이면 기체이고 ρv = p/ZvRT가 사용된다.
아임계 압력조건의 재생냉각채널 내부에서 추진제의 상변화를 고려하기위해 추진제 포화물성치들(Saturated properties)이 요구된다. 표면장력 σ과 포화온도 Tsat는 NIST 데이터를 선형보간하여 사용된다. 메탄의 기화잠열(Latent heat of evaporation) hlv은 Majer and Svoboda[15]의 hlv = 10.11e0.22Tr(1-Tr)0.388으로 계산되었다. 환산온도(Reduced temperature)는 Tr = T/Tcr이다.
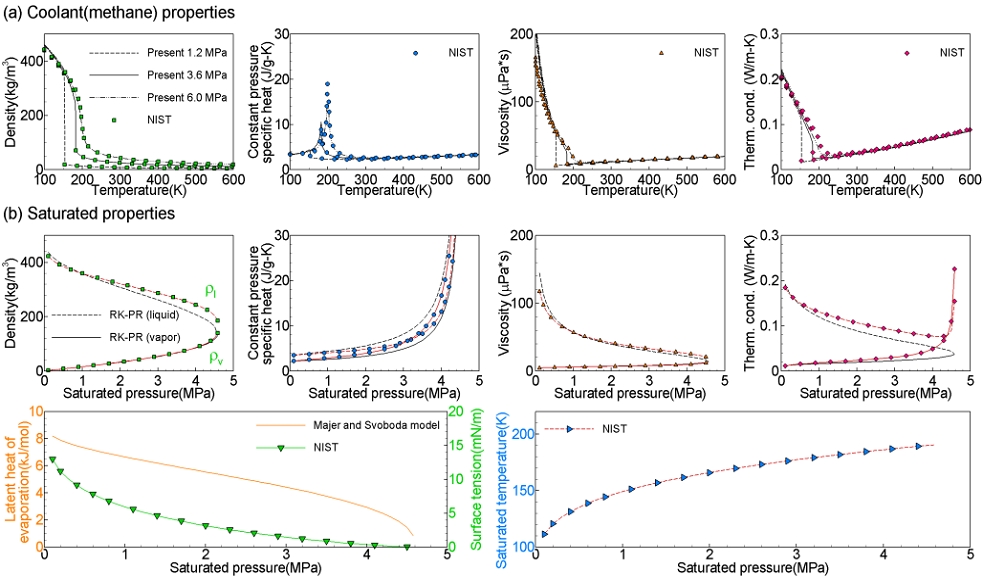
Fig. 4는 메탄에 대한 물성치 결과를 나타낸 것이다. 100% 추력단계에서 연소실 압력 6 MPa일 때, 60% 추력단계의 3.6 MPa과 20% 추력단계의 1.2 MPa을 가변추력 조건으로 설정하여 얻어진 밀도, 비열계수, 점성계수, 열전도계수가 NIST 데이터와 함께 Fig. 4(a)에서 비교되었다. 두 가지 가변추력을 가정한 아임계 압력조건에서도 잘 예측되는 것이 확인된다. Fig. 4(b)의 포화물성치는 상변화온도는 잘 예측하였지만 임계압력 4.6 MPa에 가까워질수록 RK-PR EoS가 큰 오차를 보이는 것이 확인된다. 따라서 현재 연구에서는 포화물성치의 1차원적인 특성을 고려하여 NIST 데이터를 선형보간하여 사용하였다.
2.5 복합열전달 해석을 위한 열저항법
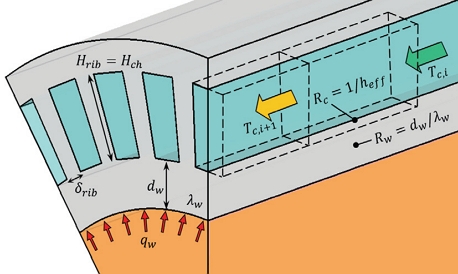
냉각채널 및 연소실 간의 복합열전달 해석은 열저항법으로 처리된다. 열저항 기반의 냉각채널 해석법의 개략도를 Fig. 5에 나타내었다. Rw와 Rc는 전도/대류 열전달의 열저항을 나타낸다. 고온가스유동을 CFD로 해석하여 얻어진 벽면온도로부터 벽면열유속이 경계조건으로 적용된다.
| (11) |
여기서 하첨자 w와 c는 연소실벽과 냉각제(메탄)를 나타낸다. 연소기 벽을 구성하는 구리합금과 스테인리스 스틸의 열전도계수 λw는 온도 변화에 대해 실험적으로 얻어진 값을 선형보간하여 얻어진다. 유효열전달 계수는 핀효율 ηfin을 고려하여 heff = ηfinhcv이고, 열전달계수는 Dittus-Boelter[5]상관식 등 Nu상관식으로 얻어진다.
| (12) |
여기서, dh는 수력직경, Rec = ρcucdh/μc, Prc = μccp,c/λc이다. 재생냉각채널 리브(Rib) 형상에 의한 핀효율 ηfin는 다음과 같다[16].
| (13) |
| (14) |
여기서 채널 리브 높이는 Hrib = Hch이고, δrib은 두께를 나타낸다. 냉각채널이 모두 연결된 하나의 채널이면 δrib = 0이고 핀효율 ηfin은 1이다.
재생냉각 채널유로에서의 메탄의 온도증가는 로 계산되어진다. 총 압력손실 식 의 마찰계수 Cf는 국부적인 Re와 dh으로 무차원화된 표면거칠기를 통해 Idelchik[17]의 테이블을 보간하여 사용된다. Δx는 격자크기이다.
2.6 수치해석 절차
ANSYS Fluent[11]를 사용하여 해석이 수행되고 열저항법에 기반한 재생냉각 해석은 UDF로 구현되었다. SIMPLEC 알고리즘이 선택되었고 대류항 차분법은 2차 풍상차분법이 적용되고 잔차 10-6을 수렴조건으로 선택하였다. 냉각채널과 연소실이 로켓엔진 사이클을 기반으로 열적으로 연계되기 때문에 냉각채널 출구온도 Tc,out가 일정해질 때까지 반복계산이 수행되었다.
2.7 수치해석방법 검증
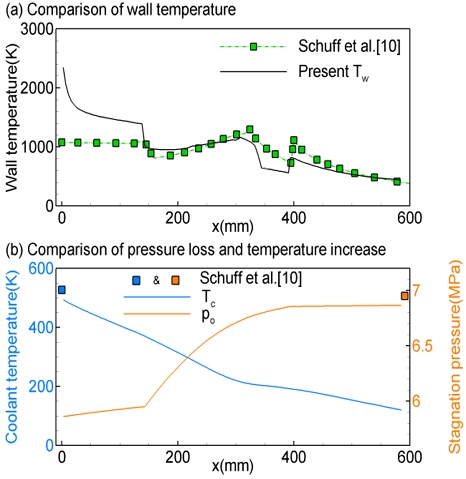
열저항법을 기반으로 로켓엔진의 팽창식 사이클을 고려하는 수치해석 방법의 타당성 검토가 수행되었다. NASA CEV 엔진의 100% 추력단계에 대해 Schuff 등[10]의 벽면온도, 메탄온도, 정체압력 변화를 Fig. 6에 나타내었다. Fig. 2(b)에서 볼 수 있듯이 CEV 엔진은 효율적인 냉각을 위해 x = 150 ~ 400 mm 영역에서 채널단면 형상비 Hch/Wch를 1.25에서 9로 증가시킨 재생냉각채널을 이용한다. 따라서 Fig. 6(a)를 보면, 일반적인 노즐 벽면온도분포와 다르게 노즐목 부분에서 온도가 낮아진 결과를 보여주고 있다. 또한, 전체적인 온도분포는 Schuff 등[10]의 결과와 비슷하지만 연료분사면 근처에서 큰 차이를 보이고 있다. Schuff 등[10]의 결과는 Bartz 상관식의 연소실 벽면열유속을 경계조건으로 재생냉각이 이루어질 때 벽면온도이기 때문에 연소실의 유속과 온도가 일정한 조건의 결과이다. 그렇지만 현재연구는 벽면근처에서 경계층이 발달하는 유동변화가 CFD에 의해서 해석된 결과이기 때문에 연소실 입구근처에서 벽면온도가 다르게 나타나고 있다. 분사기가 고려되지 않고 연소된 가스가 균일한 속도분포로 유입되는 조건이기 때문에 x=0 mm에서 고온이 나타난다. 실제 연소기에서는 연소실 벽면으로부터 분사기가 일정한 간격으로 떨어져 있기 때문에 현재결과보다는 벽면온도가 낮게 나타날 것이다. 이러한 벽면온도분포는 평형조건으로 연소실해석을 수행하는 경우 일반적인 특성으로 판단된다[18]. Fig. 6(b)에서 보면, 현재연구의 차압과 온도증가는 1.00 MPa 및 377 K으로 Schuff 등[10]의 1.09 MPa 및 409 K에 비해 약 8% 작게 얻어지고 있다. 일반적으로 Bartz 상관식이 열유속을 약 10% 크게 예측하는 것으로 알려져 있기 때문에 현재해석 결과는 타당한 범위내로 판단된다[18].
3. 결과 및 토의
열저항법을 이용한 아임계 가변추력 메탄재생냉각채널 해석법에 CFD적인 상변화모델을 도입하고 Nu상관식에 대한 분석이 수행되었다.
3.1 상변화 모델 적용
아임계 압력조건의 재생냉각채널에서는 냉각제의 증발현상이 발생할 수 있다. Lee 등[19]은 증발률을 로 제안하였다. 여기서 α는 기공률(Void of fraction)이다. 제안된 모델은 유동조건에 따라 수치계수 γ(1/s)를 다르게 (약 102∼107의 범위) 설정해야 하는 문제점을 가지고 있다. 재생냉각 채널에 이 식을 적용할 경우 단면형상의 변화와 추력변화에 따라 적절한 γ를 선택하기 어려운 점이 있다. Rattner와 Garimella[20]는 γ를 제거하고 시간증분양을 도입하여 로 비정상해석을 제안하였다. Δt는 시간증분인데 너무 크면 해석이 불안정해지고 부정확하기 때문에 Δt ≦ 0.25ρcpΔx/λ로 제한된다. 현재조건에서는 steady 해석에 비해 격자수를 약 104배로 늘리거나 Δt를 매우 작게 설정하여 unsteady 해석을 진행해야 한다. 또한, 재생냉각채널에서 열저항법과 같은 형태로 열전달이 해석될 경우 Tc - Tsat에 비례하는 상변화 모델들은 냉각제의 온도가 포화온도로 유지되지 않는 비물리적인 현상이 나타나는 문제점이 있다. 따라서 냉각채널의 열전달 및 상변화 현상을 3차원적으로 다루지 않는 경우 위와 같은 상변화모델은 적합하지 않은 것으로 판단된다.
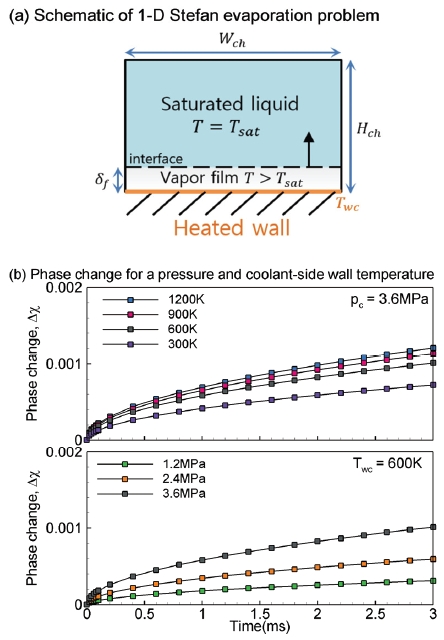
열저항법과 같이 1차원적인 열전달 평형관계를 이용하여 상변화해석이 이루어질 경우 일반적인 CFD해석과 다른 형태가 적용되어야 한다. 본 연구에서는 유체의 상(Phase)의 경계변화를 묘사하는 Stefan문제의 해를 이용하여 재생냉각채널의 열해석을 수행하는 방법을 제안한다. 상변화가 있을 때 냉각채널의 개략도는 Fig. 7(a)와 같다. 연소실벽으로부터 전달되는 열유속이 냉각제에 모두 흡수된다고 가정한다. 가열벽에서 증발이 발생되면 Stefan문제의 해로부터 기체층의 필름두께 δf를 얻을 수 있다.
| (15) |
| (16) |
여기서 t는 체류시간, ϵ은 초월방정식(Transcendental equation)의 해이고 Φ는 이다. Twc는 연소실과 인접한 냉각채널의 내벽온도이고, 초월방정식의 해 ϵ은 이분법에 의해 수치적으로 얻어졌다.
Stefan 엄밀해를 구하는 Eq. 15와 Eq. 16에서 포화상태의 메탄 물성치들과 증발잠열, 포화온도는 Fig. 4(b)와 같이 모두 포화압력에 의해 결정된다. 그러면 필름두께는 의 상수배인 로 표현된다. 따라서 상변화률에 영향을 주는 상수 C는 오직 pc와 Twc에 의한 함수임을 알 수 있다. 각 냉각채널단면에서 Wch는 일정하기 때문에 상변화률을 나타내는 기공률의 변화는 필름 두께와 채널높이 비인 Δα = δf/Hch로 얻어진다. 증기의 질량분율을 나타내는 증기건도(vapor quality)는 χ = ρvα/[ρvα + ρl(1 - α)]에 의해 계산된다.
Fig. 7(b)는 가변추력 재생냉각채널의 주요 해석조건인 채널내벽온도 Twc와 냉각채널 압력 pc에서 시간에 따른 상변화률 Δχ을 나타낸다. 시간범위는 현재 연구의 격자크기와 유속에 의해서 결정되는 각 셀의 체류시간 중 최대인 3 ms까지로 나타내었다. Fig. 7(b)를 보면 Twc가 높아질수록 Δχ가 커지고 있지만 Twc가 낮은 조건에서 벽온도증가에 따른 Δχ영향이 Twc가 높을 때 보다 크게 나타나고 있다. 이것은 ϵ이 ln(Φ)에 거의 선형적으로 비례하는 형태로 얻어지기 때문이다. 또한 동일한 Twc에서 추력단계가 높아져 pc가 증가하는 경우에도 Δχ가 증가한다.
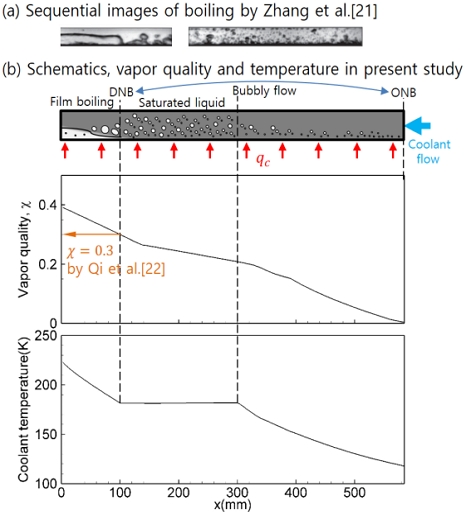
Stefan문제의 해를 이용한 재생냉각채널의 열해석 방법을 60%의 낮은 추력단계의 메탄 엔진에 대해 적용하였다. 먼저 비등현상을 고려하지 않는 일반적인 Dittus-Boelter 상관식[5]을 적용하였다. 60% 추력단계의 연소기 입구조건은 3.52 MPa의 압력과 화염온도 3528.6 K 그리고 냉각유량 19.2 kg/s가 적용되었다. Fig. 8은 60%의 추력단계로 가정된 CEV 엔진에 대해 현재방법을 적용한 해석결과와 비등유동의 개략도 및 실험이미지를 나타낸다. Fig. 8(a)는 비등이 발생된 채널의 실험 이미지 이다[21]. 핵비등으로 인해 발생한 버블은 점차 연속적으로 존재하게 되어 국부적인 열전달 계수가 급격하게 감소하는 증기로 덮인 영역이 발생하는 특징을 보인다. 이러한 지점을 DNB(Departure of nucleate boiling)로 표현하고 열유속이 갑작스럽게 감소하기 때문에 열유속의 임계점 CHF(Critical heat flux)로 정의한다. 현재 해석에는 비등 열전달을 위한 상관식이 적용되지 않았기 때문에 이러한 열유속의 변화는 확인되지 않는 해석결과이다. DNB 또는 CHF의 위치는 실험결과를 이용한다. 문헌조사에 의하면 비등 수 Bo ≈ 0.1와 증기건도 χ = 0.3 또는 χ = 0.6 위치를 주로 사용한다. Qi 등[22]은 열전달이 급격하게 감소되는 특징이 나타나는 χ = 0.3을 임계 열유속으로 설정하고 열전달 상관식을 제시하였다. Fig. 8에서는 χ = 0.3 기준을 사용하여 해석되었지만 CHF 기준은 어떤 Nu상관식을 선택하느냐에 따라 달라질 수 있다. Fig. 8(b)는 해석결과와 이를 표현하는 개략도이다. 냉각채널의 벽온도가 항상 포화온도보다 높아 전체 영역에서 비등이 일어나는 결과가 얻어지고 증기건도는 지속적으로 증가하여 출구에서 약 40%에 도달한다. 포화상 구간에서의 온도가 포화온도로 유지되고 상변화의 진행이 적절하게 얻어지는 것으로 보아 현재 연구의 상변화 해석방법이 타당하다고 판단된다.
3.2 Nu상관식 비교
지금까지 메탄액체로켓엔진 냉각채널 해석을 위해 개발된 열전달 상관식들은 다음과 같다. Pizzarelli[23]는 초임계 압력조건에서 메탄의 가성비등 현상에 의한 유동장 변화 및 열전달 저하를 고려하기 위해 CFD해석 결과들을 기반으로 Nu상관식을 제안하였다.
| (17) |
| (18) |
아임계 압력조건에서는 핵비등과 막비등의 열전달 특성이 Nu상관식에 고려되어야한다. Eq. 17과 Eq. 18는 비등열전달 특성을 고려하여 개발된 상관식은 아니지만 채널 벽면에서의 메탄의 물성치의 차이를 이용하여 유동장 변화에 의한 열전달 저하를 예측하기 때문에 비교대상으로 선택하였다.
Song 등[8]과 Liang 등[9]은 증기건도 χ = 0.6을 기준으로 다음을 제안하였다. 이들은 핵비등 영역의 상관식인 Eq. 19은 모두 동일하게 사용하였고, 막비등 구간의 상관식은 각각 Eq. 20과 Eq. 21로 다르게 제시하였다.
| (19) |
| (20) |
(Film boiling by Song et al.[8])
| (21) |
(Film boiling by Liang et al.[9])
여기서 비등 수 Bo = q/(Ghlv), Weber 수 We = G2dh/(ρlσ), 무차원 압력 수 , Lockhart-Martinelli 수 , 2상유동 레이놀즈 수 , 무차원 변수 이다. G는 질량 플럭스, g는 중력상수 9.81 m/s2이다.
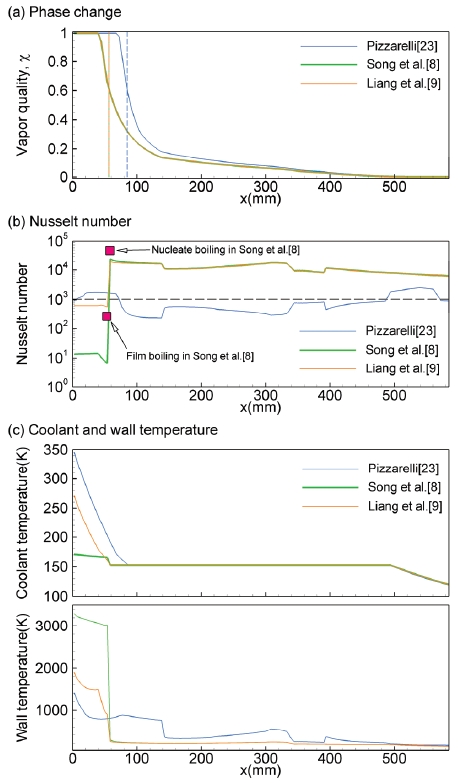
가변추력 단계 20%에서 연소실 압력 및 화염온도는 각각 1.172 MPa, 3370 K으로 냉각채널 유량은 6.4 kg/s로 감소된다. Fig. 9는 20% 추력단계에 Pizzarelli[23], Song 등[8], Liang 등[9]의 상관식을 적용해서 얻어진 증기건도, Nu, 메탄온도, 벽면온도를 보여준다. Fig. 9(a)에서 보면Pizzarelli[23] 상관식의 경우 가장 빠르게 냉각제증발을 보여주고 있다. 이것은 Fig. 9(c)에서 확인할 수 있듯이 냉각채널 벽면의 온도가 가장 높게 얻어지기 때문이다. Song 등[8]과 Liang 등[9]의 상관식은 거의 비슷한 증기건도 분포를 보여주고 있다. Fig. 9(b)는 3가지 상관식에 대한 Nu분포를 나타낸다. 로켓엔진 형상이 다르지만 Song 등[8]이 제시한 핵비등(Nu = 47700)과 막비등(Nu = 262)조건의 Nu를 비교하면 비슷한 값을 보여주고 있다. Pizzerelli[23] 상관식은 냉각제의 상변화 특성에 무관하게 Nu의 변화가 나타나고 있지만 Song 등[8]과 Liang 등[9]의 상관식은 χ < 0.6의 핵비등 영역에서 Nu가 104정도로 큰 값을 가지고 막비등(χ ≥ 0.6)이 발생하면서 Nu가 크게 감소되는 형태를 보여주고 있다. 이러한 변화는 Nu 상관식의 특성에 기인하는 것으로 판단된다. Fig. 9(c)에서 냉각채널에 유입된 액체메탄은 열전달에 의해서 핵비등이 발생하며 포화온도 Tsat에 도달하고 이러한 상변화는 기화잠열 hlv로 인해 Tc가 Tsat로 유지되게 한다. 비등열전달을 고려하지 않는 Pizzerelli[23] 상관식도 Stefan문제의 해를 이용하는 동일한 상변화모델이 적용되어 Tc가 Tsat로 유지되고 있다. 막비등 구간에서는 Nu 크기에 따라 냉각제온도와 벽온도가 다르게 나타나고 있다. 냉각채널 벽온도는 Pizzerelli[23] 상관식의 경우 1,400 K, Liang 등[9] 상관식은 1,700 K, Song 등[8]의 상관식은 3250 K로 나타났다. 막비등에 의한 열전달 저하를 고려하더라도 벽면온도 3,000 K 이상의 결과는 비물리적인 결과로 연소실 입구온도와 거의 비슷하다. Eq. 20과 21에서 막비등관련 열전달이 적절하게 고려되지 않음을 나타내는 것이다. 이러한 결과로부터 재생냉각채널의 막비등과 관련해서 현재까지의 연구들은 매우 제한적으로 이용이 가능하고 향후 Nu상관식에 대해 많은 연구가 필요함을 알 수 있다. 현재연구에서 개발된 프로그램은 그러한 재생냉각채널 열해석 및 Nu상관식 개발에 기여할 수 있을 것으로 기대된다.
4. 결 론
상변화 및 비등열전달이 고려된 가변추력 액체메탄엔진의 재생냉각채널 해석을 위해 Stefan문제의 엄밀해를 이용한 ANSYS fluent의 UDF (User-defined function)코드가 개발되었다. NASA의 25,000 lbf급 팽창식사이클 메탄엔진에 대해 100% 추력단계의 5.86 MPa 초임계 압력에서 20% 추력단계 1.172 MPa의 아임계 압력으로 변하는 조건으로 설정하였다. 냉각채널의 메탄 물성치는 RK-PR 상태방정식을 통해 얻어지고 비등조건에서 포화 물성치들은 NIST 데이터를 선형 보간하여 사용하였다.
Stefan문제의 엄밀해를 이용한 열해석방법에 의한 메탄의 상변화특성과 온도변화가 실험과 비교를 통해 확인되었다. Song 등[8], Liang 등[9], Pizzarelli[23]의 3개의 Nu상관식이 막비등이 있는 조건에서 열해석특성이 비교검토되었다. 비등현상이 고려되지 않은 Pizzarelli[23] 상관식은 핵비등과 막비등에 둔감한 Nu변화를 보여주었고, Song 등[8]과 Liang 등[9]의 상관식에서는 핵비등에 의한 열전달 향상과 막비등에 의한 Nu감소를 잘 나타내었다. 그렇지만 연소실온도에 대한 정량적인 분석이 향후 재검토될 필요가 있음을 보여주었다.
이러한 결과를 통해 UDF코드를 이용한 가변추력 메탄엔진의 재생냉각채널에 대한 핵비등 및 막비등에 열해석의 가능성을 확인하였고 추가적인 연구를 통해 로켓열설계를 위한 유용한 도구로 활용이 가능할 것으로 판단된다.
Nomenclature
| Aw : | surface area of combustor chamber wall |
| Bo : | boiling number |
| cp,v : | constant pressure specific heat of vapor |
| dg : | Gibbs free energy |
| erf : | error function |
| : | coolant mass flow rate |
| : | two-phase Reynolds number |
| Tow : | outer wall temperature |
| Tc : | coolant temperature |
| t : | time |
| X : | Lockhart-Martinelli number |
| Z : | compressibility factor |
| α : | void fraction |
| δf : | film thickness |
| λv : | thermal conductivity of vapor |
| ρv : | density of vapor |
| σ : | surface tension |
| χ : | vapor quality |
Acknowledgments
이 성과는 정부의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2016R1D1A1B02012446).
References
-
Casiano, M.J., Hulka, J.R. and Yang, V., “Liquid-Propellant Rocket Engine Throttling: A Comprehensive Review,” Journal of Propulsion and Power, Vol. 26, No. 5, pp. 897-923, 2010.
[https://doi.org/10.2514/1.49791]

-
Lee, D., Han, S. and Moon, H., “Development of 200 N-class throttleable hybrid rocket motor for lunar module application,” FirePhysChem, Vol. 1, pp. 251-259, 2021.
[https://doi.org/10.1016/j.fpc.2021.11.014]

-
Lee, W., Hwang, D., Ahn, K. and Yoon, Y., “Spray Characteristics of Effervescent Swirl Injectors for Variable Thrust,” Journal of the Korean Society of Propulsion Engineers, Vol. 23, No. 2, pp. 1-12, 2019.
[https://doi.org/10.6108/KSPE.2019.23.2.001]

-
Kim, D.H., Heo, S., Kim, I., Hwang, D., Kang, C., Lee, S., Ahn, K. and Yoon, Y., “High Pressure Spray and Combustion Characteristics of Throttleable Pintle Injector,” Journal of the Korean Society of Propulsion Engineers, Vol. 26, No. 2, pp. 60-71, 2022.
[https://doi.org/10.6108/KSPE.2022.26.2.060]

-
Dittus, F.W. and Boelter, L.K.M., “Heat Transfer in Automobile Radiators of the Tubular Type,” International Communications in Heat and Mass Transfer, Vol. 12, pp. 3-22, 1985.
[https://doi.org/10.1016/0735-1933(85)90003-X]

-
Pizzarelli, M., “The Status of the Research on the Heat Transfer Deterioration in Supercritical Fluids: A Review,” International Communications in Heat and Mass Transfer, Vol. 95, pp. 132-138, 2018.
[https://doi.org/10.1016/j.icheatmasstransfer.2018.04.006]

-
Ghiaasiaan, S.M., Two-Phase Flow, Boiling and Condensation: In Conventional and Miniature Systems, 1st Ed., Cambridge Univ. Press., U.K., 2007.
[https://doi.org/10.1017/CBO9780511619410]

-
Song, J., Liang, T., Li, Q., Cheng, P., Zhang, D., Cui, P. and Sun, J., “Study on the Heat Transfer Characteristics of Regenerative Cooling for LOX/LCH4 Variable Thrust Rocket Engine,” Case Studies in Thermal Engineering, Vol. 28, 101664, 2021.
[https://doi.org/10.1016/j.csite.2021.101664]

-
Liang, T., Song, J., Li, Q., Cui, P., Cheng, P. and Chen, L., “System Scheme Design of Electric Expander Cycle for LOX/LCH4 Variable Thrust Liquid Rocket Engine,” Acta Astronautica, Vol. 186, pp. 451-464 2021.
[https://doi.org/10.1016/j.actaastro.2021.06.015]

-
Schuff, R., Maier, M., Sindiy, O., Ulrich, C. and Fugger, S., “Intergrated Modeling and Analysis for a LOX/Methane Expander Cycle Engine: Focusing on Regenerative Cooling Jacket Design,” 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, California, AIAA 2006-4534, July, 2006.
[https://doi.org/10.2514/6.2006-4534]

- ANSYS FLUENT 12.0 Theory Guide.
-
Zhu, H., Battistoni, M., Ningegowda, B.M., Rahantamialisoa, F.N.Z., Yue, Z., Wang, H. and Yao, M., “Thermodynamic Modeling of Trans/Supercritical Fuel Sprays in Internal Combustion Engines Based on a Generalized Cubic Equation of State,” Fuel, Vol. 307, 121894, 2022.
[https://doi.org/10.1016/j.fuel.2021.121894]

-
Chung, T.-H., Ajlan, M., Lee, L.L. and Starling, K.E., “Generalized Multiparameter Correlation for Nonpolar and Polar Fluid Transport Properties,” Industrial and Engineering Chemistry Research, Vol. 27, pp. 671-679, 1988.
[https://doi.org/10.1021/ie00076a024]

-
Trummler, T., Glatzle, M., Doehring, A., Urban, N. and Klein, M., “Thermodynamic Modeling for Numerical Simulations Based on the Generalized Cubic Equation of State,” Physics of Fluids, Vol. 34, 116126, 2022.
[https://doi.org/10.1063/5.0122277]

- Majer, V. and Svoboda, V., Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation, 1st Ed., Blackwell Scientific Publications, Oxford, U.K., 1985.
-
Kim, S.-K., Joh, M., Choi, H.S. and Park, T.S., “Effective Modeling of Conjugate Heat Transfer and Hydraulics for the Regenerative Cooling Design of Kerosene Rocket Engines,” Numerical Heat Transfer, Part A, Vol. 66, pp. 863-883, 2014.
[https://doi.org/10.1080/10407782.2014.892396]

- Idelchik, I.E., Handbook of Hydraulic Resistance, 3rd Ed., Begell House, New York, U.S.A., 1996.
-
Song, J. and Sun, B., “Coupled Numerical Simulation of Combustion and Regenerative Cooling in LOX/Methane Rocket Engines,” Applied Thermal Engineering, Vol. 106, pp. 762-773, 2016.
[https://doi.org/10.1016/j.applthermaleng.2016.05.130]

- Lee, W.H., A Pressure Iteration Scheme for Two-Phase Flow Modeling, in: Multiphase Transport Fundamentals, Hemisphere Pub., Washington DC, U.S.A, 1980.
-
Rattner, A.S. and Garimella, S., “Simple Mechanistically Consistent Formulation for Volume-of-Fluid Based Computations of Condensing Flows,” ASME Journal of heat Transfer, Vol. 136, 071501, 2014.
[https://doi.org/10.1115/1.4026808]

-
Zhang, H., Mudawar, I. and Hasan, M.M., “Flow Boiling CHF in Microgravity,” International Journal of heat and Mass Transfer, Vol. 48, No. 15, pp. 3107-3118, 2005.
[https://doi.org/10.1016/j.ijheatmasstransfer.2005.02.015]

-
Qi, S.L., Zhang, P., Wang, R.Z. and Xu, L.X., “Flow Boiling of Liquid Nitrogen in Micro-Tubes: Part II - Heat Transfer Characteristics and Critical Heat Flux,” International Journal of heat and Mass Transfer, Vol. 50, pp. 5017-5030, 2007.
[https://doi.org/10.1016/j.ijheatmasstransfer.2007.08.017]

-
Pizzarelli, M., “A CFD-Derived Correlation for Methane Heat Transfer Deterioration,” Numerical Heat Transfer, Part A,, Vol. 69, No. 3, pp. 242-264 2016.
[https://doi.org/10.1080/10407782.2015.1080575]