연료과농조건에서의 기체메탄-기체산소 연소기 내 연소거동에 관한 수치해석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
연료과농조건에서의 기체메탄-기체산소 연소기의 혼합 및 연소거동을 관찰하기 위해 수치해석이 수행되었다. 당량비 2에서 3.65 구간은 내부유동 구조를 비교하고자 정상상태로 해석되었으며, 당량비 5.36은 시간에 따른 성능 변화를 관찰하고자 비정상상태로 해석되었다. 해석결과, 계산된 추력 및 연소성능이 실험값과 전반적으로 일치함이 확인되었으나, 실제의 연소 후반부에서 발생하는 비정상적인 물리현상을 구현하기 위해선 추가적인 연구가 필요한 것으로 판단된다.
Abstract
Numerical simulation was performed to observe the combustion behavior of a GCH4-GO2 combustor varying with equivalence ratio under the fuel-rich conditions. The equivalence ratio of 2 to 3.65 was analyzed in a steady state to observe the internal flow structure affected by equivalence ratio, while the equivalence ratio of 5.36 was simulated in a transient state to scrutinize the variations in performance over time. As a result, it was found that the thrust and combustion performance calculated by the simulations were in good agreement with the experimental results. However, further research is required to calculate the unsteady physics observed at the later part of practical firing.
Keywords:
CFD(Computational Fluid Dynamics), Non-premixed Combustion, Steady Diffusion Flamelet Model, Methane키워드:
비예혼합 연소, 정상 확산화염편 모델, 메탄1. 서 론
우주산업이 발달함에 따라 로켓 추진기관의 운용횟수가 많아지면서 비용의 절감 및 친환경성에 대한 수요가 높아지고 있다. 대표적 친환경성 연료인 메탄은 효율성 및 안정성이 우수할 뿐만 아니라 연소 과정에서 오염 물질의 배출이 적다는 장점을 지닌다. 또한, 메탄은 화성에서의 현지자원활용(ISRU, In-situ Resource Utilization)에 대한 가능성이 대두되면서 우주탐사를 위한 추진기관으로도 각광받는 추세이다[1].
특히, LOx-Methane 조합은 LOx-Kerosene과의 조합보다 비추력 성능 면에서 우수하고, 비용은 3배 이상 저렴하다[1,2]. 또한, 메탄은 액체수소보다 밀도가 높아 저장성이 우수하다는 장점을 지닌다. 이러한 이유로 미국, 러시아, 유럽, 일본 등 우주개발선진국은 차세대 발사체의 개발을 위한 추진기관의 연료로 메탄을 채택하고 있다.
최적의 성능을 가지는 엔진이 개발되기 위해서는 추진제의 공급조건에 따른 연소효율 및 점화 안정성 등에 대한 정보가 매우 중요하나, 메탄은 개발역사가 짧아 실험적인 데이터가 제한적이다. 이러한 정보의 부재를 해결하기 위해선 여러 운용 조건에서의 시험평가가 수행되어야 하나, 많은 시간과 비용뿐만 아니라 위험성이 수반된다. 이에 반해 수치해석은 실험적인 접근만으로는 어려운 다양한 연소 조건에서 화학반응을 모델링하고 분석할 수 있으며, 중요한 설계 인자를 사전에 도출해낼 수 있어 개발시간 및 비용을 크게 절감할 수 있다. 또한, 수치해석은 시험에서는 얻기 힘든 연소실 내의 온도 및 난류 특성에 대한 정보를 검증된 해석기법을 통해 제공할 수 있다.
이에 본 논문에서는 액체산소-기체메탄 소형로켓엔진의 연소거동에 대해 해석하기 전, 로켓엔진의 연소거동을 예측할 수 있는 해석기법을 수립하고자 수치해석이 수행되었다. 연료과농조건에서 당량비 변화에 따른 기체산소-기체메탄 연소기의 거동을 모사하고자 하였으며, 구축된 해석모델은 선행연구로 수행된 연소시험[3]에서의 추력 및 연소성능 결과와의 비교를 통해 유효성이 검증되고, 연소기 내부의 유동 구조는 수치해석 결과를 통하여 관찰되었다.
2. 시험조건
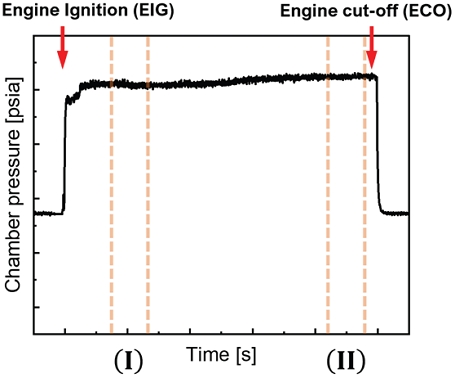
선행연구의 지상연소시험은 연료과농조건에서의 기체메탄-기체산소 연소기의 연소성능을 확인하고자 수행되었다. 시간에 따른 연소특성을 비교하고자 연소시간 내에 두 구간을 설정해 데이터가 분석되었으며, 이를 Fig. 1에 나타낸다. 구간 1은 점화 후 3.01에서 5.50 초 구간으로(EIG +3.01∼5.50 s), 구간 2는 추진제 공급 밸브가 닫히기 전 3초 구간(ECO -3.51∼-0.50 s)으로 설정되었다. 선행연구로부터 당량비가 증가할수록 연소 후반부의 특성속도 상승도 및 압력 증가가 뚜렷해짐이 확인되었으며, 이는 연소 초반부에 참여하지 않았던 미연 혼합물이 후반부에 연소에 재참여하게 되어 발생한 결과라 판단된 바 있다.
Two section where data was reduced over the combustion period.
연료과농조건에서 나타나는 비정상적인 현상으로부터 각 조건에서의 연소기 내부 유동장의 분석이 필요하다고 생각되는 바, 이에 본 논문에서는 연소거동을 예측할 수 있는 모델을 정립하고자 수치해석이 수행되었다. 각 구간에서 획득된 데이터를 토대로 해석모델이 구축되었으며, Table 1에 해석에 사용된 케이스들과 그의 당량비 및 특성속도 상승도가 요약된다. 당량비 2에서 3.65 구간은 당량비 변화에 따른 내부 연소장을 관찰하고자 정상상태로 해석되었으며, 특성속도 변화율이 가장 높은 당량비 5.36의 케이스는 시간에 따른 압력 및 특성속도의 변화를 관찰하고자 비정상상태로 해석되었다.
Experimental cases employed in the current calculations.
3. 해석기법
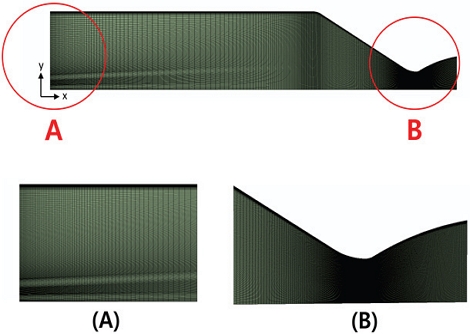
연소기의 내부 유동장은 RANS (Reynolds-averaged Navier-Stokes) 방정식으로 해석되었으며, 상용 코드인 Ansys Fluent 2021 R1[4]이 사용되었다. 해석의 수렴성을 향상시키고자 압력기반 연계 알고리즘(pressure-based coupled algorithm)을 채택하였으며, 모든 케이스에서 난류 스칼라값을 제외한 지배방정식들은 2차 풍상법(2nd-upwind scheme)으로 이산화되었다. 해석을 위한 기하학적 모델은 2차원 축 대칭 형상으로 구축되었으며, 인젝터 후단에서부터 노즐 외각 일정 영역까지가 계산영역으로 설정되었다. Fig. 2에 계산에 사용된 격자계를 나타내며, 인젝터 주입구 부분과 초음속 노즐에서의 격자가 확대되어 도시된다. 격자계는 사변형 격자가 사용되었으며, 263,445개의 셀과 265,647개의 격자점으로 구성되도록 설정하였다.
Enlarged view of the injector face region (A) and supersonic nozzle zone (B) in the grid system.
3.1 난류 모델
난류 유동을 해석하기 위해 압축성 효과를 고려한 표준 k - ϵ 난류(compressible standard k - ϵ turbulence) 모델[5,6]이 사용되었다. 난류 운동에너지(turbulent kinetic energy)인 k와 난류 소산율(turbulent dissipation rate)인 ϵ 은 각각 Eq. 1과 Eq. 2를 통해 계산되며 각 방정식의 시간에 대한 미분 항들은 정상상태 해석시 고려되지 않는다. 난류 점성계수(turbulent viscosity)는 위의 식들을 통해 도출되어 Eq. 3과 같이 정의된다. 압축성 표준 난류 모델은 난류 운동에너지 방정식 내에 팽창-소산항(dilatation dissipation)이 추가되어, 마하수 증가에 따른 난류 에너지 감소를 고려할 수 있으므로 난류 유동의 예측 성능을 향상시킬 수 있다[7].
| (1) |
| (2) |
| (3) |
3.2 연소 모델
비예혼합연소 모델(non-premixed combustion model) 중 비단열 확산화염편 모델(non-adiabatic diffusion flamelet model)이 본 계산에 적용되었다[8]. 확산화염편 모델은 난류 화염장을 1차원적인 층류화염편의 집합체로 가정하여 해석하는 방식으로, 스칼라 소산율이 미세화염구조를 지배한다[9]. 비단열 확산화염편의 1차원 상미분 방정식은 Eq. 4와 Eq. 5를 통해 기술된다.
| (4) |
| (5) |
메탄-산소 화학반응의 계산에는 21개의 화학종과 84개의 반응식이 포함된 DRM-19 메커니즘이 사용되었다[10]. DRM-19 메커니즘은 GRI-mech 1.2의 축소 모델로, 계산비용을 줄이면서도 메탄 연소의 열역학적 특성을 잘 구현해낼 수 있으며, 특히 순산소-메탄 연소의 경우, DRM-19에서 예측한 연소속도(burning velocity)와 실험결과 값이 잘 일치한다는 결과가 보고된 바 있다[11].
3.3 경계조건
해석에 사용된 경계조건들을 Table 2에 요약하여 나타낸다. 입구 조건에서의 메탄과 산소의 온도 값은 각각 298 K으로 가정하여 해석되었으며, 실험으로부터 측정된 추진제의 유량이 경계조건으로 부여되었다. 또한, 연소실과 노즐 벽면의 온도 값은 실측된 범위가 연소실의 하단부까지만 존재하여, 노즐 목과 출구부의 온도를 NASA의 CEA (Chemical Equilibrium with Application) 코드[12]로 추가적으로 계산하여 전체 온도 경계조건을 설정하였다. 마지막으로 추진제 주입구를 제외한 인젝터 단면에는 단열 및 점착 조건이 부여되었다.
Boundary conditions used in the current calculation.
4. 수치해석 결과
4.1 정상상태 해석
내부유동을 관찰하기 전, 해석기법의 유효성을 검증하기 위해 연소기의 추력 및 연소성능을 계산하였다. Fig. 3에 구간 1과 구간 2에서 계산된 당량비에 따른 특성속도 및 특성속도 효율 값을 실험값과 비교하여 나타낸다. 그림에서 볼 수 있듯이, 계산 결과는 실험결과와 전반적으로 일치함이 확인되며, 오차율은 3% 이내이다. 또한, 구간 1의 결과보다 구간 2에서의 결과에서 오차율이 감소하는 것을 관찰할 수 있는데, 이는 상대적으로 점화시간 후반부에 위치한 구간 2에서의 값이 정상상태에 더 가까운 것에 기인한 결과라 판단된다. 해석으로부터 계산된 추력 및 연소실 압력 결과는 Fig. 4에 실험값과 비교하여 도시된다. 연소실 압력에서도 모든 케이스가 허용 범위 이내의 오차율을 보이나, 당량비가 2인 케이스 GE1.x에서 두 구간 모두 추력 값에서 차이가 발생한 것을 볼 수 있다. 이는 GE1.x 케이스에서 연소시험 도중 높은 화염 온도로 인한 연소기 침식(erosion)이 발생하였는데, 이때의 노즐 목 확공 등이 비정상적 추력에 기인하는 것으로 예상된다.
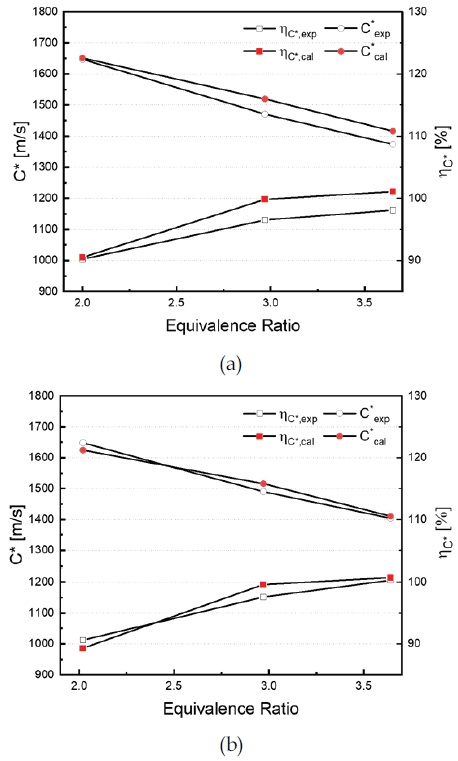
Comparison of the combustion performance between simulation and experimental results at period Ⅰ(a) and period Ⅱ(b).
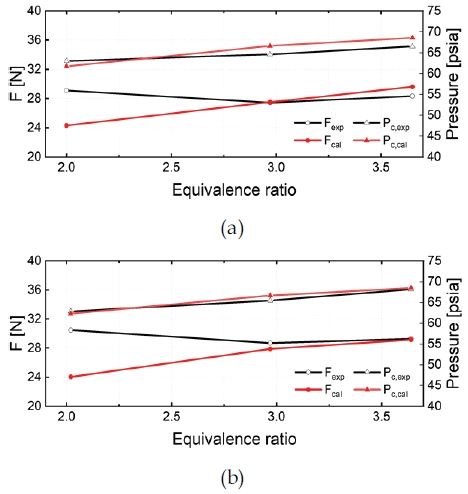
Comparison of the thrust and chamber pressure between simulation and experimental results atⅠ(a) and period Ⅱ(b).
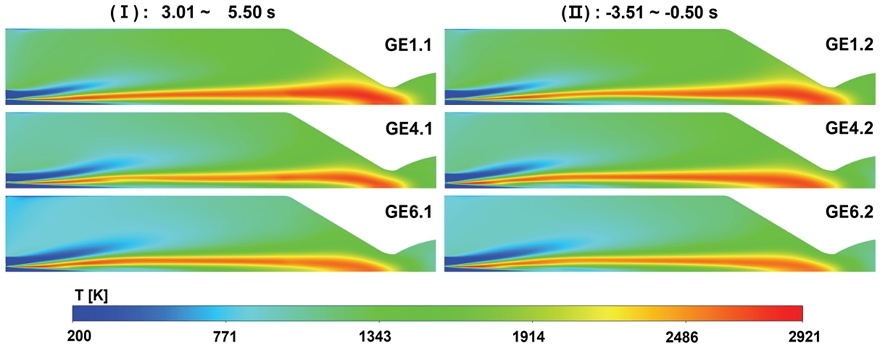
Fig. 5에 각 케이스 별 온도 분포를 비교하여 도시한다. 전체적으로 화염대가 노즐의 목 부근까지 형성되어 있음을 알 수 있으며, 당량비가 증가함에 따라 연소기 내부 고온 영역이 줄어들고, 그 최대온도가 감소함을 볼 수 있다. 이는 메탄의 유량이 증가하면서 화학양론비에서 멀어지므로, 내부 화염의 강도가 점차 약화 됨에 따라 발생한 결과로서 Fig. 3에서 보이는 당량비에 따른 특성속도 변이 경향과 일치한다.
Temperature contour results at each case.
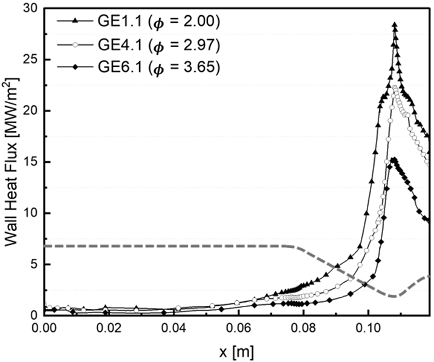
Fig. 6에 당량비에 따른 연소실 벽면에서의 열 유속의 크기를 비교하여 나타낸 선도를 도시하며, 이를 통해 모든 경우에 노즐 목에서 최대 열 하중이 발생하는 것이 확인된다. 화염대의 분포에서 볼 수 있듯이, 노즐 목 부근에서 화염의 강도가 세지므로, 열 유속의 크기 또한 같은 위치에서 급격한 변화량을 보임을 알 수 있다.
Wall heat flux distribution with equivalence ratio variation.
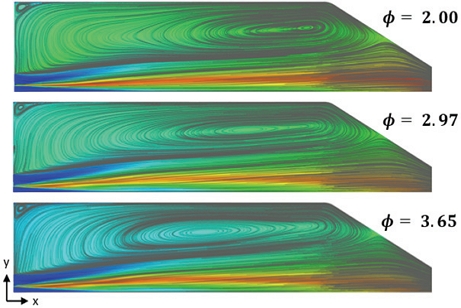
Fig. 7은 연소기 내 재순환영역을 관찰하기 위해 당량비에 따른 등온선과 유선을 함께 나타낸 그림이다. 그림에서는 메탄의 유량이 증가함에 따라 연소기 내 재순환영역의 크기가 확장되는 것이 관찰되는데, 이를 통해 당량비가 증가함에 따라 연소에 참여하지 않는 연료과농 영역의 크기가 커지며, 장시간 연소시 이 영역에서 2차 점화가 발생할 수 있다는 가능성을 시사하기도 한다.
Comparison of recirculation zone in the combustion chamber with equivalence ratio variation.
4.2 비정상상태 해석
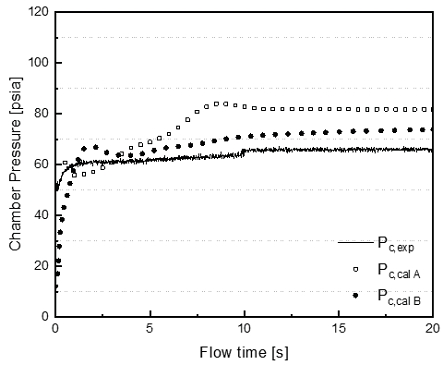
시간에 따른 특성속도 변화율이 가장 높은 당량비 5.36에서의 해석결과가 Fig. 8에 도시된다. Pc,cal A는 SIMPLEC 알고리즘을, Pc,cal B는 압력기반 연계 알고리즘을 사용하여 해석된 결과이며, SIMPLEC 알고리즘이 연소시간 내 압력 변화량을 전반적으로 과대예측하는 것을 볼 수 있다.
Comparison of chamber pressure over time between simulation and experimental results.
Table 3에는 추력 및 특성속도 결과가 요약되는데, 표에서 볼 수 있듯이 두 방식 모두 연소 후반부에서 오차율이 높아지나, 압력기반 연계 알고리즘이 실험값에 더 근접하다. 이를 통해 유동장의 변화가 큰 연소 과정을 계산할 시 압력기반 연계 알고리즘이 더 적절하다는 것이 확인된다.
Comparison of the thrust and combustion performance between simulation and experimental results.
또한, Fig. 8에서 관찰되는 지상연소시험시 연소 후반부에서 발생한 급작스러운 압력 증대가 해석결과에서는 뚜렷하게 발견되지 않는다. 이는 미연 혼합물이 연소 후반부에 반응에 재참여하는 비정상적인 물리현상을 계산해내지 못하는 연소 모델의 한계라 판단된다. 추후 이러한 실제 현상을 구현하기 위해 다른 연소 모델의 결과와 비교하거나 재순환영역의 격자 밀도를 보완하여 유동 구조를 보다 상세히 해석하기 위한 추가연구가 수행될 예정이다.
5. 결 론
액체산소-기체메탄 로켓엔진의 연소성능을 예측하기 위한 해석기법을 수립하고자, 선행연구의 일환으로 기체산소-기체메탄 예연소기에 대한 수치해석이 수행되었다. 연소기 내부 난류 화염장을 모사하기 위해 정상상태 확산화염편 모델이 선택되었으며, 총 21개의 화학종과 84개의 반응식이 본 해석에 사용되었다.
당량비 2에서 3.65 까지의 구간은 정상상태로 해석되어 각 케이스에 따른 내부유동 구조가 비교되었다. 연료과농조건에서 당량비 변화에 따른 연소기의 추력 및 연소성능 결과를 실험 실측값과 비교한 결과, 전반적으로 오차율 3% 이내의 정확성을 보이나, 당량비 2 구간인 GE1.x 케이스의 추력값에서 큰 차이를 보인다. 이는 GE1.x 케이스의 시험 도중 높은 화염온도에 기인하는 노즐 침식 및 확공 때문으로 판단된다.
각 케이스별 연소기의 내부유동을 관찰한 결과, 당량비가 증가함에 따라 화염 강도가 약해지며, 노즐 목에서의 최대 열부하의 크기가 점차 감소함을 볼 수 있다. 또한, 유선을 비교하였을 때, 메탄의 유량이 증가하면서 재순환영역의 크기가 확대되는 것이 관찰되었다. 이를 통해 연소기 내 연료과농의 영역이 커지며, 장기간 연소시 이 영역에서 2차 점화가 발생할 수 있는 가능성을 확인하였다.
당량비 5.36에서 시간에 따른 급작스러운 압력의 변화를 관찰하고자 추가적으로 계산이 수행되었다. 해석결과, 연소 후반부에 발생하는 급작스러운 압력 증대가 해석에서는 발견되지 않았는데, 이는 비정상적인 물리현상을 계산해내지 못하는 연소 모델의 한계라 판단된다.
Nomenclature
| C* : | characteristic velocity |
| k : | turbulent kinetic energy |
| ϵ : | turbulent dissipation rate |
| σk,σϵ : | turbulence model constants |
| μ : | dynamic viscosity |
| μt : | turbulent viscosity |
| Gk : | generation term |
| MT : | turbulent mach number |
| Yi : | mass fraction of i-th species |
| χ : | scalar dissipation rate |
| : | mass production rate of i-th species |
| CP : | specific heat |
| Z : | mixture fraction |
| ui : | velocity |
| h : | enthalpy |
| t : | time |
| T : | temperature |
| ρ : | density |
Acknowledgments
본 논문은 과학기술정보통신부의 재원으로 한국연구재단 미래우주교육센터(2022M1A3C2085070)의 지원을 받아 수행된 연구결과임.
References
-
Kim, J. S., Jung, H. and Kim, J. H., “State of the Art in the Development of Methane/Oxygen Liquid bipropellant Rocket Engine,” Journal of the Korean Society of Propulsion Engineers, Vol. 174, No. 6, pp. 120-130, 2013.
[https://doi.org/10.6108/KSPE.2013.17.6.120]
-
Goetz, A., Maeding, C., Brummel L. and Haeseler D., “Application of non-toxic propellants for future launch vehicles,” 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, U.T., U.S.A, AIAA 2001-3546, Jul. 2001.
[https://doi.org/10.2514/6.2001-3546]
-
Kang, Y. H., Ahn, H. J., Bae C. H. and Kim, J. S., “Combustion Characteristics of the Gaseous-methane & Gaseous-oxygen Reactants under Highly Fuel-rich Conditions,” Journal of the Korean Society of Propulsion Engineers, Vol. 25, No. 6, pp. 45-52, 2021.
[https://doi.org/10.6108/KSPE.2021.25.6.045]
- ANSYS Fluent V21.1, “ANSYS Fluent Theory Guide 2021 R1,” ANSYS, Inc., Canonsburg, P.A., U.S.A., 2021.
-
Narayan, J., “A two-equation turbulence model for compressible reacting flows,” 29th Aerospace Sciences Meeting, N.V., U.S.A., AIAA 1991-0755, Jan. 1991.
[https://doi.org/10.2514/6.1991-755]
-
Jones, W. P. and Launder. B. E. “The prediction of laminarization with a two-equation model of turbulence,” International Journal of Heat and Mass Transfer, No. 15, Vol. 2, pp. 301-314, 1972.
[https://doi.org/10.1016/0017-9310(72)90076-2]
- Gerald J.M. and Helldorff, H. V. “A Compressible Turbulence Model for High Speed Flows,” retrieved 13 Nov. from https://www.researchgate.net/publication/344933934_A_Compressible_Turbulence_Model_for_High_Speed_Flows, .
-
Peters, N., “Laminar diffusion flamelet models in non-premixed turbulent combustion,” Progress in Energy and Combustion Science, Vol. 10, No. 3, pp. 319-339, 1984.
[https://doi.org/10.1016/0360-1285(84)90114-X]
- Kim, G. H., Kim, H. J. and Kim, Y. M., “Flamelet Modeling of Soot Formation and Oxidation in a laminar CH4-Air Diffusion Flame,” Journal of the Korean Society of Mechanical Engineers, Vol. 13, No. 1, pp. 68-75, 2005.
- Chang, W. C. and Chen, J. Y., “Reduced Reaction Sets based on GRI-Mech 1.2,” retrieved 13 Nov. from http://combustion.berkeley.edu/drm/drm19.dat, .
-
Mazas, A. N., Fiorina, B., Lacoste, D. A. and Schuller, “Effects of water vapor addition on the laminar burning velocity of oxygen-enriched methane flames,” Journal of Combustion and Flame. Vol. 158, No. 12, pp. 2428-2440, 2011.
[https://doi.org/10.1016/j.combustflame.2011.05.014]
- McBride, B. J. and Gordon, S., “Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications,” NASA-RP-1311, 1996.