환형연소기에서 불안정성에 따른 유동적인 대칭성파괴 효과 Part Ⅰ: 노즐 배치의 특성
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 환형연소기 형태를 가지는 가스터빈 연소기에서 연소불안정성을 제어하는 방법을 제시하고자 하였으며, 노즐 배치와 이에 따른 당량비 변화를 통한 유동적인 대칭성파괴(Flow symmetry breaking) 효과를 비교하였다. 이를 위하여 FFT, Time signal 및 위상궤적의 모드 분석을 통하여 대칭성파괴 효과를 확인하였다. 또한, 모드분석으로 불안정한 영역과 안정된 영역을 확인하였고 이를 등고선 지도에 나타내었다. 본 연구를 통해 노즐의 당량비와 배치가 대칭이거나 노즐이 연속적으로 배치되면 불안정성이 발생하였으나, 노즐의 배치 및 당량비가 대칭성을 가지질 않는다면 당량비의 차이가 작더라도 연소불안정성이 극적으로 감소하는 것을 확인할 수 있었다.
Abstract
This research proposes a method to control combustion instability in a gas turbine combustor having an annular combustor form and compares the effect of flow symmetric braking through nozzle arrangement and the corresponding change in equivalent ratio. To this end, the symmetry breaking effect was confirmed through mode analysis of FFT, Time signal, and phase trajectory. In addition, the unstable area and the stable area were identified through mode analysis, and this was shown on the contour map. The present research shows that instability occurs when the equivalent ratio and the arrangement of the nozzles are symmetry or when the nozzles are continuously arranged, but if the arrangement and equivalent ratio are not symmetry, the combustion instability decreases dramatically even if the difference in the equivalent ratio is small.
Keywords:
Annular Combustor, Thermo-acoustic Instability, Symmetry Breaking, Longitudinal Instability키워드:
환형연소기, 열-음향 불안정성, 대칭성파괴, 종-방향의 불안정성1. 서 론
환형연소기에서 발생하는 열-음향 불안정성을 구분하는 방법에는 화염의 거동을 이미지로 취득하여 분석하는 방법과 다수의 압력센서를 이용하여 불안정성 모드를 판단하는 방법이 있으며, 대체로 다수의 압력센서를 사용하는 것이 명확한 것으로 알려져 있다. S. Candel 등이 4개의 압력센서를 사용하여 각각의 위치별 위상차를 통하여 불안정성 모드를 종-방향 모드(longitudinal mode), 방위-방향 모드(azimuthal mode), 비스듬한 모드(slanted mode), 이중 모드(dual mode) 및 흔들리는 모드(chugging mode)로 구분하였으며, 방위-방향의 불안정성 모드를 회전 모드(spinning mode)와 고정 모드(standing mode)로 구분하였다[1]. J.R. Dawson 등은 회전비율(spin ratio) 개념과 확률밀도함수(probability density function, FDF) 분포를 통하여 3 개의 압력센서에서 취득한 데이터를 시계방향의 진폭 크기와 반 시계방향의 진폭 크기를 각각 정의한 후 회전비율을 통하여 해당 값이 0의 값을 가진다면 고정 모드가 될 것이고 1 혹은 –1의 값을 가진다면 각각 시계방향 혹은 반 시계방향으로의 회전 모드를 나타낼 것이라고 보고하였다[2-3].
열-음향 불안정성을 제어하기 위하여 많은 연구들이 진행되었는데, 대표적으로 헬름홀츠 공진기(Helmholtz resonator)를 사용하거나 스피커를 장착하여 가진(forcing)을 통해 화염의 응답을 확인하여 화염전달함수(flame transfer function, FTF)로 분석하는 방법들이 있다[4-7]. 또한, Shin 등은 헬름홀츠 방정식으로 도출된 화염과 모드를 분석하여 연소불안정성을 예측하였다[8].
한편, 환형연소기에서는 대칭성파괴를 사용하여 열-음향 불안정성을 제어하는 방법이 있는데 방법에 따라서 기하학적 대칭성파괴(geometrical symmetry breaking)와 유동적인 대칭성파괴(flow symmetry breaking)가 있다[9-12]. 기하학적 대칭성파괴로는 벽막(baffles)를 설치하거나 서로 다른 형상의 노즐을 설치하는 방법이 있으며, 유동적인 대칭성파괴는 다른 선회방향 및 선회강도(swirl number)를 가지는 스월러(swirler)를 설치하거나 각각의 노즐별 유량, 당량비 및 연료를 다르게 하는 방법이 있다. 기하학적 대칭성파괴에서 벽막 설치를 통하여 대칭성파괴 결과로 기존에 시계방향으로의 회전 모드로 집중되었던 확률밀도함수 분포도가 벽막 설치에 따라서 고정 모드로 집중되는 것을 확인할 수 있으며, 유동적인 대칭성파괴에서 스월러의 방향을 서로 다르게 설치한 경우에도 마찬가지로 동일한 현상이 나타났다. T. Poinsot 등은 다수의 노즐들을 배치 및 각도에 따라서 불안정성이 감소하는 것을 확인하였으며, 노즐의 각도가 75˚와 225˚로 설치되었을 때 스플리팅 패턴 인자(splitting pattern factor)로 정의된 값이 0의 값을 가지며 대칭성파괴가 되었고 연소실 내에 반대편에 위치하는 165˚로 설치되었을 때 해당 인자가 큰 값을 가지며 불안정성이 촉진될 수 있다고 보고하였다[13].
여러 이론적인 접근법과 시뮬레이션으로 여러 유형의 버너를 구성하고 유속을 조정함으로써 환형연소기에 나타나는 방위-방향의 불안정성 모드의 빈도 및 모드(회전, 고정 및 이중)룰 제어하는 대칭성파괴 효과를 확인하였다[14-18]. 그러나, 항공기용 가스터빈 연소기의 경우 연소기 길이가 덤프면 직경보다 3~5배정도 크기 때문에 방위-방향의 불안정성보다는 종-방향의 불안정성이 주로 발생하게 되며, 종-방향의 불안정성이 훨씬 심각하다. 그럼에도 불구하고, 환형연소기에 대한 대부분의 대칭성파괴 현상은 방위-방향의 불안정성을 감쇠하는 효과에 초점을 맞추었다[19]. 또한, Kim 등은 방위-방향의 불안정성 거동과 모드를 야기하는 물리적인 메커니즘을 실험적으로 연구하였으며, 3차원 유한요소법을 이용한 음향 모드 시뮬레이션을 수행하여 계측된 실험 데이터와 비교하였다[20].
본 연구에서는 실제 항공기용 가스터빈 연소기를 모사하여 종-방향의 불안정성을 제어할 수 있는 대칭성파괴 방법을 제시하고자 한다. 대부분 환형연소기의 대칭성파괴 연구에서는 방위-방향의 대칭성파괴에 집중하였으나, 본 방위-방향의 대칭성파괴 방법을 이용하여 노즐의 당량비 분배 및 배치로 나타나는 종-방향의 불안정성 제어 현상에 집중적으로 조사하였다. 이러한 종-방향 불안정성의 대칭성파괴 연구는 아직은 부족한 실정이기 때문에 환형연소기에서의 연소불안정성 감쇠 효과 및 현상에 대한 선행적으로 수행된 결과이다.
2. 실험 장치 및 조건
2.1 실험장치 및 구성
본 연구에서 사용된 환형연소기(lab-scale annular combustor) 개략도를 Fig. 1(a)에 나타내었으며, 선행 연구에서 사용된 환형연소기 형상에서 열-방출 섭동을 측정하기 위하여 개선하였다[23]. 두 개의 혼합 챔버(mixing chamber)를 사용하여 완전 예혼합을 하였으며, 노즐에 직접 연결하여 출구로 분사되도록 설계되어 각 노즐의 공기 유량, 배치 및 각도 등을 독립적으로 제어할 수 있게 하였다. 또한, 노즐에서 균일한 유동장 형성되는지 확인하고자 화염 직접 사진을 Fig. 1(b)에 나타내었으며, 두 개의 이미지를 통해 8개 노즐 모두에서 균일한 유동장이 형성되는 것을 확인할 수 있다. Fig. 1(c)는 연소기 덤프면을 보여주고 있는데, 8개 노즐 모두 반 시계방향의 베인(vane)형 스월러로 선회강도 수는 0.83이다. 또한, 각 노즐의 선회방향과 선회강도 수는 동일하게 설정하였다.
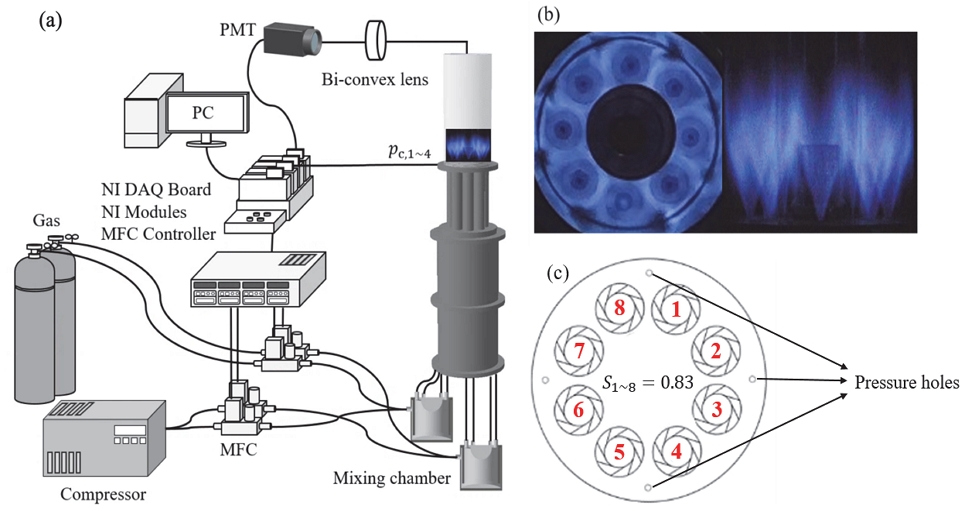
(a) Schematics diagram of annular combustor, (b) digital flame photograph, (c) combustor dump plane.
연료는 LNG 연료의 주성분인 메탄(methane, 99.95%)이며, 압축기로 공급된 공기를 사용하였다. 연료와 산화제 모두 질량유량계인 MFC를 랩뷰 소프트웨어(lab-VIEW software)와 NI 모듈(NI module, NI 9200, NI 9121)을 사용하여 제어하였으며, 유량 제어할 때 잡음(noise)을 최소화하기 위하여 유량 교정기(calibrator)와 건식 가스미터(dry gas meter)를 사용하여 신호에 따른 실제 유량을 측정하여 교정한 값을 사용하였다.
연소실 내부의 압력섭동을 측정하기 위하여 안티-노드점(anti-node point)인 덤프면에 90˚ 간격으로 4개의 piezotronics 음압센서(PCB INC., 43.62 mV/kPa)를 설치하여 압력 섭동()의 척도로 사용하였으며, 소음 레벨(sound pressure level, SPL dB)을 측정하기 위하여 Free-field형 마이크로폰(PCB INC., 378B02, M1)을 연소기 후단 100 mm 떨어진 지점에서 측정하였다. 또한, 화염 발광에 의한 동특성의 정량적인 계측을 위하여 PMT(hamamatsu, C10709, H10722-110)를 사용하였으며, OH* 자발광을 계측하기 위해 광학필터(semrock INC., 309 ± 5 nm)를 장착하여 측정하였다. 연소가스로부터 PMT 센서 보호를 위해 이격된 PMT와 노즐까지의 원거리로 인한 측정의 어려움은 양면 볼록렌즈(Bi-convex lens, 1500 mm)를 사용하여 증폭 후 초점거리를 맞춰 열-방출 섭동()을 측정하였다. 측정된 압력 및 열-방출 섭동은 시그널 컨디셔너(signal conditioner)를 통하여 10배 증폭시켜 NI 모듈로 취득하였으며, 취득한 데이터는 NI의 시그널 익스프레서 소프트웨어를 사용하여 실시간으로 확인하였다. 이를 통해 고속퓨리에변환(fast fourier transform, FFT) 및 위상궤적(phase space reconstruction, PSR), 소음 레벨, 시간 신호(time signal) 방법으로 불안정한 영역과 안정된 영역을 정의하였다[21-22].
2.2 실험조건 및 측정방법
본 연구의 실험 조건을 Table 1에 나타내었다. 각 노즐에서 분사되는 유동의 레이놀즈 수(ReD)는 2500으로 고정하였고 이때, 노즐 출구유속(u0)은 5.7 m/s가 된다. 측정은 선행 연구와 동일하게 각각의 노즐 당량비에서 점화된 후 1분 동안 유지한 후에 10 kHz의 샘플링율로 5초 동안의 데이터를 취득하였다. 또한, 덤프면에서 트랜션피스(transition piece)까지 길이로 정의되는 연소기 길이는 선행 연구를 통해 연소불안정성이 가장 크게 발생하는 550 mm로 고정하였으며, 이 길이에서 노즐의 당량비와 배치를 변경하여 대칭성파괴 효과를 관찰하였다.
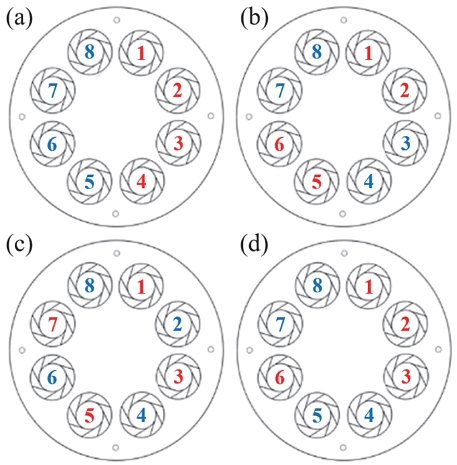
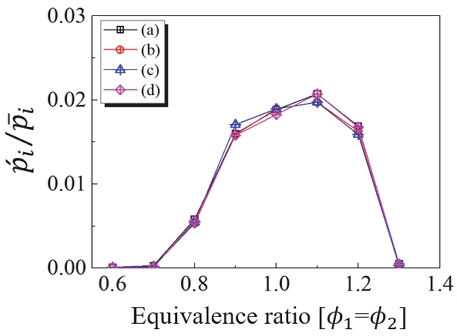
노즐의 배치를 Table 1에 나타내었는데 N은 노즐을 의미하며, 하첨자 숫자들은 해당 노즐의 번호로 Fig. 1(c)에 나와 있다. 하나의 예로 Table 1의 배치 (a)(N1, 2, 3, 4_N5, 6, 7, 8, ϕ1_ϕ2)경우에는 8개 노즐중에서 4개의 노즐들이 연속적으로 배치된 경우로 노즐 배치가 대칭성을 가지는 경우이다. 당량비(ϕ1, ϕ2)는 0.6 ~ 1.3까지 0.05 간격으로 변경하였으며, 당량비 0.55 보다 낮은 당량비에서는 희박 날림 화염(lean blow-off)이 발생하고 1.3 보다 높은 경우에는 안정 화염(stable flame)이 발생한다. Fig 3은 동일한 당량비(ϕ1 = ϕ2)에서의 압력 진폭을 나타내었다. 노즐이 동일한 당량비를 가질 때 노즐의 배치와 상관없이 비슷한 압력 진폭값을 가지며, 각각의 노즐에서 균일한 유량이 분사되는 것을 확인할 수 있다. 또한, 노즐 배치의 대칭성파괴 현상이 존재하지 않는 것을 의미한다. 당량비가 동일하지 않는 경우에는 배치 및 당량비에 대칭성파괴 현상을 확인할 수 있다.
3. 결과 및 고찰
3.1 당량비에 따른 대칭성파괴 현상
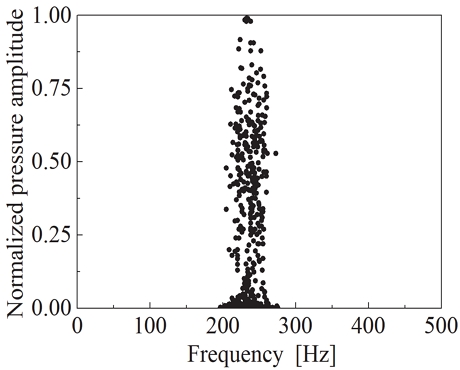
Fig. 4는 주파수에 따른 최댓값을 기준으로 정규화된 압력 진폭을 나타내었다. 210 ~ 250 Hz 사이에서 압력 진폭이 나타나며, 낮은 압력 진폭에서의 주파수는 잡음으로 인하여 넓어졌으나, 다른 주파수에서는 압력 진폭이 발생하지 않는 것을 확인할 수 있으며, 이는 종-방향의 불안정성을 제외하고 다른 모드의 불안정성이 발생하지 않는 것을 볼 수 있다.
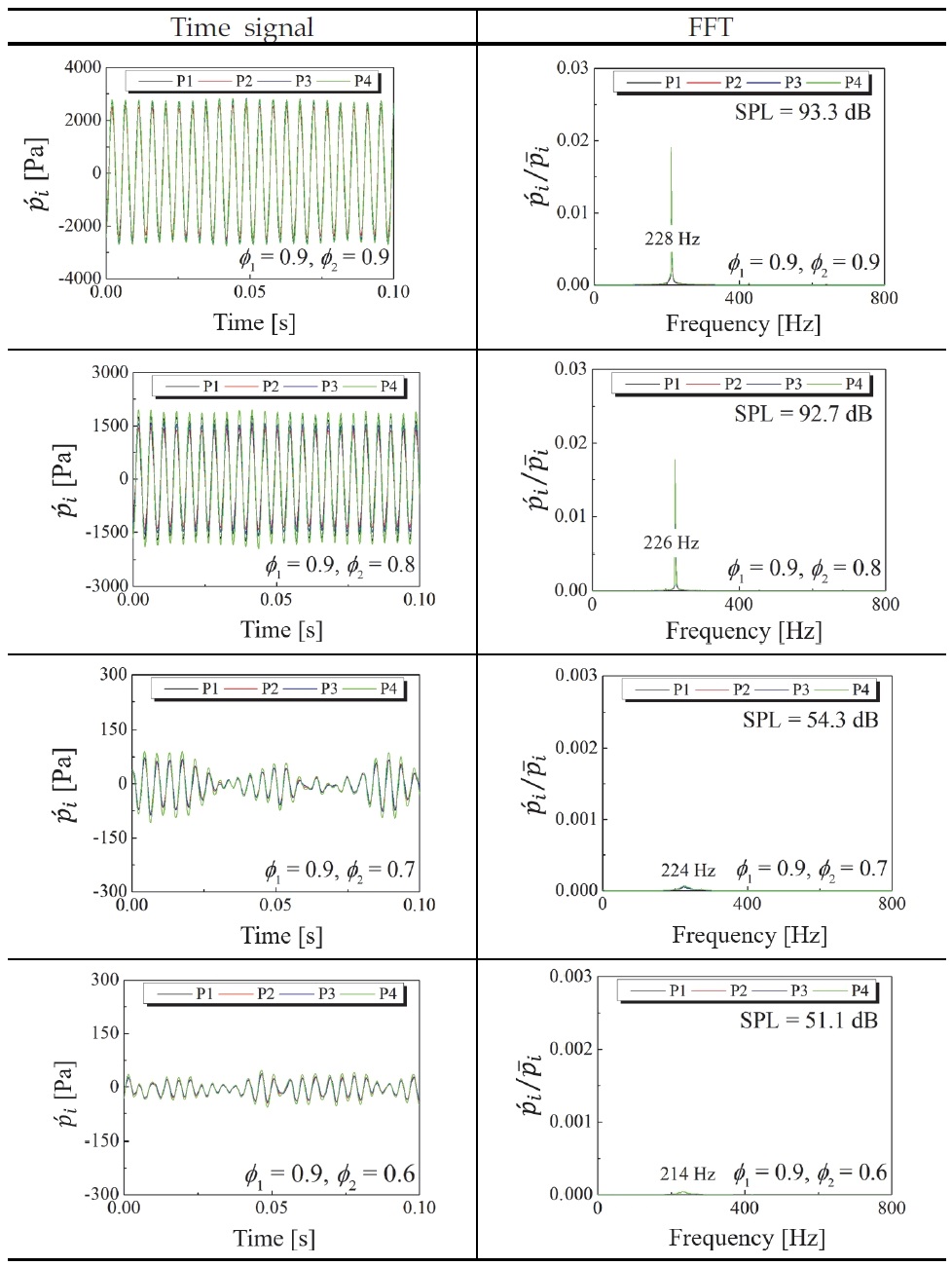
본 연구에서는 당량비에 따른 대칭성파괴 현상과 불안정성 영역을 확인하기 위해서 대표적으로 배치(a)의 당량비 ϕ1, ϕ2= 0.9, 0.9에서 ϕ1, ϕ2= 0.9, 0.6까지의 시간 신호, 소음 레벨 및 퓨리에 변환 분석을 Fig. 5에 보여주고 있다. 시간 신호는 5초 동안 측정한 51200개의 데이터 중 0.1초에 해당하는 압력 데이터로 소음의 파형이 구분되는 것을 볼 수 있다. 다수의 압력센서 위치 및 노즐 간에 당량비로 인하여 약간의 비대칭성이 보이나, 큰 차이가 없는 것을 확인할 수 있다. 또한, 다수의 압력센서 진폭을 통하여 불안정성의 모드를 구분할 수 있으며, 진폭이 동일한 파형으로 나타난다면 이는 종-방향의 불안정성을 나타낸다[1]. 종-방향의 불안정성이 아닌 방위-방향의 불안정성이 발생한다면, 종-방향의 불안정성보다 높은 주파수를 가지게 된다.
당량비가 대칭성을 가지는 ϕ1, ϕ2= 0.9, 0.9에서 압력섭동이 큰 진폭에 일정한 한계주기(limit cycle)로 진동하는 것을 확인하였고 불안정성이 크게 발생하였다. 이는 퓨리에 변환에서도 동일하게 나타났으며, 큰 진폭으로 연소불안정성이 발생한다. 이후, 당량비 차이가 증가할수록 대칭성파괴 현상이 나타나 진폭이 감소하며, ϕ1, ϕ2= 0.9_0.8에서는 당량비의 대칭성파괴가 약하게나마 발생하여 압력섭동의 진폭이 소폭 감소하지만, 높은 진폭으로 여전히 큰 불안정성이 존재하는 것을 확인할 수 있다. 그러나, 당량비 ϕ1, ϕ2= 0.9, 0.7 및 ϕ1, ϕ2= 0.9, 0.6에서는 당량비 대칭성파괴가 강하게 발생하여 진폭이 ϕ1, ϕ2= 0.9, 0.9에 비해 1/150 수준인 압력섭동의 크기가 대폭 감소하였다. 이러한 극적인 진폭 및 소음 감소현상은 모든 조건에서 동일하게 나타난다. 또한, 당량비가 감소할수록 주파수도 감소하는 것을 확인할 수 있다. 이는 총괄 당량비(global equivalence ratio)가 양론비에 멀어질수록 온도에 비례하여 주파수가 감소하는 것으로 판단된다.
연소기 후단 부근에서 측정한 압력 데이터를 이용하여 소음의 크기를 나타내었다. 소음의 크기는 20 dB의 차이가 나면 소리의 크기가 10 배 증폭하는 것을 의미하며, 40 dB은 100배 증폭하는 것이다. 즉, 20 dB 간격마다 10 배씩 증폭한다는 것을 의미한다. Fig. 3의 ϕ1_ϕ2 = 0.9_0.9에서 큰 불안정성과 함께 큰 소음이 발생하였으며, 앞서 설명하였듯이 ϕ1_ϕ2 = 0.9_0.8에서는 당량비의 대칭성파괴가 약하게나마 발생하여 소음강도도 감소하는 것을 볼 수 있다. 강한 대칭성파괴가 발생한 ϕ1_ϕ2 = 0.9_0.7 및 ϕ1_ϕ2 = 0.9_0.6에서는 ϕ1_ϕ2 = 0.9_0.9보다 40 dB 이상 감소하는 것을 확인할 수 있다. 시간 신호, 퓨리에 변환 및 음압 레벨을 통하여 불안정한 조건과 안정된 조건을 구분할 수 있다.
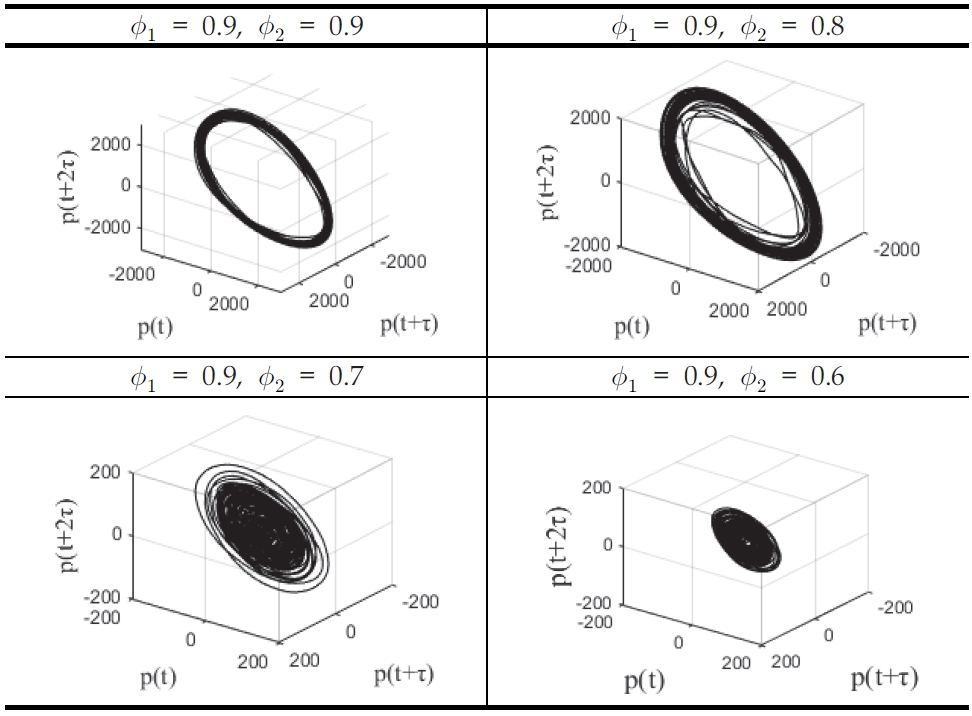
이전까지는 당량비 대칭성파괴에 따른 압력섭동의 퓨리에 변환, 시간 신호 및 음압 레벨의 불안정성에 대해서 살펴보았는데, Fig. 6는 소음이 동반된 화염을 동역학적으로 분석하는 방법인 위상궤적으로 나타내었다. 위상궤적은 특정 시간에 해당 하는 동적신호 P(t)와 τ의 위상차를 통하여 동적신호 P(t + τ)를 이용하는 방법으로, 지연시간(time delay) 값을 찾아 3차원 공간에서 입체적으로 표현함으로써 비선형시스템의 주기적인 거동을 시각적으로 구분하기 위한 대표적인 모드 분석 방법이며, τ는 압력 센서의 상관관계(correlation)를 통하여 선정하였다. 정확한 그래프 형상을 확인하기 위하여 0 ~ 0.5 초에 해당하는 압력 데이터를 이용하여 나타내었다.
이를 통하여 표현되는 위상 궤적도는 시간에 따른 데이터가 단일 혹은 복수의 어트랙터(attractor)와 한계주기진동(limit cycle oscillation)을 가지는 정도에 따라 각각 일정한 형상의 궤적을 보여준다. 궤적의 크기는 압력 진폭에 따라서 비례하며, 굵기는 어트랙터의 숫자와 잡음 등에 관련된다. 궤적도의 크기가 작은 점(point) 형태로 나타나는 고정점 어트랙터는 안정된 상태를 유지하는 거동이며, 도우넛(doughnut) 형태 및 토러스(torus) 모양의 주기 어트랙터는 불안정한 상태의 거동이다. ϕ1_ϕ2= 0.9_0.9 및 ϕ1_ϕ2= 0.9_0.8 경우에는 궤적의 크기가 크며, 토러스 모양의 주기 어트랙터를 나타내고 있다. 또한, 궤적이 일정한 굵기를 가지며, 얇으므로 복수가 아닌 단일 어트랙터에 의한 거동임을 알 수 있다. ϕ1_ϕ2= 0.9_0.7과 ϕ1_ϕ2= 0.9_0.6은 당량비의 대칭성파괴가 강하게 발생하여 궤적의 크기가 이전에 비해 1/10 수준으로 갑자기 작아지며, 기하학적으로 점과 유사한 크기로 수렴하여 고정점 어트랙터로 변경되는 것을 볼 수 있다. 이는 Fig. 5의 퓨리에 변환, 시간 신호, 음압 레벨에서 확인하였듯이 심한 소음과 진폭이 갑자기 감소하는 것과 동일하게 연소불안정성도 극격하게 감소하는 것을 볼 수 있다. 이러한 현상은 본 연구의 실험조건들에서 당량비 및 노즐 배치에 따른 대칭성파괴 조건들에서 매번 동일하게 발생하게 되면 대칭성파괴 효과가 나타나기 전에 궤적의 진폭이 커졌다가 대칭성파괴 효과가 발생함에 따라서 궤적의 진폭이 감소하면서 완전히 작아지는 거동을 보였다.
3.2 노즐 배치에 따른 대칭성파괴 현상
앞 절에서는 당량비에 대한 대칭성파괴 현상을 확인하였는데 본 절에서는 노즐의 배치에 따른 대칭성파괴 현상을 알아보고자 압력 섭동 및 열-방출 섭동에 대한 등고선 지도(contour map)를 Fig. 7에 나타내었다. Fig. 7에서도 알 수 있듯이 모든 노즐 배치 조건에서 압력과 열-방출 섭동에 대한 등고선 지도의 최대 섭동값을 가지는 구간이 동일하게 나타났으며, 인접한 노즐 간의 당량비와 노즐 배치를 제어하여 연소 시스템의 상태가 불안정한 조건에서 매우 안정된 조건으로 변경될 수 있음을 보여주고 있다.
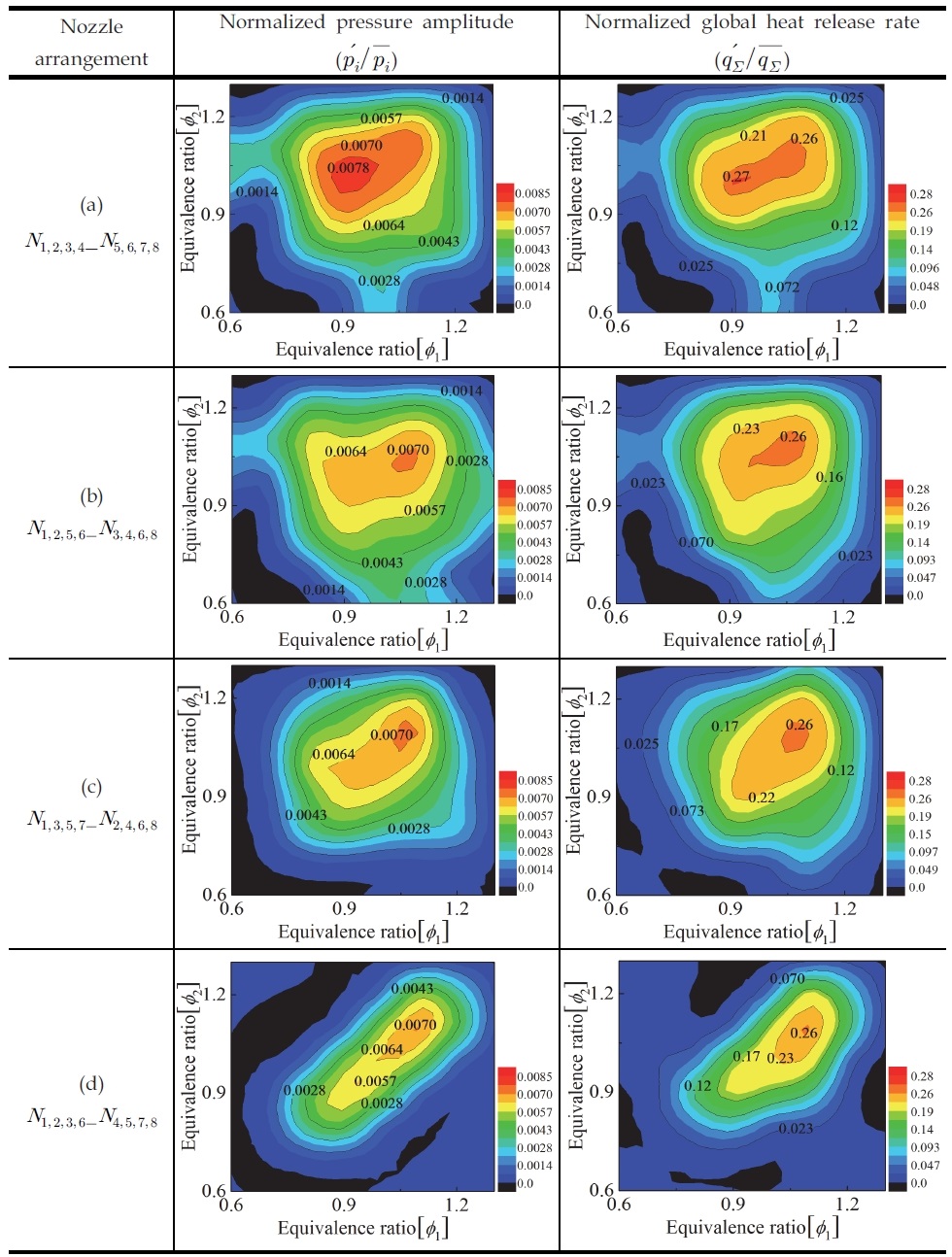
Stability maps in symmetry beaking of normalized combustor pressure amplitude, normalized heat release rate.
노즐의 배치는 Table 1에 나타내었으며, 전체적으로 노즐의 배치 조건에서 당량비가 동일한 ϕ1 = ϕ2(ϕ > 0.8) 경우에는 불안정한 영역으로 나타나며, ϕ1 > ϕ2 이거나 ϕ1 < ϕ2로 당량비가 비대칭이면서 차이가 크면 클수록 안정된 영역으로 나타남을 볼 수 있다. 이처럼 당량비의 차이가 크면 불안정성이 감소하는 것을 볼 수 있으며, 이는 화염 간에 상호작용으로 불안정성이 감소하는 것으로 판단된다. 또한, 총괄 당량비가 양론비에 가까워지게 되면 불안정성도 크게 발생하는 것을 확인할 수 있다.
먼저, Table 1의 노즐 배치(a)는 8 개의 노즐중에서 4 개의 노즐들이 연속적으로 배치되는 경우로, 다른 배치 조건들보다 뚜렷한 대칭성을 가진다. 이 경우에는 압력 섭동과 열-방출 섭동의 값이 다른 배치 조건들보다 크게 나타났으며, 불안정한 영역이 가장 넓은 것을 볼 수 있다. 노즐 배치(b)는 2 개의 노즐 간격으로 배치된 경우이다. 노즐 배치(a)처럼 4 개의 노즐이 연속적으로 배치되어 있지는 않지만, 약간의 연속성과 대칭성을 가진다. 노즐 배치(b)는 노즐 배치(a)보다 섭동의 값이 작지만, 불안정성이 발생하는 영역과 최대 섭동을 가지는 구간은 비슷한 것을 확인할 수 있다. 또한, 총괄 당량비가 양론비에 가까울수록 불안정성이 크게 발생하였으나, 노즐 배치(a)보다 당량비의 차이가 클수록 불안정성은 감소하는 것을 볼 수 있다. 노즐 배치(c)는 노즐 배치 (a), (b)와 다르게 노즐 배치가 연속적으로 되어있지는 않지만, 배치의 대칭성은 가지는 것을 볼 수 있으며, 총괄 당량비가 양론비에 가깝더라도 불안정성이 크게 발생하지 않는다. 또한, Fig. 2처럼 서로 같은 당량비를 가질 때 불안정성이 가장 크게 나타났으며, 당량비의 차이가 클수록 불안정성도 더 급격하게 감소하는 것을 볼 수 있다.
노즐 배치(a)~(c)의 경우를 통해 8 개의 노즐에서 4개씩 배치가 대칭성을 가지게 된다면 안정된 영역이 (a), (b), (c) 배치 모두 비슷한 것을 확인할 수 있다. 또한, 노즐이 연속성에 따라서 안정된 영역도 넓어지거나, 작아진다. 그러나, 불안정성 영역에서는 당량비 및 배치에 대한 대칭성파괴 효과는 다르게 나타나는 것을 볼 수 있다. 노즐 배치(d)는 노즐이 연속적으로 배치가 되어있지 않으며, 대칭성도 없는 경우이다. 이 경우엔 노즐 배치(c)와 동일하게 ϕ1 = ϕ2(ϕ > 0.8)을 제외한 나머지 영역에서는 불안정성이 거의 발생하지 않는 것을 볼 수 있으며, 대칭성을 가지지 않기 때문에 ϕ1 > ϕ2 및 ϕ1 < ϕ2 차이가 크지 않아도 불안정성이 감소하는 것을 확인할 수 있다.
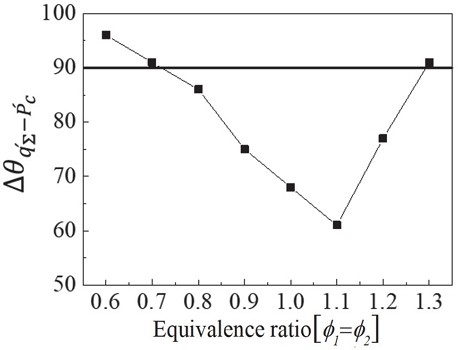
이처럼 노즐의 배치 및 당량비의 대칭성파괴 효과로 연소불안정성이 급격하게 감소하게 되며, 비대칭 제어 방식으로 다중형태의 연소기 형상에서 연소불안정성에 영향을 미칠 수 있음을 파악하였다. 불안정성이 감소하는 원인으로 다중 노즐에서 화염 간에 상호작용(interaction)으로 한계주기 거동에 큰 영향을 미친다고 판단되어 화염 간 상호작용을 설명하기 위해 Rayleigh 기준(rayleigh criterion)이 충족하는지 확인하였다. Fig. 7은 동일한 당량비에 따른 연소기 압력 및 열-방출 사이의 위상차를 나타내었는데, Fig. 3과 반비례하는 것을 볼 수 있다. Fig. 8을 통해 안정된 당량비인 0.6, 0.7 및 1.3에서는 역상(out of phase)형태이며, 불안정한 조건인 0.8 ~ 1.2까지는 열-방출과 압력섭동이 동일한 위상(in-phase)으로 레일리 기준이 충족하는 것을 확인할 수 있다. 또한, 모든 당량비 조건에서도 레일리 기준을 만족한다. 그러나, 레일리 기준이 충족한다고 해도 연료 분배와 노즐 배치의 비대칭성에 따른 연소불안정성 억제 원인을 규명에 대한 설명으로는 다소 부적절하였다.
본 연구에서는 실험적으로 노즐 배치의 대칭성파괴 현상에 대해서 초점을 맞춰서 실험을 진행하였으며, 노즐 배치의 비대칭성에 따른 연소불안정성이 감소하는 것을 확인할 수 있으나 실험적으로는 원인을 규명하기에는 많은 어려움과 추가적인 연구가 필요하다. 그러나, 노즐 배치에 따른 대칭성파괴 방법은 수치해석의 실험 데이터로 사용되기에 충분하였다.
4. 결 론
본 연구에서는 환형연소기에서 발생하는 연소불안정성을 제어하는 방법으로 노즐의 당량비 및 배치를 통해 유동적인 대칭성파괴 현상과 효과에 관해 확인하여 다음과 같은 결론을 얻었다.
1) 본 연구에서는 종-방향의 불안정성 모드를 제외하고 다른 모드의 연소불안정성은 발생하지 않는 것을 확인하였다.
2) 당량비 및 노즐 배치를 통하여 유동적인 대칭성파괴 방법으로 환형연소기의 연소불안정성을 제어할 수 있었으며, 대칭성파괴 효과에 따라서 극적으로 연소불안정성과 소음이 감소하였다.
3) 퓨리에 변환, 시간 신호, 위상궤적의 모드분석을 통하여 대칭성파괴 효과를 확인하였고 불안정한 영역과 안정된 영역을 구분되었으며, 이를 등고선 지도에 나타내었다.
4) 당량비와 노즐 배치가 대칭이거나 노즐이 연속적으로 배치된다면 불안정성이 증폭되는 것을 확인할 수 있으며, 총괄 당량비가 양론비에 가까울수록 불안정성도 더욱 증가하였다.
5) 당량비의 차이가 클수록 불안정성은 감소하는 것을 볼 수 있으며, 대칭성이 파괴된 노즐 배치에서는 당량비의 차이가 작더라도 불안정성이 극적으로 감소하는 것을 확인할 수 있었다.
6) 압력 및 열-방출 사이의 위상차가 Rayleigh 기준에 충족하는 것을 확인하였으나 특히, 노즐 배치에 따른 연소불안정성의 감소 원인을 규명하기에는 많은 어려움과 추가적인 연구가 요구된다.
Acknowledgments
이 논문은 2022년도 정부(산업통산자원부)의 재원으로 한국에너지기술평가원의 에너지기술개발사업(2020671010060, 분산발전 가스터빈용 수소전소 저 NOx 연소기 개발)과 에너지기술개발사업(20181110100290, 발전용 H급 can-type 저선회 버너 원천기술 개발)의 지원을 받아 작성되었습니다.
References
-
K. Prieur, D. Durox, T. Schuller and S. Candel, “A hysteresis phenomenon leading to spinning or standing azimuthal instabilities in an annular combustor,” Combustion and Flame, Vol. 175, pp. 283-291 2017.
[https://doi.org/10.1016/j.combustflame.2016.05.021]

-
S. Evesque and W. Polifke, C. Pankiewitz, “Spinning and azimuthally standing acoustic modes in annular combustors,” 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, pp. 1-8, 2003.
[https://doi.org/10.2514/6.2003-3182]

-
N. A. Worth and J. R. Dawson, “Effect of equivalence ratio on the modal dynamics of azimuthal combustion instabilities,” Proceedings of the Combustion Institute, Vol. 36, pp. 3743-3751, 2017.
[https://doi.org/10.1016/j.proci.2016.06.115]

-
J. Wang, P. Rubini, Q. Qin and B. Houston, “A model to predict acoustic resonant frequencies of distributed helmholtz resonators on gas turbine engines,” Applied Sciences, Vol. 9, 1419, 2019.
[https://doi.org/10.3390/app9071419]

-
N. A. Worth and J. R. Dawson, J. AM sidey, E. Mastorakos, “Azimuthally forced flames in an annular combustor,” Proceeding of the Combustion Insatitute, Vol. 36, pp. 3783-3790, 2017.
[https://doi.org/10.1016/j.proci.2016.06.107]

-
R. Balachandran, B. O. Ayoola, C. F. Kaminski and A. P. Dowling, E. Mastorakos, “Experimental investigation of the nonlinear response of turbulent premixed flames to imposed inlet velocity oscillations,” Combustion and Flame, Vol. 143, pp. 37-55, 2005.
[https://doi.org/10.1016/j.combustflame.2005.04.009]

-
Yoon, J., Joo, S., Kim, J., Lee, M., Lee, J. and Yoon, Y., “Effects of convection time on the high harmonic combustion instability in a partially premixed combustor,” Proceedings of the Combustion Institute, Vol. 36, pp. 3753-3761, 2017.
[https://doi.org/10.1016/j.proci.2016.06.105]

- Shin, Y., Jeon S. and Kim, Y., ”Combustion Instability Analysis of LIMOUSINE Burner using LES-based Combustion Model and Helmholtz Equation,” J. Korean Soc. Combus., Vol. 22, pp. 41-46, 2017.
-
C. Li, D. Yang, S. Li and M. Zhu, “An analytical study of the effect of flame response to simultaneous axial and transverse perturbations on azimuthal thermoacoustic modes in annular combustors,” Proceedings of the Combustion Institute, Vol. 37, pp. 5279-5287, 2019.
[https://doi.org/10.1016/j.proci.2018.05.121]

-
N. Noiray, M. Bothien and B. Schuermans, ”Investigation of azimuthal staging concepts in annular gas turbines,” Combustion Theory and Modelling, Vol, 15, pp. 585-606, 2011.
[https://doi.org/10.1080/13647830.2011.552636]

-
N. A. Worth and J. R. Dawson, Modal dynamics of self-excited azimuthal instabilities in an annular combustion chamber,” Combustion and Flame, Vol. 160, pp. 2476-2489, 2013.
[https://doi.org/10.1016/j.combustflame.2013.04.031]

-
J. R. Dawson and N. A. Worth, “The effect of baffles on self-excited azimuthal modes in an annular combustor,” Proceedings of the Combustion Institute, Vol. 35, pp. 3283-3290, 2015.
[https://doi.org/10.1016/j.proci.2014.07.011]

- M. Bauerheim and T. Poinsot, “Analytical methods for azimuthal thermo-acoustic modes in annular combustion chambers,” Center for Turbulence Research, pp. 77-88, 2015.
-
M. Bauerheim, P. Salas, F. Nicoud and T. Poinsot, “Symmetry breaking of azimuthal thermo-acoustic modes in annular cavities: a theoretical study,” J. Fluid Mech. Vol. 760, 431-465, 2014.
[https://doi.org/10.1017/jfm.2014.578]

-
N. Noiray, M. Bothien and B. Schuermans, “Investigation of azimuthal staging concepts in annular gas turbines,” Combust. Theory and Modelling, Vol. 15, 2011.
[https://doi.org/10.1080/13647830.2011.552636]

-
M. Bauerheim, M. Cazalens and T. Poinsot, “A theoretical study of mean azimuthal flow and asymmetry effects on thermo-acoustic modes in annular combustors,” Proceedings of the Combustion Institute, Vol. 35, 3219-3227, 2015.
[https://doi.org/10.1016/j.proci.2014.05.053]

-
G. Ghirardo and M. P. Juniper, “Azimuthal instabilities in annular combustors: standing and spinning modes,” Proceeding of the Royal Society A, 469, 2013.
[https://doi.org/10.1098/rspa.2013.0232]

-
C. Li, D. Yang, S. Li and M. Zhu, “An analytical study of the effect of flame response to simultaneous axial and transverse perturbations on azimuthal thermoacoustic modes in annular combustors,” Proceeding of the Combustion Insatitute, Vol. 37, 5279-5287, 2019.
[https://doi.org/10.1016/j.proci.2018.05.121]

-
Moon, K., Jegal, H., Gu, J. and Kim, K., “Combustion-acoustic interactions through cross-talk area between adjacent model gas turbine combustors,” Combustion and Flame Vol. 202 405-416, 2019.
[https://doi.org/10.1016/j.combustflame.2019.01.027]

-
Moon, K.H. and Kim, K.T., “Self-Excited Azimuthal Instabilities in a Can-Annular Combustion System,” J. Korean Soc. Combust., Vol. 27, 9-16, 2022.
[https://doi.org/10.15231/jksc.2022.27.1.009]

-
Lee, H., Kim, J. and Lee, K.M., “Control of the Longitudinal Instability by Symmetry Breaking in the Can Burner Simulating Annular Nozzle,” J. Korean Soc. Propulsion Engineers., pp. 66-78, 2021.
[https://doi.org/10.6108/KSPE.2021.25.2.066]

-
Guan, M. Murugesan and L.K.B. Li, “Strange Non-chaotic and Chaotic Attractors in a Self-Excited Thermoacoustic Oscillator Subjected to External Periodic Forcing,” Chaos, Vol. 28 093109, 2018.
[https://doi.org/10.1063/1.5026252]