CBT를 이용한 고체 추진제의 연소효율 도출 방법과 그레인 형상의 영향 분석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 CBT(Closed Bomb Test)시험을 통하여 고체추진제의 연소효율을 추정하는 방법을 제시하였다. CBT는 수백 기압에서 작동하므로 실기체의 영향을 고려하기 위해 Noble-Abel 상태방정식을 적용하였다. 또한 밀폐용기 벽면으로 발생하는 열손실을 고려하였다. 그레인의 연소로 인한 그레인의 체적 변화율 계산은 형상 함수(Form Function)를 적용하였으며, 총 8개의 다른 형태 그레인의 연소 효율을 도출하였다. 본 연구에서 제시한 이론모델의 적절성을 실험 결과인 압력-시간 선도와 비교하여 나타내었다. 그레인 형상과 추진제의 충진량에 따른 연소효율을 도출하였다.
Abstract
The estimation method of combustion efficiency has been introduced by using closed bomb test(CBT). The Noble-Abel equation of state was applied to consider the real gas effects to take account of high operation pressure about a couple of 100 atm. of CBT. The heat loss through the CBT wall was considered. The volume change of grain was calculated by applying form functions, which estimated combustion efficiency of 8 different gain shapes. The combustion estimation method proposed in this study was fairly validated by the comparision with the pressure-time history data of the CBT experiments. The effects of both grain shape and propellant loading density were analyzed.
Keywords:
Solid Propellant, Closed Bomb Test, Combustion Efficiency, Form Function키워드:
고체추진제, 밀폐용기실험, 연소효율, 형상함수1. 서 론
고체추진제는 다양한 에너지 발생 시스템(화포, 로켓 및 에어백 등)의 추진제로 사용되고 있다[1]. 에너지 발생 시스템 개발을 위하여 작동 영역에서의 고체추진제의 연소속도와 연소효율은 매우 중요한 설계 인자이다. 고체추진제의 연소속도는 연소실 압력에 영향을 받으며 일반적으로 압력의 n제곱에 비례한다[2]. 이 때 지수 n은 실험적으로 구할 수 있는 상수이다 (Eq. 12 참조). 또한 고체추진제의 연소속도에 영향을 미치는 인자로는 추진제의 초기 온도, 연소실의 움직임 등 추진제 외부 환경의 영향도 존재한다. 고체추진제의 연소속도를 구하는 방법으로는 drop tube, 스트랜드 버너(strand burner), CBT(closed bomb test)와 같은 실험장치를 사용할 수 있다.
인도의 High Energy Materials Research Laboratory(HEMRL)는 다양한 장치를 이용하여 고체추진제의 연소속도를 측정하는 방법을 정리하였다[3]. 일반적으로 연소속도를 측정하기 위해서 스트랜드버너 방식과 CBT가 사용되는데, 스트랜드버너 방식은 추진제를 특정 길이의 담배 모양으로 시편을 만들어 타들어 가는데 소요되는 시간을 측정하는 방법이다. 스트랜드버너 방식은 정상 상태에서의 안정적인 연소속도 데이터를 제공한다는 장점이 있지만 초고압(수백기압 이상)에서 작동하는 추진제의 연소속도 측정은 기술적으로 매우 어렵다. 그에 반해 CBT의 경우 간단하면서도 추진제의 충진량에 따라 초고압까지의 연소속도를 측정할 수 있다[4]. 또한 연소속도와 함께 추진제의 발열량은 추진제의 성능을 대표하며, 실제 발열량은 이론적 발열량과 연소효율의 곱으로 나타낼 수 있다. CBT 실험 내부는 고온고압의 환경으로 열량과 온도의 측정이 불가하므로 이에 대한 추정 방법이 필요하다. 본 연구진은 선행 연구를 통해 CBT를 이용한 추진제의 연소속도 산출방법을 제안한 바 있다[5]. 본 연구에서는 CBT에서 측정한 압력 데이터를 통해 연소효율을 추정하는 방법을 제안하고, 8개의 그레인 형상에 대한 연소효율을 도출하였다. 연소하면서 변화하는 그레인의 형상 변화율은 3차 형상 함수(Cubic Form Function)을 사용하여 계산하였다.
2. 이 론
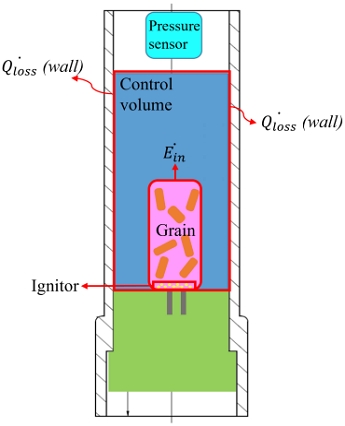
본 연구에 사용한 CBT의 형상은 실린더 형상이다(Fig. 1). 고체추진제는 실린더 용기의 하부에 놓여있으며 전기에너지로 점화되는 점화제가 그레인 아래에 놓여있다. 압력을 측정하는 압력센서는 용기의 상부에 위치한다. 본 연구를 위해 다음과 같은 가정을 한다.
- (1) 그레인 표면의 비균일 연소는 없음.
- (2) 점화제에 의한 열발생은 무시함.
- (3) 밀폐용기 내부의 압력 전파에 의한 압력 진동은 무시함.
- (4) 열손실은 용기 벽면을 통해서만 발생함.
2.1 지배방정식
CBT 내부의 물리적 현상을 모사하기 위해 검사체적을 밀폐 용기 내 추진제를 제외한 기상의 부피를 고려하였다. 추진제가 연소하면서 생성하는 연소가스의 효율을 고려한 검사체적에 따른 에너지 보존방정식은 다음과 같다.
| (1) |
여기에서 η는 연소효율을 의미하며, 2.3절에 자세히 다루었다. 검사체적 내의 에너지 변화와 생성되는 연소가스의 에너지를 고려하기 위한 항들은 다음과 같다[6].
| (2) |
| (3) |
이때 연소가 진행됨에 따라 발생하는 연소가스의 물성치들은 CEA를 사용하였다[7].
CBT에서 벽면으로의 열손실은 Saha와 Acharya[8]가 제안한 방법을 사용하였으며 다음과 같다.
| (4) |
| (5) |
CBT에서 연소 후의 연소실 내부는 고온, 고압의 환경으로 에너지가 높고 기체 분자가 매우 빠른 속도로 거동하므로 분자의 체적 및 분자 간 충돌 영향을 무시할 수 없다. 따라서 이를 모사하기 위한 실제기체 Noble-Abel 상태방정식은 다음과 같다.
| (6) |
위 식을 시간에 대해 미분하면 다음과 같다.
| (7) |
2.2 그레인 형상
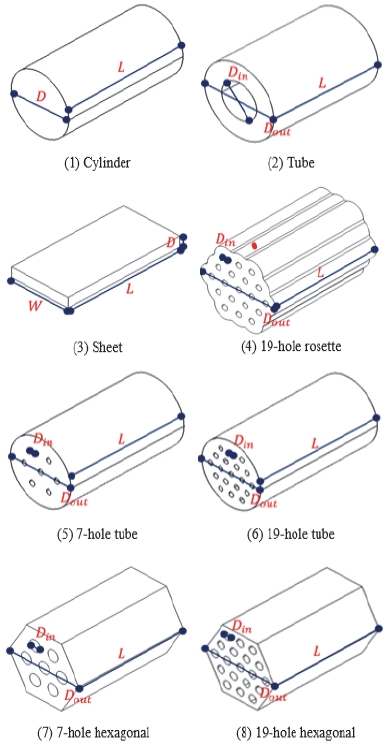
본 연구에서는 analytic method를 사용하여 기하학적 해석을 통해 총 8종의 그레인 형상을 고려하였다(Fig. 2).
각 형상은 Vittal과 Singh[9]가 제안한 방법을 사용하였으며, 기하학적 변수를 3차 형상 함수(Cubic Form Function)로 구성하면 그 관계식은 다음과 같다. 이 때 e는 추진제의 연소거리를 의미하며 시간에 따른 연소거리의 변화율은 Eq. 12의 연소속도로 나타난다.
| (8) |
| (9) |
| (10) |
각 형상 인자들은 부록에 제시하였다(Table A-1, A-2.).
| (11) |
Eq. 11은 고체추진제의 연소로 발생하는 연소가스의 질량 변화율을 형상함수로 표현된 체적분율을 통해 나타난 식이다. 이 때 는 연소속도를 의미하며 2.3절에 자세히 다루었다. 발생하는 연소가스의 질량은 Eq. 3에서 시스템 내부에너지를 변화시키고 검사체적 내 온도, 압력 또한 변화시킨다.
2.3 연소속도와 연소효율
연소속도는 연소실의 압력의 n제곱에 비례하며 그 관계는 다음과 같다[10].
| (12) |
연소속도는 시간당 연소거리의 변화량을 의미하며 단위는 [cm/s] 이며, 압력 단위는 [MPa]이다. 연소거리(e)에 대한 Eq. 8에서 연소거리 분율(f)을 구하고 체적 분율(z)에 적용하여 형상변화율을 고려하였다.
이 때 연소속도에 사용되는 상수 a와 n값은 선행 연구에서 수행한 연소속도 추정 연구[5]를 기반으로 실험데이터를 통해 구한 값을 사용하였다.
연소효율은 추진제의 이론적 발열량 대비 실제 발생하는 연소가스의 열량의 비로 정의하였으며, 이를 온도를 기준으로 연소효율을 적용할 수 있다.
| (13) |
CBT는 아주 짧은 시간(수십 msec)내에서 수백 기압의 고압 고온의 환경에서 작동하므로 열량 및 온도 측정이 불가하다. 따라서 본 연구에서는 그레인의 연소로 인해 생성된 CBT에서 측정한 압력-시간 데이터를 이용하여 연소효율을 추정하는 방법을 연구하였다. 추정된 연소효율은 고압 고온 환경에서 작동하는 CBT 내에서 실제 발열량을 측정할 수 없어 검증은 불가하지만 실제 CBT 내에서 발생하는 현상을 모사하는 데 있어 필요한 인자이다.
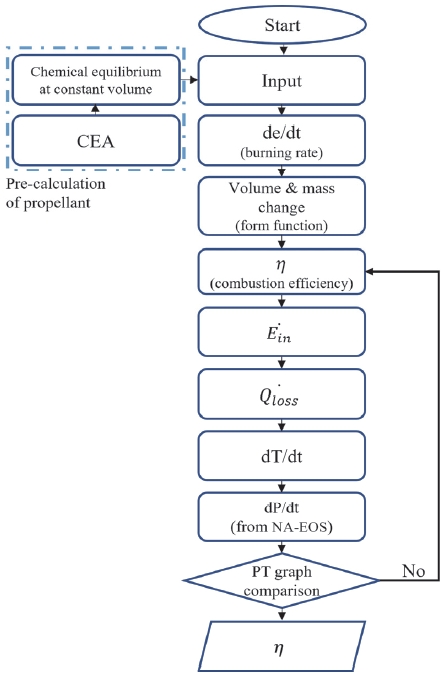
Fig. 3는 본 연구에서 적용한 연소효율 계산 흐름도이다. CEA 정적연소 모델을 통해 작동 영역에서 연소가스의 열역학 특성치와 추진제 연소에 의해 발생하는 이론 발열량을 계산하여 본 계산에 필요한 열역학 데이터를 제공한다. 압력을 고려한 연소속도를 통해 연소거리를 계산하고, 추진제의 형상을 고려한 3차 형상 함수를 적용하여 연소된 추진제량을 도출한다. 일차적으로 연소효율을 추정하여 Eq. 2, 3의 계산을 위한 필요 요소(에너지, 밀폐용기 내 온도 등)를 계산한다. 그 이후 벽면에서 발생하는 열손실을 통해 검사체적 내의 압력 변화를 예측하고 실험 데이터인 압력-시간(P-T) 선도와 비교하여 일치할 때까지 연소효율 값을 재추정하는 일련의 과정을 반복 계산하여 연소효율을 도출한다.
3. 본 론
본 연구에서 사용된 추진제는 더블베이스 추진제이며 조성은 Table 1과 같다.
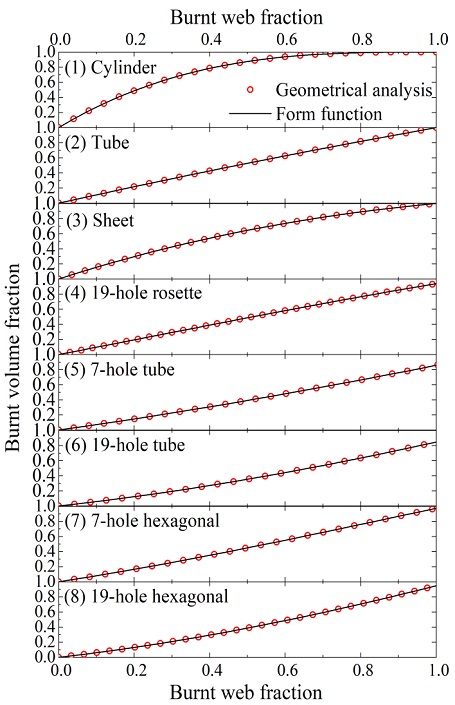
3.1 3차 형상함수 검증
2.2절에서 설명된 추진제 형상 함수를 검증하였다. 총 8종의 그레인 형상에 대해 drafting method 방법인 CAD (Computer-Aided Design) 툴인 CATIA로 계산한 결과(Geometrical Analysis)[11]와 본 연구에 사용된 형상함수는 모든 추진제 형상에 대해 잘 일치함을 알 수 있다(Fig. 4).
3.2 열손실과 충진량 효과
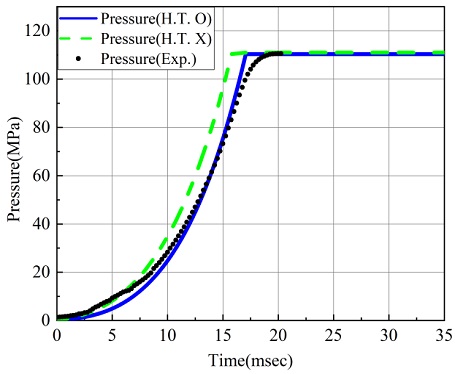
Fig. 5는 원통 7공형 그레인의 추진제 충진량(Loading Density(LD))이 0.1일 때 CBT 벽면에서의 열손실을 고려한 경우(H.T. O)와 고려하지 않은 경우(H.T. X)의 압력-시간 선도를 비교한 결과이다. 이 때 추진제 충진량(LD, g/cc)은 밀폐용기 부피 대비 총 추진제의 질량을 의미한다. LD가 같더라도 기공의 개수가 다르면 단일 그레인의 질량과 형상이 모두 다르기 때문에 충진량을 사용하였다. 열손실을 고려하지 않았을 때의 결과와 비교해서 최대 압력에 도달하기 위한시간이 약 1.8 msec차이가 발생한다. 또한 연소효율은 열손실을 고려하지 않은 경우 90%, 열손실을 고려한 경우 92%로 추정된다. 이는 벽면에서의 열손실로 인한 연소가스의 내부에너지가 감소하고 그로 인한 압력 상승률이 감소하기 때문이다. 또한 충진량에 의해 상승되는 최대압력은 실험과 해석결과 모두 약 109 MPa로 나타난다.
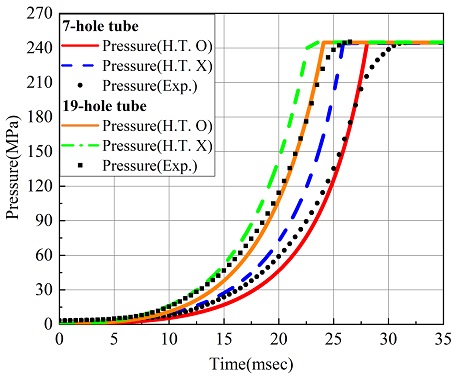
Fig. 6는 충진량(LD) 0.2일 때 원통 7공형과 원통 19공형에 따른 압력-시간 선도를 비교한 결과이다. 압력-시간 선도에서의 압력 상승 기울기는 형상에 따라 다른 것을 확인할 수 있고 19공형와 7공형에서의 비교 시 19공형에서 빠르게 증가하는 것을 확인할 수 있다. 또한 열손실의 지연시간 차이는 원통 7공형의 경우 약 1.7 msec, 원통 19공형의 경우 2 msec로 나타난다.
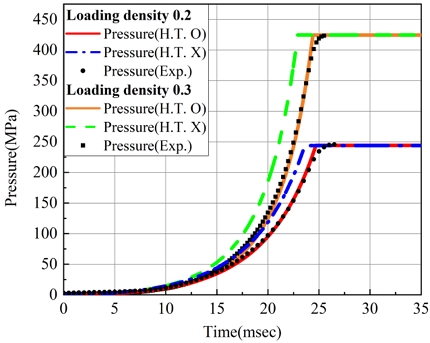
Fig. 7은 충진량(LD)에 따른 압력-시간 선도를 비교한 결과이다. 두 경우 모두 열손실을 고려한 이론 모델과 실험이 유사함을 알 수 있다. 최대 압력은 추진제의 충진량에 비례하며 충진량이 0.2과 0.3의 경우 최대압력은 각각 약 243 MPa, 약 424 MPa로 나타난다.
3.3 연소효율
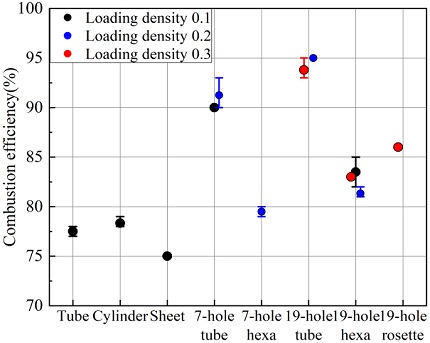
Fig. 8은 그레인 형상과 추진제 충진량에 따른 연소효율을 추정한 결과이다. 단공형은 약 77%, 원통형은 약 78.7%, 판상형은 75%의 연소효율을 나타내고 있다. 원통 7공형의 연소효율은 약 90.6%, 육각 7공형은 약 80%, 원통 19공형은 약 94.3%, 육각 19공형은 약 82.5%, 로젯 19공형은 약 87%를 나타낸다. 그러나 충진량은 연소효율에 영향을 미치지 않는 것을 알 수 있다.
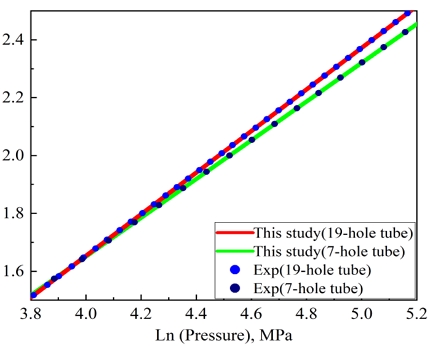
원통형, 원통 7공형, 원통 19공형의 연소효율을 비교하면 기공 개수가 많아짐에 따라 연소효율이 증가함을 알 수 있다. 이는 육각 7공형과 육각 19공형에서도 같은 경향이 나타난다. 그 원인을 분석하기 위하여 원통 7공형과 원통 19공형의 연소속도를 Eq. 12을 사용하여 구한 뒤 비교하였다(Fig. 9). 실험과 이론계산에서 모두 원통 19공형의 연소속도가 원통 7공형의 연소속도보다 빠르게 증가함을 알 수 있다. 밀폐용기 내부 압력에 의해 빠르게 증가하는 연소속도는 Eq. 11에서의 연소가스의 질량을 증가시키고 그로 인해 검사 체적의 내부에너지를 더욱 빠르게 증가시킨다. 또한 Eq. 11에서 연소 면적인 Ab가 기공의 개수에 많아짐에 따라 그레인 내부 면적이 증가하여 커진다. 따라서 빨라진 연소속도의 영향을 받는 연소면이 증가하고 이로 인한 그레인의 실제 발열량의 상승으로 이어져 연소효율의 상승으로 작용한다.
또한 같은 19공형의 형상(원통 19공형, 육각 19공형, 로젯 19공형)이더라도 즉 같은 기공의 개수를 가지고 있는데 연소효율은 육각 19공형-로젯 19공형-원통 19공형 순으로 연소효율이 증가함을 알 수 있다. 이는 위에서 기공의 개수의 증가의 원인과 동일하게 그레인 표면이 곡면의 형태일수록 그레인과 그레인의 사이에 공간이 발생하여 연소면적이 증가하기 때문이다.
4. 결 론
본 연구에서는 CBT에서 측정한 압력-시간 데이터를 이용하여 연소효율을 추정하는 방법을 제시하고 이를 적용하여 추진제의 형상과 충진량의 영향을 분석하였다. 또한 그레인 형상에 대한 형상 함수를 제시하고 검증하였다. 벽면에서의 열손실을 고려하여 이론 모델의 결과는 실험에서 측정한 압력-시간 선도와 비교하여 일치함을 확인하고, 이를 이용하여 연소효율을 도출하는 방법을 제시하였다. 최대 압력은 추진제 충진량(LD)에 비례하여 달라지는 것을 확인하였다. 그렇지만 충진량은 연소효율에 영향을 미치지 않았으며, 그레인의 기공 개수에 따라 연소효율이 변화하는 것을 확인하였다. 기공의 개수가 증가할수록 연소효율이 증가하였다. 연소효율은 기공의 개수에 따라 원통형의 경우에는 90.6%에서 94.3%, 육각형은 80%에서 82.5%로 증가하였다. 증가의 원인은 기공 수가 증가할수록 그레인의 연소면적이 증가하고 이는 연소속도를 증가시키기 때문이다. 또한 같은 기공 수임에도 육각 19공형-로젯 19공형-원통 19공형 순으로 연소효율이 증가하는데 이는 육각-로젯-원통 순으로 그레인 간의 공간이 커짐에 따라 연소면적이 증가하기 때문이다.
Nomenclature
| a : | Burning rate constant |
| Aw : | Area of wall |
| Ab : | Burning area |
| b : | Covolume |
| Cv : | Specific heat of gas at constant volume |
| Cp,f : | Specific heat of flame at constant pressure |
| Esys : | Internal energy at system |
| : | Increase energy from burnt grain |
| e : | Burn distance |
| D : | Outer diameter of propellant |
| f : | Fraction of burn distance |
| h : | Heat transfer coefficient |
| k : | Thermal conductivity |
| k1, k2, k3 : | Form function coefficients |
| mg : | Mass of gas |
| mf : | Mass of flame |
| : | Gas mass flow rate |
| : | Flame mass flow rate |
| n : | Burning rate exponent |
| P : | Chamber pressure |
| Pmax : | Maximum chamber pressure |
| Qact : | Quantity of heat of actual flame |
| Qtheo : | Quantity of heat of theoretical flame |
| : | Heat loss rate from wall |
| : | Burning rate |
| R : | Gas constant |
| t : | Time |
| T : | Temperature |
| Tm : | Mean temperature |
| To : | Initial temperature |
| Tf,act : | Temperature of actual flame |
| Tf,theo : | Temperature of theoretical flame |
| V : | Chamber volume |
| Vp : | Propellant volume |
| Vp,0 : | Initial propellant volume |
| z : | Burnt volume fraction |
| α : | Thermal diffusivity |
| ρp : | Propellant density |
| σ : | Radiation heat transfer coefficient |
| η : | Combustion efficiency |
Acknowledgments
본 연구는 방위산업기술지원센터의 지원(사업명: 화포 추진제 및 추진성능 예측 SW기술, 과제번호: UC190003D)하에 수행되었습니다.
References
-
Lysien, K., Stolarczyk, A. and Jarosz, Tomasz., “Solid Propellant Formulations : A Review of Recent Progress,” Materials, Vol. 14, 2021.
[https://doi.org/10.3390/ma14216657]

- Koněčný, P. and Z. Křižan. “Determination of black powder burning rate,” Advances in Military Technology, Vol. 3, No. 2, 11-18, 2008.
- Gupta, G., Jawale, L., Mehilal, D. and Bhattacharya, B., “Various Methods for the Determination of the Burning Rates of Solid Propellants – An Overview,” Central European Journal of Energetic Materials, Vol. 12, No. 3, pp. 593-620, 2015.
- Sung, H.-G. and Yoo, J.C., “Burning Rate Characteristics of Solid Propellant at Extremely High Pressure,” Journal of the Korean Society of Propulsion Engineers, Vol. 10, No. 3, pp. 60-66, 2006.
-
Choi, H.Y., Lee, D.S., Sung, H.G., Lee, W.M. and Kim, E.M., “Burning Rate Estimate Method of Solid Propellants at High Pressure Condition,” Journal of Korean Society of Propulsion Engineers, Vol. 26, No. 1, pp. 28-37, 2021.
[https://doi.org/10.6108/KSPE.2022.26.1.028]

-
Han, D.H., Sung, H.G. and Ryu, B.T., “Parametric Analysis and Design Optimization of a Pyrotechnically Actuated Device,” International Journal of Aeronautical and Space Sciences, Vol. 17, No. 3, pp. 409-422, 2016.
[https://doi.org/10.5139/IJASS.2016.17.3.409]

- Gordon, S. and McBride, B.J., “Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications: I. Analysis,” NASA, Cleveland, O.H., U.S.A., NASA RP-1311, 1994.
-
Saha, Krishnendu and Sumanta Acharya., “Heat transfer enhancement using angled grooves as turbulence promoters,” Journal of Turbomachinery, Vol. 136, No. 8, 2014.
[https://doi.org/10.1115/1.4025733]

-
Vittal, D. and Singh, S., “Form Function for Propellants in Closed Vessel Work,” Propellants, Explosives, Pyrotechnics, Vol. 5, No. 1, pp. 9-14, 1980.
[https://doi.org/10.1002/prep.19800050103]

-
Kubota, N., Propellants and Explosives: Thermochemical Aspects of Combustion, 3rd ed., John Wiley & Sons Inc., New York, N.Y., U.S.A., 2015.
[https://doi.org/10.1002/9783527693481]

- Y. Ata, “Numerical burnback analysis of three dimensional solid propellant grains,” M.S. - Master of Science, Middle East Technical University, 2015.