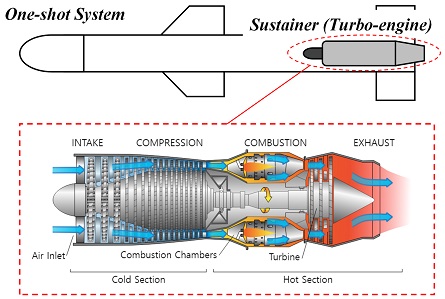
일회성 터보엔진용 구름 베어링의 저장 수명 예측에 관한 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
유도무기용 일회성 터보엔진은 장기간 저장 후에도 운용 신뢰성이 보장되어야 한다. 터보엔진의 운용 신뢰성에 큰 영향을 미치는 구름 베어링은 장시간 저장에 의해 궤도면 및 전동체에 산화층이 형성될 수 있으며, 이로 인해 미세 치수의 변화를 유발하여 고장이 발생할 수 있다. 본 연구에서는 실제 장기 저장된 일회성 터보엔진 베어링을 획득하고, 전동체 조도의 열화 데이터를 이용하여 저장 수명을 예측하였다. 저장 수명은 와이베이즈(Weibayes) 분석 방법과 선형 열화식의 계수를 난수로 생성하는 난수 생성 기반 분석 기법을 통해서 예측하였다. 본 연구에서는 두 가지 수명평가 방법의 결과를 상호 비교하고 이에 따른 장단점을 분석하였다. 향후, 추가적인 장기저장 시편을 확보하고, 명확한 고장 조도 기준을 수립하면 베어링의 저장 수명 예측정확도를 높일 수 있을 것이며, 터보엔진의 효율적인 정비 주기 설정에 기여할 수 있을 것이다.
Abstract
Operational reliability of the single-use turbo engine for guided weapons must be guaranteed even after long-term storage. Rolling element bearings have a great influence on the operational reliability of the turbo engine, however changes in micro dimensions of bearings by an oxide layers on rolling elements and raceways may cause failures after long-term storage. In this study, changes in dimensions of bearings were measured and roughness of rolling elements was used for estimating the storage life. Storage life estimation was performed via two kinds of methods, Weibayes method and random sample generation method. The results of two methods were compared and their characteristics were analyzed. This study will contribute to establish an efficient maintenance schedule for the single-use turbo engine.
Keywords:
Single-use System, Turbo Engine, Rolling Element Bearings, Residual Storage Life, Weibayes키워드:
일회성 시스템, 터보엔진, 구름 베어링, 잔여 저장 수명, 와이베이즈1. 서 론
터보엔진은 유도무기와 항공기의 추진 동력을 생성하는 추진관련 주요 부체계로 엔진에 고장이 발생할 경우 체계 전체의 기능 수행에 치명적인 문제를 일으키게 된다. 특히 유도무기에 적용되는 단수명 터보엔진의 경우 제조 후에 장기간 저장된 후에 일회성으로 사용되기 때문에, 실제 사용 시점에 엔진의 정상 작동 여부를 확약하기 어려운 문제가 있어, 장기저장에 따른 수명 및 신뢰성 평가가 필요하다[1].
터보엔진은 유입되는 공기를 압축 후 연소, 팽창 과정을 통해서 회전축의 회전 동력과 연소가스의 제트를 생성하여 추진력을 발생시키는 동력생성장치로, 압축 및 팽창 사이클을 구현하기 위해서는 임펠러 혹은 블레이드-디스크를 고속으로 회전시켜야 한다. 이러한 고속의 회전축에는 수백만 DN급(축직경(mm)×RPM), DIN 기준 P4급(ANSI/ABMA 기준 ABEC 7급) 이상의 고정밀도 등급의 구름 베어링을 적용한다. Fig. 1과 같이 일반적으로 축방향 하중을 지지하기 위한 내륜 분리형 볼베어링(Inner-race Split Ball Bearings)과 온도 변화에 의한 열적 신장을 감안한 축방향 부유식 실린더형 롤러베어링(Floating Type Cylindrical Roller Bearings)을 적용한다[2,3].
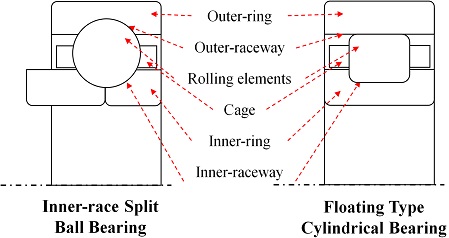
Components of bearings (left: inner-race split ball bearing, right: floating type cylindrical bearing).
일회성 단수명 터보엔진의 경우에 장기간 베어링이 엔진의 회전축에 체결된 상태로 보관 되기 때문에 노출되는 온도, 습도, 오일 접촉 등의 조건에 따라 산화, 부식되어 기능을 상실할 가능성이 존재한다. 주요 베어링 제조사인 SKF의 경우 베어링 저장 시에 온도, 습도 조건을 20℃, 75%RH 조건, 혹은 22℃, 60%RH 조건, 혹은 25℃, 50%RH 조건으로 제한하고 있으며, 개봉한 베어링의 경우 유통기한(Shelf Life)을 3년으로 설정하고 있다[4]. 하지만, 명확한 저장 수명 허용 기준 혹은 지침이 없는 상황으로, 특정 조건에서 장기간 보관되는 일회성 터보엔진용 구름 베어링의 잔존 저장 수명에 대한 명확한 평가방법을 제안하여야 할 필요가 있다.
구름 베어링의 수명 평가와 예측에 대한 연구는 다양한 베어링에 대한 성능 실험을 통해 수명데이터를 확보하기 시작한 19세기 말 Stribeck 의 연구에서 시작되었다[5]. Lundberg 와 Palmgren 은 반복적인 구름에 의한 피로 하중으로 인해 발생하는 수많은 고장 데이터를 종합하여, 동적하중계수(Basic Dynamic Load Rating)라는 값을 설정하고, 하중에 따른 수명을 판단할 수 있도록 하였다[6]. 이후, 베어링 소재의 발전과 윤활조건의 개선, 궤도면의 정밀 가공 정도를 반영하여, 기존의 L10 수명에 계수를 곱하여 수명을 교정하는 방식으로 구름베어링의 피로수명 값을 계산하고 있다[7]. 하지만, 동적하중계수에 기반한 수명평가는 베어링의 기계적 피로수명에 대한 것으로, 미운용 장기저장되는 베어링에 대한 수명평가 방법으로는 적합하지 않다.
지금까지의 장기저장 베어링에 대한 고장 및 수명 평가 연구는 주로 베어링의 윤활유 및 그리스 성분에 대한 화학적 물성 변화에 집중되었다. 아레니우스 이론(Arrhenius Principle)에 기반하면, 베어링 윤활유의 수명은 10℃ 증가에 따라 반감된다고 알려져 있다[8]. 또한, 대기 습도에 노출되어 수분을 흡수한 경우 인산염, 규산염 및 에스테르 합성유계의 수명을 단축시킨다고 보고되었으며, 이는 베어링 표면 침전물을 형성시켜 베어링 수명을 저하시키는 것으로 연구되었다. 장기저장된 그리스의 경우에도 온도 상승 및 장기 저장에 의한 영향으로 정적 마찰(Steady State Friction)의 증가와 베어링의 온도 증가를 유발하며, 결과적으로 베어링의 성능을 크게 저하시키는 것으로 확인되었다[9]. 또한, 화학적 산화반응에 의해 베어링 궤도면에 두꺼운 산화층을 형성시키고, 이는 베어링의 궤도면 조도의 상승과 구름을 방해하여 베어링의 조기 파손을 유발할 수 있다는 연구도 보고된 바가 있다[10].
유도무기에 적용되는 일회성 터보엔진용 구름 베어링에 대한 장기저장에 따른 연구보고는 보안상의 이유로 공개된 자료가 제한적이다. 공개된 자료 중 미국 국방기술정보센터(DTIC)의 연구에서는[11], 유도무기 체계의 미운용 장기저장 후 성능에 영향을 미칠 수 있는 부품으로, 밸브, 축압기, 구동기, 펌프, 실린더, 필터, 가스켓, 씰, 베어링 등을 선정하였다. 베어링의 경우 명확한 시험방법이나 수명평가 방법이 공개되어 있지 않으나 지상보다는 해저 저장 환경에서 고장률이 높은 것으로 보고되었다. 이는 앞선 언급한 연구와 같이 습도에 의한 영향으로 예상할 수 있다.
국내에서는 베어링의 장기저장에 따른 수명평가를 위한 연구로, 베어링 단품에 대한 가속노화 및 수명평가 연구가 진행된 바가 있다[12]. 해당 연구에서는 실제 저장 조건을 감안한 가속화된 온도와 습도조건에서 저장을 수행하여, 주기적으로 계측된 치수 정밀도에 대한 통계적인 분포와 수명모델을 수립하였다. 하지만 이와 같은 가속노화 시험의 경우 10년이상의 장시간을 모사하는 과정에서 과다한 고온, 다습 조건으로 부수적인 고장모드가 발생할 수 있는 한계가 있다.
이와 같이, 구름베어링은 일회성 터보엔진의 성능에 지대한 영향을 미치지만 장기간 저장 시험 데이터를 확보해야하는 한계와 공개된 자료가 제한적인 이유로 구름 베어링의 장기 저장 수명 예측에 대한 연구가 미진하며, 이로 인해 일회성 터보엔진에 대한 명확한 정비 주기를 설정하기 어려운 상황이다. 본 연구에서는 실제 운용 환경에서 장기 저장된 일회성 터보엔진에 장착되었던 베어링에서 정밀도와 관련된 데이터를 획득하고 베어링 잔존 저장 수명을 분석하기 위해 기존의 베어링 수명 분포 모델을 이용한 와이베이즈 분석법과 난수 샘플 생성을 통한 통계적 분석법을 적용하여 상호 비교하였다.
본 연구는 실제 저장환경에서 장시간 보관된 일회성 터보엔진 베어링의 데이터를 활용하고, 다양한 저장 수명을 평가하는 방안을 제시하는 점에서 의의가 있다.
2. 대상 구름 베어링 및 고장 기준
2.1 대상 구름 베어링 제원
본 연구에서 장기저장한 일회성 터보엔진은 Fig. 2와 같이 일회성 체계의 추진시스템(Sustainer)으로 사용되는 엔진이다. 엔진은 압축기, 연소기, 터빈으로 구성되며, 압축기, 터빈이 가스를 압축, 팽창시키기 위해서 로터가 중심에 위치하고 구름 베어링으로 지지된다. 이러한 터보엔진의 로터를 지지하는 베어링은 엔진에 장착한 상태로 장기 저장된 후, 분해되어 본 연구에서 장기저장 효과를 보기위한 샘플로 사용되었다. 볼베어링은 앞선 장에서 설명한 바와 같이 내륜 분리형 볼베어링이며, 롤러베어링의 경우 부유식 실린더형 롤러베어링이다. 각 베어링의 외곽 제원은 Table 1과 같다.
베어링의 제작 정밀도는 볼베어링경우 ISO Class 4, DIN 등급으로 P4 정밀도 기준을 만족하며, 롤러베어링의 경우 ISO Class 5, DIN 등급으로 P5 등급을 만족하도록 제작되었다.
본 연구에서 대상으로 한 베어링은 유도무기체계 엔진에 적용된 후 정비 시점에 분해되어 취득한 시편으로, 정비 시점인 제조 후 4,000일 시점까지 장기 저장된 베어링이다. 따라서, 정비 시점에서의 고장 여부를 판단하기 위해 장기 저장의 기준을 4,000일로 설정하였다. 분석에 사용한 베어링은 볼베어링 총 10개, 롤러베어링 총 15개이며, 대조를 위해 신품 베어링으로 볼베어링 4개, 롤러베어링 6개를 검사하여 데이터를 획득하였다.
2.2 베어링 고장 기준
구름 베어링의 정밀도 등급은 회전체의 흔들림을 제어하거나 정밀한 조립을 위한 허용치에 대한 것으로 이미 조립된 상태에서 저장된 구름 베어링의 장기저장에 의한 고장 기준으로 적절하지 않다. 구름 베어링의 손상 및 파손에 대한 용어와 원인을 규정하고 있는 ISO-15243, Rolling bearings-Damage and failures-terms, characteristics and causes 문서에 따르면, 주요 베어링 고장 모드는 구름 접촉 피로손상(Rolling contact fatigue), 마모(Wear), 부식(Corrosion), 전기적 침식(Electrical erosion), 영구변형(Plastic deformation), 크랙 및 파괴(Cracking and facture)로 구분하고 있다[13]. 앞선 연구에서처럼, 구름 베어링이 장기저장되는 동안에는 잔존 오일에 노출되거나 산화에 의한 부식과 관련한 고장 모드가 발생할 가능성이 높다. 또한, 부식에 의해서 베어링의 내, 외륜 궤도면과 전동체의 표면에 구름을 방해하는 두꺼운 층이 형성되어 베어링의 궤도면 조도(Roughness)를 변화시키는 고장 모드가 발생할 수 있다. 하지만, 현재까지 기능상 고장을 규정할 수 있는 조도 기준은 수립되지 않은 상태로, 이를 위해서는 해당 베어링에 대한 많은 성능시험을 통해 기능상 고장을 일으키는 조도 기준을 마련하여야 한다. 이는 향후 연구에서 보완되어야 할 부분으로, 본 연구에서는 유사 항공엔진용 베어링의 제조 후 출고 허용 조도 기준 값을 참고로 Table 2와 같은 고장 기준을 보수적으로 설정하였다.
3. 장기저장 베어링 검사결과 분석
장기저장 베어링 검사결과를 신품 베어링과 비교하여 앞선 장에서 고장 기준으로 설정한 조도 값이 유의미한 변화를 보이는지에 대한 검토를 진행하였다. 조도는 내, 외륜 궤도면과 전동체에 대해서 각각 평가하였다. 내륜과 외륜 조도의 경우 궤도면에서 축방향으로 조도측정을 실시하였으며, 동일 내륜 및 외륜에 대해서 각각 90도 위상 간격으로 4개 지점에서 측정하였다. 전동체의 경우 전체 전동체 중 임의로 4개의 샘플을 취득하여 이에 대한 조도를 측정하였다. Fig. 3은 각 베어링의 내, 외륜 궤도면 조도와 전동체 조도의 신품과 장기저장 간의 데이터 편차를 보여준다. 3번 볼베어링의 궤도면 조도를 제외하고는 전체적으로 조도 값이 증가하는 경향을 보이나, 정량적으로 평가하기위해 장기저장 베어링의 조도의 t-test 검정을 진행하였다. Table 3에 표시된 p-값을 기준으로 0.05 이하의 경우 두 집단의 차이가 유의미하다는 결론을 내릴 수 있다. 가장 유의미한 변화를 보이는 값은 전동체의 조도 값으로 전체 베어링에서 유의미한 차이를 보였다. 내, 외륜 궤도면 조도의 경우 2번 롤러베어링과 4번 롤러베어링에서는 유의미한 차이를 확인할 수 없으나, 그 외 베어링에서는 장기저장에 의한 변화를 보였다. 따라서, 장기간 저장에 따른 조도 증가의 명확한 효과는 내, 외륜 궤도면 보다는 전동체의 조도 결과에 크게 영향을 주는 것으로 판단할 수 있다. 따라서, 본 연구에서 고장 기준으로 전동체의 조도 값을 설정하고 저장 수명예측을 진행하였다.
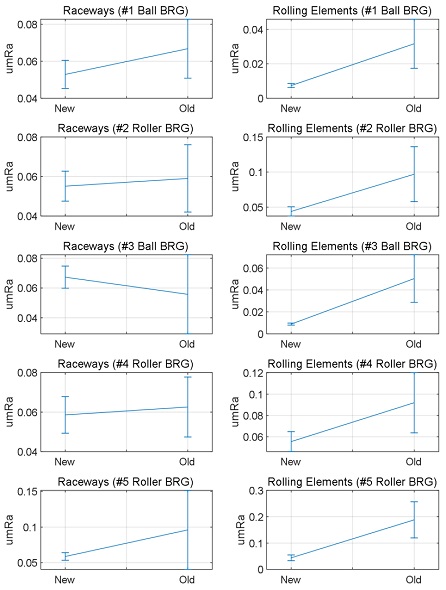
Roughness changes of bearings with long-term storage (left columns: raceways roughness, right columns: rolling element roughness).
4. 저장 수명 평가 분석법
4.1 와이베이즈 분석법
일반적인 신뢰성 평가 방법은 제품의 고장 시간에 대한 확률밀도함수를 표현한 수명 분포를 획득하고, 이를 기준으로 신뢰도, 고장률, MTTF와 같은 신뢰성 관련 지표를 계산한다. 신뢰성평가에 주로 사용되는 수명 분포 모델은 지수분포(Exponential Distribution)와 와이블분포(Weibull Distribution)로, 베어링을 포함하여 기계류 부품의 수명 분포 모델로는 다양한 고장분포의 형태를 표현할 수 있는 와이블분포를 주로 사용한다[1,14,15]. 와이블분포의 확률 밀도 함수는 다음과 같다.
| (1) |
와이블분포의 확률 밀도 함수에서 α는 분포의 형태를 정의하는 형상모수이며, λ는 특성수명이라고도 불리는 척도모수이다. 와이베이즈(Weibayes) 분석법은 와이블분포로 가정된 수명분포에서 형상모수를 알고 있는 경우, 각 샘플의 고장 시간에 대한 정보를 이용하여 와이블분포의 척도모수, 즉 특성수명을 역으로 도출하는 방법이다[16]. 와이베이즈 분석에 따른 척도모수는 다음식으로 계산할 수 있다.
| (2) |
이때, Ti 는 각 샘플의 시험 시간이며, r은 고장 샘플의 개수, N은 샘플 수를 의미한다. 만약 전체 시험 시간에 대해서 전체 샘플에 고장이 발생하지 않는다면, r = 1로 설정한 후, 위의 특성수명을 특성수명 하한값으로 설정할 수 있다. 본 연구에서는 기존의 연구를 통해서 획득한 형상모수를 이용하였으며, 볼 베어링은 2.08, 롤러 베어링은 2.79 값을 적용하였다[12]. 샘플의 고장 유무는 앞선 선정한 고장 기준인 조도 값을 기준으로 하였다.
4.2 난수 샘플 생성을 통한 통계적 분석법
난수 샘플 생성을 통한 통계적 분석법은 Fig. 4와 같은 순서에 따라 진행한다. 먼저, 앞선 장에서 장기저장 베어링에서 가장 변화가 유의미한 결과를 보인 전동체의 조도 데이터를 이용하여 시간에 따른 열화 특성을 표현하는 열화 모델을 구현한다. 본 연구에서 열화모델은 다음의 1차식을 적용하였다.
| (3) |
이 때, y 는 조도값을 의미하며, t는 저장 시간을 의미한다. 상기의 선형 열화모델식을 기반으로 앞선 3장의 신품 베어링과 장기저장 베어링의 조도 값 조합에 대해서, 각 조도 값의 데이터 쌍을 연결하는 열화모델의 계수인 β1과 β2 값을 계산한다. 다음으로, 계산된 β1, β2 값에 대한 분포를 정규분포 모델로 근사하면, 선형 열화모델에 대한 확률적인 모델을 확보할 수 있다. 선형 열화모델식의 계수를 앞서 확보한 정규분포 모델에 기반한 난수 생성함수를 이용하여 장기저장 시간에 따른 다수의 가상 조도 값을 계산한다. 이러한 다수의 가상 열화 샘플을 종합하여 고장 기준을 초과하는 고장 시점에 대한 분포를 획득할 수 있다. 특정한 수명 분포를 가정하지 않았기 때문에, 고장 시간에 대한 분포는 새로운 Kernel 분포에 기반한 수명분포 모델로 근사하고, 수명을 예측하였다.
5. 베어링 저장 수명 평가 결과
먼저, 와이베이즈 분석법을 이용하여 베어링의 저장 수명을 평가하기 위해서, 시험 시간과 고장 샘플의 개수를 산정하였다. 시험 시간은 실제 저장 기간인 4,000일이며, 고장 기준인 전동체 조도값을 기준으로 각 베어링의 고장 유무를 판단하였다.
총 25개의 저장 베어링 샘플 중에서 1번 볼베어링, 2번 롤러베어링, 3번 볼베어링, 4번 롤러베어링의 조도값은 기준값을 벗어나지 않았으며, 5번 롤러베어링에서 2개의 샘플이 기준을 초과하여 고장으로 판단하였다. 와이베이즈 분석을 위해서는 샘플의 수가 충분히 확보되어야 신뢰도가 높아지므로, 볼베어링과 롤러베어링으로 두 개의 샘플 집단을 구분하여 해석하였다. 따라서, 볼베어링의 경우 무고장 샘플로 가정하고, 특성 수명과 B10 수명의 하한값 계산하였으며, 롤러베어링의 경우 총 15개의 샘플 중 2개의 샘플이 고장인 경우에 대해 Eq. 2의 와이베이즈 분석식에 적용하여, 점추정 특성수명(척도모수)과 B10을 계산하였다. B10 수명은 다음의 계산식을 통해서 10%의 샘플이 고장나는데 걸리는 시간을 도출하였다.
| (4) |
본 연구에서는 관련 연구결과를 참고로, 볼베어링의 형상모수(Shape Parameters)는 2.08, 롤러베어링의 형상모수는 2.79를 Eq. 2에 적용하였다[12].
그 결과, 볼베어링의 경우 신뢰수준 90%를 기준으로 특성 수명 하한값이 22.6년, B10 수명이 7.7년이 계산되었으며, 롤러베어링의 경우 22.9년의 특성 수명, 10.2년의 B10 수명을 확인하였다. 이를 종합하여 Table 4에 정리하였다. 볼베어링은 장기저장 기간 동안 고장이 발생하지 않았지만, 와이베이즈 분석에 기반할 경우 수명의 하한값 만을 보수적으로 특정할 수밖에 없기 때문에 과소평가되었을 가능성이 있다.
다음으로 난수 샘플 생성을 통한 통계적 분석방법으로, 먼저 신품 베어링의 조도 값에서 장기저장된 베어링의 조도 값으로 열화되는 데이터를 근사하는 선형 근사식을 계산한다. 데이터가 신품 데이터, 장기저장 데이터, 이렇게 2개의 데이터만 존재하므로 1차식으로 근사할 경우 1차식의 계수인 β1과 β2를 계산할 수 있다. 이 때, 1차식의 계수는 동일 종류의 베어링에 대해서 도출한 열화식이므로, 이에 대한 1차 열화식의 계수의 편차는 측정 오차에 기인한다고 볼 때, 정규분포를 가진다고 볼 수 있다. 따라서, Fig. 5와 같이 각 베어링의 1차 열화식의 계수값을 근사할 수 있는 정규분포 모델을 도출하였다. 샘플수가 한정되어있어 명확한 정규분포형상을 보이지 않으나, 추가적인 샘플 획득 시에 신뢰성 높은 정규분포모델을 확보할 수 있을 것이다.
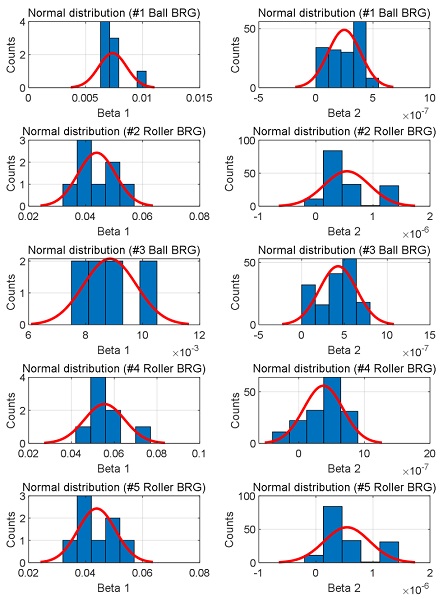
Normal distribution estimations of degradation model coefficients (left column: raceways roughness, right column: rolling element roughness).
이후, 열화식의 계수값에 대한 정규분포모델로 난수 생성을 통한 열화 샘플을 생성하고, 전동체 조도가 Table 2에 설정한 기준을 초과하는 경우를 고장이라고 판단하면, Fig. 6과 같이 각 베어링별로 수명분포모델을 구현할 수 있다. 빨간색 선은 수명분포를 근사하는 Kernel 분포모델로 비선형적인 수명분포를 잘 근사하는 것을 확인할 수 있다. 각 베어링의 수명분포에서 B10 수명 값을 추출하면, 1번 볼베어링의 경우 49.9년, 2번 롤러베어링은 16.3년, 3번 볼베어링은 30.5년, 4번 롤러베어링은 20.9년, 5번 롤러베어링은 7.4년으로 계산되었다. 와이베이즈 분석법과 동일하게 볼베어링, 롤러베어링으로 집단을 구분하여 B10 수명을 재계산하면, 볼베어링은 35.5년, 롤러베어링은 10.0년으로 계산된다.
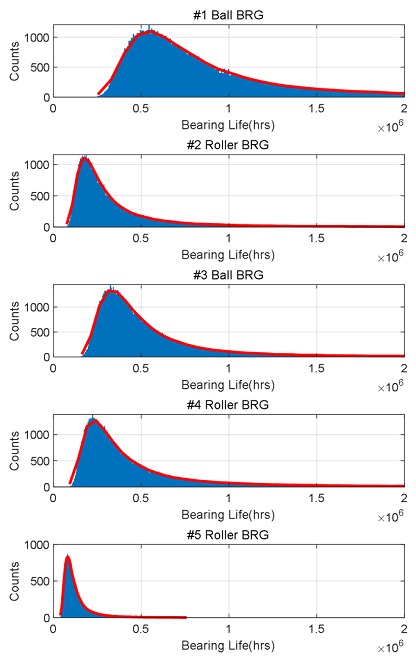
Storage life distributions of bearings and Kernel distribution fittings (from the top: #1 ball bearing, #2 roller bearing, #3 ball bearing, #4 roller bearing, #5 roller bearing).
와이베이즈 분석법과 난수 샘플 생성(Random Sample Generation, RSG)을 통한 통계적 분석법 결과를 정리하면 Table 5와 같다.
볼베어링과 롤러베어링으로 집단을 분류하고 저장수명을 예측한 결과를 비교하면, 롤러베어링의 경우 와이베이즈방법과 난수 샘플 생성 방법이 유사한 결과를 보임을 알 수 있다. 이는 롤러 베어링에서 고장 데이터가 발생하여, 이를 기반으로 와이베이즈 분석에서도 점추정이 가능하였고, 두 기법 모두 유사한 수명을 보인 것으로 판단된다. 하지만, 볼베어링의 경우 고장 데이터가 발생하지 않아 와이베이즈 분석법에서는 점 추정이 불가능하고, 수명 하한값만을 제시할 수 있기 때문에 낮은 수명으로 예측하게 되어, 수명 예측을 신뢰도가 떨어짐을 볼 수 있다.
난수 샘플 생성 방법의 경우 실제 계측데이터를 기반으로 새로운 수명 분포를 획득하기 떄문에 각 베어링별로 수명 예측이 가능하였다. 볼베어링과 롤러베어링으로 샘플 집단을 구분할 경우와 비교했을 때, 가장 낮은 수명을 보이는 3번 볼베어링이 볼베어링 집단의 B10 수명에 크게 영향을 주는 것으로 보이며, 롤러베어링 집단의 B10 수명은 5번 롤러베어링이 가장 큰 영향을 주는 것으로 판단된다. 장기저장된 베어링의 샘플 중에서 5번 베어링에서 2개의 샘플이 고장 조도 기준을 넘어간 것과 결과가 부합됨을 알 수 있다. 또한, 난수 샘플 생성 방법의 경우 볼베어링의 경우처럼 고장이 발생하지 않은 집단 내에서도 수명이 취약한 부품을 추출할 수 있다는 장점이 있다.
본 연구에서 예측한 베어링의 장기저장 수명예측 결과는 와이베이즈 분석법에 따르면 하한 수명 기준 7.7년, 난수 샘플 생성 방법의 경우 롤러베어링 집단에서 10.0년 가량이다. 본 연구의 수명 예측 결과가 보수적인 조도 허용 기준을 활용한 점을 감안할 때 예측결과는 대상엔진의 정비 주기인 4,000일(10.9년)에 유사한 결과를 보인다.
비록 두 가지 수명평가 방법이 서로 상이한 가정을 통해서 접근한 방법이나, 상대적으로 집단별 샘플수가 많은, 볼베어링, 롤러베어링으로 구분한 샘플집단 구분에서는 유사한 결과를 얻을 수 있다. 하지만, 집단별 샘플이 적거나, 무고장 샘플만 존재하는 경우 와이베이즈 분석법으로는 하한 수명만을 평가하여 보수적인 결과만을 얻게되는 한계가 존재한다. 하지만, 상대적으로 계산이 용이하여 다수 샘플이 존재하는 경우에는 유용할 것으로 보인다. 샘플 수가 적을 경우, 혹은 명확한 고장 샘플이 없는 경우에는 난수 샘플 생성 방법이 명확한 수명값을 얻는데 유리하다. 하지만, 선형 근사식으로 근사하는 과정과 선형 근사식의 계수를 정규분포로 가정한다는 점이 한계로 작용할 수 있다. 따라서, 샘플 수와 고장 데이터의 유무에 따라 적절한 방법을 선정하여 평가를 해야한다.
6. 결 론
본 연구에서는 일회성 터보엔진에 조립되어 장기간 저장되는 구름 베어링의 저장 수명을 예측할 수 있는 두가지 접근법에 대해서 소개하였다. 기존의 저장 시험을 통해 구름 베어링에 대한 수명분포모델의 형상모수를 알고 있는 경우, 와이베이즈 분석법에 의해서 비교적 간단한 절차를 통해서 수명을 예측할 수 있다. 하지만, 와이베이즈 분석법의 경우 수명분포모델에 대한 정보가 필요하며, 샘플에서 고장 샘플이 존재하지 않거나 샘플이 적은 경우에는 점추정이 불가하거나 신뢰도가 떨어지는 한계가 존재한다. 이를 보완하기 위해서 고장 데이터를 난수로 생성하는 난수 샘플 생성 방법을 소개하였다. 이 방법의 경우 실제 열화 데이터를 근사하는 열화 모델을 수립하고, 열화 모델의 계수를 근사하는 분포모델로 난수를 생성하여 실제 샘플 개수가 적은 경우에도 이를 보완할 수 있다. 또한, 기존의 수명분포모델에 한정되지 않고 새로운 수명분포모델을 획득하여 수명을 예측할 수 있다는 장점이 있다. 하지만, 열화 모델의 계수를 분포모델로 가정한다는 가정이 필요하다는 점에서 한계는 존재할 수 있다.
베어링의 수명예측 혹은 신뢰성 평가의 경우 지속적으로 운용되는 베어링에 대한 연구에 집중되어 있어, 장기저장되는 엔진용 베어링에 대한 시험데이터와 수명모델 구현 방법에 대한 연구가 부족한 상황이다. 본 연구는 이러한 측면에서 유도무기와 같은 일회성 터보엔진의 시스템 수명을 평가하는데 필요한 베어링의 저장수명을 예측하고, 창정비 주기를 설정하는데 유용하게 적용할 수 있는 방법을 제시하였다고 판단한다.
향후 추가적인 연구를 통해서, 다양한 저장시간에 대한 베어링 샘플과 데이터를 확보하여 보다 신뢰도가 높은 수명예측 결과를 획득하고자 한다. 또한, 장기저장과 관련한 명확한 조도 고장 기준이 아직 마련되지 않은 상태로, 고장이라고 판단할 수 있는 허용 조도 값 선정을 위한 연구를 진행해야 할 것이다.
Nomenclature
| α : | Shape parameter of the Weibull distribution |
| λ : | Scale parameter of the Weibull distribution |
| t : | Time |
| Ti : | Test period of each sample |
| r : | Number of failure samples |
| N : | Number of samples |
| β1 : | Bias of the linear degradation model |
| β2 : | Slope of the linear degradation model |
| μi : | Average of samples |
| σi : | Standard deviation of samples |
| B10 : | Time at which 10% of samples will have failed |
| RSG : | Random sample generation method |
Acknowledgments
본 연구는 국방과학연구소와 LIG넥스원의 지원으로 수행된 연구임(과제명: 장기운용 베어링 검사결과 분석 기술용역).
References
-
Chang, M.-S., Lee, C.-S., Park, J.-W., Kim, Y.-I. and Kim, S.J., “Storage Reliability Assessment of Springs for Turbo Engine Components,” Journal of the Korean Society of Propulsion Engineers, Vol. 23, No. 4, pp. 42-49, 2019.
[https://doi.org/10.6108/KSPE.2019.23.4.042]

-
Kim, S.J., “Analytical Consideration of the Radial Clearance to Reduce Cage Slip of the Turbo Engine Roller Bearing,” Journal of Mechanical Science and Technology, Vol. 35, No. 7, pp. 2827-2839, 2021.
[https://doi.org/10.1007/s12206-021-0606-0]

-
Kim, S.J. and Kim, Y.R., “A Study of Loading Conditions for Developing the High-speed Bearings of the Gas-turbine Engine,” Journal of the Korean Society of Propulsion Engineers, Vol. 19, No. 4, pp. 102-109, 2015.
[https://doi.org/10.6108/KSPE.2015.19.4.102]

- Super-precision Bearings, SKF, March 2016.
-
Harris, T.A. and Barnsby, R.M. “Life Rating of Ball and Roller Bearings,” Proc. IMechE, Part J: J. Engineering Tribology, Vol. 215, No. 6, pp. 577-595, 2001.
[https://doi.org/10.1243/1350650011543817]

-
Lundberg, G. and Palmgren, A., “Dynamic Capacity of Rolling Bearings,” J. Appl. Mech., Vol. 16, No. 2, pp. 165-172, 1949.
[https://doi.org/10.1115/1.4009930]

- ISO, Rolling bearings-dynamic load rating and rating life, ISO 218:2007, Geneve, Switzerland, 2007.
- Khonsari, M. and Booser, E.R., “Predicting Oil and Grease Life,” Machine Design, March 2003.
-
Varenberg, M., Kligerman, Y., Halperin, G., Nakad, S. and Kasem, H., “Assessing Workability of Greased Bearings after Long-term Storage,” Friction, Vol. 7, pp. 489-496, 2019.
[https://doi.org/10.1007/s40544-018-0255-1]

- Susanne, B.-F., “Test Method for Simulating the Aging and Oxidation Stability of Lubricants,” Machinery Lubrication, March 2005.
- Mitcheel, J.C., “Storage Reliability of Missile Materiel Program. Storage Reliability Summary Report. Volume III. Hydraulic and Pneumatic Devices,” ADA053409, 1978.
- Yang, H.-S., Chang, M.-S., Park, J.-W., Kim, Y.-I. and Kim, S.J., “Accelerated Degradation Test for Bearings of Engine Assembly,” 50th KSPE Spring Conference, Jeju, Korea, KSPE 2018-1069, 2018.
- ISO, Rolling Bearings-damage and Failures-terms, Characteristics and Causes, ISO 15243:2017, Geneve, Switzerland, 2017.
-
Bertsche, B., Reliability in Automotive and Mechanical Engineering: Determination of Component and System Reliability, Springer-Verlag Berlin Heidelberg, Germany, 2008.
[https://doi.org/10.1007/978-3-540-34282-3]

- Park, T.-K., Chang, M.-S., Sung, B.-J., Choi, B.-O. and Yang, C.-K., “Durability Evaluation of the Radiator for Construction Equipment Through Weibayes Analysis,” Proceedings of KSME Spring Conference, pp. 530-535, 2014.
-
Nicholls, D. and Lein, P., “Weibayes Testing: What is the Impact if Assumed Beta is Incorrect?,” Annual Reliability and Maintainability Symposium, pp. 37-42, 2009.
[https://doi.org/10.1109/RAMS.2009.4914646]