
고밀도 금속 플라즈마 전기전도도 예측모델
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 현대적 전기식 기폭관의 해석 모델링을 대상으로 실용적 적용이 가능한 금속성 플라즈마 조성비 및 전기전도도 계산모델이 제시되었다. 현 플라즈마 모델은 기폭관 브릿지 전기폭발 현상 시 발생하는 고밀도 플라즈마 영역의 비이상 플라즈마 효과 보정을 포함하였다. 구리 플라즈마를 대상으로 한 계산 결과는 넓은 온도 범위 및 고밀도 영역에서 해당 측정 결과와 전반적으로 잘 일치하여 기폭관 모델링 대상 적용에 적절함을 보여주었다.
Abstract
This study introduces the calculation model of ionization composition and electrical conductivity for metallic plasma for practical application to modeling and simulation of modern electrical detonators. The present model includes the correction for non-ideality of dense plasma conditions which are expected in electrical explosion of bridge in detonators. The computational results for copper plasma show favorable agreement with experimental data for a wide range of plasma temperature and high density conditions and the model is proper for detonator modeling with good prediction accuracy.
Keywords:
Metallic Plasma, Metallic Bridge Burst, Plasma Electrical Conductivity, Prediction Model키워드:
금속 플라즈마, 금속 브릿지 버스트, 플라즈마 전기전도도, 예측모델1. 서 론
폭발도선(exploding bridgewire, EBW), 폭발박막(exploding bridge film, EBF), 폭발포일(exploding foil initiator, EFI) 등 형태의 현대적 초소형 기폭장치는 구리, 알루미늄, 백금 등 금속성 도선 또는 박막 브릿지의 전기폭발에 기반하여 장착 화약의 기폭이 진행된다[1,2]. 브릿지 버스트 현상을 포함하는 이러한 브릿지 전기폭발 현상에서는 전기에너지 투입 및 주울 발열에 따라 브릿지가 액화 및 기화 단계를 거쳐 플라즈마화가 급격히 진행됨이 주요 물리현상이 된다. 따라서 전기식 기폭관 또는 착화시스템의 모델링 및 성능 해석연구에 금속성 플라즈마의 신뢰성 있는 전기전도도 예측이 매우 중요하다. 금속성 플라즈마 물성 해석의 중요성은 기폭장치 이외에도 금속 표면에서 플라즈마 삭마가 발생하는 전열화학포, 레일건 등의 여러 첨단 방산기술에도 함께 적용된다[3,4].
금속성 플라즈마의 전기전도도 모델 및 계산방법은 이상적, 완전 이온화 플라즈마 가정에 따른 Spitzer 모델[5]을 기초로 비이상 플라즈마 효과 등을 포함하며 발전되어 왔다[6-9]. 최근에는 양자분자 동역학(quantum molecular dynamics, QMD) 시뮬레이션을 이용한 플라즈마 물성 해석모델도 제시되고 있다[10].
본 연구에서는 기폭장치의 금속 플라즈마 발생 현상, 특히 브릿지 버스트로 대표되는 금속편 전기폭발에 나타나는 50,000K 고온 및 10 g/cm3 질량밀도 정도까지의 고밀도 영역의 금속성 플라즈마[11]를 대상으로 하여 플라즈마 전기전도도 해석모델 및 예측 결과 검증을 보여준다. 해당 열플라즈마 영역은 비이상 플라즈마 효과가 심화되는 영역이다. 여기서 제시되는 금속성 플라즈마 해석모델은 현대적 기폭장치 내 구리로 대표되는 금속 재질 도선 또는 박막의 전기폭발 모델링 및 전산해석 대상 실용적 적용성 확보를 목적으로 한다.
2. 금속성 플라즈마 물성 해석모델
2.1 금속성 플라즈마 상태 관계식
현 연구에서는 먼저 구리 플라즈마의 열역학적 국소 평형상태를 가정하였으며, 50,000K 정도의 고온 영역 해석을 위해서 구리 원자종의 4차 이온화까지를 해석 및 계산에 포함하였다. 기설정되는 플라즈마 온도와 압력 또는 온도와 질량밀도 조합에 대하여 열 플라즈마 상태의 비이온화 원자종과 이온화된 금속 원자종 그리고 전자의 입자밀도(number density)는 다음의 Saha 이온화 방정식으로 표현된다[5].
| (1) |
| (2) |
위에서 ne는 전자밀도(electron density)이며, ni, Ii 및 Zi는 각각 이온화된 i번째 원자종에 대한 입자밀도, 이온화에너지 및 이온 상태의 전자분배함수이다. Eq. (1)은 첨자 i = 0, 1, 2, 3, 4에 대해 적용되며 각각 Cu, Cu+, Cu2+, Cu3+, Cu4+와 같은 이온화 상태를 나타낸다. DeBroglie 파장 길이 Λ는 다음과 같이 주어진다.
| (3) |
여기서 kB와 ℏ는 각각 Boltzmann 상수와 Planck 상수이며, me는 전자질량이다. 상대적 고압 및 상대적 저온 상황의 플라즈마에 대하여 비이상 플라즈마(non-ideal plasma) 현상의 영향이 크게 나타난다. 따라서 이온화에너지의 저감을 고려해야 하기에 i번째 이온화에 대한 에너지 저감 ΔIi는 다음과 같이 일반적으로 계산된다.
| (4) |
위의 식에서 ec는 전자 전하량, ϵ0는 진공유전율이며 λD는 Debye 길이로 다음과 같다.
| (5) |
하지만 Eq. 4로는 브릿지 버스트 현상 등에서 발생할 것으로 예상되는 수 GPa의 초고압력 상태를 포함하는 넓은 온도 및 압력 범위를 다룰 때는 적합하지 않을 것으로 판단된다[11]. 이에 따라 최근 연구에서 제시한 다음의 이온화에너지 저감 모델을 채용하였다[8].
| (6) |
위의 식에서 플라즈마 이온화 상태 i에 대응하는 ion-sphere radius인 az는 다음과 같다.
| (7) |
Eq. 7에서 nh는 이온화원자 및 비이온화원자를 모두 포함한 원자밀도(heavy species density)이다. 한편 α는 플라즈마 이온화도(degree of ionization)로서 다음과 같이 계산될 수 있다.
| (8) |
이상기체 가정을 도입하여 압력과 온도의 관계를 나타내는 플라즈마 상태방정식과 질량밀도 관계식은 다음과 같다.
| (9) |
| (10) |
여기서 플라즈마 기체상수는 이며 mi와 는 각각 이온화 상태 i에 해당하는 원자의 질량, 그리고 원자들 전체의 평균 질량이다. 다만 여기서는 구리 등의 순수 금속 물질에 대한 플라즈마를 다루기에 두 질량 사이의 차이는 없다.
2.2 금속성 플라즈마 전기전도도 모델
금속성 플라즈마의 전기전도도(σe) 또는 그 역수인 비저항(ρe)의 계산에는 앞서 언급된 전자밀도, 이온화원자 및 비이온화원자 밀도 등 플라즈마 조성비의 함수 등으로 표현되는 전자-이온화 원자 및 전자-비이온화 원자 간의 충돌을 각각 고려한 Zollweg과 Liebermann[12]의 계산모델이 흔히 사용된다.
| (11) |
브릿지 버스트 시에 해당하는 고압 또는 고밀도 플라즈마의 비이상 플라즈마 조건에 대하여 기존의 전통적 모델을 소폭 개선한 다음의 각 관계식을 이용하여 플라즈마 비저항 또는 전기전도도를 구할 수 있다.
| (12) |
| (13) |
위에서 α0는 전체 원자밀도에 대한 비이온화원자의 비율(n0/nh)이다. 구리 플라즈마에 대한 electron-neutral cross section은 = 1.5×10-18 m2의 값을 사용했으며, Eq. 13의 이온-전자 충돌에 의한 전기전도도 모델에서 쿨롱 로그함수를 전통적 모델과 비교하여 수정되었다. 또한 위의 보정계수 γe는 전자간 산란 효과를 고려하는 Zaghloul[8]의 제안에 따른 다음의 관계식을 이용하였다.
| (14) |
Eq. 13의 Coulomb logarithm은 여러 형태가 존재하지만 여기서는 Powell과 Zielinski[12]의 연구에 제시된 다음의 관계식을 사용하였다. 참고로 n+는 이온화된 원자들만의 밀도(positive ion density)이다.
| (15) |
한편 Burgess 모델[13]에서는 금속체의 기화 및 플라즈마화 상태의 비저항을 온도와 압력만의 함수로서 산술식 형태의 반실험적 관계식을 이용하여 표현된다.
| (16) |
| (17) |
| (18) |
| (19) |
여기서 온도와 밀도의 단위는 eV 및 g/cm3이다. 위의 관계식에 나타나는 구리 플라즈마 대상의 상수들은 다음과 같이 주어진다: C1 = 1.5, C2 = 0.26, C3 = 2.23×10-3, C4 = 0.146, C5 = 7.68. 이러한 관계식은 그 간편성으로 기폭장치 전기폭발 현상 시뮬레이션에 자주 이용되고 있는데[2,14], 현 연구에 제시된 전기전도도 모델과 비교 분석될 것이다.
3. 구리 플라즈마 전기전도도 해석 및 토의
현 해석연구에서는 현대적 전기식 기폭관의 금속성 박막 및 도선의 전기폭발 및 플라즈마 팽창 초기에 나타나는 10,000∼60,000K 고온 영역 및 질량밀도 10 g/cm3 정도까지의 고밀도 영역의 금속성 플라즈마 발생 모델링 적용을 목적으로 플라즈마 전기전도도 해석모델 및 해석결과를 소개한다. 현 모델은 다양한 금속 소재에 적용될 수 있지만 여기서는 기폭관 브릿지 소재로 흔히 사용되는 구리 재질의 고온, 고밀도 열플라즈마를 대상으로 한다.
먼저 Fig. 1은 1기압 및 100기압 압력 조건에서 온도 변화에 따른 구리 플라즈마의 이온화 조성비 변화가 나타나 있다. 상대적 저압인 1기압에서는 온도 증가에 따라 약 10,000K 온도에서의 1차 이온화에 이어 20,000K 정도에서 구리 원자의 2차 이온화가 시작되며, 더 이상의 고온에서 3차 및 4차 이온화가 순차적으로 시작된다. 한편 100기압의 상대적인 고압 경우를 보면 좀 더 높은 온도에서 각 차별 이온화가 시작되는 등 전체적으로 플라즈마 이온화 정도가 낮아짐을 볼 수 있다.
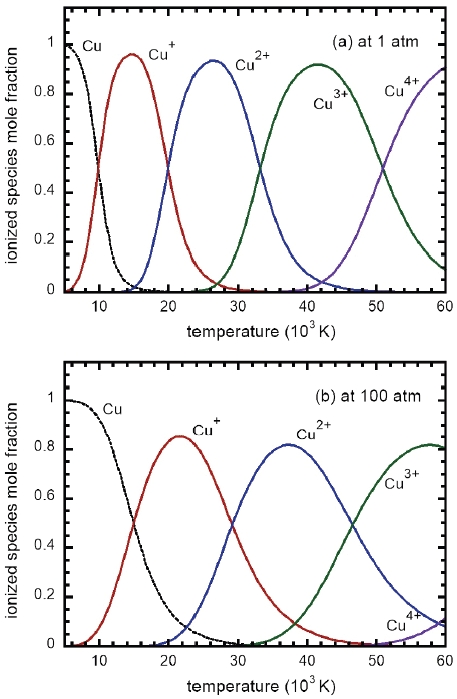
Molar composition of ionized metallic species for copper plasma with change of plasma temperature at given pressures of (a) 1 atm and (b) 100 atm.
Fig. 2에서는 여러 압력 조건에서 온도에 따른 플라즈마 이온화도 변화가 보이는데, Eq. 4의 이온화 저감 모델을 사용한 Rolader와 Batteh[3]의 해석과 비교되었다. 플라즈마 이온화 조성비는 두 모델 사이에 약간의 차이를 보이지만 상당히 일치하며, 다만 3차 이온화까지를 고려한 비교 대상 해석의 특성으로 인하여 고온 영역에서 유의미한 차이를 보여, 브릿지 전기폭발을 대상으로 한다면 금속 원자의 4차 이온화까지 고려할 필요성이 있다. 이러한 온도 및 압력에 따른 구리 플라즈마의 이온화 경향성은 브릿지 재질로 자주 적용되는 알루미늄 등 일부 타 재질의 금속 플라즈마와 상당히 유사한 경향성을 보이며 이는 타 연구에서도 확인할 수 있다[1,3].
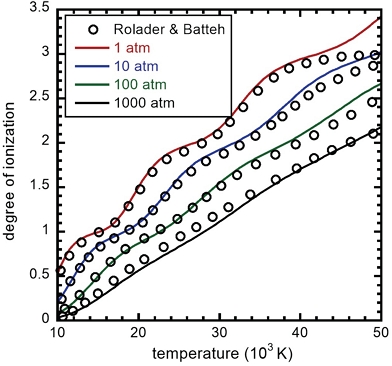
Plasma degree of ionization for copper plasma with change of plasma temperature at different levels of pressures. The symbols represent analytical results by Rolader and Batteh [3].
고압 또는 고밀도 열플라즈마에서 비이상 플라즈마 효과는 다음과 같은 플라즈마 비이상도로 추정할 수 있다[16].
| (20) |
이러한 비이상도가 충분히 낮으면(Γ < 0.1) 이상 플라즈마로 취급된다. 반면 비이상도가 상대적으로 높다면, 0.1 < Γ < 1 영역에서는 제한적인 비이상도 효과가 나타나며 여기서 제시하는 플라즈마 모델이 적용될 수 있다. 반면 Γ > 1이면 비이상 효과가 매우 크게 나타나기에 현 모델이 부적절할 수 있다. Fig. 3은 0.1 MPa∼1 GPa의 넓은 압력 범위에서 60,000K 고온까지의 플라즈마 비이상도가 나타나 있다. 이 결과로 보아서 현 모델의 이온화에너지 저감 모델이 유효함을 보여준다.
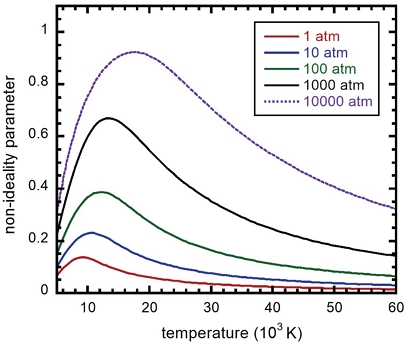
Plasma non-ideality parameter for copper plasma with change of plasma temperature at different levels of pressures.
이번에는 10,000K부터 50,000K까지 각기 설정된 플라즈마 온도에 대하여 질량밀도 10 g/cm3까지의 초고밀도 영역을 포함하여 밀도 변화에 따른 구리 플라즈마의 이온화 조성비 변화가 Fig. 4에 나타나 있다. 전반적으로 모든 온도에서 질량밀도 0.1 g/cm3 이상의 고밀도 영역에서는 좀 더 복잡한 경향에 따른 금속 원자의 고차 이온화가 발생함을 볼 수 있다. 이는 Fig. 5에 나타난 바와 같이 동일 조건에서의 플라즈마 이온화도가 고밀도 영역에서 급격히 증가하는 경향성에서도 파악할 수 있다. 이는 원자 간 쿨롱 결합 효과가 증가하며 저밀도의 열화 이온화 경향에서 고밀도의 압력 이온화 구간으로 천이함을 보여준다. 여기서도 고밀도 금속성 플라즈마 해석에는 4차 이온화 이상의 고려가 필요함이 나타난다.
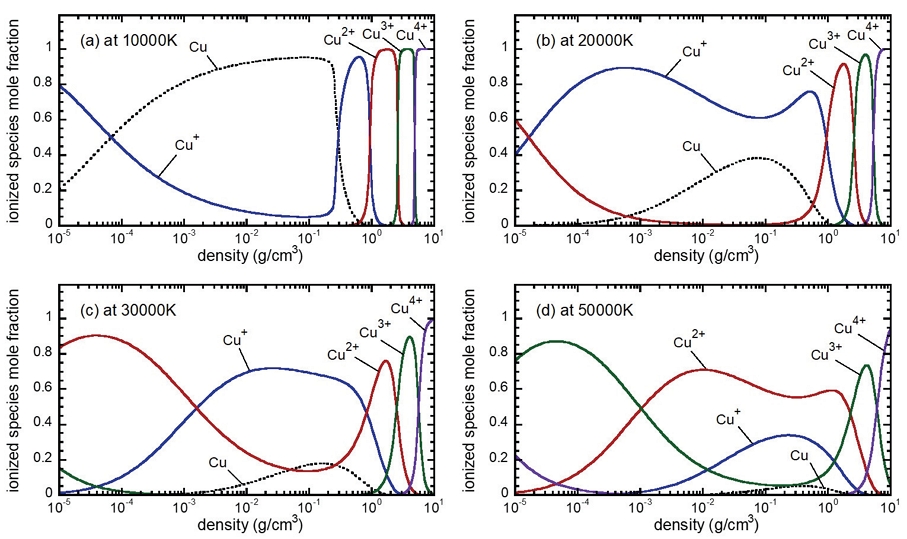
Molar composition of ionized metallic species for copper plasma with change of of mass density at given plasma temperatures of (a) 10,000K, (b) 20,000K, (c) 30,000K, and (d) 50,000K.
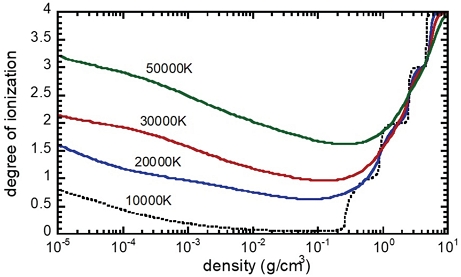
Effects of mass density on plasma degree of ionization for copper plasma at different levels of plasma temperature.
이와 같은 플라즈마 조성비 계산을 기반으로 하여 앞서 제시된 플라즈마 전기전도도 모델에 따른 구리 플라즈마의 전기전도도가 Fig. 4와 동일한 온도 및 질량밀도 영역에 대하여 계산되었다. 해당 해석 결과는 Fig. 6에 정리되었으며, DeSilva와 Katsouros[17]의 플라즈마 실험 측정 결과 및 Clérouin 등[10]의 QMD 시뮬레이션 결과와 함께 비교되었다. 또한 앞서 언급된 반실험적 Burgess 모델[13]의 예측 결과도 함께 수록되어 있다.
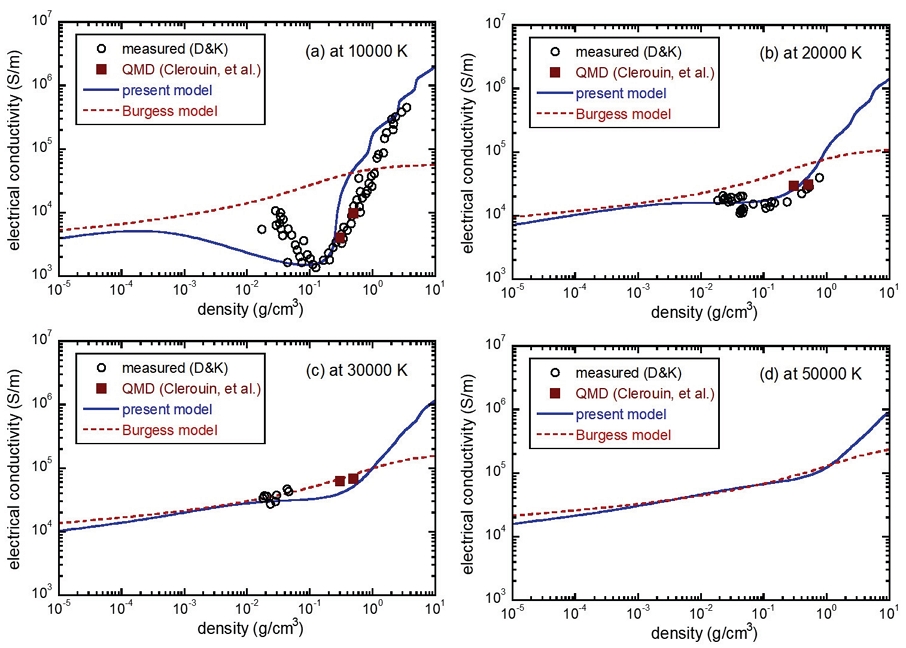
Electrical conductivity of ionized metallic species for copper plasma with change of of mass density at given plasma temperatures of (a) 10,000K, (b) 20,000K, (c) 30,000K, and (d) 50,000K. The circular symbols represent experimental results by DeSilva and Katsouros [17], while filled square symbols are from QMD simulations by Clérouin, et al. [10]. Dotted lines represent the results from Burgess model [13].
전반적 경향성을 살펴보면 동일한 질량밀도 영역에서 구리 플라즈마 전기전도도는 비이온화 원자 조성비가 상당히 낮은, 즉 이온화도가 높은 상대적 고온에서 좀 더 단순한 변화를 보여준다. 이에 비교하여 Fig. 6(a)의 10,000K과 같은 상대적 저온에서는 밀도 변화에 따른 비선형적 경향성이 두드러지게 나오는데 Fig. 4(a)와 비교하여 볼 때 비이온화 원자 조성비가 높음과 일치함을 볼 수 있다. 이는 전체 플라즈마 비저항에서 전자와 이온화 원자 간 충돌 효과에 따른 비저항 성분의 비율을 나타내는 Fig. 7에서도 확인할 수 있다. 또한 전자와 비이온화 원자 간 충돌 효과에 따른 비저항 예측 모델링이 상대적으로 좀 더 어려움을 확인할 수 있다.
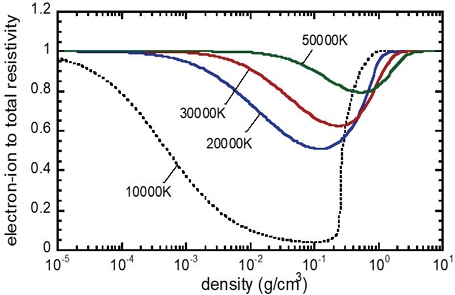
Effects of mass density on the ratio of electron-ion resistivity to total resistivity for copper plasma at different levels of plasma temperature.
현 플라즈마 전기전도도 모델은 측정 결과와 전반적 밀도 및 온도 영역에서 상당히 일치함을 보여준다. 열화 이온화 현상이 주를 이루는 저밀도 영역에 비교하여, 고밀도 영역에서는 압력 이온화 현상이 지배적인데, 비이상 플라즈마 현상이 심화되며 Burgess 모델이 부정확해짐이 나타나며 기폭관 브릿지 거동 모델링 적용에는 부적절할 것으로 판단된다.
Fig. 6에 함께 비교된 QMD 시뮬레이션 결과는 비선형성이 크게 나타나는 상대적 저온 및 고밀도 조건에서도 측정 결과와 좀 더 잘 일치한다. 하지만 QMD 시뮬레이션은 대규모 계산자원이 필요한 해석방법이기에 기폭관 설계 모델링 등에서 요구되는 실용적 플라즈마 물성 모델이 되기에는 현시점에서 부적당할 수 있다.
4. 결 론
현 연구에서는 현대적 기폭관의 금속성 브릿지 전기폭발 모델링에 적절히 적용할 금속성 플라즈마 전기전도도 계산모델이 소개되었으며, 브릿지 재질로 흔히 사용되는 구리를 대상으로 플라즈마 조성비 및 전기전도도 해석 결과를 측정 데이터 등과 비교하며 검증하였다. 여기서 제시된 실용적 전기전도도 모델이 비이상 플라즈마 효과가 강하게 발현되는 브릿지 버스트 등 관심 플라즈마 발생 현상의 고밀도 영역에서도 상당한 정확도로 금속성 플라즈마 전기전도도를 잘 예측함이 확인되었다.
Acknowledgments
본 연구는 금오공과대학교 학술연구비에 의하여 지원된 논문이다(과제번호: 2019-104-002).
References
-
Kim, K., Kim, K.-H. and Jang, S.-G., “Bridge Burst Characteristics of Aluminum and Copper Thin-Film Bridges in Electrical Initiation Devices,” Korean Journal of Metals and Materials, Vol. 56, No. 3, pp. 235-243, 2018.
[https://doi.org/10.3365/KJMM.2018.56.3.235]

-
Wang, G., He, J., Zhao, J., Tan, F., Sun, C., Mo, J., Xong, X. and Wu, G., “The Techniques of Metallic Foil Electrically Exploding Driving Hypervelocity Flyer to More Than 10 km/s for Shock Wave Physics Experiments,” Review of Scientific Instruments, Vol. 82, pp. 095105-1-8, 2011.
[https://doi.org/10.1063/1.3633773]

-
Rolader, G. E. and Batteh, J. H., “Thermodynamic and Electrical Properties of Railgun Plasma Armatures,” IEEE Transactions on Plasma Science, Vol. 17, No. 3, pp. 439-445, 1989.
[https://doi.org/10.1109/27.32252]

-
Kim, K., “Transient Flowfield Characteristics of Polycarbonate Plasma Discharge from Pulse-Powered Electrothermal Gun Operation,” Journal of Thermal Spray Technology, Vol. 17, No. 4, pp. 517-524, 2008.
[https://doi.org/10.1007/s11666-008-9204-2]

- Spitzer, L., Physics of Fully Ionized Gases, Interscience, New York, NY, U.S.A., 1956.
-
Zollweg, R. J. and Liebermann, R. W., “Electrical Conductivity of Nonideal Plasmas,” Journal of Applied Physics, Vol. 62, No. 9, pp. 3621-3627, 1987.
[https://doi.org/10.1063/1.339265]

-
Kovitya, P., “Physical Properties of High-Pressure Plasmas of Hydrogen and Copper in the Temperature Range 5000-60000 K,” IEEE Transactions on Plasma Science, Vol. PS-13, No. 6, pp. 587-594, 1985.
[https://doi.org/10.1109/TPS.1985.4316478]

-
Zaghloul, M. R., “A Simple Theoretical Approach to Calculate the Electrical Conductivity of Nonideal Copper Plasma,” Physics of Plasmas, Vol. 15, No. 4, pp. 042705-1-8, 2008.
[https://doi.org/10.1063/1.2903902]

-
Kim, D.-K. and Kim, I., “Calculation of Ionization Balance and Electrical Conductivity in Nonideal Aluminum Plasma,” Physical Review E, Vol. 68, pp. 056410-1-6, 2003.
[https://doi.org/10.1103/PhysRevE.68.056410]

-
Clérouin, J., Noiret, P., Blottiau, P., Recoules, V., Siberchicot, B., Renaudin, P., Blancard, C., Faussurier, G., Holst, B. and Starrett, C. E., “A Database for Equations of State and Resistivities Measurements in the Warm Dense Matter Regime,” Physics of Plasmas, Vol. 19, pp. 082702-1-15, 2012.
[https://doi.org/10.1063/1.4742317]

- Kim, K, Kwak, H.S., Kim, K.-H. and Jang, S.-G., “Analytic Study on Plasma Expansion of Thin-Film Bridge Burst and Flyer Acceleration in Exploding Foil Initiator,” 45th Korean Society of Propulsion Engineers Fall Conference, Gyeongju, Korea, pp. 655-659, Nov. 2015.
- Powell, J. D. and Zielinski, A. E., “Theory and Experiment for an Ablating-Capillary Discharge and Application to Electrothermal-Chemical Guns,” U.S. Army Ballistic Research Laboratory, Technical Report, BRL-TR-3355, 1992.
- Burgess, T. J., “Electrical Resistivity Model of Metals,” 4th International Conference on Megagauss Magnetic-Field Generation and Related Topics, Santa Fe, NM, U.S.A., 1986.
-
Luo, B.-Q., Sun, C.-W., Zhao, J.-H. and He, J., “Unified Numerical Simulation of Metallic Foil Electrical Explosion and Its Applications,” IEEE Transactions on Plasma Science, Vol. 41, No. 1, pp. 49-57, 2013.
[https://doi.org/10.1109/TPS.2012.2227827]

-
Batteh, J., Powell, J., Sink, D., and Thornhill, L., “A Methodology for Computing Thermodynamic and Transport Properties of Plasma Mixtures in ETC Injectors,” IEEE Transactions on Magnetics, Vol. 31, No. 1, pp. 388-393, 1995.
[https://doi.org/10.1109/20.364656]

-
Kim, K., “Numerical Simulation of Capillary Plasma Flow Generated by High-Current Pulsed Power,” International Journal of Thermal Sciences, Vol. 44, No. 11, 2005, pp. 1039-1046.
[https://doi.org/10.1016/j.ijthermalsci.2005.04.007]

-
DeSilva, A. W. and Katsouros, J. D., “Electrical Conductivity of Dense Copper and Aluminum Plasmas,” Physical Review E, Vol. 57, No. 5, 1998, pp. 5945-5951.
[https://doi.org/10.1103/PhysRevE.57.5945]
