가스터빈 회전부 림 씰 두께 증가에 따른 씰링 효율 변화에 대한 수치해석 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
가스터빈 림 씰 연구의 주요 목표 중 하나는 고온의 주 유동 유입을 차단하여 디스크 내부의 열 손상을 방지하는 것이다. 이를 위해 지금까지 림 씰의 형상에 대한 연구와 함께 이를 개선하기 위한 연구도 수행되었다. 또한, 실제 터빈에 림 씰 형상을 적용하기 위해서는 터빈 작동 시에 발생할 수 있는 다양한 상황에 대한 연구가 필요하다. 따라서 본 연구에서는 수치해석을 통해 회전부 림 씰 위치의 두께가 변화하는 상황에 대해 연구하였다. 연구는 반지름 방향으로 로터 림 씰이 상향된 경우와 림 씰 내부 방향으로 로터 디스크가 확장된 상황을 모사하여 진행하였다. 그 결과, 유입되는 이차유동의 양에 따라 각 경우에서 서로 다른 내부 압력과 씰링 성능 및 유동이 발생함을 확인하였다.
Abstract
One of the main goal of gas turbine rim seal research is to prevent thermal damage at rotor-stator disk by preventing hot gas of main flow in turbine passage. To increase sealing performance, several studies related to the improvement of rim seal configuration have been conducted. In addition, research based on actual operating condition is needed in order to apply effective turbine rim seal configuration. In this study, numerical simulation was conducted with variation of rotor rim seal thickness. Radial and axial expansion cases were tested numerically in this study. As a result, the cases showed different pressure distribution, sealing performance and flow characteristics according to the amount of secondary flow.
Keywords:
Rim Seal, Ingestion, Sealing Effectiveness, Rotor Rim Seal Thickness키워드:
림 씰, 주 유동 유입 현상, 씰링 효율, 회전부 림 씰 두께1. 서 론
가스터빈의 이차 유로 시스템은 터빈을 이루고 있는 고온 부품에 냉각 공기를 공급하여 효과적인 냉각을 달성할 수 있게 함으로써 가스터빈의 효율 및 수명을 증가시키는 역할을 한다. 이차 유로 시스템의 림 씰 시스템은 가스터빈의 고정자와 회전자 사이 간극으로 고온의 주 유동이 유입되는 것을 방지하는 장치이다. 림 씰 시스템에서의 효율적인 냉각을 위해 림 씰의 하부 영역인 휠 스페이스(Wheel space)에서는 냉각 공기가 공급되며, 림 씰 상부 영역에서는 다양한 림 씰 형상을 도입한다. 림 씰 시스템에서 소모되는 냉각 공기가 감소되면, 전체 시스템의 효율이 향상되는 효과가 있기 때문에 최소한의 냉각 공기를 이용하여 최대한의 주 유동 유입 차단을 이루는 것은 림 씰 연구에서 핵심적인 목표 중 하나이다.
림 씰에서의 주 유동 유입은 다양한 원인으로 인하여 발생하며, 이를 이해하고 분석하기 위한 연구들이 과거에 진행되었다. Owen[1]은 회전 효과에 의한 주유동의 유입 현상에 대하여 연구하였으며, 이를 분석하기 위해 orifice model을 도입하였다. 추가적으로, 그는 회전 효과 및 주유동의 압력 분포에 의한 림 씰 내부 유입 현상을 동시에 예측할 수 있는 orifice model을 제안하였다[2]. Haluca 등[3]은 베인의 위치 및 블레이드의 유무가 씰링 효율에 미치는 영향에 대한 연구를 진행하였다.
림 씰의 다양한 형상 및 터빈 가동 조건에 대한 연구 또한 진행되었다. Savov 등[4]은 단일 및 이중 림 씰에서의 씰링 효율에 대한 연구를 진행하였고, Scobie 등[5]은 씰링 효율을 상승시킬 수 있는 새로운 림 씰의 형상에 대한 연구를 진행하였다. Patinios 등[6]은 전방 림 씰과 후방 림 씰에서 유량 계수의 변화에 따라 발생하는 압력 계수 및 씰링 효율의 차이에 대해 연구하였다. Choi S.M. 등[7]은 회전수 및 이차유량의 변화에 따른 압력 및 씰링 효율의 변화에 대하여 연구하였다.
림 씰과 관련된 선행 연구는 주로 림 씰 주변의 유동, 림 씰 형상 및 가동 조건으로 제한되어 있었기에 본 연구는 실제 터빈 가동 시에 발생할 수 있는 조건을 모사하여 해당 효과를 분석하고자 한다. 따라서 본 연구에서는 회전부 림 씰에서 두께의 변화가 발생한 경우 림 씰 내부의 압력 및 씰링 효율 변화에 대한 연구를 수치해석을 통해 진행하였다.
2. 연구 방법
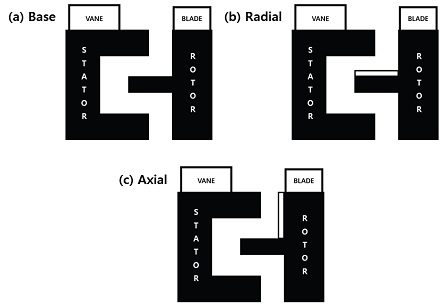
가스터빈 림 씰 연구와 관련해서, 현재 림 씰의 형상 변화 및 간극 변화에 대한 연구가 활발히 진행되고 있는 상황이다. 또한, 실제 가스터빈이 가동되는 경우 고온, 고압의 상황에서 디스크 및 블레이드가 회전하므로 이에 따른 전향 디스크 상황(디스크가 축 방향 전방으로 밀리는 현상) 및 전향 계단 상황(축의 오정렬 등으로 인해 반지름 방향으로 단차가 발생하는 상황)이 발생하게 되며, 이를 적용한 연구를 진행하였다. 따라서, 본 연구에서는 Fig. 1과 같이 기본 형상(baseline case), 반경 방향 증가 형상(radial case), 축 방향 증가 형상(axial case)의 3가지 상황에 대한 수치해석을 진행하였다. 기본 형상은 이중 림 씰의 형상을 가지고 있으며, 고속 회전 실험 리그의 림 씰 형상과 동일한 형태이다[7]. 반경 방향 증가 형상은 기본 형상에서 반지름 방향으로 열팽창 혹은 단차가 발생하였을 경우를 모사한 형상이며, 회전부 첫 번째 씰이 반지름 방향으로 1.5 mm 두께가 증가한 형태이다. 축 방향 증가 형상의 경우 기본 형상에서 축 방향으로 열팽창 혹은 전향디스크 상황이 발생한 것을 모사하였으며, 회전부 디스크의 두께가 축 방향으로 1.5 mm 증가한 형상이다. 회전부 림 씰 두께의 증가는 노즐 입구 높이의 약 5% 길이로 선정하였으며, 이는 림 씰 간극의 약 1/3을 차지한다.
림 씰 주변에서 발생하는 유동 특성을 고려하여, 비정상상태 유동을 분석할 수 있는 URANS(Unsteady Reynolds - averaged Navier - Stokes) 해석 방법이 사용되었다. 해석 프로그램은 ANSYS 19.2 상용 소프트웨어를 사용하였으며, 난류 모델로는 k-ω SST turbulence model과 transition gamma model이 적용되었다.
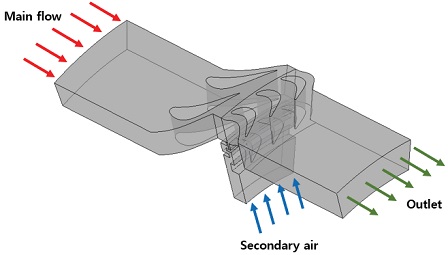
해석에 사용된 유동 도메인은 Fig. 2에 나타낸 것처럼 각각 20° 섹터에 2개의 베인과 3개의 블레이드로 구성되어 있다. 베인과 휠 스페이스의 유동 도메인은 정지 도메인으로, 회전 블레이드의 유동 도메인은 회전 도메인으로 설정하였다. 정지 도메인과 회전 도메인의 피치 비율은 1이다. 주 유동은 베인을 통과하여 출구 위치로 배출되며, 림 씰의 하부 휠-스페이스에서는 이차유동이 유입되어 주 유동의 유입을 방지한다.
Fig. 3은 해석을 실행한 유동 도메인과 격자를 나타낸다. 해석에 이용된 가스터빈의 형상은 실제 가스터빈에서 사용되는 형상을 상사하여 제작하였다. 베인과 휠 스페이스의 도메인은 정지 도메인으로 설정을 하였고, 블레이드를 지나는 유동의 도메인은 회전 도메인으로 설정하여 해석을 진행하였다. 정지 도메인과 회전 도메인 사이의 인터페이스는 transient rotor-stator 모델을 사용하여 해석을 진행하였다. 주 유동 및 이차유동이 유입되는 입구의 구속 조건은 질량 유량 조건을 사용하였으며, 블레이드 도메인을 통해 배출되는 출구 조건은 총 압력 조건을 사용하였다. 격자는 ANSYS ICEM 소프트웨어를 사용하여, 모든 계산 영역은 다중 블록 hexa 격자로 생성되었다. 벽 영역의 y+의 값은 1보다 작게 설정되었으며, 해석에서 1,200만 개의 격자 개수를 선택하였다.
본 연구에서 해석은 RANS 해석을 수행한 뒤, 해당 결과를 초기 값으로 URANS 방법 내에서 결과를 수렴시키는 과정을 거쳤다. 이후, 해당 결과를 초기 값으로 설정한 URANS 해석을 추가적으로 진행하여 최종 순간 및 평균된 결과 값을 획득하였다. 수치해석에서 사용된 timestep은 1.885X10-5로 설정되었으며, 이는 블레이드가 0.25도 회전할 때의 시간이다. 압력 분석의 경우, 블레이드가 회전하는 동안의 유입과 유출 경향을 파악하기 위하여 총 2,880개의 timestep 동안의 압력 평균값을 사용하였다.
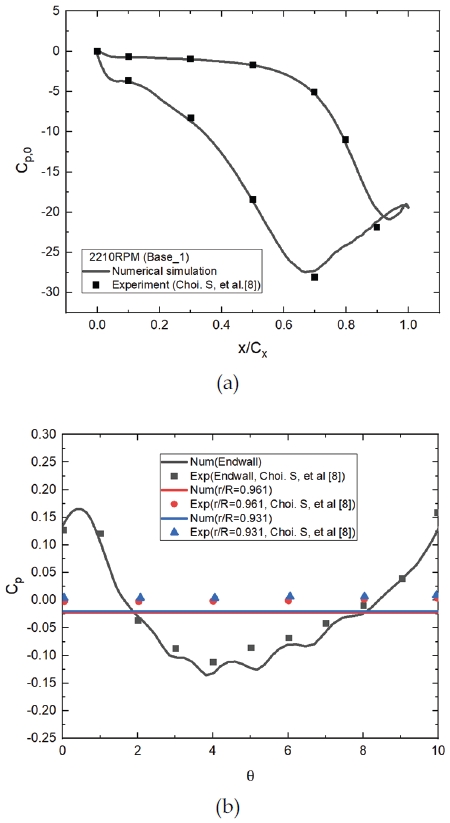
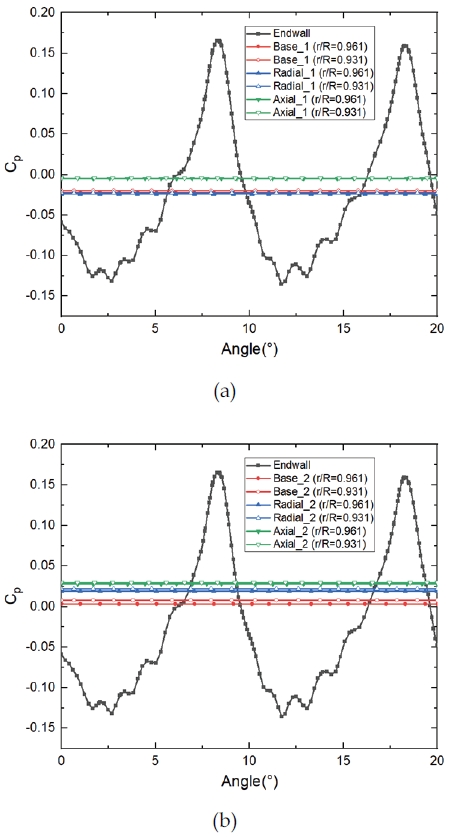
결과의 유효성을 평가하기 위해, 실험에서의 결과와 수치해석의 결과를 비교하였다. 압력 측정의 위치는 베인의 표면 및 후연면에서 후방 3 mm 떨어진 위치이며, 실험 장치와 일치하는 작동 조건에서 수치 시뮬레이션을 수행했다. 이후 이차 유량의 변화에 대하여 수치해석이 수행되었다. 수치 해석의 조건은 Table 1에 제시하였다. 해석 조건은 유량 계수(Flow coefficient) 및 회전 레이놀즈 수에 대해 실제 가스터빈에서 사용되는 운용 조건을 상사한 값을 사용하였다. Fig. 4(a)는 베인 중앙부에서 실험값과 수치해석 값의 압력계수 비교 결과이고, Fig. 4(b)는 엔드월과 림 씰 내부에서 실험값과 수치해석 값의 압력계수 비교 결과 그래프이다. 실험값은 Choi. S 등[8]에서 2,210 RPM, 이차유동 0.0222 kg/s 조건의 데이터를 사용하였다. 압력 계수는 베인 중앙부, 엔드월, r/b=0.961(between seal, 중앙부 씰), r/b=0.931(Second seal, 정지부 두 번째 씰)의 위치에서 측정되었으며, Eq. 1, 2와 같이 압력계수를 계산하였다. 그 결과, 수치해석과 실험의 결과는 주 유동 위치에서는 일치하였으며 (Fig. 4(a)), 엔드월 위치와 림 씰 내부에서는 일부 차이가 발생함을 확인하였다(Fig. 4(b)). 이와 같은 차이가 발생하는 이유는 림 씰에서의 비정상 유동 현상 때문이다. 림 씰 내부는 주 유동과 냉각 유량의 혼합이 활발하게 발생하는 위치이며, 반복되는 유동의 유입과 유출로 인해 림 씰 내부에는 크고 작은 와류가 발생하고 림 씰의 끝단에서는 유동의 박리가 발생한다. 회전에 의한 지속적인 비정상 유동의 발생에 따라 해석에서의 예측이 실제와 차이가 발생하게 되며, 림 씰 내부는 비정상 유동의 효과가 크기 때문에 주 유동 위치에 비해 압력 측정의 결과에 차이가 나게 된다. 그러나 해석에서의 결과는 참고한 논문 데이터의 오차 범위 내에 위치해 있으며, 이에 따라 해석 결과를 통해 실제 결과를 모사할 수 있다고 판단하여 추가적인 수치해석 및 결과 분석을 진행하였다.
| (1) |
| (2) |
3. 연구 결과
3.1 압력 분석
림 씰 내부 유동 특성을 파악하기 위해 압력 분석을 진행하였다. 베인의 후연부를 지난 주 유동은 베인의 형상으로 인해 원주방향으로 높낮이가 다른 압력 분포가 발생한다. Owen[2]에 의하면, 씰 내부의 압력보다 주 유동의 압력이 높아져 유동의 유입이 주로 발생하는 위치와 주 유동의 압력이 낮아져 유동의 누설이 주로 발생하는 위치가 존재하게 된다. 하지만 빠른 속도로 회전하고 있는 블레이드의 영향 또한 있기 때문에, 이에 대한 영향 또한 고려할 수 있는 방법이 시간(timestep)에 따른 압력의 평균값이며, 회전부가 회전을 하는 동안에 발생하는 평균적인 압력을 확인하게 되면 주로 어느 위치에서 유동의 유입과 유출이 발생하는지 파악할 수 있다. Fig. 5에는 엔드월에서의 위치와 림 씰 내부에서의 압력계수가 제시되어 있다. 엔드월에서의 압력이 림 씰의 압력보다 높은 경우에는 주 유동의 림 씰 내부 유입이, 엔드월에서의 압력이 림 씰의 압력보다 낮은 경우에는 이차유동의 외부 유출이 발생한다고 예상할 수 있다. Axial_1 의 경우, r/R=0.961과 r/R=0.931 위치에서 Base_1에 비해 높은 압력이 발생하였다. 반면, Radial_1의 경우 r/R=0.961과 r/R=0.931 위치에서 모두 압력 계수가 소폭 감소함을 확인하였다. 더 높은 이차유량이 유입된 Radial_2와 Axial_2의 경우, Base_2에 비해 림 씰 내부에서의 압력 상승을 확인하였다. 이를 통해, 수치해석을 통해 확인한 모든 경우에서 기존의 형상보다 주 유동의 내부 유입이 적거나 유사하게 발생함을 예측할 수 있다.
Comparison of pressure coefficient at (a) secondary air = 0.0222 kg/s, (b) secondary air = 0.0444 kg/s.
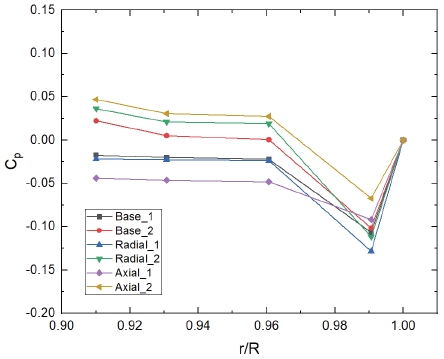
Fig. 6은 원주방향의 압력의 분포를 평균하여 r/R의 위치에 따라 도식화한 그래프이다. 전체적으로 휠-스페이스 내부에서 정지부 첫 번째 씰(first seal)까지 압력이 감소하는 경향을 보이며, 엔드월에서의 압력 계수는 정지부 첫 번째 씰보다 항상 높은 경향을 보인다. 이차유동의 양이 증가함에 따라 내부 압력이 증가하였고, 이에 따라 주 유동의 유입이 차단되는 효과가 나타남을 예상할 수 있다. 정지부 첫 번째 씰 위치에서는 축 방향 증가 형상이 제일 높은 압력 계수의 상승을 보였으며, 반대로 반경 방향 증가 형상에서는 압력 계수의 감소 현상이 나타났다.
3.2 씰링 효율 분석
림 씰 연구에서는 주 유동의 차단 정도를 나타내기 위해 “씰링 효율(Sealing effectiveness)”이라고 불리는 매개변수를 주로 사용한다. 씰링 효율은 아래의 Eq. 3과 같이 산출되었다. 씰링 효율을 산출하기 위하여 이차유동의 CO2농도가 1∼2%가 되도록 공기에 CO2 기체를 추가적으로 혼합한 뒤, 측정부에서의 CO2 농도를 측정하여 Eq. 3과 같이 씰링 효율을 산출하였다. 여기서 c는 측정부의 CO2농도, c0는 초기 유입된 이차유동의 CO2농도, c∞는 공기(ambient air)의 CO2농도이다. 주 유동의 유입이 증가할수록 씰링 효율은 0과 가까워지며, 유입이 감소할수록 씰링 효율은 1과 근접하게 된다.
| (3) |
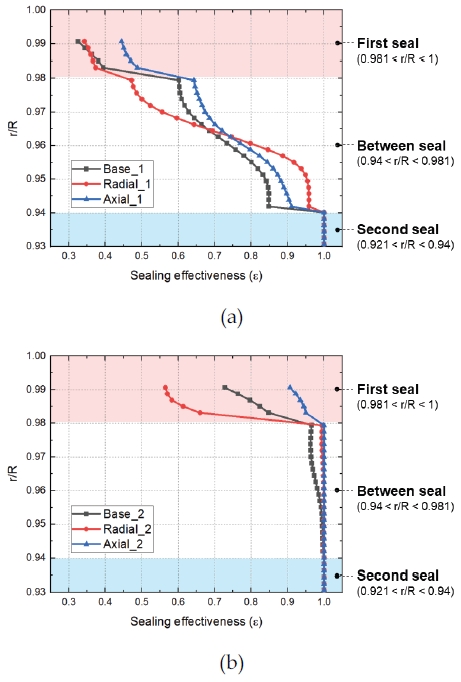
Fig. 7은 림 씰의 반지름 방향 위치에서의 씰링 효율을 나타낸 그래프이다. 붉은 색으로 표시된 구역은 정지부 첫 번째 씰이 위치한 영역, 흰색은 중앙부 씰 영역, 그리고 파란색은 정지부 두 번째 씰이 위치해 있는 영역이다. Fig. 7(a)에서 정지부 두 번째 씰 영역에서는 모든 case에서 씰링 효율이 1이며, 해당 영역까지의 주 유동 유입은 측정되지 않았다. 중앙부 씰 영역의 경우, r/R<0.964 위치에서의 씰링 효율이 Radial_1(+13%), Axial_1(+7.3%), Base_1 순으로 높게 측정되었다. 하지만 r/R>0.964 영역에서는 Radial_1의 씰링 효율이 급격하게 하락(-22.4%)하여 제일 낮은 수치의 씰링 효율이 발생하였고, Axial_1은 Base_1에 비하여 높은 씰링 효율(+6.8%)을 유지하였다. 정지부 첫 번째 씰 영역에서는 중앙부 씰의 r/R>0.964 영역의 경향과 동일한 경향이 나타나지만, 주 유동의 유입이 활발하게 이루어지는 영역이기 때문에 대체적으로 낮은 씰링 효율이 발생한다.
Comparison of sealing effectiveness at (a) secondary air = 0.0222 kg/s, (b) secondary air = 0.0444 kg/s.
Fig. 7(b)의 경우, Fig. 7(a)와 비교하여 두 배의 이차유량이 유입되었기 때문에 전체적으로 높은 씰링 효율의 경향이 나타난다. 중앙부 씰과 정지부 두 번째 씰의 영역까지 모든 case에서 0.95 이상의 씰링 효율의 값이 지속적으로 나타났다. 정지부 첫 번째 씰의 위치에서는 Axial_2(+24.6%), Base_2, Radial_2(-22.4%) 순으로 높은 씰링 효율이 나타났으며, Axial_2에서는 축 방향 림 씰의 간극이 줄어든 영향을 직접 받아 씰링 효율이 Base_2에 비해 증가하였다.
3.3 유동 분석
림 씰에서는 주 유동의 유입 상황과 냉각 유동의 유출 상황이 시간에 따라 다르게 발생하게 된다. 냉각 유량의 유출은 림 씰 내부에 영향을 주지 않지만, 주 유동의 유입은 림 씰 내부의 열 손상을 발생시킬 수 있기 때문에 주 유동의 유입 현상에 대한 분석은 중요하다.
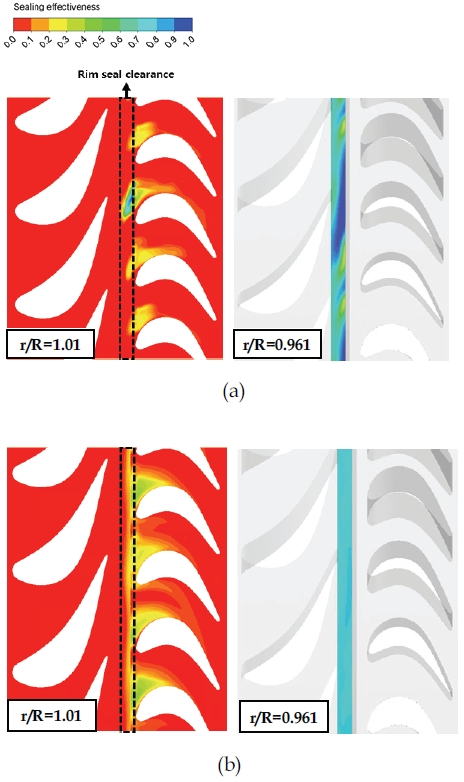
Fig. 8(a)는 Base_1에서 씰링 효율 순간 컨투어를 나타낸다. r/R=1.01의 경우, 냉각 유량의 유출이 로터 블레이드 근처에서 발생하며, 블레이드 흡입 면을 따라서 진행함을 알 수 있다. 또한, 냉각 유량의 유출량은 각 블레이드의 위치에 따라서 다르게 나타나게 된다. r/R=0.961 위치에서는 대체로 높은 씰링 효율이 발생하며, 불규칙한 형태의 씰링 효율 분포가 발생한다. 이는 중앙부 씰이 주 유동과 냉각 유동의 혼합이 활발하게 이루어지는 위치이기 때문이다. 반면, Fig. 8(b)의 씰링 효율 평균 컨투어는 블레이드의 위치에 따라서 비교적 반복적인 씰링 효율 분포가 나타난다. r/R=0.961 위치에서는 전체적으로 약 0.8에 가까운 일정한 수준의 씰링 효율의 분포가 관찰되며, 디스크 회전의 영향이 지배적인 위치임을 알 수 있다.
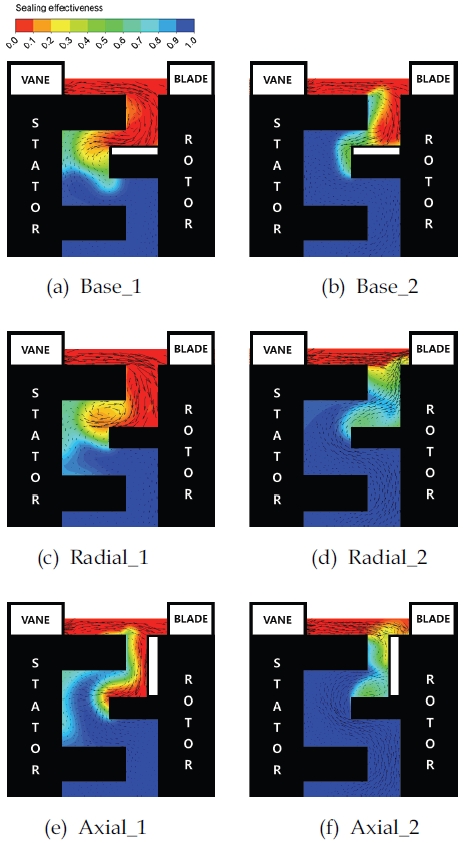
Fig. 9는 각 케이스에서 주 유동이 최대로 유입되는 상황에서의 씰링 효율 컨투어와 속도 벡터를 나타낸 그림이다. Fig. 9(a)에서, 간극 사이로 유입된 주 유동은 회전부 첫 번째 씰 상부를 따라 림 씰 내부로 진입하고, 끝단에서 박리되어 와류를 형성한다. Fig. 9(c)에서는 중앙부 씰 위치로 유입되는 주 유동이 정지부 첫 번째 씰 하부 벽을 따라 정지부 벽면으로 유입되는 경향을 보인다. 이는 정지부 첫 번째 씰과 회전부 첫 번째 씰 사이의 간극이 좁아지며 박리된 유동이 근처의 정지부 첫 번째 씰 하부 벽으로 재부착의 발생이 용이해지기 때문이다. Fig. 9(e)에서는 중앙부 씰 내부로 주 유동이 크게 유입이 되지 않고 주로 회전부 첫 번째 씰을 따라 유입되는 경향이 관찰된다. 또한, 정지부 근처 벽에서는 높은 씰링 효율이, 회전부 근처 벽에서는 낮은 씰링 효율이 발생하였다.
Fig. 9(b), (d), (f)에서는 중앙부 씰 내부로의 주 유동의 유입이 대부분 차단되며, Fig. 9(d)의 경우 정지부 첫 번째 씰 위치로의 주 유동 유입이 가장 크게 발생함을 알 수 있다.
4. 결 론
본 연구는 로터 디스크에서 축방향과 반지름 방향으로 두께의 변화가 발생한 경우에 대해 림 씰에서의 압력, 씰링 효율 및 유동 변화를 수치해석으로 분석하였다.
반경 방향의 단차가 발생하였을 때, 유입된 이차유량이 0.0222 kg/s 인 경우 내부 압력이 크게 변하지 않았지만, 중앙부 씰 상부 위치에서의 씰링 효율이 21.7% 증가하였고 하부 위치에서는 13% 감소하였다. 유입된 이차유량이 0.0444 kg/s 인 경우, 내부 압력이 상승하여 중앙부 씰에서의 씰링 효율이 상승하였지만, 정지부 첫 번째 씰에서 주 유동 유입이 크게 발생하여 씰링 효율이 22.4% 감소하였다.
축 방향의 단차가 발생하였을 때, 유입된 이차유량이 0.0222 kg/s 인 경우에는 중앙부 씰 위치에서 약 7% 내외로 씰링 효율이 증가하였다. 유입된 이차유량이 0.0444 kg/s 인 경우 내부 압력의 증가가 발생하였으며 Base 형상에 비해 정지부 첫 번째 씰 위치에서의 씰링 효율이 약 24.6% 증가하였다.
Nomenclature
| Cp : | Pressure coefficient |
| Cx : | Axial chord length of vane |
| c : | Concentration of local position |
| c0 : | Concentration of cooling flow inlet |
| c∞ : | Concentration of ambient air |
| p : | Pressure |
| pt : | Total pressure at inlet |
| R : | Radius of vane endwall |
| r : | Radius |
| Vin : | Inlet velocity |
| x : | Axial direction |
| Ω : | Rotation speed |
| ε : | Sealing effectiveness |
| ρ : | Density |
| θ : | Circumferential angle |
Acknowledgments
본 연구는 2019년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구이며(20193310100030), 2020년도 산업통상부의 재원으로 수행한 한국에너지기술평가원(KETEP) 인력양성사업(No. 20204030200110)의 일환으로 수행되었습니다. 또한, 한화에어로스페이스의 지원을 받아 수행되었으며 이에 감사드립니다.
References
-
Owen, J. Michael. “Prediction of Ingestion Through Turbine Rim Seals-Part 1: Rotationally-Induced Ingress,” Turbo Expo: Power for Land, Sea, and Air. Florida, U.S.A., pp. 1071-1082, June 2009.
[https://doi.org/10.1115/GT2009-59121]

-
Owen, J. Michael. “Prediction of Ingestion Through Turbine Rim Seals-Part 2: Externally-Induced and Combined Ingress,” Turbo Expo: Power for Land, Sea, and Air, Florida, U.S.A., pp. 1083-1093, June 2009.
[https://doi.org/10.1115/GT2009-59122]

-
Hualca, F.P., Horwood, J.T., Sangan, C.M., Lock, G.D. and Scobie, J.A., “The effect of vanes and blades on ingress in gas turbines,” Journal of Engineering for Gas Turbines and Power, Vol. 58653, pp. V05BT15A0082020, 2019.
[https://doi.org/10.1115/GT2019-90987]

-
Savov, Svilen S., Nicholas R. Atkins and Sumiu Uchida, “Comparison of single and double lip rim seal geometry,” Turbo Expo: Power for Land, Sea, and Air, Seoul, Korea, pp. V05AT15A003, June 2016.
[https://doi.org/10.1115/GT2016-56317]

-
Scobie, J.A., Teuber, R., Li, Y.S., Sangan, C.M., Wilson, M. and Lock, G.D., “Design of an improved turbine rim-seal,” Journal of Engineering for Gas Turbines and Power, Vol. 138, No. 2, 022503, 2016.
[https://doi.org/10.1115/1.4031241]

-
Patinios, M., Scobie, J.A., Sangan, C.M. and Lock, G.D., “Performance of Rim-Seals in Upstream and Downstream Cavities over a Range of Flow Coefficients,” International Journal of Turbomachinery, Propulsion and Power, Vol. 2, No. 4, 21, 2017.
[https://doi.org/10.3390/ijtpp2040021]

-
Choi, S.M., Choi, S. and Cho, H.H., “Effect of Various Coolant Mass Flow Rates on Sealing Effectiveness of Turbine Blade Rim Seal at First Stage Gas Turbine Experimental Facility,” Energies, Vol. 13, No. 16, 4105, 2020.
[https://doi.org/10.3390/en13164105]

-
Choi, S., Bang, M., Choi, S.M., Cho, M.H., Moon, H.K. and Cho, H.H., “Unsteady hot gas ingestion through the double rim-seals of an axial gas turbine,” International Journal of Mechanical Sciences, Vol. 207, 106664, 2021.
[https://doi.org/10.1016/j.ijmecsci.2021.106664]