고압에서 작동하는 고체 추진제 연소속도 추정 방법

1. 서 론

화포의 성능은 고체 추진제의 연소 엔탈피, 장약 질량, 연소속도에 큰 영향을 받는다. 전체 방출 에너지는 조성비에 따른 연소 엔탈피와 장약의 질량으로 결정되나, 탄이 빠른 속도로 움직이며 부피가 변화하기 때문에 연소속도 또한 최종 탄속에 큰 영향을 미치게 된다. 일반적인 고체 추진제의 연소속도는 주로 추진제 조성비에 의해 영향을 받는다. 또한 연소속도는 연소실 압력과 연소 전 추진제의 초기 온도, 연소 표면을 흐르는 가스의 속도, 연소실의 움직임 등 추진제 외부 환경의 영향을 받는다[1]. 시간당 추진제가 연소하는 양을 의미하는 연소율은 일반적으로 연소실의 압력의 n제곱에 비례한다. 또한 추진제의 초기 온도가 증가하면 예열에 필요한 시간이 감소하므로 연소속도가 증가한다.

인도의 High Energy Materials Research Laboratory(HEMRL)[2]는 다양한 장치를 이용하여 고체 추진제의 연소속도를 측정하는 방법을 정리하였다. Crawford[3]에 의해 고안된 Crawford bomb method는 추진제에 퓨즈선(fuse wire)을 포함, 최상단에서 점화가 시작되어 각 퓨즈선 간 거리와 경과한 시간을 나누어 연소율을 계산하는 방식으로 일반적인 압력(약 100기압 이하) 범위에서 널리 사용하는 연소속도 측정 방법이다. Song 등[4]은 초음파 변환기를 이용하여 매질에 방사한 후 연소하는 면에서 반사되어 돌아오는 역학적 파동을 측정하는 방식으로 추진제의 연소속도를 측정하는 초음파 측정 기법(Ultrasonic measurement technique)을 적용하였다. Eisenreich 등[5]은 밀폐용기에 석영 창을 설치하여 광학 및 분광학적 방법으로 추진제의 연소속도를 관찰하는 방법을 적용하였다. Sung 등[6]은 특정 고연소속도 고체추진제는 초고압(약 280기압 이상)에서 연소속도에 압력 상승률의 효과를 고려해야 하며 이로 인하여 압력지수가 0.4에서 0.8로 증가함을 제시하였다. 밀폐용기실험(Closed Bomb Test: CBT)은 초고압(200 cc 기준 약 120기압 이상)에서 측정한 압력 데이터를 이용하여 연소속도를 측정하는 방법이다[7].

본 연구에서는 국내에서 진행된 적 없는 초고압 환경에서의 고체 추진제의 연소속도를 추정하는 방법을 정립한다. CBT에서 측정한 압력 데이터와 추진제 조성에 따른 열역학 특성값을 이용하여 화포용 추진제의 연소속도를 계산하는 방법을 소개하며, 해외 프로그램(BRLCB)의 연소속도 지수/상수 결과를 비교하여 정확성을 검증하였다. BRLCB는 1982년에 개발되었으며 고체 추진제의 연소속도 추정, CBT 0D 성능해석과 시간에 대한 추진제 표면적 변화 등 다양한 분석이 가능한 프로그램이다.

2. 이 론

2.2 추진제 조성 별 열역학 특성

추진제의 연소 에너지를 예측하기 위해서 각 추진제의 열역학 특성값을 확보할 필요가 있다. 추진제의 연소 생성물은 원료 조성과 연소 조건 등에 따라 다르게 나타난다.

CBT는 정적연소이며 추진제의 연소로 발생하는 에너지는 내부에너지로 전환된다. 연소 후의 연소실 내부는 고온, 고압의 환경으로 일반적인 환경에서 기체의 거동을 묘사하는 이상기체 상태 방정식과는 달리 고압의 영향을 고려할 필요가 있다. 이상기체 가정에서는 기체 분자의 질량은 고려하나 분자 체적의 영향은 무시한다. 그러나 CBT의 고온, 고압의 환경에서는 에너지가 높고 기체 분자가 매우 빠른 속도로 거동하므로 분자의 체적 및 분자 간 충돌 영향을 무시할 수 없다. 따라서 이를 모사하는 실제기체 Noble-Abel 상태방정식은 다음과 같다.

$\[ P\left(V-m_{g}b\right)=m_{g}RT \]$

(3)

Covolume은 고온, 고압의 환경에서 기체 분자의 체적을 고려하는 보정 항으로 기체 분자의 유효체적을 의미한다.

Lennard-Jones potential(12-6 potential)은 상호 분자 간 potential을 이용하여 각 기체 분자의 유효 반경을 정의한다. 이 모델은 전기적으로 중성인 원자나 분자 간 약한 척력과 인력에 대한 영향을 고려한다. 기체 분자의 유효 반경은 분자 간의 potential이 0인 지점까지의 거리로 정의한다. 분자의 potential은 다음과 같다.

$\[ \varphi \left(r\right)=4ϵ\left({\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right) \]$

(4)

Table 1은 일부 기체 분자의 Lennard-Jones potential parameter이다. 이를 이용하여 Virial Equation of State에서 사용하는 Second virial coefficient와 Third virial coefficient를 구할 수 있다. 이는 각각 다음과 같다.

$\[ B\left(T\right)=\frac{2}{3}\pi N_A{\sigma }^3\sum _{j=0}^{\infty }{b}^{\left(j\right)}{\left(\frac{k_{B}T}{ϵ}\right)}^{-\left(2j+1\right)/4} \]$

(5)

$\[ C\left(T\right)={\left(\frac{2}{3}\pi N_A{\sigma }^3\right)}^2\sum _{j=0}^{\infty }{c}^{\left(j\right)}{\left(\frac{k_{B}T}{\epsilon }\right)}^{-\left(j+1\right)/2} \]$

(6)

Table 1.

Lennard-Jones potential parameter.

위 식은 각각 무차원 인자 T*와 t*의 함수로 구성된 무차원 변수 B*와 C*를 이용하여 각각 Ref.[9]의 Table Ⅱ-A, C에서 확인할 수 있다.

$\[ B\left(T\right)=b_{0}B\text{*}\left(T\text{*},t\text{*}\right),C\left(T\right)={b_0}^{2}C\text{*}\left(T\text{*},t\text{*}\right) \]$

(7)

$\[ b_0=\frac{2}{3}\pi N_A{\sigma }^3,T\text{*}=T\frac{k_B}{ϵ},t\text{*}={\mu }^2/\sqrt{8}ϵ{\sigma }^3 \]$

(8)

앞선 방식으로 구한 Second virial coefficient와 Third virial coefficient는 각 화학종의 값이다. 따라서 연소가스를 구성하는 혼합물의 virial coefficient는 mixing rule을 이용하여 구할 수 있다. Second virial coefficient는 서로 다른 분자의 상호작용을 고려하는 Second-order mixing rule을, Third virial coefficient는 First-order mixing rule을 적용한다. 각 mixing rule은 다음과 같다.

$\[ B\left(T\right)=\sum _i^{}\sum _j^{}{x}_i{x}_j{B}_{i,j} \]$

(9)

$\[ C\left(T\right)=\sum _i^{}{x}_i{C}_i \]$

(10)

$\[ {\sigma }_{i,j}=\frac{1}{2}\left({\sigma }_i+{\sigma }_j\right) \]$

(11)

$\[ {ϵ}_{i,j}=\frac{\sqrt{{\sigma }_i^3{\sigma }_j^3}}{{\sigma }_{i,j}^3}\times \sqrt{{ϵ}_i{ϵ}_j} \]$

(12)

따라서 혼합물의 Second virial coefficient와 Third virial coefficient를 이용하여 covolume을 구할 수 있으며 이는 다음과 같다.

$\[ b=\frac{{\left(1/MW\right)Bv}^2+{\left(1/MW\right)}^{2}Cv}{v^2+\left(1/MW\right)Bv+{\left(1/MW\right)}^{2}v} \]$

(13)

2.3 추진제 형상

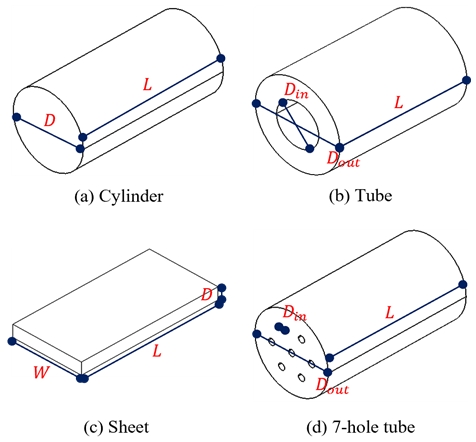
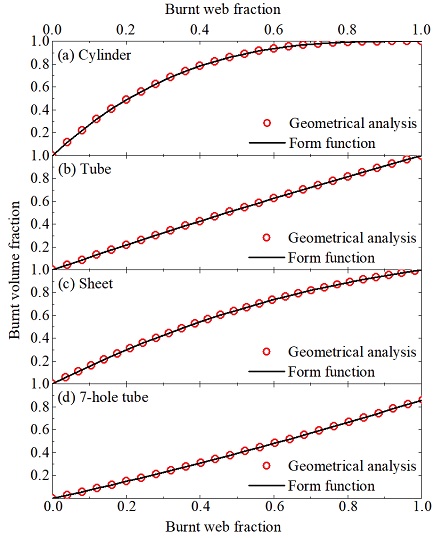
본 연구에서는 총 4종의 추진제 형상을 고려하며 Fig. 1과 같다. Vittal과 Singh[10]가 제안한 방법을 이용하였으며 각 형상의 기하학적 변수를 3차 형상 함수(Cubic form function)로 구성한다. 형상 함수는 연소한 추진제의 체적 분율 z를 연소거리 분율 f에 대한 함수로 나타낼 수 있다. 이는 다음과 같다.

$\[ z=f\left(k_1+k_{2}f+k_3{f}^2\right) \]$

(14)

Fig. 1

Propellant grain configuration

연소한 추진제의 체적 분율은 다음과 같이 정의한다.

$\[ z=\frac{V_{p,0}-V_p}{V_{p,0}}=1-\frac{V_p}{V_{p,0}} \]$

(15)

3. 요소 모델 검증

3.1 열역학 특성값 검증

본 연구에서는 서로 다른 2종류의 추진제 조성을 이용하여 열역학 특성값을 검증하였다. 각 추진제의 조성은 Table 2와 같다.

Table 2.

Propellant composition.

각 추진제별 충진양(Loading density)을 다르게 하여 Covolume을 비교하였으며 밀폐용기 내 연소 모델은 CEA의 정적연소 계산을 사용하였다[12]. 계산된 Covolume은 고온, 고압의 환경을 고려하여 화학 평형을 계산하는 BLAKE와 비교하였다[13]. 계산 결과는 각각 Tables 3, 4와 같다. 모든 추진제에서 Second virial coefficient와 Third virial coefficient는 생성되는 연소가스의 조성에 큰 차이가 없기 때문에 충진양에 무관하여 거의 일정한 값을 가진다. BLAKE와 비교하였을 때, virial coefficient는 최대 7%의 오차를 나타낸다. 반면에 충진양이 높을수록 Covolume의 값이 작아지는 경향을 보이며 오차 또한 최대 6% 결과를 보인다.

Table 3.

Covolume of propellant case 1.

Table 4.

Covolume of propellant case 2.

3.2 형상 함수 검증

2.3절에서 구성한 형상 함수를 검증하기 위해 4종의 추진제 형상(Fig. 1)별로 기하학적 방법을 이용하여 계산한 부피와 형상 함수를 이용하여 계산한 부피를 비교하였다. Fig. 2는 Web의 변화에 따른 연소한 체적 분율을 나타내며 각 추진제 형상에 대해 정확히 일치하는 결과를 보인다.

Fig. 2

Comparison between the form function and geometrical analysis.

4. 연소속도 분석

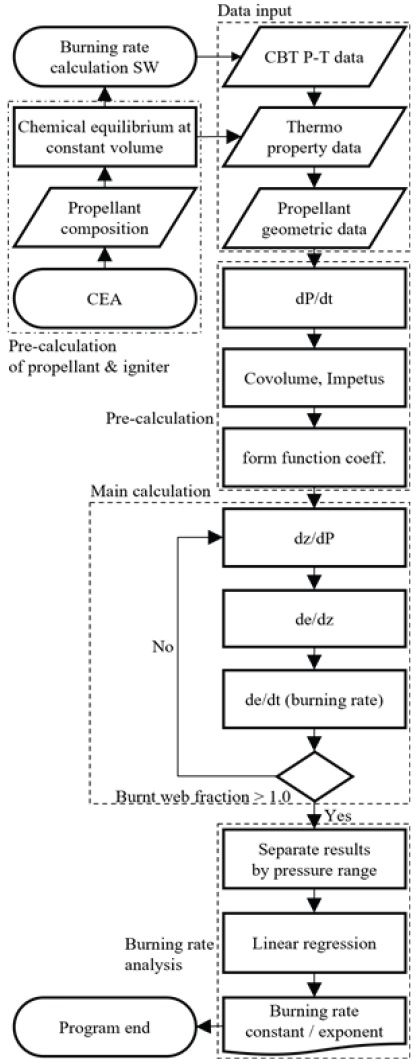
연소속도 분석은 선형성이 보장되면서 고압 영역인 25-75%의 구간에서 수행한다[14]. Fig. 3은 연소속도 분석 방법을 간략히 나타내었다. 연소속도 계산을 위해 해당 추진제의 CBT 압력 데이터, CEA에서 정적연소 계산을 통해 얻은 추진제 및 점화제의 열역학 물성치와 해당 추진제의 형상 정보를 계산하여 입력한다. CBT 압력 데이터로부터 dP/dt, 열역학 물성치로부터 Covolume 및 Impetus, 형상 정보로부터 해당 형상의 형상 함수 인자(form function coefficient)를 계산한다. 이후 2절에서 제시한 dz/dP와 de/dz를 이용하여 de/dt (연소율)을 계산한다. 계산된 연소율을 연소실 내부 압력에 따라 범위를 나누어 선형회귀분석을 하여 연소속도 지수/상수를 추정한다.

Fig. 3

Flow chart for burning rate analysis program.

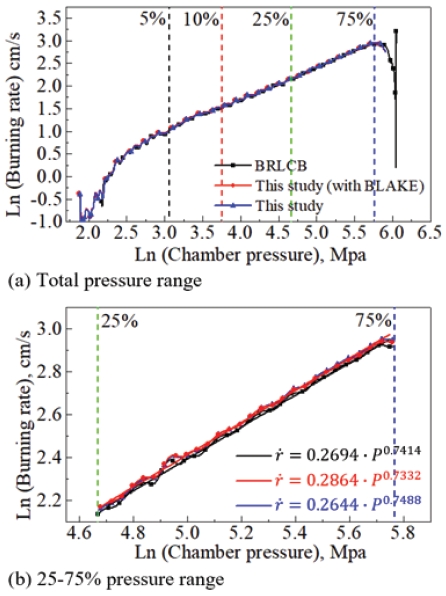
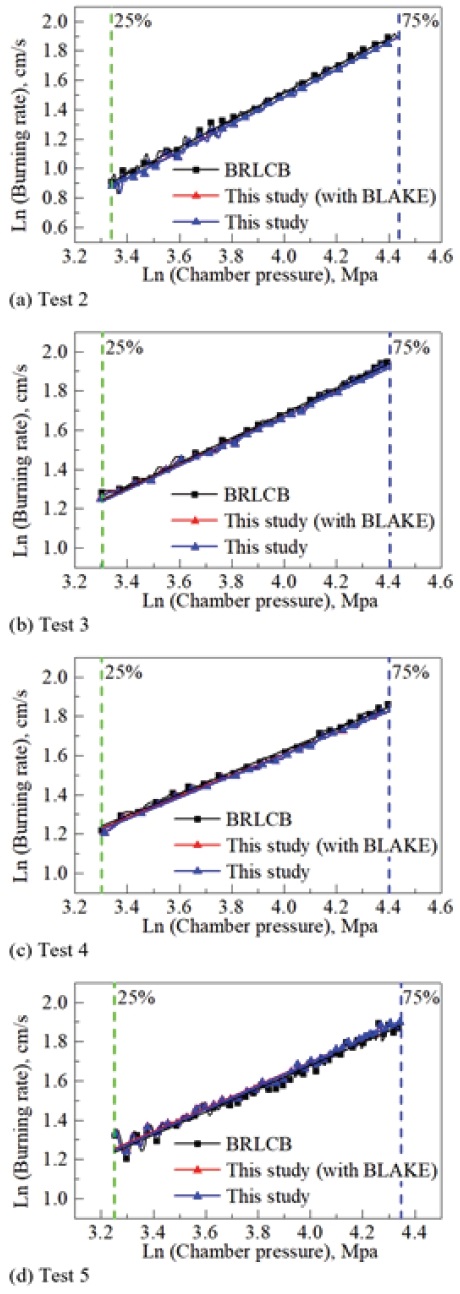
Table 5는 동일한 형상에 대해 서로 다른 추진제 조성(추진제 Case 1과 Case 2) 또는 동일한 추진제 조성에 대해 서로 다른 형상에 대해 연소속도 지수/상수를 분석하였다. 연소속도 지수/상수 계산을 BRLCB의 계산 결과와 비교 검증하였다. Tables 6-7은 계산된 연소속도 지수/상수와 오차를 나타낸다. Figs. 4-5는 연소실 압력에 대해 계산된 추진제의 연소율을 나타낸다.

Table 5.

Test specification.

Table 6.

Analysis result of test 1.

Table 7.

Analysis results of other tests.

Fig. 4

Comparison of burning rate of test 1.

Fig. 5

Comparison of burning rate.

모든 경우에서 연소속도 지수/상수는 약 6%의 오차가 발생한다. Test 1과 2는 원통 7공 추진제로 sliver가 발생하는 시점의 연소실 내 압력은 각각 최대 압력의 84%, 91%로 연소속도 추정에 영향을 주지 않는다. 또한 Covolume의 차이가 연소속도 추정에 미치는 영향을 확인하기 위해 BLAKE에서 계산된 값 (Figs. 4-5에서 “with BLAKE”로 표기)과 본 연구에서 계산한 값을 이용하여 연소속도 추정을 진행하였다. 모든 경우에서 5% 이내의 연소율 차이를 보이는 것을 확인할 수 있으며 Covolume 값의 차이는 연소율 추정에 큰 영향을 미치지 않는 것을 확인할 수 있다.

5. 결 론

본 연구에서는 밀폐용기(CBT) 내 화포 추진제의 CBT 압력 데이터를 이용하여 추진제의 연소속도를 추정할 수 있는 방식을 도출하였다.

연소가스 조성과 열역학 특성값을 도출하였으며 추진제 형상에 대해 형상 함수를 구성하여 연소에 의한 추진제 형상 변화율을 계산하였다. 본 연구에서 도출된 연소속도는 해외 BRLCB 코드 결과와 비교하여 검증하였다. 고압 영역에서의 연소속도 지수/상수가 약 6% 이내의 오차를 갖는 것을 확인하였다. Sliver가 발생하는 원통 7공형 형상의 경우에는 sliver가 발생하는 시점이 이미 연소 후반부에 위치하여 연소율 추정에 영향을 미치지 않는다. 또한 Covolume 차이에 의한 연소율의 차이를 확인하기 위해 BLAKE에서 계산된 열역학 특성값을 적용하여 연소율 추정을 진행하였으며 모든 test에서 약 5% 이내의 차이가 존재하나 연소율에는 큰 영향은 미치지 않는다.

Acknowledgments

본 연구는 방위산업기술지원센터의 지원(사업명: 화포 추진제 및 추진성능 예측 SW기술, 과제번호: UC190003D)하에 수행되었습니다.

References

• Cho, M.G., Heo, J.Y. and Sung, H.G., “Unsteady Internal Ballistic Analysis for Solid Rocket Motors with Erosive Burning,” Journal of the Korean Society of Propulsion Engineers, Vol. 13, No. 2, pp. 17-25, 2009.
• Gupta, G., Jawale, L., Mehilal, D. and Bhattacharya, B., “Various Methods for the Determination of the Burning Rates of Solid Propellants – An Overview,” Central European Journal of Energetic Materials, Vol. 12, No. 3, pp. 593-620, 2015.
• Crawford, B.L., Huggett, C., Daniels, F. and Wilfong, R.E.,“ Direct Determination of Burning Rates of Propellant Powders,” Analytical Chemistry, Vol. 19, No. 9, pp. 630-633, 1947. [https://doi.org/10.1021/ac60009a004]
• Song, S.J., Kim, H.J., Ko, S.F., Oh, H.T., Kim, I.C., Yoo, J.C. and Jung, J.Y., “Measurement of Solid Propellant Burning Rates by Analysis of Ultrasonic Full Waveforms,” Journal of Mechanical Science and Technology, Vol. 23, No. 4, pp. 1112-1117, 2009. [https://doi.org/10.1007/s12206-009-0302-y]
• Eisenreich, N., Kugler, H.P. and Sinn. F., “An Optical System for Measuring the Burning Rate of Solid Propellant Strands,” Propellants, Explosives, Pyrotechnics, Vol. 12, No. 3, pp. 78-80, 1987. [https://doi.org/10.1002/prep.19870120304]
• Sung, H.-G. and Yoo, J.C., “Burning Rate Characteristics of Solid Propellant at Extremely High Pressure,” Journal of the Korean Society of Propulsion Engineers, Vol. 10, No. 3, pp. 60-66, 2006.
• Celmins, A., “Solid Propellant Burning Rate Measurement in a Closed Bomb,” ARMY BALLISTIC RESEARCH LAB, Aberdeen Proving Ground, M.D., U.S.A., BRL-R-1840, 1975.
• Kubota, N., Propellants and Explosives: Thermochemical Aspects of Combustion, 3rd ed., John Wiley & Sons Inc., New York, N.Y., U.S.A., 2015. [https://doi.org/10.1002/9783527693481]
• Hirschfelder, J.O., Curtiss, C.F. and Bird, R.B., Molecular Theory of Gases and Liquids, John Wiley & Sons Inc., New York, N.Y., U.S.A., 1964.
• Vittal, D. and Singh, S., “Form Function for Propellants in Closed Vessel Work,” Propellants, Explosives, Pyrotechnics, Vol. 5, No. 1, pp. 9-14, 1980. [https://doi.org/10.1002/prep.19800050103]
• NATO., “Derivation of Thermochemical Values for Interior Ballistic Calculation,” STANAG 4400, 1993.
• Gordon, S. and McBride, B.J., “Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications: I. Analysis,” NASA, Cleveland, O.H., U.S.A., NASA RP-1311, 1994.
• Freedman, E., “BLAKE - A Thermodynamics Code Based on TIGER: User’s Guide and Manual,” ARMY BALLISTIC RESEARCH LAB, Aberdeen Proving Ground, M.D., U.S.A., ARBRL-TR-02411, 1982. [https://doi.org/10.21236/ADA121259]
• Oberle, W.F. and Kooker, D.E., “BRLCB: A Closed-Chamber Data Analysis Program Part 1. Theroy and User’s Manual,” ARMY RESEARCH LAB, Aberdeen Proving Ground, M.D., U.S.A., ARL-TR-36, 1993. [https://doi.org/10.21236/ADA260493]