
알루미늄/니켈 나노박막다층 내 수직방향 이종금속 반응파 전파 해석연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 나노에너지 기술 해석연구에서는 알루미늄/니켈 나노 다층박막구조 내 이종금속 반응파의 박막층 수직방향 전파현상을 대상으로 모델링 및 해석을 진행하였다. Al/Ni층이 교차하는 반무한영역에서 열 및 화학종 확산 방정식을 기반으로 1차원적 전산해석을 수행하였다. 해석결과로 이종금속 반응파의 수직방향 정상 전파 확립 등 반응파 특성을 발견하였다. 수평방향 전파현상 해석과 비교하여 이와 같은 나노구조물에서 반응파 자체전파속도에 대한 방향성 변화 영향이 매우 약하게 나타남을 확인하였다.
Abstract
Present modeling study of nanoenergetics focuses on the numerical simulation of reaction wave propagation in normal direction across nanoscale multilayers of aluminum and nickel combination. The governing equations for atomic and thermal diffusion are employed in one-dimensional semi-infinitely alternating Al/Ni multilayered structures and the numerical results show the established patterns of quasi-steady intermetallic reaction waves. Also, the reaction wave speed is confirmed to be highly independent of reaction wave directions in such nanoenergetic structures.
Keywords:
Nanoscale Multilayers, Reaction Wave Propagation, Aluminum/Nickel Layer, Numerical Modelling키워드:
나노 박막다층구조, 반응파 전파, 알루미늄/니켈 박막쌍, 해석모델1. 서 론
최근 들어 금속성 나노구조체 기반의 나노에너지 기술이 다양한 초정밀 에너지 응용분야에서 주목을 받고 있다. 방산 및 추진기술에서도 화약, 추진제 등 고에너지 물질 점화 및 연소 시스템의 소형화 및 경량화, 에너지밀도 증가, 점화성능 향상 및 정밀 조정, 그리고 시스템 안전성 및 신뢰성 향상 등 많은 기술적 장점으로 활발한 관련 연구개발 활동이 진행되고 있다[1]. 관련 세부기술로서 나노 금속입자 또는 나노 테르밋 복합분체 등의 활용이 있으며[2,3], 본 연구의 대상이 되는 이종금속 나노박막층 조합으로 구성되는 반응성 나노 박막다층구조가 또다른 대표적 기술이다[4-6].
대개 기상박막증착 등 MEMS 공정으로 제작되는 이종금속 나노 박막다층구조는 반응 점화 시에 이종금속간 화학반응의 빠른 점화성 및 높은 발열을 동반하는 고속 반응파 전파특성을 보인다[4]. 그동안 알루미늄/니켈(Al/Ni), 보론/티타늄(B/Ti) 등 다양한 금속조합의 박막다층구조를 대상으로 실험적 연구 및 간소화 모델을 이용한 이론해석 연구가 수행되었다[5-8]. 또한 이러한 이종금속 박막다층구조의 뛰어난 에너지 분출특성을 활용하여 고에너지물질 착화기의 점화성능 향상 가능성에 대한 실험 및 모델링 연구들이 진행된 바 있다[9-12].
이종금속 나노 박막다층구조 내 반응파 점화 및 전파에 관한 해석적 연구는 주로 박막층을 따르는 수평방향 전파현상을 대상으로 하였는데[7,8,13], 이에 비하여 박막다층 수직방향으로의 반응파 전파현상은 아직 심도깊게 다루어진 바가 별로 없다. 본 해석연구에서는 앞서의 반응파 수평전파 선행연구[13,14]에서 개발된 해석기법을 기반으로 하여 Al/Ni 조합의 나노 다층구조 내 수직방향 이종금속 반응파 전파에 관한 전산 시뮬레이션 및 현상 분석을 시도한다.
2. 박막다층구조 내 반응파 수직전파 해석모델
본 연구의 모델링 및 해석연구 대상은 Fig. 1(a)에 묘사한 바처럼 Al/Ni 이종금속 나노 다층박막으로서 수십 나노미터 내외 나노두께의 알루미늄과 니켈 박막층이 서로 교차하여 연속적으로 적층되어 구성되는 나노구조체이다. 알루미늄과 니켈 간의 이종금속반응에 의한 발열 반응파의 자체전파는 여기서는 박막다층의 수직방향(x방향)으로 진행되어 1차원적 물리현상으로 모델링이 가능하다. 이종금속반응에 따른 다층구조 내 발열 및 온도에 따른 물성치 변화를 고려한 비정상 에너지 방정식과 반응 발열률 모델식은 다음과 같이 표현될 수 있다[8,13,14].
| (1) |
| (2) |
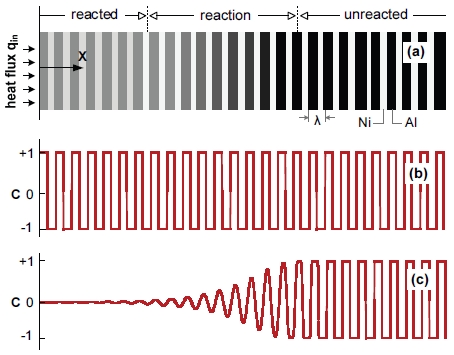
Schematic of nanoscale bimetallic multilayers of aluminum and nickel (a) with initial atomic species concentration (b) and reaction wave propagation in Al/Ni multilayers (c).
여기서 각 금속 박막층의 질량밀도(ρi), 비열(ci), 열전도도(ki) 등은 해당 금속층에 대하여 온도의 함수로서 주었다. Eq. 2의 이종금속 반응 발열률은 화학종 농도(C)의 시간변화율 제곱에 비례한다는 실험적 고찰을 기반으로 한다[7]. 또한 ΔHf는 Al + Ni ⟶ NiAl 화학반응의 반응열(330 cal/g)이다.
이종금속 박막층 간의 양방향 원자 확산에 따른 화학종 농도 변화는 다음과 같은 비정상 확산방정식 및 확산계수로 표현할 수 있다.
| (3) |
| (4) |
이종금속층의 화학종 농도는 Shvab-Zeldovich 무차원 변환변수 개념을 채용하여 순수 알루미늄은 C = +1, 순수 니켈은 C =╶1로 정의하였다. Al/Ni 화학반응이 니켈 알루미나이드(NiAl)로 진행되면 그 농도 변수값이 양쪽에서 0에 접근한다. 이종금속 화학반응은 Arrhenius 반응모델을 따른다고 가정하였다. Al/Ni 이종금속 반응 해석에 필요한 활성화 에너지(Ea) 및 전지수인자(pre-exponential factor, D0) 값들은 타 이종금속 조합에 비하여 비교적 잘 확립되었으며, 반응전파 측정시험 분석에 따라 Ea = 137 kJ/mol, D0 = 2.18×10-6 m2/s로 주어진다[5].
Al/Ni 나노 박막다층의 반응 점화는 Fig. 1(a)와 같이 반무한 다층구조의 한쪽 면에서 짧은 일정시간 동안 점화 가능 최소 열유속을 적용하여 모사하였으며, 인근 다층구조의 온도가 일정 이상 유지되면 더 이상의 외부 에너지 자극없이 이종금속 반응이 시작되어 Fig. 1(c)와 같이 박막다층 수직방향으로 전파된다. 이러한 열유속 점화조건이 레이저 조사 또는 금속저항 브릿지를 이용한 열적 점화 등 실제 점화방식과도 일치하며, 자세한 설정은 선행연구를 참조한다[13,14].
Al/Ni 금속다층의 접촉면에서 이종원자 예혼합(premixing)이 없다고 가정하면 화학종 농도의 초기조건은 Fig. 1(b)와 같이 박막다층 수직방향으로 +1과 ╶1 사이의 연속적 단위 계단함수 형태로 표현된다. 하지만 박막다층 제조공정 및 그 이후에 접촉면의 예혼합 현상은 불가피하게 발생한다. 이러한 예혼합층 존재 효과를 해석에 포함하기 위하여 박막다층 수평방향 전파 해석연구에서도 채용한 다음과 같은 예혼합층 모델[14]을 여기서도 이용하였다. 따라서 ±w 두께의 예혼합층 영역에서 초기 화학종 농도는 다음처럼 표현된다.
| (5) |
여기서 w는 예혼합 두께이며 x’는 각 접촉면 기준 박막다층 수직방향 좌표이다. 한편 초기온도는 모든 박막다층 영역에서 300 K로 주었다.
위와 같은 이종금속 박막다층 구조의 모델링을 이용하여 Al/Ni 다층구조 내 이종금속간 화학반응 점화 및 반응파의 수직방향 전파 현상 분석을 위한 박막다층 온도 및 화학종 농도의 비정상 1차원적 해석계산을 다물리 전산해석 패키지인 COMSOL MULTIPHYSICS를 이용하여 수행하였다.
3. 박막다층 해석결과 및 토의
본 이종금속 박막다층 해석연구의 전산해석 대상은 나노 두께의 Al/Ni 박막쌍이 한 쪽으로 무한히 반복되는 다층구조에서 박막다층 수직방향으로의 이종금속 화학반응 점화 및 반응파 자체전파 현상이다. Al/Ni 복합박막 한쌍의 두께는 λ = 60 nm를 기본으로 설정하였다. 앞서 언급한 Al/Ni 이종금속 반응의 1:1 몰비와 더불어 각 금속 질량밀도 및 몰질량을 고려하면 Al/Ni 박막쌍 내 각 금속 두께비는 약 1.5:1이다. 따라서 각 금속층의 개별 두께는 tAl = 36 nm, tNi = 24 nm이다.
반무한영역에서 진행되는 이종금속 반응파 전파 해석을 위해서 박막다층의 해석 길이는 충분해야 하는데, 여기서는 총 1,024개의 Al/Ni 박막쌍으로 1차원적 해석영역을 설정하였다. 격자는 한 박막쌍 당 51개를 배치하였으며 반응영역 내 화학종 농도 및 발열률이 가파르게 변하는 이종금속 접촉면 인근에 격자를 좀 더 조밀하게 배치하였다. 또한 격자 민감도 시험을 진행하여 현 격자계가 충분함을 확인하였다. 또다른 해석영역 끝단은 단열 경계조건으로 단순하게 처리하였다. 접촉면의 예혼합 두께는 Al/Ni 박막다층 점화시험 측정결과 분석[7]에 따라 w = 1.2 nm을 기본값으로 주었다.
이러한 Al/Ni 박막다층의 기본 형상조건(λ = 60 nm)에 대하여 이종금속 반응점화 이후 형성된 반응파 전파현상 해석결과가 Fig. 2와 Fig. 3에 마이크로초 단위 시간별로 화학종 농도 및 온도분포, 그리고 반응 발열률 분포로 나타나 있다. 먼저 Fig. 3(b)를 관찰하면 주어진 10 ns의 열유속 점화조건에 따라 이종금속 반응이 0.25 μs 이내에 점화되어 높은 발열을 동반하여 반응파 자체 전파가 이루어짐을 볼 수 있다. 초기에 3 μs 정도의 시간 구간에서는 점화 효과 및 열유속 가열로 인하여 비정상 반응파 변화 현상을 보인다. 그 이후에는 온도와 발열률 분포 형상과 각 시간 당 반응파 진행 위치 간격이 일정하게 유지됨을 보아 반응파의 정상 전파가 수립됨이 나타난다.
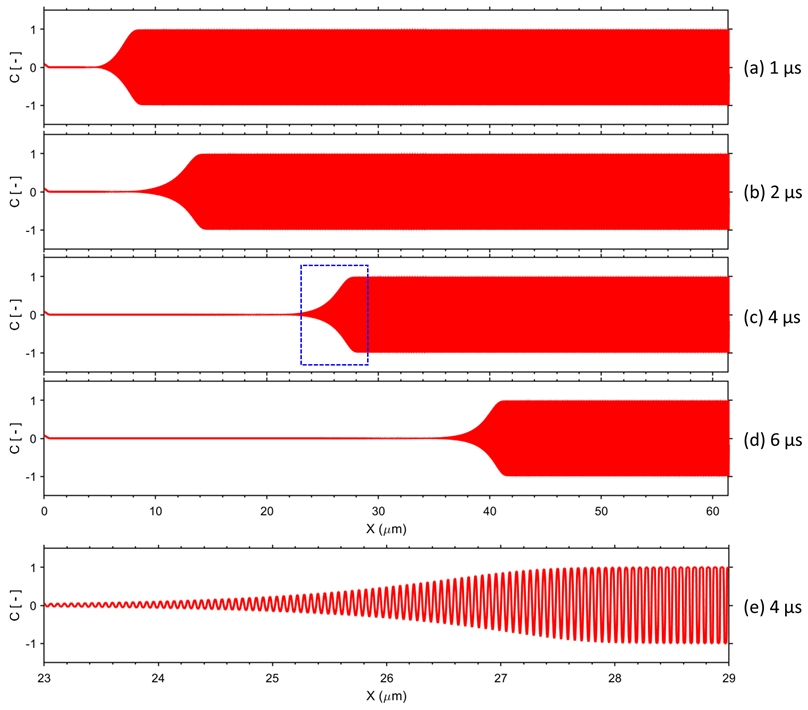
Time progress of atomic species concentration distribution in Al/Ni multilayers: the case of bilayer spacing λ = 60 nm and premixing thickness w = 1.2 nm. Dotted box at 4 μs represents the zone for (e).
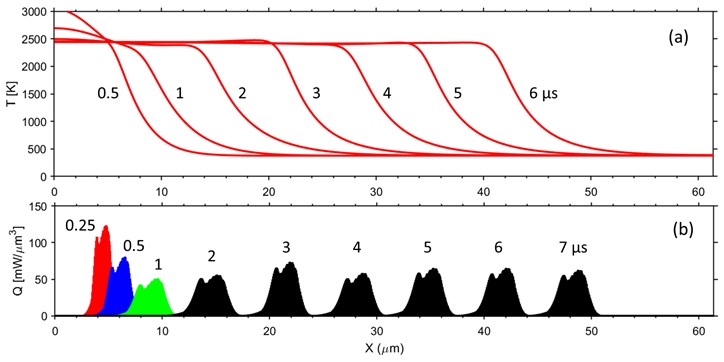
Time progress of (a) temperature and (b) reaction heat generation distributions in Al/Ni multilayers: the case of bilayer spacing λ = 60 nm and premixing thickness w = 1.2 nm.
Fig. 2의 시간적 화학종 농도 분포의 시간 간격별 변화에서도 이러한 반응파의 선형적 전파를 확인할 수 있으며 반응영역 길이는 약 6 μm로 80여개의 Al/Ni 박막쌍에 해당한다. 개별적 이종금속층 내 화학종 농도 변화를 좀 더 잘 관찰하기 위해서 Fig. 2(e)에는 Fig. 2(c)의 4 μs 시간대에 대하여 23-29 μm의 반응영역의 화학종 농도 분포가 나타나 있다. 참고로 동일 시간에 대하여 온도분포를 화학종 농도 분포와 함께 비교해보면 반응파 앞쪽의 예열영역(4 μs 경우 40 μm까지)을 발견할 수 있다. 예열영역은 복합다층의 유효 열전도성에 큰 영향을 받으며 반응파 자체 전파속도에도 지대한 영향을 미치게 된다.
동일 Al/Ni 박막다층 사양에 대하여 이번에는 시간-공간좌표에 대한 온도 및 화학종 농도 변화가 Fig. 4에 나타나 있다. 여기서도 초기 약 3 μs 내의 비정상 효과와 그 이후의 이종금속 반응파 자체전파 확립 현상이 관찰된다. 특히 Fig. 4(a)에서 점화를 위한 열유속 효과는 초기 2-3 μs 정도 이내에 사라지며 시간에 따른 기반응영역과 비반응영역 구분을 특정하는 반응파 및 예열영역 전파특성이 시간-공간도표에서 확연히 선형적임이 보인다.
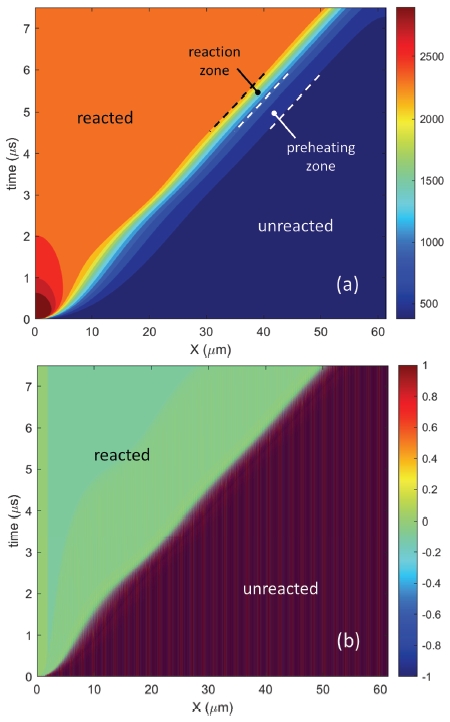
Time-space contours of (a) temperature and (b) atomic species concentration in reacting Al/Ni multilayers (the case of λ = 60 nm and w = 1.2 nm).
Fig. 3(b)에서 시간별 발열률 분포 형태를 관찰하면 반응영역 내 두 위치에서 최고점이 나타난다. 이를 볼 때 총 발열률은 발생 위치가 다른 두 발열분포의 합으로 분석할 수 있다. 예로 5 μs 시간대의 반응영역은 약 34.5-37 μm의 반응파 전파방향 기준 전반구간과 그 보다 상대적으로 짧고 발열률이 낮은 약 32.5-34.5 μm의 후반구간으로 나눌 수 있다. 이러한 두 구간에서의 박막다층 반응현상을 세밀히 관찰하기 위해서 각 구간의 일부 영역에 대한 발열률 및 화학종 농도분포가 Fig. 5에 나타나 있다. Fig. 5(a)와 (b)에 보이는 반응파 선단의 전반위치에서는 박막다층 접촉면 인근의 좁은 영역의 Al/Ni 반응을 보인다. 이에 비교하여 Fig. 5(c)와 (d)의 반응파 후단위치에서는 접촉면 반응이 상당히 진행된 후 각 금속층 내부영역에서의 반응성이 확인된다.
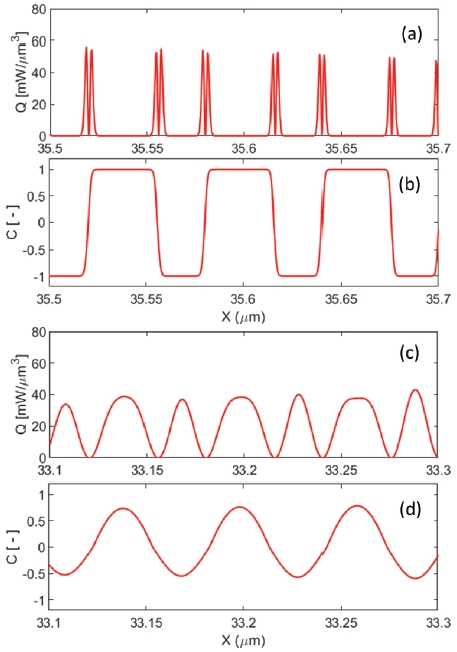
Detailed view of reaction heat generation and atomic species concentration for (a, b) front and (c, d) rear locations at time of 5 μs (the case of λ = 60 nm and w = 1.2 nm).
Fig. 6에는 λ = 60 nm의 Al/Ni 박막다층 내 수직방향 반응파 위치의 시간적 변화가 나타나 있다. 반응파 위치는 점화 시작점(x=0)에서 화학종 농도가 C = ±0.5에 도달하는 지점 평균을 기준으로 산출하였는데, 발열률 최고 위치, 일정 온도값 위치 등으로 선정하여도 큰 차이는 없었다. 여기서도 예혼합 두께가 w = 1.2 nm일 때 초기 3 μs 시간대 이후에 반응파의 선형적 자체전파가 확인되며 그 기울기의 선형회기분석으로 구한 반응파 전파속도는 약 6.5 m/s이다.
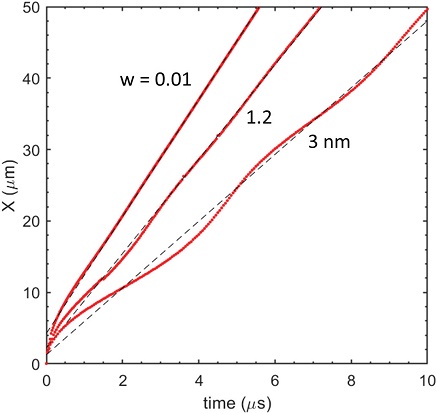
Effects of atomic premixing on time traces of reaction wave in Al/Ni multilayers (the case of bilayer spacing λ = 60 nm).
다음으로 동일 박막쌍 두께에 대하여 Al/Ni 접촉면 예혼합 정도의 영향성을 분석하기 위하여 예혼합이 거의 없는 경우(w = 0.01 nm)와 예혼합 두께가 증가한 w = 3 nm일 때의 시간적 반응파 위치를 Fig. 6에 함께 포함하였다. 예상대로 예혼합 효과가 없는 경우에는 반응파 전파속도가 약 7.9 m/s로 증가하며 매우 짧은 시간 내에 반응파 전파의 선형성이 수립된다.
반대로 w = 3 nm인 경우에는 반응파 전파속도의 상당한 감소(약 4.6 m/s)가 있으며, Fig. 6과 같이 상당한 비정상성이 나타난다. 반응파 수평전파 해석연구[14]에서는 예혼합 영향이 큰 경우에 초기 열유속 점화조건의 영향과는 별개로 주기적 비정상성이 관찰된 바가 있다. 여기의 반응파 수직방향 해석에서도 동일 현상으로 추정한다. 하지만 이를 확인하기 위해서는 해석영역 및 계산시간의 대폭적 확장이 불가피하여 추가적 연구가 필요한 부분이다.
예혼합 두께를 조밀하게 변화시키며 해석을 진행하여 앞서 언급한 방법으로 반응파 전파속도를 산출하였으며 그 결과가 Fig. 7에 정리되어 있다. 예혼합 두께가 1 nm 정도 이상으로 증가하면서 반응파 전파속도가 급격하게 떨어지는 경향을 보인다. 더욱 심한 주기적 비정상성을 보이는 w = 7 nm 경우에서 전파속도가 0.52 m/s로 낮아지며, 그 이상의 예혼합 정도에서는 점화조건을 어떻게 조정해도 Al/Ni 반응 점화가 나타나지 않는다.
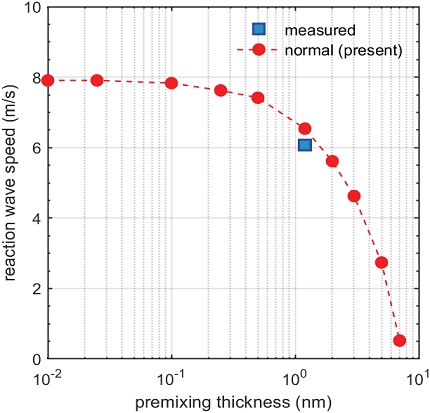
Effects of atomic premixing on propagation speed of reaction wave in Al/Ni multilayers (the case of bilayer spacing λ = 60 nm).
마지막으로 박막쌍 두께를 변화시키며 반응파 수직전파 해석을 진행하여 반응파 전파속도에 미치는 영향을 알아보았다. 동일한 예혼합 조건(w = 1.2 nm)에 대하여 10에서 200 nm까지의 박막쌍 두께 범위에 대한 종합적 결과를 Fig. 8에 정리하였다. 박막쌍 두께가 감소하면 반응파 전파속도가 상당히 증가하는 경향을 보이기는 하지만 일정 예혼합 두께에 의한 영향으로 λ = 15 nm 정도에서 최고 속도가 나타난다.
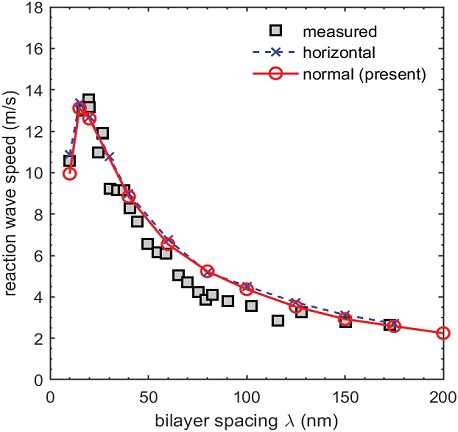
Effects of bilayer spacing on propagation speed of reaction wave in Al/Ni multilayers (the case of premixing thickness w = 1.2 nm).
여기에는 Al/Ni 박막다층 내 반응파 수평전파 대상 전파속도 측정시험[7]과 2차원적 해석[14] 결과가 함께 수록되어 있다. 이를 본 연구의 수직전파 속도 해석결과와 비교하면 거의 동일한 전파속도가 나타남을 알 수 있다[15,16]. 따라서 현 연구대상 이종금속 박막다층과 같은 나노 크기의 에너지구조물에서는 반응파 전파의 방향 의존성이 매우 약하게 나타나기에 3차원적 나노 박막다층 구조 등의 해석모델링에서도 현재의 저차원 모델링이 유효할 것으로 판단된다.
4. 결 론
본 나노구조 에너지 해석연구에서는 Al/Ni 이종금속 조합의 나노 박막다층구조 내 이종금속 반응파의 박막층 수직방향 자체전파를 대상으로 Shvab-Zeldovich 화학종 농도변수 기반 모델링 및 1차원적 전산해석을 수행하였다. 박막쌍 두께 60 nm 형상의 박막다층의 점화 시에 정상 반응파의 선형적 전파 특성을 확인할 수 있었다. 또한 박막층 수평방향 반응파 전파와 비교하여 박막쌍 두께 및 예혼합 두께 별 반응파 자체전파속도는 별 다른 차이가 없기에 나노 두께의 박막다층 구조에서도 반응파 전파특성의 방향 의존성이 매우 약하게 나타남을 확인할 수 있었다.
Acknowledgments
본 연구는 금오공과대학교 학술연구비에 의하여 지원된 논문이다(과제번호: 2019-104-002).
References
-
Mukasyan, A.S., Rogachev, A.S. and Aruna, S.T., “Combustion Synthesis in Nanostructured Reactive System,” Advanced Powder Technology, Vol. 26, pp. 945-976, 2015.
[https://doi.org/10.1016/j.apt.2015.03.013]

-
Dreizin, E.L., “Metal-Based Reactive Nanomaterials,” Progress in Energy and Combustion Science, Vol. 35, pp. 141-167, 2009.
[https://doi.org/10.1016/j.pecs.2008.09.001]

-
Son, S.F., Asay, B.W., Foley, T.J., Yetter, R.A., Wu, M.H. and Risha, G.A., “Combustion of Nanoscale Al/MoO3 Thermite in Microchannels,” Journal of Propulsion and Power, Vol. 23, pp. 715-721, 2007.
[https://doi.org/10.2514/1.26090]

-
Adams, D.P., “Reactive Multilayers Fabricated by Vapor Deposition: A Critical Review,” Thin Solid Films, Vol. 576, pp. 98-128, 2015.
[https://doi.org/10.1016/j.tsf.2014.09.042]

-
Gavens, A.J., Van Heerden, D., Mann, A.B., Reiss, M.E. and Weihs, T.P., “Effect of Intermixing on Self-Propagating Exothermic Reactions in Al/Ni Nano- laminate Foils,” Journal of Applied Physics, Vol. 87, pp.1255-1263, 2000.
[https://doi.org/10.1063/1.372005]

-
Gachon, J.C., Rogachev, A.S., Grigoryan, H.E., Illarionova, E.V., Kuntz, J.J., Kovalev, D.Yu., Nosyrev, A.N., Sachkova, N.V. and Tsygankov, P.A., “On the Mechanism of Heterogeneous Reaction and Phase Formation in Ti/Al Multilayer Nanofilms,” Acta Materialia, Vol. 53, pp. 1225-1231, 2005.
[https://doi.org/10.1016/j.actamat.2004.11.016]

-
Knepper, R., Snyder, M.R., Fritz, G., Fisher, K. and S., Knio, O.M., and Weihs, T.P, “Effect of Varying Bilayer Spacing Distribution on Reaction Heat and Velocity in Reactive Multilayers,” Journal of Applied Physics, Vol. 105, pp. 083504-19, 2009.
[https://doi.org/10.1063/1.3087490]

-
Salloum, M. and Knio, O.M., “Simulation of Reactive Nanolaminates Using Reduced Models: I. Basic Formulation,” Combustion and Flame, Vol. 157, pp. 288-295, 2010.
[https://doi.org/10.1016/j.combustflame.2009.06.019]

-
Baginski, T.A., Taliaferro, S.L. and Fahey W.D., “Novel Electro-Explosive Device Incorporating a Reactive Laminated Metallic Bridge,” Journal of Propulsion and Power, Vol. 17, pp. 184-189, 2001.
[https://doi.org/10.2514/2.5726]

-
Tanaka, S., Kondo, K., Habu, H., Itoh, A., Watanabe, M., Hori, K. and Esashi, M., “Test of B/Ti Multilayer Reactive Igniters for a Micro Solid Rocket Array Thruster,” Sensors and Actuators A: Physical, Vol. 144, pp. 361-366, 2008.
[https://doi.org/10.1016/j.sna.2008.02.015]

- Choi, J. and Kim, K., “A Three-dimensional Modeling of Microscale Thin-film Initiator with Boron/titanium Multilayers,” Journal of Propulsion and Energy, Vol. 1, pp. 66-73, 2020.
-
Kim, K., “A Microscale Explosive Initiator Integrated with a Reactive Thin-Filmed Metallic Bridge of Boron/Titanium Laminated Layers,” Microsystem Technologies, Vol. 27, pp. 1379-1388, 2021.
[https://doi.org/10.1007/s00542-018-4265-8]

-
Kim, K., “Analysis of Self-Propagating Intermetallic Reaction in Nanoscale Multilayers of Binary Metals,” Metals and Materials International, Vol. 23, pp. 326-335, 2017.
[https://doi.org/10.1007/s12540-017-6379-4]

-
Kim, K., “Numerical Investigation of the Self-Propagation of Intermetallic Reaction Waves in Nanoscale Aluminum/Nickel Reactive Multilayer Foils,” Korean Journal of Metals and Materials, Vol. 57, pp. 97-107, 2019.
[https://doi.org/10.3365/KJMM.2019.57.2.97]

-
Salloum, M. and Knio, O.M., “Simulation of Reactive Nanolaminates Using Reduced Models: II. Normal Propagation,” Combustion and Flame, Vol. 157, pp. 436-445, 2010.
[https://doi.org/10.1016/j.combustflame.2009.08.010]

-
Kim, K. and Park, J.Y., “Computational Study of Intermetallic Reaction Propagation in Nanoscale Boron/Titanium Metallic Multilayers,” Journal of the Korean Society of Propulsion Engineers, Vol. 21, pp. 10-17, 2017.
[https://doi.org/10.6108/KSPE.2017.21.3.010]
