가스터빈 블레이드의 얇은 벽에서의 팬 형상 홀 최적화
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
가스터빈 블레이드를 고온의 주유동으로부터 보호하기 위해 다양한 냉각 기법이 연구되었고, 팬 형상 홀을 포함한 다양한 막냉각 홀 형상에 대해서도 연구가 수행되어왔다. 하지만, 소형 가스터빈에 대한 수요가 증가함에 따라 얇은 벽에 적용할 수 있는 막냉각 홀에 대한 연구가 필요하다. 이에 따라 본 연구에서는 수치해석을 통하여 분사율 1과 2에서 팬 형상 홀의 형상 변수의 영향을 연구하였다. 또한, 원형부 길이와 전방향 및 횡방향 확장각, 세 가지 변수에 대하여 최적화를 수행하였다. 각 분사율에서 최적화된 두 형상은 유사한 형상 변수와 냉각 성능을 갖는 것으로 나타났다.
Abstract
Several cooling techinques have been studied for protecting gas turbine blades from hot gas. In terms of film-cooling techniques, various shapes of film cooling holes have been studied including fan shaped holes, which are used on gas turbine blades. However, owing to increasing demands on smaller gas turbines, a research on film-cooling holes on thin walls is required. This study was conducted at blowing ratios of 1 and 2, using numerical analysis. Through the numerical analysis, the effect of geometrical parameters on the effectiveness of fan-shaped hole film cooling was studied. Moreover, optimization was performed on three geometrical parameters: metering length, lateral expansion angle and forward expansion angle. As a result, we realized that the optimal fan-shaped holes on each blowing ratio were found to have very similar geometry and cooling performance.
Keywords:
Gas Turbine Blade, Film Cooling, Fan Shaped Holes, Optimization키워드:
가스터빈 블레이드, 막냉각, 팬 형상 홀, 최적화1. 서 론
가스터빈의 효율과 출력을 향상시키기 위해서 가스터빈의 입구 온도가 지속적으로 증가하고 있으며, 이에 따라 높아진 열부하를 감소시키기 위하여 가스터빈 블레이드 냉각에 대한 연구가 진행되어 왔다.
막냉각은 가스터빈 블레이드의 표면을 냉각하는 방법으로, 막냉각 홀을 통해 분사된 냉각 유체가 주유동으로부터 부품에 전달되는 열유속을 저감시키는 기법이다.
막냉각에서 냉각 성능을 나타내는 단열 막냉각 효율은 홀 형상에 따라 상이하게 나타난다. 원형홀은 홀의 입구와 출구의 면적이 동일한 형상으로 높은 분사율에서 막냉각 효율이 감소하는 단점을 가진다. 이는 홀 출구에서의 냉각 유체 분사 속도가 높아짐에 따라 냉각 유체가 블레이드 표면을 잘 덮지 못해 나타나는 현상으로, 이를 해결하기 위하여 홀 출구의 면적을 홀 입구보다 넓힌 확장홀에 대한 연구가 수행되어 왔다.
Cho와 Rhee[1]는 원뿔형의 확장홀에 대한 연구를 수행하였으며, 확장각에 따른 막냉각 성능의 변화를 확인하였다. Schoeder와 Thole[2]는 팬 형상 홀에 대한 연구를 수행하였으며, 홀 길이가 6D인 홀에 대한 막냉각 성능 연구를 수행하였다. 이 밖에도 팬 형상 홀에 대한 다양한 연구가 수행되었다[3-5]. 또한, 보다 높은 냉각 성능을 얻고자 최적 홀 형상에 대한 연구 역시 이루어지고 있다[6,7].
위와 같은 연구들은 대부분 홀의 길이가 6D 이상인 형상에 대하여 수행되었다. 그런데 가스터빈 블레이드를 소형화하기 위해서는 얇은 벽에 적용할 수 있는 형상에 대한 연구가 필요하며, 이는 홀의 길이가 짧은 형상에 대한 연구의 필요성으로 이어진다.
선행 연구에 따르면 팬 형상 홀은 횡방향 확장각이 10° 이상이고 전방향 확장각이 10° 이하일 때 높은 냉각 성능을 갖는다. 하지만, AR가 커짐에 따라 냉각 성능이 향상되는 경향과 큰 확장각에서 유동박리가 나타난다는 유동특성을 고려했을 때, 홀 길이가 짧아짐에 따라 높은 냉각 성능을 가지는 확장각의 크기가 달라질 것이다. 또한, Park[8]에서 연구한 것과 같이 2D 이상의 원형부 길이를 얇은 벽에 적용하기에는 어려움이 있으므로, 원형부 길이에 대한 연구 역시 필요하다.
따라서, 본 연구에서는 얇은 벽에 적용된 팬 형상 홀의 원형부 길이와 횡방향 및 전방향 확장각 변화에 따른 영향을 확인하고, 막냉각 성능을 향상하기 위한 최적화를 수행하였다.
2. 연구 방법
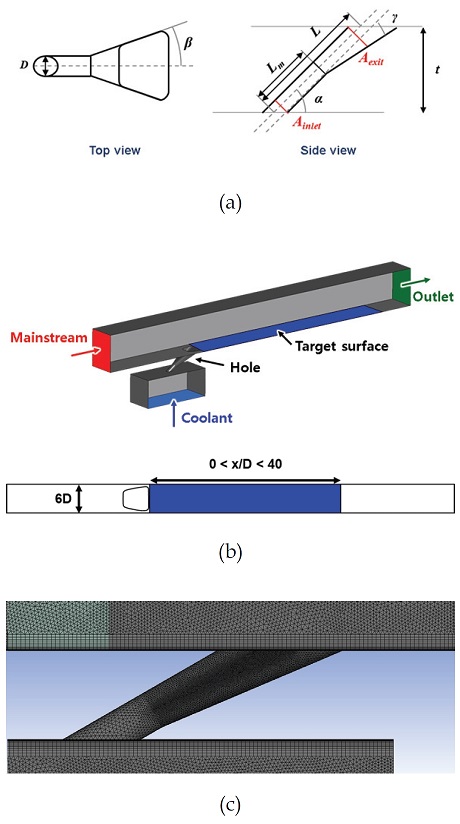
Fig. 1에는 팬 형상 홀의 형상 변수와 막냉각 효율 측정 위치, 격자가 제시되어 있다. D는 원형부의 단면 지름이고, t는 벽의 두께, L은 홀의 원형부와 확장부를 포함한 전체 길이, Lm은 원형부의 길이, α는 분사각, β는 횡방향 확장각, γ는 전방향 확장각이다. 본 논문에서 D는 0.8 mm이며, t/D는 약 2.3으로 홀 길이가 5 이하인 얇은 벽에서의 막냉각을 연구하였다. 또한, 홀과 홀 사이의 간격을 고려하여 횡방향 확장각은 23˚ 이하로 설정하였다.
팬 형상 홀의 연구에 앞서, 수치해석 결과를 실험결과와 검증하는 과정을 거쳤다. 실험의 경계조건과 수치해석의 경계조건은 경계층 밖에서의 주유동 속도와 난류강도가 각각 10 m/s와 0.35%로 동일하다. 수치해석은 ANSYS CFX 17.2 소프트웨어를 사용하였으며, k-ω 난류 모델에서 약 850만 개의 비정렬 격자에서 수행되었다[10]. 이를 비교한 결과는 Fig. 2에 제시되어 있다. 최적화는 0 < x/D < 40에서의 면적 평균 막냉각 효율을 기준으로 수행되었다. 해석점을 설정할 때에는 Latin Hypercube Sampling을 이용하였으며, 최적점을 얻기 위하여 Kriging method를 사용하였다[11,12].
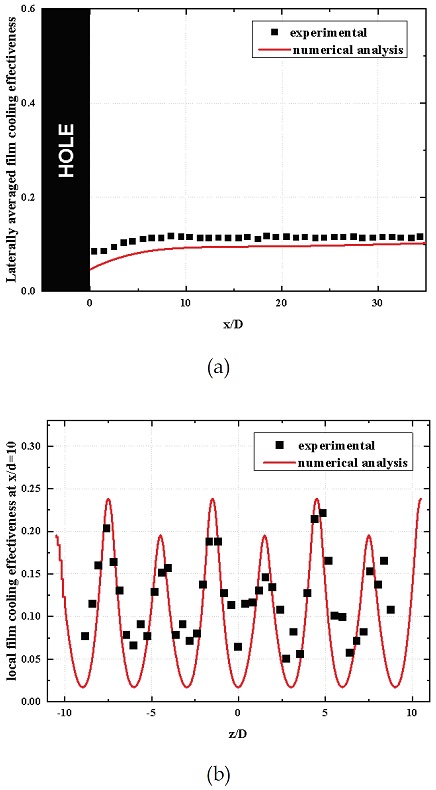
Validation results (a) laterally averaged film cooling effectiveness contour (b) local film cooling effectiveness @ x/D = 10.[9].
3. 연구 결과
3.1 변수 영향 분석
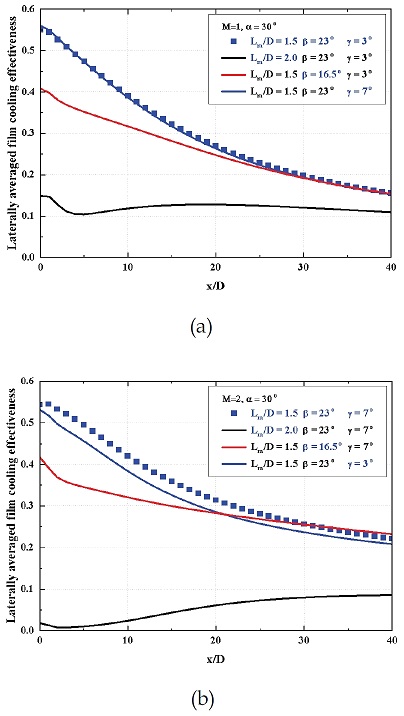
변수의 영향을 분석하기 위해서 우선 Table 2와 3과 같이 분사율(M) 1과 2에서 총 6개의 형상에 대한 해석을 수행하였다. 그리고 각 분사율에서 가장 높은 면적 평균 막냉각 효율을 가지는 형상을 기준으로 하여 원형부 길이(Lm/D)와 횡방향 확장각(β), 전방향 확장각(γ)의 영향을 비교할 수 있는 형상을 비교한 그래프는 Fig. 3에 제시되어 있다.
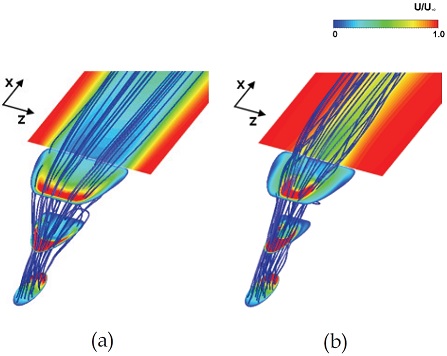
Fig. 3(a)에서 볼 수 있듯이, 분사율 1에서 원형부 길이가 1.5와 2인 두 형상 간의 차이가 가장 크게 나타났다. 원형부 길이가 2인 형상의 경우 4 < x/D < 15 영역에서 횡방향 평균 막냉각 효율이 증가하는 구간이 나타났는데, 이는 Fig. 6(b)에서처럼 냉각 유체의 코어가 바닥면에 부착되지 못한 상태로 분사되었다가 점차 바닥면으로 부착되면서 높아지기 때문으로 보인다. 그 이후에는 주유동과 섞이면서 다른 형상들과 같이 후류로 갈수록 횡방향 평균 막냉각 효율이 감소하였다. 전방향 확장각이 3˚인 형상과 7˚인 형상에서의 횡방향 평균 막냉각 효율은 거의 유사하게 나타났다. Fig. 3(b)에서도 분사율 1과 같은 경향이 나타났는데, 분사율 1과 비교하여 2배의 냉각 유량을 분사하기 때문에 AR가 더 큰 7˚의 전방향 확장각을 가지는 형상에서 가장 높은 막냉각 효율을 가지었다.
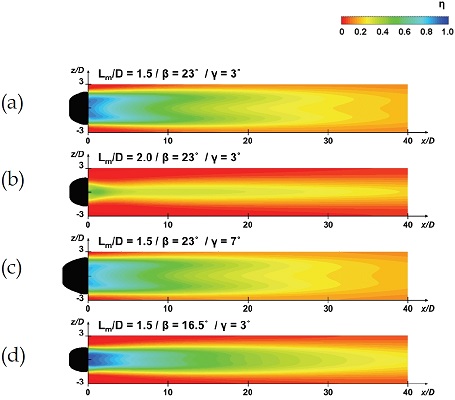
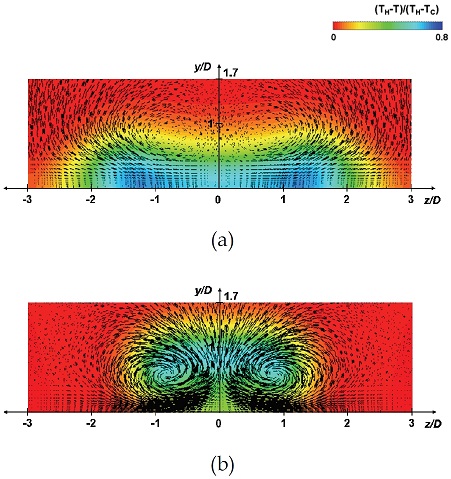
Fig. 4에 제시된 막냉각 효율 분포를 봐도 원형부 길이가 1.5이고 β가 23˚일 때, 두 가지 전방향 확장각에 대하여 유사한 막냉각 효율 분포가 나타났다. 또한, 횡방향 확장각이 16.5˚인 형 상보다 23˚인 형상에서 냉각유체가 z방향으로 더 넓은 면을 덮으면서 막냉각 효율이 향상되었다. 원형부 길이가 2.0일 때에는 –1 < z/D < 1 외의 영역에서의 막냉각 효율이 0.2 이하로 나타났는데 이는 Fig. 5와 Fig. 6에서 볼 수 있듯이, 냉각 유체가 넓고 고르게 분사되지 않고 바닥면(y/D = 0)에 잘 부착되지 못한 상태로 주유동과 만나 강한 콩팥 와류를 형성하여 주유동이 바닥면으로 유입되기 때문이다.
3.2 홀 형상 최적화
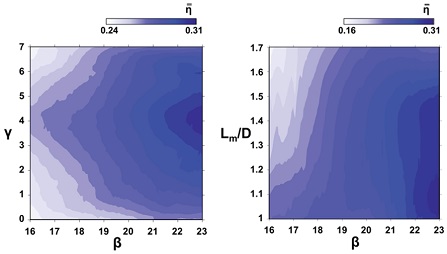
형상 변수가 막냉각 성능에 주는 영향을 통해, 분사율 1과 2에서 팬 형상 홀을 최적화하기 위한 범위를 설정하였고(Fig. 7 참조), 해당 범위 내에서 최적 형상을 도출하였다. Fig. 7에는 분사율 1에서의 형상 변수에 따른 반응면이 제시되어 있다. 반응면에 따르면 횡방향 확장각이 커질수록 높은 냉각 성능을 가지고 전방향 확장각은 4˚에서 최적값을 가진다는 것을 알 수 있다. 이는 횡방향 확장각이 커짐에 따라 z방향으로 더 넓은 면적을 냉각 유체가 고르게 덮을 수 있으며, 원형부 길이는 냉각 유체가 분사되는 형태에 영향을 주기 때문으로 보인다.
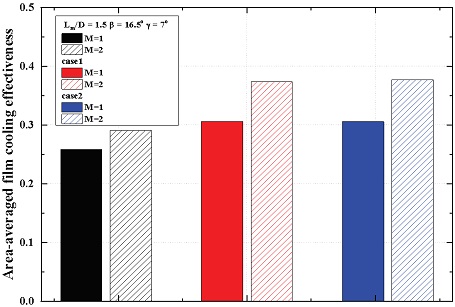
Fig. 8과 Fig. 9에는 분사율 1과 2에서 얻은 최적 형상(case 1, 2)의 막냉각 효율 분포와 면적 평균 막냉각 효율이 제시되어 있다. 두 형상은 모두 0 < x/D < 40의 영역에서 0.1 이하의 막냉각 효율 분포가 거의 나타나지 않았다. Case 1과 Case 2는 β와 γ가 동일하고 원형부 길이(Lm/D)가 0.2만큼 차이가 나는 형상으로, Fig. 8(a)와 (c), (b)와 (d)에서 매우 유사한 막냉각 효율 분포를 가지었고 면적 평균 막냉각 효율 또한 유사한 값을 가지었다. 이를 통해, 얇은 벽에 적용된 팬 형상 홀은 1.1 < Lm/D < 1.3 범위에서는 원형부 길이의 큰 영향을 받지 않는다고 할 수 있다.
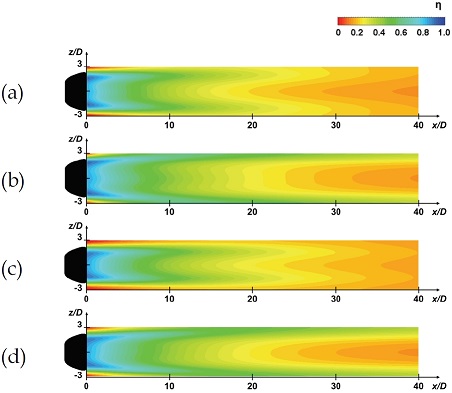
Film cooling effectiveness contour of optimized fan shaped hole (a) case 1 at M = 1, (b) case 2 at M = 2, (c) case 2 at M = 1, (d) case 2 at M = 2(case 1: Lm/D = 1.1, β = 23.0˚, γ = 4.0˚, case 2: Lm/D = 1.3, β = 23.0˚, γ = 4.0˚).
4. 결 론
본 연구에서는 수치해석을 통해 얇은 벽에 적용된 팬 형상 홀의 형상 변수에 의한 냉각 성능 변화를 비교하였고, 최적화 기법을 적용하여 분사율 1과 2에서의 최적 형상을 도출하였다. 본 논문에서 다룬 3 가지 형상 변수 중에서 횡방향 확장각이 냉각 성능에 가장 큰 영향을 주었고, 원형부 길이와 전방향 확장각은 범위 내에서 최적값을 가지었다. 분사율 1에서의 최적 형상은 Lm/D = 1.1, β = 23.0˚, γ = 4.0˚이고, 분사율 2에서는 Lm/D = 1.3, β = 23.0˚, γ = 4.0˚이다. 해당 형상들은 Lm/D = 1.5, β = 16.5˚, γ = 7˚ 형상보다 분사율 1에서 약 19%, 분사율 2에서 약 29% 향상된 냉각 성능을 가지었다.
Nomenclature
| AR : | Area ratio(Aexit/A∈ ≤ t) |
| D : | Hole diameter |
| L : | Hole length |
| M : | Blowing ratio ((ρCUC)/(ρHUH)) |
| p : | Hole pitch |
| t : | Wall thickness |
| T : | Temperature |
| U : | Velocity |
| x : | Coordinate in the streamwise direction |
| y : | Coordinate in the vertical direction |
| z : | Coordinate in the lateral direction |
| α : | Injection angle |
| β : | Lateral expansion angle |
| γ : | Forward expansion angle |
| η : | Adiabatic film cooling effectiveness, ((TH-Taw)/(Th-Tc) |
| ρ : | Density |
Subscripts
| C : | Coolant flow |
| H : | Mainstream flow |
| aw : | Adiabatic wall |
Acknowledgments
본 연구는 2019년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구입니다(20193310100030). 또한, 2020년도 산업통상부의 재원으로 수행한 한국에너지기술평가원(KETEP)의 인력양성사업(No. 20204030200110) 일환으로 수행되었으며, 이에 감사드립니다.
References
-
Cho, H.H., Rhee, D.H. and Kim, B.G., “Enhancement of Film Cooling Performance Using a Shaped Film Cooling Hole with Compound angle Injection,“ JSME International Journal Series B Fluids and Thermal Engineering, Vol. 44, No. 1, pp. 99-110, 2001.
[https://doi.org/10.1299/jsmeb.44.99]

-
Schroeder, R.P. and Thole, K.A., ”Adiabatic Effectiveness Measurements for a Baseline Shaped Film Cooling Hole,“ Turbo Expo: Power for Land, Sea, and Air, American Society of Mechanical Engineers, Vol. 45721, p. V05BT13A036. 2014.
[https://doi.org/10.1115/GT2014-25992]

-
Saumweber, C. and Schulz, A., “Effect of Geometry Variations on the Cooling Performance of Fan-shaped Cooling Holes,“ Turbo Expo: Power for Land, Sea, and Air, Vol. 43147, pp. 905-919, 2008.
[https://doi.org/10.1115/GT2008-51038]

-
Chen, A.F., Li, S.J. and Han, J.C., “Film cooling with forward and backward injection for cylindrical and fan-shaped holes using PSP measurement technique,“ American Society of Mechanical Engineers, Vol. 45721, p. V05BT13A042. 2014.
[https://doi.org/10.1115/GT2014-26232]

-
Li, W., Li, X., Ren, J. and Jiang, H., “A Novel Method for Designing Fan-Shaped Holes With Short Length-to-Diameter Ratio in Producing High Film Cooling Performance for Thin-Wall Turbine Airfoil,“ Journal of Turbomachinery, Vol. 140, No. 9, 2018.
[https://doi.org/10.1115/1.4041035]

-
Lee, K.D., Husain, A. and Kim, K.Y., “Multi-objective Optimization of a Laidback Fan Shaped Film-cooling Hole Using Evolutionary Algorithm,“ International Journal of Fluid Machinery and Systems, Vol. 3, No. 2, pp. 150-159, 2010.
[https://doi.org/10.5293/IJFMS.2010.3.2.150]

-
Wang, C.H., Zhang, J.Z. and Zhou, J.H., “Data Mining Optimization of Laidback Fan-shaped Hole to Improve Film Cooling Performance,“ Journal of Central South University, Vol. 24, No. 5, pp. 1183-1189, 2017.
[https://doi.org/10.1007/s11771-017-3521-x]

-
Park, S.H., Kang, Y.J., Seo, H.J., Kwak, J.S. and Kang, Y.S., “Experimental Optimization of a Fan-shaped Film Cooling Hole with 30 Degrees-injection Angle and 6-hole Length-to-diameter Ratio,“ International Journal of Heat and Mass Transfer, Vol. 144, pp. 118652, 2019.
[https://doi.org/10.1016/j.ijheatmasstransfer.2019.118652]

-
Park, S., Jung, E.Y., Kim, S.H., Sohn, H.S. and Cho, H.H., “Enhancement of Film Cooling Effectiveness Using Backward Injection Holes,“ International Journal of Thermal Sciences, Vol. 110, pp. 314-324, 2016.
[https://doi.org/10.1016/j.ijthermalsci.2016.08.001]

- ANSYS CFX V17.2, “ANSYS CFX Theory Guide 17.2,” ANSYS, Inc., Canonsburg, P.A., U.S.A., 2015.
-
Shields, M.D. and Zhang, J., “The Generalization of Latin Hypercube Sampling,“ Reliability Engineering & System Safety, Vol. 148, pp. 96-108, 2016.
[https://doi.org/10.1016/j.ress.2015.12.002]

-
Martin, J.D. and Simpson, T.W., “Use of Kriging Models to Approximate Deterministic Computer Models,“ AIAA Journal, Vol. 43, No. 4, pp. 853-863, 2005.
[https://doi.org/10.2514/1.8650]