PIC-DSMC 방법을 이용한 전기추력기 플룸 해석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
2000년 대에 들어 가파르게 성장하고 있는 우주비행체용 전기추진시스템의 안정적인 운영기술 개발을 위해, PIC-DSMC를 이용하여 전기추력기의 배기플룸의 거동을 해석하였다. 해석 방법에서 Boltzmann 관계식을 이용한 Simple Electron Fluid Model을 적용하였고, 원자-이온 간 충돌에 의해 발생하는 전하 교환 및 운동량 교환을 함께 고려하였다. 본 연구의 해석결과는 실험에서 계측한 플라즈마 전위값을 비교적 잘 예측하였다. 추력기 출구 근처에서는 활발한 입자 간 충돌 및 원자-이온 간 전하 교환으로 인해, 느린 이온 및 빠른 원자가 생성되었으며, 추력기 배기플룸의 궤적 및 속도에 중요한 영향을 미칠 것으로 예측되었다.
Abstract
To develop technologies for the stable operation of electric propulsion systems, the exhaust plume behavior of electric thrusters was studied using PIC-DSMC(particle-in-cell and direct simulation Monte Carlo). For the numerical analysis, the Simple Electron Fluid Model using Boltzmann relation was employed, and the charge and momentum exchanges due to atom-ion collisions were considered. The results of this study agreed with the plasma potentials measured experimentally. Near the thruster exit, active collisions among particles and charge exchanges created slow ions and fast atoms, which were expected to significantly affect the trajectory and velocity of the thruster exhaust plume.
Keywords:
Satellite Thuster, Electric Propulsion System, Hall Thruster, Plume Analysis, PIC-DSMC키워드:
위성 추력기, 전기추진시스템, 홀 추력기, 플룸 해석1. 서 론
전기식 우주추진시스템이 실제 우주비행체에 실제 적용되기 시작한 시점은 1960년대 초반이다. 초기에는 단순한 기능시연을 위한 미션을 수행하였으나, 이후 점차 그 수요가 확대되어 자세제어 및 궤도유지 미션에 활발히 적용되었다. 2000년대에 들어서는 더 높은 추력과 운영시간을 요하는 정지궤도 위성의 궤도상승(Orbit raising)임무에도 성공적으로 적용되고 있으며, 2018년 기준, 전 세계에서 발사되고 있는 정지궤도 위성의 약 50%가 전기추력기를 장착하고 있을 정도로 그 수요가 빠르게 증가하고 있다[1,2].
우리나라에서도, 대표적인 전기추력기인 홀 추력기 및 이온 추력기에 대한 실험적 연구가 소수의 연구진들에 의해 꾸준히 이어져왔으며, 2013년에는 과학기술위성 3호에 국내에서 개발한 10 mN 급 홀 추력기가 장착되어 성공적으로 운영된 바 있다[3]. 그러나, 그에 반해, 전기추력기 내부현상 또는 배기플룸의 거동을 예측하기 위해 전산해석방법을 적용한 국내연구는 극히 드문 실정이다[4].
우주추진시스템의 배기플룸은 우주공간이라는 희박환경에서 큰 폭으로 팽창, 확산될 수 있으며, 경우에 따라 비행체의 카메라, 태양전지 등 주요장비들을 오염시킬 수 있어, 그 거동을 정확하게 예측할 필요가 있다. 그러나, 지상시험을 통해, 우주추진시스템의 플룸 거동을 예측하는 경우, 진공챔버 용량의 한계, 중력에 의한 영향 등으로 인해 지상시험결과와 실제 시스템운영 특성에 차이가 있을 수 있다. 따라서, 이를 보정기 위한 전산해석연구는 안정적인 우주추진시스템개발에 필수적인 요소라고 할 수 있다.
전기추력기의 전산해석은 PIC(Particle-In-Cell) 방법을 이용한 해석이 가장 널리 활용되고 있다[5]. PIC 방법은 격자계 셀 내부의 모사입자(Simulated Particle)에 가해지는 전자기력을 계산하여, 모사입자의 가속도를 산출하고, 이를 이용하여 모사입자를 전진시키는 입자추적기법의 한 종류이다. 그러나, PIC 방법은 입자 간의 충돌모델을 포함하고 있지 않으므로, 추력기 배기플룸과 같이 입자의 수밀도가 높은 영역을 해석하기 위해서는 별도의 입자충돌 모델을 포함해주어야 한다.
모사입자간의 충돌을 정확하게 모사해주기 위한 방법으로 PIC-MCC (Particle-In-Cell Monte Carlo Collisions) 와 PIC-DSMC (Particle-In-Cell Direct Simulation Monte Carlo) 방법이 많이 사용된다. PIC-MCC 방법은, 한 개의 모사입자에 대해, 이 입자가 주변에 분포하는 표적입자 클라우드(Target Particle Cloud)와 충돌할 확률을 계산하여, 충돌여부를 결정한다. 이때, 표적입자 클라우드는 모사입자가 아니므로, 충돌 후 표적입자의 운동상태는 추적되지 않는다. 따라서, PIC-MCC 방법은 기본적으로 충돌 전후에 에너지 보존 및 운동량 보존에서 오차가 발생하며, 이 오차값이 큰 경우 별도의 보정과정을 필요로 한다[6]. 그러나, PIC-DSMC 방법은 2개의 모사입자를 선정하고, 상호 간의 충돌확률을 이용해 충돌여부를 결정하며, 충돌 후에도 2개 입자의 거동을 모두 추적하므로, 전체 입자군의 에너지 보존 및 운동량 보존이 성립한다. 따라서, PIC-DSMC 방법이 추력기 플룸해석에 있어서 가장 정확한 결과를 제시하는 방법이라 할 수 있다.
전기추력기의 배기플룸을 이루는 플라즈마는 이온과, 중성원자 및 자유전자를 모두 포함한다. 이 중 자유전자는 이온 및 중성원자에 비해 이동속도가 매우 빠르기 때문에, PIC 방법으로 전자를 추적하기 위해서는 시간 간격을 대게 10-12 sec 수준으로 짧게 두어야 한다[7]. 이렇게 전자를 입자로 두고 추적하는 경우, 계산용량이 엄청나게 증가하게 되는데, Adam 등[8]은 소형 홀 추력기의 (플룸영역을 제외한) 내부유동장 해석연구에서 100 μsec 의 해석결과를 얻기 위해 약 1개월 정도의 계산시간이 소요되었다고 밝혔으며, 해석 조건에 따라 통상적으로 수개월의 계산시간이 소요되는 것으로 보고되고 있다[7].
따라서, 연구개발과정에서 수용가능한 수준의 계산시간 및 계산정확도를 확보하기 위한 방법으로, 자유전자를 입자로 두지 않고 유체로 가정하는 Hybrid-PIC 방법이 널리 사용되고 있다[9-11]. 이 방법은 자유전자를 유체로 두지만, 원자 및 이온 등은 입자로 해석하므로, 일반적인 연속체 가정의 전산해석방법과 달리, 희박기체 영역에서의 분자동역학적 특성 분석이 가능하다.
자유전자를 유체로 모델링하는 방법도, 크게 2가지로 분류된다. 첫 번째는 자기장의 세기가 무시할 만큼 작고, 해석영역 내 전자의 온도가 균일하다는 가정을 적용하여, 볼츠만 관계식으로 전위(Electric Potential)를 계산하는 Simple Electron Fluid Model이다[10,11]. 두 번째는, 보다 상세한 모델로, 해석영역 내 전자온도분포를 고려하여, 전자유체의 연속방정식과 에너지방정식을 함께 해석하는 Detailed Electron Fluid Model이다[9,10].
본 연구에서는, 전기 추력기 플룸에서의 입자 간 충돌효과를 잘 고려할 수 있는 PIC-DSMC 방법을 이용하여, 홀 추력기의 플룸을 해석하고, 해석결과의 타당성을 평가하였다. 전산해석을 위한 코드는 OpenFOAM 기반의 PIC-DSMC 코드인 pdFoam을 사용하였으며, 전자는 유체로 가정하는 Hybrid-PIC 모델을 적용하였다. 현재, pdFoam은 전자 모델로 Simple Electron Fluid Model만 구현되어 있어, 본 연구에서도 이를 사용하였다. 그러나, 기존의 pdFoam에 포함되지 않은 몇 가지 모델 및 기능을 추가하여 해석코드의 활용성을 개선하였다.
2. 전산 해석 방법
2.1 pdFoam 개요
본 연구에서는 HyStrath 연구그룹의 OpenFOAM 기반 PIC-DSMC 코드인 pdFoam을 수정, 보완하여 활용하였다[12]. pdFoam은 모든 OpenFOAM 프로그램이 그러하듯, 격자계 및 병렬계산에 제한이 없으며, 사용자의 전문성에 따라 타 프로그램과 통합, 개선도 가능하다. 기존의 다양한 OpenFOAM 코드들의 주요 Library들을 접목, 활용할 수 있다는 점은 최대의 장점이라고 할 수 있다.
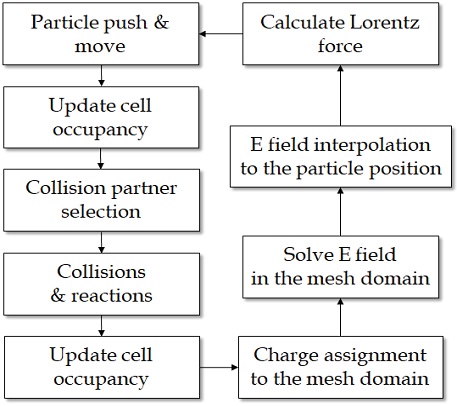
Fig. 1에는 pdFoam의 해석 알고리즘을 나타냈다. 그림의 왼쪽 상단에서 시작하면, 우선, 입구조건 및 입자의 속도, 가속도 등을 이용하여, 입자를 주입, 이동시키고, 격자셀 내 입자구성을 갱신한다. 이후 충돌입자를 선택하고, 충돌조건 만족 여부를 판정하여, 입자를 충돌시키게 되는데, 경우에 따라 입자 간 화학반응을 계산한다. 충돌 및 화학반응에 따른 격자셀 내 입자구성변화를 갱신한 후에는, 이온입자의 전하값을 격자계에서의 전하값으로 변환하여, 전기장을 해석한다. 그리고, 해석된 격자계의 전기장값을 입자 위치 값으로 다시 변환하여, 전자기력을 계산한다. 이후, 입자에 작용하는 힘, 속도, 속력을 이용하여, 입자를 이동시키는 처음으로 돌아간다.
보다 상세한 입자충돌모델 및 코드 구성 내용은 참고문헌[12]에 상세하게 서술되어 있으므로, 본 논문에서는 전기추력기의 플룸해석을 위해 pdFoam에 추가 개선된 내용을 중심으로 소개하기로 한다.
2.2 원자-이온 간 전하 교환 및 운동량 교환 모델
현재 활용되고 있는 대부분의 홀 추력기와 이온추력기는 제논(Xe)가스를 연료로 사용한다. 제논 가스는, 추력기의 종류에 따라, 다양한 방법으로 이온화되어 제논이온(Xe+, Xe2+)이 되며, 이들 이온은 로렌츠 힘에 의해 추력기 노즐 방향으로 가속되어, 추력을 발생시킨다.
추력기 내부의 모든 제논가스가 100% 이온화되는 것은 아니므로, 전기추력기의 배기플룸은 중성의 제논원자, 제논이온 및 자유전자를 포함한다. 이때, 전자기력(로렌츠 힘)의 영향을 받지 않는 제논원자는 추력기 출구에서 속력이 느리지만, 전자기력을 받는 제논이온은 속력이 매우 빠르다. 추력기의 배기플룸에 포함된 느린 제논원자와 빠른 제논이온은 하류로 이동하며 서로 충돌하여 운동량을 교환(MEX, Momentum Exchange)하기도 하고, 다음의 식과 같이 서로 전하를 교환(CEX, Charge Exchange)하기도 한다[9-11,13].
| (1) |
이러한 전자의 교환 과정에서, 전자를 얻은 빠른 이온은 빠른 원자가 되고, 전자를 빼앗긴 느린 원자는 느린 이온이 되므로, 배기플룸 내 가스는 다양한 조성과 속도분포를 갖게 된다. 특히 느린 이온은 배기플룸의 전기장 분포에 중요한 영향을 미치며, 나아가 배기플룸의 확산 정도에도 영향을 준다[14]. 배기플룸의 확산 정도는 비행체의 주요장비의 오염도와 직결되므로, 원자와 이온 간의 전하 교환 및 운동량 교환은 위성을 비롯한 우주비행체의 수명을 올바로 예측하기 위해 필수적으로 고려해야할 물리현상이라고 할 수 있다[14,15].
pdFoam은 원자-이온 간 전하 교환과 운동량 교환을 고려하고 있지 않아, 본 연구에서 관련 모듈을 작성하여, 추가하였다. 이때, 전하 교환과 운동량 교환의 충돌면적(Collision Cross Section) σ는 다음과 같이 Miller 등[16]의 실험데이터에 기반한 관계식을 사용했다. 또한, Boyd 등[17]의 연구결과로부터 전하 교환의 확률을 0.5로 가정할 수 있으므로, 전하 교환과 운동량 교환의 충돌면적은 동일하다고 가정하였다[11,15]. 아래의 식에서 Elab 은 Laboratory Ion Energy이다.
| (2) |
| (3) |
또한, 원자와 원자 간 충돌은 VHS(Variable hard sphere)을 이용하여 고려하였다[18].
2.3 전자 유체 모델
pdFoam은 전자를 입자로 해석하는 Fully Kinetic 방법과 전자를 유체로 모델링하는 Hybrid 방법을 모두 제공한다[12]. 이때, Hybrid 방법의 경우 Simple Electron Fluid Model을 전자유체모델로 사용하여 전위값을 계산한다.
pdFoam에서 적용한 전위계산 방법을 살펴보면, 우선 전자에 대해 등온(Isothermal), 정전(Electrostatic), 자기장 영향 무시 등을 가정하여, Boltzmann 관계식(Eq. 4)을 이용, 전자의 수밀도를 계산하고, 이 값을 Poisson 방정식에 대입하여, 전위값을 계산하였다[12].
그러나, 자유전자 발생량이 많은 추력기 내부 및 외부의 경우, 자유전자가 추진제 가스에 집중적으로 분포되어 있어, Boltzmann 관계식으로 계산한 전자의 수밀도값이 실제 값과 차이가 있을 수 있다. 이 경우 계산된 전위값에 왜곡을 가져올 수 있으므로, 본 연구에서는, pdFoam의 방법을 수정하여, 준중성 플라즈마 (Quasi-neutral Plasma) 가정으로, 전자의 수밀도를 이온의 수밀도 값과 동일하게 두고(Eq. 5)[9], 이를 Boltzmann 관계식(Eq. 4)에 대입하여 전위를 계산하였다[11,15]. 이때, 아래의 식에서 φ, kB, Te, n은 전위, 볼츠만 상수, 전자온도 및 수밀도를 각각 나타낸다.
| (4) |
| (5) |
2.4 기타 개선 사항
효율적인 전산해석을 위해 pdFoam에서 제공하지 않는 기타 기능과 모델을 추가하였다.
첫째로, 효율적인 축대칭 문제 해석을 위한 반경방향 가중기법을 적용하였다. DSMC의 축대칭 문제 해석의 경우, 중심축에 가까운 격자셀의 체적이 작게 계산되므로, 유사한 수준의 입자 수밀도를 유지할 경우, 중심축 주변에 매우 적은 수의 모사입자가 배치되어, 정확한 입자 간 충돌 및 거동을 모사하기 힘들게 된다. 따라서, 중심축에서 멀어질수록 입자수를 비롯한 기타물리량에 대한 가중치를 적용하여, 계산 효율을 극대화하는 접근방법이 많이 사용되고 있다. pdFoam의 경우, 이러한 가중 처리 방법을 포함하고 있지 않아, 축대칭 계산 시 매우 많은 입자수를 사용해야하는 문제가 있다. 따라서 본 연구에서는 pdFoam에 반경방향 가중기법을 적용하여, 계산을 효율화하도록 개선하였다.
둘째로, 원자-전자 충돌 이온화 모델을 포함시켰다. 홀 추력기의 경우, 음극에서 발사되는 전자가 홀 추력기 내부로 유입되고, 홀 효과에 의해 원운동 가속돼 원자와 충돌하며, 이로 인해 충돌한 원자 중 일부가 이온화된다. 본 논문에서는 추력기 배기플룸의 거동만을 해석하여, 원자-전자 충돌 이온화 현상을 관찰하지는 않았으나, 향후 홀 추력기 내부의 주요현상을 고찰하기 위해 원자-전자 충돌 이온화 모델을 pdFoam에 추가하였다.
3. 전산해석 결과
3.1 전산 해석 예제 정의
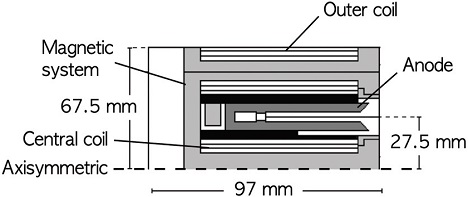
앞서 설명한 바와 같이 수정, 개선된 pdFoam을 이용하여, 미시건 대의 D55 홀 추력기의 배기플룸의 거동에 대해서 해석하였다. D55 홀 추력기는 많은 연구자들에 의해 다양한 실험 및 전산해석이 수행되어 연구결과가 비교, 검증된 바 있다[10,11,19-22]. D55 홀 추력기는 내경 50 mm, 외경 60 mm의 환형 챔버로 구성되어 있으며, 4.76 mg/s 의 제논을 연료로 사용하고, 비추력은 약 1,819 초이다[19]. D55 홀 추력기의 형상은 Fig. 2에 나타난 바와 같다. 본 연구에서는 Domonkos 등[20]과 Zakharenkov 등[21]의 실험결과를 기준으로 전산해석을 수행하였다.
D55 홀 추력기의 플룸을 해석하기 위해 추력기 출구 및 하류영역을 계산영역으로 두고, 전산해석을 수행하였다. 계산용량 절감을 위해 2차원 축대칭으로 가정하였으며, Boyd[19]의 접근방법과 같이 3차원 해석을 필요로 하는 음극의 영향은 무시하였다.
Fig. 3에는 계산영역의 형태 및 경계조건을 표시하였으며, Table 1에 전산해석에서 사용한 추력기 출구 조건을 기록하였다. 이때, Case 1은 추력기 출구 부근을 측정한 Domonkos 등[20]의 실험결과에 적용된 조건이며, Case 2는 추력기 하류영역을 측정한 Zakharenkov 등[21]의 실험결과에 적용된 조건이다. 또한, Fig. 3에서 계산영역의 출구(Outlet)는 입자가 경계면 외부로 이동할 때 삭제처리하는 deletion patch를 적용하였고, 벽면(Wall)은 diffuse wall 조건을 적용하였으며, 해석영역의 초기조건은 진공으로 두었다. 시험장치 및 우주공간에 존재하는 입자는 무시하였다.
몇몇 연구자들은 이들 실험 결과를 재현하기 위한 전산해석을 수행함에 있어서, 서로 다른 해석 조건을 사용한 바 있다[10,11,19,22]. 이는 전기추력기 플룸 해석연구에 다양한 불확실성이 존재한다는 반증이기도 하다. 본 연구에서는 Choi 등[22]이 적용한 해석조건을 대부분 수용하였으며, 일부에 대해서는 타당한 가정을 통해 수정하여 적용하였다. 우선, 본 연구에서는, Kim 등[23]의 연구에서 환형 홀 추력기의 경우 Xe2+ 이온이 추력기 플룸의 전위값에 큰 영향을 주지 않는다는 실험결과에 착안하여, 간단한 해석을 위해, Xe2+ 를 고려하지 않았으며, 따라서, 실험조건의 Xe2+ 수밀도를 Xe+ 수밀도에 합산하여 적용하였다. 또한, 실험 데이터에 따르면, 추력기 출구 근처에서 전자온도가 약 10 eV이고, 추력기 하류영역에서는 약 3 eV로 계측되었는데, Boyd[19] 는 Boltzmann 관계식(Eq. 4)에서 전자온도 Te를 하류값인 3 eV로 가정하였고, Choi[10]와 Wang 등[11]은 상류값인 10 eV로 가정하였다. 본 연구에서는 중간값인 6.5 eV를 적용하였다. 또한 Choi[10]와 Wang 등[11]은 추력기 출구에서의 전위를 0 V에서 147 V 사이에 분포하는 함수 형태로 모델링 하였으나, 본 연구에서는 중간값인 73.5 V를 적용하였다.
본 연구에서 사용한 격자계의 최소간격은 약 2 mm 이며, 시간 간격은 5×10-8 초 이다. 계산 결과 약 60,000 시간증분(Time step) 후 정상상태에 도달하였으며, 정상상태에서 계산영역 내 모사입자 수는 약 93만 개로 나타났다. 전산해석에 25 core CPU를 사용했을 때, 소요된 계산시간은 약 33 시간이다.
3.2 실험결과와의 비교 및 검증
앞 절에서 설명한 D55 홀 추력기 플룸해석 예제에 대해 전산해석을 수행하고, 실험값과 비교분석하였다.
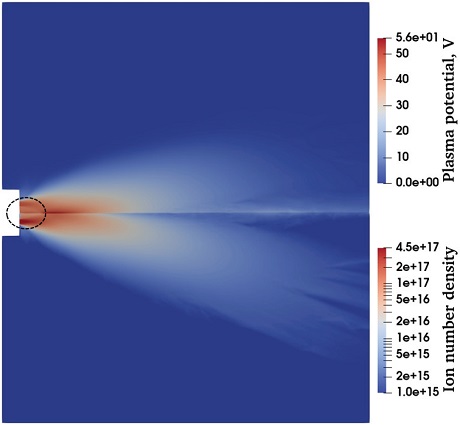
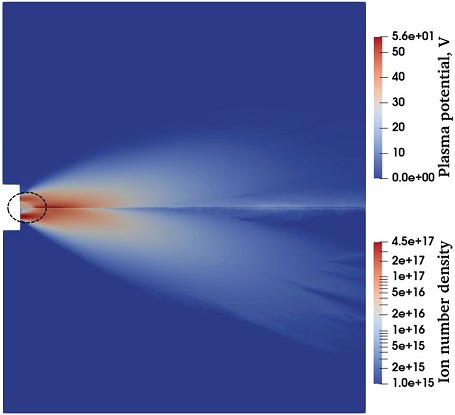
Fig. 4에는 Case 1에 대해 추력기 출구 하류 영역에서 제논이온의 수밀도 분포를 나타냈다. 그림을 살펴보면, 추력기 출구 부근에서는 이온의 수밀도가 입구조건과 유사하게 높게 나타나고 있으나, 하류로 갈수록 값이 급격하게 감소하고 있음을 알 수 있다. 이는 희박기체 공간에서 추진제가 주변공간으로 급격히 확산되면서 나타나는 전형적인 패턴이다. 추력기 하류에도 이온의 양이 없는 것은 아니지만, 추력기 출구 근처에 비해 지나치게 수밀도가 낮기 때문에, Fig. 4과 같이 이온의 수밀도 분포를 실스케일로 표시한 경우에는, 배기플룸의 거동을 육안으로 구분하기 어렵다.
Fig. 5에는 제논이온의 수밀도와 함께 추력기 주변공간의 전위분포를 함께 나타냈다. 이때, 수밀도 분포는 플룸 영역의 특성을 잘 확인할 수 있도록, 로그스케일로 표시하였다. 그림을 살펴보면, 추력기 출구에서 분사된 추진제가 희박기체영역으로 확산되고 있는 모양이 잘 나타나고 있다. 또한 전위값과 이온 수밀도의 분포패턴이 매우 유사하게 나타나고 있음도 확인할 수 있는데, 이는 Eq. 4에 나타낸 볼츠만 관계식에 의한 것으로 볼 수 있다. 식에 나타난 바와 같이, 전위 값은 전자 수밀도의 로그값에 비례하는데, 준중성 플라즈마 가정에 의해 전자의 수밀도와 이온의 수밀도가 서로 동등하므로, 이와 같은 패턴이 나타난 것이다. 볼츠만 관계식에서는 전자의 온도 또한 일정한 것으로 가정하게 되는데, 전자온도가 일정하지 않거나, 특정 방향으로의 전류가 강하게 나타나는 등 볼츠만 관계식의 가정이 성립하지 않는 경우, 전위분포와 이온 수밀도간의 상관관계는 달라질 수 있다.
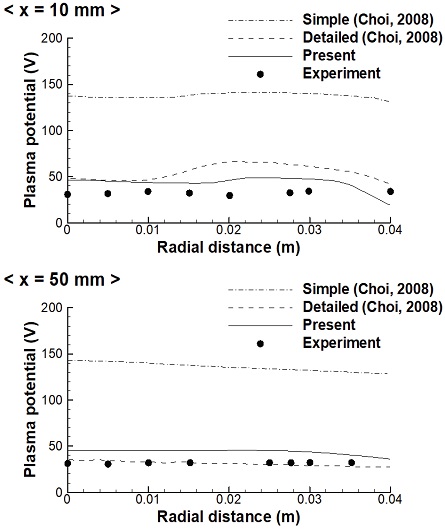
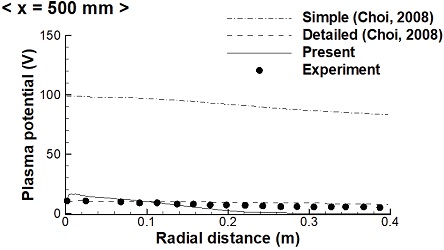
Fig. 6과 7에는 추력기 출구에서부터 축방향으로 10 mm, 50 mm, 500 mm 위치에서 반경방향 거리에 따른 전위값 분포를 실험값과 비교하여 나타냈다. 이때, 실험데이터의 부재로 인해, 10 mm, 50 mm 위치에서의 데이터는 Case 1의 조건을 이용하여, Domonkos 등[20]의 실험값과 비교하였고, 500 mm 위치에서의 데이터는 Case 2의 조건을 이용하여, Zakharenkov 등[21]의 실험값과 비교하였다. 그림에 나타난 바와 같이 본 연구의 해석결과가 실험값과 비교적 근접한 결과를 보여주고 있음을 알 수 있다. 여기서, 함께 비교한 전산해석 결과는 Choi[10]의 해석결과를 사용하였다.
본 연구의 해석결과는 동일한 Simple Electron Fluid Model을 적용한 Choi[10]의 데이터에 비해 개선된 결과를 보여주고는 있으나, 실험값과의 절대비교에 있어서는 해석결과가 실험결과보다 다소 높게 나타나고 있다. 또한, Choi[10]의 Detailed Electron Fluid Model을 적용한 결과와의 비교에서는, x= 10 mm 경우를 제외한 다른 모든 데이터에서 Detailed Electron Fluid Model이 본 연구의 결과보다 실험값을 더 잘 예측하는 것으로 나타났다. 현재 사용된 단순한 모델의 문제점을 개선하고, Detailed Electron Fluid Model 등 보다 상세한 모델을 적용하는 경우, 보다 정확한 결과 도출이 가능할 것으로 판단된다.
3.3 원자-이온 간 전하 교환의 영향
2.2절에서 강조한 바 있듯이, 전기추력기 배기플룸에서의 원자-이온 간 전하교환은 플룸에 의한 전기장 형성과 플룸 확산에 중대한 영향을 미친다고 알려져 있다. 이에 대한 영향을 확인하기 위해, Case 1 조건에 대해, 원자-이온 간 전하 교환을 고려하지 않도록 설정한 상태(w/o CEX)에서 추가적인 전산해석을 수행하였다. 이때, 원자-이온 간 운동량 교환의 경우에는, 특별한 모델이 적용되지 않은 일반적인 DSMC 코드를 사용한 것으로 가정하여 VHS 모델을 적용하여 해석하였다[18].
Fig. 8에는 추력기 출구 주변의 전위와 이온수밀도 분포를 나타냈다.
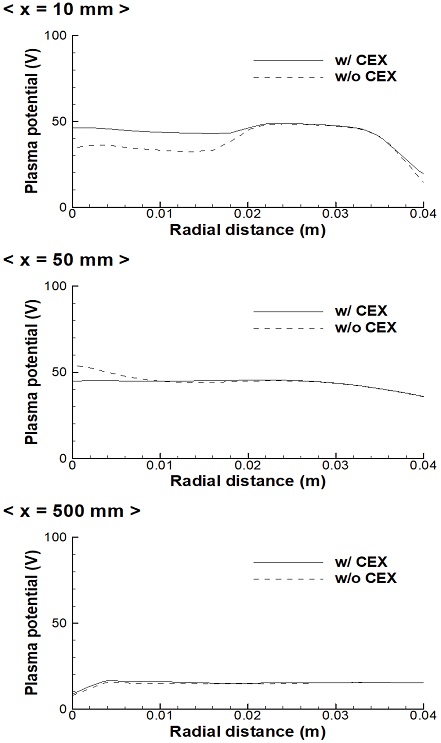
Fig. 5와 8을 비교해보면 전체적으로 거의 유사한 분포를 보인다고 생각할 수 있으나, 추력기 출구와 가까운 거리의 영역(점선 영역)을 살펴보면 극명한 차이를 확인할 수 있다. 원자-이온 간 전하 교환을 고려한 Fig. 5의 경우에는 추력기 출구 근처의 축 중심부에도 많은 양의 이온이 분포하고 있으며, 이로 인해 전위값도 높게 나타나고 있다. 그러나 전하 교환을 고려하지 않은 경우에는 같은 영역에서 이온의 수밀도 및 전위값이 현저하게 낮게 나타나고 있음을 알 수 있다.
이러한 특성에 대한 정량적인 분석을 위해, 추력기 출구에서부터 축방향으로 10 mm, 50 mm, 500 mm 위치에서 반경방향 거리에 따른 전위값을 발췌하여 Fig. 9에 나타내 비교하였다. 그림에 나타난 바와 같이, 추력기 출구와 가까운 영역(x= 10 mm, 50 mm)에서는 전하 교환을 고려한 경우와 그렇지 않은 경우가 축 중심부 근처에서 확연한 차이를 보이고 있다. 그러나, 이러한 경향은 추력기 출구에서 멀어질수록 감소하여, x= 500 mm 인 영역에서는 전하 교환을 고려한 경우와 그렇지 않은 경우의 결과가 거의 차이가 없음을 알 수 있다. 이는 추력기 출구 근처에서는 입자들의 수밀도가 높기 때문에 입자 간 충돌이 빈번하게 발생하고, 이로 인해, 원자-이온 간 전하 교환이 활발하게 나타나는 것으로 해석할 수 있다. 반면에, 입자들의 수밀도가 현저하게 낮아지는 추력기 출구 하류 영역에서는 입자 간 충돌발생빈도도 적기 때문에, 원자-이온 간 전하 교환 효과가 크지 않은 것으로 볼 수 있다.
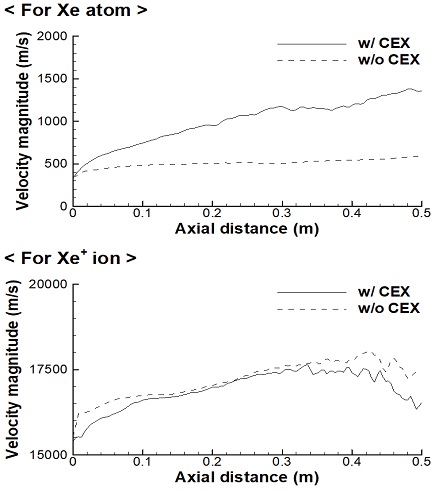
2.2절에서 설명한 바 있듯이, 원자-이온 간 발생하는 전하 교환은, 원자와 이온 간의 속력 교환의 결과를 초래한다. 즉, 추력기 출구에서 전자기력에 의해서 가속된 빠른 이온이, 전하 교환을 거쳐 빠른 원자로 바뀌게 되며, 이 과정에서 느린 원자는 느린 이온으로 탈바꿈되는 것이다. 이러한 현상을 확인하기 위해, 추력기 출구 중심부(r= 27.5 mm)에서 축방향 거리에 따른 제논 원자 및 이온의 속력의 크기를 산출하여 Fig. 10에 나타냈다. 그림에서 확인할 수 있듯이, 전하 교환을 고려하지 않은 경우에는 원자의 속력이 거의 일정한 수준을 유지하고 있으나, 전하 교환을 고려한 경우에는 그렇지 않은 경우보다 속력이 현저하게 높게 나타나고 있음을 알 수 있다. 반면 이온의 경우에는 전하 교환을 고려한 경우가 그렇지 않은 경우보다 속력이 낮게 나타나고 있어, 앞서 설명한 이론과 일치함을 확인할 수 있다. 이때, 이온입자는 플룸 내에서 전기장의 영향을 받아, 감가속 되므로, 전하 교환의 영향이 단순하지는 않으나, 그림 상에서 많게는 1000 m/s 이상의 속력차이가 나타나고 있다.
이렇듯, 추력기 출구 중심부 근처에서는, 전자교환 유무에 따라, 입자 수밀도, 전위, 입자 속도 등의 물리량의 차이가 현저하게 나타나고 있다. 그러나, Fig. 5와 8의 등고선(Contour) 상에서 볼 때, 추력기 출구 중심부 근처 이외의 영역에서는 전자교환 유무에 따른 변화를 확인하기 어렵다. 등고선은 공간상에 어떤 물질이 있을 때, 같은 값의 물리량을 갖는 물질의 위치를 이은 선이다. 따라서, 희박기체 공간과 같이, 극소량의 물질(원자 및 분자)이 넓은 영역에 이격, 분산되어 있는 경우, 등고선을 이용한 분석이 어려울 수 있다.
이를 보완하기 위해, Fig. 11에는 Xe 원자 및 Xe+ 이온 입자들의 공간적 위치 분포를 나타냈다. 그림을 살펴보면, Xe+ 이온(빨간색 입자)이 추력기 출구의 역방향 상류 영역(점선으로 표시)까지 이동해 있음을 알 수 있다. 이는 추력기 출구 중심부 근처에서 전위값이 높기 때문에, Xe+ 이온이 로렌츠 힘을 받아 역방향으로 이동한 것으로 추정할 수 있다(Fig. 5, 8의 전위값 참조). 반면, 로렌츠 힘을 받지 않는 Xe 원자(파란색 입자)는 Xe+ 이온에 비해 매우 적은 양만이 추력기 역방향 상류에 위치하고 있다. 또한, 이러한 Xe+ 이온의 역류현상은 전자교환을 고려하지 않은 경우(Fig. 11 위 그림)보다, 이를 고려한 경우(Fig. 11 아래 그림)에서 더욱 두드러지게 나타남을 확인할 수 있다. 이는 전자교환을 통해 발생하는 저속의 이온(Fig. 10 참조)이 로렌츠 힘의 영향권에서 느리게 이동하며, 로렌츠 힘을 받아 넓게 확산한 것으로 볼 수 있다. 이러한 현상은 추력기 모델에 따라, 실험 상에서도 매우 두드러지게 나타나는데, 이온입자가 추력기 출구면과 평행하게 분포하여, CEX wing으로 불리기도 한다[24,25].

Spatial distribution of Xe(Blue sphere) and Xe+(Red sphere) particles(Upper: Without CEX, Lower: With CEX).
이렇게 전하교환 현상에 의해 증대된 추력기 배기플룸의 역류현상은 비행체 주요 장비들의 오염을 유발할 수 있다. 따라서, 전기추력기를 우주비행체에 적용하기 위해서는 입자 간 충돌을 상세히 고려한 PIC-DSMC 해석이 필요하며, 특히 추력기 출구 근처에서 활발하게 발생할 수 있는 전하 교환에 대한 고려가 필수적이다.
4. 결 론
입자 간 충돌 효과를 정확하게 고려할 수 있는 PIC-DSMC 방법을 이용하여, D55 홀 추력기의 배기플룸의 거동을 해석하였다. 이때, 전자는 유체로 가정하여, Boltzmann 관계식을 이용한 Simple Electron Fluid Model을 적용하였으며, 원자-입자 간 전하 교환 및 운동량 교환을 모두 고려하였다.
본 연구의 전산해석 결과는, 단순한 전자 모델을 적용했음에도 불구하고, 실험에서 계측한 플라즈마 전위값을 비교적 잘 예측하였다. 또한, Boltzmann 관계식에 나타난 바와 같이, 플라즈마 전위는 이온 수밀도의 로그값과 직결되어 서로 유사한 공간적 분포를 보였다.
원자-이온 간 전하 교환의 효과를 확인하기 위해 수행한 추가적인 전산해석결과에서, 전하 교환을 고려한 경우, 속력이 매우 빠른 원자와 속력이 느린 이온의 생성이 확인되었다. 또한, 추력기 출구 부근에서는 전하 교환 모델 고려 여부에 따라 전위 분포 및 이온 수밀도 분포의 변화가 두드러지게 나타났으며, 전하 교환을 고려한 경우에는 그렇지 않은 경우보다, Xe+ 이온의 확산 및 역류 현상이 더욱 강화되었다.
추력기 출구 근처에서는 입자 간 충돌에 의해 원자-이온 간 전하 및 운동량이 교환되는 현상이 발생하며, 이로 인해 입자들의 궤적 및 속도가 달라질 수 있다. 따라서, 전기추력기를 장착한 우주비행체의 안정적인 운영을 위해서는 PIC-DSMC 방법을 이용한 입자 간 충돌 및 전하 교환, 운동량 교환에 대한 고려가 필수적이다.
References
-
Lev, D., Myers, R.M., Lemmer, K.M., Kolbeck, J. and Koizumi, H., “The Technological and Commercial Expansion of Electric Propulsion,” Acta Astronautica, Vol. 159, pp. 213-227, 2019.
[https://doi.org/10.1016/j.actaastro.2019.03.058]

-
Kim, H., Kim, S. and Won, S., “Current Status and Trends of Research and Development on Electric Thruster, Part I: Overseas,” Journal of Korean Society of Propulsion Engineers, Vol. 23, No. 6, pp. 95-108, 2019.
[https://doi.org/10.6108/KSPE.2019.23.6.095]

-
Cho, H., Ryu, K., Cha, W., Lee, J., Seo, M. and Choi, W., “STSAT-3 Hall Thruster Propulsion System Development,” Journal of Korean Society for Aeronautical and Space Sciences, Vol. 38, No. 8, pp. 834-841, 2010.
[https://doi.org/10.5139/JKSAS.2010.38.8.834]

-
Han, D., Joe, M., Shin, J., Sung, H. and Kim, S., “Numerical Analysis on Plasma Particles inside Electro-magnetic Field using Particle-in-cell Method,” Journal of Korean Society for Aeronautical and Space Sciences, Vol. 45, No. 11, pp. 932-938, 2017.
[https://doi.org/10.5139/JKSAS.2017.45.11.932]

-
Birdsall, C.K. and Langdon, A.B., Plasma Physics via Computer Simulation, Adam Hilger, New York, N.Y., U.S.A., 1991.
[https://doi.org/10.1201/9781315275048]

- Brieda, L., “Multiscale Modeling of Hall Thrusters,” Ph.D. Dissertation, Department of Aerospace Engineering, The George Washington University, Washington, DC, U.S.A., 2012.
-
Boeul, J., “Tutorial: Physics and Modeling of Hall Thrusters,” Journal of Applied Physics, Vol. 121, 011101, 2017.
[https://doi.org/10.1063/1.4972269]

-
Adam, J.C., Heron, A., Laval, G., “Study of Stationary Plasma Thrusters using Two-dimensional Fully Kinetic Simulations,” Physics of Plasmas, Vol. 11, No. 1, pp. 295-305, 2004.
[https://doi.org/10.1063/1.1632904]

-
Cai, C., “Numerical Studies on Plasma Plume Flows from a Cluster of Electric Propulsion Devices,” Aerospace Science and Technology, Vol. 41, pp. 134-143, 2015.
[https://doi.org/10.1016/j.ast.2014.12.018]

-
Choi, Y., “Particle Simulation of Plume Flows from an Anode-Layer Hall Thruster,” Ph.D. Dissertation, The University of Michigan, Department of Aerospace Engineering, Ann Arbor, M.I., U.S.A., 2008.
[https://doi.org/10.2514/1.28384]

-
Wang, J., Chen, L., Jiang, Y. and Lee, C., “Particle Simulation of an Anode-layer Hall Thruster Plume using an Anisotropic Scattering Model,” Acta Astronautica, Vol. 175, pp. 19-31, 2020.
[https://doi.org/10.1016/j.actaastro.2020.05.023]

-
Capon, C.J., Brown, M., White, C., Scanlon, T. and Boyce, R.R., “pdFOAM: A PIC-DSMC Code for Near-Earth Plasma-body Interactions,” Computers and Fluids, Vol. 149, pp. 160-171, 2017.
[https://doi.org/10.1016/j.compfluid.2017.03.020]

-
Araki, S.J. and Wirz, R.E., “Ion-Neutral Collision Modeling using Classical Scattering with Spin-Orbit Free Interaction Potential,” IEEE Transactions on Plasma Science, Vol. 3, pp. 470-480, 2013.
[https://doi.org/10.1109/TPS.2013.2241457]

-
Boyd, I.D., “Review of Hall Thruster Plume Modeling,” Journal of Spacecraft and Rockets, Vol. 38, No. 3, pp. 381-387, 2001.
[https://doi.org/10.2514/2.3695]

-
Guiliano, P.N. and Boyd, I.D., “Particle Simulation of Collision Dynamics for Ion Beam Injection into a Rarefied Gas,” Physics of Plasmas, Vol. 20, 033505, 2013.
[https://doi.org/10.1063/1.4794954]

-
Miller, J.S., Pullins, S.H., Levandier, D.J, Chiu, Y. and Dressler, R.A., “Xenon Charge Exchange Cross Sections for Electrostatic Thruster Models,” Journal of Applied Physics, Vol. 91, No. 3, 984, 2002.
[https://doi.org/10.1063/1.1426246]

-
Boyd, I.D. and Dressler, R.A., “Far Field Modeling of the Plasma Plume of a Hall Thruster,” Journal of Applied Physics, Vol. 92, No. 4, pp. 1764-1774, 2002.
[https://doi.org/10.1063/1.1492014]

- Bird, G.A., Molecular Gas Dynamics and the Direct Simulation of Gas Flows, Oxford Press, New York, N.Y., U.S.A., 1994.
-
Boyd, I.D., “Computation of the Plume of an Anode-Layer Hall Thruster,” Journal of Propulsion and Power, Vol. 16, No. 5, pp. 902-909, 2000.
[https://doi.org/10.2514/2.5658]

-
Domonkos, M.T., Marrese C.M., Haas J.M. and Gallimore, A.D., “Very Near-Field Plume Investigation of the D55,” AIAA Paper, 1997-3067, 1997.
[https://doi.org/10.2514/6.1997-3062]

- Zakharenkov, L., Semenkin, A.V. and Lebedev, Y.V., “Measurement Features and Results of TAL D-55 Plume,” International Electric Propulsion Conference Paper, 2005-184, 2005.
-
Choi, Y., Keidar, M. and Boyd, I.D., “Particle Simulation of Plume Flows from an Anode-Layer Hall Thruster,“ Journal of Propulsion and Power, Vol. 24, No. 3, pp. 554-561, 2008.
[https://doi.org/10.2514/1.28384]

-
Kim, H., Lim, Y., Choe, W. and Seon, J., “Effect of Multiply Charged Ions on the Performance and Beam Characteristics in Annular and Cylindrical Type Hall Thruster Plasmas,“ Applied Physics Letters, Vol. 105, 144104, 2014.
[https://doi.org/10.1063/1.4897948]

-
Hofer, R.R., Jankovsky, R.S. and Gallimore, A.D., “High-Specific Impulse Hall Thrusters, Part 1: Influence of Current Density and Magnetic Field,“ Journal of Propulsion and Power, Vol. 22, No. 4, pp. 721-731, 2006.
[https://doi.org/10.2514/1.15952]

-
Roy, R.I., Hastings, D.E. and Gatsonis, N.A., “Modelling of Ion Thruster Plume Contamination,“ International Electric Propulsion Conference Paper, 93-142, 1993.
[https://doi.org/10.2514/6.1994-3138]