스크램제트 추진 시스템의 비행 제어를 통한 연소기의 추력 분석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
공기 흡입식 극초음속 비행체인 스크램제트의 공력 데이터를 기반으로 하여 꼬리날개 각도와 발생 추력을 제어 입력으로 가지는 PID 기반 제어기를 설계했다. 일정한 비행 동압을 가지는 상승궤적과 순항 이후 목표지점을 타격하는 궤적을 기준으로 입력하여 해당 궤적을 추종하는 비행 시뮬레이션을 수행했다. 시뮬레이션 결과에 대해서 초기 상승궤적과 순항 궤적에 대해 비행체 모델에 요구되는 추력을 계산하여 수소 연료 이중 모드 스크램제트 연소기에 요구되는 연료 유량 분석을 위한 연소해석을 진행했다. 본 연구의 연소해석은 독립적으로 개발된 흡입구, 연소기, 노즐, 외부 공력 모델을 통합한 모델에 대해 진행되어 공기 흡입식 극초음속 비행체 통합 설계에 대한 기반을 마련했다.
Abstract
The PID controller with fin angle and thrust as control input was designed based on the aerodynamic data of scramjet system. Flight simulation following a given trajectory which strike the target point after climb and cruise with constant dynamic pressure was conducted. After that, the required thrust for the climb and cruise was calculated and the required fuel flow rate for the hydrogen fuel dual mode scramjet combustor was analyzed. The combustor analysis of this study which conducted on integrated model of independently developed inlet, combustor, nozzles and external aerodynamic models, laying the foundation for the integrated design of the air breathing hypersonic system.
Keywords:
Hypersonic Vehicle, Dual Mode Scramjet Combustor, Combustion Analysis키워드:
극초음속 비행체, 이중 모드 스크램제트 연소기, 연소해석1. 서 론
스크램제트의 엔진은 흡입구, 격리부, 연소기와 노즐로만 구성되어 아음속 영역에서는 운용될 수 없는 등, 설계 조건 이외의 영역에서는 성능의 저하가 커진다. 또한, 엔진 내부의 연소기를 비롯하여 흡입구, 노즐 등을 포함한 스크램제트 추진 시스템의 상태변수는 비선형성을 띠고 있으며 서로 연계되어 있으므로 엔진제어를 포함한 비행 제어를 위해서는 전체 비행 구간에서 시스템의 분석이 필요하다.
본 연구에서는 고정형상 흡입구와 수소 연료 초음속 연소기를 가지는 기준 모델에 대해서 임의의 비행 조건에서 형상 모델의 외부와 내부 유동의 특성을 계산하여서 이론적으로 요구되는 추력을 연료 유량에 대해서 발생하는 실제 추력과 비교하여 추진 시스템을 분석하고자 한다.
특히 흡입구 성능은 비행 받음각에 대해 민감하며 이는 연소기에서 연소 불안정으로 이어질 수 있으므로, 임의로 설계한 받음각 범위를 벗어나지 않는 비행 궤적을 계산하는 연구는 여럿 진행된 바 있다. Murillo[1]는 비행 동압과 받음각 구속조건을 가지는 스크램제트 추진 시스템의 상승궤적 최적화 관련 연구를 수행하였으며, Groves[2]는 선형화한 스크램제트 추진 시스템에 대해 최적 제어기법을 적용한 제어 결과를 보여주었다. 따라서 적절한 추진 시스템 분석을 위해서는 비행체의 궤적 제어에서 받음각 조건을 제한하여 흡입구에 설계 범위 이내의 유동 조건을 제공하는 것은 필수적이며 이를 위해 제어기 설계단계에서 실시간으로 받음각을 제한할 수 있는 알고리즘을 제안했다.
이에 대한 제어 결과를 통해 상승과 순항 단계에서 비행 조건과 요구 추력 프로파일을 분석하였으며 엔진 모델이 주어진 비행 조건에서 요구 추력을 만족시키는 데 필요한 연료 유량을 분석하여 전체 비행 구간에서의 질량 변화율을 추정했다.
본 논문은 다음과 같은 순서로 쓰였다. 2장에서는 본 연구에 적용된 비행체의 외부 공력과 흡입구, 연소기 모델을 소개했다. 3장에서는 외부 공력을 이용하여 상승과 순항 비행에서의 비행 조건을 분석하였다. 이를 통한 제어기의 설계 과정과 결과를 4장에서 분석하였으며 5장에서 그에 대한 연소기 분석을 진행했다.
2. 비행체 모델
2.1 외부 공력
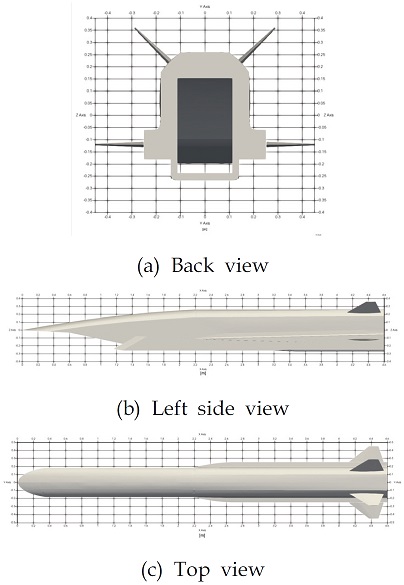
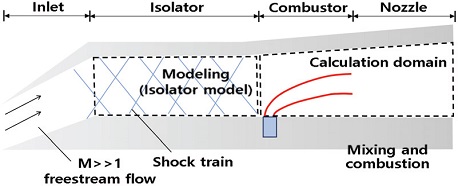
본 연구에서는 Fig. 1과 같이 꼬리날개와 흡입구를 포함한 엔진 형상을 가진 스크램제트 추진 시스템을 대상으로 하였다.
Scramjet vehicle model.
넓은 비행 구간에 대해서 해당 모델의 공력 데이터를 얻기 위해서 비교적 짧은 시간 내에 결과를 얻을 수 있는 국소 표면 경사 법을 사용하였다[3]. 해당 데이터는 엔진 내부 분석이 포함되지 않고 추력이 고려되지 않은 외부 공력 데이터이며 해당 분석 방법은 X-51A 형상에 대해서 CFD 결과와 비교하여 검증이 완료되었다[4]. 이를 통해 얻어낸 데이터는 이후 시스템 분석과 꼬리날개 각도와 요구 추력을 제어 입력으로 가지는 제어기 설계에 사용됐다.
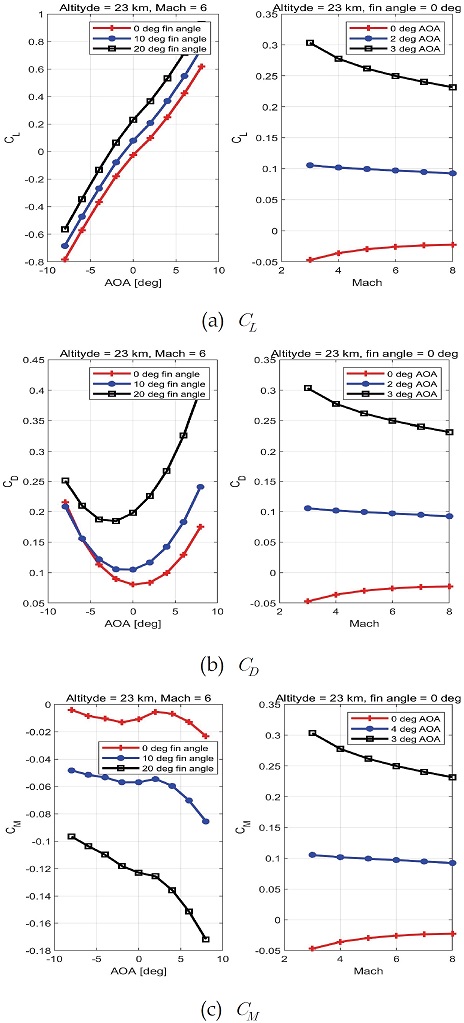
공력 데이터는 꼬리날개의 비대칭적인 움직임과 두 쌍의 꼬리날개가 다른 값을 가지는 경우를 가정하지 않고 Table 1에 나와 있는 조건에 대해서만 사용했다. 제어기 모델은 4차원으로 그리딩된 공력 데이터에 대해 선형 보간을 통하여 사용하도록 하였으며 양력, 항력, 종축 모멘트 계수가 꼬리날개 각도에 비례하는 등의 결과를 Fig. 2에서 확인할 수 있다.
Grid data and aerodynamic parameters.
Aerodynamic data with various flight conditions.
2.2 흡입구
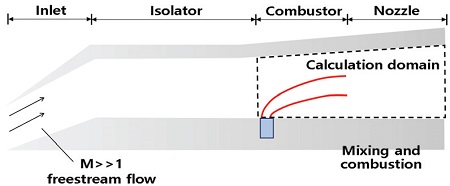
앞 절의 공력 데이터에 대한 추진 시스템의 분석을 위해 Fig. 1과 같은 형상을 기준으로 하여 설계된 SC01-A 흡입구 모델을 사용했다[5]. SC01-A 모델은 고도 23 km, 마하 4에서 6 조건에서 전산해석이 수행되어 정상상태에 대해서 흡입구 출구 유동 조건이 분석되었다. 본 연구에서는 격리부에서 유동의 변화를 분석하기 위해 연소기에서 램, 스크램제트 모드의 판별과 격리부 분석을 할 수 있도록 했다. 그러므로 SC01-A 모델에서 격리부를 제외하고 같은 형상을 가지는 흡입구 모델에 대해 분석을 진행했다. 다양한 비행 조건에서 흡입구에 발생하는 경사충격파 전후의 유동 데이터를 분석하여 비행 고도, 마하수, 받음각에 대한 흡입구 출구 유동의 압력, 온도, 밀도, 마하수 정보를 1차원 값으로 계산하여 연소기 모델에 값을 전달했다.
연소기 내부에 주입되는 연료의 인젝터는 Fig. 4, 5처럼 strut type으로 가정됐으며 주입구 길이와 혼합 길이 등을 결정하기 위한 분사 모델에 대한 세부사항은 Birzer 등에 의해 실험을 기반으로 제작된 모델을 사용했다[7].
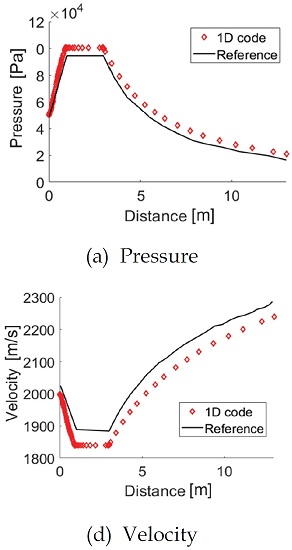
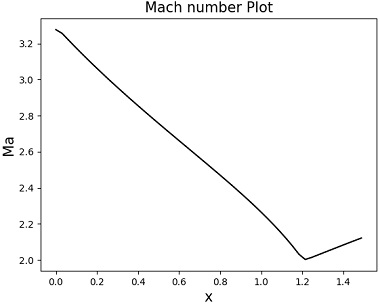
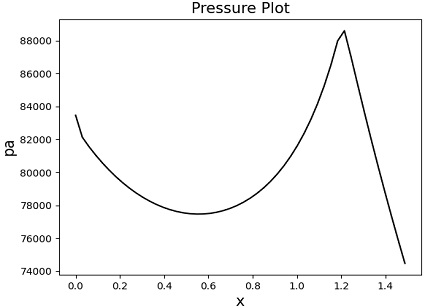
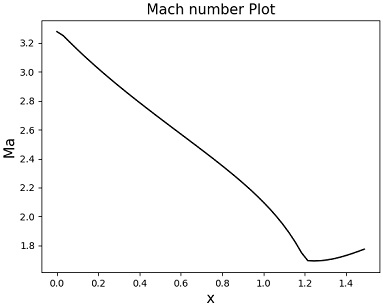
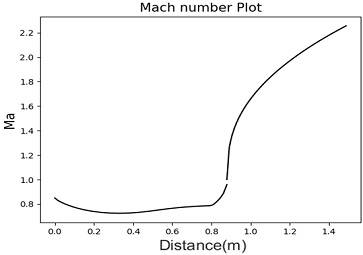
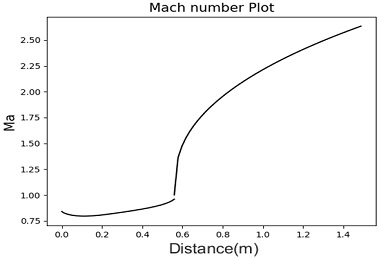
해당 솔버는 유체의 지배방정식과 아레니우스식 기반의 연소 모델을 준 1차원 해석 모델에 도입하였으며 변화하는 비행 조건에서 연소 상태를 유지하기 위해 비행 조건과 당량 비에 따라 결정되는 램제트 모드와 스크램제트 모드 사이의 전환을 분석하여 연소해석을 진행할 수 있도록 개발되었다. 솔버의 검증을 위해서 Fig. 3처럼 연소해석 결과가 선행 문헌과 비교됐으며 Table 2의 조건에서 수행한 것처럼 선행 문헌의 결과를 잘 재현했음을 확인했다[6,8].
Comparison of Combustor Analysis Results[6].
Combustor conditions.
연소기의 램모드와 스크램모드 판별 및 분석을 위해 주어진 격리부 입구 조건을 연소기 입구 조건으로 가정한 뒤, 연소기 내부의 아음속 지점 존재 여부 확인을 통해 모드를 판별하였으며, 램모드에서는 열 질식(Thermal choking)이 발생하는 위치를 계산하여 격리부 입구 조건에 대한 연소기 입구 조건을 계산하도록 했다[6].
다음으로 해당 솔버가 임의의 조건에서도 연소기 내부의 해석이 가능함을 보이기 위하여 Table 3, Table 4의 조건에서 동일 모델로 여러 당량 비에 대하여 연소해석을 진행하였다.
Flight Conditions.
Isolator Conditions.
Schematic of Scram mode Combustor.
Schematic of Ram mode Combustor.
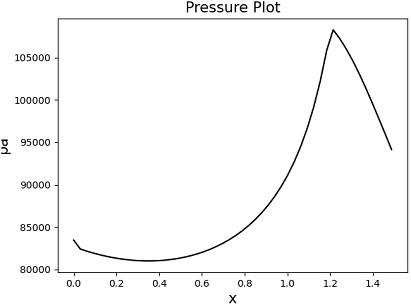
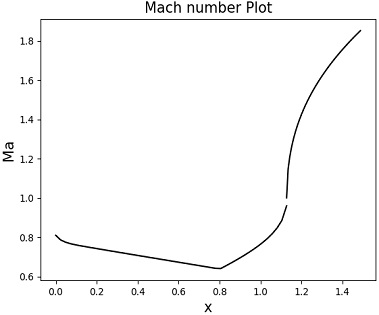
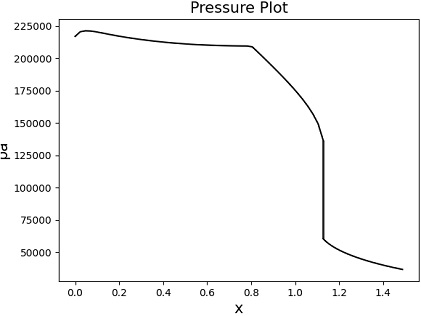
동일 조건으로 당량 비 0.20, 0.22, 0.30에서 해석이 진행되었으며 각 조건에서 당량 비에 따라 스크램제트 연소기 내부 마하수는 감소, 압력은 증가하였음을 Figs. 6∼11에서 확인할 수 있다. 당량 비를 0.3까지 증가시켰을 때 연소기 내부 유동이 아음속이 되어 램제트 모드로 연소기 내부 해석이 이루어졌다.
Equivalence ratio 0.20 Mach Plot.
Equivalence ratio 0.20 Pressure Plot.
Equivalence ratio 0.22 Mach Plot.
Equivalence ratio 0.22 Pressure Plot.
Equivalence ratio 0.30 Mach Plot.
Equivalence ratio 0.30 Pressure Plot.
3. 비행 조건 분석
3.1 순항 비행
목표 고도와 마하수에 대한 순항조건을 찾기 위해 각 조건에 대해서 요구되는 추력, 꼬리날개 각도, 받음각을 계산했다. 그때의 비행경로 각과 종축 각속도는 모두 0으로 두었으며 순항조건 탐색 과정에서 질량 변화는 없다고 가정하였다. 비행체의 순항 동역학에 모델 파라미터를 적용하기 위해 Table 1의 값들을 아래 식에 대입하여 각 비행 지점에 대해 순항조건을 만족하도록 하는 값을 찾았다.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
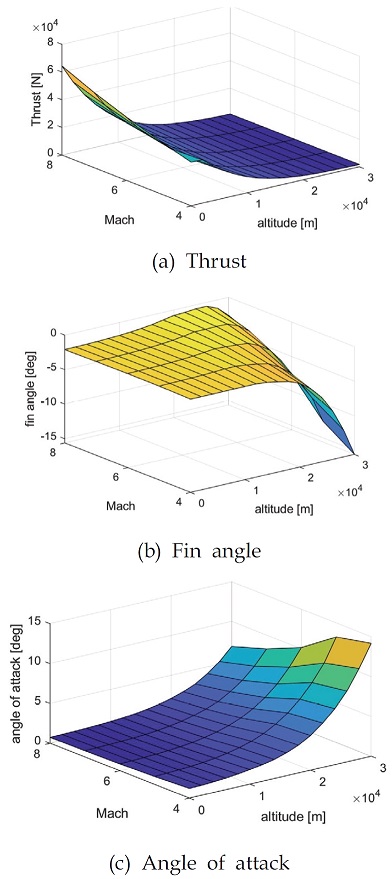
Fig. 12에서 여러 비행 조건에서 순항 동역학을 만족하는 추력, 꼬리날개 각도, 받음각 값을 확인할 수 있다. 고도가 올라감에 따라 대기 압력과 함께 비행 동압이 감소하여, 순항을 위한 추력이 감소하였고 양력 향상을 위해 받음각이 증가했음을 확인할 수 있다.
Trim conditions for various flight conditions.
3.2 상승 비행
본 연구에서는 비행체에 구조적 안정성을 줄 수 있도록 일정한 동압을 가지는 궤적을 따라 상승한다고 가정하였다. 또한, 일정한 동압으로 상승할 경우 상승 가속도에 따라 상승궤적 전체에서 요구되는 비행 조건을 미리 결정할 수 있어 그에 대한 추진 시스템 분석을 간편하게 진행할 수 있다[10]. 가속도가 acc로 주어지면 해당 시점의 고도와 마하수에 대해서 일정한 동압으로 상승하기 위한 비행경로 각은 아래 Eq. 12과 같다.
| (12) |
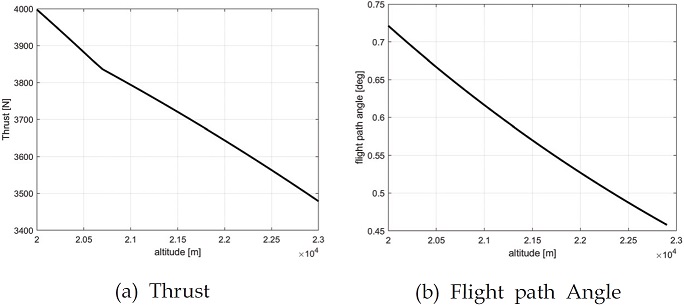
고도 20 km 마하 4.737부터 고도 23 km 마하 6까지 가속도 2 m/s2으로 상승할 때, 3.1절과 같은 방식으로 구한 요구 추력과 Eq. 12를 사용하여 계산한 비행경로 각을 Fig. 13에서 확인할 수 있다.
Climb conditions for 2 m/s2 acceleration.
4. 제어기 모델
4.1 3-loop 제어기 구성
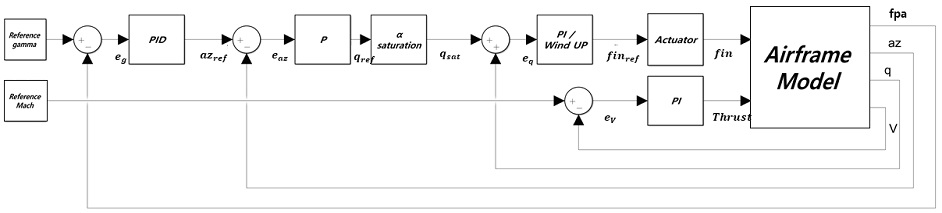
3 자유도로 가정된 스크램제트 추진 시스템 제어를 위해 Fig. 14와 같이 꼬리날개 각도와 추력을 제어 입력으로 받는 제어 루프를 구성하였다. 기준 입력으로 주는 궤적을 추종하기 위해 내부 루프로 종축 각속도, z축 가속도, 비행경로 각을 피드백하여 꼬리날개의 입력값을 계산하고 마하수를 추종하기 위해 속력을 피드백하여 추력 입력값을 계산했다.
Block diagram of a PID controller.
4.2 받음각 구속조건
받음각 구속조건을 적용하기 위해 임의로 받음각의 경계를 지정하고 제어 루프에 반영되도록 하였다. 혼합압축 흡입구 형상에서 음의 받음각은 흡입구에서 흐름의 유출이 발생하기 쉽고 엔진 내부에서 연소를 위한 유동의 압축이 충분히 일어나지 않아 엔진 성능에 영향을 미칠 수 있으므로 받음각의 경계 αmin과 αmax를 -4도에서 6도로 설정했다. 이후 제어기 내부에서 받음각이 경계 조건에 근접하면 임의로 각속도 명령을 제어하여 설정한 영역 내부의 받음각 조건으로 비행할 수 있도록 했다.
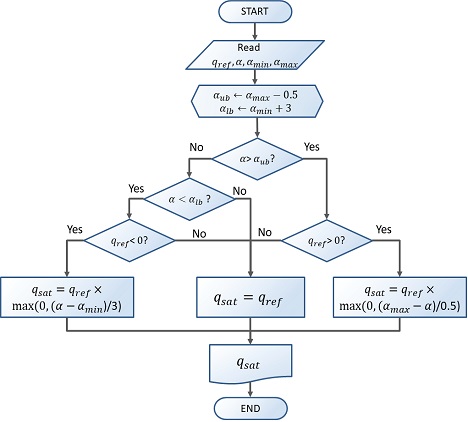
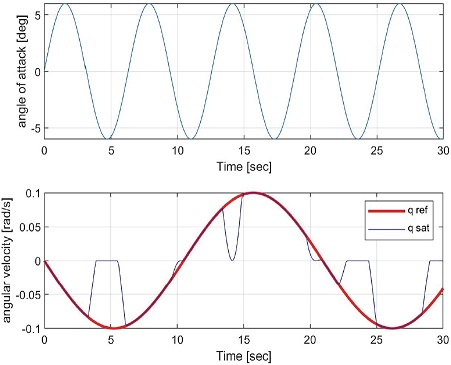
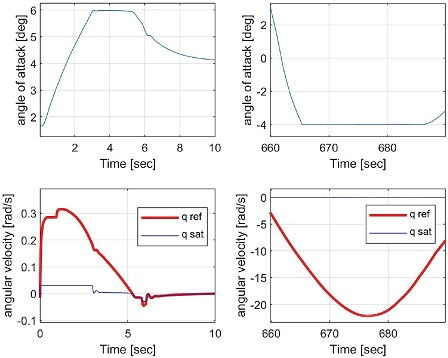
이를 위해 Fig. 15의 알고리즘을 이용하여 기존의 각속도 명령 값인 qref를 Fig. 16의 예시처럼 실제 명령 값인 qsat로 조정하여 입력하도록 했으며 받음각이 경계 조건에 접근함에 따라 각속도 명령의 절댓값을 감소시켜 입력함으로써 받음각이 경계 내부에 유지되도록 하였다. 3∼6 초 구간에서 받음각이 지정한 하한선에 접근하고 각속도 명령이 음수일 때 qsat가 기존의 명령 값보다 절댓값이 작은 값으로 수정된 결과를 확인할 수 있으며 13∼16 초 구간에서 반대의 경우를 볼 수 있다.
Flow chart for α constraints algorithm.
Example of angular velocity input.
4.3 게인 튜닝
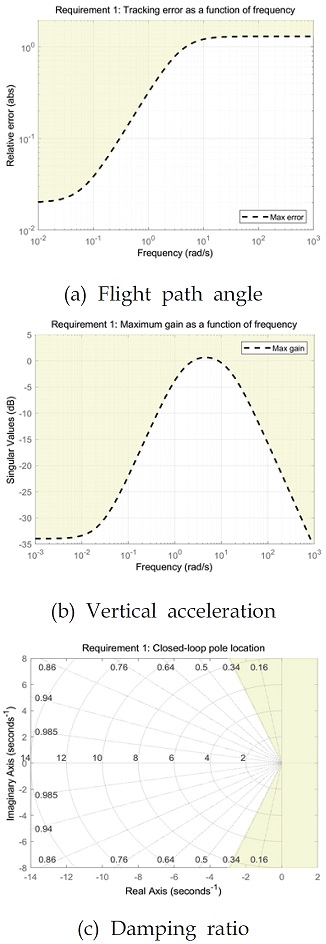
3.2절에서 탐색 된 순항 지점을 기준으로 스크램제트 추진 시스템을 선형으로 근사하여 각각의 선형 시스템에 대한 게인값을 찾았다. 게인 튜닝을 위해 Fig. 17처럼 비행경로 각과 종축 각속도에 대해 빠른 응답시간과 적은 정상상태 오차를 가지고, 내부 루프에 대해 측정 잡음과 교란을 제거할 수 있으며 최소한의 감쇠비를 가질 수 있도록 조건을 설정했다.
Tuning goals.
4.4 궤적 시뮬레이션 결과
제어기는 고도와 마하수를 기준 입력으로 받아 실시간으로 요구되는 비행경로 각과 마하수를 추종하도록 설계되었다. 제어기의 입력은 꼬리날개 각도와 요구되는 추력이며 추력은 동체에 평행하다고 가정하였으며 연소기 분석을 위해 질량 변화는 없다고 가정하였다.
경로는 20 km 상공에서 일정한 동압을 유지하며 상승하여 고도 23 km에서 마하 6으로 순항한 후 1,200 km 지점에 있는 목표에 닿는 궤적으로 하였다. 순항 고도와 마하수는 3.2절의 순항조건에서 순항 받음각이 설계 범위 내에 들어올 수 있게 하는 임의의 값을 선정하였으며 상승 가속도는 2 m/s2으로 고정하였다.
Fig. 18에서 0∼10 초와 660∼690 초에서 받음각과 각속도 명령의 결과를 확인할 수 있다. 각 구간에서 받음각이 한계치에 근접하여 각속도 명령이 수정되고 받음각이 경계선 내부에서 유지됐다.
Angular velocity input result.
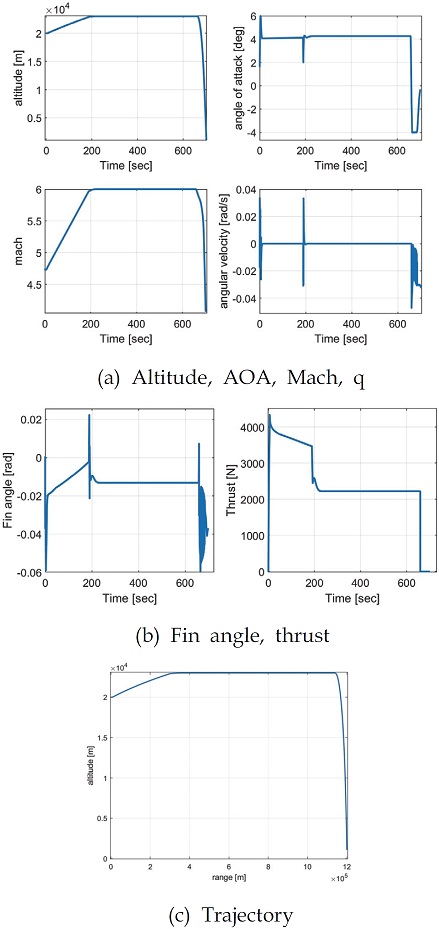
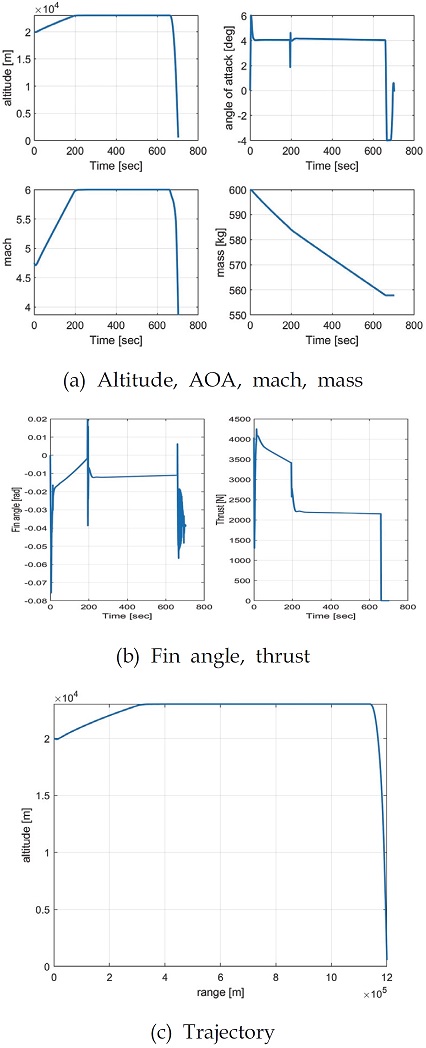
Fig. 19에서 시간에 따른 고도, 받음각, 마하수, 종축 각속도 결과와 전체 구간에서 제어 입력을 확인할 수 있으며 그에 따른 궤적을 확인할 수 있다.
Control results (constant mass).
초기 조건인 20 km 부근과 순항 비행을 시작하는 23 km 부근을 제외하면 Fig. 13에서 계산한 상승궤적에서의 요구 추력과 입력된 추력이 동일함을 Fig. 20에서 확인할 수 있다.
Analytic and real required thrust.
5. 연소기 분석
5.1 상승 구간
4장에서 제어기 설계를 통해 이론적으로 상승 시 요구되는 추력이 제어 입력과 유사한 결과를 보임을 확인하였다. 이를 바탕으로 실제 비행체의 엔진 모델이 요구되는 추력을 발생시키는 데 필요한 연료 유량을 분석할 수 있다.
비행 조건을 흡입구 형상에 적용하여 연소기 입구의 유동 조건을 계산하였고, 연료 유량 조절을 통해 연소기 출구의 유동 조건 분석했다. 추력은 완전팽창 노즐을 가정하여 간단한 모멘텀 식을 사용하여 계산하였다.
상승 구간 연소기 분석을 위해 제어 결과에서 고도 20,500 m, 22,500 m의 비행 조건을 사용하였으며 상세한 비행 조건을 Table 5에서 확인할 수 있다.
Flight conditions in climb phase.
상승궤적에서 비교적 큰 추력이 요구되어 램제트 모드로 연소기가 작동했으며 Table 5에서 요구된 추력이 Table 6의 격리부 입구 조건에 대해서 Table 7의 연소기 조건을 통해 계산된 발생 추력과 해당 조건에서 유사한 결과를 보임을 확인할 수 있다. 각 구간에서 연소기 내부 마하수는 Fig. 21, 22와 같으며 격리부 내의 의사 충격파에 의해 연소기 입구 마하수가 1 이하로 떨어졌음을 볼 수 있다.
Isolator inlet conditions in climb phase.
Combustion results in climb phase.
Combustor mach (20,500 m).
Combustor mach (22,500 m).
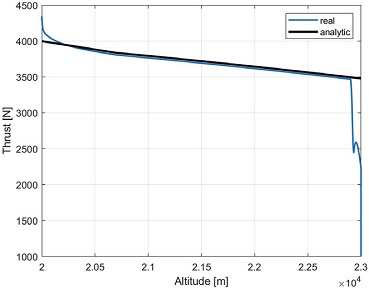
이를 통해 상승 구간에서 비행체의 질량 변화를 간단히 추정하면 그에 따른 순항 비행 조건을 계산해볼 수 있다. 두 조건에서 발생 추력과 연료 유량 값을 사용해 상승 구간 전체에서 발생 추력에 연료 유량이 비례하도록 가정했을 때 상승궤적을 그려보면 Fig. 23과 같으며 상승 과정에서 16 kg가량의 연료를 소모하여 23 km에 도달하였고 이후에 순항 단계로 진입했음을 볼 수 있다.
Control results in climb phase.
5.2 순항 구간
상승 이후 23 km 고도에서 마하 6의 속도로 순항 단계로 진입한 직후의 비행 조건을 이용하여 순항 시작 시점의 요구 추력과 그에 대한 연소기 분석을 진행할 수 있다.
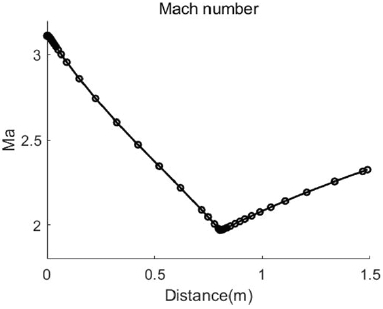
Table 8의 순항 시작 시점에서 비행 조건과 요구 추력에 대해서 격리부 입구 조건은 Table 9과 같이 계산되었다. 해당 격리부 입구 조건에 대해서 대략 2000 N의 요구 추력을 발생시키기 위해 스크램제트 모드로 연소기가 작동되어 Table 10의 결과를 도출했으며 그때의 연소기 내부 마하수는 Fig. 24와 같다.
Flight conditions in cruise phase.
Isolator inlet conditions in cruise phase.
Combustion results in cruise phase.
Combustor mach (23,000 m).
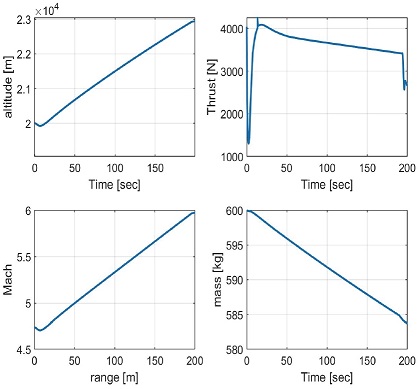
순항 단계에서 비행체의 질량 변화를 간단히 추정하기 위해 전체 순항 구간을 스크램제트 모드로 비행한다고 가정하여 해당 조건에서의 연료 유량을 순항 단계에서의 질량 변화율이라 가정했다. 그때의 궤적을 Fig. 23의 상승궤적을 포함하여 그려보면 Fig. 25와 같으며 시간에 따른 비행체 질량 변화와 함께 전체 구간에서 받음각 제한조건 이내로 비행하며 주어진 궤적을 추종한 결과를 확인할 수 있다.
Control Results (Mass varies with time).
대략 450 초 가량의 순항을 통해 26 kg의 연료를 소비하였으며 상승궤적을 포함해 총 42 kg의 연료를 사용하여 목표지점인 1,200 km 지점에 도달하였다.
6. 결 론
기준 궤적을 받음각 구속조건을 만족하는 범위 내에서 추종하도록 하는 제어기를 설계했다. 등동압 궤적을 기준으로 하여 전체 궤적에서 요구되는 추력을 이론적으로 계산했으며 설계한 제어기에서 이론적인 요구 추력과 유사한 추력 입력으로 기준 궤적을 추종했음을 확인했다.
이후 비행 조건과 연료 당량비에 따른 연소기의 모드 판별과 발생 추력에 대해 분석했으며 상승과 순항 단계에서 분석한 연소기 조건을 통해 전체 구간에서 질량 변화율을 추정할 수 있었다. 최종적으로 제어기가 질량 변화와 받음각 제한조건에서 기준 궤적을 잘 추종하는 결과를 보였다. 이를 통해 모델의 외부 공력 데이터와 흡입구 및 연소기 모델을 성공적으로 통합하여 이후 제어 및 연소를 고려한 비행체의 통합 설계에 기여할 수 있을 것으로 보인다.
Nomenclature
| acc : | Acceleration |
| az : | Longitudinal acceleration in body fixed coordinate frame |
| e : | Error |
| Fx, Fz : | Force in body fixed coordinate frame |
| fin : | Fin angle |
| fpa : | Flight path angle |
| g, g0 : | Gravity, standard gravity |
| h : | Altitude |
| Iyy : | Pitch moment of inertia |
| m : | Mass |
| q : | Angular velocity |
| RE : | Earth radius |
| U, W : | Speed in body fixed coordinate frame |
| V : | Velocity |
| α : | Angle of attack |
| Θ : | Pitch angle |
| ρ : | Air density |
Subscripts
| g : | flight path angle |
| lb, ub : | lower and upper bound |
| min, max : | minimum and maximum value |
| ref : | reference input |
| sat : | saturated input |
Acknowledgments
본 연구는 스크램제트 복합추진시스템 특화연구실 과제(과제코드: 16-106-501-035)의 지원을 받아 수행하였으며, 이에 감사드립니다.
References
- Murillo, O.J., “A fast ascent trajectory optimization method for hypersonic air-breathing vehicles,” Ph.D. Dissertation, Department of Aerospace Engineering, Iowa State University, Ames, Iowa, United States, 2010.
-
Groves, K.P., Sigthorsson, D.O., Serrani, A. and Yurkovich, S., “Reference command tracking for a linearized model of an air-breathing hypersonic vehicle,” AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, U.S.A., AIAA 2005-6144, Aug. 2005.
[https://doi.org/10.2514/6.2005-6144]
- Lee, M.S. and Kim, H.G., “Development of unstructured hypersonic panel code for rapid aerodynamic analysis using local surface inclination method,” 53th KSPE Autumn Conference, Busan, Korea, pp. 212-216, Nov. 2019.
- Lee, M.S., Lee, J.I., Kim, K.H. and Kim. H.J., “Unstructured Panel Code Development for Efficient Aerodynamic Analysis of Air-Breathing Hypersonic Vehicles,” International Journal of Aeronautical and Space Sciences. (to be published)
- Lee, J.W. and Kang, S.H., “Design Improvement and Performance Evaluation of 2D Scramjet Inle,” 54th KSPE Spring Conference, Korea, KSPE 2020-1061, Jul. 2020.
- Yang, J.H., Nam, J.H., Kang, S.H. and Yoh, J.I., “Numerical Investigation of Dual Mode Ramjet Combustor using Quasi 1-Dimensional Solver,” Journal of The Korean Society for Aeronautical and Space Sciences. (to be published)
-
Birzer, C. and Doolan, C.J., “Quasi-One-Dimensional Model of Hydrogen Fueled Scramjet Combustors,” Journal of Propulsion and Power, Vol. 25, No. 6, pp. 1220-1225, Nov. 2009.
[https://doi.org/10.2514/1.43716]
-
Torrez, S.M., Scholten, N.A., Micka, D.J., Driscoll, J.F., Bolender, M.A., Doman, D.B. and Oppenheimer, M.W., “A scramjet engine model including effects of precombustion shocks and dissociation,” 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit., Hartford, U.S.A., AIAA 2008-4619, Jul. 2008.
[https://doi.org/10.2514/6.2008-4619]
-
Ikui. T., Matsuo, K. and Nagai, M., “The Mechanism of Pseudo-Shock Waves,” Bulletin of JSME, Vol. 17, No. 108, pp. 731-739, Jun. 1974.
[https://doi.org/10.1299/jsme1958.17.731]
-
Driscoll, J.F., Torrez, S.M. and Driscoll, J.F., “Minimum-fuel ascent of a hypersonic vehicle using surrogate optimization,” Journal of Aircraft, Vol. 51, No. 6, pp. 1973-1986, 2014.
[https://doi.org/10.2514/1.C032617]