액체 추진제 공급시스템의 정특성 모델링 및 검증
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
액체로켓엔진의 추진제 공급시스템의 각 요소와 전체 시스템에 대한 보편적 모델에 실험계수를 적용한 수학적 모델링 기법을 소형 액체로켓엔진을 모사한 수류 시험 장치를 통한 실험 결과로부터 검증하였다. 유체저항요소와 펌프의 압력 변화에 대한 예측을 수행하였으며 예측 정확도 향상을 위해 구성요소 모델링에 대하여 실험계수를 적용하였다. 이를 위해 각 구성요소에 대해 유동의 지배방정식이나 이미 알려진 경험식을 기반으로 실험계수의 도출 방안에 대하여 정리하였으며 사용한 상용품의 실험계수를 제시하였다. 모델링을 통한 예측 결과는 실험 데이터와 비교적 잘 일치하였다. 실험 데이터와의 검증을 통해 시뮬레이션의 정확도에 영향을 미치는 인자에 대해 분석하고 시스템 해석의 정확도 향상 방안에 대하여 제안하였다.
Abstract
The mathematical modeling applying experimental coefficients to a conventional model was validated through the hydraulic test for the components and the full system of a small-sized liquid rocket engine’s propellant supply system. According to the simulations, pressures difference for the fluid resistance components and the pump were mainly predicted. In order to improve the modeling accuracy, the loss coefficients obtained by the empirical method were applied to the modeling. Based on the governing equation of the flow or the well known empirical equation, the method of deriving the empirical coefficients was summarized and the coefficients were presented for the commercial products used in this study. The prediction results by modeling were in good agreement with the experimental data. Through the comparison with the experimental data, the factors affecting the accuracy of the simulation were analyzed and improving methods of the accuracy was proposed.
Keywords:
Liquid Rocket Engine, Electric-pump Cycle, Propellant Supply System, Cold Flow Test키워드:
액체로켓엔진, 전기펌프 사이클, 추진제 공급시스템, 수류 시험1. 서 론
액체로켓의 추진제 공급계에 대한 해석은 요구 추력을 만족하는 추진제 유량에 대하여 유체저항요소에서의 차압 및 압력손실을 도출하고 이로부터 연소실에 요구 압력을 공급하는 가압 시스템의 성능을 도출하는 과정으로 진행된다. 따라서 구성요소들 사이의 유량에 따른 압력변화 예측은 엔진 성능 해석에 있어 필수적인 요소이다. 따라서 액체로켓엔진의 사이클과 무관하게 모든 사이클의 공통 요소인 가압시스템과 유체저항요소에 대한 정밀한 모델링 기법 확보는 액체로켓엔진 개발에 있어 중요한 요소로 고려된다. 유체저항요소는 보통 배관, 오리피스, 밸브 등의 추진제의 저항으로 작용하는 요소로 구성되어 있다. 일반적으로 이러한 요소들에 대한 모델링은 물리적 특성에 기반한 이론적 모델링에 실험 데이터를 통해 습득한 실험계수를 추가하는 방식으로 수행된다[1]. 대표적인 우주선진국의 액체로켓엔진 모델링&시뮬레이션 프로그램으로 미국 NASA의 ROCETS[2], 일본 JAXA의 REDS[3] 및 유럽의 ESPSS[4]가 존재한다. 해당 프로그램들은 방대한 실험 데이터로부터 도출한 성능 곡선을 내장하고 있으며 실험 결과를 통해 프로그램의 성능을 검증하여 높은 정확도를 확보하였다. 이와 같이 높은 정확도를 목적으로 하는 모델링&시뮬레이션 프로그램의 개발을 위해서 실험 데이터가 필수적으로 요구된다.
언급한 프로그램 외에도 성능 해석의 정확도 향상 및 검증을 목적으로 엔진 시스템의 추진제 공급계를 모사한 시험 장치를 이용한 연구는 국내외적으로 다양하게 수행되었다[5]. Spiller 등[6]은 상용 기어펌프를 사용하여 전기펌프 사이클 엔진을 모사한 실험 장치를 구성하였으며, 매질로는 hydraulic oil Agip OSO 46을 사용하였다. 실험을 통해 회전수에 따른 펌프의 양정과 유량에 따른 압력손실의 성능 곡선을 도출하였다. Talik 등[7]은 추력 2.2 kN급 전기펌프 사이클 엔진의 산화제 펌프를 설계하고 매질을 물로 사용하여 유량에 대한 펌프 양정의 성능 곡선을 도출하였다. 김형민 등[8]은 체적 유량 8 m3/h, 펌프 설계 양정 18 m에 대한 수류 시험 장치를 구성하여 펌프의 출구와 유체저항요소에서의 압력을 측정하여 일부 구성요소에 대해 실험 계수를 도출한 바 있다. 그러나 앞서 언급된 선행연구들은 추진제 유량 1 kg/s 정도 혹은 그 이상을 가지는 중소형 엔진의 추진제 공급계에 대하여 모사한 것으로 그 이하의 소량의 유량에 해당하는 소형 엔진에 대한 모델링 및 검증 결과는 보고된 바가 없으며 사용한 구성품의 실험계수 및 도출방안에 대하여 제시한 바가 없다.
추진제 공급계 시험에 있어 상용품을 적용하는 경우 시험 장치 구축이 용이하여 널리 이용될 수 있지만, 이론적 모델링에서 필요로 하는 정보를 습득하기 어렵다는 문제가 따른다. 이에 본 연구에서는 상용구성품을 이용하여 추진제 공급장치를 구성하고, 적용한 구성품에 대해 이론에 근거한 실험 계수를 예비 실험을 통해 도출하여 모델링에 적용하는 방안을 제안하고자 하였다. 이와 더불어 0.1∼0.2 kg/s 정도의 매우 작은 유량을 가지는 소형 액체로켓엔진을 대상으로 기존에 잘 알려져 있는 공급계 모델링[1]을 정리하여 이에 대한 정확도를 수류 실험 결과를 통해 평가하고자 하였다. 이를 위해 각 구성요소에서의 실험계수를 도출하고 이를 적용한 모델링 결과와 실험 결과와의 오차를 확인하였다. 또한 실험 데이터의 정확도가 시뮬레이션 결과에 미치는 영향에 대해 분석하였으며 시스템 단위 검증 결과를 통해 요소설계 프로그램의 정확도 향상 방안을 제시하였다. 본 논문에 기술된 모델링, 측정된 실험계수 그리고 제시된 실험결과는 소형 액체로켓엔진에 대한 성능해석 연구에 도움이 될 것으로 기대된다.
2. 구성요소 모델링 기법 및 검증
2.1 구성요소 수학적 모델링
본 절에서는 유체저항요소인 배관, 곡관, 볼 밸브, 니들 밸브의 수류실험 데이터로부터 추출한 실험계수 및 이론적⋅경험적 모델링과 펌프 모델링에 대하여 기술한다. 유체저항요소에 대한 모델링은 차압과 압력손실 예측이 목적이다. 배관의 경우 벽면의 마찰 및 곡관 등 형상의 특성이 바뀌는 지점이 존재하므로 얘기치 못한 압력손실을 발생시킨다. 이와 달리 밸브의 경우 유체의 흐름을 제어하기 위해 사용되는 구성요소로, 내부의 면적변화를 통해 인위적으로 차압을 발생시킨다. 유체저항요소에서의 압력손실 및 차압은 Eq. 1의 손실계수와 동압의 곱으로 표현되며[1] 연속 방정식을 적용하면 유량과 면적의 함수로도 표현이 가능하다. 압력손실 및 차압 모델링의 높은 신뢰성을 확보하기 위해서는 보다 정확한 손실계수(K)를 추정하는 것이 중요하다.
| (1) |
배관
배관을 흐르는 유체에 대해 정상상태, 비압축성 가정을 바탕으로 마찰로 인한 압력손실은 유체의 평균속도, 배관의 직경, 배관의 길이 그리고 마찰계수로 표현하는 Eq. 2의 Darcy-Weisbach 방정식을 사용하여 모델링하는 방식이 보편적이다[1]. Darcy-Weisbach equation은 Bernoulli 방정식과 연속 방정식으로부터 유도되는 이론식으로 무차원 마찰계수(f)를 사용하여 직선 도관의 압력손실을 계산 가능한 식이다.
| (2) |
| (3) |
마찰계수는 경험적 방식으로 추정하며 Moody chart가 실용적으로 사용된다. Moody chart는 10,000개 이상의 실험결과를 분석한 것으로 유동 특성에 따라 4개의 영역대로 나누어 레이놀즈 수, 거칠기 및 직경의 함수인 Eq. 3로 표현된다[9]. Rec는 난류로의 천이구간에서의 레이놀즈 수를 의미한다.
곡관의 마찰계수는 배관과 동일하게 레이놀즈 수에 의존하며[9], 곡률반경이 고려되지 않은 기역자 형태의 부드럽게 굽은 곡관의 압력손실은 굽힘각(θ)에 따라 Eq. 4의 경험식으로 추정 가능하다[10, 11]. 마찰계수(f)는 배관과 동일하게 Moody chart를 기반으로 레이놀즈 수에 따른 경험적 모델링 방식을 사용하여 앞의 Eq. 3을 적용한다.
| (4) |
터빈유량계
실제 엔진에서 비행 중에 엔진 상태진단을 위해 각종 계측장치들이 부착되며 지상 시험 장치에서도 마찬가지로 데이터 습득을 위해 계측장치의 설치가 요구된다. 따라서 보다 정확한 엔진 성능예측을 위해서는 이러한 계측장치들이 성능에 미치는 영향을 분석해야 한다. 본 연구에서는 터빈유량계를 추가로 적용하였다. 터빈유량계는 유동에 수직으로 설치되어 로터의 회전 속도가 유체의 체적 유량에 비례하는 원리를 이용하여 유량을 도출하는 장치이다. 유체의 운동에너지를 로터의 회전운동 에너지로 변환하는 장치이기 때문에 타 방식에 비하여 압력손실이 크게 발생한다는 단점이 존재한다. 이는 하나의 유체저항요소로 작용한다. 터빈유량계는 회전에 따른 저항특성 변화가 존재하나 모델링의 용이성을 위해 고정면적에 대한 유체저항요소로 가정하면 Eq. 1을 이용하여 압력손실의 예측이 가능하다. 손실계수는 방식, 크기, 조건, 용도 등에 따라 다르기 때문에 일반적으로 실험 데이터를 통해 손실계수를 도출한다.
볼밸브
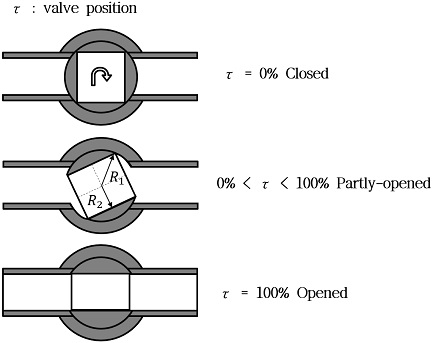
볼밸브는 내부에 관로가 존재하는 볼 형상의 디스크를 회전시킴으로써 유동흐름의 면적을 조절하여 유량 및 압력을 제어하는 장치이다. 0°∼90° 범위로 회전조작이 가능하며, 주로 0°의 폐쇄 또는 90°의 개방에 대한 개폐용도로 사용하나, 목적에 따라 회전율을 조절하여 유량 및 압력제어 용도로 사용하기도 한다[12]. Fig. 1에 볼밸브를 간략하게 도식화하여 원리를 나타내었다.
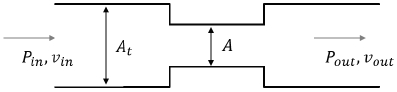
볼밸브 내부의 관로가 전후단의 배관과 단면적이 동일하다고 가정하면 볼밸브 내부의 형상은 Fig. 2와 같이 간략하게 나타낼 수 있다. 전후단의 배관의 면적(At)과 볼밸브의 내부 유효면적(A)을 통해 Bernoulli’s equation과 연속 방정식에 따라 볼밸브에서의 차압은 Eq. 5로 이론적 모델링이 가능하다[12].
| (5) |
배관의 면적과 볼밸브의 내부 유효 면적의 비는 이론적으로 Eq. 6의 밸브 개도와 내부 형상의 함수로 나타낼 수 있다[12].
| (6) |
Eq. 5은 면적변화에 의한 차압 모델링으로 마찰에 의한 압력손실은 고려하지 않고 있다. 하지만 실제로 면적변화가 존재하지 않아도 마찰에 의한 압력손실 및 복잡한 내부 구성으로 인해 개방조건에서도 압력강하가 발생한다. 따라서 실험적으로 볼밸브의 손실계수를 추정하는 방식이 사용된다. 본 연구에서는 수류 시험 장치에 사용한 상용 볼밸브에 대하여 이론적으로 차압이 발생하지 않는 개방조건에 대해 수류 시험을 진행하여 볼밸브의 압력손실에 대한 실험계수(Kball)를 도출하여 모델링에 적용하였다. 따라서 볼밸브에서의 압력강하는 Eq. 7로 모델링 가능하다.
| (7) |
니들밸브
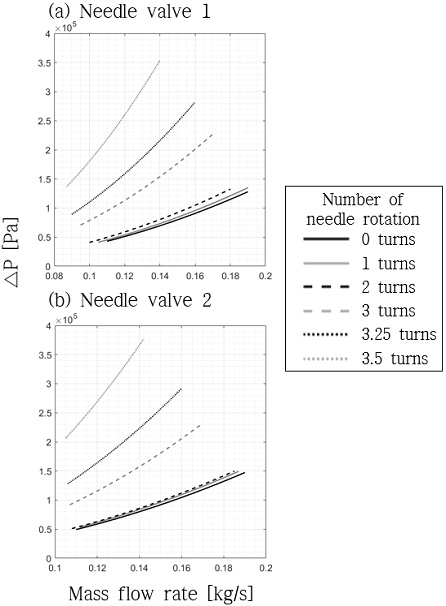
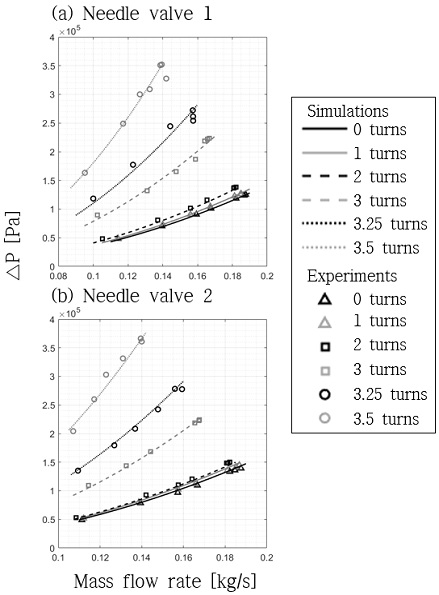
니들밸브는 스템(stem)을 이용하여 유동 흐름의 면적을 조절하여 유량 및 압력을 제어하는 장치이다. 스템 조절축의 회전수에 따라 관로에 설치되어 있는 스템의 높낮이를 조절하여 유동 흐름의 면적을 제어하는 원리이다. 조작이 간편하여 주로 미세한 유량 및 압력 제어의 용도로 사용한다. 볼밸브와 마찬가지로 면적에 대한 내부형상은 Fig. 2로 간략하게 나타내어 차압은 Eq. 5로 모델링하는 것이 일반적이다. 하지만 회전수에 따른 배관의 면적과 니들 밸브 내부 유효 면적 비는 니들밸브의 사양에 따라 다르기 때문에 보다 실용적인 방법으로 면적 비를 무시하고 실험 데이터를 통해 회전수에 따른 차압에 대한 경험식을 작성하여 모델링 하는 것이 유용할 수 있다. 니들밸브의 최대 회전수(Xt)와 회전수(X)의 차이에 대한 비율을 Eq. 8의 Turn ratio(Tr)로 정의하면 니들밸브의 차압은 Eq. 9로 유량과 Turn ratio의 3차 다항식으로 표현된다. 니들밸브의 실험계수(α, β, γ, δ)는 니들밸브의 사양에 따라 다르며 본 연구에서는 수류 시험 장치에 사용한 상용 니들 밸브에 대하여 실험을 통해 손실이 고려된 실험계수를 도출하였다. 본 논문에서 제시하고 있는 모든 실험계수는 121케이스의 유량조건에 대한 수류 실험 데이터로부터 curve fitting을 통해 도출하였다. 이를 통해 니들밸브 1과 니들밸브 2에 대한 성능곡선을 작성하였으며 Fig. 3에 나타내었다.
| (8) |
| (9) |
펌프
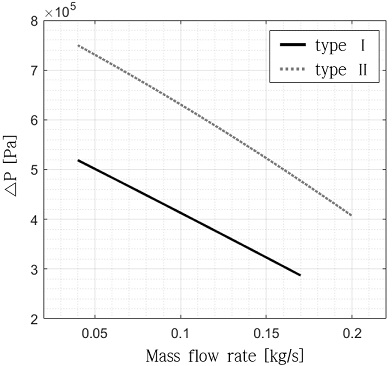
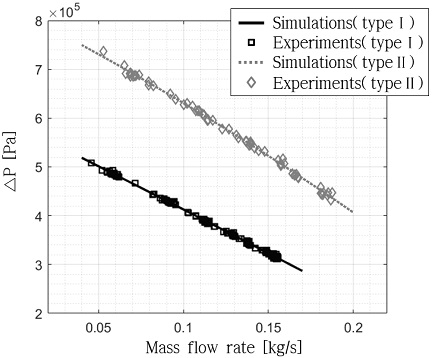
Affinity law에 의해 원심펌프의 압력은 유량의 제곱에 비례한다[13]. 이에 따라 토출압력과 입구압력의 차이를 Eq. 10과 같이 유량에 대한 2차 함수로 모델링 하였다. 본 연구에서는 가압성능이 다른 두 개의 상용 펌프에 대하여 수류 시험으로부터 습득한 실험 데이터를 통해 Eq. 10의 손실이 포함된 실험계수(ε, ζ, κ)를 도출하였고 이를 통해 펌프 토출 압력과 입구 압력의 차인 압력 증가에 대한 모델링을 수행하였다. 또한 실험계수를 이용하여 Fig. 4에 최대 가압 5 bar 상용펌프(type Ⅰ)와 최대 가압 7 bar 상용펌프(type Ⅱ)의 유량에 대한 압력 증가의 성능 곡선을 나타내었다.
| (10) |
2.2 수류 시험 결과를 통한 모델링 검증
본 절에서는 2.1절의 구성요소의 수학적 모델링의 검증을 위한 수류 시험 장치의 구성을 2.2.1절에 다루고 있다. 2.2.2절에는 수류 시험을 통해 각 요소별 모델링을 검증한 결과를 제시하고 있으며 2.2.3절에는 실험 데이터의 편차가 검증에 미치는 영향에 대해 다루고 있다.
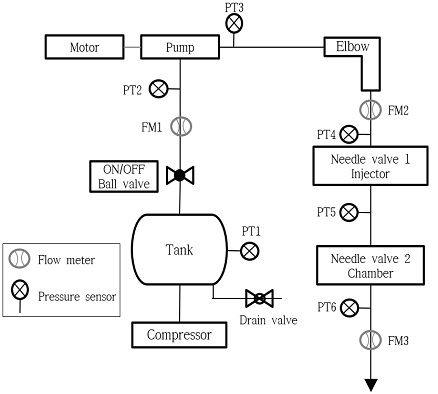
모델링 기법의 검증을 위해 구축된 소형 액체로켓엔진을 모사하는 수류 시험 장치의 구축된 모습은 Fig. 5에 제시하였다[14]. 작동유체로는 물을 사용하였으며 탱크의 부피는 25 L로 압축기로 공기를 가압하여 탱크의 가압가스로 사용하였다. 전체 시험의 진행의 안전이나 유량 공급의 단속을 위하여 탱크 후단에 볼 밸브를 설치하였고, 가압을 위하여 엔진의 전기펌프에 해당하는 펌프-모터 어셈블리를 구성하였다. 펌프-모터 어셈블리는 유연웨스텍社의 ‘S-1502’ 모델을 사용하였다. 펌프 후단에는 곡관 및 인젝터를 모사하는 니들 밸브 1과 연소실을 모사하는 니들 밸브 2를 구성하였고 최대 5 bar(type Ⅰ)와 최대 7 bar(type Ⅱ)의 가압성능을 갖는 두 개의 상용펌프를 선정하였다. 소형 액체로켓엔진의 추진제 공급계 모사를 위하여 유량 0.1∼0.2 kg/s 수준의 수류 시험 장치를 구성 하였다.
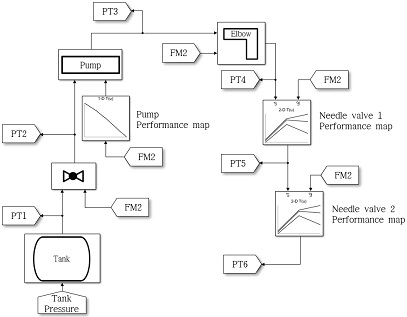
Fig. 6은 수류 시험 장치의 개략도로 구성요소 및 유량과 압력 측정 지점을 나타낸다. 압력은 탱크(PT1), 볼 밸브 후단(PT2), 펌프 후단(PT3), 곡관 후단(PT4), 니들 밸브 1 후단(PT5) 그리고 니들 밸브 2 후단(PT6)의 총 6개의 지점을 측정한다. 압력센서는 Sensys社의 ‘PHP-C-0010-BCTJ-FC’모델을 사용하였으며 유량계는 KOMETER社의 ‘NK-250’모델을 사용하였다. 유량은 펌프 전단(FM1), 펌프 후단(FM2), 시스템 최 후단(FM3)의 총 3개의 지점을 측정하며, 배수 유량을 측정하여 유량계 보정을 수행하였다.
배관, 터빈유량계
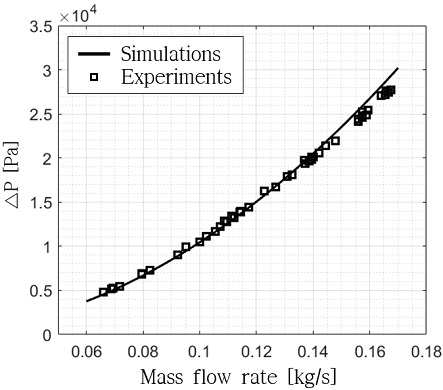
곡관을 포함한 배관의 압력손실 모델링은 시뮬레이션 결과와 실험에서 PT3와 PT4에서 측정된 압력의 차이로 검증하였다. 배관 및 곡관의 손실계수는 Eq. 2-4로부터 경험식을 사용하여 계산하므로 별도의 실험계수 도출은 수행하지 않았다. PT3와 PT4사이에는 배관과 곡관뿐만 아니라 터빈유량계가 존재하기 때문에 유량계로 인한 추가적인 압력손실을 고려해야 한다. 이를 고려하기 위해 실험을 통해 유량계의 손실계수를 도출하여 유량계를 하나의 압력손실 요소로 가정하여 해석에 포함하였다. 본 연구에서 도출한 모든 실험계수는 MKS 단위계를 기준으로 하였으며 도출된 터빈유량계의 손실계수 (KFM)는 3.31×103으로 Eq. 1에 적용하여 터빈유량계에서의 압력손실을 모델링하였다. 수류 시험 장치의 설계 유량 범위에서 46 케이스에 대하여 실험을 수행하여 시뮬레이션 결과와 비교한 것을 Fig. 7에 나타내었다. 또한 실험 데이터의 재현성을 평가하기 위해 동일 유량 조건에 대하여 3번의 실험을 수행하여 각 구성요소에 대하여 상대표준편차(RSD, Relative Standard Deviation)를 구하였다. 상대표준편차는 표준편차와 데이터의 평균값의 비율로 실험의 정밀도를 평가하는 성능계수로 Eq. 11에 상대표준편차의 수식을 제시하였다. 특정 실험 데이터의 값(xi)과 모든 데이터의 평균값(m)의 차를 제곱한 것을 실험 횟수(N)로 나눈 것의 제곱근은 표준편차이며 이를 평균값으로 나눈 것이 상대표준편차 이다. PT3와 PT4의 차이의 경우 최대 상대표준편차는 1.46%이다. 본 연구에서는 각 케이스 별 오차의 절댓값을 평균한 것을 오차의 평균으로 정의하였으며 모든 요소에 대한 오차의 평균은 동일하게 평가하였다. 결과적으로 곡관과 터빈유량계를 포함한 배관에 대하여 최대 5.98%, 평균 2.65%의 오차를 보였다.
| (11) |
볼밸브, 터빈유량계
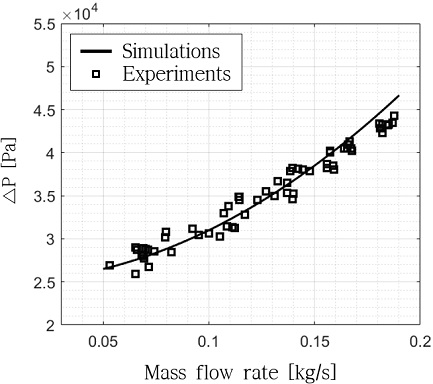
볼밸브의 압력손실 모델링은 시뮬레이션 결과와 실험에서 PT1와 PT2에서 측정된 압력의 차이로 검증하였다. 수류 시험 장치에서 실험의 On/OFF 용도로 볼 밸브를 사용하였기 때문에 완전 개방 조건에서 실험을 수행하였다. 내부면적 비는 1이므로 볼 밸브에서의 압력손실은 Eq. 7에 따라 Eq. 12로 모델링 가능하다. 배관과 마찬가지로 PT1과 PT2 사이에 터빈유량계가 존재하기 때문에 터빈유량계의 압력손실을 고려하여 볼밸브의 손실계수를 도출하였다. 볼밸브의 손실계수는 실험 데이터로부터 1.89×103으로 도출되었다. 64케이스에 대하여 실험을 수행하여 시뮬레이션 결과와 유량에 대한 압력손실을 비교한 것을 Fig. 8에 나타내었다. PT1과 PT2의 차이의 경우 최대 상대표준편차는 4.05%이며 결과적으로 최대 6.43%, 평균 3.31%의 오차를 보였다.
| (12) |
니들밸브
니들밸브는 회전축을 조절하여 실험의 유량을 조절하는 역할로 0, 1, 2, 3, 3.25, 3.5회전에 대하여 시뮬레이션 결과와 실험 결과를 비교한 것을 Fig. 9에 나타내었다. 니들밸브 1은 PT4와 PT5에서 측정된 압력의 차이를, 니들밸브 2는 PT5와 PT6에서 측정된 압력의 차이를 실험에서 측정된 압력강하로 정의하였다. 마찬가지로 유량에 대한 압력강하를 검증하였으며 회전수와 유량에 대한 차압 경험식에 도출한 실험계수를 적용하여 압력강하를 예측하였다. 도출된 실험계수는 니들 밸브 1의 경우 α=5.91×10-4, β=1.64×10-3, γ=1.52×10-3, δ=6.94×10-5이며, 니들 밸브 2의 경우 α=3.65×10-4, β=1.26×10-3, γ=1.41×10-3, δ=7.45×10-5이다. 모델링 검증을 위해 니들 밸브 1과 니들 밸브 2에 대하여 42케이스의 실험을 수행하였다. 니들밸브 1에 해당하는 PT4와 PT5의 차이의 최대 상대 표준편차는 3.15%이며 니들밸브 2에 해당하는 PT5와 PT6는 0.78%이다. 결과적으로 니들 밸브 1의 경우 최대 11.1%의 오차, 평균 2.74%의 오차를 보였고 니들 밸브 2의 경우 최대 6.89%, 평균 2.68%의 오차를 보였다.
펌프
펌프는 추진제를 모사한 매질을 가압하는 장치로 본 연구에서는 성능 곡선을 사용하여 모델링하였다. 성능 곡선의 실험계수는 type Ⅰ의 경우 ε=-2.48×105, ζ=-1.76×106, κ=5.88×105이며, type Ⅱ의 경우 ε=-1.59×106, ζ=-1.76×106, κ=8.23×105으로 도출되었다. 유량에 대한 압력 증가를 type Ⅰ은 121케이스, type Ⅱ는 64케이스의 실험을 통해 검증하였으며 PT3와 PT2에서 측정된 압력의 차이를 압력 증가로 정의하였다. 최대 상대표준편차는 1.11%이며 Fig. 10은 시뮬레이션 결과와 실험 결과와의 비교 검증을 나타낸다. type Ⅰ의 경우 최대 1.05%, 평균 0.49%의 오차를 보였으며 type Ⅱ의 경우 최대 1.39%, 평균 0.74%의 오차를 보였다.
실험 결과의 정확도가 시뮬레이션 오차에 미치는 영향을 확인하기 위해 각 구성요소에 대한 검증 결과를 Table 1에 정리하였다. 동일 조건에서 수행한 3개의 실험 데이터의 상대표준편차(RSD, Relative Standard Deviation)의 최댓값과 시뮬레이션과 실험 데이터간의 평균오차 및 최대오차를 비교하였다. 결과적으로 배관과 니들밸브 2를 제외한 구성요소에 대하여 최대 상대표준편차가 평균오차보다 크고 최대오차보다는 작은 결과를 보였다. 실험 데이터의 편차가 평균 오차 및 최대 오차와 비교하였을 때 무시 가능한 작은 값을 가지지 않기 때문에 이를 통해 필수적으로 발생하는 실험 데이터의 편차가 시뮬레이션의 정확도 평가에 상당한 영향을 주었을 것이라 사료된다.
3. 요소설계 프로그램 개발 및 검증
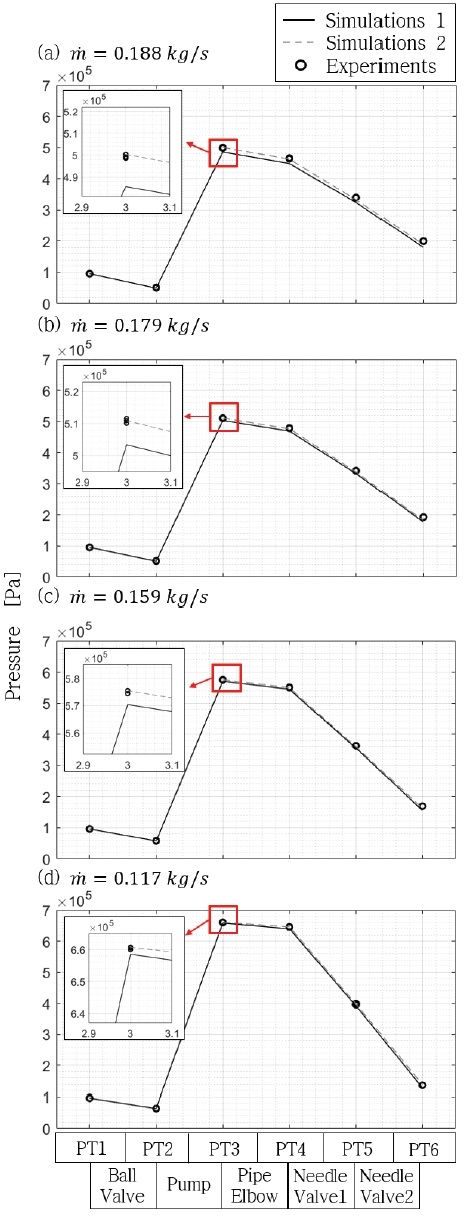
선행연구로부터 검증된 전기펌프 사이클의 액체로켓엔진 요소설계 프로그램[10]을 이용하여 소형 액체로켓엔진을 가정하는 수류 시험 장치모사 프로그램을 개발하였다. 상용 프로그램 matlab 기반 simulink로 수류 시험 장치 모사 프로그램을 작성하였으며 simulink 모델은 Fig. 11에 나타내었다. 2.2절에서 검증한 요소설계 모델링 기법을 각 단위모듈에 적용하여 공급계 전체 시스템 해석을 목적으로 하였다. 실험으로부터 도출된 각 구성요소의 실험계수는 Table 2에 정리하였다. 펌프는 type Ⅱ 상용펌프를 기준으로 하였고 프로그램 내에 니들 밸브와 펌프의 성능 곡선을 내장하였다. 프로그램 검증을 위해 4 케이스의 유량 조건에 대하여 시뮬레이션과 수류 실험 결과를 Fig. 12에 비교하였다. 시뮬레이션 결과는 Simulations 1이며 수류 실험 결과는 Experiments이다. Fig. 12 (a)는 유량이 0.188 kg/s 조건, (b)는 0.179 kg/s 조건, (c)는 0.159 kg/s 조건, (d)는 0.117 kg/s 조건이다. x축은 각 구성요소 사이의 지점으로 Fig. 6의 수류 시험 장치의 압력 측정 지점과 동일하게 정의하였다. y축은 해석 및 측정된 절대압력이며 실험 데이터의 편차를 확인하기 위해 동일한 조건의 3회의 실험 데이터를 도시하였다. 또한 3회의 실험 데이터의 시각적 구분을 위해 모든 유량조건에서 PT3 지점에서의 확대 그림을 같이 나타내었다. 유량 조건에 대한 각 지점의 오차를 Table 3에 정리하였으며 고유량 범위일수록 모든 지점에서 전반적으로 오차가 높아지는 경향성을 보인다. 이는 (1)압력손실이 유량의 제곱에 비례하기 때문에 유량이 증가함에 따라 압력에 대한 오차가 증가하여 나타나는 경향성 또는 (2)저 유량 모사가 목적인 시험 장치에 대하여 넓은 범위에 대해 실험을 수행하였기 때문에 나타나는 경향성이 원인이라 분석된다. 유량이 0.188 kg/s 조건의 경우 PT6에서 약 10%의 오차를 보이는데 이는 PT3 지점에서 발생한 오차의 절대적인 값이 이후 지점에서 보상되지 않고 그대로 유지되기 때문이다. 특히 펌프와 같은 가압시스템의 경우 압력의 절대적인 값이 크기 때문에 작은 오차율이라도 차이 값이 그대로 유지되어 후단의 상대적으로 절대적인 값이 작은 압력손실 요소들의 오차율을 크게 증가시킬 수 있다. 만약 펌프(PT3)에서의 오차가 없었을 경우를 가정하여 Fig. 12에 Simulations 2로 해석 결과를 나타내었다. PT3의 값은 실험 데이터를 사용하였으며 이후 PT4, PT5, PT6의 구성요소 모델링은 Simulation 1과 동일하게 하였다. 유량 조건에 대한 각 지점의 오차를 Table 3 하단에 제시하였으며 결과적으로 Simulation 1보다 모든 지점 및 유량에서 오차가 감소한 것을 확인할 수 있다. 따라서 구성요소 단위의 검증과 별개로 전체 시스템에 대한 검증이 필요함과 특히 펌프와 같은 가압시스템의 정확도가 중요함을 본 결과를 통해 제시할 수 있다. 가압시스템의 정확도 향상 방안 연구, 특정 구성요소에서 발생한 오차가 후단의 구성요소에 미치는 영향 최소화 연구 또는 시스템의 요구 정확도를 만족시키기 위한 정량적 평가를 통한 각 구성요소의 정확도 관리전략에 대한 추가적인 연구가 필요할 것으로 보인다.
4. 결 론
본 논문에서는 유량 0.1∼0.2 kg/s 수준의 전기펌프 사이클을 가정한 소형 액체로켓엔진의 각 구성요소에 대한 모델링 기법을 제시하고 모사 수류시험 장치를 통한 실험결과로부터 구성요소 모델링 기법을 검증하였다. 검증한 구성요소로는 유체저항요소인 배관, 곡관, 터빈유량계, 볼밸브 그리고 니들 밸브가 있으며 가압 시스템으로는 펌프가 있다. 실험 데이터로부터 볼밸브, 니들밸브, 펌프, 터빈유량계의 실험계수를 도출하는 방법을 정리하였으며 이를 통해 수류 시험 장치에 사용된 상용품의 실험계수를 제시하였다. 배관과 곡관은 이론 및 경험식으로부터 손실계수를 예측하였다. 구성요소단위로 모델링 기법을 검증하였으며 실험 데이터의 상대표준편차가 모델링 정확도에 상당부분 영향을 미침을 확인하였다. 시스템 단위 검증을 위해 시뮬레이션 정확도를 4가지의 유량조건에 대하여 각 구성요소의 오차를 실험 결과와 비교하였다. 전체 시스템의 경우 단위구성요소 시뮬레이션과 달리 이전 구성요소에서 발생한 오차가 그대로 유지되어 후단 구성요소의 오차를 증가시키는 것을 확인하였다. 따라서 절대적인 값이 큰 가압시스템의 높은 정확도 확보는 시스템의 전반적인 정확도 향상에 요구되는 부분이다. 또한 각 구성요소에서의 정확도와 시스템의 정확도와의 관계를 도출하여 특정 시스템 정확도를 만족시키기 위한 각 구성요소의 정확도 관리 전략을 제시하는 것이 필요하며 추후 연구를 통해 보완하고자 한다.
Nomenclature
| A : | Area (m2) |
| B : | Impeller blade angle (degree) |
| D : | Diameter (m) |
| e : | Roughness (m) |
| f : | Friction coefficient |
| g : | Gravitational acceleration (m/s2) |
| H : | Pump exit height (m) |
| K : | Loss coefficient |
| L : | Length (m) |
| N : | Number of experiments |
| NV : | Needle valve |
| P : | Pressure (Pa) |
| PT : | Pressure transducer |
| R : | Ball valve radius (m) |
| Re : | Reynolds number |
| Tr : | Turn ratio |
| xi : | Experimental value |
| X : | Number of needle valve turn |
| v : | Fluid flow average velocity (m/s) |
| m : | Mean of experimental data |
| : | Mass flow rate (kg/s) |
| Ω : | Rotation speed (rad/s) |
| θ : | Band angle (degree) |
| ρ : | Density (kg/m3) |
| τ : | Ball valve position (%) |
Subscripts
| c : | Critical |
| in : | Inlet |
| out : | Outlet |
| t : | Total |
| ball : | Ball valve |
| FM : | Flow meter |
Acknowledgments
본 연구는 방위사업청과 국방과학연구소의 지원으로 수행되었으며 이에 감사드립니다. (계약번호 UD180046GD).
References
-
Juyeon, L., Seung-Won, C., Donghui, H., Wonkeun, K., Jaecheong, L., Hwanil, H., Tae-Seong, R. and Hyoung Jin, L., “Research trend analysis on modeling and simulation of liquid propellant supply system,” Journal of the Korean Society of Propulsion Engineers, Vol. 23, No. 6, pp. 39-50, 2019.
[https://doi.org/10.6108/KSPE.2019.23.6.039]

-
Binder, M., “An RL10A-3-3A rocket engine model using the Rocket Engine Transient Simulator(ROCETS) software,” 29th Joint Propulsion Conference and Exhibit, Monterey, CA, p. 2357, Jun. 1993.
[https://doi.org/10.2514/6.1993-2357]

- Kimura, T., Takahashi, M., Wakamatsu, Y., Hasegawa, K., Yamanishi, N. and Osada, A., “Rocket Engine Dynamic Simulator (REDS),” JAXA-1349-1113, 2004.
- Moral, J., Perez Vara, R., Steelant, J. and De Rosa, M., “ESPSS simulation platform,” Space Propulsion, May 2010.
-
Wonkeun, K., Jaecheong, L., Hyoungjin, L., Tae-Seong, R. and Hwanil, H., “Overseas research trends of an electric-pump cycle for application in upper-stage propulsion systems,” Journal of the Korean Society of Propulsion Engineers, Vol. 24, No. 1, pp. 64-77, 2020.
[https://doi.org/10.6108/KSPE.2020.24.1.064]

-
Spiller, D., Stabile, A. and Lentini, D., “Design and testing of a demonstrator electric-pump feed system for liquid propellant rocket engines,” Aerotecnica Missili & Spazio, Vol. 92, No. 3-4, pp. 123-130, 2013.
[https://doi.org/10.1007/BF03404670]

-
Talik, J., Luce, J., Froelich, J.C., Shang, M., Rasheed, R.M. and Roland, J.S., “Electric propellant feed-system for amateur class high altitude sounding rockets,” AIAA SPACE and Astronautics Forum and Exposition, Orlando, F.L., U.S.A., AIAA 2017-5132, Sep. 2017.
[https://doi.org/10.2514/6.2017-5132]

- Taeho, K., Yushin, J. and Woongsup, Yoon., “Modeling of the liquid rocket engine transients,” Journal of the Korean Society of Propulsion Engineers, Vol. 15, No. 1, pp. 45-54, 2011.
- Moody, F., “Friction factors for pipe flow,“ Transactions of the A.S.M.E., Vol. 66, pp. 671-684, 1944.
- Juyeon, L., Tae-Seong, R., Hwanil, H. and Hyoung Jin, L., “Performance analysis and mass estimation of a small-sized liquid rocket engine with electric-pump cycle,” International Journal of Aeronautical and Space Sciences, Accepted.
- Taekyu, L., Sangbok, L. and Tae-Seong, R., “Pipe network analysis for liquid rocket engine with gas-generator cycle,” 2012 KSPE Spring Conference, Korea, pp. 52-57, May 2012.
- Lozano-Tovar, P.C., “Dynamic models for liquid rocket engine with health monitoring application,” M.S. Thesis, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, 1998.
- Lobanoff, S. and Robert, R., “Centrifugal pumps: design and application,“ Elsevier, 2013.
- Wonkeun, K., Jaecheong, L. and Hwanil, H., “Fundamental experimental setup of an electric-pump cycle for space propulsion systems,” 53rd KSPE Fall Conference, Busan, Korea, pp. 59-60, Nov. 2019.