고온 환경에서 무한 튜브 검출기의 적용에 관한 타당성 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
액체로켓엔진 연소기와 가스터빈에 사용되는 동압센서는 고온의 환경에서 작동되어야 하므로 보통 리세스 마운트로 체결된다. 리세스 마운트 방식은 고온의 연소가스로부터 센서를 보호할 수 있으나 튜브-캐비티 시스템에서 튜브 공진이 발생한다. 본 연구에서는 이를 줄이기 위해 ITP를 도입하였다. 과거 문헌에서 제안한 ITP 모델을 실험 결과와 검증하고 응답특성을 분석하였다. 이 모델을 이용하여 기하학적 형상과 물리량을 변화시켜 주파수 응답 분포를 변화시킴으로써 ITP를 설계하기 위한 가이드라인을 제안하였다.
Abstract
Dynamic pressure sensor used in liquid rocket engine combustor and gas turbine is recess-mounted usually because it should work in high temperature environment. Although recess-mounted method can protect it from combustion gas in high temperature, tube resonance occurs in a tube-cavity system. To reduce it, the infinite tube probe(ITP) was introduced in this study. The ITP model suggested in previous literature was validated with experimental data and frequency response characteristics were analyzed. Guidelines for designing the ITP were suggested as frequency response profiles varied with geometric information and physical properties using this model.
Keywords:
Infinite Tube Probes, Natural Frequency, Pressure Transducer키워드:
무한튜브검출기, 고유주파수, 압력센서1. 서 론
1.1 연구 배경 및 목적
지금까지 가스터빈과 같이 1000 K 수준의 고온에서 동압을 측정하기 위한 센서가 개발되어 왔지만 아직도 로켓과 같은 3000 K이상의 초고온의 연소시스템에서 동압을 측정하는 것은 어려운 일이다.
국내에서 로켓 연소기에 사용되고 있는 동압 센서는 PCB사의 123A22와 구조적으로 보완된 123B22[1]를 사용 중이고 센서의 열손상을 방지하기 위해 냉각수와 헬륨을 공급하는 방식이다. 냉각수를 사용할 경우 물의 끓는점으로 인해 저주파 노이즈 발생의 우려가 있고 헬륨을 사용할 경우 연소장에 영향을 줄 수 있기 때문에 문제가 될 수 있다. 한편, 유럽 DLR의 연구그룹에서 발표한 연구 문헌[2,3]에서는 Kistler사의 6021A 시리즈의 최대 700 ℃까지 견딜 수 있는 고온용 센서[4]를 사용하고 있다. 이들 그룹은 센서를 플러쉬 마운트로 연결하고 열 손상되기 전까지 사용한다. 그러나 국내에서 고가의 센서를 플러쉬로 연결하여 열손상이 될 때마다 폐기하는 것은 어려운 일이다. 이 때문에 냉각수와 헬륨을 사용하지 않는 센서를 이용하여 공진 문제를 최소화하여 동압을 측정하는 방법을 찾는 것은 중요하다고 볼 수 있다.
현재까지 제안된 동압측정을 위해 센서를 장착하는 방법은 크게 두 가지로 나눌 수 있다. 하나는 플러쉬 마운트(Flush Mount)로 연결해서 측정하는 방법이고 다른 하나는 리세스 마운트(Recess Mount)를 두어 측정하는 방법이다. 플러쉬 타입의 경우 내부 유도관이 없기 때문에 음향학적인 문제로부터 자유롭다. 그러나 리세스 방식의 경우 고온의 연소가스로부터 센서를 보호할 수는 있으나 음향학적인 공진 문제가 대두된다.
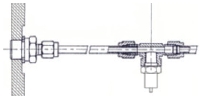
한편, 이와는 달리 무한한 배관을 이용하는 방법은 배관 내부에 진행파만을 형성하여 신호의 왜곡없이 측정을 가능하게 한다. 이를 Infinite line pressure probe[5] 혹은 Semi Infinite Line Tube Pressure Probe[6] 방법으로 알려져 있다. 이러한 방법은 가스터빈, 로켓과 같은 고온의 환경에서 작동하는 시스템에서 주로 사용된다[7-11]. 이 장치는 연소기로부터 나오는 유도관의 중간에 T자형으로 분기하여 수직 분기점은 동압 센서를 연결하고 유입구와 평행인 출구 쪽에는 무한대에 가까운 유한한 튜브를 연결한다. 이 유한한 튜브의 끝단은 캡으로 막거나 혹은 개방되는 구조를 가지고 있다. 물리적으로 보면 연소기 내부에서 발생한 압력파는 유도관을 따라 긴 튜브의 끝단까지 전파하면서 센서면을 통과하고 점성에 의해 압력파는 사라진다. 이때 튜브의 끝단에서 발생하는 반사파는 소산되므로 이론적으로는 존재하지 않는다[6]. 따라서 Infinite Tube Probe(이하 ITP로 지칭함)도 리세스 방식의 한 방법으로 음향학적 공진문제를 해결하는 방법으로 볼 수 있다.
ITP의 설계의 핵심은 이론적으로 넓은 주파수 도메인상에서 반사파를 최소화하는 것이다. 이는 마치 무 반향실에서 소음이 발생하면 진행파만 존재하고 반사파가 없기 때문에 울림이 없는 상태와 비슷하다[12]. 배관 내부에서 반사파를 최소화하는 메커니즘은 파동의 감쇠(Attenuation)와 관련이 있다. 이 매커니즘은 크게 두 가지로 나눌 수 있다. 첫번째는 유동장이 없는 상황에서 배관의 직경이 작을 경우 경계층에서의 음향 감쇠가 나타난다. 두번째는 유체에서의 점성과 열전도와 관련된 감쇠가 있다. 이들 원인들 중 배관 경계층에서의 음향 감쇠가 지배적이다[13].
아직까지 국내에서는 ITP에 대해 가스터빈 분야 등에서 일부 쓰이고 있는 것으로 보이나 이에 대한 국내 기술적인 문헌을 찾기 어렵다. 따라서 본 연구의 목적은 액체로켓엔진 연소기를 위한 기술적인 사전 검토이다. 이를 위해 먼저 ITP에 관한 과거 문헌 검토를 통해 물리적인 현상을 이해하였다. 또한 최근 검증된 Boyle의 이론식을 바탕으로 기본 설계를 위한 계산 코드를 만들었고 그들의 시험 결과와 비교를 통해 계산코드를 검증하였다.
이와 같은 이론식을 이용하여 물리적인 현상을 이해하는 것은 기본 설계를 위해 중요하기 때문에 본 연구에서는 변수 조정을 통한 응답 특성을 모사하고 분석함으로써 물리적인 현상을 이해하고자 하였다.
기본적으로 연구자가 요구하는 응답특성의 범위는 서로 다르고 기하학적 형상의 요구사항도 다르기 때문에 변수 조정을 통한 응답 특성의 경향성 파악은 연구자에게 설계를 위한 유용한 정보를 제공한다. 마지막으로 앞서 변수 조정과 응답 특성의 경향성에 관한 분석 결과를 바탕으로 액체로켓엔진 연소기를 대상으로 ITP의 기본 설계의 사례를 제시하였다.
1.2 ITP에 관한 문헌 조사
이미 Kim & Choi[14]는 HR(Helmholtz Resonator) 모델과 공압 모델(Pneumatic Model)에 대해 비교 분석한 결과를 제시하였다. ITP는 진행파가 튜브의 끝단 경계점에서 반사되지 않도록 하기 위해 긴 배관이 되도록 설계하므로 이 현상을 이해하기 위해서는 공압 모델이 적용되어야 한다.
공압 배관에서 압력의 감쇠현상의 이론적인 규명은 1949년 Taback[15]에 의해 이루어졌다. 그의 모델은 전력시스템과 공압시스템의 수학적인 상사성에 기반하여 모델이 만들어졌고 실험적으로 검증되었다. 이후 1950년에 Iberall[16]이 이론적인 모델을 제시하였다. 그의 모델은 단순화된 유체역학적 지배방정식을 이용하여 유도되었다.
1955년 Blackshear 등[17]은 screeching 연소 매커니즘을 이해하기 위한 계측 장비를 개발하기 위해 ITP에 관한 연구를 처음으로 진행하였다. 실험 결과로부터 튜브 내부에서 발생하는 높은 진폭의 비선형적인 음향 감쇠를 설명하는 이론을 제안하였다. 그러나 감쇠율을 이용하는 방법으로 완전한 이론적인 ITP 기술은 아니었다. 당시 Iberall이 제안했던 수학적 모델을 바로 적용하지는 않았던 것으로 보인다.
Iberall이 제안한 수학적 모델을 기반으로 1965년 Bergh & Tijdeman[18]은 튜브와 캐비티(Cavity)로 이루어진 N개의 세트(Set)에 대한 주파수 응답 모델을 개발하였다. 그들의 모델과 실험치의 비교에서 대부분은 좋은 결과를 보여주었지만 일부 불일치한 경우도 있었다.
이후 1984년 Englund & Richards[8]는 Bergh & Tijdeman의 모델을 이용하여 ITP의 주파수 응답을 계산하였다. 그들은 블레이드 wake를 계측하기 위해 ITP를 이용하여 계측하였다. 그들이 설계한 ITP는 가급적 센서를 플러쉬 마운트 체결을 위해 평평한 타원형 검출기(Flat-oval Probe)로 설계하였다. 주파수 응답 특성을 보면 저주파수에서 진폭비가 1에 가깝고 0.9∼1.0 kHz까지 감쇠한다. 저주파수에서 진폭비의 진동은 배관의 끝단에서 반사파 때문에 나타나는 현상이다. 5 kHz 이상에서 진폭비의 진동은 센서의 탭 부피와 배관 끝단에서의 반사하는 압력파 때문에 나타난다고 하였다.
1989년 Salikuddin등[9]은 ITP를 개발하여 고온환경에서 고주파 계측을 수행하였고 기존 냉각 방식의 센서의 계측 결과와 비교하였다. 그에 의하면 당시까지 몇몇 문헌[17,19,20]으로부터 최대 5 kHz까지 ITP를 사용해 왔고 이 한계는 당시 고주파 발생기가 없었기 때문으로 보았다. Salikuddin등은 특별히 제작된 고주파 발생기를 이용하여 80 kHz까지 ITP를 시험하였다. 그들은 원형관(Circular Tube)과 납작한 타원 형태의 튜브(Cross-section Flattened Oval Tube)를 사용한 배관 단면 형태의 변화, 센서와 튜브 사이의 부피 변화, 온도의 변화 등을 SPL(Sound Pressure Level) 분포를 통해 조사하였다.
2005년도 Ferrara등[13]은 충격파관과 음향 스피커를 이용하여 ITP의 주파수 응답 특성을 결정하였다. 2007년 Zinn & Herbermann[12]는 가스터빈의 고온환경에서 동압을 계측하기 위해 CTP(Cavity Type Probe)와 ITP를 비교 시험하였다. 여기서는 전자의 경우가 더 높은 주파수 범위에서 계측할 수 있는 것으로 보고하였다.
2007년 Wegner등[7]은 짧은 튜브 압력 검출기(Short Tube Pressure Probe)와 ITP의 성능을 마이크로 터빈을 대상으로 비교하였다. 연료/산화제의 혼합기의 밀도 변화에 따라 온도는 변화하고 이에 따라 음향의 임피던스가 변화한다. 그러므로 갑작스런 온도 기울기 변화는 반사파를 만들어내고 이에 따라 음향 증폭을 발생시킬 수 있다고 하였다.
이후 ITP와 관련하여 많지는 않지만 조금씩 관심을 갖고 접근하는 연구자들이 존재하고 있었고 2018년 Gejji등[21]은 폭굉파(Detonation Wave)에 대해 ITP, 플러쉬, 리세스 마운트를 한번에 설치해서 계측을 수행했다. 그들은 ITP에서 플러쉬 마운트 대비 36∼54%, 리세스에 대해 5∼28%의 진폭 감쇠가 발생하였고 시간 지연이 발생했다고 보고하였다.
2018년 Naples등[11]은 RDE(Rotating Detonation Engine)에서 ITP를 충격파관(Shock Tube)를 대상으로 실험하였다. ITP는 실제 압력 대비 70∼85%의 값을 보여주었다. 압력 센서의 캐비티 부피가 신호 지연 효과가 크게 나타났다. 따라서 이 부피를 최소화하는 것이 중요하다고 하였다. 튜브 직경은 1.78, 3.35, 4.93 mm를 조사하였고 1.78 mm과 4.93 mm가 강한 충격파의 반사파를 보이는 것으로 나타났다.
그들은 2019년 후속 연구[6]로 직경, 센서 리세스, 센서 마운트 방법, 가스화학종, 엔진 작동 주파수를 변화하여 검출기의 응답특성을 조사하였다. ITP의 경우 플러쉬 마운트 센서에 비해 50∼90%의 감쇠가 발생하였고 모든 ITP가 20 kHz를 넘어서면서 PSD(Power Spectral Density)가 줄어드는 경향을 보였다. 여기서도 그들은 센서와 배관사이 캐비티의 부피가 중요하다고 하였다.
2018년 Boyle 등[22]은 항공기의 터보팬의 소음 저감에 관심을 갖고 연구를 진행하였다. 그들은 노이즈 계측을 위해 터보팬 후단에 ITP를 장착하여 압력 변동을 측정하였다. 2019년 그들은 ITP에 대한 상세한 후속연구 결과[23]를 발표하였다. 그들은 1/4 인치(inch)와 1/8 인치의 배관에 대해 분기되어 긴 튜브와 연결되는 포트를 캡으로 막고 응답 특성을 계측하였다. 그리고 Bergh & Tijdeman의 식을 변형한 응답함수 식을 이용하였고 예측치를 실험값과 비교하여 좋은 결과를 보여주었다.
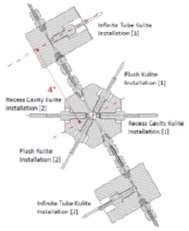
지금까지 언급한 과거 ITP의 응용 사례 및 형상을 Table 1에 정리하였다. 대부분 충격파관에 대해 응용연구가 진행되었고 온도센서가 연결되는 마운트를 기준으로 주로 피팅을 사용하여 연결되는 구조를 갖고 있다.
2. 주파수 응답 모델 및 매개변수 선정
2.1 주파수 응답 모델
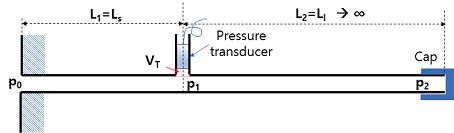
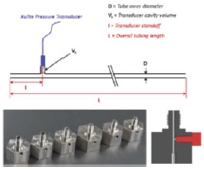
ITP를 설계하기 위해서는 Fig. 1에 나타낸 개략도에서 알 수 있듯이 두 가지 구속조건인 기하학적인 길이와 배관 내부를 구성하는 매질이 존재하고 이에 대한 가이드라인이 필요하다. 기하학적인 조건에는 배관의 직경 d와 연소실에서의 소음원(p0)으로부터 센서까지 길이 LS의 설정이 있고 이론적으로 센서로부터 긴 튜브끝단까지 길이 LI는 무한대이어야 한다. 그러나 현실은 유한한 길이를 가져도 무한대와 동일한 성능을 보이는지에 대해 검토가 이루어져야 한다. 매질의 특성에는 점성, 열전도, 밀도 등이 있고 물리량으로 파생되는 음속이 이에 해당한다. 이와 같은 설계 변수의 가이드라인을 얻기 위해서는 정밀한 물리 모델이 필요하다.
ITP의 수학적인 모델은 Iberall[16]과 Bergh & Tijdeman[18] 그리고 Samuelson[19]의 이론적인 작업에 기반한다. 이후 Boyle[23]은 이들 모델을 기반으로 실험적으로 간단히 적용할 수 있는 모델을 제안하였다. Boyle이 최종 제안한 ITP 모델은 다음과 같다.
| (1) |
| (2) |
여기서 기하학적인 정보로 각 구간별 길이 조건과 배관의 직경이 포함된다. 그리고 센서와 배관 사이의 부피가 전달함수를 결정하는 변수로 포함되어 있다. α는 shear wavenumber로 다음의 Eq. 3과 같이 무차원 변수로 정의한다.
| (3) |
수학적인 의미는 관성효과와 점성효과의 비율을 의미하고 비정상 Reynolds 수로 간주한다. 물리적으로는 배관 직경과 경계층 두께의 비율을 의미한다[24]. Eq. 1과 2에서 Φ는 전파상수, nT는 polytropic exponent를 의미한다[18,23].
반사계수(Reflection Coefficient) Q는 배관 끝단의 경계조건으로 캡으로 막혔을 경우 Q=1이고 열린 상태이면 Q=-1이다. 만일 무한대이면 Q=0으로 표현한다. 본 연구에서 검토된 LI는 길이가 유한하고 끝단은 캡으로 막는 것이 일반적이기 때문에 검증을 제외한 모든 계산 조건(Table 2)에서 고려된 Q는 1로 고정하였다. 이와 같은 식은 근본적으로 Bergh & Tijdeman의 식으로부터 비롯되었기 때문에 ITP 내부의 온도(T)가 일정하다는 모델이 성립하는 가정은 동일하다.
2.2 매개변수 선정 및 계산 조건
Boyle이 제안한 모델에 대해 복소수 계산을 위한 검증된 프로그램을 작성하였고 고온의 연소기에 적용하기 위해 여러 변수를 조정하여 ITP 적용 타당성을 검토하고자 하였다. Boyle의 연구에서 사용된 모델은 근본적으로 Bergh & Tijdeman의 결과를 바탕으로 유도되었기 때문에 구속조건도 모두 동일하다. 즉 벽면은 일정한 온도를 유지해야 하고 매질의 온도 변화는 없다. 그러나 실제로는 연소실의 고온 가스가 ITP 배관을 타고 나오면서 주변의 대기 온도와 열전달이 일어나므로 ITP 끝단으로 갈수록 온도는 하강하여 어느 지점에서는 대기 온도와 평형상태에 이를 것이다.
본 연구에서 사용된 모델에서는 이와 같은 상황을 모사하지 못하므로 여러 온도 변수를 고려하여 ITP 설계에 고려해야 한다. 매개 변수 조정에 의한 주파수 응답 특성의 변화를 분석하기 위해 선정된 변수는 총 5가지이다. LS와 LI의 효과는 이미 Boyle의 결과로부터 잘 알려졌지만 온도의 변화에 따른 결과는 알려지지 않는 관계로 총 5가지 변수를 모두 선정하여 케이스 연구를 진행하여 종합적으로 평가하였다(Table 2).
대형 가스터빈과 같은 연소기는 다소 큰 직경의 ITP를 사용하고 있으나 현재 개발 중인 로켓 연소기는 주로 정압센서 계측을 위해 1/8 인치와 1/4 인치의 튜브 규격치를 사용하기 때문에 Table 2의 #5와 같이 이들 두 가지를 선택하였다.
3. 계산 결과
3.1 프로그램 검증결과
Fig. 2는 프로그램 검증을 위해 Boyle의 실험 결과와 계산결과를 비교 분석하였다. Fig. 2 (1A, 1B)는 ITP에서 LI의 긴 튜브를 제외하고 캡(Cap)을 씌우지 않은 경우(Q=-1)에 대한 주파수 응답 특성과 위상 분포를 보여주고 있고 Boyle이 제안한 예측식이 실험치를 잘 따르는 것을 확인할 수 있다.
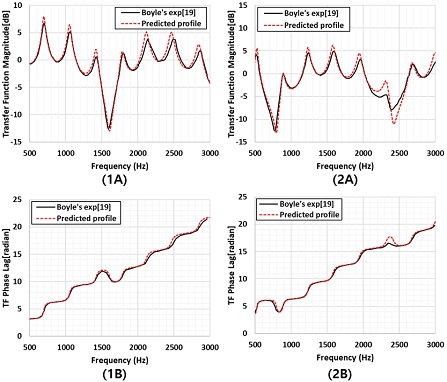
Comparison of experimental(solid line) and analytic models(dashed line) for the uncapped(1A, 1B) and capped ITP(2A, 2B)[23].
Fig.2 (2A, 2B)은 LI의 긴 튜브를 제외하고 캡을 씌운 경우(Q=1)에 대한 주파수 응답 특성과 위상분포를 실험적으로 보여주고 있고 이를 재현한 프로그램을 검증하여 좋은 결과를 보여주고 있다. 캡을 안 씌운 경우에 비해 캡을 씌운 경우가 2000 Hz 이상에서 모델 예측이 다소 떨어진다. Fig. 2의 결과는 Boyle의 연구 결과에서 캡까지 거리인 LI가 주어지지 않아 105 mm로 가정하여 계산한 결과이다. 캡으로 막아 캡의 공간에 의해 2 mm 정도 증가한다고 가정할 경우 정확도는 더 좋아진다. 본 연구에서는 Fig. 2를 개발된 코드의 검증 결과만으로 제시하였기 때문에 자세한 논의는 논외로 한다.
3.2 매개 변수 변화에 따른 전달함수와 위상의 변화
앞 절에서 실험치와 예측결과를 통해 모델의 예측 능력과 프로그램을 검증하였고 본 절에서는 각 변수의 조정을 통해 주파수 응답 특성의 변화와 위상 변화의 경향을 분석하였다. 예측 결과에 사용된 물리량은 모두 연소기 대상으로 CEA 계산[25]을 통해 얻은 물리량을 이용하여 계산에 활용하였다.
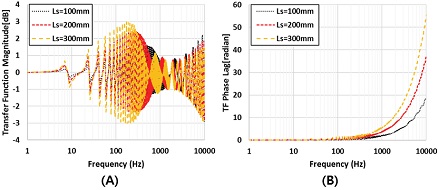
먼저, 센서와 인접한 LS의 변화에 따른 주파수 응답 특성을 분석하였다. LS는 실제 연소기에 내부 벽면 센서 포트로부터 외부에 도출된 튜브의 길이를 포함하여 ITP 센서 마운트까지 거리를 최소 100 mm로 예상되고 200 mm, 300 mm의 3가지 경우에 대해 분석을 수행하였다.
Fig. 3과 같이 주파수 응답의 진폭은 약 10 Hz 이하 저주파수에서 0 dB에서 시작하고 10 Hz 근처에서부터 진동이 발생한다. 10∼1000 Hz 사이의 주파수 응답 파형이 관찰되고 LS가 증가함에 따라 이 파형의 진폭 변동은 커지며 포락 파형(Envelope Wave)은 전체적으로 저주파수 대역으로 이동하는 경향을 보였다. 1000 Hz를 초과하면서 파형은 LS에 관계없이 증가하는 양상을 보인다.
Fig. 3 (B)의 위상 지연(Phase Lag)은 100 mm인 경우가 가장 낮게 분포하고 300 mm가 가장 높다. 고주파에서 나타나는 위상 지연 효과는 특성주파수 분석시에는 문제가 없지만 위상을 고려한 분석시에는 주의해야 한다. 따라서 LS는 가급적 하드웨어에 가깝게 위치하는 것이 위상 지연을 최소화할 수 있다.
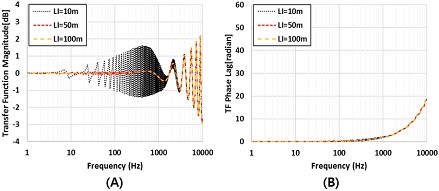
Fig. 4는 LI의 변화에 따른 주파수 응답 특성을 분석하였다. 10 m인 경우 10∼1000 Hz 사이 포락파와 함께 파형이 동시에 나타나지만 50 m, 100 m에서는 포락파만 관찰이 되고 파형은 사라졌다. 1000 Hz 이후 진동은 서로 다른 LI에 대해 큰 차이가 없었다. 따라서 10∼1000 Hz는 LI의 길이에 영향을 받는 것을 알 수 있다. 이와 같은 현상은 이미 Englund & Richards에 의해 보고되었고 그들은 튜브의 끝단에서 발생하는 반사파에 의해 나타난다고 하였다[8]. 이를 줄이기 위해서는 LS를 짧게 하는 것도 중요하지만 LI를 길게 설계해야 한다. 한편, LI의 변화에 따른 위상의 큰 변화는 관찰되지 않았다.
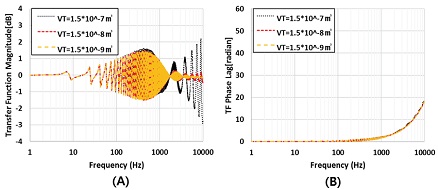
Fig. 5는 센서와 ITP의 튜브사이의 부피를 변화함에 따른 주파수 응답 특성을 관찰하였다. 10∼1000 Hz 구간에서는 VT의 변화에 따른 주파수 응답 파형의 큰 변화는 관찰되지 않았다. 하지만, 1000 Hz 이상에서 나타나는 파형은 부피가 작을수록 파형의 크기는 줄어든다. 이 결과도 Englund & Richards에 의해 보고되었고 그들의 경우 5 kHz 이상에서 이와 비슷한 현상을 보고하였다. 이 같은 현상의 원인은 탭 부피와 튜브의 끝단에서 반사된 압력파에 의해 일어난 것으로 밝히고 있다[8]. 위상의 경우 큰 변화는 관찰되지 않았다.
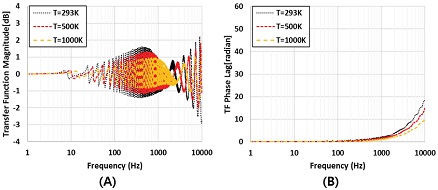
Fig. 6은 온도에 따른 주파수 응답 특성 결과를 보여준다. 온도가 증가함에 따라 10∼1000 Hz의 파형의 크기는 감소하는 경향을 보이고 1000 Hz 이상에서 관찰되는 파형의 크기는 모두 증가하는 양상을 보인다.
전체 포락 파형은 온도가 증가함에 따라 고주파수 측으로 이동하는 경향을 보인다. 위상의 경우 온도가 높을수록 낮은 위상 분포를 보인다.
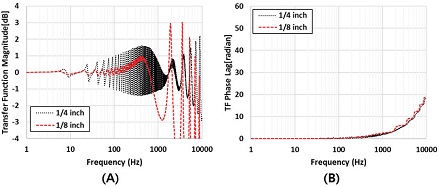
Fig. 7은 배관의 직경변화에 따른 응답특성 결과를 보여준다. 1/4 인치의 튜브는 1/8 인치 튜브에 비해 10∼1000 Hz 구간에서 큰 진동이 관찰된다. 1000 Hz 이상에서는 오히려 1/8 인치 튜브가 더 큰 진동폭을 보이고 있다. 위상은 1/8 인치 튜브의 고주파수 영역에서 진동이 다소 관찰이 되나 전체적인 경향은 비슷하다.
4. ITP 내부 온도의 사전 시험 결과 및 설계 사례
4.1 ITP 내부 온도의 사전 시험 결과
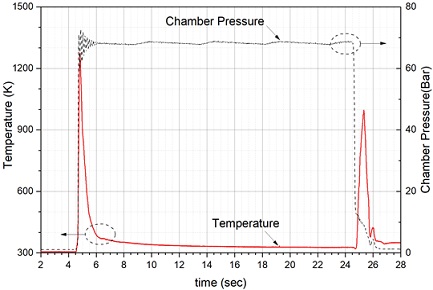
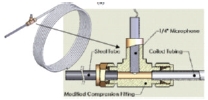
앞서 Boyle의 이론식은 Bergh & Tijdemnan의 연구결과에서 유도된 식을 포함하므로 유도관 내부의 온도는 일정한 것으로 가정하고 있다. ITP를 사용할 경우 ITP 내부의 온도는 연소실 온도보다 낮지만 고온으로 예상할 수 있다. 이를 확인하기 위해 Fig. 8과 같이 정압 유도관에 열전대(Thermocouple)를 장착하여 사전 테스트를 진행하였다. 유도관 끝단은 정압센서가 연결되어 막혀있다.
열전대는 연소실 외부 표면 기준 약 60 mm 이격시켜 설치하였고 이는 배관 간섭과 상용 튜브의 결합에 있어 최적이다. 따라서 앞서 수행한 변수 조정에 따른 연구 결과에서 LS = 100 mm의 이격 거리는 현실적이라 할 수 있다.
연소실 측면에 열전대를 설치하고 연소시험을 진행한 결과를 Fig. 9에 나타내었다. 연소압은 약 70 bar까지 상승하였고 정상 연소 구간에서 안정적으로 연소가 이루어졌다. 온도는 점화 구간인 4 – 6 초 사이에서 약 1270 K까지 상승하였다가 정상 연소 구간 시작 시점인 6 초에 도달하면서 온도는 급격하게 감소한다. 이는 점화초기 생성된 연소가스가 정압 유도관으로 유입이 된 후 유도관 반대쪽은 정압 센서와 온도센서로 막혀있기 때문에 더 이상 진행하지 못하고 정체된 것으로 보인다. 따라서 유도관 내부 온도는 정상 연소구간에 도달하면서 급격하게 떨어져서 약 326 K에 이르게 된다. 마지막으로 연소 종료구간에서 발생하는 충격에 의해 연소가스가 유도관으로 다시 유입이 되면서 온도는 다시 급격하게 상승했다가 떨어지는 경향을 보인다.
이와 같이 정상 연소구간에서 연소실 내부는 고온이지만 60 mm 정도 이격 거리를 둘 경우 거의 상온에 근접할 정도로 상당히 낮은 온도 분포를 보인다. 이 때문에 ITP를 실제 적용할 때 ITP의 내부 온도는 연소실 내부 온도보다 상당히 낮을 것으로 예상할 수 있다.
4.2 액체로켓엔진 연소기 기준 계산 결과 분석
앞서 ITP 설계 모델을 이용하여 변수를 조정함으로써 응답 특성을 비교하였다. 이를 통해 기하학적 형상 변경의 가이드 라인을 제시하였다.
정리하면, LS는 가급적 작아야 하고 LI는 반사파를 줄이기 위해 길게 설계해야 한다. 그리고 센서와 튜브사이의 부피는 최대한 줄여야 한다. 이러한 가이드 라인은 관찰하고자 하는 주파수 범위에 따라 응답 특성을 다르게 설계해야 하므로 설계 방향성만을 제시할 수 있다.
본 절에서는 각 변수 변화에 따른 주파수 응답 특성과 위상의 경향을 분석하고 설계 변수를 조정하여 ITP를 설계한 예를 제시하였다. 로켓 엔진 연소기의 경우 1/4, 1/8 인치 튜브를 주로 사용하고 최대 10 kHz까지 주파수 분석을 수행하고 있다. 즉, 응답 특성은 10 kHz까지 0 dB 근처에 있어야 한다.
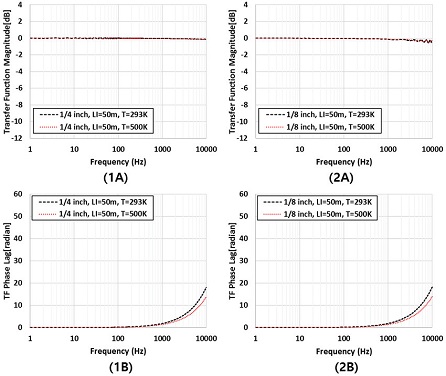
앞서 변수 조정을 통한 응답 특성의 경향을 분석한 가이드라인을 기준으로 시행착오로 계산하였다. 1/4 인치 튜브를 기준으로 LS = 100 mm, LI = 50 m VT = 1.5☓10-9 m3의 기하학적 크기와 상온인 293 K와 500 K의 온도에 대한 계산 결과를 Fig. 10 (1A, 1B)에 나타냈다. 앞서 사전 시험 결과 ITP의 내부 온도가 400 K을 초과하지는 않을 것으로 예상되지만 기본 설계에서 변수 조정을 통해 응답특성 변화를 분석하는 것이 목적이므로 최대 500 K까지로 설정하고 결과를 검토하였다.
Fig. 10(1A, 1B)에 나타낸 응답특성에서 10∼1000 Hz의 진동은 미세하게 관찰이 되나 0 dB을 기준으로 거의 평평한 그래프를 보인다. 다만, 10 kHz 근처에서 음의 dB 영역으로 감소하는 경향을 보이나 그래프 상으로는 미미하다.
위상의 경우 10 kHz 기준 최대 20 라디안(Radian) 근처까지 관찰된다. 위상은 LS에 크게 영향을 받으므로 LS가 존재하는 한 불가피하게 나타나는 현상이다. 가스터빈과 같이 만일 능동 제어를 할 경우 시간 지연은 필연적이므로 이에 대한 적절한 대비책이 필요하다고 할 수 있다.
Fig. 10 (2A, 2B)과 같이 1/8 인치 튜브의 경우 전달함수와 위상을 직경을 제외하고 1/4 인치 튜브와 동일한 기하학적 정보를 바탕으로 계산하였다. 10 kHz에서 1/4 인치 튜브와는 다르게 1/8 인치 튜브의 경우 응답특성이 음의 dB 영역으로 더 많이 감소하는 경향을 보인다. 그러나 10 kHz에서 dB 감소를 감수할 경우 계측데이터에 미치는 영향은 적으리라 판단된다. 위상의 경우 1/4 인치에서 나타난 결과와 동일하다.
5. 결 론
본 연구에서는 ITP를 대상으로 Boyle의 모델을 이용하여 기하학적 변수와 온도 변화에 따른 응답특성을 분석하였다. 기하학적 정보로는 측정 대상 포트로부터 센서까지 길이 LS, 센서 포트에서 긴 튜브 끝단까지 LI와 센서 표면과 튜브 사이의 부피 VT, 튜브의 직경이 있다. 이와 함께 매질의 온도를 관찰하였다. Boyle의 모델은 실험 결과와 비교하여 타당한 결과를 보였고 이를 바탕으로 변수 조정을 통한 응답특성 변화를 관찰하였다.
그 결과 LS의 경우 하드웨어에서 구현 가능한 최대한 짧은 길이로 하고 LI의 경우 시험 설비 주변 공간을 고려하여 길게 해야 응답 특성에서 나타나는 10∼1000 Hz의 진동을 줄일 수 있다. VT의 경우 부피를 작게 해야 1000 Hz 이상 영역에서 전달함수 진동을 줄일 수 있다. 튜브의 직경이 증가하면 1000 Hz 이상 영역이 줄어드나 10∼1000 Hz의 진동이 발생할 수 있다. 이 경우 LS와 LI를 조정해서 이를 줄일 수 있다.
협소한 공간과 고온의 연소실에서 발생하는 동압을 측정해야 하는 상황에서 ITP는 하나의 대안이 될 수 있다. ITP 설계는 목표 응답 특성 범위와 시험장 상황에 따라 기하학적 크기를 조정해야 한다. 그 이유는 LI가 100 m 수준만 되어도 상당히 많은 공간을 차지하고 주변 간섭이 작을 경우 Ls를 비교적 짧게 설계하여 위상 지연을 최대한 줄이는 방향으로 설계를 할 수도 있기 때문이다.
본 연구 결과는 ITP를 제작하기 전 사전 모사를 위해 변수에 따른 응답 특성의 경향성 변화를 예측함으로써 연구자가 원하는 응답 특성 범위를 설정하여 제작할 수 있는 유용한 도구 및 정보를 제공한다.
향후 튜브와 센서 사이의 부피를 최소화하기 위한 방안과 ITP의 튜브 연결시 불연속적인 부분이 존재하지 않는 설계에 대해 검토가 추가적으로 필요하다.
Nomenclature
| c : | Speed of sound |
| d : | Inner diameter of a tube |
| I : | Imaginary unit |
| Jp : | Bessel function of the first kind of order p |
| LS : | Short tube length |
| LI : | Infinite tube length |
| nt : | Polytropic exponent in tube |
| Q : | Reflection coefficient |
| R : | Tube radius |
| VT : | Transducer volume |
| α : | Shear wavenumber |
| γ : | Heat capacity ratio |
| Φ : | Propagation constant |
| μ : | Viscosity |
| ρ : | Density |
| ω : | Angular frequency |
Acknowledgments
본 연구는 “한국형발사체개발사업(KSLV-II)”의 지원으로 수행되었습니다.
References
- Rocket Motor ICP® Pressure Sensor, Installation and Operating Manual. PCB Piezotronics, Inc.
-
Armbruster, W., Hardi, J., Suslov, D. and Oschwald, M., “High-Speed Flame Radiation Imaging of Thermoacoustic Coupling in a High Pressure Research Thrust Chamber,“ Presented at the 2018 Joint Propulsion Conference, Cincinnati, Ohio, 2018.
[https://doi.org/10.2514/6.2018-4951]

- Armbruster, W., Gröning, S., Hardi, J. and Oschwald, M., “Analysis of High Amplitude Acoustic Pressure FIeld Dynamics in a LOX/H2 Rocket Combustor,” p. 12.
- High Temperature Pressure Sensor for Gas Turbine- and Thermoacoustics Applications. Kistler.
-
Van de Wyer, N., Brouckaert, J.F. and Miorini, R.L., “On the Determination of the Transfer Function of Infinite Line Pressure Probes for Turbomachinery Applications,“ Presented at the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 2012.
[https://doi.org/10.1115/GT2012-69563]

-
Naples, A., Knisely, A. M., Hoke, J. and Schauer, F., “Infinite Line Pressure Probe and Flush Transducer Measurements in a Rotating Detonation Engine Channel,“ Presented at the AIAA Scitech 2019 Forum, San Diego, California, 2019.
[https://doi.org/10.2514/6.2019-2022]

-
Wegner, M., Nance, D. and Ahuja, K., “Characterization of Short and Infinite-Line Pressure Probes for In-Duct Acoustic Measurements Under Hostile Environment,“ Presented at the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 2007.
[https://doi.org/10.2514/6.2007-3443]

- Englund, R. and Richards, W.B., The Infinite Line Pressure Probe, Publication NASA Technical Memorandum 83582. 1984, p. 17.
-
Salikuddin, M., Burrin, R. and Brown, W., “Design and Characterization of a High Temperature and High Frequency Infinite-Line Pressure Probe,“ Presented at the 12th Aeroacoustic Conference, San Antonio, TX, U.S.A., 1989.
[https://doi.org/10.2514/6.1989-1116]

-
Spurling, J.A., “Using a Semi-Infinite Tube to Measure Pressure Oscillations in Solid Rocket Motors,“ Presented at the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, 2015.
[https://doi.org/10.2514/6.2015-3976]

-
Naples, A., Hoke, J.L. and Schauer, F.R., “Quantification of Infinite Line Pressure Probe Response to Shocks and Detonation Waves,“ Presented at the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida, 2018.
[https://doi.org/10.2514/6.2018-1886]

-
Zinn, H. and Habermann, M., “Developments and Experiences With Pulsation Measurements for Heavy-Duty Gas Turbines,“ Presented at the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, Canada, 2007.
[https://doi.org/10.1115/GT2007-27475]

-
Ferrara, G., Ferrari, L. and Sonni, G., “Experimental Characterization of a Remoting System for Dynamic Pressure Sensors,“ Presented at the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, Nevada, USA, 2005.
[https://doi.org/10.1115/GT2005-68733]

-
Kim, H. and Choi, H.S., “A Comparative Study of Frequency Response Models for Pressure Transmission System,” Journal of the Korean Society of Propulsion Engineers, Vol. 24, No. 2, 2020, pp. 83-93.
[https://doi.org/10.6108/KSPE.2020.24.2.083]

- Taback, I., The Response of Pressure Measuring Systems to Oscillating Pressures, Publication Technical Note NO. 1819. Langley Aeronautical Laboratory Langley Air Force Base, Va., 1949.
-
Iberall, A.S., “Attenuation of Oscillatory Pressures in Instrument Lines,” Journal of Research of the National Bureau of Standards, Vol. 45, No. 1, p. 85, 1950.
[https://doi.org/10.6028/jres.045.008]

- Blackshear, P.L., Rayle, W.D. and Tower, L.K., Study of Screeching Combustion in a 6-Inch Simulated Afterburner, Publication NACA TN 3567. 1955, p. 60.
- Bergh, H. and Tijdeman, H., “Theoretical and Experimental Results for the Dynamic Response of Pressure Measuring Systems,“ Publication Report. NLR-TR-F. 238. National Aero and Astronautical Research Institute(NATIONAAL LUCHT- EN RUIMTEVAARTLABORATORIUM), 1965.
-
Samuelson, R.D., Pneumatic Instrumentation Lines and Their Use in Measuring Rocket Nozzle Pressure, Publication RN-DR-0124, 4212042. Nuclear Rocket Operations, Aerojet-General Corporation, 1967, p. RN-DR--0124, 4212042.
[https://doi.org/10.2172/4212042]

-
Salikuddin, M., “Application of Impedance Tube Technique in the Measurement of Burning Solid Propellant Admittances,“ Ph.D. Thesis. Georgia Institute of Technology, 1978.
[https://doi.org/10.2514/6.1979-167]

-
Gejji, R.M., Walters, I.V., Beard, S., Lemcherfi, A., Sardeshmukh, S.V., Heister, S.D. and Slabaugh, C.D., “Transducer Installation Effects on Pressure Measurements in PGC Devices,“ Presented at the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida, 2018.
[https://doi.org/10.2514/6.2018-0158]

-
Boyle, D.K., Henderson, B.S. and Hultgren, L.S., “Core/Combustor-Noise Baseline Measurements for the DGEN Aeropropulsion Research Turbofan,“ Presented at the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, Georgia, 2018.
[https://doi.org/10.2514/6.2018-3281]

-
Boyle, D.K., Henderson, B.S. and Hultgren, L.S., “Transfer-Function Determination for Infinite-Tube-Probe Pressure Transducers with Application to Turbofan Core/Combustor Noise,“ Presented at the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 2019.
[https://doi.org/10.2514/6.2019-2588]

- Beltman, W.M., “Viscothermal Wave Propagation Including Acousto‐elastic Interaction,“ PhD thesis. University of Twente, 1998.
- Gordon, S. and McBride, B.J., Computer Program for Calculation Complex Chemical Equilibrium Compositions and Applications, Publication NASA RP 1311. 1994, p. 64.