[ Technical Paper ]

Journal of the Korean Society of Propulsion Engineers - Vol. 24, No. 2, pp.83-93

ISSN: 1226-6027 (Print) 2288-4548 (Online)

Print publication date 01 Apr 2020

Received 30 Dec 2019 Revised 24 Feb 2020 Accepted 05 Mar 2020

DOI: https://doi.org/10.6108/KSPE.2020.24.2.083

압력전달시스템을 위한 주파수응답모델들의 비교 연구

김현준^a^{, *} ; 최환석^a

A Comparative Study of Frequency Response Models for Pressure Transmission System

Hyeonjun Kim^a^{, *} ; Hwan-Seok Choi^a

aCombustion Chamber Team, Korea Aerospace Research Institute, Korea

Correspondence to: ^* E-mail: kris@kari.re.kr

Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

압력전달시스템의 주파수응답특성의 효과 때문에 동압센서를 하드웨어에 flush 마운트 형태로 설치해야 한다. 그러나 측정을 위한 포트 주변의 협소한 조건 혹은 고온의 연소가스로부터 센서가 손상되는 것을 막기 위해 벽면 안쪽에 recess 마운트 방식을 설계하기도 한다. 압력전달시스템에서 동압 신호의 왜곡이 발생하기 때문에 동적 응답 특성을 반드시 고려해야 한다. 본 연구에서는 섭동 모델과 2차 축소 모델을 실험치와 비교하였고 주파수응답모델을 선택하기 위한 가이드라인을 제시하였다.

Abstract

Dynamic pressure transducer needs to be flush-mounted on hardware due to frequency response characteristics of pressure transmission system. However, it is sometimes necessary to be mounted in recessed configuration due to insufficient space for sensor installation and for protection of sensor from thermal damage. Dynamic response characteristics should be considered due to distortion of original dynamic pressure signal in the pressure transmission system. In this study, small perturbation model and 2nd order reduced model were compared with experiments and a guideline for selecting a frequency response model was suggested.

Keywords:

Dynamic Pressure Sensor, Frequency Response Model, Pressure Measuring System

키워드:

동압센서, 주파수응답모델, 압력측정시스템

1. 서 론

1.1 연구 배경 및 목적

동압 측정을 위한 센서는 반드시 flush 마운트로 체결해야 한다. 하지만 공간적인 이유와 고온 노출에 따른 센서 보호 등의 이유로 동압 센서는 압력전달시스템(유도관)을 설계하여 측정하고자 하는 위치로부터 떨어져서 계측을 하기도 한다. 특히, 가스터빈의 경우 연소실의 온도가 1200 K 수준인데 반해 로켓 엔진의 연소기는 이보다 훨씬 높은 3000 K을 상회하는 고온에서 동작하는 시스템이기 때문에 연소실의 동압 측정을 더욱 어렵게 한다.

이를 극복하기 위해 센서와 접촉하는 면을 포함하는 부피(volume of cavity)와 이를 연결하는 튜브(tube)로 이루어진 기하학적 형상(이하 압력전달시스템으로 지칭함)을 이용하여 연소실의 고온에 센서가 손상되지 않고 연소실 내부의 동압 변동을 안정적으로 측정할 수 있도록 설계를 한다. 그러므로 압력전달시스템의 주파수응답특성을 알아야 바람직한 측정 범위를 알 수 있다. 즉, 보편적인 동압 센서 고유의 공진주파수(>25 kHz[1])와는 관계없이 측정 가능한 주파수는 주로 압력전달시스템의 공진주파수에 지배를 받는다.

이러한 공진주파수를 빠르게 얻기 위해 본 연구에서는 기존에 많이 이용하는 집중계 모델인 이차계(2nd order system)와 가장 엄밀한 해석적 설계식인 섭동(perturbation) 모델을 비교 분석하여 이들 모델들의 적절한 적용 방법에 대한 가이드라인을 제공하고자 한다.

1.2 동적응답모델의 문헌 조사

압력전달시스템의 동적응답특성을 예측하기 위한 해석적 모델은 크게 두 가지 방식으로 구분된다. 첫 번째는 시스템을 집중계(lumped system)로 모델링하여 이차축소모델(2nd order reduced model)을 이용하여 해석하는 방법[2-6]이다. 두 번째는 연속체 역학을 바탕으로 섭동 이론(small perturbation theory)을 이용하여 지배 방정식으로부터 전달함수를 얻는 방법이다[7]. 이와 같은 해석적 모델의 해는 기본 설계 단계에서 빠르게 공진주파수를 확인할 수 있는 유용한 방법이다.

집중계에 의한 해석 방법은 압력전달시스템에 채워져 있는 매질을 하나의 가스 덩어리로 간주하겠다는 의미이다[8]. 이차 모델은 이미 Whitmore & Leondes[5]가 단순화된 파동 방정식에서 역 라플라스 변환을 통해 유도됨을 보였다. 즉, 이차 계는 1차 공진주파수에 대한 2차 축소 방정식(reduced equation)으로 이해될 수 있다. 이 방정식의 주파수 응답 특성은 다음과 같다.

p 1 p 0 = 1 1 - ω ω n 2 2 + 4 h 2 ω ω n 2

(1)

이 모델은 간단하며 문헌[4]에도 소개되어 있어 초기 연구자들이 가장 먼저 접근하게 되는 모델이다. 여기서 공진주파수는 다음과 같다.

f n = c 2 π A t L e f f V v

(2)

상기 식은 Helmholtz 공진기의 공진주파수를 의미한다. 여기서 L_eff은 유효길이(effective length)로 매질의 점성 경계층 두께를 무시할 경우 L_eff=L+δ_i+δ_e의 관계식을 갖는다. 이 식은 튜브 길이에 관한 끝단보정계수(end-correction factor)를 필요로 한다[9-11].

물리적으로는 실제 진동하는 매질의 길이가 튜브 내부의 가스의 길이보다 더 크기 때문에 공진주파수 식에서의 길이는 기하학적인 길이가 아닌 실제 진동하는 매질 길이의 효과를 고려해야 한다[12]. 즉, 매질의 진동이 유도관의 외부에 영향을 미치기 때문에 관을 기준으로 공진기 내부의 보정길이와 공진기 외부의 보정길이를 고려해야 한다[13-15]. 이는 배관 출구에서 진동하는 매질을 시각적으로 표현하는 수치 계산 결과에서도 잘 드러난다[16]. 개방된 끝단을 갖는 파이프(open-ended pipe)에서 플랜지가 있는 경우 δ = 8R_t/3π ≈ 0.85R_t이고 플랜지가 없는 경우는 δ = 0.6R_t이다(Rayleigh 모델이라 명명함)[17].

그러므로 Helmholtz 공진기의 노즐 목에서 보정길이는 외부에 플랜지가 있는 경우 δ = (0.85+0.85)R_t = 1.7R_t이고 외부에 플랜지가 없는 경우에는 δ = (0.85+0.6)R_t = 1.4R_t이다[17]. 더욱 정밀한 보정길이 예측 모델의 경우 Ingard[9]가 1953년에 내부 보정길이를 제안하였고 Ji[18]는 외부 보정길이 보정식을 제안하였다. 그러나 상기 모델들은 모두 적용에 제한 사항이 있고 본 연구에서는 Rayleigh 모델이 실험값을 충분히 모사하고 있어서 이 모델을 대상으로만 검토하였다.

한편, 공압전달시스템(pneumatic transmission system) 분야에서 Schuder & Binder[19]는 공압 제어 시스템을 모사하기 위해 1차원 질량, 에너지, 운동량 방정식을 선형화하여 전기 회로 시스템과 비슷한 형태로 방정식을 유도하였다. 이후 Hougen 등[20]은 위 식을 2차 방정식으로 확장하였고 그의 식으로부터 공진주파수 계산식을 재정리 하였다. 그리고 Whitmore & Leondes[5]가 파동 방정식으로부터 얻은 1차 공진주파수만을 고려하여 2차 방정식을 유도하였다. 그 식에서 사용된 공진 주파수 계산식은 기본적으로 Hougen[20]의 공진주파수와 동일하였다. 그는 V_eff = V_v + (L_tA_t)/2의 유효 부피를 제시하였고 공진주파수 식은 다음과 같이 표현된다.

f n = c 2 π A t L V v + L t A t 2 = c 2 π L 12 + V v V t

(3)

위 식의 우변은 Hougen 등[20]의 식이고 부피비가 0 ≤ V_v/V_t ≤ 100 조건에서 1/2의 상수 값 대신 0.3905의 보정 값을 제안하기도 하였다[21]. 위 관계식을 이용하면 압력전달시스템의 첫 번째 고유 진동수를 얻을 수 있다. 한편, 감쇠율은 다음과 같은 관계식을 변형시켜 쓰이고 있다[1,2,5,6,22].

h = 4 μ ρ R t 2 ω n

(4)

여기서 감쇠율은 여전히 실험치와 차이가 있고 적절한 예측 모델이 존재하지 않는다[6]. 그러므로 감쇠율을 주로 실험을 통해 얻는데 여러 수학적 방법론이 존재한다[2,23].

집중계 모델의 제한 사항을 볼 때 그 한계점이 명확하기 때문에 많은 연구자들은 자연계 현상을 보다 정확하게 이해하기 위해 분포 매개변수 모델(distributed parameter model)과 같은 더욱 복잡한 모델에 관심을 가졌다[24]. Iberall[25]이 분포 매개변수 모델을 유도한 이후 Bergh와 Tijdeman[7]은 cavity와 tube가 N개의 set로 직렬 연결되는 구조에 관한 완전한 모델을 제시하였다. 그의 해는 삼각함수와 베셀(Bessel) 함수로 이루어진 상당히 복잡한 구조를 갖는다.

이 해는 몇 가지 가정을 통해 유도되었기 때문에 이 가정을 이해할 필요가 있다. 먼저, 섭동(perturbation) 방법을 사용하였기 때문에 압력, 밀도, 온도의 변동 성분은 평균치에 비해 작아야 한다. 층류 조건에 이상 기체를 가정하였고 배관 끝단에서 효과가 무시될 정도로 길이가 긴 L/d >> 1 조건을 만족해야 한다. 벽면의 열전달율이 매질보다 커서 튜브 벽면에서의 온도 변동을 무시할 수 있어야 한다. 센서와 인접한 cavity에서 압력과 온도는 공간적으로 집중계로 간주한다. 센서 자체의 공진주파수가 압력전달시스템의 주파수보다 커야 한다[7,26].

이 수학적 모델은 많은 문헌[8,26-31]에서 검증이 되었고 일정한 벽면 온도와 층류 유동일 때 기체와 액체 압력 측정 시스템의 주파수 응답특성을 계산하는 도구로 사용되고 있다. 한편, cavity와 유도관 1 set만을 고려할 경우 식은 다음과 같이 단순화된다.

P 1 P 0 = 1 cosh ⁡ φ L t + V v V t σ + 1 k n φ L t s i n h φ L t

(5)

여기서, σ는 압력 센서의 다이어프램의 변형으로 인한 cavity의 무차원 계수를 의미한다. 센서의 다이어프램을 강체라 가정할 때 σ=0으로 간주한다. k는 cavity에서의 polytropic index로 공기에 대해 cavity 내부가 열역학적으로 등압과정이면 0, 등온과정이면 1이고 등엔트로피 과정이면 1.4이다[32]. 음향은 기본적으로 압축 팽창이 공간적으로 나타나기 때문에 매질 부피의 변화가 빠르게 나타나면 단열과정으로 나타나고 그 속도가 느리면 등온과정으로 나타난다[33]. 이와 같은 현상을 고려하여 Svete는 공기에 대해 수치 계산을 위해 평균값인 1.2를 사용하기도 했다[26]. 나머지 변수들은 Bergh & Tijdeman 모델[7] 관련 문헌에서 참고할 수 있다.

Kobayashi[8]등은 이와 같은 집중계와 분포 매개변수 모델에 관한 상호 비교를 위해 실험과 해석값을 비교 분석하였다. 그의 결과에서 L/d ≥ 20의 경우 Bergh & Tijdeman 모델이 실험값과 거의 일치하였다. 다른 문헌에서는 L/d ~ 6의 비교 결과도 비교적 정확한 결과를 보여주었다[30]. 심지어 L/d = 2에서도 시험 결과와 잘 일치하였으나 L/d = 1에서는 이 모델이 과대평가된 공진주파수를 나타내었다[34]. 따라서 Bergh & Tijdeman 모델[7]은 L/d >> 1에서 만족할 만한 예측을 보이는 것으로 볼 수 있다.

이와 같은 두 가지 종류의 해석적 접근방법은 몇 가지 가정이 고려되기 때문에 그 한계와 적용 범위가 제한된다. 따라서 무분별하게 적용하면 잘못된 결과를 얻을 수 있다. 이 때문에 접근방법에 있어서 가이드라인이 필요하다.

본 연구에서는 압력전달시스템의 공진주파수보다 작은 주파수인 사용가능주파수를 얻는 것이 목적이다. 각각의 모델들은 진폭과 위상에 대해 검증이 이미 잘 이루어져 있어서 사용가능주파수를 얻는데 이용되는 진폭에 주로 초점을 맞추어 각각의 모델들을 비교 분석하였다.

2. 실험 데이터를 이용한 코드 검증 및 해석해와 실험치의 비교 분석

2.1 주파수응답모델 분류

본 비교 연구에서는 집중계와 Bergh & Tijdeman 모델을 분석하기 위해 MATLAB 프로그램으로 구현하여 비교 분석을 수행하였다.

본 연구에서는 Table 1과 같이 Bergh & Tijdeman 해석식[7]과 2차 모델에서 사용되는 유효길이[17,35] 및 공압의 동특성 연구에 사용되는 유효 부피[5,20]에 따른 변화에 대해 과거 실험 결과와 비교 분석하여 주파수 특성을 분석하였다.

Table 1.

Three types of frequency response models.

2.2 실험치와 해석해의 비교

Fig. 1 ~ Fig. 6까지는 Bergh & Tijdeman의 단일 연결 튜브(single connecting tube) 실험 결과에서 L/d >> 1인 실험 결과와 각 모델을 모두 비교한 결과를 보여준다. 먼저, Fig. 1은 L/d = 2143에서 실험치와 모델을 이용한 해석 결과를 보여주고 있다. Bergh & Tijdeman 모델이 가장 정확한 예측 결과를 보여주었고 Whitmore & Leondes는 Bergh & Tijdeman 모델을 이용한 첫 번째 공진주파수 영역과 거의 동일한 예측 결과를 보여준다. 반면, Rayleigh 모델은 예측 실패하였다.

Fig. 1

Comparison of experiment and analytic models for single pressure measuring system, L/d = 2143, d = 1.4 mm (Bergh & Tijdeman[7]).

Fig. 2

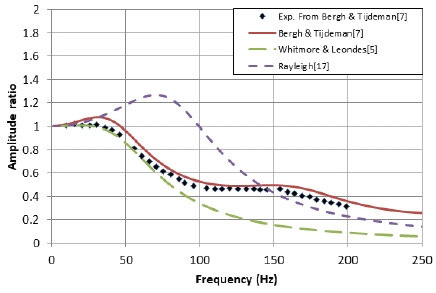
Comparison of experiment and analytic models for single pressure measuring system, L/d = 1020, d = 0.98 mm (Bergh & Tijdeman[7]).

Fig. 3

Comparison of experiment and analytic models for single pressure measuring system, L/d = 629, d = 1.59 mm (Bergh & Tijdeman[7]).

Fig. 4

Comparison of experiment and analytic models for single pressure measuring system, L/d = 629, d = 1.59 mm (Bergh & Tijdeman[7]).

Fig. 5

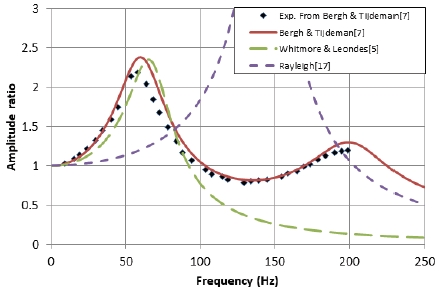
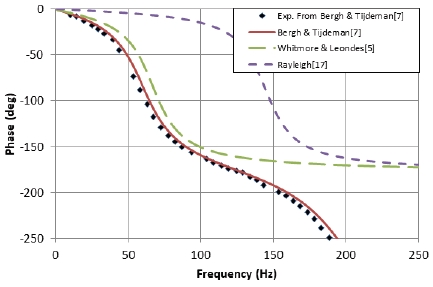
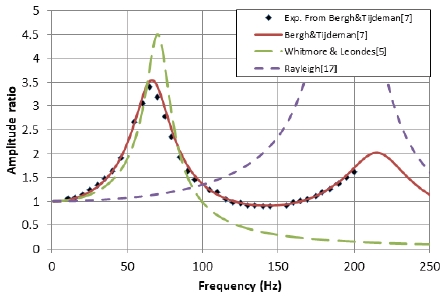
Comparison of experiment and analytic models for single pressure measuring system, L/d = 500, d = 2.18 mm (Bergh & Tijdeman[7]).

Fig. 6

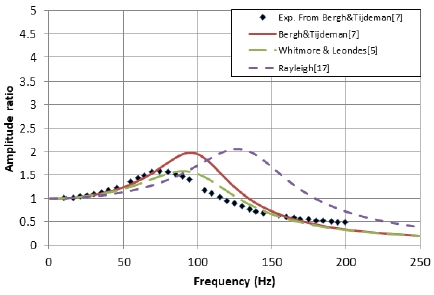
Comparison of experiment and analytic models for single pressure measuring system, L/d = 476, d = 1.05 mm (Bergh & Tijdeman[7]).

Fig. 2는 L/d = 1020에서의 비교 결과를 보여준다. Bergh & Tijdeman 모델이 실험치에 비해 다소 높은 예측치를 보이나 전체 경향을 잘 모사해 주고 있고 Whitmore & Leondes 모델은 첫번째 공진주파수를 가장 잘 모사하고 있다.

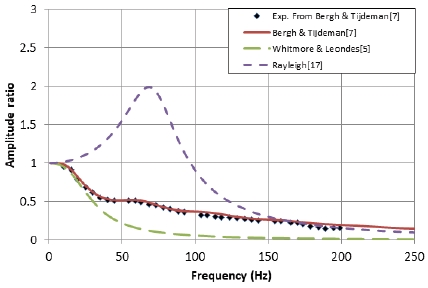
Fig. 3에는 L/d = 629에서의 결과를 비교하였다. 여전히 Bergh & Tijdeman과 Whitmore & Leondes 모델이 실험치를 가장 비슷하게 예측했다. Fig. 4는 L/d = 629에서의 위상을 비교하였다. 약 53 Hz의 공진주파수가 존재하는 구간에서 급격한 위상 변화가 관찰되었다. 본 연구에서 관심이 있는 사용가능주파수는 공진주파수보다 낮은 영역인 저주파수 영역이다. 이 영역에서는 위상의 변화가 크지 않고 사용가능주파수는 진폭 비로 정의되므로 본 연구에서는 주로 진폭 비에 초점을 맞추어 분석하였다.

Fig. 5는 L/d = 500에서 각각의 모델들의 결과를 실험치와 비교하였다. Bergh & Tijdeman 모델이 가장 정확한 공진주파수를 모사하고 있는 것을 확인할 수 있다. Whitmore & Leondes의 모델도 실험치를 비교적 잘 모사하고 있지만, 그 크기는 다소 과대평가되어 나타나고 있다. 한편, 고전적인 Helmholtz 공진기의 유효길이를 반영한 Rayleigh의 모델을 적용할 경우 약 200 Hz의 공진주파수를 얻어서 실험치와 상당한 차이를 보였다.

Fig. 6에는 L/d = 476에서 각 모델들의 결과를 실험치와 비교하였다. Whitmore & Leondes와 Bergh & Tijdeman 모델은 실험치의 공진주파수 위치에서 다소 벗어나 있지만 두 모델의 그래프 형태는 서로 비슷한 경향을 보인다. Rayleigh 모델은 예측이 실패했다.

Fig. 7은 Johnson[28]의 단일 연결 튜브의 L/d=860에서 실험 결과를 이용하여 예측한 결과를 보여준다. 기하학적 형상 정보는 제시되어 있지만, 온도와 압력의 정확한 물리량이 알려지지 않은 관계로 상온(25℃)으로 가정하고 공기의 압력을 변화시켜 본 연구에서 사용한 모델 중 가장 일치한 결과를 보이는 모델을 기준으로 결과를 분석하였다. Whitmore & Leondes의 모델은 Bergh & Tijdeman의 모델과 마찬가지로 서로 비슷한 공진주파수 결과를 보였고 Whitmore & Leondes 모델의 감쇠율이 과도하여 실험치와 차이가 다소 발생하였다. 여전히 Rayleigh 모델은 예측이 실패하였다.

Fig. 7

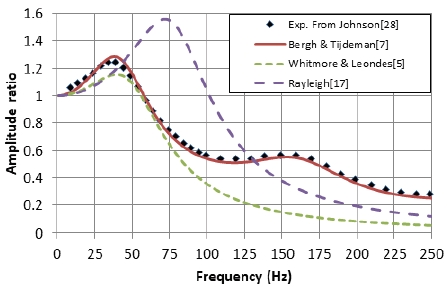
Comparison of experiment and analytic models for single connecting tube, L/d = 860, d = 1.18 mm (Johnson[28]).

Fig. 8에는 Johnson[28]의 단일 연결 튜브의 L/d = 14.4에 대해 비교하였다. 분석 결과 Whitmore & Leondes의 모델이 가장 정확한 공진주파수 예측 결과를 보였다. 이 결과로 볼 때 L/d = 10 근처에서부터 Bergh & Tijdeman 모델의 공진주파수 예측 정확도가 다소 떨어지는 것으로 보인다.

Fig. 8

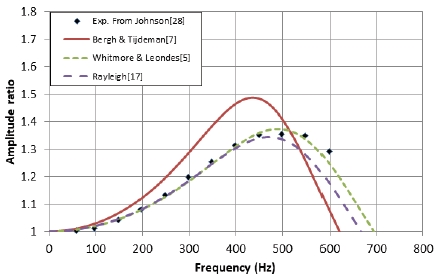
Comparison of experiment and analytic models for single connecting tube L/d = 14.4 d = 0.508 mm (Johnson[28]).

Fig. 9은 Singh[36]의 Helmholtz 공진기에 관한 시험 결과에서 L/d = 1.8에 대해 앞서 언급한 3가지 모델과 비교하였다. 이번에는 Rayleigh 모델을 제외하고 모든 모델이 실험치에 비해 과대평가된 결과를 보인다.

Fig. 9

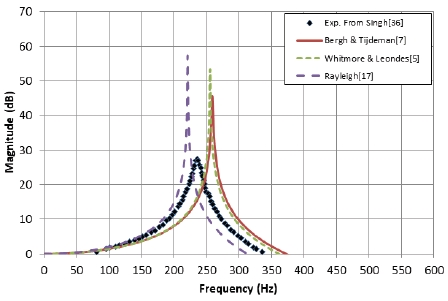
Comparison of experiment and analytic models for single connecting tube, L/d = 1.8, d = 52.5 mm (Singh[36]).

지금까지 결과로 볼 때 L/d >> 10 근처 영역에서는 Whitmore & Leondes와 Bergh & Tijdeman 모델이 공진주파수를 가장 잘 예측하고 L/d가 1 ~ 10 근처에서 Rayleigh 모델 또한 공진주파수를 비교적 잘 예측하기 시작하는 것으로 보인다.

2.3 L/d와 공진주파수의 관계

앞선 결과로부터 L/d에 따라 예측 모델의 정확도가 서로 상이한 결과를 보여주었기 때문에 L/d에 따른 공진주파수의 변화를 알아볼 필요가 있다. 앞선 결과들은 서로 다른 문헌의 데이터를 검토하였기 때문에 기하학적인 형상과 물성치가 서로 달라 L/d에 따른 공진주파수의 경향을 직접적으로 판단할 수 없다. 그러므로 L/d에 따른 공진주파수의 실험 데이터가 필요하다.

Kobayashi등[8]은 L/d의 변화에 따라 1차 공진주파수를 Bergh & Tijdeman 모델과 이차계의 공진주파수 모델(Rayleigh 모델)을 이용하여 실험치와 비교하였다.

본 연구에서는 그의 결과에 Whitmore & Leondes 모델을 추가하여 비교 분석하였다. 문헌에서 제시된 기하학적 형상과 압력을 사용하였고 온도와 물성치가 주어져 있지 않은 관계로 공기에 대해 온도를 조정하였다. 이 실험에서는 cavity가 없는 유도관만 존재하는 센서 마운트를 사용하였기 때문에 Rayleigh 모델에 외부 보정계수 δ_e = 0.85R_t 모델만 적용하였다.

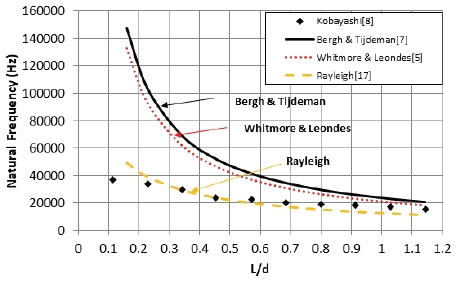
Fig. 10에서 L/d가 작은 영역에서 공진주파수는 Bergh & Tijdeman 모델과 Whitmore & Leondes 모델은 예측이 실패하였고 Rayleigh 모델이 실험치와 비슷한 경향을 보였다. Rayleigh 모델은 L/d ~ 1까지는 실험치에 가까운 공진주파수를 예측하였고 이후로 다소 과소평가된 공진주파수를 예측하였다.

Fig. 10

Natural frequencies at small L/d(Kobayashi[8]).

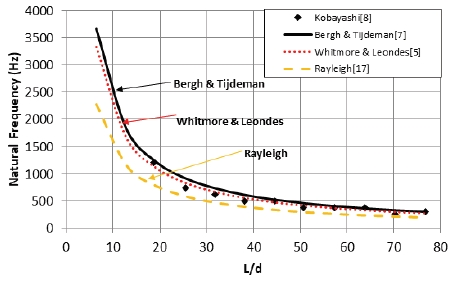
L/d가 큰 영역에서는 약간의 편차는 존재하지만 Bergh & Tijdeman과 Whitmore & Leondes 모델이 실험치를 잘 따르고 있다(Fig. 11). 반면, Rayleigh 모델은 실험치와 차이가 다소 존재한다.

Fig. 11

Natural frequencies at large L/d(Kobayashi[8]).

정리하면, L/d가 클수록 모델에 따른 공진주파수의 차이가 작게 나타나고 있고 L/d가 작을수록 Bergh & Tijdeman과 Whitmore & Leondes 모델은 예측이 명백히 실패한다는 점을 알 수 있다. 이는 이들 모델이 기본적으로 L/d >> 1의 가정에서 유도되었기 때문이다.

이와 같은 Kobayashi등의 문헌에 제시된 시험 데이터와의 비교 분석으로부터 L/d가 클수록 Bergh & Tijdeman과 Whitmore & Leondes 모델을 사용하는 것이 적절해 보이고 L/d가 작은 영역에서는 Rayleigh 모델을 사용하는 것이 더 좋은 예측 결과를 보여준다.

3. L/d와 사용가능주파수 영역과의 관계

압력 유도관으로부터 올바른 계측 범위를 판단하기 위해 공진주파수만을 기준으로 평가할 수는 없다. 공진주파수 근처에서는 측정된 동압이 증폭되어 나타나기 때문에 공진주파수로부터 떨어진 영역을 기준으로 삼아야 한다. 이상적으로는 진폭 비(amplitude ratio)가 1인 영역을 기준으로 해야 하지만 물리적으로 완벽한 1인 영역은 제한적이므로 허용할 수 있는 가이드라인을 정해야 한다.

센서 제조사들은 센서 자체의 공진주파수가 존재하므로 사용 가능한 주파수 범위를 공진주파수의 약 20% 수준으로 엄밀하게 정하고 있다. 이는 허용 가능 오차가 5%(p₁/p₀ = 1.05) 정도가 된다. 이렇게 하면 측정 가능 범위가 줄어들기 때문에 오차 범위를 10%(p₁/p₀ = 1.1) 혹은 3 dB(p₁/p₀ = 1.4)까지로 정하기도 한다[37]. 그러나 통상적으로 공진주파수의 25% 까지를 사용 가능한 주파수 범위[8]로 정하고 있고 이는 허용 오차 범위 5 ~ 10%의 수준이다. 따라서 압력 유도관의 공진주파수를 기준으로 오차 범위를 어디까지 정할 것인지는 연구자가 직접 결정해야 한다.

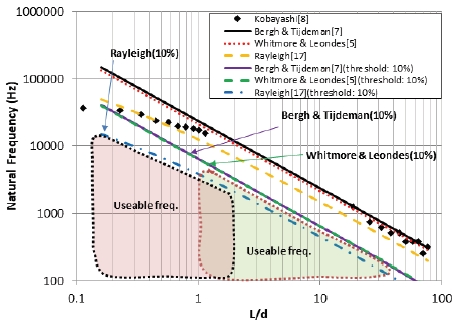
Fig. 12에는 Kobayashi등의 문헌의 데이터로부터 공진주파수와 함께 10% 오차를 허용할 경우 사용가능주파수 영역을 표시하였다. L/d < 1 경우 Rayleigh 모델의 10% 오차 허용시 그래프를 경계로 저주파수 영역이 사용가능주파수 영역이고 L/d >> 1의 경우 Whitmore & Leondes 모델의 10% 오차 허용시 그래프를 경계로 저주파수 영역이 사용가능주파수를 의미한다. L/d가 1 근처에서 두 모델의 예측이 서로 비슷한 경향을 보인다. 이 부분은 향후 연구가 더 필요하다.

Fig. 12

Natural frequencies and usable frequency range with 10 % error at overall L/d (Kobayashi[8]).

L/d >> 1 영역에서는 Bergh & Tijdeman과 Whitmore & Leondes 모델이 거의 비슷한 공진주파수를 예측하였고 사용가능주파수 범위는 줄어들지만 두 가지 모델이 거의 비슷하다. 따라서 두 가지 모델의 어느 것을 사용해도 결과에 큰 영향을 주지 않을 것이다. 그러나 기본 설계 단계에서 비교적 간단한 모델이 실제 적용하기가 용이하기 때문에 Bergh & Tijdeman 모델과 같이 코딩이 요구되는 복잡한 모델보다는 Whitmore & Leondes의 이차계 모델이 사용 측면에서 더 유리하다.

한편, L/d < 1 영역에서는 앞의 두 모델의 정확도가 떨어지므로 Rayleigh 모델을 사용하는 것이 적절해 보인다. Rayleigh 모델의 예측 결과 사용가능주파수가 더욱 크게 줄어든 것을 확인할 수 있다.

4. 결 론

본 연구에서는 과거에 연구되어온 Bergh & Tijdeman 모델과 이차계 모델인 Whitmore & Leondes와 Rayleigh 모델을 비교 분석하였다.

L/d >> 1의 경우 기본적으로 Bergh & Tijdeman 모델을 사용하는 것이 좋으나 코딩을 해야 할 정도로 복잡하므로 이차계 모델인 Whitmore & Leondes 모델을 이용해 공진주파수를 예측하는 것이 가장 간단한 방법이다.

L/d < 1의 경우 공진주파수 예측에 있어 오차가 다소 존재하긴 하지만 여전히 기존 Rayleigh 모델 적용이 적절해 보인다. 그러나 향후 이 영역에서 좀 더 정확한 공진주파수 예측 모델 개발이 필요해 보인다.

지금까지 검토한 모델들은 한계가 분명히 존재하기 때문에 모든 실험 조건에 대해 항상 만족한다고 볼 수는 없다. 그러나 제안된 모델 중에 어느 모델을 선택하는 것이 가장 적절한지에 대한 가이드라인을 줄 수 있고 이를 통해 동압 측정을 위한 압력전달시스템의 공진주파수와 사용가능주파수를 비교적 쉽고 빠르게 파악할 수 있다.

Nomenclature


A_t :	Cross-sectional area of tube
c :	Speed of sound
d :	Diameter of tube
h :	Damping ratio
k :	Polytropic index for the fluid in the cavity
L_eff :	Effective length
L = L_t :	Tube length
n :	A complex polytropic index of the fluid in the tube
p₀ :	Amplitude of pressure oscillation in cavity
p₁ :	Amplitude of pressure oscillation at the inlet of the cavity
R_t :	Radius of tube
V_v :	Pressure transducer volume
V_t :	Tube volume
μ :	Dynamic viscosity of the fluid
ρ :	Density of the fluid
σ :	Dimensionless increase in transducer volume due to diaphragm deflection
φ :	Complex wave propagation factor
ω :	Angular frequency
ω_n :	Natural angular frequency
δ_i :	Interior end-correction factor
δ_e :	Exterior end-correction factor

Acknowledgments

본 연구는 “한국형발사체개발사업(KSLV-II)”의 지원에 의하여 수행되었습니다.

References

Doebelin, E. O. Measurement Systems: Application and Design, McGraw-Hill, New York, 1990.
Bajsic, I., Kutin, J., and Zagar, T. “Response Time of a Pressure Measurement System with a Connecting Tube,” Instrumentation Science & Technology, Vol. 35, No. 4, 2007, pp. 399-409. [https://doi.org/10.1080/10739140701436579]
Goody, M. C., and Simpson, R. L. An Experimental Investigation of Pressure Fluctuations in Three-Dimensional Turbulent Boundary Layers: Defense Technical Information Center, Fort Belvoir, VA, 1999. [https://doi.org/10.21236/ADA390236]
Holman, J. P. Experimental Methods for Engineers, McGraw-Hill/Connect Learn Succeed, Boston, 2012.
Whitmore, S. A., and Leondes, C. T. “Pneumatic Distortion Compensation for Aircraft Surface Pressure Sensing Devices,” Journal of Aircraft, Vol. 28, No. 12, 1991, pp. 828-836. [https://doi.org/10.2514/3.46105]
Winroth, P. M. “Characterization of and Correction for Pressure-Measurement Installation,” Centres, Competence Center for Gas Exchange (CCGEx), 2017, p. 11.
Bergh, H., and Tijdeman, H. Theoretical and Experimental Results for the Dynamic Response of Pressure Measuring Systems. Publication Report. NLR-TR-F. 238. National Aero and Astronautical Research Institute(NATIONAAL LUCHT- EN RUIMTEVAARTLABORATORIUM), 1965.
Kobayashi, H., Leger, T., and Wolff, J. M. “Experimental and Theoretical Frequency Response of Pressure Transducers For High Speed Turbomachinery,” International Journal of Turbo and Jet Engines, Vol. 17, No. 2, 2000. [https://doi.org/10.1515/TJJ.2000.17.2.153]
Ingard, U. I. “On the Theory and Design of Acoustic Resonators,” Journal of the Acoustical Society of America, Vol. 25, No. 6, 1953, pp. 1037-1061. [https://doi.org/10.21236/ada395634]
Kim, S., and Kim, Y.-H. “Resonance Frequency Shifts of Helmholtz Resonator Array Panel Brought by Change in Resonator Arrangements,” Korean Society for Noise and Vibration Engineering(KSNVE), 2005, pp. 97-100.
Ver, I. L., and Beranek, L. L., Eds. Noise and Vibration Control Engineering: Principles and Applications. Wiley, Hoboken, N.J, 2006.
Dickey, N. S., and Selamet, A. “Helmholtz Resonators: One-Dimensional Limit for Small Cavity Length-to-Diameter Ratios,” Journal of Sound and Vibration, Vol. 195, No. 3, 1996, pp. 512-517. [https://doi.org/10.1006/jsvi.1996.0440]
Mekid, S., and Farooqui, M. “Design of Helmholtz Resonators in One and Two Degrees of Freedom for Noise Attenuation in Pipelines,” Acoustics Australia, Vol. 40, No. 3, 2012, pp. 194-202.
Monteiro, M., Marti, A. C., Vogt, P., Kasper, L., and Quarthal, D. “Measuring the Acoustic Response of Helmholtz Resonators,” The Physics Teacher, Vol. 53, No. 4, 2015, pp. 247-249. [https://doi.org/10.1119/1.4914572]
Webster, E. S., and Davies, C. E. “The Use of Helmholtz Resonance for Measuring the Volume of Liquids and Solids,” Sensors, Vol. 10, No. 12, 2010, pp. 10663-10672. [https://doi.org/10.3390/s101210663]
Kirby, R., and Duan, W. “Sound Radiation from the Open End of Pipes and Ducts in the Presence of Mean Flow,” Acoustics, 2017, p. 9.
Lawrence E. Kinsler, Austin R. Frey, Alan B. Coppens, and James V. Sanders. Fundamentals of Acoustics, John Wiley & Sons Inc., 2000.
Ji, Z. L. “Acoustic Length Correction of Closed Cylindrical Side-Branched Tube,” Journal of Sound and Vibration, Vol. 283, No. 3-5, 2005, pp. 1180-1186. [https://doi.org/10.1016/j.jsv.2004.06.044]
Schuder, C. B., and Binder, R. C. “The Response of Pneumatic Transmission Lines to Step Inputs,” Journal of Basic Engineering, Vol. 81, 1959, pp. 578-584. [https://doi.org/10.1115/1.4008563]
Hougen, J. O., Martin, O. R., and Walsh, R. A. “Dynamics of Pneumatic Transmission Lines,” Control Engineering, Vol. 10, No. 9, 1963, pp. 114-117.
Elson, J. P., and Soedel, W. “Criteria for the Design of Pressure Transducer Adapter Systems,” International Compressor Engineering Conference, 1972, p. 6.
Whitmore, S. A., and Fox, B. “Improved Accuracy, Second-Order Response Model for Pressure Sensing Systems,” Journal of Aircraft, Vol. 46, No. 2, 2009, pp. 491-500. [https://doi.org/10.2514/1.36262]
Casiano, M. J. Extracting Damping Ratio From Dynamic Data and Numerical Solutions. Publication NASA/TM 2016-218 227. 2016, p. 42.
Stecki, J. S., and Davis, D. C. “Fluid Transmission Lines-Distributed Parameter Models Part 1: A Review of the State of the Art,” Proceedings of the Institution of Mechanical Engineers, Part A: Power and Process Engineering, Vol. 200, No. 4, 1986, pp. 215-228. [https://doi.org/10.1243/PIME_PROC_1986_200_032_02]
Iberall, A. S. “Attenuation of Oscillatory Pressures in Instrument Lines,” Journal of Research of the National Bureau of Standards, Vol. 45, No. 1, 1950, p. 85. [https://doi.org/10.6028/jres.045.008]
Svete, A., and Kutin, J. “Optimal Dimensions of Connecting Tubes for Dynamic Measurements of Pressure,” Journal of Physics: Conference Series, Vol. 1065, 2018, p. 162006. [https://doi.org/10.1088/1742-6596/1065/16/162006]
Fisher, A., Watkins, S., and Watmuff, J. “Dynamic Calibration of Pressure Measurement Systems: An Improved Method,” 18th Australasian Fluid Mechanics Conference, 2012, p. 4.
Johnson, R. B. A Technique for Measuring Unsteady Pressures. NAVAL Postgraduate School, 1968.
Holmes, J. D., and Lewis, R. E. “The Dynamic Response of Pressure - Measurement Systems,” 9th Australasian Fluid Mechanics Conference, 1986, p. 4.
Boerrigter, H. L., and Charbonnier, J. M. Design and Calibration of an Unsteady Pressure Measurement System,. Presented at the ICIASF'97 Record. International Congress on Instrumentation in Aerospace Simulation Facilities, 1997.
van Ommen, J. R., Schouten, J. C., vander Stappen, M. L. M., and van den Bleek, C. M. “Response Characteristics of Probe-Transducer Systems for Pressure Measurements in Gas-Solid Fluidized Beds: How to Prevent Pitfalls in Dynamic Pressure Measurements,” Powder Technology, Vol. 106, No. 3, 1999, pp. 199-218. [https://doi.org/10.1016/S0032-5910(99)00078-9]
Yunas A. Cengel, and Michael A. Boles. Thermodynamics: An Engineering Approach. McGraw-Hill, 2003.
Jakevicius, L., Demcenko, A., and Mardosaite, R. “Ultrasound Attenuation Dependence on Air Compression or Expansion Processes,” Ultragarsas, Vol. 65, No. 1, 2010, pp. 42-46.
Walter, T., Gossweiler, C., and Willson, B. “Application of an Improved Model for the Determination of Acoustic Resonances in Indicator Passages for Combustion Pressure Measurements in Large Bore Gas Engines,” Kistler, p. 14.
Rayleigh, J. W. S. The Theory of Sound. London: The Macmillan Company, 2nd edn. Reprinted 1945, New York: Dover Publications, 1876.
Singh, S. Tonal Noise Attenuation in Ducts by Optimising Adaptive Helmholtz Resonators. MS thesis. The Univ. of Adelaide, Australia, 2006.
Piezoelectric Accelerometers: Theory and Application. Metra Mess- und Frequenztechnik, 2001.

#	System	Models (effective length & volume)	Reference
1	2nd order system	L_eff = L_t+δ_i+δ_e δ = 0.85R_t	Kinsler[18] Rayleigh[17]
2	2nd order system	V_eff = V_v+L_tA_t/2	Whitmore & Leondes[5], Hougen et al[20]
3	Perturbation model	-	Bergh & Tijdeman[7]