코로게이트 3층 샌드위치 패널 구조체 물성 및 구조해석

1. 서 론

산업에서 광범위하게 사용되는 구조물로써의 3층 합금 샌드위치 패널은 구조체의 경량성과 비교적 높은 강성을 갖는 특성으로 특히 주익, 벽면, 빔 구조물, 미익 등의 항공우주 분야에 널리 적용되고 있다. 코로게이트 패널을 포함하여 일반적인 3 층 샌드위치 패널들은 상대적으로 고강도 두 개의 박판 외피와 비교적 후판의 저밀도 및 저강도의 내부의 코어(core)와의 결합 형태로 이루어져있으며 높은 비강도가 그 특징이다[1]. 대표적으로 널리 이용되는 샌드위치 패널 중의 하나인 허니콤(honey comb) 샌드위치 패널에 있어 코어는 외판에 수직으로 접합하게 되며 이 때 선접촉 만으로 유지되므로 외부하중에 의해 접합력을 상실할 수 있는 단점을 갖는 반면 코로게이트 패널은 외피와의 면접촉을 유지하므로 구조강도 면에서 보다 유리하다.

본 연구에서는 기계적 물성의 획득을 위해 코로게이트 변형거동에 기반을 둔 분석식(analytical closed form)이 이용되었으며 이 때 외피의 영향이 반영될 수 있도록 위의 식은 수정되었다. 또한 본 구조체는 일축 섬유강화 복합재와 유사한 형태를 가지므로 복합재 균질화 기법을 통해 기계적 물성이 예측되었으며 두 가지 기법을 통해 얻은 물성은 3층 구조체의 형상 변수에 따른 각 하중에서의 구조해석에 적용되었으며 물성획득 기법에 대한 비교도 포함되었다.

2. 코로게이트 샌드위치 패널의 기계적 물성

일반적으로 샌드위치 패널의 외피는 주요 하중을 버티는 역할을 감당하며 내부 코어는 외부 하중을 전달하는 용도로 적용된다. 다양한 3층 샌드위치 구조체의 모델링에 관한 전반적인 조사 및 정리/비교가 이루어진 바 있다[2]. 코로게이트 패널을 포함하여 3층 샌드위치 패널들에 대한 직접적인 모델링은 수치해석상 고비용이 발생하는 특성상, 외피와 코어의 상세한 형상을 갖는 패널 자체에 대한 모델링보다 패널의 유효 기계적 물성으로 대체되는 것이 보편적이다.

코로게이트 패널은 이방성 탄성계수를 갖는다. 이에 3층 패널에 대해 임의의 여러 얇은 층의 적층 구조물 혹은 이방성 후판으로 간주하여, 탄성계수 등에 대해 유효 기계적 물성을 획득하는 기법이 이용된 바 있으며 이 때 보정기법을 통한 전단계수가 얻어졌다[3-5]. 한편 일부 샌드위치 패널에 대한 극히 국부적 유한요소 해석 또는 실험을 통해 얻은 유효 탄성계수들은 분석식에서의 결과와 비교되었으며, 주기적 구조를 갖는 샌드위치 패널에 대해 근사확장기법을 이용한 균질화를 적용하여 유효 물성을 획득하는 기법도 소개되었다[6-13]. 위의 기법들 외에 다른 기법을 소개하여 그 유용성을 보이고자 한다.

한편 일축방향으로 주기성을 갖는 3층 코로게이트 패널은 섬유강화 복합재와 유사성을 갖고 있으므로 2 개상(phase)으로 이루어진 복합재 균질화기법이 적용될 수 있다[10,12]. 여러 개의 상이 존재하는 복합재에 대한 균질화에는 Mori-Tanaka, 자가일치(self-consistent) 기법 등이 있으며 그 중에서도 저밀도 게재물 복합재에 주로 사용되는 Mori-Tanaka 기법이 비교적 간단한 유도과정을 요구한다. 더욱이 Mori-Tanaka 이론은 복합재의 근사적 기계적 물성을 얻는 기법 중에서 가장 간단한 기법으로 비교적 정확한 물성을 획득하는 도구로 보편적으로 활용되고 있다[14]. 특히 섬유강화 일축 복합재의 경우 섬유방향 탄성계수는 혼합분율로 무리 없이 근사화할 수 있으나 교차방향(transverse)의 계수를 얻는데 혼합법칙의 적용은 한계가 있다.

본 연구에서는 코로게이트 패널에 대한 분석식 및 복합재 균질화기법 이용, 유효물성이 얻어졌으며, 이를 바탕으로 실린더 구조체에서의 특정 하중조건에 대한 구조해석이 수행되었다.

3. 코로게이트 패널의 물성

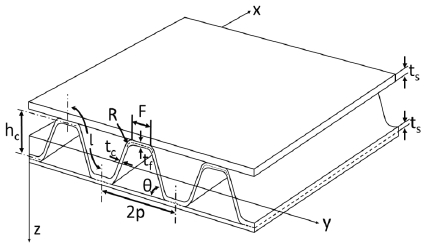
본 연구에서 구조해석에서 적용된 코로게이트 3 층 샌드위치 패널 형상과 주요치수는 Fig. 1에서 보는 바와 같으며 이를 바탕으로 분석식을 통한 각 방향별 탄성계수가 획득되었다.

Fig. 1.

Geometry of corrugated panel.

분석식[1]에 기초하여 획득된 기계적 물성획득 가정을 보여준다. 코로게이트 층의 유효 탄성계수($$ {\tilde{E}}_x$$)와 전단계수($$ {\tilde{G}}_{xy}$$, $$ {\tilde{G}}_{zx}$$)는 아래와 같다.

하지만 위의 식에서 외피의 영향이 고려되지 않았으므로 외피 두께의 영향이 반영될 필요가 있으며 이에 복합재와 마찬가지로 혼합법칙이 적용되면 아래와 같은 식으로 수정될 수 있다.

한편 유효 전단계수의 zx성분은 외피의 영향을 거의 받지 않으므로 아래와 같다.

코어 y 방향의 유효 탄성계수는 다음과 같다.

여기서,

마찬가지로 외피의 영향이 포함되면 위의 식은 아래와 같이 수정된다.

유효 탄성계수 $$ {\tilde{E}}_z$$도 두께방향에 대해 외피 영향을 거의 받지 않으므로 다음과 같이 표현 된다.

한편 다음은 유효 전단계수 yz 성분이다.

각 성분별 포아송 비는 다음과 같다.

여기서

위의 분석식과 같이 유효 탄성계수들이 획득될 수 있는 반면 한편 앞서 언급되었듯이 복합재 균질화기법을 기반으로 유효 물성이 획득될 수 있다[14]. 코로게이트 3층 샌드위치 구조물의 구성은 게재물(inclusion)과 기저물(matrix)의 2개의 상(phase)으로 구분된다. 여기서의 게재물은 코로게이트 층, 기저물은 외피를 포함한 나머지 공간으로 간주될 수 있다. 다음 과정에서는 편리상 x, y, z의 각 방향은 1, 2, 3 성분으로 표시되었다. 일축 방향의 게재물(하첨자 “I”)과 균일 메트릭스(하첨자 “M”)의 각각의 강도 성분은 아래로 표현된다.

균질화를 위해서 게재물의 형상을 반영하는 Eshelby 텐서가 요구되며, 이 때 메트릭스 내에 축방향으로 일정한 주기적로 결합된 게재물에 대해 다음과 같이 표현될 수 있다[15].

그 밖의 다른 성분들은 “0”이다. 위의 형상 Eshelby 텐서는 코로게이트 층에 대해 일축방향 실린더 형상으로 가정되었으나, 주기적인 코로게이트 층에 대한 특정 Eshelby 텐서가 존재하지 않으므로 본 연구에서는 위에서 제시된 텐서가 균질화의 근사를 위해 적용되었다.

여기서 하첨자 “r”은 각 상을 나타낸다. 여기서, $$ M_{ijkl}{|}_r=L_{ijkl}^{-1}{|}_r$$이다. 또한 각 상의 국소부위(local) 응력 및 변형율은 다음과 같다.

여기서 A_ijkl|_r, B_ijkl|_r은 각각의 “r” 상에 대한 변형율, 응력 집중인자 텐서(concentration factor tensor)를 나타내며 다음과 표현된다.

여기서 “|₀” 표시는 참고 매개(reference media)를 의미하며 게재물의 부피분율이 작을 때 기저물로 대체될 수 있다. 따라서 여러 상을 갖는 복합재에서의 균질화 혹은 유효 강도 텐서의 각 성분, 변형율 및 응력은 아래와 같이 표현된다.

한편, 2 개의 상을 갖는 복합재에서의 변형율 집중인자 텐서는 다음과 같이 간략화된다.

그럼, 일축 강화 게재물이 혼합된 패널에 대한 강성 텐서의 각 성분은 다음으로 나타낸다.

다음은 균질화를 거친 유효 탄성계수이다.

한편 $$ {\tilde{E}}_3$$는 코로게이트의 형상에 크게 좌우되므로 위의 복합재 균질화기법을 통해 획득되기보다는 앞의 분석식에서 얻은 값이 적용되었다.

위의 결과를 이용하면, 강성 텐서의 각 성분은 다음과 같이 정리될 수 있다.

4. 구성 간 물성 비교

본 구조해석에 이용된 소재로는 외피의 경우 17-4PH, 코로게이트 코어로는 AISI 321이 사용되었으며 각 소재의 상온 및 고온 물성은 다음의 Table 1에 열거되었다.

Table 1.

Material properties at room and elevated temperatures.

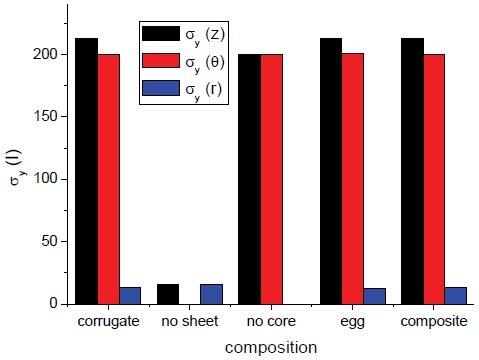
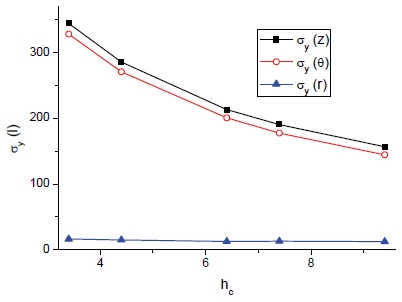
아울러 비교를 위해 코어가 egg-box 형상을 갖는 3층 샌드위치 패널 구조체에 대한 비교도 포함되었다. 한편 방향별 항복강도의 경우도 마찬가지로 복합재에서 보편적으로 이용되고 있는 혼합분율 법칙이 각 layer가 차지하는 상대적 면적에 비례하여 적용되었다. 후에 다시 언급될 예정이나 두께 방향 항복응력 및 탄성계수가 축방향에 비해서 상대적으로 상당히 낮은 수준이다.

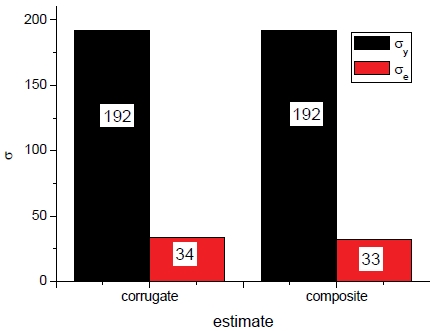
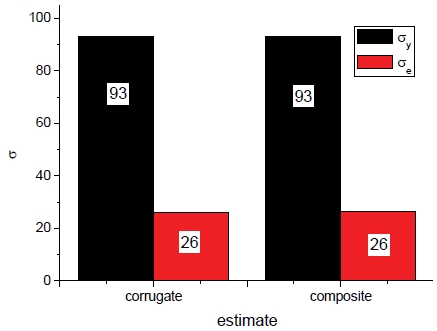
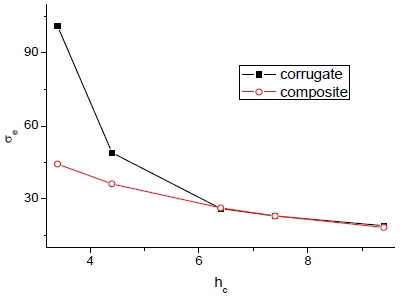
Fig. 2와 3에서는 각각의 샌드위치 패널의 구성에 따른 등가 및 방향별 항복강도를 각각 보여준다. 또한 외피가 제거된 상태를 제외하고 비슷한 수준의 등가 항복강도를 보이며 코어 층이 제거된 경우에는 상대적으로 약간 낮은 값을 보이나 감소량은 크지 않은 것으로 나타났다.

Fig. 2

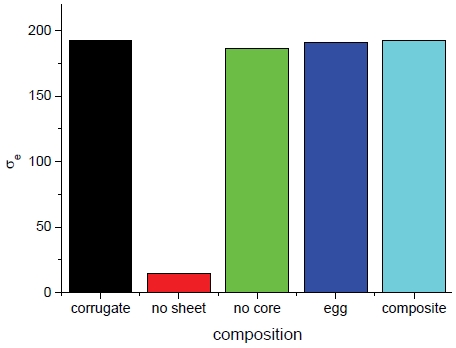
Composition on σe (corrugate: analytical and composite: homogenization).Fig. 2의 약어 설명- corrugate: corrugate sandwich panel analytical closed form- no sheet: outer sheets removed- no core: corrugate core removed- egg: egg-box sandwich panel- composite: composite homogenization

Fig. 3

Composition on σy(I) (corrugate: analytical and composite: homogenization).

외피 제거상태에서는 모든 방향에서 낮은 항복강도를 가지므로 구조체로서의 기능을 거의 상실한 반면 코어 층이 제거상태에서는 두께 또는 반경방향의 강도가 전혀 존재하지 않는다.

Table 2에는 상온에서의 2가지 피치(p)에 대한 코로게이트 분석식과 복합재 균질화 기법으로 얻은 기계적 물성의 비교를 보여주고 있다. 여기서 코로게이트 층의 축방향은 “z” (Fig. 1의 “x”)로 나타내며 코로게이트 분석식이 약간 높은 값을 보이며, 두께방향은 “r” (Fig. 1의 “z”)의 경우에는 같은 값을 보인다. 더욱이 앞서 언급되었듯이 두께방향 탄성계수(E_r)는 축방향 및 횡방향에 비해서 상당히 낮은 값을 보인다.

Table 2.

Corrugated sandwich panel mechanical properties obtained using analytical closed form and composite homogenization.

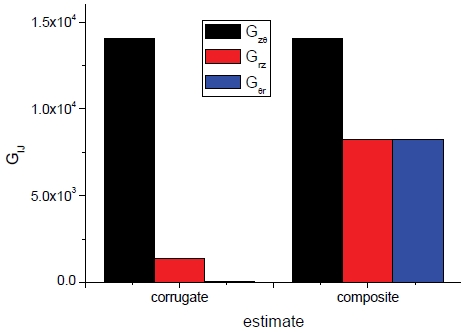
Fig. 4는 전단계수에 대한 물성획득 기법의 비교를 보여주며 “θ”는 원주방향 혹은 코로게이트의 횡방향(transverse)을 나타낸다. 두 가지 기법으로는 동일한 G_zθ이 얻어지며, G_rz 및 G_θr의 경우에는 복합재 균질화 기법이 높은 값을 보인다. 더욱이 복합재 균질화 기법이 적용되면 G_rz = G_θr으로 이는 일축 섬유강화 복합재의 균질화 기법을 가정한 것에 기인하며 따라서 균질화기법의 적용의 한계라고 할 수 있다. 두 가지 기법에 따른 물성과 변형거동에 대해서는 구조해석 결과와 함께 구체적으로 언급될 예정이다.

Fig. 4

Estimate on GIJ shear modulus (corrugate: analytical and composite: homogenization).

5. 구조해석 결과 및 분석

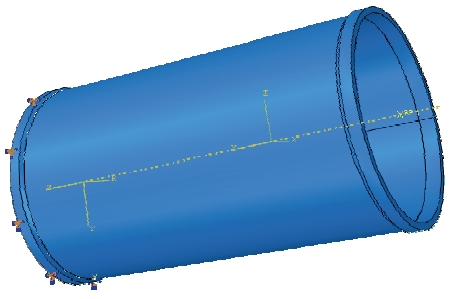
본 구조해석에서 사용된 형상은 Fig. 5에서 보는 바와 같이 코로게이트 샌드위치 패널이 원통으로 말린 구조체이다. 기계적 물성을 결정하는 독립변수로는 코어 층의 높이(h_c), 피치 간격(p), 접합부 폭F), 각 층의 외피 및 코어 두께(t_c, t_s) 등이 있으며 위의 변수의 변화에 따른 변형거동이 분석되었다.

Fig. 5

Cylindrical corrugated sandwich panel.

본 연구에서 사용된 가상의 하중조건은 다음의 Table 3과 같으며 각각 온도별로 측면 모멘트(M_Σ), 축방향 압축(N_c) 및 실린더 내/외면의 압력차(ΔP) 등으로 주어졌다.

Table 3.

Loading conditions.

Fig. 6과 7은 각각 하중조건 1 (상온, 측면하중) 및 2 (고온, 측면하중, 압축, 압력)에 대해 물성획득 기법에 따른 등가 항복강도와 발생된 등가응력 최대값과의 비교를 보여주고 있다.

Fig. 6

σy and σe for loading 1 (corrugate: analytical and composite: homogenization).

Fig. 7

σy and σe for loading 2 (corrugate: analytical and composite: homogenization).

여기서 p=6, h_c=6.4, F=4 mm 형상의 패널이 적용되었으며, 물성획득 기법에 따른 차이가 거의 없는 것으로 밝혀졌으며 또한 구조안전성(Δσ=σ_y - σ_e)도 충분히 확보된 것으로 나타났다.

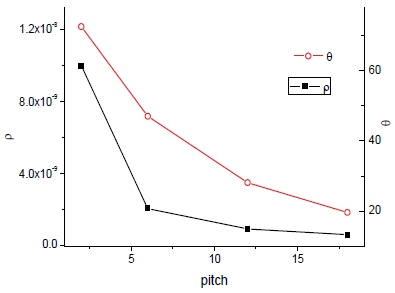
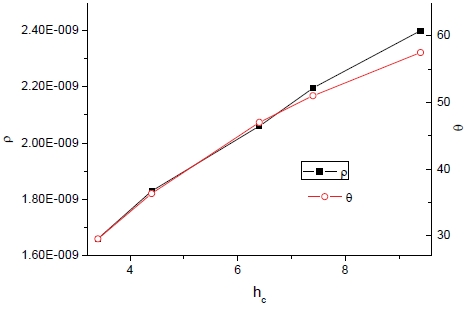
Fig. 8은 피치(p)변화에 따른 코로게이트 샌드위치 패널의 비중(ρ) 및 각도형상(θ)을 나타내며 피치의 증가에 따라 중량과 코로게이트 각도가 감소하며 하지만 동시에 피치 증가에 따른 그 영향은 점차적으로 완만해지는 것이 관찰된다. 더욱이 각도의 감소로 코로게이트 성형이 용이해지며 또한 과다한 성형에 따른 국부적 두께감소가 발생하지 않는 것도 기대할 수 있다.

Fig. 8

Effect of p on ρ and θ.

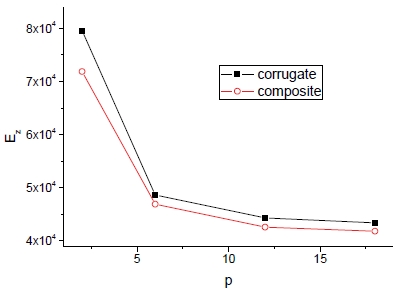
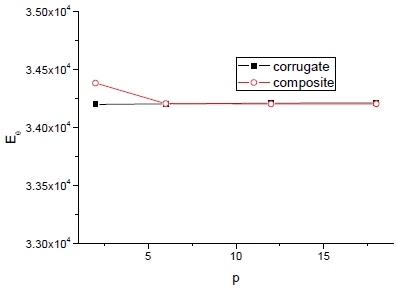
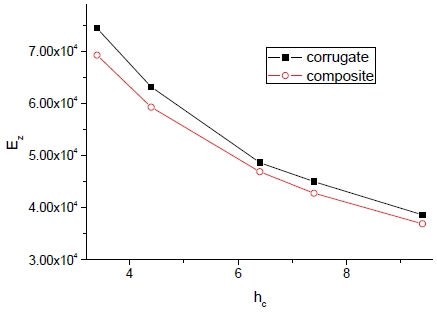
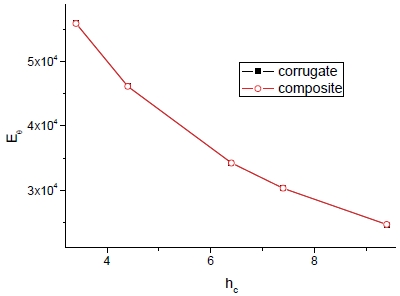
Fig. 9와 10은 피치 증가에 따른 방향별 유효 탄성계수(E_z, E_θ)의 변화를 보여준다.

Fig. 9

Effect of p on Ez.

Fig. 10

Effect of p on Eθ.

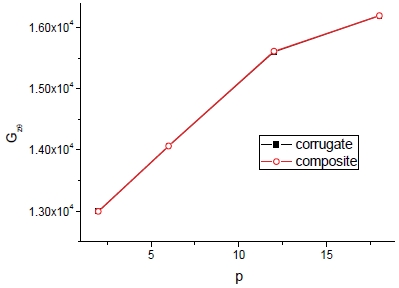
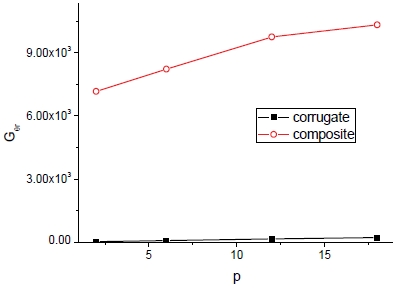
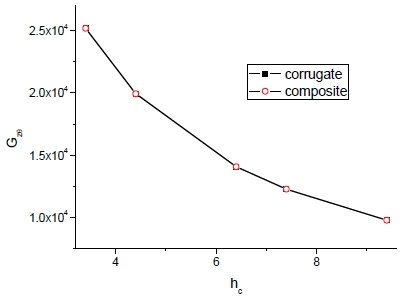
피치에 따른 축방향 탄성계수(E_z)의 현저한 감소가 두드러지며 물성획득 기법에 따라 차이는 있으나 각 기법간의 폭은 거의 일정하다. 한편 횡방향에 대해 피치가 어느 일정수준에 도달하면 거의 변화가 없으며 또한 물성획득 기법에 대한 차이도 없다. 피치에 따른 전단계수의 변화는 Fig. 11과 12에서 보는 바와 같다.

Fig. 11

Effect of p on Gzθ.

Fig. 12

Effect of p on Gθr.

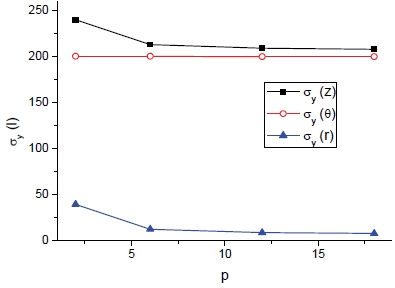
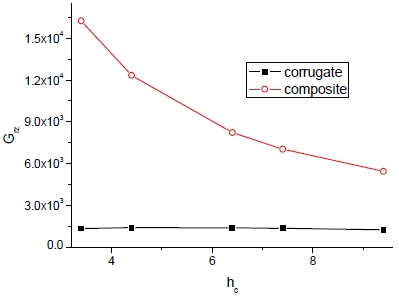
피치에 따라 전단계수는 증가하며 G_zθ의 경우 두 가지의 기법에 따른 차이가 없으나 G_θr의 경우에는 그 차이가 현저하다. Fig. 13은 방향별 항복강도를 보여주고 있으며 피치의 증가에 따라 σ_y(z)와 σ_y(r)는 감소하나 σ_y(θ)에는 변화가 거의 없는 것이 관찰된다.

Fig. 13

Effect of p on directional yield strength.

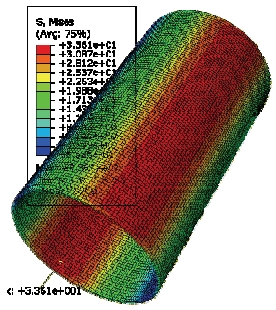
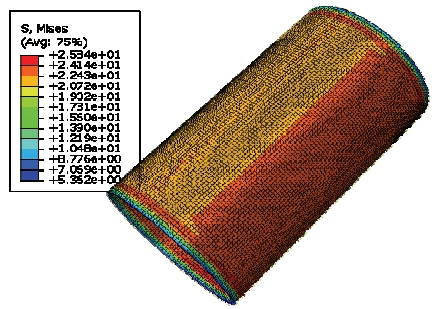
Fig. 14와 15는 Table 3의 하중조건에 따른 코로게이트 샌드위치 패널을 이용한 실린더 구조체에 대한 구조해석결과 응력 분포 예를 나타낸 것으로 이 때 p=6, F=4와 h_c=6.4 mm의 코로게이트 형상이 사용되었다. 측면 하중에 의해 일정한 폭의 최대 응력부위가 발생하는 것이 관찰된다. 주어진 하중에 대해 발생한 최대응력을 근거로 구조안전성이 분석되었다.

Fig. 14

Stress distribution withloading condition 1.

Fig. 15

Stress distribution with loading condition 2.

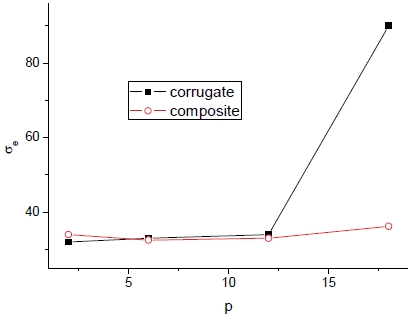
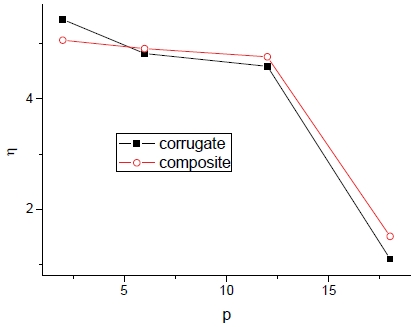
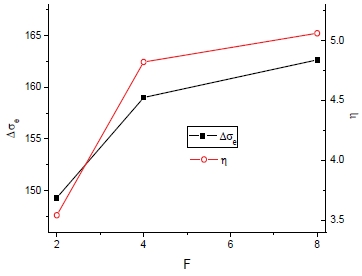
다음의 Fig. 16과 17은 피치 p의 변화에 따른 등가응력의 최대값(σ_e|_max) 및 구조안전율(η=σ_y/σ_e-1)의 변화를 보여준다.

Fig. 16

Effect of p on σe, loading 1.

Fig. 17

Effect of p on η, loading 1.

여기서 피치에 따라 등가응력은 증가하며 이로 인해 구조안전율 감소하는 것이 관찰된다. 이는 주어진 피치 형상에 따라 응력 값은 변하나 항복강도에는 큰 변화가 없는 것으로 말미암은 것이다. 따라서 피치의 증가로 패널의 제작성은 용이해질 수 있으나 구조적으로 불리하다는 것이 밝혀졌다. 물성획득 기법에 따라서 발생되는 응력에 차이가 있으나 결과적인 구조안전성에는 응력의 격차만큼의 차이는 발생치 않는다.

Fig. 18은 코로게이트 층의 높이(h_c)에 의한 비중 및 각도(θ)의 증가를 보여주고 있다.

Fig. 18

Effect of hc on ρ and θ.

또 이에 따른 탄성계수(E_z, E_θ)의 변화는 Fig. 19와 20에서 보는 바와 같으며 h_c의 증가에 따라 탄성계수는 감소하며 E_z에서는 코로게이트 분석식이 약간 높게 평가하는 반면 E_θ에 관련해서는 두 가지 획득기법에 대해서 동일한 값을 보이는 것이 특징이다. 한편 Fig. 21과 22에는 전단계수의 변화를 나타내고 있다. h_c의 증가에 따라 G_zθ는 감소하며 물성획득기법에 따른 차이는 없다. G_rz의 경우 복합재 균질화 기법에서는 감소하나 코로게이트 분석식에서는 상대적으로 거의 변화가 없는 것이 관찰된다.

Fig. 19

Effect of hc on Ez.

Fig. 20

Effect of hc on Eθ.

Fig. 21

Effect of hc on Gzθ.

Fig. 22

Effect of hc on Grz.

또한 h_c에 따른 방향별 항복강도의 변화는 Fig. 23에서 보여주고 있으며 축방향과 횡방향에서의 감소가 뚜렷이 나타나고 있다.

Fig. 23

Effect of hc on σy(I).

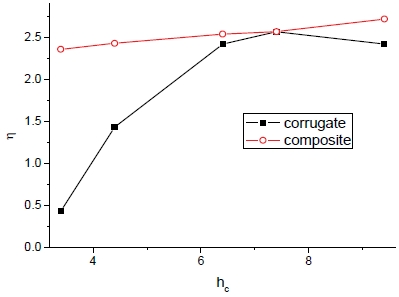
위에서 얻은 탄성계수를 사용하여 얻은 등가응력과 구조안전율은 Fig. 24와 25에서 보는 바와 같으며 구조해석에는 하중조건 2가 적용되었다. h_c의 증가에 대해서 등가응력(σ_e)는 감소하며 비교적 작은 h_c 값에서는 물성획득 기법 간의 예측된 탄성계수 차이 발생에 따른 등가응력의 차이가 발생하나 h_c의 증가로 그 차이는 감소하다가 거의 일치하게 된다. 아울러 구조안전율(η=σ_y/σ_e-1)은 증가하는 것이 관찰된다. 하지만 복합재 균질화 기법으로는 η가 지속적으로 완만하게 증가하나 코로게이트 분석식으로는 급격한 증가 후 다시 감소하는 현상이 발견된다.

Fig. 24

Effect of hc on σe, loading 2.

Fig. 25

Effect of hc on η, loading 2.

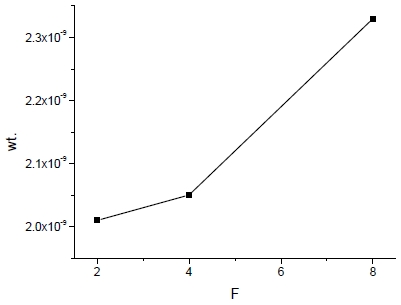
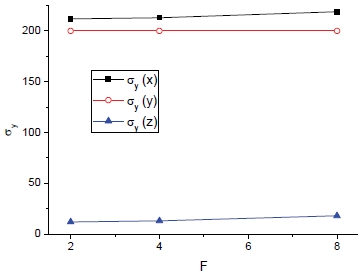
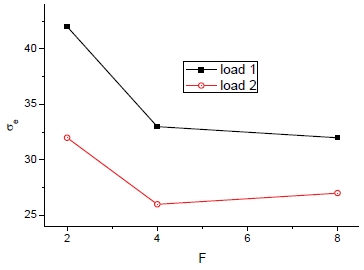
코어 접합부 폭(F)에 따른 중량 및 방향별 항복강도는 Fig. 26과 27에서 보는 바와 같다. F에 따라 중량과 항복강도는 소폭 증가하는 것이 관찰된다.

Fig. 26

Effect of F on weight (p=6, hc=6.4).

Fig. 27

Effect of F on yield stress directional.

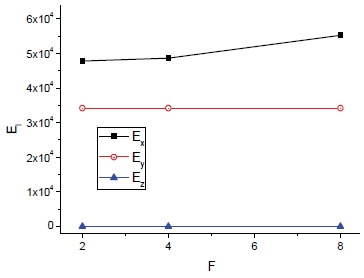
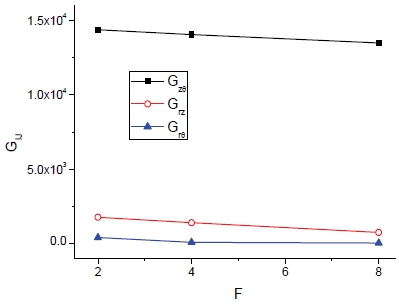
또한 코로게이트 분석식을 통해 F에 따른 탄성계수 및 전단계수는 Fig. 28과 29와 같으며 F에 따라서 약간 증가하나 그 영향은 다른 형상 변수 p나 h_c의 영향에 비해 작은 것이 특징이다.

Fig. 28

Effect of F on normal modulus.

Fig. 29

Effect of F on shear modulus.

Fig. 30과 31에는 F에 따른 등가응력 변화를 보여주며 하중조건에 대해 응력이 감소하는 것을 볼 수 있으며 구조안전율도 동시에 향상된다.

Fig. 30

Effect of F on equivalent stress.

Fig. 31

Effect of F on Δσe & η, loading 1.

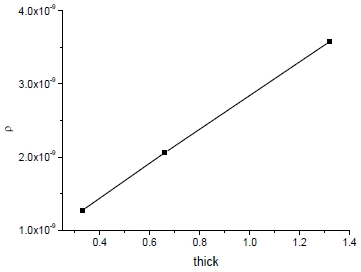
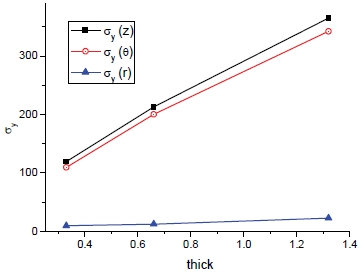
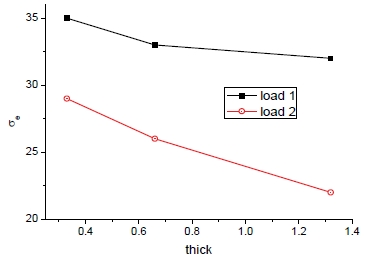
Fig. 32와 33은 외피 및 코어의 두께의 동일한 증가에 따른 밀도 및 방향별 항복강도의 변화를 보여준다. 여기서 두께의 증가에 따라 샌드위치 패널의 밀도 및 항복강도가 거의 비례적으로 증가함이 관찰된다.

Fig. 32

Effect of thickness on density.

Fig. 33

Effect of thickness on yield directional.

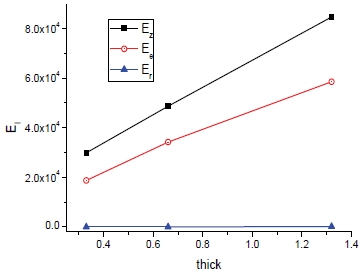
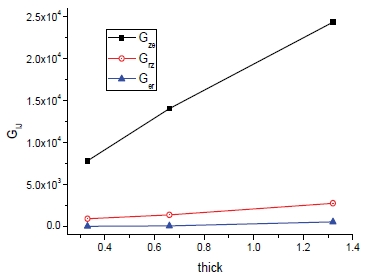
탄성계수(E_I)와 전단계수(G_IJ)의 두께에 따른 변화는 다음의 Fig. 34와 35와 같으며 예상된 바와 마찬가지로 물성도 E_r을 제외하고 거의 비례적인 관계를 보인다.

Fig. 34

Effect of thickness on normal modulus.

Fig. 35

Effect of thickness on shear modulus.

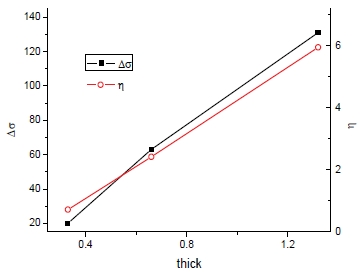
두께에 따라 응력 차이(Δσ=σ_y-σ_e)는 증가하며 구조안전성도 향상된다(Figs. 36, 37).

Fig. 36

Effect of thickness on σe.

Fig. 37

Effect of thickness on Δσ & η.

하지만 각 층 두께에 따른 구조체의 중량이 증가하므로 주어진 하중조건에 대해서 적당한 구조안전성을 확보할 수 있는 범위에서 최적의 형상이 선정되어야한다.

6. 결 어

본 연구에서는 코로게이트 3층 샌드위치 패널 구조체와 관련하여 코로게이트 분석식 및 일축 강화 복합재 균질화기법을 통해서 유효 기계적 물성이 획득되었으며 외피의 영향을 반영할 수 있도록 코로게이트 분석식은 수정되었다. 더욱이 두 가지 물성획득 기법간의 차이가 비교되었으며 이를 이용하여 원통형 3층 샌드위치 패널 구조체에 대한 구조해석에 적용되었으며 또한 각 형상 변수에 따른 샌드위치 패널에서의 물성 변화와 원형형 구조체의 변형거동이 분석되었다.

코로게이트 피치(p)의 증가에 대해 중량 및 코어의 각도가 감소하며 경량화 및 제작성 용이해질 것으로 예상되며 황방향 강도 σ_y(θ) 변화는 거의 없으나 축방향 및 반경방향의 강도는 다소 감소하는 것이 관찰되었다. 코어 층의 높이(h_c)에 따라서 중량 및 코어의 각도는 증가하며 항복강도는 감소함에도 불구하고 응력의 감소로 구조안전성은 오히려 증가한다. 한편 접합부의 폭에 따라 물성에 변화가 다소간 발생하나 그 효과는 다른 형상변수에 비교하여 상대적으로 미미한 것으로 밝혀졌다. 각 층의 소재의 두께에 따라 중량, 물성 및 구조안전성을 현저하게 증가함이 관찰된다.

한편 물성획득 기법에 따라서 방향별 탄성계수에는 다소간의 차이가 발생하나 구조해석을 통해서 얻은 응력 및 구조안전성에는 큰 차이가 없는 것으로 밝혀졌다.

References

• Ko, W.L. “Elastic Constants for Super-plastically Formed-Diffusion Bonded Corrugated Sandwich Core”, NASA Technical Paper 1562.
• Noor, A.K., Burton, W.S., and Bert, C.W., “Computational Models for Sandwich Panels and Shells”, Appl. Mech. Rev., Vol. 49, pp. 155-199, 1996. [https://doi.org/10.1115/1.3101923]
• Isaksson, P., Krusper, A., and Gradin, P.A., “Shear Correction Factors for Corrugated Core Structures”, Composite Structures, Vol. 80, pp. 123-130, 2007. [https://doi.org/10.1016/j.compstruct.2006.04.066]
• Fung, T.C., Tan, K.H., and Lok, T.S., “Elastic Constants for Z-Core Sandwich Panels”, J. Struct. Eng., Vol. 120, pp. 3046-3055, 1994. [https://doi.org/10.1061/(ASCE)0733-9445(1994)120:10(3046)]
• Martinez, O.A., Sankar, B.V., Haftka, R.T., and Bapanapalli, S.K., “Micromechanical Analysis of Composite Corrugated-Core Sandwich Panels for Integral Thermal Protection Systems”, AIAA JOURNAL, Vol. 45, pp. 2323-2336, 2007. [https://doi.org/10.2514/1.26779]
• Lok, T.S. and Cheng, Q.H., “Elastic Stiffness Properties and Behavior of Truss-Core Sandwich Panel”, J. Struct. Eng., Vol. 126, pp. 552-559, 2000. [https://doi.org/10.1061/(ASCE)0733-9445(2000)126:5(552)]
• Carlsson, L.A., Nordstrand, T., and Westerlind, B., “On the Elastic Stiffnesses of Corrugated Core Sandwich”, J. of Sandwich Structures and Materials, Vol. 3, pp. 253-267, 2001. [https://doi.org/10.1106/BKJF-N2TF-AQ97-H72R]
• Buannic, N., Cartraud, P., and Quesnel, T., “Homogenization of Corrugated Core Sandwich Panels”, Composite Structures, Vol. 59, pp. 299-312, 2003. [https://doi.org/10.1016/S0263-8223(02)00246-5]
• Chang, W.S., Ventsel, E., Krauthammer, T., and John, J., “Bending Behavior of Corrugated-Core Sandwich Plates”, Composite Structures, Vol. 70, pp. 81-89, 2005. [https://doi.org/10.1016/j.compstruct.2004.08.014]
• He, L., Cheng, Y.S., and Liu, J., “Precise Bending Stress Analysis of Corrugated-Core, Honeycomb-Core and X-core Sandwich Panels”, Composite Structures, Vol. 94, pp. 1656-1668, 2012. [https://doi.org/10.1016/j.compstruct.2011.12.033]
• Bartolozzi, G., Pierini, M., Orrenius, U., and Baldanzini, N., “An Equivalent Material Formulation for Sinusoidal Corrugated Cores of Structural Sandwich Panels”, Composite Structures, Vol. 100, pp. 173-185, 2013. [https://doi.org/10.1016/j.compstruct.2012.12.042]
• Kooistra, G.W., Deshpande, V., Wadley, H.N.G., “Hierarchical Corrugated Core Sandwich Panel Concepts”, Journal of Applied Mechanics, Vol. 74, pp. 259-268, 2007. [https://doi.org/10.1115/1.2198243]
• Lok, T.S. and Cheng, Q.H., “Free and Forced Vibration of Simply Supported, Orthotropic Sandwich Panel”, Computers Structures, Vol. 79, pp. 301-312, 2001. [https://doi.org/10.1016/S0045-7949(00)00136-X]
• Abaimov, S.G., Khudyakova, A.A., and Lomov, S.V., “On the Closed Form Expression of the Mori-Tanaka Theory Prediction for the Engineering Constants of a Unidirectional Fiber-Reinforced Ply”, Composite Structures, Vol. 142, pp. 1-6, 2016. [https://doi.org/10.1016/j.compstruct.2016.02.001]
• Pavan, R.C., Creus, G.J., Maghous, S., “A Simplified Approach to Continuous Damage of Composite Materials and Micromechanical Analysis”, Composite Structures, Vol. 91, pp. 84-94, 2009. [https://doi.org/10.1016/j.compstruct.2009.04.044]