개방형 사이클 액체로켓엔진 시동해석 코드 개발 및 평가
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문에서는 개방형 사이클 액체로켓엔진의 시동해석을 위해 개발된 해석 코드의 수학적 모델을 제시하였다. 추진제 공급 배관에서의 추진제 충진 과정을 포함하여 엔진을 구성하는 대부분의 요소를 고려하였다. 한국형발사체 시험발사체에 사용된 75톤급 엔진의 시동해석을 수행하였으며, 해석 결과와 실험 결과가 잘 일치함을 보임으로써 시동해석 코드의 타당성을 증명하였다.
Abstract
In this paper, mathematical models of a simulation code are presented. The simulation code was developed for the startup analysis of an open cycle liquid rocket engine (LRE). Most of the components comprising an LRE, including the priming process in the propellant feeding line, were considered. A startup simulation of a 75-tonf LRE, which was used for the KSLV-II test launch vehicle (TLV), was performed. The simulation results showed good agreement with the engine acceptance test results, thus proving the validity of the startup simulation code.
Keywords:
Startup Simulation, Liquid Rocket Engine, KSLV-II, TLV, Mathematical Model키워드:
시동해석, 액체로켓엔진, 한국형발사체, 시험발사체, 수학적 모델1. 서 론
액체로켓엔진의 시동 과정은 엔진 작동 과정에서 가장 중요한 부분으로서, 엔진 연소시험 전에 시동 해석을 통해 시동 구간에서의 엔진 동적 특성을 미리 파악하는 것이 필요하다. 또한 엔진 시동 시, 밸브 및 점화장치 등의 작동 순서에 따라 엔진시동 특성이 변하기 때문에 다양한 경우의 수를 미리 해석으로 평가하는 것이 필요하다. 특히 한국형발사체에 사용되는, 등유-액체 산소를 추진제로 사용하는 개방형 가스발생기 사이클 엔진의 경우, 시동 과정은 1~2초 이내의 짧은 시간에 이뤄지는데, 연소기 또는 가스발생기로의 연료와 산화제 유입 순서가 바뀌거나 추진제 혼합비가 설계 값에서 크게 벗어나는 경우, 엔진이 손상되거나 심할 경우에는 엔진이 폭발할 수도 있다. 시동해석 코드가 없던 시절 러시아의 경우, 엔진 개발 시험 중 발생한 엔진 파손의 30% 이상이 시동과정에서 발생한 것으로 보고되었다[1]. 한편, 미국의 경우에도 Space Shuttle Main Engine (SSME) 개발 시에는 시동해석 코드의 도움을 받지 못하였는데, SSME의 시동 절차를 확립하는 데에만 1년의 시간, 50차례의 시험과 많은 수의 엔진이 사용되었다고 보고되었다[2].
상기와 같이 엔진 시동 과정의 중요성 때문에, 그리고 엔진 개발 기간 및 비용 절감을 위해 해외 발사체 선진국에서는 로켓엔진 시동해석 코드 개발 연구를 활발하게 수행해 왔다[2-10]. 액체산소 및 액체수소와 같은 극저온 추진제를 사용하는 엔진의 해석[2-4,10]에서는 추진제 밀도 변화를 고려하였고, 저장성 추진제를 사용하는 엔진의 해석[5,6]에서는 추진제를 비압축성으로 간주하였다. 시동해석 코드는 전통적인 텍스트 코딩 방식뿐만 아니라 GUI (Graphic User Interface) 방식[7-9]으로도 개발이 수행되고 있다. 대부분의 시동해석 코드는 로켓엔진을 연구 또는 개발하는 기관에서 in-house 코드로 개발을 시도해 왔다. 단, 일부 문헌[8]과 같이 유공압 시스템 상용 해석 코드인 AMESim을 이용하여 시동 해석을 한 경우도 있으나 일반적이지는 않다.
국내에서도 액체로켓엔진 시동해석에 대한 연구가 보고 되었으나 대부분 유공압 시스템 상용 해석 코드인 FloMASTER를 이용하였다[11-13]. 상용 해석 코드를 사용하지 않은 시동해석 연구[14,15]도 일부 있으나 연소기를 제외한 파워팩 해석 결과만을 제시하였다. 국내에서 in-house 시동해석 코드를 이용하여 액체로켓엔진 전체 시스템에 대해 해석하고 이를 실험 결과와 비교한 연구는 아직까지는 보고된 바 없다.
본 논문에서는 in-house 액체엔진 시동해석 코드에 적용된 개방형 가스발생기 사이클 액체로켓엔진의 수학적 모델을 제시하였다. 또한 한국형발사체(누리호)의 시험발사체에 사용된 75톤급 엔진의 시동해석 결과와 수락시험 결과의 비교를 통하여 in-house 시동해석 코드의 타당성을 검증하였다.
2. 액체로켓 엔진의 수학적 모델
2.1 엔진 구성
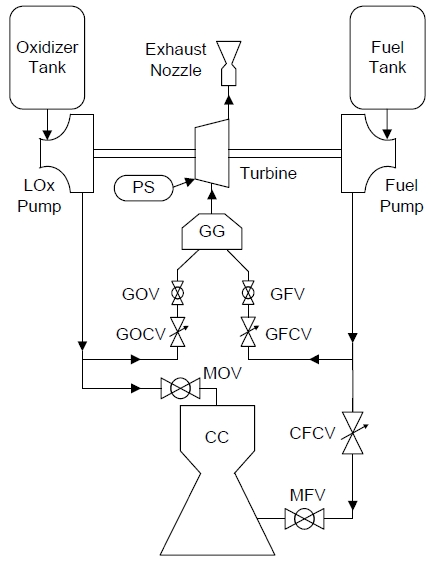
본 연구의 대상인 75톤급 엔진은 개방형 가스발생기 사이클로서, 추진제로 등유와 액체산소를 사용한다. 엔진 구성은 Fig. 1과 같다. 연소기와 가스발생기의 냉각은 연료 재생냉각 방식이다. 추진제 펌프와 터빈은 단일 축으로 연결되어 있다. 엔진 시동 시, PS의 연소 가스가 터빈을 회전시켜 터보펌프를 작동시키고, 이후에는 GG의 연소 가스가 터빈을 회전시키게 된다. 터빈을 통과한 연소 가스는 모두 배기 노즐을 통해 외부로 배출된다.
Schematic diagram of KSLV-II 75-tonf LRE.
2.2 배관 유동 모델
본 연구에서는 1차원 배관 유동 해석을 위해 lumped parameter model을 사용하였다. 배관 유동 모델은 배관뿐만 아니라 연소기 및 가스발생기의 재생냉각 채널, 매니폴드 및 인젝터에도 적용되었다. 추진제는 비압축성 유체로 가정하였으며 열전달은 고려하지 않았다. 배관 유동 모델은 추진제의 priming (또는 filling) 과정을 포함하는데, 본 연구를 위해 선행 연구에서 소개한 배관 유동 모델[16]에 추가된 항은 다음과 같다. 추진제 탱크로부터 엔진 입구까지의 추진제 배관 길이가 수직으로 매우 길기 때문에 중력에 의한 수두를 고려하기 위해 ρgHy 항을 추가하였다. 또한 펌프 양정, Ph 항도 추가하였다. 수정된 배관 유동 모델의 미분방정식은 Eq. 1, 유한차분 방정식은 Eq. 2와 같다.
| (1) |
| (2) |
ay : hydraulic resistance of the given pipelineby : intertial resistance of the given pipelineGy : flow rate throught given pipeline, Hy : heightPin : inlet pressure, Pout : outlet pressureΔt : time increment, g : acceleration of gravityn : current time step, n+1 : following time step
2.3 터빈 모델
터보 펌프의 터빈 출력, Wt는 Eq. 3과 같이 표현된다[17]. L0ad는 작동가스의 이용가능 에너지라고 부르며, 단위질량의 작동가스가 등엔트로피 팽창을 하면서 한 일이다. Eq. 3에서 터빈 효율, ηt은 Eq. 4와 같다[21]. 이때 u는 터빈 팁의 속도, π는 터빈 압력비(P1t/P2), cad는 단열 가스 속도로서 의 관계를 가진다. 계수 Ai, Bi는 상수이며 실험값이다.
| (3) |
| (4) |
2.4 펌프 모델
터보 펌프의 출력, Wp는 Eq. 5와 같이 표현된다[17]. Ph는 펌프 양정(Pa), ηp는 펌프 효율이다. bi, ci는 상수이며 실험값이고, nt은 터보펌프 회전속도(rev/s)이다.
| (5) |
2.5 터보 펌프 에너지 평형 모델
터빈 출력(Wt), 산화제 펌프 출력(Wp,o), 연료 펌프 출력(Wp,f)과 회전체의 관성에 대한 에너지 평형 관계는 Eq. 6과 같다. 단, 기계마찰에 의한 출력 손실은 작으므로 무시하였다. J는 터보펌프 회전체의 회전 관성 모멘트이다.
| (6) |
2.6 연소 모델
연소기 및 가스발생기의 연소에서 연소 지연은 없으며, 추진제가 연소실로 분사된 즉시 완전 기화되어 연소된다고 가정하였다. 연소기, 가스발생기의 압력은 Eq. 7과 같이 이상기체 방정식을 사용하여 계산하였다. 이때 mo, mf는 각각 연소실로 유입된 산화제와 연료의 질량이다.
| (7) |
Eq. 7에서 가장 중요한 요소는 연소가스의 기체상수(R)와 온도(T)이다. 본 연구에서는 Gibbs 자유에너지 최소화 기법을 적용한 in-house 연소해석 코드[18]를 사용하여 혼합비에 따른 R, T를 구하였다. 그러나 가스발생기와 같은 극단적인 연료(등유) 과잉 혼합비 조건에서는 연소 온도가 낮고, 연소가스 체류 시간이 상대적으로 짧아 화학평형상태라고 볼 수 없으므로 상기 코드와 같이 화학평형 조건에서 계산한 연소가스의 물성값은 신뢰할 수 없다고 알려져 있다[19]. 따라서 연료 과잉 혼합비 조건에서 연소가스의 비열비와 기체상수는, CEA 코드[20]에서 연소 생성물 중, 탄소(graphite)를 제외하고 계산하는 방식[19]을 사용하여 획득하였다. 한편, 가스발생기 혼합비에 따른 연소가스 온도는 가스발생기 수락시험[21]을 통해 얻은 값을 사용하였다.
3. 시동해석 코드
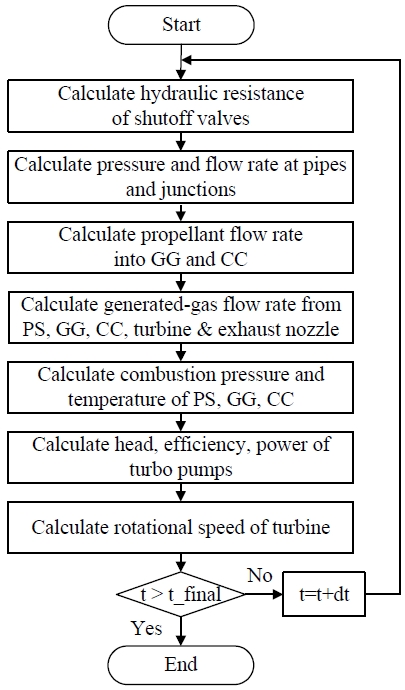
시동해석 코드는 MATLAB을 사용하여 개발하였으며 RETSIM (Rocket Engine Transient Simulation Code)으로 명명하였다. 사용된 함수(서브루틴)는 총 11개로, 배관 유동, 분기배관(junction) 유동(2종), 펌프 성능, 터빈 성능, 연소기 압력, 가스발생기 압력, 가스 유량, 파이로 스타터 압력 및 개폐밸브 유량계수 등을 계산한다. 계산 순서도는 Fig. 2와 같다.
Calculation flow chart of RETSIM code.
4. 엔진시동 해석 및 실험 결과 비교
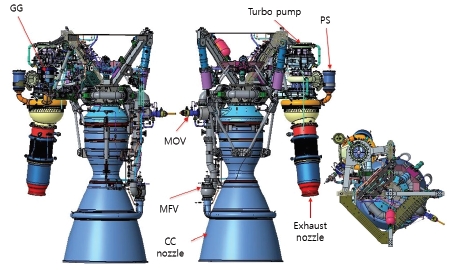
In-house 시동해석 코드를 이용하여 한국형발사체(누리호)의 시험발사체 인증모델에 사용된 75톤급 엔진[Figs. 1, 3]에 대한 시동해석을 수행하였으며 엔진 수락시험 결과와 비교하였다.
Figure of KSLV-II 75-tonf LRE[11].
배관 유동 모델이 적용된 배관의 개수는 총 36개로 Table 1과 같다. 엔진 시동 순서는 MFV 개방, PS 작동, MOV 개방, GFV 개방, GOV 개방 순이다.
Number of pipes.
해석 시, 시간 증분, Δt는 0.2 msec로 계산하였으며 실험 데이터의 sampling rate은 1 kHz이다.
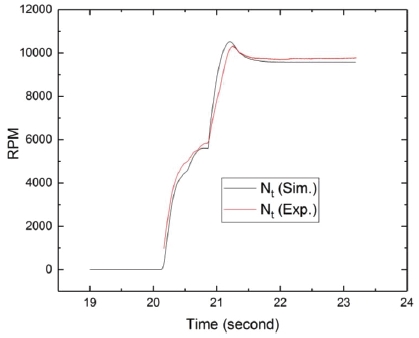
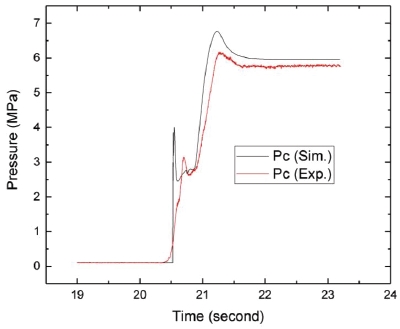
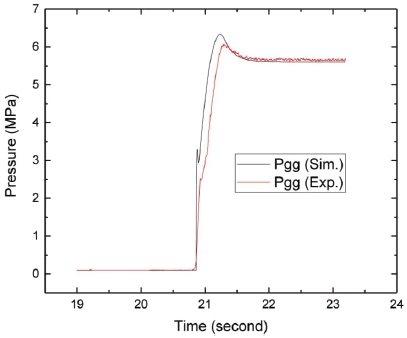
Figs. 4~8은 해석결과와 실험결과를 도시한 것이다. 터보펌프 회전 속도, Nt (RPM)의 경우, Fig. 4와 같이 천이 구간 및 정상 상태에서 해석결과와 실험결과가 거의 일치하고 있다. 참고로 약 1,000 RPM 미만의 회전 속도는 실험값이 수집되지 않았는데, 이는 해당 센서의 특성에 기인한다. Fig. 5의 연소기 연소압의 경우, 전반적으로는 해석결과가 실험결과보다 조금 높으나 비교적 천이 구간을 비슷하게 따라가고 있다. 특히 21.2초 부근에서의 오버슈트(overshoot)를 거의 같은 시간에 나타내고 있다. 이와 같은 연소압의 오버슈트는 PS 작동 시간 및 개폐밸브의 개방 시간과 밀접한 관계가 있다. 오버슈트에 의한 과도한 압력 상승은 시스템에 위험을 초래할 수 있으므로, 시동해석을 통해 오버슈트가 과도하게 발생하지 않는 적절한 시동 시퀀스를 미리 얻을 수 있다. 한편, 20.5초 부근에서 해석값은 실험값과 달리 순간적으로 급격히 상승한다. 이와 같은 차이의 원인은 다음과 같다. 즉, 해석에서는 액체산소를 비압축성 유체로서 기화하지 않는다고 가정하였으나, 실제로는 시동초기에 액체산소가 연소기 내부로 유입될 때 기화가 된다. 따라서 연소기 내부 유동은 액체와 기체가 섞인 다상 유동이 되고, 기화된 산화제로 인해 연소기 내부에 배압이 형성되면서 산화제 유입을 방해하게 된다. Fig. 6의 가스발생기 연소압도 연소기와 같은 이유로 해석값이 실험값보다 천이 구간에서 더 빨리 상승하였다.
Turbo pump rotational speed.
Combustion chamber pressure.
Gas generator pressure.
Fuel pump head.
Oxidizer pump head.
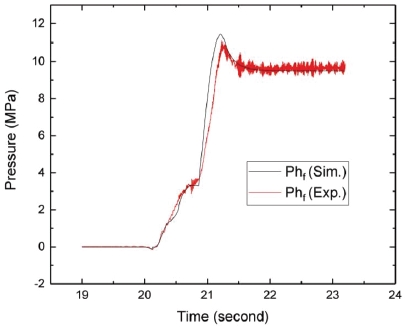
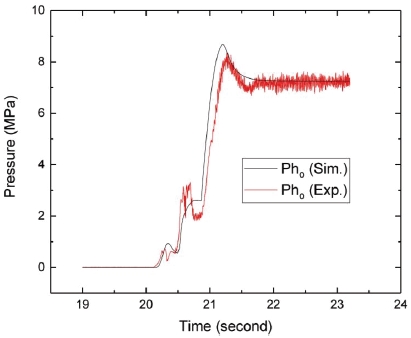
Fig. 7, 8은 각각 연료 및 산화제 펌프의 양정이다. 연료 펌프 양정은 해석결과와 실험결과가 거의 일치하고 있다. 반면에 산화제 펌프 양정은 전반적으로는 비슷하나 20.5~20.9초 구간에서 다소 차이가 있다. 이러한 차이는 연소 압력과 마찬가지로 산화제 기화 현상에 기인하는 것으로 판단된다.
한편, 정상 상태에서의 연소기 연소압(Pc), 가스발생기 연소압(Pgg), 연료 펌프 양정(Phf), 산화제 펌프 양정(Pho) 및 터보펌프 회전속도(Nt)에 대한 해석값과 실험값을 Table 2에 비교하였다. 최대 오차는 연소기 연소압에서 2.58% 수준으로, 해석값과 실험값이 잘 일치하고 있음을 보여준다.
Comparison of steady state results.
5. 결 론
In-house 액체로켓엔진 시동해석 코드를 사용하여 한국형발사체(누리호)의 시험발사체 인증모델에 사용된 75톤급 엔진의 시동해석을 수행하였으며 엔진 수락시험 결과와 비교하였다. 본 시동해석 코드는 액체산소의 기화를 고려하지 않는다. 따라서 연소기와 가스발생기의 연소압과 산화제 펌프 양정의 경우, 시동 천이 일부 구간에서 실험 결과와 다소 차이가 발생하였다. 그러나 전반적으로 시동 천이 구간을 상당히 정확하게 예측하였으며 특히, 오버슈트가 발생하는 시점을 정확히 예측하였다.
액체로켓엔진 개발 과정 중에는 수많은 설계 변경이 발생하고 이에 따른 시동 시퀀스 수정이 필요하다. 또한 엔진 시험 중, 직관적으로는 이해하기 힘든 물리적 현상이 발생하기도 한다. 제한된 예산과 개발 기간 내에서 상기와 같은 문제들을 실험을 통해 파악하고 해결하기는 매우 어렵다. 따라서 본 시동해석 코드가 한국형발사체 엔진 개발 및 차세대 발사체의 엔진 개발 과정에서 중요한 역할을 할 것으로 기대된다.
Nomenclature
| A : | throat area of nozzle or orifice |
| Cd : | discharge coefficient of nozzle or orifice |
| G : | mass flow rate of fluid |
| P1t : | inlet total pressure |
| P2 : | outlet static pressure |
| R : | gas constant |
| T1t : | inlet total temperature |
| k : | specific heat ratio |
| CC : | combustion chamber |
| CFCV : | CC fuel control valve |
| GG : | gas generator |
| GFCV : | GG fuel control valve |
| GFV : | GG fuel shutoff valve |
| GOCV : | GG oxidizer control valve |
| GOV : | GG oxidizer shutoff valve |
| MFV : | main fuel shutoff valve |
| MOV : | main oxidizer shutoff valve |
| PS : | pyro starter |
| ⍴ : | density of fluid |
Acknowledgments
[이 논문은 한국추진공학회 2019년도 춘계학술대회(2019.5.29-31, 라마다프라자 제주호텔) 발표논문을 심사하여 수정·보완한 것임.]
References
-
Kalnin, V.M. and Sherstiannikov, V.A., “Hydrodynamic Modelling of the Starting Process in Liquid-propellant Engines,” Acta Astronautica, Vol. 8, pp. 231-242, 1981.
[https://doi.org/10.1016/0094-5765(81)90033-3]
- Martin, M.A., Nguyen, H.H., Greene, W.D., and Seymour, D.C., “Transient Mathematical Modeling for Liquid Rocket Engine Systems: Methods, Capabilities, and Experience,” 5th International Symposium on Space Propulsion, Chattanooga, Tennessee, U.S.A., 2003.
-
Durteste, S., “A Transient Model of the VINCH Cryogenic Upper Stage Rocket Engine,” 43rd AIAA/ ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, D.H., U.S.A., AIAA 2007-5531, 2007.
[https://doi.org/10.2514/6.2007-5531]
-
Liu, K. and Zhang, Y., “A Study on Versatile Simulation of Liquid Propellant Rocket Engine Systems Transients,” 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Huntsville, A.L., U.S.A., AIAA 2000-3771, 2000.
[https://doi.org/10.2514/6.2000-3771]
-
Ramesh, D. and Aminpoor, M., “Nonlinear, Dynamic Simulation of an Open Cycle Liquid Rocket Engine,” 43rd AIAA/ASME /SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, D.H., U.S.A., AIAA 2007-5507, 2007.
[https://doi.org/10.2514/6.2007-5507]
-
Karimi, H., Nassirharand, A., and Beheshti, M., “Dynamic and Nonlinear Simulation of Liquid-Propellant Engines,” Journal of Propulsion and Power, Vol. 19, No. 5, 2003.
[https://doi.org/10.2514/2.6187]
- Ordonneau, G., Albano, G., and Masse, J., “CARINS: A Future Versatile and Flexible Tool for Engine Transient Prediction,” 4th International Conference on Launcher Technology “Space Launcher Liquid Propulsion,” Liege, Belgium, 2002.
- Vaney, R., Thomas, V., and Lekeux, A., “Transient Modelling of Cryogenic Rocket Engines A Modular Approach,” 4th International Conference on Launcher Technology “Space Launcher Liquid Propulsion,” Liege, Belgium, 2002.
- Atsumi, M., Ogawara, A., Akazawa, K., and Takeishi, K., “Development of Visual Integrated Simulator for Rocket Engine Cycle,” 4th International Conference on Launcher Technology “Space Launcher Liquid Propulsion,” Liege, Belgium, 2002.
- Kanumuri, A., Wakamatsu, Y., Shimura, T., Toki, K., and Torii, Y., “Start Transient Analysis of Turbopump-fed LOX/LH2 Rocket Engine (LE-5),” National Aerospace Laboratory of Japan NAL-TR-868, 1985.
- Moon, Y., Park, S., and Jung, E., “Startup Analysis of KSLV-II 75 tonf Class Liquid Rocket Engine,” 2016 KSPE Spring Conference, Korea, pp. 769-772, 2016.
- Moon, Y. and Jung, E., “A Startup Analysis of KSLV-II Liquid Rocket Engine by Ignition Sequence of Gas Generator-Combustion Chamber,” 2016 KSPE Fall Conference, Korea, pp. 1010-1012, 2016.
- Park, S., Cho, W., and Moon, Y., “Improvement of the Startup Transient Analysis on the Liquid Rocket Engine using the TP+GG Coupled Test Result,” 2011 KSPE Fall Conference, Korea, pp. 821-826, 2011.
-
Lee, S. and Moon, I., “Simulator Development for Startup Analysis of Staged Combustion Cycle Engine Powerpack,” Journal of the Korean Society of Propulsion Engineers, Vol. 19, No. 5, pp. 62-70, 2015.
[https://doi.org/10.6108/KSPE.2015.19.5.062]
-
Lee, S. and Moon, I., “Startup Analysis of Staged Combustion Cycle Engine Powerpack,” Journal of the Korean Society of Propulsion Engineers, Vol. 20, No. 3, pp. 1-8, 2016.
[https://doi.org/10.6108/KSPE.2016.20.3.001]
- Jung, T. and Han, S., “Pipe Flow Model for a Liquid Rocket Engine Startup Analysis,” 2015 SASE Spring Conference, Korea, pp. 166-169, 2015.
- Belyaev, E.N., Chvanov, V.K., and Chervakov, V.V., Mathematical Modelling of Liquid Rocket Engine, Moscow Aviation Institute Press, Moscow, Russia, 1999.
- Jung, T., “Combustion Analysis Program of Liquid Propellent Rocket Engine,” Aerospace Engineering and Technology, Vol. 7, No. 2, pp. 163-167, 2008.
- Kim, S., “Non-Equilibrium Combustion Modeling of Extremely Fuel-Rich Kerosene-LOx Gas Generators,” KARI REG-TM-2004–007, 2004.
- Gordon, S. and McBride, B.J., “Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications,” NASA RP-1311, 1996.
- Moon, Y., Nam, C., Ha, S., and Park, S., “Test Requirement of 75 tonf Liquid Rocket Engine 5G(QM),” KARI L2-ES-01289, 2017.