Center Body 위치와 Cone 각도에 따른 Center Body Diffuser의 유동특성 및 시동에 대한 수치적 연구

2.1 Center Body diffuser 원리

초음속 디퓨저에 사용되는 기본적인 원리는 1-D Normal shock 이론으로 노즐에서 배출된 가스의 운동량으로 인하여 진공챔버 내부에 연행효과를 발생시켜 챔버의 압력을 강하시키고, 디퓨저의 적정한 위치에서 수직 충격파를 발생시켜 유동 압력의 회복 및 배출하는 것이다. CBD의 경우에 노즐에서 가속된 초음속 유동의 plume이 강한 운동량을 가진 상태에서 분사되어 노즐 바깥의 진공 챔버에 연행효과를 발생시킨다. 연행효과로 인하여 챔버의 내부 유체가 초음속 유동과 같이 디퓨져 바깥으로 빠져나가 챔버 내부의 압력은 하강하여 저압 환경으로 모사하게 된다. 노즐에서 배출된 가스는 디퓨져 바깥으로 배출되는 과정에서 CB로 인하여 디퓨저 내부의 단면적이 감소하게 된다. 단면적의 감소로 인하여 경사충격파, 경계층, 재순환 영역이 발달된다. 그리고 초음속에서 아음속으로 감속된 유동을 디퓨저 후단부의 단면적 확장으로 인하여 추가적인 감속을 유도된다. 그로 인해 내부 유동의 압력이 디퓨저 바깥의 외기와 가까운 압력으로 회복되어 배출된다. 이러한 CBD의 특성 중, 초음속 유동의 압력이 회복되는 과정에서 CB와 초음속 유동에서 발생되는 충격파 및 경계층의 상호작용이 발생한다. 노즐에서 분사된 초음속 유동의 감속 및 압력 회복의 과정에서 CB의 형상에 의한 초음속 유동에 미치는 영향이 영향을 받는다. 그리고 CB에 의한 영향이 디퓨저의 시동압력 및 디퓨저의 내부 유동의 형상에도 영향을 미친다.

2.2 초음속 디퓨저의 시동

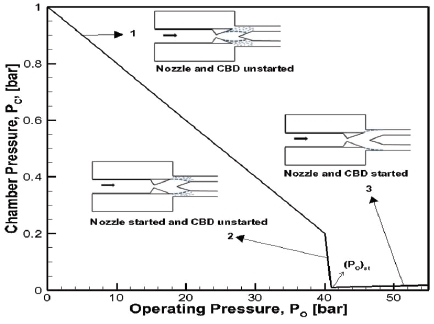
고고도의 저압을 모사할 수 있는 초음속 디퓨저의 시동조건은 nozzle에서 분사되는 가스에 의한 연행효과를 발생시킬 수 있는 plume이 형성되어 진공 챔버의 압력강하를 발생시켜 진공 챔버의 압력이 저압 환경 모사에 충분한 상태에 도달되기 시작한 상태를 디퓨저의 시동이라고 한다. Fig. 1은 이전에 연구된 CAED의 유동 현상을 참고하여 CBD의 형상에 맞추어 디퓨저의 시동 과정의 형상을 나타낸 것이다[4]. Fig. 1에 나타낸 CBD에서 노즐의 plume의 형성과 형태, 디퓨저 시동 여부에 따라서 디퓨저 내부 유동의 형태를 각각 ‘1’, ‘2’, ‘3’으로 나타내었다. 이 때 ‘1’의 상황은 노즐과 디퓨저가 모두 시동되지 않은 상태이다. ‘1’의 상태에서는 노즐에 충분한 입력 압력(p_o)이 인가되지 않아서 발생된다. 낮은 p_o로 인하여 초음속 유동이 노즐 확장부 끝단까지 가속되지 못하고 노즐 확장부의 중간에서 유동 박리가 발생된 상태이다. 또한 노즐의 plume이 진공 챔버에 충분한 연행효과를 발생시키지 못하여 진공 챔버의 고고도 모사가 가능한 저압이 충분히 모사되지 못하여 디퓨저또한 시동되지 못한다. Fig. 1에서 ‘2’상태는 노즐은 시동이 되었으며 디퓨져는 시동이 되지 않은 상태이다. ‘1’ 상태에서 보다 높은 압력을 노즐에 인가하여 노즐에서 가속된 초음속 유동이 노즐 확장부 끝까지 가속된다. 하지만 노즐에서 발달되는 plume이 디퓨저 벽면까지 도달하지 못하였으며, 초음속 유동의 운동 모멘트가 부족하여 진공 챔버에 충분한 연행효과를 일으키지 못한다. 그래서 진공 챔버의 저압 환경이 모사되지 못하였다. 또한 진공 챔버가 디퓨저 바깥의 외기와 격리되지 않고 외기의 영향을 받는 상태이다. Fig. 1의 ‘3’의 상태는 노즐과 디퓨저 모두 시동이 된 상태이다. 초음속 유동은 노즐 끝까지 내부 유동박리 없이 가속되었고 노즐에서 발달된 plume은 높은 운동 모멘트를 가지고 디퓨저 벽면에서 진공 챔버에 연행효과를 발생시켜 챔버 내부 압력을 감소시킨다. 연행효과로 인하여 진공챔버는 고고도 모사가 가능한 저압 환경을 모사된다. 또한 초음속 유동에 의하여 디퓨저 외부 대기와 진공 챔버가 격리되어 디퓨저는 고고도 엔진을 테스트하기 적합한 환경이 모사한다.

Fig. 1

Start-up of nozzle and diffuser according to inlet pressure[3,4]

2.3 Center Body diffuser 형상 및 설계 변수

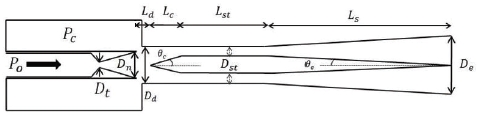
본 연구에서 해석한 CBD의 형상은 Fig. 2와 같은 형태로 설계되었으며, 디퓨저의 설계 변수는 Table 1과 같다. CBD의 설계 변수에서 노즐 팽창비(ϵ), CB 이차목 길이(L_st), 디퓨저 확산부 길이(L_s), 디퓨저 출구 직경(D_e)은 고정변수로 설정하였다. CB의 디퓨저 내부의 위치와 CB의 cone 각도에 따른 유동특성 및 시동 압력을 해석하기 위하여, 노즐과 CB사이의 거리(L_d)와 CB의 각도(θ_c)는 설계 변수로 설정하였다. Table 1의 CBD의 형상 수치는 실험에 사용된 축소형 CBD의 형상이다. 축소형 CBD 실험을 통한 결과와 수치해석을 통한 결과를 비교하기 위해서 축소형 CBD와 동일한 형상과 치수를 이용하여 수치해석을 진행하였다.

Fig. 2

Schematic of CBD and parameters.

Table 1.

Design parameters of CBD.

2.4 CFD 난류 모델

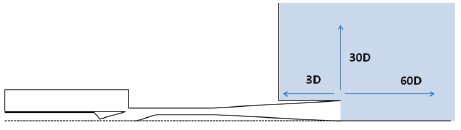
CBD의 유동 해석을 위하여 상용 해석프로그램인 Ansys Fluent v14.5를 사용하였다. 작동 유체는 비연소 조건을 가정하여 질소를 선정하였다. CBD와 비슷한 초음속 디퓨저인 이차목 디퓨저(STED)에 대한 선행 연구를 따르면, 초음속 디퓨저 확산부에서 유동 박리점의 위치가 디퓨저 바깥 외기의 영향을 받는다는 결과가 있다[5]. 따라서 선행 연구 결과를 참고하여 CBD의 해석에서 외기의 영향을 고려하여 Fig. 3과 같이 디퓨저 바깥의 외기의 유동 조건을 설정하였다. Fig. 3에 나타낸 외기의 크기는 디퓨저 확산부의 지름인 D_e를 기준으로 설정되었다.

Fig. 3

Schematic of CBD geometry considering diffuser external ambient.

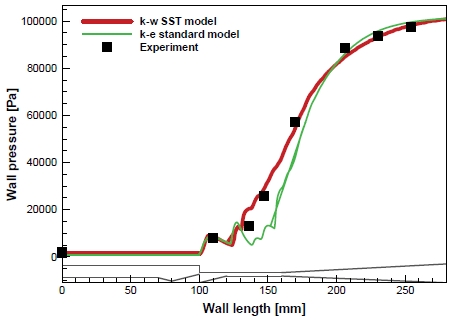
유동해석은 축대칭(axisymmetric) 조건을 적용하였다. 디퓨저 내부의 초음속 유동과 같은 유체 유동을 해석할 때, 실제 유동을 가깝게 모사 할 수 있는 난류 모델을 선택하여 해석이 진행되어야 한다. 본 연구에서 해석에 사용될 난류 모델을 선택하기 위하여 CBD의 축소형 모델을 이용한 실험 값과 standard k-ϵ과 SST k-ω모델 중 SST k-ω을 이용하여 수치해석으로 구한 CBD 내부 벽면의 압력을 비교하여 CBD의 해석에 이용할 난류 모델을 선택하였다. 난류모델 선정에서 Standard k-ε모델을 적용할 때는 Y+가 30~300으로 하였고 SST k-ω 모델에서는 Y+를 5이하로 격자를 생성하였다. Fig. 4는 선행연구에서 축소형 CBD 모델을 이용한 실험 데이터와 각각의 다른 난류모델을 사용한 수치해석 값을 비교한 결과이다[5]. Fig. 4의 결과를 통하여 CBD의 벽면의 압력을 standard k-ϵ 난류모델과 SST k-ω난류모델 중, SST k-ω 난류모델이 실험 값에 standard k-ϵ의 결과보다 더 근사하게 계산되었다. 그리고 CFD에 사용될 난류 모델을 선택에 있어서, 난류모델이 가진 특성을 파악하여 비교하였다. 본 연구에 사용될 CBD와 같은 초음속 디퓨저의 내부에서는 여러 가지 충격파와 재순환 영역, 유동박리와 같은 복잡한 유동과 유동의 압축성 효과를 잘 해석할 수 있어야한다. 하지만 standard k-ϵ모델은 경계층 내부를 벽면함수를 이용하여 모사하기 때문에 유동박리에 대한 정확한 예측이 불가능하다. 그래서 CBD에서의 경사충격파 이후 생성되는 경게층 및 재순환영역을 해석하는데 어려움이 있다. 그러므로 standard k-ϵ모델보다 SST k-ω모델이 유동 박리점과 디퓨저 벽면 근처의 경계층 및 전단층, CB 근방에서 발생되는 재순환영역과 압축성 유동을 계산하는데 적합한 난류 모델로 판단된다. 축소형 CBD 모델을 이용한 실험 데이터와 해석 데이터의 결과 비교 및 난류모델의 특성을 고려하여 CBD의 수치해석에 SST k-ω모델이 실제 현상을 해석하는데 적합하다고 판단되어 SST k-ω모델을 이용하여 수치해석을 진행하였다.

Fig. 4

Comparison of turbulence models and experimental data along the diffuser wall[3].

2.5 Center Body diffuser의 CFD 해석 geometry 분류

CBD 내부에서 CB 위치와 CB의 형상이 디퓨저 내부의 유동특성과 디퓨저 시동 압력에 미치는 영향을 알아보기 위하여 진행되었다. Table 3는 CB cone 각도가 고정된 상태에서 CB의 위치에 따라 CBD의 geometry를 분류하였다. CB cone 각도는 15°를 기준으로 고정하였다. 그 이유는 선행연구에서 L_d/D_st가 0.28인 지점에서 15도의 CB cone angle 형상에서 가장 낮은 압력으로 diffuser가 시동이 가능한 것으로 해석된 결과가 있다[5]. 또한 다른 선행연구의 결과에서 CB의 위치가 노즐에 근접하여 있을 경우 초음속 유동이 챔버 내부로 침입할 수 있다는 결론을 고려하였다[6]. 따라서 CB 위치에 따른 배기가스의 운동 모멘트와 CB의 적절한 위치에 대한 해석을 위하여 Table 3과 같은 CB의 여러 위치의 사례를 해석 대상으로 고려하였다. Table 4는 CB의 위치를 D_st의 3배의 길이만큼 노즐과 떨어진 곳에 고정하였다. 또한 선행 연구에서 CB cone 각도를 5°, 15°, 22.5°로 해석하여 15°의 각도에서 가장 모멘트 손실이 적었다는 결과를 참고하여 Table 4에서 CB cone 각도를 세밀하게 나누어 CB cone 각도에 따른 내부 유동 특성과 낮은 압력에서의 디퓨저 시동의 요인에 대하여 해석을 진행하였다[5].

Table 3.

Analyzed cases of CBD according to position of CB.

Table 4.

Analyzed cases of CBD according to CB cone angle.

2.6 CBD 해석 결과 비교

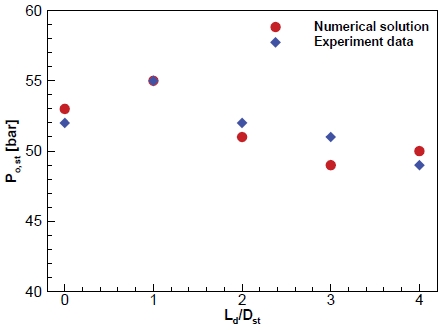
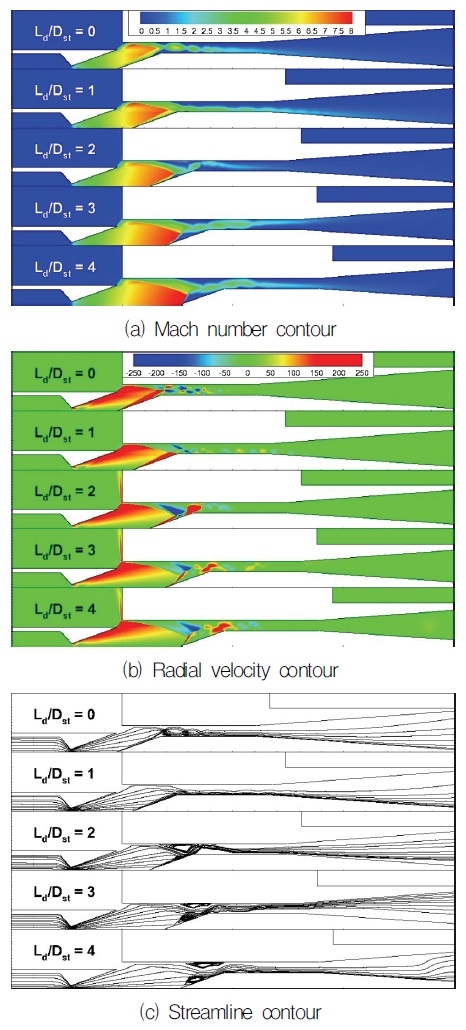
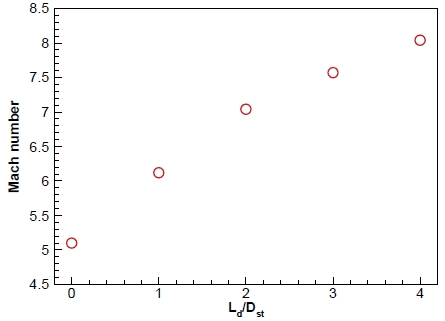
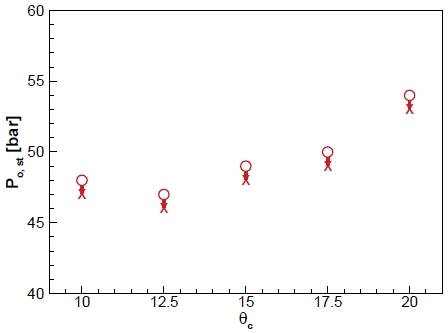
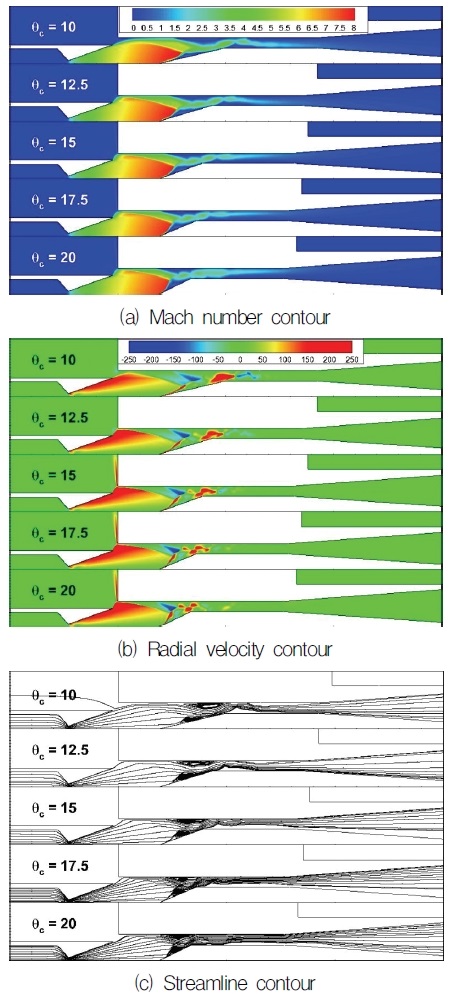
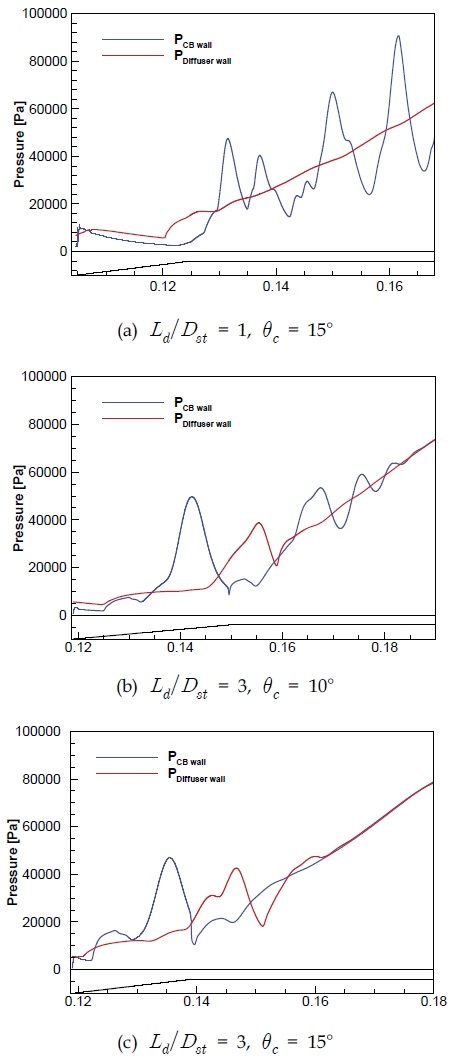
CB의 형상과 위치로 인해 노즐에서 분사된 초음속 유동이 영향을 받는다. 고고도의 저압모사를 위하여 노즐 내부에서 유동박리가 없어야하며, 노즐 주변의 챔버의 압력은 고고도와 비슷한 저압을 모사해야한다. 챔버의 내부 압력은 노즐에서 가속된 초음속 유동의 모멘텀으로 인한 연행효과로 챔버 내부의 유체가 초음속 유동과 함께 Diffuser 바깥으로 빠져나가게 되어 챔버 내부의 압력이 낮아진다. 따라서 CB의 위치 및 cone 각도에 따른 초음속 유동의 유동특성을 파악하기 위하여 수치해석을 진행하였다. CB 위치에 따른 CB와 초음속 유동의 유동 특성을 비교를 위해, 각각의 0D~4D의 CB 위치를 가진 디퓨저의 수치해석 결과를 비교하였다. Fig. 5는 CB 위치에 따른 디퓨저 시동압력을 나타낸 그래프이고 Fig. 6는 CB 위치에 따라 해석한 수치해석 결과를 마하수, 유동의 횡방향 속력을 나타낸 것이다. CB 위치에 따른 내부 유동을 비교하였을 때, CB가 노즐에서 멀어질수록 유동의 모멘텀이 증가되는 것을 Fig. 6(a)와 Fig. 7로 확인할 수 있다. 또한 CB 위치에 의하여 경사충격파의 형성 위치와 재순환 영역이 달라지는 결과를 확인하였다. Fig. 6(c)의 streamline으로 L_d/D_st가 0, 2인 경우에 경사충격파 및 재순환 영역이 CB cone 끝단에 형성되었고 L_d/D_st가 1의 경우에서는 분명하게 나타나지 않았다. L_d/D_st가 3 이상의 경우에 경사충격파 및 재순환 영역이 CB cone 전단에 발생되는 것이 나타난다. 따라서 Fig. 7를 고려하여, CB 위치는 유동 모멘텀 발달에 영향을 미친다. 그리고 CB와 초음속 유동의 상호작용으로 인하여 발생되는 강한 경사충격파의 형성 위치에 영향을 미치는 것으로 판단된다. Fig. 1의 ‘1’과 ‘2’의 차이를 유동 모멘텀과 plume 크기의 차이로 고려하였을 때, Fig. 5에서 L_d/D_st가 0부터 2의 경우, plume이 발달하면서 시동압력이 감소하는 경향을 보여야 한다. 하지만 plume은 발달하였지만 오히려 L_d/D_st=1 경우에 시동압력이 감소하지 않고 상승하는 결과를 얻었다. 그런 의미로, 시동압력의 가장 큰 차이를 보인 L_d/D_st=1, 3의 디퓨저 내부 유동 결과를 비교하였다. 두 조건의 차이점으로 L_d/D_st=1 조건과 달리 3의 경우에 초음속 유동 구간에서 강한 경사충격파가 발생되었다. 또한 Fig. 6(b)를 통하여, 경사충격파 이후의 초음속 유동 방향이 달라지는 것이 나타났다. 따라서 수치해석 결과로, 강한 경사충격파의 형성과 초음속 유동의 방향 변화가 낮은 압력에서 디퓨저가 시동되는 원인으로 판단된다. CB 위치에 따른 디퓨저 시동압력과 유동 특성을 고려하여, 유동 방향에 영향을 미칠 것으로 예상되는 CB cone 각도를 변화시켜 수치해석을 진행하였다. Diffuser 축소부의 유로는 CB로 인하여 중앙이 막힌 원형을 띄며 유로가 좁아진다. 또한 CB를 피하여 유동이 흘러야 초음속 유동의 모멘텀이 유지될 수 있다. 따라서 적절한 위치의 CB와 CB cone 각도를 통해 초음속 유동의 형태를 유도하여 2차목 구간에서 초음속 유동이 Diffuser 벽면과 CB 표면에 치우치지 않도록 하는 것이 중요하다. Fig. 5에서 가장 시동압력이 낮았고 CB cone 전단에 경사충격파가 나타난 L_d/D_st가 3인 CB 위치에 θ_c에 따른 CBD를 해석하였다. Fig. 8은 θ_c에 따른 시동 압력을 나타내고 Fig. 9은 θ_c에 따른 디퓨저 내부 유동 나타내었다. Fig. 8를 통해 θ_c에 따라 CBD의 시동압력이 달라지는 것이 확인되었다. 그리고 Fig. 9를 통해, θ_c에 영향을 받아 경사충격파 형성 각도가 달라지는 것이 나타나며. 재순환 영역의 발달과 유동 방향의 변화가 영향을 받는 것을 확인하였다. θ_c를 따라 경사충격파 각도가 상승할 때, 초음속 유동의 방향 변화가 더 높았으며, 재순환 영역의 확장이 나타났다. θ_c의 초음속 유동에 대한 영향을 확인하기 위해 Fig. 9의 시동압력이 비슷한 θ_c가 10°, 15°조건의 유동 수치해석 결과를 비교하였다. Fig. 10의 (b)와 (c)를 통해, 낮은 θ_c로 경사충격파의 각도가 낮게 형성되면 초음속 유동이 CB 표면에 shock train이 형성되었다. Fig. 10의 벽면에서의 압력 그래프를 통해, 경사충격파의 각도가 낮을 경우에 공통적으로 이차목 구간에서 CB표면에 shock train의 영역이 넓게 나타났다. 경사충격파의 형성 및 Diffuser wall과 CB 표면에서의 압력 결과로 CB 위치와 θ_c가 초음속 유동에 영향을 미치며 Diffuser 시동 압력에 영향을 주는 것으로 판단된다.

Fig. 5

Comparison of starting pressure according to CB position at 15 ̊ of θc.

Fig. 6

Flow characteristics of CBD according to CB position at the 55 bar (po).

Fig. 7

Comparison of mach number at front of CB cone according to CB position.

Fig. 8

Comparison of start pressure according to variable θc (Ld/Dst = 3).

Fig. 9

Flow characteristics of supersonic flow according to variable θc.

Fig. 10

wall pressures of CBD according to CB position and θc.