하이브리드 로켓의 저주파불안정성에 미치는 당량비 영향 직접수치해석

1. 서 론

하이브리드 로켓은 다른 화학 로켓과 달리 비교적 안정한 연소를 하는 것으로 알려져 있다[1-7]. 그럼에도 100 Hz미만의 저주파수 연소불안정(Low Frequency Instability)이 발생하고 있으며, 이 연소불안정의 발생은 고체연료의 열 관성에 의한 열적지연(thermal lag)이 주요한 원인인 것으로 알려져 있다[2]. 최근의 연구결과에 의하면 저주파수 연소불안정의 발생은 500 Hz대역의 압력 및 열방출 진동의 상호 간섭과 매우 밀접한 관련이 있는 것으로 밝혀졌다[3-6]. 특히, Moon 등[4]은 광자수를 측정하는 장치(PMT : Photomultiplier Tube)를 이용하여 연소압력과 함께 열방출의 진동을 측정하여 상호관계를 분석하였다. 그의 결과에 의하면 500 Hz대역의 압력진동(p′)뿐 아니라 동일한 주파수 대역의 열방출 진동(q′)도 함께 나타나는 것으로 확인되었다. 더욱이 저주파수 연소불안정이 시작할 때는 두 종류의 500 Hz대역 진동이 상호 결합하는 것으로 확인되었다. 즉, 안정한 연소가 유지되면 두 진동은 음의 결합(negative coupling)을 형성하지만 저주파수 연소불안정이 발생하면 500 Hz대역의 p′, q′은 양의 결합(positive coupling)을 유지하는 것이 관찰되었다. 따라서 500 Hz대역의 압력과 열방출 진동의 발생과 위상차 변화에 의한 상호 결합관계의 변화는 하이브리드로켓 연소의 저주파수 불안정성을 이해하는 데 매우 중요한 인자임을 알 수 있다.

이와 관련하여, Kim 등[5]은 LES 계산에 의한 수치계산을 통하여 500 Hz대역의 압력진동의 발생 원인에 대한 연구를 진행하였다. 그 결과에 의하면, 축 방향 산화제 유동과 연료 기화에 의한 수직방향의 기화유동이 상호작용하여 경계층 영역 부근에서 작은 크기의 와류가 생성되며 후연소실로 유입되면서 500 Hz대역의 압력 진동이 나타나는 것으로 알려졌다. 따라서 500 Hz대역의 압력진동은 연소실에서 발생하는 음향 가진에 의한 음향파의 발생과는 무관한 것으로 확인되었다. 한편, 500 Hz대역의 압력진동과 같은 주파수대역의 열방출 진동의 발생은 주연소실에서 기화한 미연연료(unburned Fuel)가 후연소실에서 추가적으로 연소하기 때문에 발생하는 것으로 밝혀졌다. 이때 추가적인 연소는 후연소실로 유입되는 작은 크기의 와류 내부에서 발생하므로 압력진동과 동일한 주파수 대역 특성을 갖는 것으로 보인다. 그럼에도 500 Hz대역의 압력과 연소 진동이 저주파수 불안정이 발생하면 위상차가 π/2 이하로 유지되어 양의 결합을 형성하며, 안정한 연소에서는 위상차가 π/2 이상으로 이동하여 음의 결합으로 변화하는 원인에 대한 충분한 연구는 이루어지지 않았다.

이와 관련하여 Hong 등[8]은 하이브리드 로켓 연소실과 같이 분출효과를 포함하지는 않았지만, 후향 계단이 있는 연소실에 대하여 유입온도와 당량비를 변화시키면서 연소압력의 주파수 특성 변화를 실험적으로 연구하였다. 결과에 의하면 당량비의 변화에 의하여 연소압력의 진동특성이 영향을 받아 새로운 주파수 대역으로 천이하며 열방출 진동과의 위상차도 변화하는 것이 관찰되었다. 이 연구에서 사용한 연소실 형상과 난류유동 특성은 하이브리드 로켓 연소실 형상은 서로 다르지만, 당량비의 변화가 연소압력 및 열방출 진동의 주파수 특성과 위상차에 영향을 줄 수 있음을 의미하고 있다.

따라서 본 연구에서는 하이브리드 로켓의 저주파수 연소불안정현상 발생과 매우 밀접한 관련이 있는 500 Hz대역의 압력진동 및 연소반응률 진동의 위상차에 연소 당량비 변화가 미치는 영향에 대하여 직접수치모사(direct numerical simulation) 방법을 사용하여 전산해석을 수행하였다. 수치모사에는 계산영역으로 들어오는 유동의 온도와 조성의 변화를 통하여 당량비 천이를 고려하였다. 특히 당량비 변화가 연소압력과 연소 진동 사이의 위상차 변화에 미치는 영향을 정량적으로 계산하였다.

2. 수치해석

수치해석 방법으로, 하이브리드 로켓 후연소실의 반응 유동장을 정밀하게 해석하기 위해 직접수치해석 기법을 적용하였다. 공간 미분 항에는 6차 정확도를 갖는 유한차분법(finite difference scheme)을 적용하고 시간 미분 항에는 3차 정확도를 갖는 외재적 Runge-Kutta 방법을 적용하였다[9]. 반응 유동장 해석을 위해 연속방정식, 운동량, 화학종 보존방정식을 해석하였고, 메탄의 연소반응 해석을 위해 2단계 아레니우스 모델과 5개 화학종을 이용했다. 본 연구에 사용된 화학반응모델계수는 Table 1에 나타난 바와 같다[10].

Table 1.

2-Step Reaction model for CH4/O2[10].

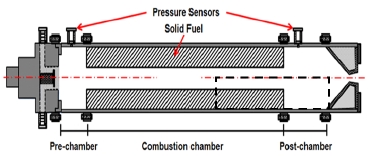
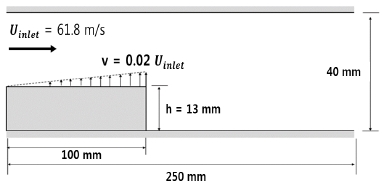
Fig. 1은 시험에서 사용한 하이브리드 로켓 연소실을 도시한 것이다. 본 연구에서 계산영역은 시험모델의 고체연료 일부와 및 후연소실을 포함하고 있으며, Fig. 1의 점선으로 표시한 부분을 발췌하여 Fig. 2에 도시하였다. 그림에 나타난 바와 같이 100 mm길이의 고체연료가 후향 계단의 형상으로 존재하며, 연료상단에서 휘발가스가 축 방향에 따라 선형적으로 분출한다고 가정하였으며 최대분출속도(v)는 실험 결과에 근거하여 유동 유입속도의 0.02배로 설정하였다[11]. 해석영역으로 유입되는 유동은 상류에서 1차 연소가 이루어진 연소가스가 유입되는 것으로 설정하였으며, 고체연료에서 분출된 휘발가스와 혼합되고, 후연소실에서 추가연소가 발생하는 것으로 설정하였다. 이 때 유동의 유입속도는 실험결과에 근거하여 U_{∈ ≤ t} = 61.8 m/s로 고정하였다.

Fig. 1

Schematic of hybrid rocket combustor model[3].

Fig. 2

Calculation domain of hybrid rocket.

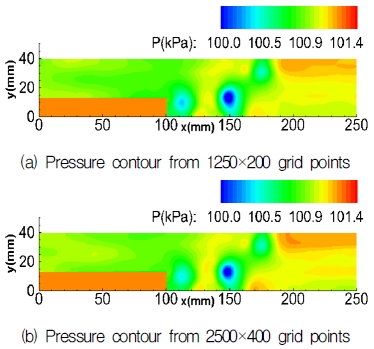
Fig. 3은 본 연구에 사용한 격자계와 4배 증가시킨 격자계의 압력분포를 비교하여 나타낸 그림이다. 그림을 통해 본 연구에서 사용한 약 25만개의 격자계와 격자수를 4배 증가시킨 경우에도 동일한 해석결과를 나타내는 것을 확인하여, 층류조건 해석에 적절한 격자수임을 확인하였다. 2차원 형상에 대하여 수치계산을 수행하였으며, 경계조건에는 계산영역 내에서 발생하는 압력파가 입, 출구에서 반사되지 않는 무반사 조건을 적용하였으며, 상하 경계는 1000K 등온벽면 조건을 적용하였다 [12,13].

Fig. 3

Grid resolution study between (a) 1250×200 and (b) 2500×400 grid points.

수치계산에 사용된 그 밖의 계산조건은 Table 2와 같다. 앞서 언급하였듯이 본 연구의 목적은 당량비 변화가 연소압력과 열방출 진동의 위상차 변화와 그 발생원인에 대하여 정량적인 분석을 하는 데 있다. 따라서 적절한 입구조건의 변화를 통하여 당량비 변화를 모사하였다. 하이브리드 로켓 연소과정에서 당량비 변화는 주연소실에서 발생하며 이로 인하여 연소온도와 연소가스 조성이 변화한다. 특히 당량비 변화에 따라서 연소 후 생성가스에 포함되는 산소와 물의 농도가 변화하므로 본 수치계산에서는 연소온도와 연소가스의 물과 산소의 조성비를 조정하여 당량비 변화를 모사하였다, Table 2는 계산에 사용된 네 가지 경우의 계산조건을 정리한 표이다.

Table 2.

Numerical test conditions.

3. 해석 결과

3.1 일반적인 유동패턴 (Case 1, 기준조건)

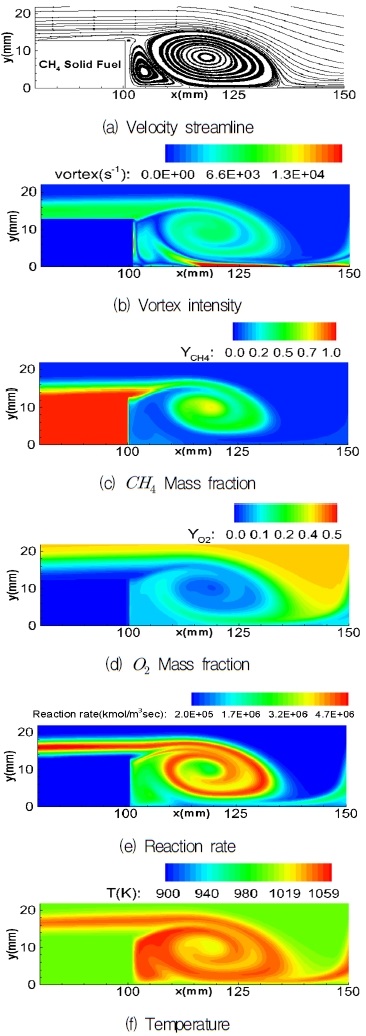
하이브리드 로켓 연소실 내부 반응유동장의 특성을 파악하기 위해 기존의 Case 1 조건을 기준조건으로 하여 직접수치해석을 수행하였다. Fig. 4에는 후향 계단 하류에 생성되는 와류의 모습을 나타내었다. Fig. 4 (a)와 (b)는 계단 후단의 유선분포 및 와류강도를 나타낸 그림이다. 그림에 나타난 바와 같이 확장영역에서 계단 위와 아래의 속도차이로 인해 재순환영역이 형성되는 것이 보인다. Fig. 4 (c)와 (d)에는 동일한 데이터에 대해 메탄과 산소의 분포를 나타냈다. 그림에서 보듯이 메탄과 산소가 와류를 따라 재순환영역으로 유입되어 혼합되고 있음을 알 수 있다.

Fig. 4

General vortex generation at backward facing step for case 1.

Fig. 4 (e)와 (f)에는 연소반응률 및 온도분포를 보여주고 있는데, 그림에 나타난 바와 같이 고온의 메탄과 산소가 고체연료 상부와 재순환영역에서 혼합되어 추가로 반응하며, 이로 인해 재순환 영역 내에서의 온도가 유입유동의 온도보다 상승하였음을 알 수 있다.

후향 계단을 지나는 반응유동은 주기적으로 와류를 형성하고 떨어져 나가면서 이동한다. 이때 와류 내부에서 연소가 진행되며 온도와 압력변화가 발생한다. Fig. 5에서 보듯이 와류가 계단에서 생성된 후에 빠져나가고 있으며, 후향 계단 하류에서 새로운 와류가 생성되어 이동하는 현상이 주기적으로 나타난다. Fig. 6는 와류의 이동에 따라서 나타나는 압력분포를 보여주고 있다. 계산영역에서의 압력분포를 살펴보면 와류영역에서 낮은 압력이 형성되는 전형적인 와류유동특성을 보이고 있으나, 시간에 따라 전체적인 압력이 주기적으로 상승, 하락하고 있음을 알 수 있다. 이러한 계산영역 내 전체적인 압력의 주기적인 변화는 연소반응에 의한 발열 및 팽창에 의한 것으로 추정할 수 있다.

Fig. 5

Sequential image of temperature contours for one cycle in computational domain.

Fig. 6

Sequential image of pressure contours for one cycle in computational domain.

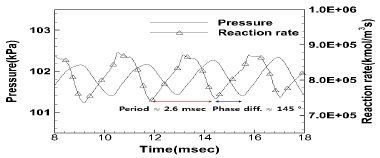
계산영역 내부 평균 압력의 주기적인 변화와 연소반응률 간의 상관관계를 확인하기 위해 Fig. 7에 고체연료를 제외한 유동장 영역에 대하여 평균 압력 및 연소반응률의 시간 변화를 도시했다. 그림에서 보듯이, 평균 압력 및 연소반응률이 동일한 주기(2.6 msec) 및 주파수(384 Hz)로 상승, 하락을 반복하는 것을 알 수 있다. 그러나 평균 압력 및 연소반응률의 위상은 일치하지 않고 있다. 두 진동의 위상차(∆Φ)는 저점기준으로 대략 145 °로 측정된다. 이는 연소반응에 의한 유동의 온도상승 및 팽창효과가 압력파로 전체 연소실로 확장되는 데 걸리는 시간에 의한 것으로 볼 수 있으며, 연소실험에서 관찰한 현상과 동일한 특징을 보여주고 있다[3,4,6].

Fig. 7

Oscillations of pressure and reaction rate for Case 1 Tinlet = 1000 K, ∆Φ ≃ 145 °.

Kim 등의 연구에서와 달리 본 결과에서 500 Hz 대역의 열유동 진동이 나타나지 않은 이유는 연소기 입구에서의 난류강도를 고려하지 않아, 500 Hz 열유동 진동의 주된 원인이 되는 작은 와류가 발생하지 않았기 때문인 것으로 추정할 수 있다[5].

3.2 유입유동의 온도 변화

앞 절에서는 기준조건에 대해 계산결과를 분석하여 와류발생, 압력과 온도의 주기적 변화 등의 주요현상을 살펴보았다. 후향 계단을 지나면서 와류가 형성되며, 이 영역에서 연료 및 산화제가 혼합되어 연소반응에 의한 압력진동이 유도되는 현상을 확인하였다. 따라서 본 절에서는 당량비 변화에 따른 압력진동과 연소반응률 진동의 위상변화를 확인하기 위해 당량비 변화에 따른 유입유동의 온도를 변화하여 전산해석을 수행하여 고찰하였다.

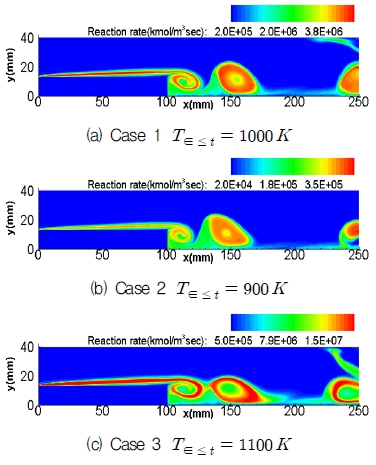
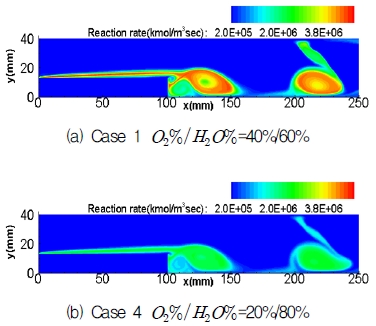
Fig. 8은 Case 1, Case 2, Case 3의 연소반응률 분포를 나타낸 그림이다. 와류의 형태를 비교하고자 서로 다른 분포 등고선 값을 적용하였으며, 각 그림은 최하류 측 와류의 중심이 계산영역의 출구에 도달했을 때를 동일하게 적용하여 비교하였다. 그림을 살펴보면, 연소반응률은 온도와 화학종농도의 지수형태로 표현되므로, 연료 및 산화제의 분포 및 온도변화에 따라 연소반응이 집중되는 영역분포가 달라지고 있으나, 모든 경우에 대해 연소반응 구간이 와류영역을 중심으로 분포하고 있으며, 공통적으로 후향 계단에서 새로운 와류가 생성되는 주기성을 나타내고 있다. 또한, 유입유동의 온도가 높을수록, 더 활발한 연소반응이 이루어지고 있음을 알 수 있다.

Fig. 8

Reaction rate contour for each case.

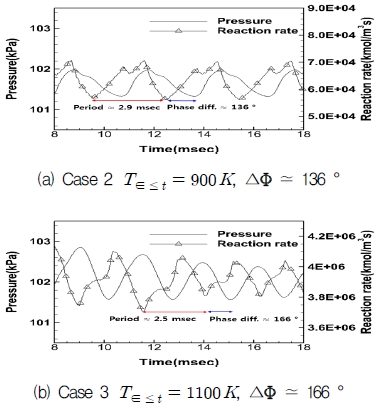
유입유동의 온도변화가 계산영역의 평균 압력 및 연소반응률에 미치는 영향을 보다 자세히 살펴보기 위해 Case 2, 3의 고체연료를 제외한 유동장 영역에 대하여 평균 압력 및 연소반응률의 시간변화를 Fig. 9 (a), (b)에 각각 나타냈다.

Fig. 9

Oscillations of pressure and reaction rate for (a) Case 2, (b) Case 3.

그림을 살펴보면, 압력과 연소반응률의 파형은 경우에 따라 다르게 나타나고 있으며, 저점기준의 주기(주파수)는 Case 2의 경우 약 2.9 msec(344 Hz), Case 3의 경우 약 2.5 msec(400 Hz)로 소폭 변화하는 것이 확인되었다. 압력과 연소반응률 간의 위상차를 살펴보면 Case 2의 경우 약 136 °, Case 3의 경우 약 166 °로 확연한 변화를 보이고 있다. 이는 3.1 절에서 나타낸 Case 1의 위상차 약 145 °와 차이를 보이고 있어, 유동유입 온도의 변화가 압력 및 연소반응률 진동의 주기에는 큰 영향을 주지 않지만, 위상차에 분명한 영향을 주는 것을 알 수 있다.

3.1절에서 언급한 바 있듯이, 연소반응률과 압력진동의 위상차는 연소반응에 의한 온도상승 및 팽창효과가 압력파로 전체 연소실로 확장되는 데 걸리는 시간에 의한 것으로 볼 수 있다. 압력파의 속도, 즉 음속은 온도의 제곱근에 비례하므로, 유입유동 온도 변화가 음속 변화를 초래하여, 위상차가 발생한 것으로 분석된다.

3.3 유입유동의 조성 변화

본 절에서는 당량비 변화에 따른 유입유동의 조성변화가 평균 압력과 연소반응률 진동의 위상변화에 어떤 영향을 미치는지 살펴보았다.

Fig. 10은 Case 1과 4에 대하여 새로운 와류가 생성되기 직전 시점의 연소반응률 분포를 나타낸 그림이다. 유사한 주기적 거동의 시간적 구간을 발췌하기 위해 동일한 물리적 시간이 아닌 동일한 유동패턴을 갖는 시점을 선택하여 비교하였다. 그림에 나타난 바와 같이 화학종의 조성의 변화 영향으로 연소반응률의 절대적인 크기는 다르지만, 두 경우 모두 와류영역에 연소반응이 집중되고 있고, 와류의 생성 위치 및 움직임 또한 매우 유사하게 나타나고 있음을 알 수 있다. Case 4가 Case 1보다 낮은 연소반응률을 보이는 이유는 Case 4의 경우 유입되는 산소의 양이 Case 1에 비해 적기 때문인 것으로 해석할 수 있다.

Fig. 10

Reaction rate contour for each case.

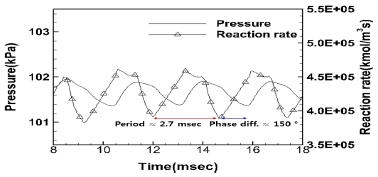
Fig. 11은 Case 4의 고체연료를 제외한 유동장 영역에 대하여 압력 및 연소반응률의 공간적 평균값을 시간에 따라 나타낸 그림이다. 그림을 보면 저점기준의 주기(주파수)는 약 2.7 msec(370 Hz)이며 압력과 연소반응률 진동의 위상차는 약 150 °로 확인되었다. 기준조건인 Case 1과 비교하면, 주기는 거의 동일하고, 위상차는 약 5 °정도로 소폭 변화가 있는 것으로 나타났다.

Fig. 11

Oscillations of pressure and reaction rate for Case 4 ∆Φ ≃ 150°.

따라서, 본 결과로부터, 당량비 변화에 의해서 압력과 연소반응률 사이의 위상변화가 발생하며, 유입유동의 조성변화보다 온도변화에 의한 위상변화가 더 두드러지고 있음을 알 수 있다.

4. 결 론

하이브리드 로켓의 연소에서 주연소실의 당량비 변화가 연소 압력 및 발열량 진동 사이의 위상변화에 미치는 영향을 정량적으로 확인하기 위하여 직접수치해석을 수행하였다. 당량비 변화를 모사하기 위해 유입유동의 온도, 산소/물의 조성비율을 변화하여 모두 네 가지 경우에 대한 전산해석을 수행하였다.

계산 결과에 의하면, 후향 계단 하류에서 와류가 생성되고, 벽면에서 분출된 연료가 미연소 유동과 혼합되어 와류내부에서 추가적인 연소현상이 관찰되었다. 입구 조건에 따라 와류의 모양 및 연소반응률의 크기의 변화가 관찰되기도 하였으나, 와류의 생성, 이동 및 배출되는 현상은 거의 동일하게 관찰되었다. 또한, 계산영역의 평균압력과 연소반응률의 시간변화를 살펴본 결과, 주기는 동일하지만, 위상차가 변화하는 현상들이 확인되었다.

당량비 변화로 인해 유입유동의 온도가 변화한 경우에는, 진동의 주기는 큰 변화가 없지만, 위상차는 크게 변화하는 것이 관찰되었다. 당량비 변화의 결과로, 유입유동의 조성만을 변화시킨 경우에는, 주기는 거의 동일하고, 위상차는 소폭 변화하는 것으로 나타났다.

따라서, 당량비 변화가 압력 및 연소반응률 진동의 위상변화의 원인이 된다는 기존의 연소시험결과를 수치계산으로 확인하였으며, 이러한 위상변화의 주된 원인이 당량비 변화에 따른 유입유동의 온도변화임을 알 수 있었다. 유입유동의 온도변화는 압력파의 이동속도, 즉 음속의 영향을 주어 압력과 연소반응률 진동의 위상변화를 일으킨 것으로 해석할 수 있다.

Acknowledgments

본 연구는 한국연구재단(과학기술정보통신부)의 우주핵심기술개발사업 (NRF-2017M1A3A3A02016374)에 의해 지원받았습니다. 이에 감사드립니다.

References

• R.M. Jenkins, J.R. Cook, "A Preliminary Analysis of Low Frequency Pressure Oscillations in Hybrid Rocket Motors", 31st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, San Diego, C.A., U.S.A., AIAA 95-2690, Jul.), (1995. [https://doi.org/10.2514/6.1995-2690]
• A. Karabeyoglu, S. De Zilwa, B. Cantwell, and G. Zilliac, "Transient Modeling of Hybrid Rocket Low Frequency Instabilities", 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, A.L., U.S.A, AIAA 2003-4463, Jul.), (2003. [https://doi.org/10.2514/6.2003-4463]
• Park, K.S., and Lee, C.J., "Low Frequency Instability in Laboratory- scale Hybrid Rocket Motors", Aerospcase Science and Technology, 42, p148-157, (2015). [https://doi.org/10.1016/j.ast.2015.01.013]
• Moon, Y.J., and Lee, C.J., "Dynamics of Post Chamber Flame and Combustion Pressure in Hybrid Rocket", 52nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Salt Lake City, U.T., U.S.A, AIAA 2016-4869, Jul.), (2016.
• Kim, D.Y., and Lee, C.J., "Destabilization of the Shear Layer in the Post Chamber of a Hybrid Rocket", Journal of Mechanical Science and Technology, 30(4), p1671-1679, (2016). [https://doi.org/10.1007/s12206-016-0323-2]
• Lee, D.E., Moon, Y.J., and Lee, C.J., "Equivalence Ratio Variation and Pressure Oscillations in the Hybrid Rocket Combustion," AIAA Propulsion and Energy Forum, 53rd AIAA/SAE /ASEE Joint Propulsion Conference, Atlanta, G.A., U.S.A, AIAA 2017-4904, Jul.), (2017.
• Koo, W., and Lee, C.J., " The Visualization of Unstable Combustion in Hybrid Rocket", Journal of the Korean Society of Propulsion Engineers, 11(4), p46-51, (2007).
• Hong, S., Shanbhogue, S.J., Speth, R.L., and Ghoniem, A. F., "On the Phase between Pressure and Heat Release Fluctuations for Propane/Hydrogen Flames and Its Role in Mode Transitions", Combustion and Flame, 160(12), p2827-2842, (2013). [https://doi.org/10.1016/j.combustflame.2013.07.001]
• Wray, A.A., "Minimal Storage Time Advancement Schemes for Spectral Methods", NASA Ames Research Center MS-202, (1990).
• Bibrzycki, J., and Poinsot, T., "Reduced Chemical Kinetic Mechanisms for Methane Combustion in O₂/N₂ and O₂/CO₂ Atmosphere", Working note ECCOMET WN/CFD/10/17, (2010).
• Park, C., and Lee, C.J., "Vortices Generation in the Reactive Flow on the Evaporative Surface", Journal of Mechanical Science and Technology, 29(2), p563-570, (2015). [https://doi.org/10.1007/s12206-015-0116-z]
• Kim, J.W., and Lee, D.J., "Generalized Characteristic Boundary Conditions for Computational Aeroacoustics", AIAA Journal, 38(11), p2040-2049, (2000). [https://doi.org/10.2514/2.891]
• Poinsot, T.J., and Lele, S.K., "Boundary Conditions for Direct Simulations of Compressible Viscous Flows", Journal of Computational Physics, 101(1), p104-129, (1992). [https://doi.org/10.1016/0021-9991(92)90046-2]