터보펌프 인듀서에서 캐비테이션 시작점의 특성 및 예측에 관한 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
터보펌프 인듀서에서 발생하는 캐비테이션은 시작점부터 점차 발달하여 임계점, 그리고 급격한 양정 하락으로 이어지는 붕괴점의 과정으로 진행된다. 본 연구에서는 터보펌프 인듀서에서 발생하는 캐비테이션 시작점에 대한 특성과 경험식을 사용한 예측을 평가해 보았다. 타원 평판의 캐비테이션 시작점 경험식은 터보펌프 인듀서의 시작점도 비교적 잘 예측하는 것으로 나타났다. 하지만, 선박용 프로펠러에서 이용되는 경험식의 경우 터보펌프 인듀서의 결과와 큰 차이를 보였다. 터보펌프 인듀서의 캐비테이션 시작점은 날개 수가 증가할수록 빨라졌지만, 현절비와는 무관한 것으로 나타났다.
Abstract
The cavitation of a turbopump inducer develops from the inception to a critical point, and encounters breakdown finally. In this study, we evaluated the characteristics and predictions of cavitation inception for the turbopump inducer using empirical equations. The empirical equation for the elliptical plate predicted the generation of cavitation inception of the turbopump inducer relatively well. However, in case of the marine propeller, it showed a considerable difference owing to the Reynolds number of the operating point. The cavitation inception occurred earlier as the number of blades increased. However, the solidity had no major impact on the cavitation inception because the cavitation occurred locally at the tip of the leading edge.
Keywords:
Turbopump, Inducer, Cavitation inception, Empirical equation키워드:
터보펌프, 인듀서, 캐비테이션 시작점, 경험식1. 서 론
액체로켓엔진에 사용되는 터보펌프는 연료와 산화제를 고압의 상태로 연소실에 공급하는 역할을 한다. 고속, 고압으로 작동되는 터보펌프는 이로 인하여 캐비테이션이 발생하는데, 이를 방지하기 위하여 인듀서(Inducer)를 장착하여 높은 흡입성능을 유지하게 된다. 인듀서는 회전차(Impeller) 앞전에서 캐비테이션을 방지하기 위한 최소한의 양정 상승을 목적으로 하고 있기에 큰 현절비(Solidity)로 설계하게 된다.
터보펌프 인듀서의 캐비테이션은 처음 발생하는 시작점(Inception)에서 일정 비율의 양정이 낮아지는 임계점(Critical point)을 지나 양정이 급격하게 떨어지는 붕괴점(Breakdown)으로 진행되는데, 터보펌프 인듀서에서는 임계점이 중요한 요소이기 때문에 이에 대한 많은 연구가 진행되어왔다[1-3]. 따라서 본 연구에서는 지금까지 수행되지 않은 터보펌프 인듀서의 캐비테이션 시작점의 정확한 예측을 위한 선행차원의 의미로 터보펌프 인듀서의 캐비테이션 시작점에 대하여 연구해 보고자 한다. 캐비테이션 시작점을 정확하게 예측하고 이를 기반으로 시작점을 늦출 수 있는 방법이 개발된다면 자연적으로 임계점 및 붕괴점이 지연되는 효과가 있을 것이다. 터보펌프의 임계점이 낮아지는 것은 입구 압력에 대한 운전 가능 영역이 확대되는 것이기 때문에 시작점에 대한 연구가 의미 있다고 판단하였다.
외부에서 일이 가해지지 않는 익형(Airfoil)의 경우 양정을 정의 할 수 없기에 임계점에 대한 개념이 없고, 선박용 프로펠러에 대한 캐비테이션은 수력성능적인 접근보다 소음이나 진동이 중요한 관점이기 때문에 임계점보다는 캐비테이션의 발생에 초점을 맞추어 연구가 진행되는 실정이다[4-11]. 그렇기 때문에 상대적으로 많은 연구가 수행된 익형 및 선박용 프로펠러의 캐비테이션 시작점에 사용된 경험식을 기초연구 차원으로 레이놀즈 수(Reynolds Number)나 순환(Γ, Circulation) 등의 값을 터보펌프 인듀서에서 사용하는 정의로 바꿔 적용하여 예측하여 보았다. 우선 본 연구를 위하여 수행된 시험의 흡입성능 결과와 가시화를 통하여 캐비테이션 시작점의 특성을 살펴보고, 이와 더불어 인듀서의 날개수와 현절비가 캐비테이션 시작점에 미치는 영향도 평가해 보았다. 이와 관련된 내용은 향후 인듀서에 캐비테이션 시작점을 정확하게 예측할 수 있는 경험식 도출에 참고가 될 것으로 생각된다.
2. 연구 방법
2.1 시험 방법
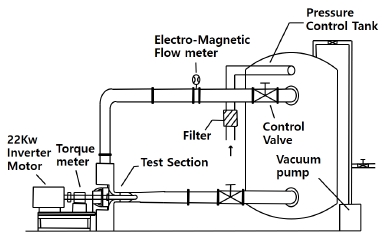
본 연구에 사용된 인듀서는 날개 수가 2개이고, 현절비는 2인 축류 방식의 나선형으로 설계 하였다. 현절비는 날개 길이(C, Chord length)와 날개 사이의 거리(P, Pitch)의 비로 정의한다. 이에 대한 제원을 Table 1에 나타내었다. 시험 장치는 상온의 물인 작동 유체가 순환하는 폐회로(Closed loop) 방식으로 구성하였다. 인듀서는 모터로 구동되며, 배관 하류에 장착된 유량계로 유량을 계측하였다. 인듀서 입구와 출구의 압력은 정압계로 측정하여 양정을 구하였고, 캐비테이션 시험의 경우 유체의 용존 산소를 제거하여 사용하였다. 또한 진공펌프를 이용하여 입구 압력을 낮추었으며, 가시화를 위하여 아크릴로 제작한 케이싱에 초고속 카메라를 사용하여 인듀서 케비테이션의 형상 및 발달 과정을 관측하였다. Fig. 1은 이에 대한 전체 도식을 나타낸 그림이다.
2.2 수치해석 방법
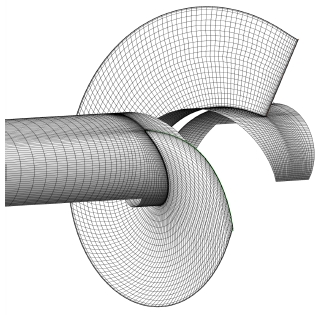
수치해석을 위한 인듀서는 정렬격자로 생성하였고, 계산상의 편의를 위하여 단일 유동통로(Single passage)를 대상으로 하여 유동해석을 수행하였다. 캐비테이션 수치해석의 수렴을 위하여 입구 길이는 직경의 10배에 해당하는 길이로 정하였고, 격자 검증을 통하여 약 150,000개로 구성된 격자를 선택하였다. 이에 대한 인듀서의 격자 형상을 Fig. 2에 나타내었다. 경계조건으로 입구에는 전압을, 출구에는 질량유량을 사용하여 수력성능을 평가하였다. 회전 좌표계와 고정 좌표계의 경계면에는 프로즌로터(Frozen-rotor)의 인터페이스 조건을 주었으며, Shear stress transport(SST) 난류 모델을 채택하여 벽에서의 y+는 10~30을 유지하였다. 흡입성능 계산을 위한 캐비테이션 모델로는 선형화된 Rayleigh-Plesset Equation을 적용하였다.
3. 캐비테이션 특성
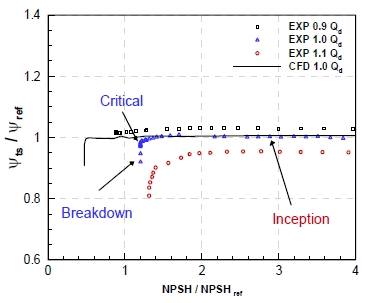
캐비테이션은 액체의 온도가 기화점 이상이거나, 압력이 증기압 이하로 되었을 때 기포가 발생하는 현상이다. 일반적으로 터보펌프 인듀서의 흡입성능 시험은 입구 압력을 낮춰가며 진행하는데, 이때 발생하는 현상은 다음과 같은 과정으로 나타난다. 캐비테이션이 발생하지 않는 영역(High NPSH)에서부터 입구 압력을 낮추게 되면 처음으로 캐비테이션이 발생하게 되는데, 이를 시작점(Inception)이라한다. 이후 캐비테이션은 점차적으로 더 크게 성장하여 어느 순간 양정이 낮아지는 현상이 나타난다. 이 지점을 임계점(Critical point)으로 정하는데, 각각의 터보펌프 특성에 맞게 캐비테이션이 발생하지 않는 영역에서의 양정 대비 1%, 3%, 혹은 5% 낮은 지점을 임계점으로 정한다. 이후 양정하락은 계속 이어지게 되고 어느 순간 양정이 급격하게 떨어지게 되는 붕괴점(Breakdown)에 도달하게 된다. 임계점 이후부터 붕괴점까지 터보펌프는 설계 양정만큼의 압력 상승을 하지 못하기 때문에 이보다 높은 입구 압력에서 터보펌프를 작동시켜야 한다. 즉, 캐비테이션 임계점은 터보펌프의 작동되는 입구 압력의 범위를 정하게 되므로 중요한 설계요소로 여겨진다. Fig. 3과 Fig. 4는 시험을 수행하여 얻은 캐비테이션 흡입성능 곡선을 나타낸 그래프와 각 영역에 해당하는 캐비테이션의 형상을 나타낸 그림이다.
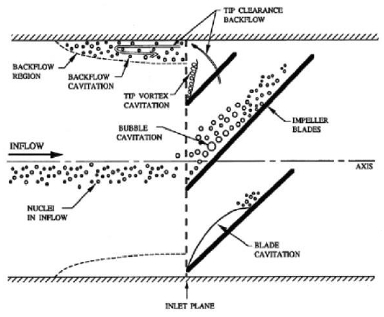
터보펌프 인듀서의 캐비테이션 시작은 인듀서 앞전(Leading edge)의 팁에서 발생한다. 소용돌이 형상으로 발생하기에 이를 소용돌이 캐비테이션(Tip vortex cavitation)이라고 한다. 이후 소용돌이 캐비테이션이 커져가며 끝에서 기포가 떨어지는 현상(Bubble cavitation)이 발생하는데 여기까지를 일반적으로 캐비테이션의 시작으로 간주하고 있다. 시작점을 지난 캐비테이션(Blade cavitation or attached cavitation)은 날개를 따라 더욱 두껍고 길게 발달하게 된다. 이와 관련하여 캐비테이션 형상의 종류를 Fig. 5에 나타내었다[12]. 캐비테이션과 관련된 용어로는 입구 압력을 양정단위로 나타낸 유효흡입양정(NPSH, Net positive suction head)과 무차원으로 나타낸 캐비테이션 수(σ, Cavitation number)가 있다. 이에 대한 정의를 Eq. 1과 Eq. 2에 나타내었다.
| (1) |
| (2) |
캐비테이션 수는 입구의 전압(Pt)과 증기압(Pv)의 차이를 인듀서 날개 앞전 팁의 접선속도(Ut)기준으로 얻어지는 동압의 비로 정의하고 있다. 터보펌프가 운전 될 때에는 양정 하락이 발생하지 않아야하기 때문에 임계점 이상의 입구압력이 확보되는 것이 중요하다. 그래서 설계의 관점으로 캐비테이션 임계점은 운전이 가능 할 수 있는 최소한의 필요한 압력이고, 이러한 이유로 필요유효흡입양정(NPSHr, Required NPSH)이라는 용어로도 사용되고 있다.
4. 캐비테이션 시작점
인듀서의 캐비테이션 시작점을 예측하는 경험식을 구하기 위해서는 다양한 변수에 대한 시험 및 유동해석을 통하여 얻어야 하겠으나 선행연구 차원으로 다른 분야에서 연구된 경험식을 인듀서를 대상으로 하여 평가해 보고자 한다.
4.1 익형 및 평판
Eq. 3과 Eq. 4는 McCormick[13]이 타원 모양의 평판과 직사각형 모양의 평판에 대한 캐비테이션 시작점을 경험식으로 나타낸 식이다.
| (3) |
| (4) |
| (5) |
| (6) |
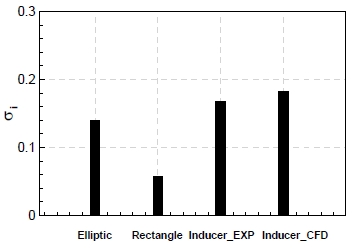
두 경험식에 사용된 레이놀즈 수는 경계층이 없는 영역의 입구 속도(U∞)와 타원 및 직사각형 평판의 길이(L)를 대표 속도와 길이로 사용하고 있다. 이에 대한 식을 Eq. 5에 나타내었다. 두 경험식은 레이놀즈 수는 동일한 지수를 적용하였고, 받음각(α, Angle of attack)에 대한 지수와 계수를 다르게 설정하여 캐비테이션 시작점을 예측하고 있다. 터보펌프의 인듀서의 날개 역시 같은 반경 기준으로 단순하게 보면 2차원의 익형 형상이고, 받음각은 입사각(Incidence angle)과 같은 개념이기에 위의 경험식을 적용시켜도 된다고 판단하였다. Eq. 6은 인듀서에서 일반적으로 사용하는 레이놀즈 수의 정의이다. 이 식으로 얻은 레이놀즈 수의 값을 경험식에 적용하여 터보펌프 인듀서의 캐비테이션 시작점을 예측해 보았다. Fig. 6은 이에 대한 인듀서의 시작점을 예측한 결과이다. 직사각형 평판보다 타원 평판이 더 정확하게 예측하는 것을 확인하였다. 이는 위에서 언급한 것처럼 인듀서 날개는 타원형과 비슷한 익형의 형상으로 설계되기 때문에 타원 평판 경험식의 받음각과 레이놀즈 수에 해당하는 지수 값이 좀 더 적절하다고 판단하였다.
4.2 프로펠러
선박용 프로펠러의 캐비테이션은 날개의 끝(Tip), 허브(Hub), 뿌리(Root), 간극(Gap) 등에서 발생하는데, 프로펠러의 캐비테이션 시작점은 일반적으로 정수압 및 회전의 영향으로 날개 끝에서 소용돌이의 형태로 발생한다. 인듀서의 경우 날개 끝에서 소용돌이가 나타난다면, 프로펠러의 경우는 축을 기준으로 날개 끝에서 소용돌이가 발생한다는 차이점이 있다[10]. Fig. 7은 프로펠러 날개에서 발생하는 소용돌이 캐비테이션을 나타낸 그림이다. 프로펠러의 캐비테이션 시작점 경험식은 Rankine vortex 모델을 기본으로 하고 있다. Vortex 반경 안쪽영역은 와도(ω, Vorticity)가 일정하고 점성 효과가 지배적인 영역으로 간주하고 있고, 이에 더하여 Vortex의 세기(Γ)가 주어지면 반경에 따른 접선속도는 Eq. 7과 Eq. 8로 정해진다.
| (7) |
| (8) |
Spreiter와 Sacks[14]는 Rankine vortex 모델을 운동 방정식에 적용하여 프로펠러의 접선속도와 압력의 관계를 정의하고 증기압을 고려하여 캐비테이션이 발생하는 최소의 압력을 캐비테이션 수로 나타내었다. 캐비테이션의 시작은 속도가 가장 빠른 날개 끝에서 발생하기 때문에 반경에 대한 경계 조건으로는 최대 속도를 가지는 프로펠러의 반경으로 사용하고 있다. 이에 대한 내용의 운동방정식을 Eq. 9에서부터 Eq. 11로 정리하여 Eq. 12의 경험식으로 제시하였다.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Eq. 12에 제시된 C와 D는 프로펠러의 날개 길이와 직경을 의미한다. 선박용 프로펠러에서 발생하는 캐비테이션은 프로펠러 앞전에서 원주방향의 현상으로만 평가하고 있다. 인듀서의 앞전 역시 프로펠러와 유사한 방식으로 볼 수 있는데, 단순하게 보면 두 경우 모두 반경이 다른 두 원형 중 내측 원형이 회전하는 Couette flow 현상으로 볼 수 있다. 또한 내측 원형 안쪽은 프로펠러와 인듀서가 유체에 일을 가해준다는 현상도 동일하다. 차이점이 있다면 프로펠러의 경우 외측 원형은 점착 조건(No slip condition)을 고려하여 반경이 무한대인 반면, 인듀서의 경우는 케이싱이 외측 원형에 해당하고, 두 원형 사이의 공간은 간극(Tip clearance)에 해당한다고 보면 될 것이다. 따라서 프로펠러에서 사용하는 경험식을 인듀서에 적용시켜도 무방하다고 판단하였다. 프로펠러의 시작점에 사용된 레이놀즈 수는 Eq. 13으로 정의하는데 대표속도로 입구 속도와 프로펠러 팁 속도의 제곱평균제곱근(RMS) 개념을 적용하고 있다. 이는 대형 선박의 경우 100 rpm 정도의 낮은 회전속도로 운전되기에 입구속도를 무시하지 못하고 고려해야하기 때문이다. 하지만 터보펌프는 고속으로 회전하기에 높은 팁 속도에 비하면 입구속도는 무시해도 무방하므로 위에 언급한 Eq. 6의 식을 사용하고 있다. 선박용 프로펠러에서 사용하는 계수 및 지수는 경험적으로 k는 0.055, x는 0.52, 그리고 y는 0.4를 제시하고 있다. 이 경험식에 인듀서의 레이놀즈 수를 대입시켜 캐비테이션 시작점을 예측해 보았고, 그 결과를 Table 2에 나타내었다. 시험 결과와 상당한 차이를 보이고 있는데, 레이놀즈 수가 원인이 될 수 있다고 판단하였다. 프로펠러 캐비테이션 시작점의 경험식은 순환, 날개 길이와 직경, 그리고 레이놀즈 수 이렇게 총 4개의 변수로 되어 있다. 이 중에 날개 길이와 직경은 형상에 의하여 명확하게 정의되는 변수이고, 순환은 두 경우 모두 접선 속도를 사용하는 동일한 정의에 의하여 얻어지는 값이다. 따라서 레이놀즈 수에 해당하는 부분이 차이를 발생시키는 원인이라고 생각하였다. 실제 프로펠러는 104~105의 레이놀즈 수 영역에서 운전되고 있지만, 인듀서는 고속으로 회전하기에 프로펠러와는 다른 107의 영역에서 운전되고 있다. 따라서 프로펠러에서 사용되고 있는 경험식에서 레이놀즈 수를 반영하는 지수 값은 인듀서에는 적용하기 힘든 것으로 판단하였다. 뿐만 아니라 순환에 해당하는 x, 및 k에 선택된 값 역시 인듀서에 적용시키기에는 아직 검증이 안 되었다고 판단하였다.
4.3 날개 수 및 현절비
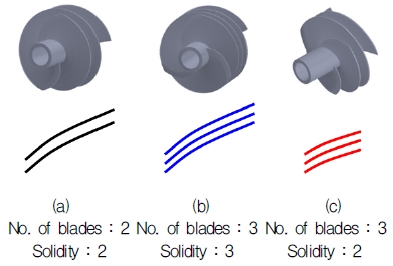
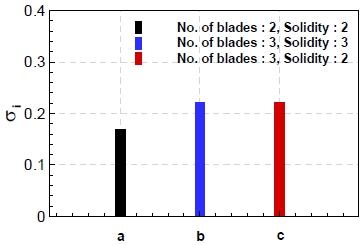
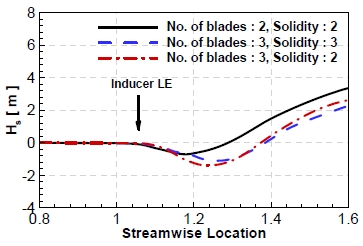
인듀서의 여러 변수 중에서 직경, 입, 출구 날개 각도와 같은 변수는 설계요구양정 및 흡입성능을 위해 중요한 변수로 설정이 된다. 이를 제외하고 캐비테이션의 관점으로 의미가 있는 변수로는 날개 수(Z, Number of blades)와 현절비(S, Solidity)가 있는데, 이 두 변수가 캐비테이션 시작점에 미치는 영향을 평가해 보았다. 본 연구 결과는 향후 터보펌프 인듀서의 캐비테이션 시작점의 경험식을 도출하는데 도움이 될 것으로 생각된다. 날개 수가 2와 3, 현절비가 2와 3에 해당하는 인듀서 세 종류를 선정하여 이를 대상으로 캐비테이션 시험을 수행하였다. Fig. 8은 인듀서 형상을 나타낸 그림이고, Fig. 9는 이 세 형상을 대상으로 시험을 수행하여 얻은 인듀서의 캐비테이션 시작점 결과를 나타낸 그래프이다. 캐비테이션 시작점은 날개 수가 증가할수록 빨리 발생하였지만, 현절비의 영향은 없는 것으로 나타났다. 이는 Fig. 4의 캐비테이션 가시화에서 확인한 것처럼 인듀서의 캐비테이션 시작점은 앞전(LE, Leading edge)의 끝(Tip)에서 국소적으로 발생하는 현상으로 현절비는 동일한 날개 수의 인듀서인 경우라면 입구의 원주방향의 형상과 상관없는 축 방향의 날개 길이와 관련 있기에 캐비테이션 시작점과 관련이 없는 것을 확인하였다. Fig. 10은 유동해석을 수행하여 인듀서 앞전에서의 정압을 나타낸 그래프이다. 유동해석 결과 역시 현절비와 상관없이 날개 수에 의해서만 앞전에서 압력이 차이나는 것으로 보아 위의 결과를 신뢰할 수 있다고 판단하였다.
5. 결 론
터보펌프 인듀서에서 발생하는 캐비테이션 시작점에서의 기포 형상 및 특성을 확인하였고, 인듀서의 날개 형상과 비슷한 익형 및 프로펠러에서 사용되는 경험식을 적용하여 캐비테이션 시작점을 예측하였다. 그리고 설계 변수 중 날개 수와 현절비가 캐비테이션 시작점에 미치는 영향에 대하여 평가해 보았다. 결과를 분석하여 얻은 결론은 다음과 같다.
- (1) 타원 평판의 경험식은 인듀서의 시험 및 유동해석 결과와 비교적 잘 일치했다. 하지만 직사각형 평판은 큰 차이를 보였다. 이는 두 경우 모두 레이놀즈 수에 같은 지수를 적용하였기 때문에 받음각에 대한 영향 및 계수의 차이로 볼 수 있는데, 타원 평판의 받음각에 해당하는 지수 값이 인듀서의 캐비테이션 시작점을 좀 더 잘 예측한다고 볼 수 있었다.
- (2) 선박용 프로펠러의 경험식은 Rankine vortex 모델을 발전시켜 얻은 것으로, 이를 사용하여 예측한 인듀서의 시작점은 시험 결과와 큰 차이를 보였다. 이는 운전 영역에서 레이놀즈 수의 차이로 프로펠러의 경험식에서 적용되는 레이놀즈 수에 대한 지수 값은 인듀서에 적용하기 힘든 것으로 판단하였다.
- (3) 터보펌프 인듀서의 캐비테이션 시작점은 현절비의 변화와는 관계없고, 날개 수가 많아질수록 더 높은 입구압력에서 발생하는 것을 확인하였다. 이는 캐비테이션의 시작점이 인듀서 앞전 팁에서 국부적으로 발생하는 현상이기 때문에 축 방향 길이와 관련이 있는 현절비의 영향은 없는 것으로 나타났다.
References
- Hong, S.S., Park, B., Kwak, H., Kim, D.J., Lee, H., and Kim, J., “Full-Speed Suction Performance Test of a Turbopump for a 75 Ton Class Rocket Engine", Proceeding of the 2013 KSPE Conference, p95-98, (2013).
-
Lee, G.M., Kang, S.H., and Lee, K.H., “Cavitation Test of a High Pressure Turbopump", The KSFM Journal of Fluid Machinery, 7(4), p16-23, (2004).
[https://doi.org/10.5293/kfma.2004.7.4.016]

- Jung, K.N., Park, J.H., Kim, Y,K., and Kim, H.C., “A Study of NPSH required Performance Improvement for a Centrifugal Vertical Pump", Proceeding of the 2009 KSME Conference, p126-131, (2009).
- Kang, T.J., and Park, W.G., “Cavitating Flow Analysis of 2-D Blade”, Proceeding of the 2012 KSCFE Conference, p54-57, (2012).
- Arakeri, V.H., and Acosta, A.J., “Cavitation inception on axisymmetric bodies at supercritical Reynolds number”, Journal of ship research, 20(1), p40-50, (1976).
- Amromin, E.L., “Scaling effect of cavitation inception on a 2D eppler hydrofoil”, Journal of fluid engineering, 124, p186-193, (2008).
- Hsiao, C.T., and Chahine, G.L., “Scaling of tip vortex cavitation inception for a marine open propeller”, 27th Symposium on naval hydrodynamics, (2008).
-
Lee, C.S., Han, J.M., Kim, J.H., and Ahn, B.K., “Propeller Tip Vortex Cavitation Control Using Water Injection”, Journal of the Society of Naval Architects of Korea, 47(6), p770-775, (2010).
[https://doi.org/10.3744/snak.2010.47.6.770]

-
Lee, P.H., Ahn, B.K., Lee, C.S., and Lee, J.H., “An Experimental Study on Noise Characteristics of Propeller Cavitation Inception”, Journal of the Society of Naval Architects of Korea, 48(1), p1-7, (2011).
[https://doi.org/10.3744/snak.2011.48.1.1]

-
Park, S.I., Lee, S.J., You, G.S., and Suh, J.C., “Vortex Cavitation Inception Delay by Attaching a Twisted thread”, Journal of the Society of Naval Architects of Korea, 51(3), p259-264, (2014).
[https://doi.org/10.3744/snak.2014.51.3.259]

- J. Hundemer, and M. Abdel-Maksoud, “Prediction of tip vortex cavitation inception on marine propellers at an early design stage”, 7th International symposium on cavitation, CAV2009-143, (2009).
- Brennen, C.E., Hydrodynamics of pumps, Oxford university press, p288, (1994).
- McCormick, B.W., “On cavitation produced by a vortex trailing from a lifting surface”, Journal of basic engineering, p369-379, (1962).
- Spreiter, J.R., and Sacks, A.H., “The rolling up of the trailing vortex sheet and its effect on the downwash behind wings”, Journal of aeronautical science, 18(1), p21-32, (1951).