추진체계 개념설계단계에서 불확실성 고려방법에 대한 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
고속 추진체계의 개발 초기는 자료의 부족, 비용 제약, 지상에서 실제 비행환경 모사의 어려움 등으로 불확실 요소들을 확률분포의 형태로 모델링하기 어려운 실정이다. 이러한 이유로 본 연구에서는 이중연소 램제트를 대상으로 전문가들의 경험에 의한 연소효율 정보를 수집하여 이를 에비던스 이론으로 모델링하여 불확실성을 정량화 하였다. 정량화한 불확실성 정보를 이용하여 흡입구와 연소기의 출구면적에 대하여 추력여유와 열질식의 불확실성을 고려한 신뢰성 최적설계를 수행하였다. 한정된 불확실 정보를 가지고 엔진의 개념설계가 가능함을 확인할 수 있었다.
Abstract
At the early stages of development of high-speed propulsion systems, associated uncertainties cannot be easily modeled into probabilistic distributions, owing to the lack of test data, cost, and difficulty of simulating real-flight environments on the ground. To tackle this issue, in this research, the combustion efficiencies of dual-combustion ramjet engines are assumed to have been provided by experts and quantified by evidence theory. Using quantified uncertainty, the inlet area and combustor exit are optimized while satisfying reliability margins of thrust and thermal choking. The result shows a reasonable design of the engine under uncertain circumstances.
Keywords:
Uncertainty Quantification, Evidence Theory, Dual Combustion Ramjet, Reliability Based Design Optimization키워드:
불확실성의 정량화, 에비던스 이론, 이중연소 램제트, 신뢰성 최적화1. 서 론
일반적인 최적설계는 입력변수나 모델링의 불확실성을 고려하지 않기 때문에 설계 값은 제약조건은 만족하지만 설계여유를 전혀 가지지 못한 결과를 보여준다. 입력변수나 모델링의 불확실성을 고려하기 위하여 최적설계단계에서 각종 불확실 요소를 수학적으로 모델링하여 반영하는 신뢰성 최적설계(RBDO: Reliability Based Design Optimization)기법이 연구되고 있다. 그렇지만 실제 시스템 개발, 특히 고속추진체계 개발 분야에서 신뢰성 최적설계 기법을 적용하기는 쉽지 않다. 불확실한 변수들을 확률분포를 가지는 확률변수로 모델링하기 위해서는 많은 량의 데이터가 필요한데, 고속 추진체계분야는 사용할 수 있는 데이터의 양은 매우 제한적이기 때문이다. 비용등의 문제로 지상시험 시험설비를 갖추기가 어렵고, 설사 설비를 확보하였더라도 지상시험 조건을 비행환경과 동일하게 가져가기는 매우 어렵기 때문이다.
불확실성에는 지식이나 경험이 부족하기 때문에 발생하는 인지적(epistemic) 불확실 요소와 온도 환경조건과 같이 제어할 수 없는 불확실 요소(random)가 있다[1]. 인지적 불확실요소에 대하여 Shaper[2]는 Dempster의 연구를 기반으로 Dempster-Shaper 이론이라고 불리기도 하는 에비던스 이론(evidence theory)을 제안하였다. 에비던스 이론은 Belief(Bel)와 Plausibility(Pl)이라는 두 매개변수를 각각 불확실성의 최소값과 최대값으로 정의한다. 만일 Bel 과 Pl이 동일하다면 이는 전통적인 확률과 동일한 의미를 가지므로 전통적인 확률은 에비던스 이론의 특별한 경우로 볼 수 있다. 에비던스 이론에서 제시하는 확률 값은 불연속적인 특성을 가지므로 계산시간이 매우 많이 필요하여 그동안 공학분야에서는 잘 적용되지 않았다. 초기에 Oberkampf 와 Helton[3]이 에비던스 이론을 간단한 수식에 적용하였으며, Bae 등[4]이 비교적 큰 규모의 공학문제에 이를 적용한 바 있다. 최적설계 문제에 에비던스 이론을 최조로 적용 한 이는 Agawal 등[5]이다. Mourelatos 등[6]이 매우 효율적인 EBDO(Evidence Based Design Optimization)개법을 제안하였다.
본 논문에서는 DCR(Dual Combustion Ramjet)엔진의 초기 설계단계에서 에비던스 이론을 이용하여 불확실성을 정량화하였다. DCR엔진은 두 개의 연소기, 즉 가스발생기와 초음속 연소기로 이루어져 있다. 두 연소기의 연소효율은 지상시험 자료도 없을 뿐 아니라 수치계산으로 구하기도 어려워 전통적인 방식으로 확률변수를 모델링하기 쉽지 않다. 이에 따라 이 분야의 경험과 지식을 가진 전문가들이 연소기의 효율을 추정하였다. 이 데이터는 구간(interval)별로 제시되어 있으며 상호 인접, 분리 및 중첩 등을 통하여 Bel과 Pl이라는 두 가지 변수를 가지는 불확실성 값으로 추정하였다. 나아가 계산된 불확실성 값을 이용하여 흡입구와 노즐면적을 결정하기 위한 최적설계를 수행하였다.
2. DCR 엔진모델링
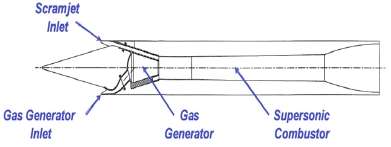
DCR엔진은 1977년 JHU/APL에서 최초로 제기된 개념이다. 이름과 같이 두 개의 연소기를 가지는 데, 고온의 가스를 발생시키는 가스발생기와 초음속 연소가 이루어지는 초음속 연소기가 직렬형태로 배치되어 있다. 아음속 흡입관을 통해 가스발생기로 유입된 공기는 가스발생기내부에서 일부 연소가 이루어진 후, 고온 가스상태 연료가 초음속으로 배출된다. 이 가스상태의 연료는 초음속 흡입관을 통해 유입된 공기와 혼합되어 초음속 연소관에서 연소가 이루어지는 구조이다.
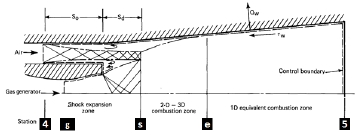
DCR 분야의 대부분의 연구는 Billig 등[7, 8]에 의해 이루어 졌다. Fig. 2는 DCR엔진의 형태를 보여주고 있다. 가스발생기의 출구에서 shock train의 끝단 s까지를 shock expansion zone이라 부른다. 초음속 흡입구를 통과한 공기흐름은 여기를 지나면서 연속적인 충격파를 발생시키며 가스발생기의 출구흐름의 압력 Ps과 동일한 수준을 가지게 된다. s-e구간은 연소영역으로서 반경방향/축방향 연소구배가 형성된다. 많은 실험[9]에서 유효 연소면적(AS)이 실제 연소기 면적과 같아지는 e지점에서 연소압력 Pe가 Ps와 동일해 지는 것을 확인하였다. 이 결과로부터 질량보존, 운동량보존 및 에너지 보존관계 식을 유도하였다.
| (1) |
만일 연소기가 일반적인 축대칭 형상이라면 면적과 압력의 관계는 다음과 같이 유도된다.
| (2) |
여기서 ε은 Billig[9]에 의해 정의된 엔트로피 한계조건으로서 다음과 같이 표현된다.
| (3) |
Fig. 2의 영역4-5구간 벽면압력은 Eq. 2와 Eq. 3을 적분하여 얻을 수 있다.
| (4) |
Eq. 2로부터 면적 관계식은 다음과 같다.
| (5) |
Eq. 5로부터 A5와 영역4와 영역g의 다른 모든 변수를 알고 있을 때, Eq. 1과 Eq. 5를 조합하여 영역5의 변수와 PS를 계산할 수 있다. 그 외 흡입구, 가스발생기 및 노즐 등의 변수들에 계산은 참고문헌[11]에 기술되어 있다.
3. 결정론적 해석
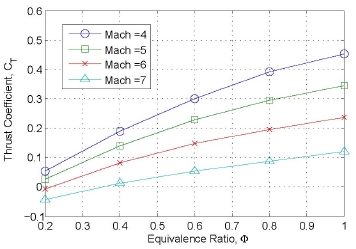
DCR엔진의 모델링을 통해 주어진 조건에서 엔진의 추력 등을 계산할 수 있다. Fig. 3은 고정된 형상에서 당량비와 마하수에 따른 Net Thrust 계수를 보여주고 있다. 당량비가 증가할수록 추력계수가 증가하는 일반적인 경향을 볼 수 있다. 속력이 증가할수록 추력계수가 감소하는 것은 Ram항력의 증가 때문인 것으로 판단된다.
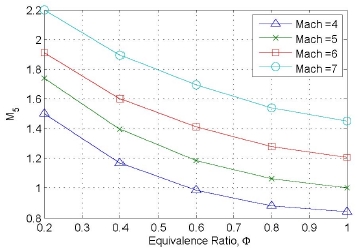
Fig. 4는 초음속 연소기의 노즐 끝단에서의 연소흐름의 마하수를 보여주고 있다. Reyleigh관계식에 의해 일정한 면적의 도관을 지나는 초음속흐름의 속도는 열량이 증가할수록 감소된다. 비록 초음속 연소기 노즐의 면적은 노즐끝단으로 갈수록 증가(A5/Ae=1.668)하지만 열량의 유입이 더 크기 때문에 연소속력이 줄어드는 것으로 생각할 수 있다.
4. 에비던스 이론
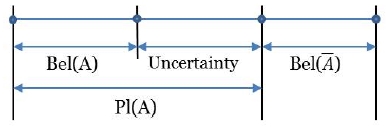
에비던스 이론은 지식이나 경험의 부재에서 오는 인지적 불확실요소를 정량화하는데 유용한 도구이다. 확률분포로 모델링할만한 데이터가 없는 상태에서 전문가들이 경험과 공학적인 지식에 기반하여 불확실 변수의 범위와 이 범위 내에서 구간별로 가중치를 제시한다. 에비던스 이론은 하나의 변수에 대하여 각 전문가들이 제시한 값들을 조합하고, 이를 다른 불확실 변수와 조합하여 전체 시스템의 불확실성을 계산하는 방식이다. 전문가들은 불확실 설계변수를 구간별로 가중치를 가지는 여러 개의 구간으로 나누어 구간별로 가중치를 제시하는데, 이를 BPA(basic probability assignment)라 부른다. BPA는 참 값이 이 구간 안에 존재할 가능성을 나타내는 우도(likelihood)의 의미를 가진다. 하나의 불확실 변수에 대하여 다수의 전문가들은 각기 다른 BPA를 독립적으로 제시하게 되는데, 이때 제시되는 구간은 서로 겹칠 수도 있고 전혀 다를 수도 있다. Evidence의 정량화된 표현인 m은 0에서 1사이의 값을 가지며, 전통적인 확률값과 상이한 개념이다. 집합 A의 부분집합인 집합 B의 모든 BPA, m(A)의 합을 Belief라 부른다. 반면, 집합 A와 교집합 성분을 가지는 집합 B의 BPA, m(A)의 합을 Plausibility라고 부른다. 따라서 Belief(A), 또는 Bel(A)는 집합 A의 최소값이며, Plausibility(A) 또는 Pl(A)는 집합 A의 최대값이 된다.
| (6) |
전문가들이 제시하는 불확실 변수의 범위와 구간별 가중치가 일치하지 않으므로 이를 적절히 조합하여 하나의 BPA로 산출하는 과정이 필요하다. 다음은 Dempster‘s rule에 따라 여러 BPA를 하나의 BPA로 조합하는 과정이다. 만일, 두 명의 전문가 의견 m1과 m2 로 정의되는 두 개의 BPA가 있다면, m(A)는 집합 B와 집합 C의 교집합 구간에서만 정의되는 m을 가리킨다. Dempster‘s rule에 따라 Eq. 7과 같이 두 개의 m을 하나의 m으로 조합할 수 있다.
| (7) |
여기서
로서 1-K는 조합된 m(A)를 정규화하기 위해 나누어 주는 값이다. 여기서 Pl(A)는 1에서 Bel()를 뺀 값과 같다.
| (8) |
Fig. 5는 Bel(A)과 Pl(A)의 관계를 보여준다. 여기서 Bel(A) 와 Bel() 사이에는 불확실성이 존재하므로 두 값의 합은 반드시 1이 될 필요는 없다. 만일 Bel(A) 과 Pl(A)은 같은 값을 가지다면 이는 전통적인 의미의 확률이 된다. 결론적으로 Bel(A) 과 Pl(A)의 관계는 다음과 같다.
| (9) |
5. 불확실성 정량화
본 연구단계에서 DCR엔진의 가스발생기 연소효율(ηg)과 초음속 연소기의 연소효율(ηc)은 지상시험이 불가능 했으며, 전산해석으로도 얻기 어려운 변수였다. 이에 두 변수를 유사분야의 경험을 가진 전문가들로부터 Table 1과 같이 얻었다. 두 명의 전문가가 각 변수에 대하여 구간과 BPA를 제시하였다. 여기서 BPA는 일종의 가중치와 유사한 개념이다. Eq. 6의 Dempster의 방식을 적용하여 BPA를 조합하였다. 예를 들어, ηc에서 두 전문가가 제시한 것 중에서 중첩된 구간은 [0.86-0.88], [0.88-0.90], [0.90-0.92], [0.92-0.93], [0.93-0.94]이다. [0.86-0.88] 구간에서 BPA는 0.2(mExp1) × 0.3(mExp2) = 0.06이 된다. 계산된 1-K=0.4이므로 m[0.86-0.88] = 0.15이다. 이와 같은 방식으로 각 변수에 대해 BPA를 조합하면 Table 2와 같은 결과를 얻는다.
Table 2는 각각의 변수들에 대해 BPA를 조합한 결과이다. 다음 단계는 모든 변수에 대해 BPA를 조합하여야 한다. Table 2에서 ηg와 ηc는 각각 3개와 5개의 조합으로 구성되었으므로 두 변수의 구간의 BPA 조합은 Table 3과 같이 총 15개가 된다.
Table 3은 가스발생기 연소효율(ηg)과 초음속 연소기의 연소효율(ηc)이라는 두 개의 불확실한 변수의 구간과 각 구간에서 정의된 BPA(필기체)를 보여주고 있다. 다음단계는 각 구간에서 성능변수의 최대값과 최소값을 계산하는 일이다. 성능변수는 추력효율(CT)와 노즐 출구 마하수(M5)이다. 예를 들어 ηg의 첫째구간인 [0.83, 0.90]과 ηc의 첫째구간인 [0.86,0.88]에서 CT를 계산하여야 한다. 만일, 이 구간에서 CT가 단조증가(또는 감소)하면 네 모서리점만 계산하면 되지만, 아닐 경우, 비선형 최적계산을 통해 최대값과 최소값을 구해야 하므로 훨씬 많은 계산이 필요하게 된다.
Table 3은 가스발생기 연소효율(ηg)과 초음속 연소기의 연소효율(ηc)이라는 두 개의 불확실한 변수의 구간과 각 구간에서 정의된 BPA(필기체)를 보여주고 있다. 다음단계는 각 구간에서 성능변수의 최대값과 최소값을 계산하는 일이다. 성능변수는 CT와 노즐 출구 마하수(M5)이다. 예를 들어, ηg의 첫째구간인 [0.83, 0.90]과 ηc의 첫째구간인 [0.86,0.88]에서 CT를 계산하여야 한다. 만일 이 구간에서 CT가 단조증가(또는 감소)하면 네 모서리점만 계산하면 되지만, 아닐 경우, 비선형 최적계산을 통해 최대값과 최소값을 구해야 하므로 훨씬 많은 계산이 필요하게 된다.
본 논문에서는 추력의 한계를 주어진 비행조건에서 항력을 이길 수 있는 최대값인 0.11으로 설정하였다. 각 구간에서 CT의 최대값이 0.11보다 작은 경우, 최소값만 0.11보다 작은 경우를 찾았다. 최대값이 0.11보다 작은 경우는 Bel이며, 최소값이 0.11보다 작으면 Pl을 의미한다.
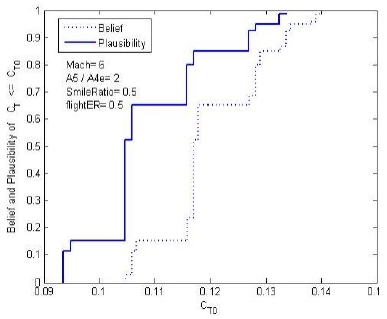
Fig. 6은 주어진 비행조건에서 엔진이 내야 하는 추력(CT0) 보다 더 큰 추력(CT)을 낼 수 있는 가능성의 정도를 나타내는 누적 Bel함수(CBF, Cumulative Belief Function)와 누적 Pl함수(CPF, Cumulative Plausibility Function)를 계산한 결과를 보여주고 있다. 예를 들어 DCR엔진에게 요구되는 추력계수 CT0가 0.11일 때, 엔진이 이보다 작은 추력 가질 Belief의 정도는 0.15이며 Plausibility의 정도는 0.65이다. 즉, 이 엔진의 추력계수가 0.11보다 낮을 가능성이 0.15~0.65 사이에 존재하는 것으로 이해할 수 있다.
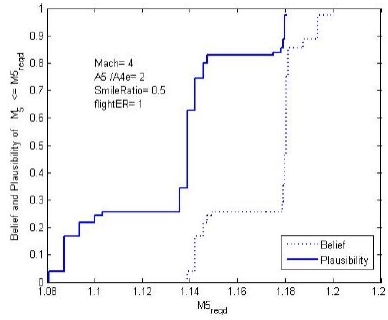
Fig. 7은 노즐 출구마하수 M5가 1보다 클 가능성의 정도인 Belief와 Plausibility를 계산한 결과이다. Fig. 4와 같이 초음속 연소흐름에서 열량이 유입됨에 따라 노즐 출구 마하수가 감소하게 되어 열질식(thermal choking)이 발생할 수 있다. 이를 방지하기 위하여 노즐출구 마하수가 1이상이 될 Belief와 Plausibility를 계산하였다. 다행스럽게도 M5가 1보다 작은 가능성은 없으므로 이 엔진은 thermal choking 관점에서는 충분히 안전한 것으로 생각할 수 있다.
전문가들이 제시한 BPA(Table 1)가 불연속적이므로 누적 Belief와 누적 Plausibility도 계단형태의 불연속성을 가지게 된다. Belief와 Plausibility 사이의 간격은 신뢰도의 불확실성으로 표현된다. 만일, 계산에 사용할 연소효율의 데이터가 무한히 많아 하나의 확률분포로 정의할 수 있다면, Belief와 Plausibility는 동일한 값을 가지게 되어 하나의 누적확률분포(CDF)로 Fig. 6과 Fig. 7을 표현할 수 있다.
6. 에비던스 기반 최적화
신뢰성 설계에서 설계 요구조건을 만족할 일반적인 확률 값은 95%이상이다. Fig. 6과 같이 설계한 DCR엔진이 추력 요구조건을 만족할 가능성의 정도는 0.35~0.85로서 0.95보다 작은 수준이므로 보다 보수적인 설계가 필요하다. 이에 따라 Fig. 6의 에비던스 이론으로 구한 Plausibility를 최적설계의 제약함수로 설정하여 최적설계를 수행하였다.
| (10) |
여기서 목적함수 f는 비추력 Isp의 역수이며, 설계변수 d는 흡입구 면적비(α), 노즐 면적비(A5/Ae) 그리고 당량비(ΦER)이다. x는 불확실변수로서 가스발생기 연소효율(ηg)과 초음속 연소기의 연소효율(ηc)이다. 제한조건은 제약함수 g가 제한요구값 greqd 보다 작을 Plausibility의 정도가 일정수준 이하가 되도록 정의하였다. 제약함수의 제한요구값은 CT가 주어진 비행조건에서 항력을 이길 최소값인 0.17보다 크게, M5는 1보다 큰 조건으로 설정하였다. pf는 허용가능한 Plausibility의 정도로서 0.3, 0.1, 0.01로 줄여가면서 최적해를 구하였다. 최적계산은 Direct 알고리즘[10]을 사용하였다. Eq. 10의 최적설계 문제에 각 변수들을 대입하여 Eq. 11과 같이 정리하였다.
| (11) |
Table 4에 결정론적 최적설계 결과(deterministic optimization)와 EBDO결과를 비교하였다. 결정론적 최적설계에서 목적함수는 Eq. 11과 동일하며, 제약함수는 CT와 M5가 각각 0.17과 1.0이하를 만족하는 조건으로 설정하였다. 최적화 결과, 목적함수는 가장 높은 Isp를 발생시키고 있다. 그러나 추력계수와 M5가 각각 제한요구 값과 동일한 활성(active)상태이다. 불확실요소에 의해 설계변수나 모델링에 작은 변동이 발생하면 시스템은 추력이 부족하거나 thermal choking 상태에 빠지게 되는 위험성이 있다.
이러한 문제를 해결하기 위하여 EBDO는 제약함수를 허용 가능한 Plausibility의 정도가 정의된 pf 값보다 작도록 정의하였다. 예를 들어, Eq. 11에서 pf가 0.3이면, M5가 1보다 작을(thermal chocking 발생) 가능성(plausibility)이 0.3이하가 되도록 설계 값을 구하는 문제가 된다. 계산결과를 보면, pf가 줄어들수록 허용 가능한 Plausibility의 정도가 줄어들므로 목적함수인 Isp값이 감소하는 보수적인 결과를 보여준다. 즉, 성능(목적함수)를 양보하는 대신, 시스템의 신뢰도(제한함수)를 확보하는 방식이다. Table 4의 함수 계산횟수는 결정론적 최적화와 EBDO 각각 103과 105 수준이다. EBDO에서는 바깥 루프는 최적화 계산을 수행하며, 매 최적계산마다. 각 제한함수의 Plausibility를 만족하기 위한 내부 루프가 있으며, Plausibility 계산에는 각 BPA마다 최고값과 최소값을 찾아야 하므로 계산 횟수는 더욱 증가하게 된다.
7. 결 론
에비던스 이론을 이용하여 인지적 불확실 요소에 대한 불확실성을 정량화하고, 최적설계를 수행하였다. 에비던스 이론은 시험자료나 계산결과를 얻기 힘든 분야에서 전문가의 의견과 같은 제한적인 정보를 가지고 불확실성을 정량화 하는데 유용한 도구임을 확인할 수 있었다. 향후 EBDO의 계산효율을 증대시키는 문제는 풀어야 할 숙제이다.
Nomenclature
| α : | ratio of intake area to body area |
| ΦER : | equivalence ratio |
| cf : | skin friction coefficient |
| ϵ : | entropy limit |
| ηg : | combustion efficiency of gas generator |
| ηc : | combustion efficiency of combustor |
| Isp : | specific impulse |
| CT : | thrust coefficient |
| M5 : | Mach no. at nozzle exit |
| A5 : | area at nozzle exit |
Acknowledgments
[이 논문은 한국추진공학회 2017년도 춘계학술대회(2017. 5. 31 - 6. 2, 라마다프라자 제주호텔) 발표논문을 심사하여 수정 · 보완한 것임.]
References
-
Oberkampf, W. L., Helton, J. C., and Sentz, K., “Mathematical Representation of Uncertainty”, AIAA42nd Non-Deterministic Approaches Forum, Seattle, WA, U.S.A., AIAA-2001-1645, April, (2001).
[https://doi.org/10.2514/6.2001-1645]

- Shafer, G., “A Mathematical Theory of Evidence”, Princeton Univ. Press, Princeton, NJ, (1976).
-
Oberkampf, W. L., and Helton, J. C., “Investigation of Evidence Theory for Engineering Applications”, AIAA Non-Deterministic Approaches Forum, Denver, USA, AIAA 2002-1569, April), (2002.
[https://doi.org/10.2514/6.2002-1569]

-
Bae, H.-R., Grandhi, R. V., and Can_eld, R. A., “Epistemic Uncertainty Quantification Techniques Including Evidence Theory for Large-Scale Structures”, Computational Structure, 82(13-14), p1101-1112, (2004).
[https://doi.org/10.1016/s0045-7949(04)00086-0]

-
Agarwal, H., Renaud, J. E., Preston, E. L., and Padmanabhan, D., "Uncertainty Quantification Using Evidence Theory in Multidisciplinary Design Optimization", Reliability Engineering and System Safety, 85(1-3), p281-294, (2004).
[https://doi.org/10.1016/j.ress.2004.03.017]

-
Mourelatos, Z.P., and J. Zhou, "A design optimization method using evidence theory", Journal of Mechanical Design, 128(4), (2006).
[https://doi.org/10.1115/1.2204970]

-
Billig, F. S., Waltrup, P.J., and R. D. Stockbridge, “Integral Rocket Dual Combustion Ramjets : A New Propulsion Concept”, Journal of Spacecraft and Rockets, 17(5), p416-424, (1980).
[https://doi.org/10.2514/3.57760]

- Billig, F. S., “Ramjet with Supersonic Combustions”, AGARD-LS-167, (1984).
-
Billig, F.S., and Dugger, G.L., “The interaction of shock waves and heat addition in the design of supersonic combustors“, Symposium (International) on Combustion, 12(1), p1125-1139, (1969).
[https://doi.org/10.1016/s0082-0784(69)80490-x]

- Lophaven, S., Nielsen, H., and Sondergaard, J., A MATLAB Kriging Toolbox, Technical University of Denmark, Kongens Lyngby, Technical Report No. IMM-TR-2002-12, (2002).
- Jong-Ryul Byun, Joongki Ahn, Hyungul Yoon, and Jin-Shik Lim, “Preliminary Performance Analysis of a Dual Combustion Ramjet Engine”, Journal of the Korean Society of Propulsion Engineers, 15(5), p72-81, (2011).