배플이 장착된 로켓 연소기의 선형 안정성 해석

1. 서론

로켓엔진 연소기를 설계하고 시험할 때 중요한 일 중 하나는 고주파 연소불안정을 방지하는 것이다. 열음향 연소불안정은 연소기 내에서 에너지가 발생하는 열적인 과정과 압력진동에 해당하는 음향장과의 상호작용으로 연소에너지가 음향진동과 동조하여 지속적으로 진동상태를 유지하는 것으로, 연계과정 중 주도과정에 대한 규명과 진동발생 및 진행에 대한 해석연구가 진행되고 있다.

고주파 연소불안정에 대한 실험적인 연구는 특정형상의 연소기를 대상으로 비연소상태의 음향특성 시험 및 연소상태에서 화염전달함수 특성을 측정하는 것이다. 음향특성 실험은 연소기의 여러 위치에서 외란을 부가하여 외란 전파에 대한 반사, 투과 및 흡수특성을 시공간으로 정량화 하여 음향장의 응답특성을 구한다. 분사과정 또한 연소불안정에 미치는 영향이 크기 때문에 이에 대한 특성실험이 중요하지만, 연소를 수반하는 경우 상호연계 특성을 분리하기 어렵다. 따라서 로켓 연소기에서 널리 사용하는 와류형 분사기의 분무특성 실험[1]과 같이 상온에서 분사기만의 동특성 측정결과를 보고하는 것이 일반적이다[2,3].

연소불안정 선형해석은 질유량, 열방출 및 연소압력의 섭동 간 상관성을 평가함으로서 자발적으로 야기되는 진동여부를 도출하는 것이다. 열방출 및 연소압력 섭동 간 위상이동(phase shift)을 민감시간지연(τ)과 압력지수(n)로 구성한 단순모델이 제안된 이후 기상 및 액상추진제를 대상으로 선형해석을 적용하여 연소불안정을 해석한 다수의 연구결과가 보고 된 바 있으며[4,5], Mitchell 등은 음향공명기 및 배플을 갖는 연소기 내 유체유동에 대한 해석모델을 선형 및 비선형 해석하여 비교 타당성을 입증하였다[6,7]. 단순 시간지연 연소모델인 n - τ 모델을 이용한 고주파 연소불안정 해석 연구로, Kobayashi 등은 고주파불안정에 영향을 미치는 세부과정으로 분사 및 연소가 연계하여 연소불안정에 미치는 영향을 비교분석하였다[9].

2. 연소기의 선형 열음향 해석

2.1 연소기내 고주파 불안정해석

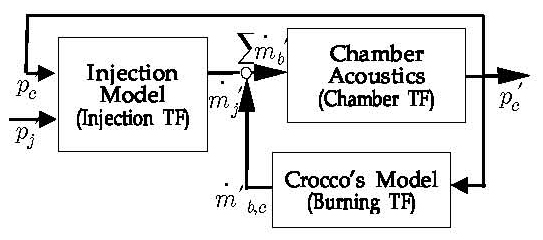
로켓엔진 연소기의 고주파 불안정성은 연소와 관련된 추진제 분사, 연소 및 연소기내 음향유동 특성이 연계된 폐회로에 기인한다. 따라서 연소기의 고주파 연소불안정 동적 특성은 연소기 내 음향과 커플 된 열-유동에 대한 선형해석 모델과 Crocco의 시간지연 개념의 단순 모델을 이용하여 Fig. 1과 같이 세분된 개별과정의 입력함수에 대한 응답함수로 표현되는 전달함수로 이해할 수 있다[4,9].

Fig. 1

Schematic diagram of combustion.

2.4 연소기 전달함수(Z_c)

연소기 전달함수는 연소가스 섭동에 대한 연소압력 섭동을 나타내는 응답함수로 다음과 같이 연소기 어드미턴스로 표현된다.

$\[ \frac{1}{Z_c}\equiv Y_c\left(s\right)=\frac{\dot{m}{\text{'}}_b\left(s\right)}{p\text{'}\left(s\right)} \]$

(3)

연소기내 압력섭동 및 연소가스의 상관관계를 구하기 위해 가스유동을 등 엔트로피 조건 압축성 유체이며, 와류유동이 없다는 가정 하에 다음과 같이 질량 및 모멘텀 식을 풀어 음향장 내 압력 및 속도 관계식인 파동식을 구한다.

$\[ \frac{D\rho }{Dt}+\rho \nabla \cdot u=0 \]$

(4)

$\[ \rho \frac{Du}{Dt}+\frac{1}{\gamma }\nabla p=0 \]$

(5)

여기서 압력, 밀도 및 가스 속도를 무차원화하여 표현하고, 속도포텐셜 함수를 적용하면 다음 Eq. 6 및 Eq. 7로 표현할 수 있다.

$\[ \begin{array}{c}u=\nabla \phi \hfill \\ p\text{'}=-\gamma [\frac{\partial \phi \text{'}}{\partial t}+(\overline{u}\cdot \nabla \left)\phi \text{'}\right]\hfill \end{array} \]$

(6)

$\[ \frac{{\partial }^2\phi \text{'}}{\partial t^2}-{\nabla }^2\phi \text{'}+\overline{u}[\nabla (\overline{u}\cdot \nabla \phi \text{'}\left)\right]+2\overline{u}\frac{\partial }{\partial t}(\nabla \phi \text{'})=0 \]$

(7)

또한, 상기 식에서 섭동부분을 섭동진폭과 시간 섭동분(e^st)으로 나누어 표현하면, 연소기 내 평균유동은 축(z)방향으로만 존재하므로 마하수로 무차원화하여 표현할 수 있다. 이로부터 선형화 한 유동식은 Eq. 8과 같다.

$\[ \begin{array}{c}\phi \text{'}=\phi e^{st}\\ p=-\gamma [s\phi +M\frac{\partial \phi }{\partial z}]\\ s^2\phi -{\nabla }^2\phi +2sM\frac{\partial \phi }{\partial z}+M^2\frac{{\partial }^2\phi }{\partial z^2}=0\end{array} \]$

(8)

Eq. 8의 경계조건으로 분사면(z = 0)과 노즐면(z = L)을 적용하는데, 연소면은 분사면으로부터 n - τ 시간지연관계를 이용하여 Eq. 9의 경계조건을 적용하고, 노즐에서의 경계조건은 Eq. 10과 같다.

$\[ \dot{m\text{'}}=\overline{\dot{m}}\cdot n\left(p\text{'}\right(t)-p\text{'}(t-\overline{\tau }\left)\right) \]$

(9)

그리고,

$\[ \begin{array}{c}{\left.\frac{\partial \phi }{\partial z}\right|}_{z=0}+{\left.M\frac{p}{\gamma }\right|}_{z=0}={\left.Mn\left(1-e^{-i\omega \tau }\right)p\right|}_{z=0}\\ {\left.\frac{\partial \phi }{\partial z}\right|}_{z=L}={\left.M\frac{\gamma -1}{2\gamma }p\right|}_{z=L}\end{array} \]$

(10)

연소기 어드미턴스를 구하기 위해서는 분사면 및 노즐에서의 경계조건인 Eq. 10을 적용한 후 연소 면에서 두 식을 연속시켜 Eq. 11의 연소기 어드미턴스 식을 얻는다[8].

$\[ Y_c=\frac{{\dot{m}}_b\text{'}}{p\text{'}}=\frac{1}{\overline{u}}(Y_d-\frac{\overline{{\rho }_u}{a}_u}{\overline{{\rho }_d}{a}_d}{Y}_u)+\frac{1}{\gamma } \]$

(11)

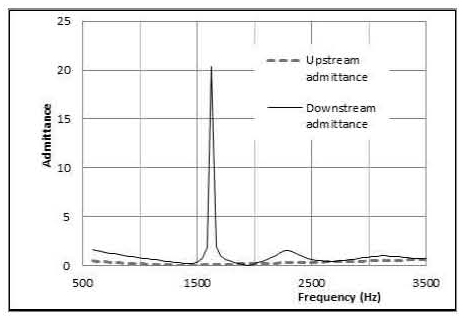
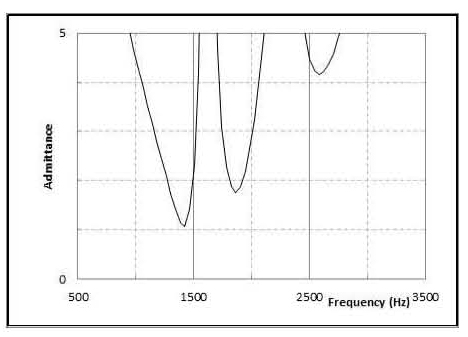
Eq. 11에서 Y_u는 Eq. 10의 분사면 경계조건 (z = 0)을 적용하여 구한 상류 어드미턴스이며, Y_d는 연소기 노즐입구 경계조건(z = L)을 적용한 연소기 하류 어드미턴스 이며, ρ_ua_u 및 ρ_da_d는 각각 상류 및 하류의 평균밀도 및 음속이다. 또한 γ 는 비열비이다.

이로부터 Table 1 형상의 원통형 연소기에 대한 어드미턴스 계산결과는 Fig. 2 및 Fig. 3과 같다.

Table 1.

Specification of combustion chamber.

Fig. 2

Up and down-stream admittance.

Fig. 3

Chamber admittance.

2.5 주파수 해석에 따른 연소불안정 평가

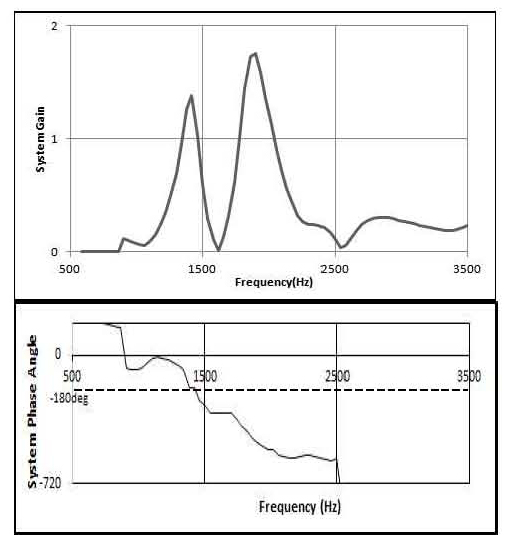
연소불안정 해석은 관심을 갖는 주파수범위에서 주파수에 따른 연소 시스템 이득을 계산하는 것으로 이를 위해 전술한 세부과정 전달함수의 특성파악이 필요하다. 시간미분을 주파수 도메인으로 전환하는 주파수분석방법은 전달함수의 특성을 효과적으로 파악할 수 있다[10,11]. 즉 s 대신 복소 주파수(s → jω, α =0)를 대입하여 계의 이득 및 위상각을 구하는데, 대표적인 계산결과로 계의 이득과 위상각은 Fig. 4와 같다.

Fig. 4

System gain and phase angle.

계의 안정성은 관심주파수에서 이득 여유와 위상 여유를 판단하는 것으로 실제 적용에서는 위상각이 -180°에서 이득 값이 1 이상인 경우 불안정한 것으로 판정한다. 즉 안정한계에 대한 시스템 특성식 Eq. 12를 만족하는 조건으로 Eq. 13을 적용한다[5].

$\[ 1-Z_c(Y_I+Y_B)=1-F\left(s\right)=0 \]$

(12)

$\[ \begin{array}{c}\left|F\left(j\omega \right)\right|=1\hfill \\ \left|\text{arg}\left\{F\left(j\omega \right)\right\}\right|=\pm \pi \hfill \end{array} \]$

(13)

단, Eq. 13의 위상 조건을 고려할 때 연소시스템의 세부 단계 전달함수에서는 시간지연 만 발생하므로, -180° 위상각이 물리적인 의미를 갖지만 주기함수의 특성에 따라 +180°를 병기한다.

2.6 연소기제원 및 운영조건

해석에 사용하는 연소기는 원통형으로 구성하였으며, 노즐부의 수축반각 30〫 를 적용하였다. 연소기의 형상 값은 Table 1과 같이 특성길이로 나누어 무차원으로 정규화하였으며, 연소기 운영조건은 정상상태 평균값을 기준으로 압력은 연소압력, 질유량은 추진제 총질유량으로 나누어 무차원화 하여 Table 2에 정리하였다.

Table 2.

Operating condition.

3. 해석결과

3.2 배플장착에 따른 고주파 안정 효과

연소기내에 배플이 장착된 경우 Eq. 8은 배플 공간 및 나머지 연소공간에서 별도의 해를 구한 다음 두 영역의 접촉면에서 이들을 일치시켜 최종 해를 구한다.

3.2.1 배플 길이에 따른 댐핑효과

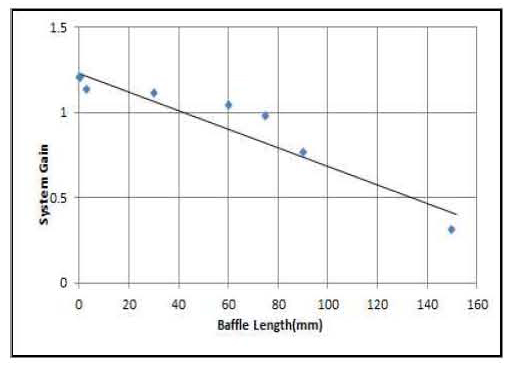
접선방향의 연소 불안정을 해소하는 방법으로 널리 사용하는 방법은 분사면 부근의 연소기 공간에 배플을 설치하여 연소면의 공간을 분할하는 것이다. 다만, 연소기 내부의 구조물 설치를 위해서는 냉각이 필요하므로 적정길이의 배플을 선정하는 것은 의미 있는 일이다. 이에 따라 3개의 날개를 갖는 배플을 길이를 3mm로부터 150mm 까지 늘이면서 시스템 이득을 계산하여 결과를 Fig. 5에 제시했다. 전술했듯이 계가 안정하기 위해서는 1 이하의 이득 값을 가져야하며, 결과에서 보듯이 배플의 길이가 증가함에 따라 시스템은 안정해지는 것으로 나타났다.

Fig. 5

Overall system gain with various baffle length.

한편 시스템 이득은 배플의 길이증가에 따라 거의 선형으로 떨어지는 것을 알 수 있었다. 실제 계산에 적용한 Crocco의 n - τ 모델에서는 연소 면에서 연소가 집중하여 완료된다는 가정을 적용하였기 때문에 배플 길이 증가에 따라 안정성이 증가하는 것은 Mitchell[6]의 계산결과와 부합하며, 배플 내에서 댐핑의 주요한 요인 중 하나는 배플 내 유동손실에 기인하기 때문으로 볼 수 있다.

3.2.2 배플 개수에 따른 댐핑 효과

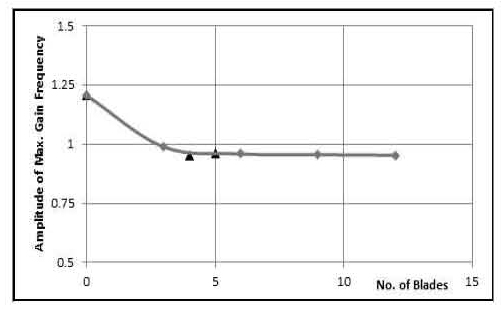
배플 개수가 계의 안정성에 미치는 효과를 파악하기 위해, 배플 장착 시 시스템 이득이 1 이하 값을 갖도록 축방향 배플 길이가 75mm인 배플을 계산 기준으로 삼았다. 이후 배플 개수를 3개에서 12개까지 증가시켜 이에 해당하는 시스템 이득을 구하여 결과를 Fig. 6에 제시했다.

Fig. 6

Overall system gain with various baffle blade numbers.

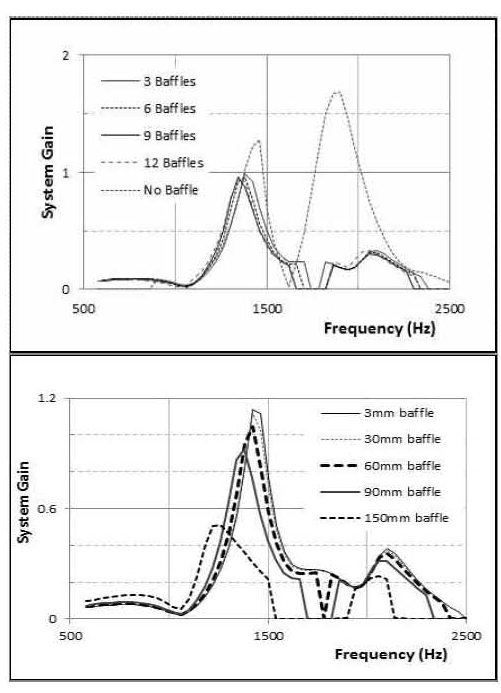
Fig. 6의 시스템 이득 값은 1T 모드에 해당하는 것으로, 피크 값을 갖는 주파수에서 이득의 최대값이 나타난다. 전체적으로 배플 개수가 3개 이상에서는 이득 값은 거의 변하지 않았다. 즉, 배플 개수 증가가 안정성에 미치는 영향은 제한적인 것으로 나타났다.

3.2.3 배플 효과에 따른 주파수 이동 효과

관심 주파수 영역에서 시스템 이득이 피크 값을 갖는 주파수와 연소기의 음향모드에 해당하는 고유주파수를 비교하였다. 관심 대상은 순수 1T 음향모드에 해당하는 주파수이며, Fig. 7에 보인 바와 같이 1T 이상의 높은 주파수인 1940Hz의 피크는 배플을 설치함에 따라 급격히 감소하므로 시스템의 안정성에 미치는 영향이 작다. 그러나 1T 모드의 피크 주파수는 배플의 개수가 증가함에 따라 점차 낮은 주파수로 이동하여 12개 배플의 경우에는 1340Hz까지 낮아졌다. 이러한 주파수 이동은 배플의 길이가 증가하는 경우에도 유사하게 나타났으며, 150mm 배플 길이의 경우 1220Hz까지 낮아져 주파수 이동 폭은 전체 시스템 댐핑이 커질수록 증가하였다.

Fig. 7

Frequency shift of max. system gaina) with respect to the baffle numbersb) with respect to the baffle length.

4. 결론 및 향후 계획

액체산소 및 케로신을 추진제로 하는 액체로켓 연소기의 고주파 연소불안정을 해석하기 위해 선형해석을 수행하였다. 연소기내 고주파 연소불안정을 야기할 수 있는 분사 및 연소 프로세스에 대한 단순모델을 적용하고, 연소기 내 음향과 커플된 유동식을 시-공간 변수분리 후 선형화를 수행하였다. 원통 좌표로 표현된 2차 미분식은 분사면 및 노즐입구를 경계조건으로 적용하여 해를 구했다.

시스템의 안정성 판정을 위해 주파수 해석을 수행하였으며, 관심 영역 주파수인 1T 모드에서 시스템 이득 및 위상각을 구해 시스템의 불안정여부를 판정하였다. 1T 모드 안정성 확보 방안으로 길이 75mm인 3개의 날개를 갖는 배플을 기준으로 배플 효과를 검토하였다. 배플 설치에 따라 시스템 이득이 중립 안정조건 이하로 떨어져 1T 모드 불안정이 해소 된다. 배플 길이 증가에 따라 시스템 이득이 계속 낮아지므로 안정성 향상에 미치는 효과가 지속적으로 증가하지만, 배플 개수 증가가 1T 모드 안정성에 미치는 효과는 급격히 떨어지는 결과를 얻었다. 또한 배플 길이 및 개수 증가에 따른 형상변경으로 연소기의 고유 음향모드 주파수는 낮은 주파수방향으로 천이하는 것을 확인할 수 있었다.

해석에 적용한 연소모델은 특정한 시간지연을 갖는 연소면에서 연소가 집중하는 단순모델을 적용하여 실제 연소현상과는 달리 배플의 효과를 과도 평가할 것으로 판단된다. 향후 연소영역을 임의의 위치로 확장하는 연소모델을 적용하고 연소면 경계조건을 확장하는 연구를 통해 실제 사용하고 있는 복잡한 로켓엔진 연소기의 불안정 특성 해석결과를 도출할 수 있을 것으로 생각한다.

References

• Yi, Y., Hong, M., and Lee, S.Y., “Experimental Study on the Merged Angle of Mixed-Interaction Regions of Sprays from Two Pressure-Swirl Injectors”, Journal of ILASS-KOREA, Vol. 16(No. 4), p195-200, (2011).
• Bazarov, V., and Yang, V., “Liquid -Propellant Rocket Engine Injector Dynamics”, Journal of Propulsion and Power, Vol. 14(No. 5), p797-806, (1998). [https://doi.org/10.2514/2.5343]
• Kim, D., Im, J., Koh, Hl, and Yoon, Y., “Effect of Ambient Gas Density on Spray Characteristics of Swirling Liquid Sheets”, Journal of Propulsion and Power, Vol 23(No.3), p603-611, (2007). [https://doi.org/10.2514/1.20161]
• Fang, J., “Application of Combustion Time-lag Theory to Combustion Stability Analysis of Liquid and Gaseous Propellant Rocket Engines”, 22nd Aerospace Science Meeting, Reno, NV USA, >AIAA paper 84-0510, 09-12), Jan., (1984.
• Hutt, J.J., and Rocker, M., Liquid Rocket Engine Combustion Instability, Vol. 169 Progress in Astronautics and Aeronautics AIAA Inc., Washington, DC, USA, Ch. 12, (1995).
• Baer, M. R., and Mitchell, C. E., “A Theoretical Evaluation of Rigid Baffles in Suppression of Combustion Instability”, Colorado State University, Fort Collins, Colorado, USA, NASA CR-134986, (1976).
• Mitchell, C. E., Liquid Rocket Engine Combustion Instability, Vol. 169 Progress in Astronautics and Aeronautics AIAA Inc., Washington, DC, USA, Ch. 15, (1995).
• Nguyen, T. V., “Computer code for use in high frequency combustion stability analyses”, Aerojet TechSystems Company, Thermodynamic analysis report 9980:1807, (1988).
• Kobayashi, K., Daimon, Y., Iizuka, N., Tamura, H., Mitani, T., and Onodera, T., “Studies on Combustion Instability for Liquid Propellant Rocket Engines”, 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, AIAA, July-Aug.), (2011. [https://doi.org/10.2514/6.2011-6028]
• Schulze, M., and Sattelmayer, T., “A Comparison of Time and Frequency Domain Descriptions of High Frequency Acoustics in Rocket Engines with Focus on Dome Coupling”, Aerospace Science and Technology, Vol. 45, p165-173, (2015). [https://doi.org/10.1016/j.ast.2015.05.007]
• Sattelmayer, T., Schmid, M., and Schulze, M., “Impact of Injector Mass Flow Fluctuations on Combustion Dynamics in Liquid Engines”, Journal of Spacecraft and Rockets, Vol. 52(No. 5), p1417-1429, (2015). [https://doi.org/10.2514/1.A33287]