베이지안 확률기법을 이용한 당량비 오차분석에 관한 연구
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
엔진 당량비의 제어오차가 요구범위를 불만족할 확률을 분석하였다. 당량비의 제어오차는 무작위 불확실요소와 인식론적 불확실요소로부터 동시에 영향을 받는다. 무작위 불확실요소는 일반적으로 확률분포가 주어지므로 민감도 기반의 신뢰성 해석기법을 이용해 쉽게 해석이 가능하다. 확률분포를 알기 어려운 인식론적 불확실요소를 다루기 위해서는 새로운 접근법이 필요하다. 무작위 불확실요소에 대한 신뢰성 해석결과를 베이지안 추론에 이용함으로서 엔진 당량비의 제어오차가 요구범위를 불만족할 확률에 대한 확률분포를 구할 수 있었다. 이러한 접근은 무작위 불확실요소와 인식론적 불확실 요소가 동시에 존재하는 공학시스템 해석에 유용하게 사용될 수 있다.
Abstract
This paper analyzes the probability of failure for the equivalence ratio error. The control error of the equivalence ratio is affected by the aleatory and epistemic uncertainties. In general, reliability analysis techniques are easily incorporated to handle the aleatory uncertainty. However, the epistemic uncertainty requires a new approach, as it does not provide an uncertainty distribution. The Bayesian inference incorporates the reliability analysis results to handle both uncertainties. The result gives a distribution of failure probability, whose equivalence ratio does not meet the requirement. This technique can be useful in the analysis of most engineering systems, where the aleatory and epistemic uncertainties exist simultaneously.
Keywords:
Bayesian Statistics, Reliability Analysis, Equivalence Ratio키워드:
베이지안 확률기법, 신뢰성 해석, 당량비1. 서 론
공기흡입식 엔진을 원활하게 작동시키기 위해서는 흡입구를 통해 유입된 공기량에 대응하여 적절한 양의 연료를 공급해 주어야 한다. 흡입기량에 비해 연료공급량이 지나치게 많거나 적으면 연소효율이 낮아지고, 고열로 인해 엔진 구성품에 손상이 발생할 수 있다. 흡입공기량과 연료 공급량의 비는 당량비(equivalence ratio, φ)로 표현할 수 있다.
본 연구는 엔진시스템이 당량비 제어오차 범위(예를 들어, 명령 당량비대 실제 운용되는 당량비의 차이가 명령대비 5%이내)에서 작동할 확률을 구하는 문제를 다루고 있다. 공기흡입식 엔진에서 흡입공기량은 기체에 장착된 센서로 부터 얻는 대기정보(air-data)와 흡입구에서 측정한 압력 및 온도 등을 조합하여 추정한다. 일반적으로 압력센서와 온도센서는 제조사로부터 오차범위와 함께 제공된다. Full scale대비 %로 표현되는 각 센서의 오차는 정규분포의 특성을 가지며 오차의 범위는 3σ 값으로 이해하여 적용할 수 있다. 서로 독립적인 각 센서의 오차가 공기흡입량 추정에 미치는 영향은 결합 확률분포(JPDF, Joint Probability Density Function)의 형태로 표현된다. 결합 확률분포는 몬테칼로(Monte Carlo) 시뮬레이션 기법이나 민감도 기반 신뢰성(reliability) 해석기법인 FORM(First Order Reliability Method)을 이용하여 구할 수 있다.
문제는 연료공급량 제어오차이다. 연료공급장치는 여러 구성품이 복잡하게 조립된 장치이므로 명령대비 출력오차가 항상 발생하게 된다. 시험을 통해 오차원인을 식별할 수도 있으나 시험물의 수량과 시험 가능횟수가 제한되어 있어 쉽지 않다. 흡입구센서 오차와는 달리, 연료공급장치의 제어오차는 시험자료가 매우 한정적이므로 이를 적절한 수준의 신뢰도와 표준오차를 가지는 확률분포로 모델링하기가 어렵다.
제한된 횟수의 시험결과를 통계적으로 모델링하기 위하여 베이지안(Bayesian) 통계기법을 이용하였다. 베이지안 통계학은 전통적인 빈도주의(frequentism) 통계학과는 대비되는 개념이다. 빈도주의 통계학은 확률을 객관적으로 해석하여 확률변수(parameter)는 고정되어 있다고 인식하는 반면, 베이지안 통계학은 확률을 우리가 알고 있는 주관적인 믿음의 정도로 정의하여, 확률변수에 대한 불확실성을 확률분포로써 설명하고 있다.
공학분야에서 대두되는 불확실 요소는 크게 무작위(aleatory) 불확실요소와 인식론적(epistemic) 불확실 요소로 나눌 수 있다. 무작위 요소는 센서오차, 제작공차, 재료물성치 등과 같이 더 이상 줄일 수 없는 성격을 가진다. 일반적으로 무작위 불확실 요소는 확률분포가 제공되거나, 변동에 대한 정보가 많기 때문에 확률분포를 쉽게 모델링할 수 있다. 반면, 인식론적 불확실 요소는 정보나 지식의 부재에서 기인하므로 불확실 정도를 줄일 수는 있으나 이를 위해서는 시간과 비용이 투입되어야 한다. 연구개발과정에서 두 가지 불확실 요소는 대부분 동시에 나타나므로 이를 통합적으로 고려해주는 연구[1-2]가 필요하다.
일단 불확실 요소의 확률분포를 알면, 이를 이용하여 여러 불확실 요소가 전체 시스템에 미치는 영향인 결합 확률분포를 계산하는 것은 어렵지 않다. 결합 확률분포를 계산하는 대표적인 방법으로 몬테칼로 시뮬레이션이 있으나, 확률변수의 개수가 많거나 구하고자 하는 확률 값이 작아질수록 시뮬레이션 횟수가 기하급수적으로 증가하는 단점이 있다. 그러므로 계산 시간이 많이 필요한 CFD나 CAE해석 등에는 시스템의 민감도 정보를 이용한 FORM와 같은 신뢰성 해석기법[3]을 사용하는 것이 좋다. 본 연구에서도 확률분석에 FORM을 이용하였다.
대부분의 시스템에서는 무작위 불확실 요소와 인식론적 불확실 요소가 동시에 나타나므로 이를 함께 고려해주는 연구가 필요하다. 당량비 제어오차는 무작위 불확실 요소인 흡입구 센서오차와 인식론적 불확실요소인 연료공급장치 오차에 의해 발생한다. 엔진의 당량비 제어오차가 설계 범위를 벗어날 확률을 실패확률(pf, probability of failure)로 정의하였다. 흡입구센서 오차에 의한 당량비 제어 실패확률을 계산하더라도 연료공급장치의 변동으로 실패확률 계산결과는 매번 달라질 수밖에 없다. 즉, 베이지안의 관점에서는 실패확률(pf)값 자체도 확률분포를 가지게 된다.
2. 이항분포 모델의 베이지안 추론
베이지안 통계학은 18세기에 제안된 개념이나 그 모호성과 주관성, 그리고 많은 계산 량으로 그동안 주류인 빈도주의 통계학으로부터 외면 받아왔다. 다행히 20세기 이후부터 컴퓨터의 발전과 더불어 현대 경제학, IT 및 공학 등 분야에서 활발히 이용되고 있다. “동전이 던져 앞면이 나올 확률이 50%이다”라는 진술을 빈도주의자는 “동전던지기를 무한히 반복하면 그중 50%는 앞면이 나온다”라고 표현하는 반면, 베이즈주의자는 “앞면이 나올 확신은 50%이다”라고 확률을 주관적인 믿음의 정도로 표현하는 것이다. 표본의 개수가 무한히 증가하면 빈도주의 확률이나 베이즈 확률은 동일한 값으로 수렴한다. 문제는 표본의 개수가 제한적인 경우이다.
베이즈 통계학은 사전지식(prior knowledge)과 객관적인 우도(likelihood, 시험자료)를 조합하여 사후확률분포를 계산하는 구조이다. 특정분야의 지식과 경험을 가진 전문가로부터 사전확률을 추출하고, 이를 시험자료와 조합하면 비록 적은량의 시험자료를 가지고도 의미 있는 모수를 추정할 수 있는 장점이 있다. 만일 빈도주의 통계기법을 이용한다면, 의미 있는 확률 값을 구할 때까지 시간과 비용을 투입하여 시험을 수행해야 할 것이다.
대부분의 공학문제들은 반복수행 시, 성공 또는 실패, 발생 또는 미 발생, 만족 또는 불만족 등의 이항(binomial)성격을 가지고 있다. 가스터빈 엔진의 당량비 제어오차는 특정한 확률로 성공(규격만족)과 실패(규격초과)라는 베르누이 시행(Bernoulli sequence, 각 사건이 통계적으로 서로 독립이며 발생확률이 정해져 있다)이면, 이항(binomial)확률분포를 따른다.
Eq. 1은 사건이 일어날 확률이 p, 일어나지 않을 확률이 1-p인 모델에서 N회 시행 중, x회의 사건이 일어날 확률(X)을 계산하는 이항확률분포의 PMF(Probability Mass Function)이다.
| (1) |
이 식에서는 발생확률 p가 주어졌기 때문에 X를 구하는 것은 어렵지 않다. 반대의 경우인 N회 시행에서 성공횟수 x를 알고 있을 때, 발생확률 p를 구하는 문제는 Eq. 2의 베이지안 추론을 통해 가능하다.
| (2) |
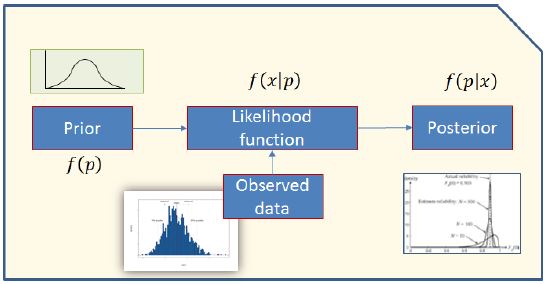
여기서 f(p)는 사전확률분포(prior distribution)이며, f(x|p)는 우도함수로서 시험자료 등을 통해 구한다. Fig. 1은 사전확률을 우도함수와 결합하여 사후확률(posterior distribution)을 계산하는 베이지안 추론구조를 나타내고 있다. 만일, 계산된 사후확률f(p|x)는 새로운 자료f(x|p)가 추가되면 사전확률 f(p)로 바꾸어 다시 사후확률을 계산하는데 이용된다.
본 연구에서는 최초 사전확률에 대한 정보가 없으므로 f(p)= U(0,1) 균등분포로 가정하였다. 이항분포에서 모든 확률을 합한 분모는 1이 되며, 우도함수는 이항확률분포를 따르므로 이를 다시 정리하면 Eq. 3과 같은 베타(beta)분포의 형태를 가지게 된다.
여기서 α = x + 1, β = N - x + 1이 된다. 즉, 베이지안 추론에서 이항분포의 공액(conjugate)분포는 베타분포가 되어 쉽게 확률을 구할 수 있다.
| (3) |
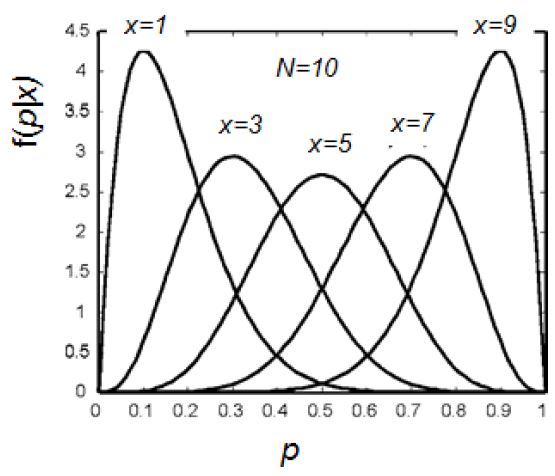
Fig. 2는 N=10인 조건에서 x를 달리한 베타분포를 보여주고 있다. 총 시행횟수 N에서 성공횟수 x가 증가할수록 확률분포 f(p)의 중앙값인 p는 우측으로 치우치는 것을 알 수 있다. 시행횟수(N)가 증가할수록 p의 범위는 좁아지게 된다. 즉, 정보의 양이 증가할수록 보다 정확한 확률을 계산할 수 있게 되는 것이다.
3. 시스템 구성
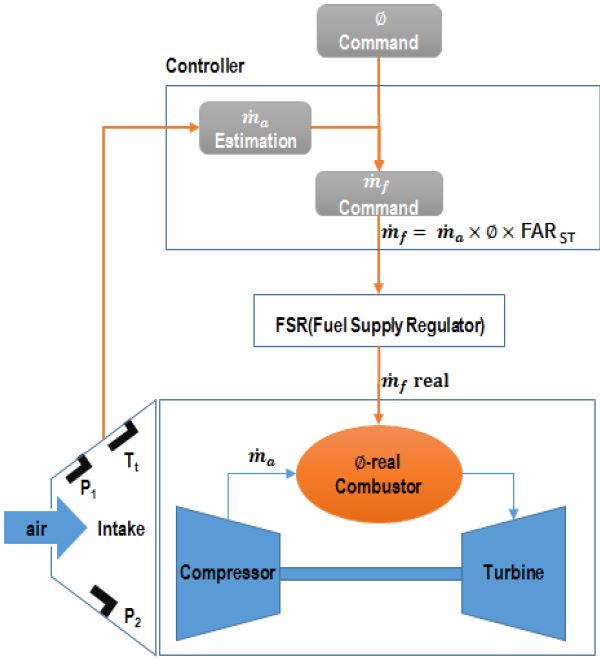
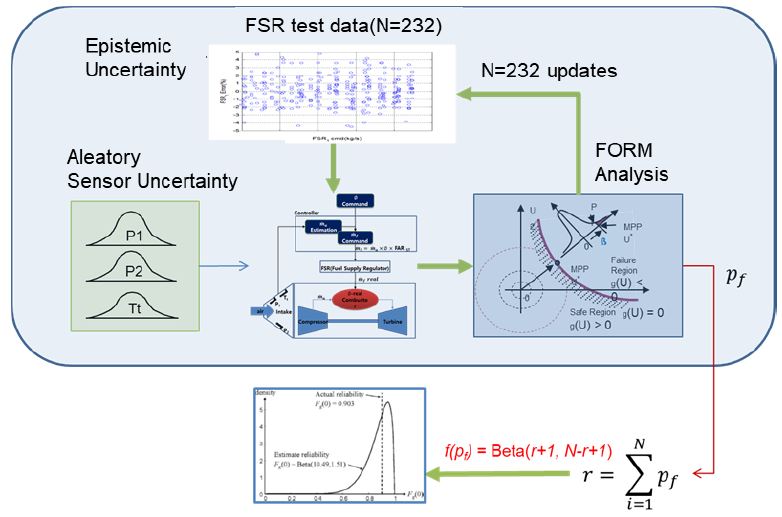
Fig. 3은 연료공급량 결정을 위한 공기흡입 엔진의 구성을 보여주고 있다. 흡입공기량()은 흡입구에 장착된 2개의 압력센서(P1, P2)와 1개의 온도센서(Tt)를 이용하여 추정한다. 각 센서는 서로 독립적이며 정규분포를 가지는 무작위 불확실요소이다. 엔진제어기(controller)에서는 흡입구 센서에서 측정된 정보를 이용하여 공기량을 추정한다. 추정한 공기량()과 당량비(Φ) 명령 그리고 연료의 이론 연공비(FARST, stoichiometric fuel air ratio)를 곱하여 엔진에 공급해 주어야 할 연료량()명령을 생성한다. 흡입구 각 센서의 오차에 대해서는 확률분포가 있으므로 MCS 나 FORM을 이용해 공급 연료량의 결합 확률분포를 쉽게 계산할 수 있다.
연료공급장치(FSR, Fuel Supply Regulator)의 특성으로 인해 명령 연료 유량과는 실제 연소기로 공급된 유량에는 차이가 발생한다. 이러한 오차에 대한 시험자료는 매우 제한적이기 때문에 확률분포로 모델링하기 어렵다. 결과적으로 엔진 연소기에 공급되는 연료량은 흡입구 센서와 연료공급장치의 오차에 의해 처음 의도한 명령유량과는 차이가 발생하게 되어, 엔진구조물이나 연소효율에 영향을 미치게 되는 것이다.
Table 1에 흡입구 센서의 오차특성을 정리했다. 각 센서는 통계적으로 서로 독립이며, 정규분포를 가진다(N.I.D.). 예로 0.0267값을 가지는 P1센서의 COV(Coefficient of Variation)은 표준편차가 평균값의 2.67% 수준임을 의미한다.
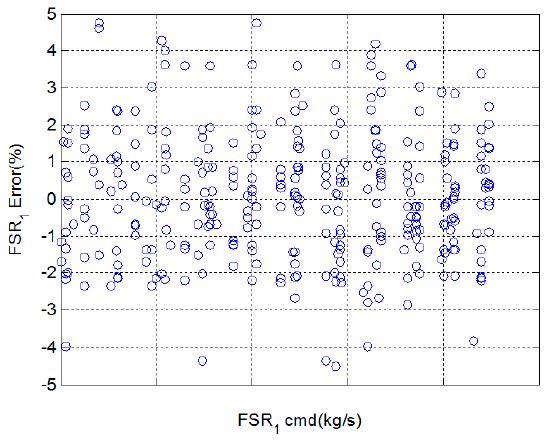
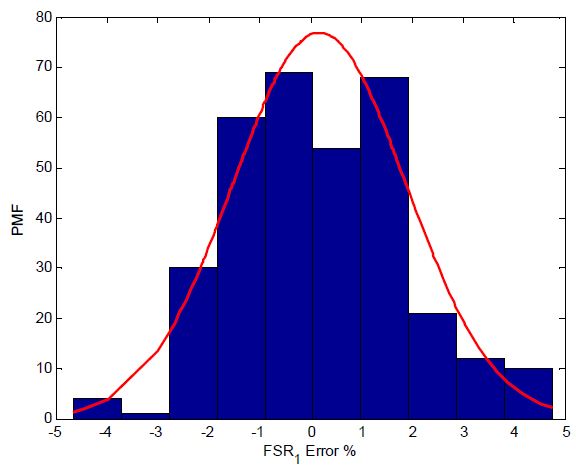
Fig. 4는 연료공급량 오차에 대한 총 232개 시험결과이다. 각각의 데이터는 명령 연료유량 대비 토출 연료유량의 차이를 %로 표현한 값이다. 각 연료공급조건에서 ±5% 이내의 공급오차량(명령대비)이 발생하고 있으나, 데이터 개수의 제한으로 오차의 정확한 확률분포는 알 수 없는 상태이다. Fig. 5는 FSR1 유량오차(%)를 확률질량함수(PMF)로 나타내고, 이를 정규분포로 적합(fitting)결과이다. 연료공급오차의 PMF가 정규분포(붉은색 실선)와 잘 맞지 않는 것을 볼 수 있으므로 연료공급오차는 흡입구 센서오차와는 달리 정규분포로 모델링하기 어렵다는 것을 알 수 있다. 정규분포가 아닌 가장 적합한 확률분포를 찾을 수 있으나 이 또한 제한된 시험자료의 량으로 만족스러운 결과를 얻기 어렵다. 연료공급오차의 확률분포를 추론하기 위하여 베이지안 기법을 적용하기로 하였다.
4. 당량비 오차분석
시스템의 성공 또는 실패확률을 계산하기 위한 베이지안 추론기법을 엔진의 당량비 오차분석에 적용하였다. 엔진의 당량비 오차(명령 당량비 대비 출력 당량비의 차이)가 명령 기준 ±3% 이내에서 작동할 확률을 구하기로 한다. 명령당량비는 0.625로 설정했다. 즉, 엔진 제어기에서 당량비 명령 φ=0.625로 주었을 때, FSR이 당량비 오차 3%(0.606 ≤φ ≤ 0.644) 보다 범위 밖에서 연료를 공급할 확률 pf의 확률분포 f(pf)를 구하는 문제다.
| (4) |
Fig. 6은 당량비의 오차를 분석하는 절차를 보여주고 있다. FSR시험자료는 Fig. 4와 같이 232개를 확보하였다. 각 FSR시험조건에서 흡입구 센서오차 정보만을 이용하여 [당량비 제어오차가 ±3%를 벗어날] 실패확률 pf를 계산했다. 이 값은 몬테칼로 시뮬레이션을 통해 구할 수도 있으나 본 연구에서는 계산시간을 줄이기 위하여 민감도 기반의 FORM을 이용하였다. N=232번의 시행으로부터 얻은 각각의 실패확률 pf 을 모두 더한 값 x는 시스템의 실패에 대한 기대 횟수(expected number)로 치환할 수 있다.
| (5) |
총 시행횟수 N=232 과 Eq.5의 기대횟수 x를 가지고 Eq. 3의 베타분포를 계산하면 실패확률에 대한 사후 확률분포를 알 수 있다.
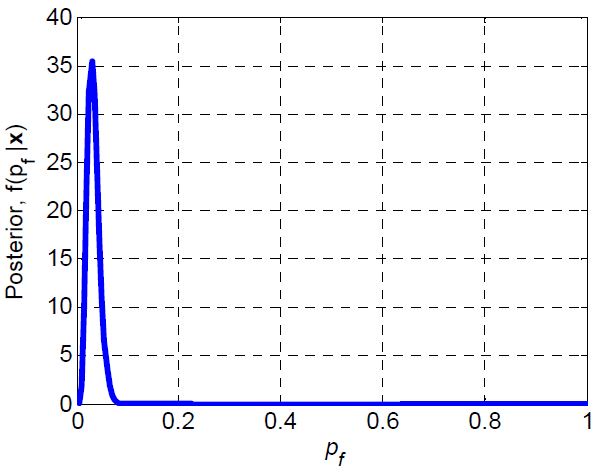
Fig. 7은 실패확률의 사후 확률분포를 계산한 결과이다. 사후 확률분표가 그림의 왼쪽에 좁은 범위에서 분포하고 있는 것을 볼 수 있다. 실패확률(당량비 제어오차가 3%를 벗어날 확률)의 확률 분포인 것이다. 실패확률이 약 0.05를 중심으로 좌우로 분포하고 있으므로 이 엔진 시스템이 규격(당량비 제어오차가 3% 이내)을 불만족할 가능성이 5% 정도임을 말해주고 있다.
FSR 오차에 관한 시험자료가 부족하므로 계산된 실패확률 pf는 하나의 결정된 값이 아니라 분포 f(pf)로 표현되고 있다. FSR시험자료가 증가할수록 Fig. 7의 분포범위는 좁아지게 된다. 만일, 무한히 많은 시험자료를 확보하게 된다면 그림의 분포는 하나의 값으로 수렴하게 되며, 그 값은 빈도주의 통계학을 이용하여 계산한 것과 동일한 값을 가지게 될 것이다.
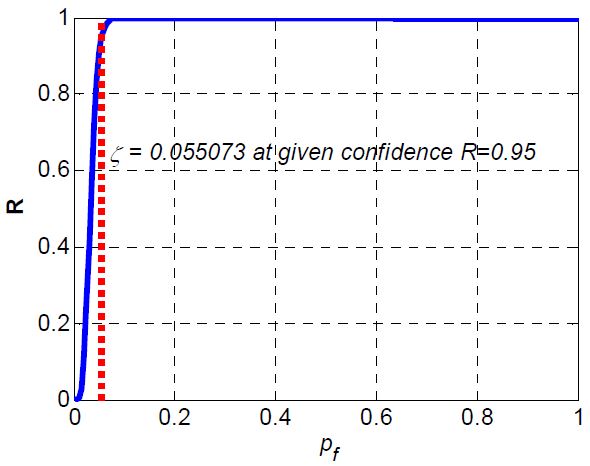
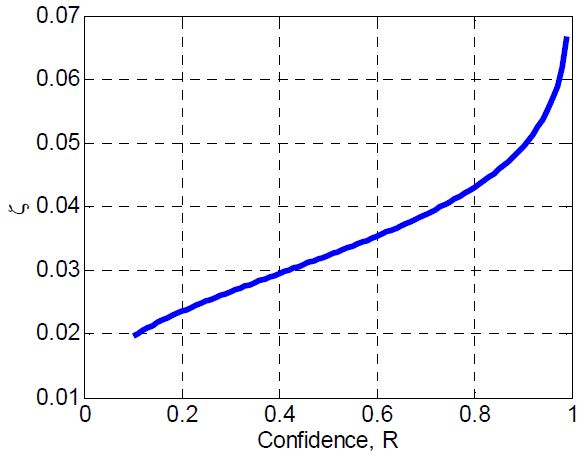
Fig. 8은 Fig. 7의 사후확률분포를 누적확률함수(cdf, cumulative distribution function)로 나타낸 것이다. 정량적인 분석이나 신뢰성 최적설계의 문제구성을 위하여 신뢰수준(R, confidence level)을 정의 하고 신뢰수준 R을 벗어나는 확률의 누적값ζ를 Eq. 6과 같이 계산하였다. 여기서 ζ는 실패확률의 누적확률 값이다.
| (6) |
신뢰수준 R= 0.95에서 실패확률은 누적확률 ζ는 0.055로 계산되었다. 즉, 당량비 제어오차 3%를 벗어날 확률은 95% 신뢰수준으로 약 5.5% 정도라고 이해할 수 있다.
Fig. 9와 같이 신뢰수준을 낮출수록 누적확률 ζ는 줄어들게 된다. 만일 신뢰수준을 0.4로 낮춘다면 오차규격을 불만족할 확률은 3% 수준으로 낮아지게 되는 것이다. 신뢰수준을 높이면 실패확률도 높아지게 된다. 해석결과에 대한 높은 신뢰수준을 높게 가져갈수록 더욱 보수적인 결과를 얻게 되는 당연한 이치다.
5. 결 론
대부분의 공학시스템에서는 오차에 대한 확률분포가 있는 무작위 불확실성 요소와 오차정보가 제한된 인식론적 불확실요소가 공존하게 된다. 두 가지 불확실 요소를 동시에 고려하기 위한 베이지안 추론모델을 엔진의 당량비 오차분석에 적용하여 의미 있는 결과를 도출하였다. 이 방법은 실패확률에 대한 확률분포를 제공해 주기 때문에 기존의 인식론적 불확실 요소를 처리하기 위해서 사용하는 worst case scenario를 적용하는 것에 비해 나은 설계결과를 보여 준다. 연구결과를 실제 개발현장에서 적용하기 위해서 당량비 제어오차 감소를 위해 역으로 엔진 센서나 FSR의 오차를 얼마 이하로 감소시켜야 하는 지에 대한 민감도를 분석을 수행할 필요가 있다.
Nomenclature
| pf : | probability of failure |
| : | air mass flow rate |
| : | fuel mass flow rate |
| Φ : | equivalence ratio |
| MCS : | Monte Carlo Simulation |
| FORM : | First Order Reliability Method |
| FSR : | Fuel Supply Regulator |
| N.I.D. : | Normal and Independently Distributed |
References
-
Gunawan, S., and Papalambros, P., “A Bayesian Approach to Reliability-Based Optimization with Incomplete Information“, Journal of Mechanical Design, 128(4), p909-919, (2006).
[https://doi.org/10.1115/1.2204969]

- Youn, B.D., and Wang, P., “Bayesian Reliability-based Design Optimization Using Eigenvector Dimension Reduction Method“, Structural and Multidisciplinary Optimization, 36(2), p107-123, (2008).
- Ayyub, B.M., and Halder, A., “Practical Structural Reliability Technique”, Journal of Structural Engineering, 110(8), p1707-1724, (1984).