냉각채널의 각도와 직경 변화에 따른 채널 내 압력 손실에 관한 수치적 연구
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
냉각채널에서의 압력 손실을 수치적으로 연구하기 위하여 채널의 축 방향에 대한 각도, 채널 내부의 유체의 유속, 채널의 직경을 변화시키며 수치해석을 진행하였다. 채널의 축 방향에 대한 각도 변화에 따라서 압력 손실은 큰 변화가 없었다. 하지만 일반적으로 알려진 대로 채널의 직경이 커지면 압력손실이 감소하고, 유체의 유속이 느려지면 압력손실이 감소하는 경향은 두드러지게 나타났다. 이러한 결과는 무차원화 하여 정량화하였고, 기존 채널내부의 압력손실에 대한 경험식과 비교하여 기존 경험식의 타당성을 확인하였다. 본 연구에서 획득한 정보는 향후 냉각채널을 설계할 때 압력손실을 고려함에 있어 도움이 될 것으로 판단된다.
Abstract
The pressure loss in a cooling channel was investigated by conducting a numerical analysis, which was performed with a different channel angle in the axial direction , velocity of flow, and diameter of channels. The pressure loss did not change much with respect to the different channel angle. However, the pressure loss tended to decrease if the diameter of the channel increased and the velocity of the flow decreased. The results were quantified by a nondimensional method and compared to an existing experimental equation to validate them. The data obtained by this study would be helpful in the design process of a cooling channel considering the pressure loss.
Keywords:
Pressure Loss in Channel, Cooling Channel, Angle of the Channel, Diameter Ratio of the Channel키워드:
채널 내 압력손실, 냉각채널, 채널 각도, 채널 직경비1. 서 론
액체로켓엔진의 연소실과 노즐은 3,000 K 이상의 고온, 고압의 환경에서 작동되기 때문에 작동되는 시간동안 안정적인 작동을 위해서는 냉각 시스템 구축이 필수적이다. 이를 위해 열 차폐 코팅, 막 냉각, 재생냉각 등의 다양한 방법을 적용한다. 이 중 연소실 내벽에 냉각채널을 만들어 연료를 흘려보내어 연소실 벽을 냉각시키고, 온도가 올라간 추진제를 연소에 참여시켜 엔탈피 이득을 얻는 재생냉각이 효율적인 냉각 방법으로 평가되어 일반적으로 널리 사용된다[1,2].
열전달 관점에서 냉각채널을 설계할 때, 효과적인 냉각과 연소기 내벽이 구조적 건전성을 위해서는 소재 온도가 적절한 구조 강도를 가질 수 있는 온도 내에서 사용하여야 하며, 이 온도는 소재의 용융점보다는 훨씬 낮은 온도여야 한다. 또한 냉각채널 내 추진제의 유동이 빠르고, 흐르는 추진제와 채널이 닿는 표면적이 넓을 때 재생냉각에 의한 냉각효과가 증가된다[3,4]. 그리고 엔진시스템 측면에서는 냉각채널에서의 압력 손실이 정확히 예측되어야만 공급시스템에서의 공급 압력을 설정할 수 있기 때문에 냉각채널에서의 압력손실에 대한 정확한 예측이 필수적이다[5].
하지만 냉각효과를 증가시키기 위해 추진제의 유속을 증가시키면 냉각채널에서 압력손실이 증가하게 된다. 또한 채널의 수와 전열면적은 연소실의 크기에 따라 제한이 있고, 제작상의 비용 및 시간 소모까지 고려해야하기 때문에 적절한 타협점에서 설계가 이루어진다. 또한 냉각채널설계 시 로켓엔진 펌프의 토출압력이 이미 규격에 따라 정해져 있기 때문에 타당한 냉각채널설계를 위해서는 펌프의 토출압력에 따라 냉각채널 내부에서 발생되는 압력손실에 대하여 정확하게 예측할 수 있어야 한다[6].
많은 유체역학 서적 및 자료들에서 마찰손실에 따른 유체의 압력손실에 대한 경험식들을 제시하고 있지만, 실제 냉각채널을 모사한 형상에 대해 직접적으로 활용할 수 있는 자료는 국내에서 찾기가 힘든 상황이다. 이에 따라 본 연구에서는 냉각채널의 폭과 너비, 축 방향에 대한 각도, 냉각채널 내 추진제의 유속을 변수로 하여 수치해석을 진행하였다. 수치해석의 결과는 기존의 유체역학적 관내 압력손실에 관한 식과 비교를 수행하였다. 본 연구결과는 재생냉각채널을 설계하는데 있어서 압력손실을 예측하는데 도움이 될 것으로 판단된다.
2. 관련 이론
관 내 압력손실은 유체역학적으로 해석할 때 Eq. 1과 같이 손실계수, 채널 내 유속, 밀도의 함수로 표현된다.
| (1) |
이 때 손실계수(ζov)는 ζov = ζloc + ζfr로서, 벽면마찰에 의한 손실계수(ζfr)와 유동방향이나 단면적이 변하면서 생기는 국부적인 손실계수(ζloc)로 구분할 수 있다. 재생냉각 채널에서는 두 손실이 모두 발생하지만 채널의 단면적에 비해 길이가 매우 길기 때문에 마찰손실에 비해 국부적인 손실이 매우 작다[7]. 그리고 실제 로켓 연소기의 재생냉각채널에서 생기는 국부적인 손실은 채널의 분기, 합류 및 방향전환 등에 의해서 발생하는 것이지만 본 연구에서 대상으로 하는 직선형 채널과 나선형 채널에서의 국부적인 손실은 아주 작다. 그러므로 마찰손실만을 고려하여 연구를 수행하였다. 벽면 마찰에 의한 마찰계수는 Eq. 2와 같이 벽면의 거칠기(Δ), 수력학적 직경(Dh), 레이놀즈수(Re)의 함수로 표현된다.
| (2) |
마찰계수는 원형단면을 가정하여 계산되기 때문에 사각단면에서는 보정계수(knon, cir)를 사용해야 한다. 따라서 재생냉각 채널에서 벽면 마찰에 의한 압력손실은 Eq. 3과 같이 보정계수, 벽면의 거칠기, 직경, 레이놀즈수의 함수로 표현된다.
| (3) |
채널의 표면이 매우 매끄러워 마찰을 무시할 수 있는 경우(smooth wall) 원형단면에서의 마찰계수는 난류유동에서 레이놀즈수에 따라 Eq. 4로 표현된다.
| (4) |
균일한 거칠기를 가지고 있다고 가정할 경우(uniform roughness wall) 마찰계수는 Eq. 5로 표현된다. Eq. 5는 참고문헌 [8]의 112쪽 table 값들을 수식화한 것으로 공학적 오차를 포함하는 식이다.
| (5) |
3. 수치해석 방법
3.1 대상 채널 형상 설정
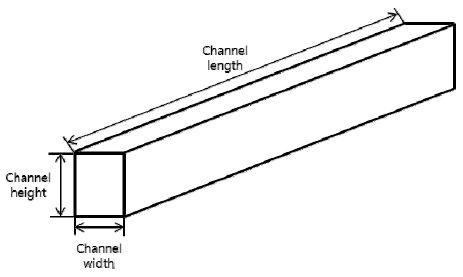
본 연구에서는 총 15종류의 케이스를 모델링하여 수치해석을 수행하였다. 냉각채널의 단면은 제작 상의 편이 및 실제 냉각채널의 형상을 고려하여 사각형 형상의 단면으로 설정하였다. 냉각채널의 단면 형상에 따른 압력손실 변화를 알아보기 위하여 CH2를 기준으로 CH1과 CH3은 채널의 너비를 고정하고 채널의 높이를 0.5 mm씩, CH4와 CH5는 채널의 높이를 고정하고 채널의 너비를 1 mm 씩 변화시켜 설정하였다. CH1~CH5는 직선채널로 길이 172 mm이며, 나머지 10개의 채널은 단면에 대한 형상은 CH1~CH5와 동일하게 설정하고, CH6~CH10은 축과의 각도 15도를 갖는 나선형 형태, CH11~CH15는 축과의 각도 30도를 갖는 나선형 형태의 채널로 냉각채널을 모델링 하였다. 15개의 냉각채널의 형상은 Table 1과 같다. 냉각채널의 형상은 선행연구의 실험에서 이용한 채널의 형상을 기초로 하여 설정하였다[7].
3.2 해석 조건
선정한 15개의 채널을 3차원 모델링하여 상용 프로그램인 ANSYS FLUENT v14.5를 통해 수치해석을 수행하였다. 작동유체는 물을 사용하였고, 상온 실험 조건(298 K)을 고려하여 ρ = 997 kg/m3 , μ = 8.93 × 10-4N ∙ s/m2 이다. 난류모델은 k - ϵ Standard Wall Function을 적용하였다. 채널 입구의 경계조건은 물의 유속으로 설정하였고 채널 출구의 경계조건은 일정한 압력을 유지하도록 설정하였다. 또한 벽면의 거칠기는 실제로도 매우 작기 때문에 매끄러운 벽면조건과 실험에서 계측된 값을 이용하였다.
4. 해석 결과
4.1 케이스별 압력 강하량 데이터
수치해석 결과는 다음 Table 2와 같다. 15개의 다양한 채널에 대해, 다양한 유속 조건에서 압력손실을 정량화 하였다. 일반적으로 재생냉각채널에서의 유속은 RD-107의 경우 최대 20~25 m/s의 값을 가지는 것으로 알려져 있다. 본 연구에서도 이 값을 바탕으로 20 m/s를 기준으로 10, 20, 30 m/s의 값을 결정하여 적용하였다.
4.2 유속 변화에 따른 압력손실 변화
일반적으로 관내 유동에서 유속이 증가하면 압력손실 또한 증가하는 것으로 알려져 있다.
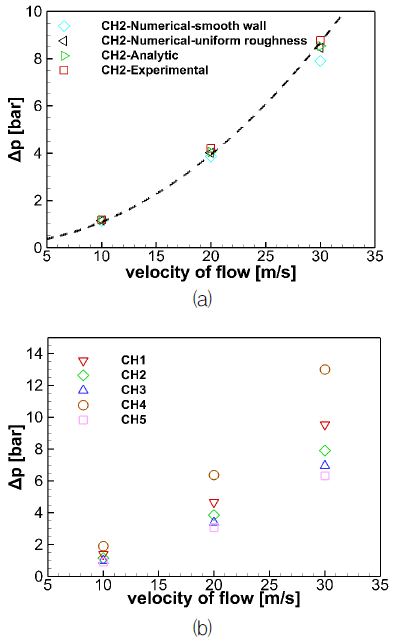
Fig. 2 (a)는 본 연구의 대상 채널과 같은 단면을 갖는 채널에 대한 선행연구[9]의 실험 결과와 경험식(Eq. 3)의 계산 결과, 매끄러운 벽면을 가정한 수치해석 결과, 균일한 거칠기를 가정한 수치해석 결과의 비교 그림이다. 이 때 해석에서 적용한 표면 거칠기는 선행연구에서 측정된 값인 1.24 μm를 사용하였다[9]. 모든 데이터의 결과 또한 유속의 제곱에 근사하게 비례하여 증가하는 경향을 보인다. 매끄러운 벽면을 가정한 경우를 제외한 나머지 세 개의 데이터는 거의 같은 압력손실 결과가 얻어짐을 알 수 있다. 본 연구에서는 벽면의 거칠기를 고려하지 않고 해석한 결과이기 때문에 실제 실험 데이터에서 더 큰 압력강하가 측정되었다고 보인다. 따라서 본 연구에서의 해석방법이 타당함을 확인할 수 있다. Fig. 2 (b)는 직선형 채널인 CH1~CH5에서 유속을 10, 20, 30 m/s 로 변경하여 얻은 데이터이다. 기존에 알려진 대로 유속이 커질수록 압력손실 또한 커지는 것을 확인할 수 있다. 유속이 증가할 때 압력손실의 증가는 채널의 단면 형상과 관계없이 유속의 제곱에 근사하게 비례하여 증가하는 경향이 Fig. 2 (a)에서와 동일하게 보인다. 유동의 동압이 유속의 제곱에 비례하는 관계이기 때문에 위와 같은 경향이 나타나는 것으로 판단된다. 그리고 상대적으로 낮은 유속인 10 m/s 조건에서는 거칠기의 영향이 아주 작아서 매끄러운 벽면조건과 균일한 거칠기 조건의 결과의 차이가 아주 미미하지만 유속이 빨라질수록 두 조건에서의 압력손실 차이는 증가하였다.
4.3 냉각채널의 단면 형상 변화에 따른 압력손실 변화
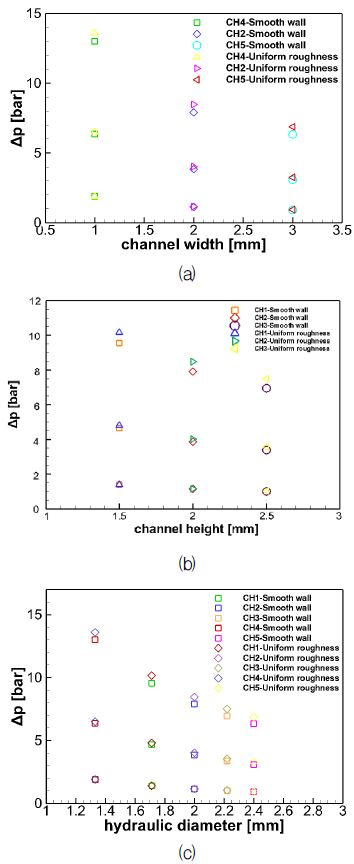
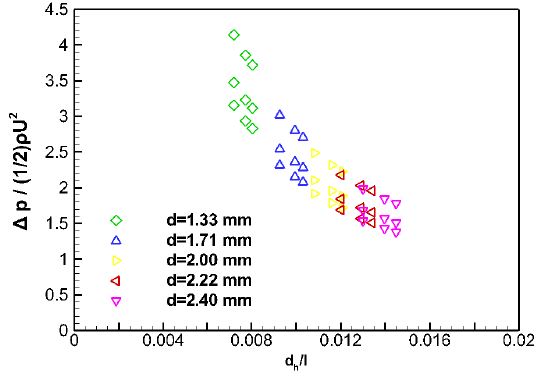
냉각채널의 너비 변화에 대한 영향을 보기 위해 기준 채널인 CH2 (너비 2 mm, 높이 2mm)에서 높이를 고정시키고 너비를 1 mm 로 줄여 CH4를, 너비를 3 mm 로 늘려 CH5를 모델링하였다. 또한 냉각채널의 높이 변화에 대한 영향을 보기 위해 CH2에서 너비를 고정시키고 높이를 1.5 mm 로 줄여 CH1를, 2.5 mm 로 늘려 CH3을 모델링 하였다. Fig. 3 (a), (b)는 유속조건 10, 20, 30 m/s에서 채널 너비와 높이를 변화 시키며 수치해석을 수행한 데이터이다. 같은 x축 상의 데이터에서 아래서부터 차례로 유속조건 10, 20, 30 m/s에서의 데이터이다. 채널의 너비, 높이 변화에 대한 압력손실은 동일하게 너비, 높이가 커지면 압력손실은 감소하는 것을 확인할 수 있었다. 기존의 관 내 압력손실에 대한 식들은 원형단면을 가정하기 때문에 수치해석 결과를 기존 경험식과 비교하기 위하여 냉각채널 단면의 너비와 높이를 Eq. 6을 통해 수력학적 직경으로 환산하였다. 유속 10 m/s 조건에서 직선형 채널인 CH1~CH5에서의 수력학적 직경 변화에 대한 압력손실 변화를 Fig. 3 (c)에 나타내었다. 여기서 A는 냉각채널의 단면적, P는 냉각채널에서 유동과 접하는 가장자리 길이에 해당한다.
| (6) |
냉각채널의 단면에 대한 변수를 수력학적 직경으로 환산하여 그린 그래프에서도 냉각채널의 너비, 높이의 경우와 같이 수력학적 직경이 증가하면 압력손실이 감소하는 경향이 나타났다. 하지만 보다 의미 있는 데이터를 얻기 위해서 무차원화를 통한 정량화가 필요하다고 판단되었다. 또한 균일한 거칠기 조건에서의 압력손실이 매끄러운 벽면 조건에서보다 모든 케이스에서 약간씩 크게 나타났다. 하지만 그 차이가 매우 작기 때문에 매끄러운 벽면을 가정하여도 무방하다고 판단된다.
4.4 각도 변화에 따른 압력손실 변화
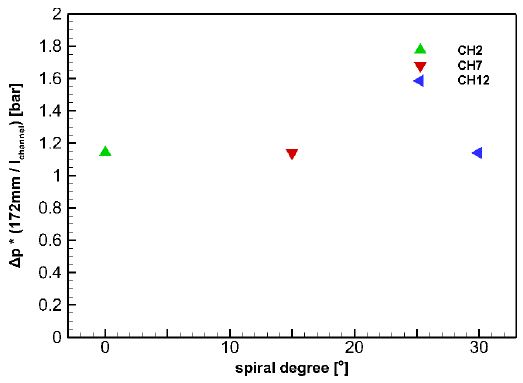
본 연구에서는 냉각채널 내 압력손실에 대한 냉각채널의 단면 형상 변화의 영향뿐만 아니라 실제 연소기에서 주로 사용되는 나선형 냉각채널의 각도에 대한 영향 또한 수치해석 수행하여 데이터를 얻었다. Fig. 4에 유속 10 m/s 조건에서 동일한 단면 형상을 갖고, 축에 대한 각도를 변화시킨 CH2, CH7, CH12에서의 압력손실을 동일 길이 조건으로 환산하여 나타내었다. 냉각채널의 축에 대한 각도 변화는 냉각채널 내부에서의 압력손실에 미치는 영향은 매우 작은 것으로 나타났다. 이 결과는 관련 이론에서 언급된 것처럼 냉각채널의 길이가 단면적에 비해 매우 길기 때문에 국부적 압력손실이 무시할 만큼 작기 때문인 것으로 판단된다. 따라서 동일한 사이즈의 연소기의 외벽에 냉각채널을 설계할 때 축에 대한 각도를 크게 하면 채널의 길이가 길어지는 효과에 의한 압력손실 증가만을 고려해도 충분히 타당하다고 판단되며, 이에 따라 냉각채널의 각도는 냉각채널의 길이에 따른 냉각효과를 고려하여 타당한 각도로 설계되어야 한다.
5. 결과 분석
본 연구의 수치해석의 결과에서 유속이 빠를수록, 냉각채널의 너비, 높이가 작을수록 채널내부에서의 압력손실이 증가하는 것이 확인 되었다. 하지만 냉각채널을 설계함에 있어서 실질적으로 참고하기 위한 데이터를 얻기 위해서는 얻어진 수치해석 결과 데이터를 정량화할 필요성이 있다고 판단되었다. 따라서 길이와 직경의 비, 레이놀즈수, 동압과 차압의 비 세 가지 무차원 인자를 바탕으로 분석하였다.
dh/l 은 냉각채널의 수력학적 직경과 길이의 비로, 채널의 형상을 나타내는 무차원수이다. 는 유동의 정압과 동압의 비로, 압력에 대한 무차원수이다. 각 무차원수 계산 결과는 Table 3, 4, 5와 같다.
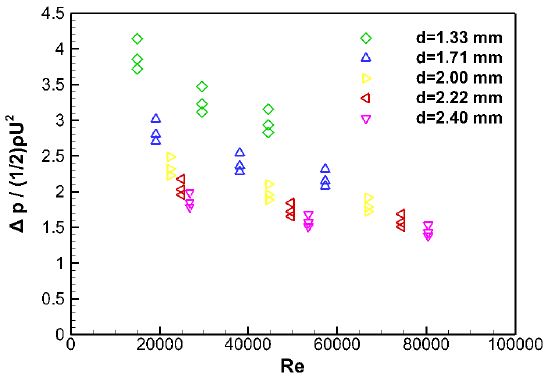
무차원화 결과를 파악하기 위해 Fig. 5, 6에서는 직경 비에 대한 압력 비, 레이놀즈수에 대한 압력 비를 그래프로 나타내었다.
직경 비와 레이놀즈수 각각의 경우 모두 증가할수록 압력비가 감소하는 것을 확인할 수 있다. 위 두 결과를 하나의 수식으로 정량화하여 기존 경험식과 비교하기 위하여 Eq. 7의 마찰계수 개념을 도입하여 또 하나의 무차원수를 계산하였다. 마찰계수 계산 결과는 Table 6과 같다.
| (7) |
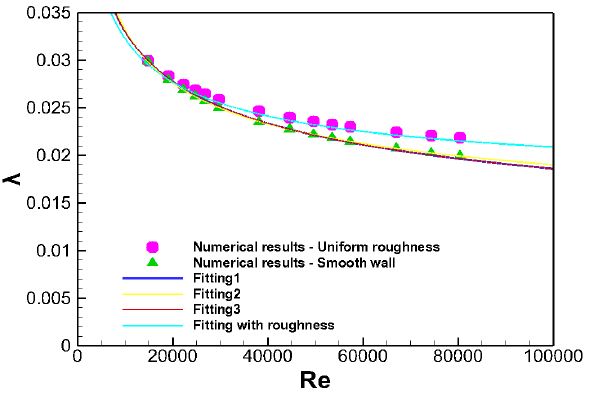
기존 경험식을 참고하여 마찰계수는 레이놀즈수의 함수로 표현될 것으로 판단하여 Fig. 7에는 레이놀즈수 – 마찰계수 그래프를 나타내었다. 각각의 채널과 유속에서 총 45개의 데이터를 얻을 수 있었다. 표면 거칠기를 고려한 경우, 고려하지 않은 경우에 비해 마찰계수가 약간씩 더 큰 값으로 계산되었다. 레이놀즈수가 증가함에 따라 그 차이는 점점 커지는 것이 확인되었다. Fig. 7은 채널의 마찰계수가 레이놀즈수의 함수로 표현 될 수 있음을 보여준다. 레이놀즈수가 증가하면 마찰계수가 감소하는 경향을 보였고 그 경향을 알아보기 위하여 수치해석 결과를 최소제곱법을 사용하여서 3가지 기존의 레이놀즈수 – 마찰계수 식과 비교하였다. fitting 식 순서는 Table 7에 나타낸 순서와 동일하며 Uniform roughness를 적용한 데이터들 또한 fitting 하여 나타내었다. fitting된 식의 가용 범위는 해석이 진행된 1.48×104≺ Re ≺8.04×104의 범위에 국한된다.
6. 결 론
냉각채널의 압력손실에 있어 냉각채널의 단면형상과 축과의 각도, 내부의 유속 변화에 대한 특성을 수치해석을 통해 파악하였다. 단면의 형상 변화에 있어서는 단면의 너비와 높이가 증가하면 압력손실은 감소하는 경향을 보였다. 단면의 너비와 높이 두 변수는 하나의 변수 수력학적 직경으로 환산하여 고려할 수 있었다. 수력학적 직경의 증가에 따라서도 압력손실이 감소하였다.
다음으로 각도에 대한 변화에 있어서 압력손실은 큰 영향을 받지 않았다. 이는 냉각 채널이 각도를 가지더라도 길이에 비해 단면적이 굉장히 작기 때문에 직선채널의 연속과 큰 차이가 없기 때문이라고 판단된다. 다만 같은 사이즈의 연소기에서라면 중심축에 대한 채널의 각도가 증가함에 따라 채널의 길이가 증가하여 압력손실이 증가할 것이다.
본 연구에서 얻은 정보는 무차원화를 통해 정량화되었다. 그 후 마찰계수 개념을 도입하고 최소제곱법을 이용한 fitting을 통해 기존의 채널 내 압력손실에 대한 경험식과 비교할 수 있었다. 기존의 경험식과 마찬가지로 수치해석 결과 또한 마찰계수가 레이놀즈수의–0.25제곱에 비례하며, fitting 식이 기존의 경험식에 근사한 것을 확인하였다.
실제 연소기에서 사용되는 재생냉각채널은 연소기의 형상이 원통형이 아니기 때문에 필요에 따라 단면적이 변하기도 하고, 분기점과 합류점이 있기도 하다. 또한 막 냉각을 위한 오리피스가 존재하는 경우 질량 유출에 유속 감소로 압력손실이 생기기도 한다. 본 연구에서 획득한 정보는 단순히 단면적이 일정한 채널에서의 압력손실만을 다루고 있다. 그렇기 때문에 실제 연소기에서 사용되는 재생냉각채널에 본 연구의 결과를 직접적으로 적용하기는 어렵다. 하지만 채널내부에서 압력손실에 대한 기존식의 타당성을 확인할 수 있었으며, 사각단면을 가지는 재생냉각채널을 고려한 경우, 압력손실을 보다 손쉽게 예측할 수 있을 것으로 판단된다.
Acknowledgments
본 연구는 민군기술협력사업(NO. 14-CM-MC-16)과 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(NO. 2016M1A3A3A02017979, 2015M1A3A3A02011346).
References
- Kim, H.J., and Choi, H.S., “Investigation of Characteristics for Cooling Parameters of a Combustor in Liquid Rocket Combustors,”, Journal of the Korean Society of Propulsion Engineers, 14(5), p45-50, (2010).
-
Yang, W., and Sun, B., “Numerical simulation of liquid film and regenerative cooling in a liquid rocket,“, Applied Thermal Engineering, 54(2), p460-469, (2013).
[https://doi.org/10.1016/j.applthermaleng.2013.02.021]

- Sutton, G.P., Rocket Propulsion Elements, 6th ed., John Wiley & Sons Inc., New York, N.Y., U.S.A., (1992).
- Michel, R.W., “Combustion Performance and Heat Transfer Characterization of LOx/Hydrocarbon Type Propellants”, Lyndon B. Johnson Space Center Contract NAS-9-15968, (1983).
- Hong, S.S., Kim, J.S., Kim, D.J., and Kim, J.H., “Performance Test of Turbopump Assembly for 75 Ton Liquid Rocket Engine Using Model Fluid,“, Journal of the Korean Society of Propulsion Engineers, 15(2), p56-61, (2011).
-
Ulas, A., and Boysan, E., “Numerical analysis of regenerative cooling in liquid propellant rocket engines,”, Aerospace Science and Technology, 24(1), p187-197, (2013).
[https://doi.org/10.1016/j.ast.2011.11.006]

-
Ahn, K., Kim, J.G., Lim, B., Kim, M., Kang, D., and Kim, S.K., “Fuel-Side Cold-Flow Test and Pressure Drop Analysis on Technology Demonstration Model of 75 ton-class Regeneratively- Cooled Combustion Chamber,“, Journal of the Korean Society of Propulsion Engineers, 16(6), p56-61, (2012).
[https://doi.org/10.6108/kspe.2012.16.6.056]

- Idelchik, I.E., Handbook of Hydraulic Resistance, 3rd ed., Begell House, New York, U.S.A., p75-148, (1996).
-
Yoon, W.J, Ahn, K.B, and Kim, H.J, “An Experimental Study on Pressure Loss in Straight Cooling Channels”, Journal of the Korean Society of Propulsion Engineers, 20(4), p94-103, (2016).
[https://doi.org/10.6108/kspe.2016.20.4.094]