밀폐용기 연소실험 시 센서위치에 따라 변화하는 압력 진동에 대한 수치적 연구
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
밀폐용기 내 Zirconium/Potassium Perchlorate의 연소를 수치적 모델링을 통해 전산해석을 수행하였다. 5차 WENO 공간차분법과 improved delayed detached eddy (IDDES) 난류모델을 사용하여 충격파가 동반되는 내부 유동구조를 모사하였고, 라그랑지안 연소모델을 통해 화약 입자를 계산하였다. 옆면 중앙에 센서가 설치된 원통형 밀폐용기 내부 유동분석을 통해 압력 진동이 발생하는 원인을 규명하였다. 또한 센서 다이어프램 깊이 변화에 따라 측정되는 압력 데이터를 실험값과 비교분석 하였다. 그 결과 센서 탭의 깊이가 약 2.36 mm 이상으로 커지면 유동속도가 아음속으로 감쇠하고 복잡한 eddy가 발생하여 측정값에 큰 불규칙성을 야기하는 현상을 관측하였다.
Abstract
A computational fluid dynamics simulation of pyrotechnic material combustion inside a cylindrical closed vessel was carried out using the Eulerian–Lagrangian method. The 5th order upwind WENO scheme and the improved delayed detached eddy turbulence model were implemented to capture shock waves. The flow structure was analyzed inside the cylindrical vessel with a pressure sensor installed at the side wall center. The analysis revealed that the pressure oscillated because of the shock wave vibration. Additionally, the simulation results with four different sensor tab depths implied that, inside the sensor tab, eddies were generated by the excessively large gap between the sensor diaphragm and the side wall. These eddies caused irregularity to the measured time-pressure curve, which is an undesirable characteristic.
Keywords:
Closed Bomb Test, Reactive Two-phase Flow, Eulerian-Lagrangian Method키워드:
밀폐용기연소실험, 반응이상유동, 오일러리안-라그랑지안 방법1. 서 론
밀폐용기 연소실험(Closed Bomb Test, CBT)은 밀폐용기 내부에서 고체연료를 점화시켜 발생하는 압력을 측정하는 실험이다. 이 방법은 주로 추진제나 화약의 성능을 측정하는데 사용된다. 하지만 다양한 형태의 파이로 작동기구[1-5]에 사용되는 Zirconium Potassium Perchlorate(ZPP)와 같이 연소속도가 빠른 화약은 점화 시 매우 큰 충격파가 발생하고, 용기 내부에서 충격파의 무작위적 반사에 의해 정확한 압력 측정 및 화약 특성분석이 쉽지 않다[6]. 이 경우 특히 압력 센서의 위치에 따라 전혀 다른 압력 데이터가 측정되기 때문에 위치에 따른 연소 및 유동 특성을 이해하고 실험을 수행할 필요가 있다. 유사한 연구로 NASA의 A. Dibbern 등[7]은 실험을 통해 압력 센서의 위치와 센서의 어댑터 직경에 따른 차이를 연구한 바 있지만 실험적 접근방법은 두꺼운 밀폐용기 내부에서 1 msec 이내에 발생하는 유동현상 가시화가 불가능하기 때문에 원인은 규명하지 못하였다.
본 연구는 전산해석을 이용한 내부 유동 관측을 통해 센서 위치에 따른 영향을 분석하여 향후 CBT 실험 시 센서 종류 및 설치위치 선택에 참고가 될 수 있도록 하였다. 강한 충격파가 동반되는 유동이기 때문에 상류 5차 WENO 기법을 사용한 improved delayed detached eddy(IDDES) [8, 9] 난류모델을 사용하였고, 라그랑지안 기법으로 연소하는 화약 입자를 개별 추적하였다.
2. 수학적 모델링
2.1 ZPP 화약의 점화 및 연소 모델링
본 연구에 사용된 연료는 ZPP(Zr 52%, KClO4 42%, Viton 5%, Graphite 1%)이다. ZPP는 압력 카트리지 내부에 약 5000 psi로 압착되어 사용되며 육안으로 관찰 시 하나의 펠렛 형태이다. 펠렛 형태의 화약은 점화 방법에 따라 연소면적에 확연한 차이가 발생한다[10]. 펠렛을 한쪽면만 열린 용기에 두고 열린 면에 점화원을 가하면 고체로켓 추진제와 같이 열린 면의 단면에서부터 타들어 가지만 반대쪽의 닫힌 면에서 점화시 내부 압력에 의한 화염전파로 펠렛이 파편화되어 빠른 연소가 일어난다. Fig. 1은 ZPP가 장착된 압력 카트리지를 대기 중에서 점화시킨 후 초고속 카메라를 통해 촬영한 스냅샷이다. 위 설명과 같이 (a) 점화 직후 자체 압력에 의해 매우 빠른 속도로 퍼져나가고 (b) 사진 상으로 여러개의 붉은 점들이 개별적으로 발광하는 것을 보아 그래뉼 형태의 ZPP가 각각 연소하는 것으로 볼 수 있다.
ZPP의 점화는 매우 빠른 속도로 일어나기 때문에 수치적 계산 시 그래뉼 단위로 고려하고 점화 직후부터 모사를 하여 모든 그래뉼이 동시 점화 되어있다고 가정하였다. 실제 그래뉼은 입도 분포가 존재하지만 시뮬레이션 상에서는 동일 분포로 가정하고, 본 연구자의 기존 연구 결과[11]에 따라 그래뉼의 직경은 17 μm로 가정하였다.
ZPP 입자의 개수(N)는 직경과 실제 장착 무게로부터 아래와 같이 계산한다.
| (1) |
Mt는 장착된 화약질량이고 dp는 입자의 평균 직경이다. 각 그래뉼이 완벽한 구 형태를 갖고 가스상(gas phase)의 연소생성물이 존재한다는 가정 하에 압력지배[12]를 받는 Vielle의 법칙에 따라 그래뉼 표면에서부터 중심 방향으로 아래의 속도()로 타들어 간다.
| (2) |
여기서 a는 연소속도 상수, n은 연소속도 지수이며, P는 입자 주변의 압력이다. 상수 a와 n은 B. L. Poulsen과 K. K. Rink[13]가 측정한 값을 사용하였다. 하나의 입자가 연소하며 외부로 방출하는 연소생성물의 질량생성률 및 열방출율은 아래와 같다.
| (3) |
| (4) |
여기서 ρzpp는 고체 ZPP의 밀도, hcomb는 ZPP의 연소 엔탈피이다. Table 1은 입자연소 모델링에 사용된 각 계수를 나타낸다.
2.2 오일러리안-라그랑지안 기법을 이용한 이상유동 해석
점화 후 연소중인 ZPP는 각각의 그래뉼 단위로 계산할 수 있기 때문에 라그랑지안 기법을 이용하여 각 입자를 개별 추적하여 계산하였다. 라그랑지안 기법은 입자의 연소 모델을 쉽게 적용할 수 있고 물리적으로 정확한 장점이 있지만 입자의 개수가 증가함에 따라 컴퓨터 리소스를 크게 차지한다. 적절한 계산 시간을 확보하기 위해 본 연구는 Message Passing Interface (MPI)를 이용한 병렬 컴퓨팅을 수행하였다.
오일러리안 기법은 2차원 Navier-Stokes 방정식을 다룬다. 복잡한 충격파가 발생하기 때문에 충격파 포착에 유리한 상류 5차 WENO 기법에 IDDES 난류모델을 사용하였고 3차 Runge-Kutta 기법으로 물리적 시간 전진을 수행한다. 지배방정식은 아래와 같다.
| (5) |
| (6) |
| (7) |
| (8) |
Eq. 5, 6, 7 및 8은 각각 질량, 모멘텀, 에너지 및 화학종 보존방정식이다. 상첨자 ㅡ 및 ~는 해당 변수의 시간평균 및 Favre 평균을 의미한다. 모든 식의 오른쪽 항에 소스텀이 존재하며 각 소스텀은 입자 연소에 의한 영향을 고려하였다. 소스텀의 정의는 아래와 같다.
| (9) |
여기서 은 하나의 격자에 존재하는 모든 ZPP 입자의 질량 방출율 합을 의미한다.
입자와 가스의 대류 열전달계수 h는 아래와 같은 Ranz-Marshall의 실험식을 사용하여 대류 열전달률과 열전도율의 비율을 의미하는 Nusselt 수를 구하고(Nu), 열전달계수로 변환할 수 있다.
| (10) |
여기서 Re는 레이놀즈주, Pr은 프란틀수이다.
ZPP연소에 의해 발생하는 가스는 실제로 여러 가스종의 혼합물이지만 계산상으로는 하나의 연소생성물로 고려하였다. 연소생성물의 물성치는 CEA[14]와 NIST[15] 데이터를 이용하여 계산하였다.
입자거동은 뉴턴의 2법칙을 이용하여 계산 가능하다. 입자의 구동 힘은 유동과의 상대속도로 인해 발생하는 저항만 고려하였고, 그 힘은 아래와 같이 표현된다.
| (11) |
여기에서 Cd는 항력계수이고 ur은 상대속도이다.
3. 수치 계산 결과
3.1 수치적 계산 도메인 및 압력 데이터 취득 방법
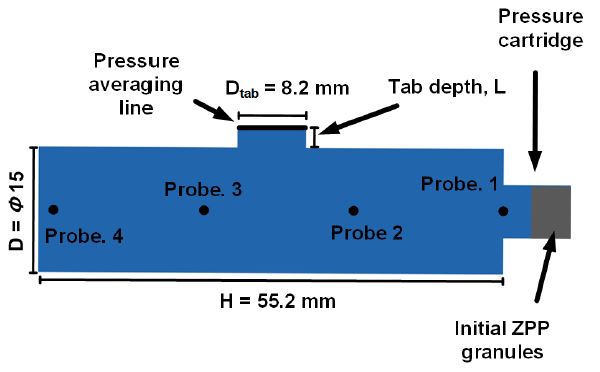
계산은 Fig. 2와 같이 10 cc 부피의 원통형 밀폐용기 CBT를 모사하였다. 용기 우측에 압력 카트리지가 장착되어있고 이 위치에 ZPP 그래뉼이 초기화된다. 모든 그래뉼은 동시점화를 가정하였다. 2-D 계산이기 때문에 10 cc 부피와 2-D도메인의 부피를 상사하여 ZPP 입자를 주입하였다. 용기의 중앙 위쪽에 압력 측정을 위한 탭이 있다. 센서 탭의 깊이 L 은 0, 0.29, 0.58, 2.32 mm 로 총 4가지 경우를 고려하였다.
3.2 밀폐용기 내부의 유동 현상 분석
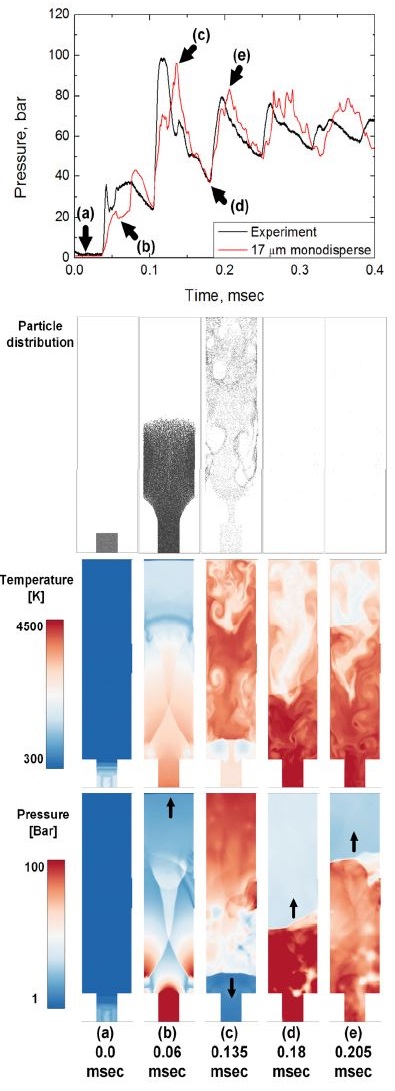
Fig. 3은 탭 길이 L = 0.29 mm 일 때 계산 결과를 실험 측정값과 비교한 것이다. 실험은 압력측정을 위해 Kistler사의 type-6005 센서를 사용하였고 주파수 필터는 사용하지 않았다. 또한 오실로스코프를 이용하여 100 MHz이 속도로 데이터를 취득하였다. 밀폐용기의 형상은 Fig.2와 같으며, 센서 다이어프램의 위치는 벽면으로부터 약 0.3 mm 뒤에 위치해있다. 실험은 세 번 진행되었으며 50 Khz의 FFT 필터 적용 후 각 결과의 오차는 약 7% 내외이다. 시간에 따른 입자분포도, 온도, 압력 분포는 압력-시간 선도에 표시된 시점과 동일하다. 압력 분포에 표시된 화살표는 충격파의 이동 방향을 의미한다. 계산 초기 상태인 Fig. 3(a)는 밀폐용기 내부유동이 정지 상태이고 입자도 압력 카트리지 내부에 존재한다. 하지만 ZPP의 급격한 연소로 인해 약 15배 이상의 압력차이가 발생할 정도의 강한 충격파가 생성된다. 충격파는 약 700 m/s의 평균 속도로 상승하고 Fig. 3(b)와 같이 윗면에 충돌 및 반사한다. 충격파의 상승에 의해 ZPP 그래뉼도 용기내부로 확산되지만 고체와 기체의 모멘텀 차이에 의해 가스보다 느리게 거동한다. 충격파가 반사되기 직전 후단의 압력은 약 15 bar 이고 온도는 약 1700 K 이지만 Fig. 3(c)와 같이 반사충격파가 하강을 하며 밀폐용기내 충격파 진행 방향의 후단의 압력은 160 bar 이상, 온도는 약 충격파 위치에서 압력-시간 선도는 국부 최대점에 도달한다. Fig. 3(d)와 같이 충격파가 하단에서 다시 반사하여 상승할 때 충격파의 상단에 위치한 센서 탭 부근은 피스톤 효과에 의해 압력이 급격히 하강하며 충격파가 탭 하단에 도달했을 때 압력-시간 선도는 국부최소점이 된다. 이후 충격파가 센서 탭을 지나가면 충격파 뒷부분의 높은 압력으로 인해 압력 - 시간 선도가 급격히 재 상승한다. 이와 같이 높은 압력차를 가지는 충격파의 계속적인 반사에 의해 센서에 압력진동이 측정되는 것이다.
3.3 용기 위치별 압력 차이
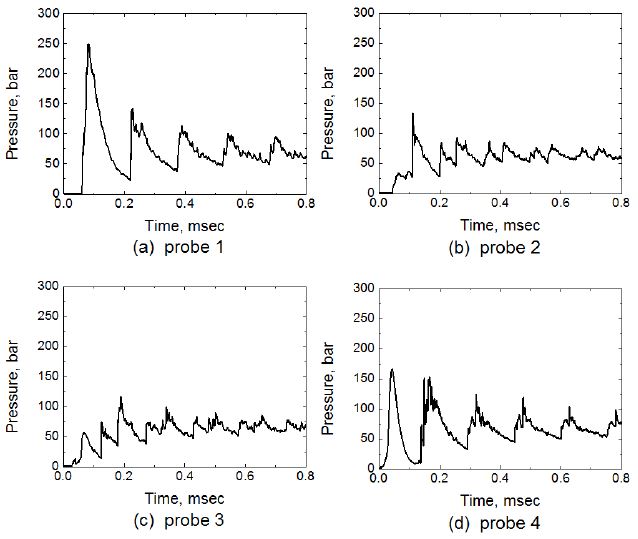
Fig. 4는 Fig. 2에 표시된 네 개의 프로브에서의 압력-시간 선도를 나타낸다. 각 점은 용기 (a) 좌측, (b), (c) 중앙 및 (d) 우측에 위치해있다. Fig. 4(a) 및 (d)는 충격파의 진동 횟수 (0.7 msec 동안 5회의 진동)와 동일한 진동 주기를 가지며 비교적 깔끔한 압력 선도가 나타난다. 단지 압력 카트리지 상단인 (a)가 초기에 더 높은 피크를 나타낸다. 또한 (a) 및 (d)는 매우 급격한 상승과 완만한 하강을 하는 파형이 나타나는데, 이는 충격파의 불연속성에 의한 특징이다. 후단의 압력이 매우 높은 충격파가 압력측정 위치를 지날 때 급격한 압력 상승이 되지만 이후 충격파 이동에 따른 피스톤 효과에 의한 압력하강 속도는 상승 속도에 비해 매우 완만하다. 반면 용기 중앙부에 위치한 (b) 및 (c)는 진폭이 비교적 작고 진동 주기가 짧고 불규칙하게 나타난다. 원인은 충격파가 압력카트리지가 존재하는 아래벽면에 충돌 후 반사될 때 높이 차이에 의해 충격파가 분할되기 때문이다. 이분된 충격파는 전 후 압력차가 감소하여 진폭이 크게 감소하고, 작은 충격파가 연이어 프로브를 지나기 때문에 (a)및 (d)에서 나타나는 하나의 큰 주기(약 0.19 msec) 사이에 (b) 및 (c) 그래프에는 2개 이상의 작은 주기가 나타난다.
3.4 센서 다이어프램 위치, L에 따른 압력 차이
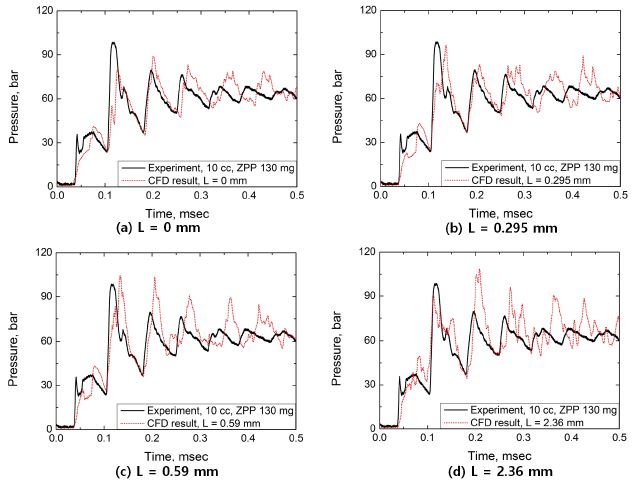
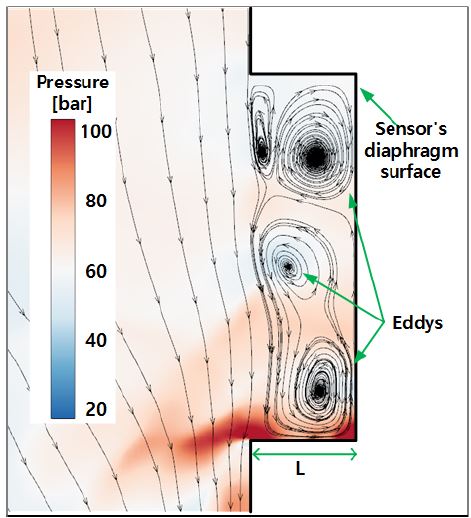
Fig. 5는 네 개의 다른 센서 다이어프램 위치(Fig. 2 에서 L)에 따른 압력-시간 선도를 실험값과 비교한 결과이다. Fig. 5(a)는 L = 0 mm 인 경우이다. 0.05 msec 이전 가장 초기에 압력이 상승할 때 실험값은 압력이 미세하게 압력 국부 최대점 (이하 “피크”) 형상을 가지고 다시 상승하지만 수치 결과는 완만한 상승을 나타낸다. 이후 실험은 두 번째 압력 피크가 가장 최대치를 나타내고 이후 점차 감소하는 반면 수치 값은 세 번째에서 가장 큰 피크를 나타내고 이후 미세하게 감소한다. 또한 네 번째 피크까지 주기는 비슷하지만 이후에는 차이가 점차 커지는데 이는 이차원 수치해석이 삼차원 소산효과를 고려하지 못하기 때문으로 추측된다. Fig. 5(b)는 L = 0.295 mm 결과이다. 네 가지 경우 중 피크의 진폭, 파형 및 주기 등이 실험과 가장 비슷하며 특히 초반에 미세한 피크도 모사된다. Fig. 5(c)는 L = 0.59 mm 로 초반의 미세한 피크가 더욱 뚜렷해 졌으나 두 번째 피크 이후의 진폭이 과다하게 예측되었다. 마지막으로 가장 긴 L = 2.36 mm인 Fig. 5(d)는 압력 선도가 매우 불규칙하게 예측되며, 시간이 지날수록 불규칙성이 강해진다. Fig. 6은 L = 2.36 mm 일 때 센서 탭 내부의 유동을 유선을 이용해 가시화한 그림이다. L 값이 0.59 mm 이하일 때와 비교해 내부 공간이 증가하여 유동속도가 크게 감쇠되면서 여러 eddy들이 발생하였고, 이로 인해 압력교란이 발생한다. 이와 같은 현상으로 인해 불규칙적인 압력 그래프가 나타난다. 위 결과는 압력센서 설치시 너무 큰 길이는 바람직하지 않음을 의미하고 만약 센서의 보호를 위해 거리를 둬야 한다면 큰 eddy가 생성되지 않을 정도의 작은 깊이로 설계를 하는 것이 바람직함을 의미한다.
4. 결 론
ZPP의 밀폐용기 연소실험을 오일러리안-라그랑지안 수치기법으로 해석하여 밀폐용기 내의 복잡한 유동 현상을 관찰하였다. 실험 측정값에서 나타난 압력진동 현상의 원인은 수치해석 결과 위, 아래로 진동하는 충격파가 센서의 다이어프램을 반복적으로 통과하기 때문인 것으로 나타났다. 충격파가 진동하면서 압력카트리지가 있는 벽면에 충돌 시 압력파가 분리되는 현상에 의해 밀폐용기 위, 아래 위치에서는 진폭이 크고 주기가 충격파 진동수와 동일한 압력이 측정되지만 중앙 부분에서는 분리된 충격파에 의해 진폭이 작고 주기가 불규칙한 압력이 측정되었다.
벽면 중앙의 센서 다이어프램 위치가 벽면과 일치할 때 실험상 측정된 초기 압력피크가 관찰되지 않았다. 다이어프램 위치 L = 0.295 mm일 때 실험과 가장 비슷한 결과가 도출되었고 다이어프램이 너무 뒤에 위치하여 센서 탭 내부 공간이 커질 경우 복잡한 와류의 발생으로 압력이 매우 불규칙하게 측정되었다. 따라서 밀폐용기 연소 실험에서 센서를 설치할 때 다이어프램의 위치를 최대한 벽면에 가깝게 설치하고 면적을 본 실험 및 수치해석에 사용된 1/4‘’ 배관규격 이하로 설정하면 보다 정확한 측정이 가능하다.
Acknowledgments
본 연구는 ‘유도탄용 고성능 PMD 기술’ 사업의 일환으로 방위사업청과 국방과학연구소의 지원으로 수행되었습니다.
References
-
Jang, S.K., Lee, H.N., and Oh, J.Y., "Performance Modeling of a Pyrotechnically Actuated Pin Puller", International Journal of Aeronautical and Space Science, 15(1), p102-111, (2014).
[https://doi.org/10.5139/ijass.2014.15.1.102]

-
Han, D.H., Sung, H.G., Jang, S.G., and Ryu, B.T., "Parametric Analysis and Design Optimization of a Pyrotechnically Actuated Device", International Journal of Aeronautical and Space Science, 17(3), p409-422, (2016).
[https://doi.org/10.5139/ijass.2016.17.3.409]

-
Braud, A.M., Gonthier, K.A., and Decroix, M.E., "System Modeling of Explosively Actuated Valve", Journal of Propulsion and Power, 23(5), p1080-1095, (2007).
[https://doi.org/10.2514/1.27414]

-
Hwang, D.H., Lee, J.H., Han, J.H., Lee, Y.J., and Kim, D.J., "Numerical Analysis and Simplified Mathematical Modeling of Separation Mechanism for the Ball-type Separation Bolt", Journal of the Korean Society of Propulsion Engineers, 20(3), p63-70, (2016).
[https://doi.org/10.6108/kspe.2016.20.3.063]

-
Kim, B.H., Kang, W.K., Jang, S.G., and Yoh, J.I., "Hydrodynamic Analysis on Shock-induced Detonation in Pyrotechnic Initiator", Journal of the Korean Society of Propulsion Engineers, 20(5), p19-30, (2016).
[https://doi.org/10.6108/kspe.2016.20.5.019]

- Han, D.H., Sung, H.G., Kwon, M.R., Ahn, G.H., Kim, J.H., and Ryu, B.T., "Multi-phase LES on the Pressure Oscillation inside a Closed Vessel Induced by a ZPP Combustion", 46th KSPE Spring Conference, Jeju, Korea, p375-378, May), (2016.
-
Dibbern, A., Sipes, W., Hagopian, M., McDougle, S.H., Saulsberry, R.L., and Crisafulli, J., "Implication of Dynamic Pressure Transducer Mounting Variations on Measurements in Pyrotechnic Test Apparatus", 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, C.O., U.S.A., AIAA 2009-4992, Aug), (2009.
[https://doi.org/10.2514/6.2009-4992]

-
Spalart, P.R., Deck, S., Shur, M.L., Squires, K.D., Strelets, M.K., and Travin, A.K., "A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities", Theoretical and Computational Fluid Dynamics, 20(3), p181-195, (2006).
[https://doi.org/10.1007/s00162-006-0015-0]

-
Shin, J.S., and Sung, H.G., "Numerical Investigation of a Model Scramjet Combustor Using DDES", International Journal of Turbo & Jet Engines, 41(1), p75-80, (2017).
[https://doi.org/10.1515/tjj-2015-0056]

- Kosanke, K.L., and Kosanke, B.J., "Parallel and Propagative Pyrotechnic Burning", Pyrotechnics Guild International Bulletin, (79), p167-172, (1992).
-
Han, D.H., Sung, H.G., and Ryu, B.T., "Numerical Simulation for the Combustion of a Zirconium/Potassium Perchlorate Explosive inside a Closed Vessel", Propellants, Explosives, Pyrotechnics, 42(10), p1168-1178, (2017).
[https://doi.org/10.1002/prep.201700068]

-
Yang, L.C., "Effects of Fuel Particle Size and Impurity on Solid-to-Solid Pyrotechnic Reaction Rate", 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, C.A., U.S.A., AIAA 2011-5581, Aug), (2011.
[https://doi.org/10.2514/6.2011-5581]

-
Poulsen, B.L., and Rink, K.K., "Modeling the Energy Release and Burn Rate Characteristics of ZPP Based Initiators", 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, F.L., U.S.A., AIAA 2011-271, Jan), (2011.
[https://doi.org/10.2514/6.2011-271]

- Gordon, S., and McBride, B.J., Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications,“, NASA Reference Publication 1311, (1994).
- “NIST chemistry WebBook,”, retrieved 15 Feb. 2017, World Wide Web location http://webbook.nist.gov/chemistry/.