[ Research Paper ]

Journal of the Korean Society of Propulsion Engineers - Vol. 22, No. 2, pp.52-58

ISSN: 1226-6027 (Print) 2288-4548 (Online)

Print publication date 01 Apr 2018

Received 09 Mar 2017 Revised 08 Sep 2017 Accepted 14 Sep 2017

DOI: https://doi.org/10.6108/KSPE.2018.22.2.052

초음속 풍동에서 발생하는 충격파의 히스테리시스 현상에 관한 연구

이익인^a ; 한그루^a ; 김태호^a ; 김희동^a^{, *}

Study on the Hysteretic Behaviors of Shock Wave in a Supersonic Wind Tunnel

Ik In Lee^a ; Geu Roo Han^a ; Teo Ho Kim^a ; Heuy Dong Kim^a^{, *}

aDepartment of Mechanical Engineering, Andong National University, Korea

Correspondence to: ^*E-mail: kimhd@anu.ac.kr

Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

유체 유동 시스템에서 히스테리시스 현상은 다양한 산업 및 공학 응용 분야에서 발생하며, 최근 이에 대한 많은 연구가 수행되어 왔다. 이러한 현상은 주로 압력비가 일시적으로 변화하는 과정에서 발생하며 초음속 풍동에 영향을 미칠 것으로 예상되나, 이에 대한 연구는 찾아보기 힘들다. 본 연구에서는 초음속 풍동 내부에서 발생하는 히스테리시스 현상을 수치해석으로 조사하였다. 비정상, 축대칭, 압축성 N-S 방정식을 유한 체적법으로 이산화 하였으며, 난류모델은 Spalart-Allmaras을 적용하였다. 본 연구의 결과로 전압의 증감에 따라, 동일한 압력비에서 발생하는 충격파의 위치가 다르게 나타났으며, 이를 통해 초음속 풍동을 효율적으로 작동시킬 수 있는 최적의 압력비를 찾을 수 있음을 알았다.

Abstract

Hysteresis phenomena are often encountered in a wide variety of fluid flow systems used in industrial and engineering applications. Hence, in recent years, a significant amount of research been focusing on clarifying the physics of the flow hysteresis appearing during the transient change of the pressure ratios and influencing the performance of the supersonic wind tunnel. However, investigations on the hysteresis phenomenon, particularly when it occurs inside the supersonic wind tunnel, are rare. In this study, numerical simulations were carried out to investigate the hysteresis phenomena of the shock waves encountered in a supersonic wind tunnel. The unsteady and compressible flow was analyzed with an axisymmetric model, and the N-S equations were solved by using a fully implicit finite volume scheme. The optimal pressure ratio was determined from the hysteresis curves, and the results can be utilized to operate the wind tunnel efficiently.

Keywords:

Supersonic Wind Tunnel, Hysteresis Phenomenon, Shock Wave Location, Internal Flows

키워드:

초음속 풍동, 이력 현상, 충격파 위치, 내부 유동

1. 서 론

히스테리시스 현상은 일반적으로 물질의 탄성, 전기 및 자성에서 쉽게 나타나며 어떤 물리량이 주기적 또는 어떤 범위를 갖고 움직였을 때, 그 이전에 물질이 경과해온 상태의 변화 과정에 의존하여 출발지로 돌아오지 못하고 다른 값으로 떨어지는 현상을 일컫는다. 그러나 최근 이러한 히스테리시스 현상은 다양한 산업 및 공학 응용분야뿐만 아니라 역학, 물리학, 수문학, 경제학 등 여려 분야에서 쉽게 접할 수 있는 현상이다. 특히 유체 부문에서는 이중모드 램제트(dual-mode ramjet), 초음속 풍동(supersonic wind tunnel), 로켓 노즐 등 많은 분야에 나타나고 있다.

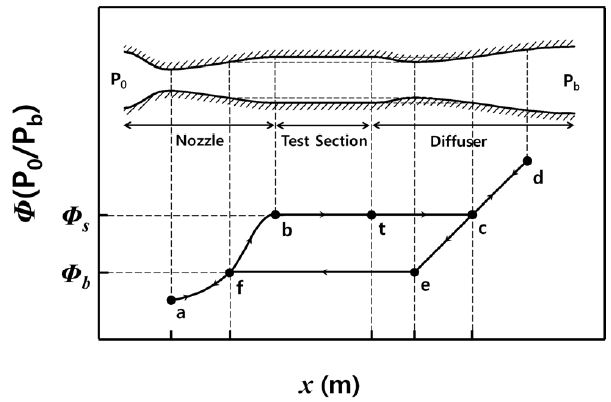
초음속 풍동에서 발생하는 히스테리시스 현상을 간략하게 Fig. 1에 나타내었다. 이론적으로 초음속 풍동에서 풍동압력비(wind tunnel pressure ratio)를 증가시키면 (a)지점인 첫 번째 노즐 목(nozzle throat)에서 수직충격파(normal shock wave)가 발생한다. 이 후 풍동압력비를 서서히 증가시키면 충격파는 풍동 출구 방향으로 이동하게 되며 (b)지점인 측정부(test section)에 충격파가 위치하게 된다. 풍동압력비를 좀 더 증가시키면 충격파는 측정부 끝단에 위치하게 되는데, 이 압력비를 시동압력비(starting pressure ratio) Ø_s라 한다. 축소유로에선 충격파가 발생할 수 없으므로 충격파는 2차목(2nd throat)인 (c)지점에서 발생하여 (d)지점으로 이동한다. 그 후 다시 풍동압력비를 감소시키면 충격파는 (c) - (e)지점을 지나 (f)지점으로 이동하게 된다. 이때 (e)지점의 압력비를 작동압력비(operating pressure ratio) Ø_b라 한다. 이러한 현상은 측정부에서 충격파와 벽면 경계층의 간섭 현상에 의하여 발생하며, 만일 비점성유동 계산을 수행한다면 작동압력비와 시동압력비는 동일할 것으로 예상된다.

Fig. 1

Hysteresis diagram in supersonic wind tunnel.

히스테리시스 현상을 적절히 이용한다면 초음속 풍동의 효율적인 운전이 가능하다. 또한 기계장치의 성능이나 수명 저하에 영향을 야기시키므로 히스테리시스 현상에 대한 정확한 이해가 필요하다.

최근 히스테리시스 현상에 관한 많은 연구가 수행되었으며, 그중에 하나로 로켓 엔진에 사용되는 추력 노즐을 예로 들 수 있다[1]. 또한 2차원 초음속 노즐에서 발생하는 히스테리시스 현상의 실험 및 수치해석적 연구는 비교적 상세히 보고된 바 있다[2,3]. 하지만 초음속 풍동에서 히스테리시스 현상이 발생하는 이유와 조건, 또한 이러한 히스테리시스 현상에 미치는 유동변수와 제어방법에 대한 구체적인 연구는 미흡한 실정이다.

본 연구에서는 Blow-Down 형식의 JAXA 1m × 1m Supersonic Wind Tunnel(JSWT) 풍동으로 2차원 대칭 수치해석을 수행하였으며, 이를 종래의 실험 결과와 비교 검증하였다. 초음속 풍동 내부에서 발생하는 히스테리시스 현상을 수치해석적으로 조사하기 위해, 풍동압력비를 선형적으로 변화시켜 충격파의 위치를 확인하였고 서로 다른 측정점에서 측정한 압력변동을 비교하였다.

2. 수치해석 방법

본 연구에 앞서, 수치해석 타당성을 조사하기 위한 선행연구로 여러 가지 격자에 대한 수치해석을 수행하였으며 여러 난류모델을 적용하여 선행 실험결과와 비교하였다. 그 결과 후술하는 바와 같은 계산영역과 계산격자를 얻을 수 있었으며, Spalart, P.R. 와 Allmaras, S.R.[4]가 제안한 Spalart-Allmaras One-Equation 난류모델을 사용한 결과 실험 결과를 잘 예측하였다.

수치해석은 상용코드인 Fluent Ver. 15.0을 사용하였다. 2차원 압축성 Reynolds-averaged Navier-Stokes 방정식을 적용하였으며, 완전 내 재적 유한 체적법(implicit finite volume scheme)을 적용하였다. 또한 압축성 유동을 고려하여 지배 방정식을 density-based solver인 coupled scheme을 적용하였으며, 수치적 안정성을 위해 AUSM-DV와 2nd order up-wind scheme을 적용하여 대류항(conective term)을 계산하였다.

본 연구에서 사용한 JAXA 1m × 1m Supersonic Wind Tunnel(JSWT)는 2개의 고압탱크에 저장된 건조 공기가 압력 조절기, 가변 2차원 노즐, 측정부(test section), 2차 목(2nd throat)을 가진 디퓨저를 통과하여 대기로 방출되는 구조이다. 측정부의 크기는 높이 1 m, 폭 1 m, 길이 1.8 m, 마하수는 1.4에서 4.0까지 설정 가능하며, 레이놀즈 수 적용 범위는 2.0×10⁷~6.0×10⁷ (1/m)이다. 작동시간(run time)은 최대 40초이다.

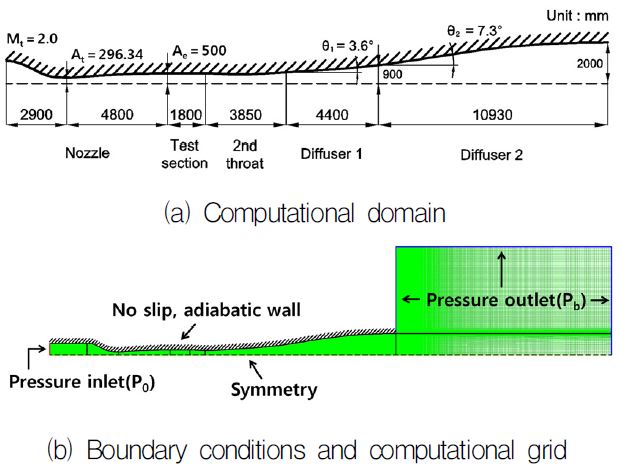
Fig. 2에서 수치해석에 사용된 JSWT 풍동의 계산영역과 경계조건을 나타내었다[5]. 본 수치해석에 사용된 계산영역의 총 격자수는 대략 20만개를 사용하였으며, 경계층이 발달하는 부분, 유동이 초크하는 목 부분, 그리고 충격파 발생예상 부분에 격자를 집중시켰다. 모든 벽면은 단열(adiabatic), 점착(non-slip) 조건을 입구는 pressure inlet, 출구는 pressure oulet 조건을 적용하였다. 입구 전압(P₀)은 115 kPa ~ 420 kPa 범위에서 변화시켰으며, 출구 배압(P_b)은 101.325 kPa로 고정하였다. 또한 전온도(T₀)는 300 K로 일정하며, 작동시간은 1.0 × 10^-5으로 1초 동안 비정상 계산을 하였다.

Fig. 2

Computational domain and boundary conditions.

본 연구에서 사용한 초음속 풍동의 2차원 노즐은 노즐 입구로부터 노즐 목까지 길이가 2900 mm, 노즐 목으로부터 출구면, 즉 측정부의 입구까지의 길이는 4800 mm 이다. 측정부의 크기는 높이 500 mm, 길이 1800 mm이며, 2차목을 가진 디퓨저의 길이는 3850 mm이다. 디퓨저 1(Diffuser 1)과 디퓨저2(Diffuser 2)의 길이는 각각 4400 mm, 10930 mm이며 디퓨저1의 확대반 각(θ₁)은 3.6°, 디퓨저2의 확대반각(θ₂)은 7.3°로 고정하였다. 또 본 연구에 사용된 설계마하수(M_t)는 2.0이며, 유로의 폭은 1000 mm로 일정하다[6].

3. 결과 및 고찰

초음속 풍동에서 발생하는 히스테리시스 현상을 조사하기에 앞서, 본 연구에서 수행한 수치해석 결과와 JSWT의 실험결과를 비교하여 타당성을 조사하였다.

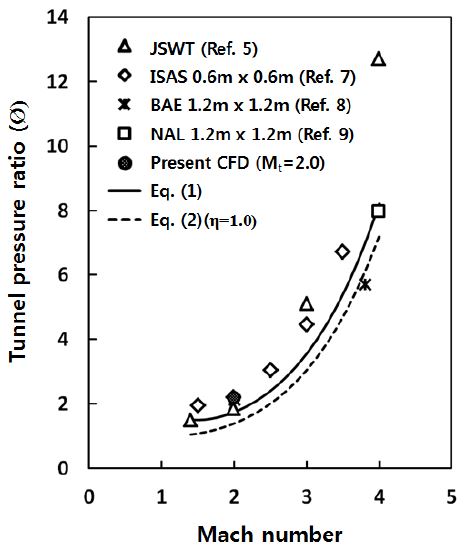
Fig. 3은 초음속 풍동에서 마하수와 풍동압력비 Ø(=상류정체실의 압력 P₀/풍동의 배압 P_b)의 관계를 선행연구에서 수행한 실험 결과와 비교하였다[5,7-8]. 그 결과, 본 연구의 수치해석 결과가 JSWT에서 수행한 실험결과와 잘 일치하였다. 디퓨저의 영향을 고려하지 않고 설계마하수(M_t)에서 측정부에 수직충격파가 발생한다고 가정하였을 경우, 시동압력비는 등엔트로피 관계식 과수직충격파 관계식으로 부터 Eq. 1로 나타난다.

ϕ = 1 + γ - 1 2 M t 2 γ γ - 1 γ + 1 2 γ M t 2 - γ - 1

(1)

Fig. 3

Mach number at various pressure ratios in wind tunnel.

Eq. 1에서 풍동 하류에 디퓨저 효율 η 를 도입하면 Eq. 1은 Eq. 2로 쓸 수 있다.

ϕ = 1 + γ - 1 2 M t 2 γ γ - 1 γ + 1 2 γ M t 2 - γ - 1 1 + γ - 1 2 η γ - 1 M t 2 + 2 2 γ M t 2 - γ - 1 - γ γ - 1

(2)

η =0인 경우, 충격파 하류의 흐름이 완전히 박리한 경우를 나타내며 η =1인 경우는 충격파 하류에서 압력이 배압까지 완전히 회복하여 디퓨저 출구에서 유속이 0인 경우를 의미한다.

그러나 Fig. 3에서 각 풍동의 시동압력비는 각각 다른 특성을 보였으며, 실제 풍동에서는 디퓨저에 의한 압력상승이 있으므로 Eq. 1에서 얻은 값보다 높은 풍동압력비에서 풍동의 시동이 예상되지만, 항상 그렇지는 않았다. JSWT는 마하수 2.0 인 부분에서 이론값과 비슷한 경향을 보였다. 그러나 마하수 3.0에서 시험에 필요한 압력 비율이 급격히 증가하는 경향이 나타났다.

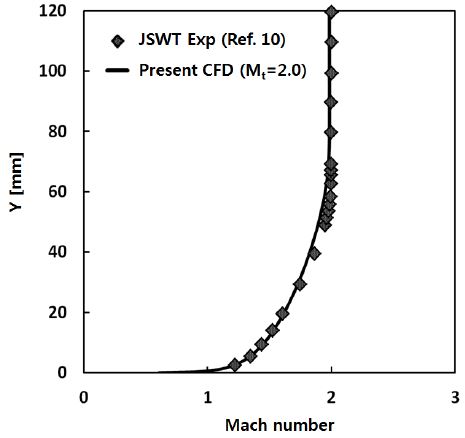
측정부에서의 경계층 두께를 마하수 2.0에서 선행연구의 실험 결과와 비교하여 Fig. 4에 나타내었다[10]. 그 결과 JSWT의 실험 결과와 매우 일치한 결과를 얻었으며, 경계층 두께는 마하수 2.0에서 대략 60 mm이다. 위에서 언급한 두 결과를 토대로 실험결과와 수치해석 결과가 잘 일치하였다.

Fig. 4

Comparison of experimental and predicted mach number in boundary layer.

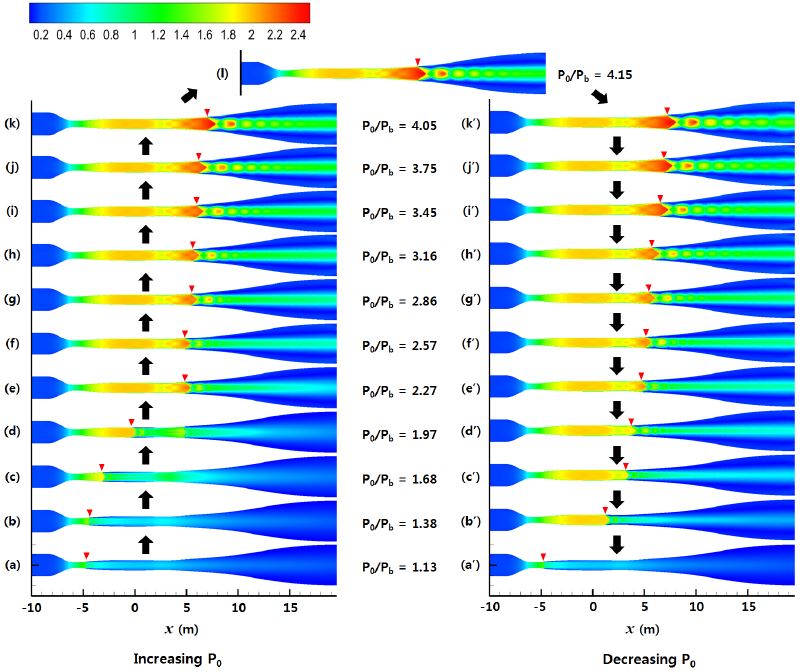
Fig. 5는 초음속 풍동에서 풍동압력비를 변화시켜 각 풍동압력비에 따른 유동장의 마하수 분포를 나타내었다. 그림의 결과들은 풍동의 배압을 고정시키고 정체실 상류의 전압을 선형적으로 증가시켜 수치해석을 수행한 후, 정체실 상류의 전압을 초기상태로 감소시킨 과정에서 얻어진 결과이다. 상류정체실 압력이 증가함에 따라 노즐 목에서 발생하는 충격파가 초음속 풍동 출구방향으로 이동하게 되며, 충격파의 형태 또한 변화된다. 충격파가 노즐 상류에 발생할 때는 수직 충격파의 형태를 띠나, 하류로 이동함에 따라 의사충격파의 형태로 변화된다. 이것은 노즐 벽면에서 발생하는 난류경계층과 충격파의 간섭현상에 기인한 것이다. 또 중요한 것은 압력비의 증감과정에서 충격파의 위치가 서로 상이하였다. 따라서 초음속 풍동의 시동압력비는 Eq. 1과 그림에서 압력비가 증가하는 과정의 압력비 2.27에서 얻어지며, 압력비가 감소하는 과정의 압력비 1.38 부근에서 작동압력비가 얻어진다는 것을 알 수 있다.

Fig. 5

Mach number contours at various pressure ratios.

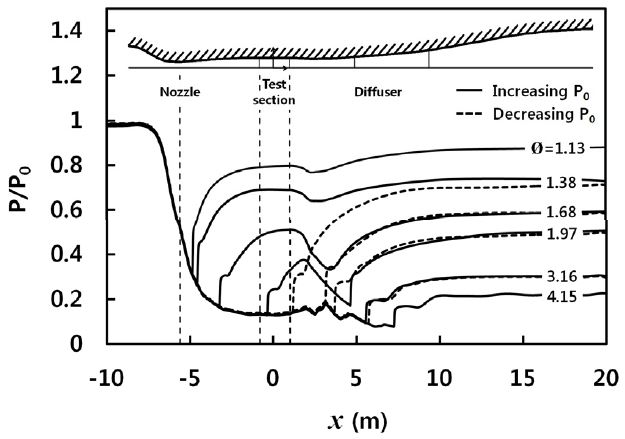
Fig. 6에서 초음속 풍동 벽면에서의 압력분포를 조사하기 위해, 횡축은 측정부 중심에서의 거리로 나타내었으며 종축은 벽면의 정압을 상류정체실 압력으로 무차원하여 나타내었다. 풍동압력비(Ø) 증가과정에서 얻은 벽면의 압력 분포를 실선으로 표시하였으며, 감소과정에서 얻은 벽면의 압력분포는 점선으로 표시하였다. 2차 목의 영향으로 압력손실의 원인이 되는 경계층 박리현상이 발생하였으며, 풍동압력비의 증가과정과 감소과정에서 발생하는 풍동내의 충격파 위치차이는 낮은 압력비에서 더 크게 나타났다.

Fig. 6

Static pressure distributions on tunnel wall.

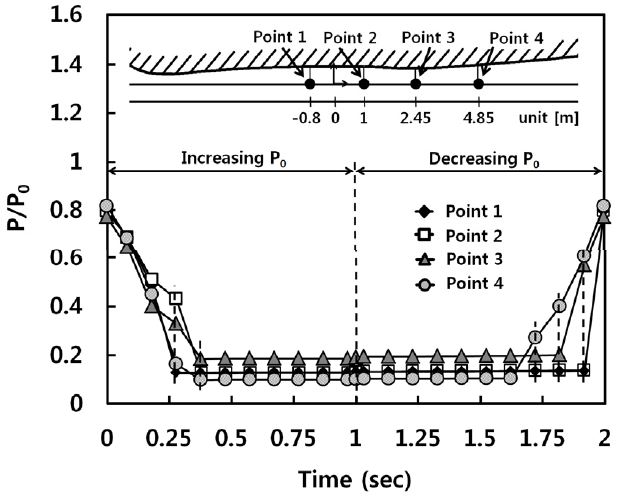
시간변화에 따른 압력변화가 어떻게 나타나는지 조사하기 위해, 서로 다른 측정점에서 정압을 측정하여 Fig. 7에 나타내었다. 횡축은 상류정체실의 압력(P₀)이 변화되는 시간을 나타냈으며, 종축은 측정점의 정압(P)을 상류정체실 압력으로 무차원 하였다. 측정점의 자세한 위치는 Fig. 7에 자세히 표시하였다. 상류정체실 압력은 초기 지점에서 1초까지 증가하며, 이후 2초까지 감소하여 초기조건으로 돌아간다. 상류정체실의 압력이 증가함에 따라 충격파는 풍동 출구방향으로 이동됨을 Fig. 5에서 앞서 설명하였다. 풍동에서 발생하는 충격파의 위치가 측정점에 근접 할수록 압력비(P/P₀)는 감소하였으며, 충격파가 모든 측정점을 지나는 지점인 t=0.4초를 기준으로 이후의 모든 측정점에서 압력비는 일정하게 유지되었다. 이러한 경향은 상류정체실의 압력감소과정에서도 나타난다. 그러나 t=1.6초를 기준으로 압력비가 증가하는 과정에서 상류정체실 압력이 증가하는 과정과 차이가 발생하였다. 초기상태에서 0.4초 부근까지 압력비가 감소되나 상류정체실 압력의 감소과정에서는 이보다 더 늦은 1.9초 부근에서 압력비가 증가하였다.

Fig. 7

Static pressure distributions along the centerline at various instances.

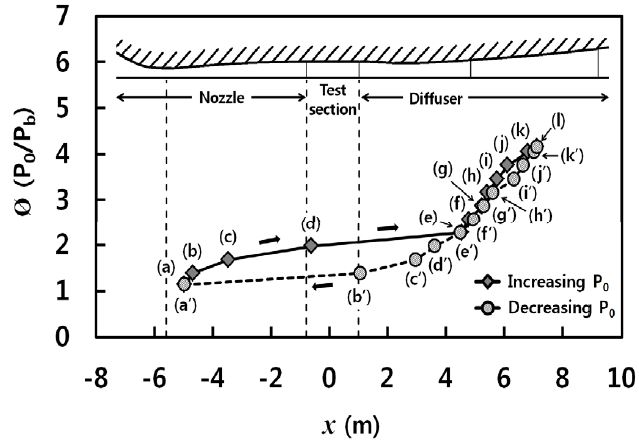
Fig. 8은 초음속 풍동에서 발생하는 충격파의 위치를 바탕으로 히스테리시스 곡선을 나타내었다. 횡축은 측정부 중심에서의 거리이며, 종축은 풍동압력비로 나타내어 비교하였다. 서로 다른 풍동압력비에서 발생하는 충격파의 위치를 심볼로 표시하였다. 상류정체실 압력이 증가함에 따라 충격파 발생 위치는 풍동 출구 방향으로 이동하였다. (e)지점에서 초음속 풍동이 시동되었으나 동일한 풍동압력비인 (e’)을 지나 (b’)에서 초음속 풍동이 작동되었다. 히스테리시스 현상은 모든 범위의 풍동압력비에서 발생하였지만, 특히 풍동압력비가 (a)~(e) 범위에서 매우 넓게 발생했다. 이러한 충격파 위치의 히스테리시스는 측정부 하류 디퓨저에서도 발생하게 되며, 따라서 작동압력비를 결정하는 경우에, 충격파의 위치를 2차 목으로부터 먼 하류까지 위치하도록 압력비를 변화시키면 풍동의 효율이 감소하게 된다. 실제의 풍동 운전은 충격파를 2차 목 바로 하류에 위치하도록 압력비를 증가시킨 후, 압력비를 감소시켜 작동압력비를 얻는 것이 가장 바람직하다.

Fig. 8

Hysteresis diagrams for shock wave locations.

4. 결 론

본 연구에서는 초음속 풍동에서 발생하는 히스테리시스 현상을 조사하기 위해, 2차원 비정상 압축성 Reynolds-averaged Navier-Stokes 방정식을 적용하여 수치해석을 수행하였다. 초음속 풍동에서 풍동압력비를 변화시켜 내부에 발생하는 충격파의 위치를 토대로 히스테리시스를 분석하였으며, 아래와 같은 결과를 얻었다.

(1) 상류정체실의 압력이 증가할수록 초음속 풍동에서 발생하는 충격파의 위치는 풍동 출구 쪽으로 이동하였다.

(2) 상류정체실의 전압이 시간에 따라 선형적으로 증감하였을 때, 동일한 풍동압력비에서 발생하는 충격파의 위치가 서로 다르다.

(3) 상류정체실 전압이 증가하는 과정과 감소하는 과정에서 발생하는 충격파의 위치를 비교하였을 때, 상류정체실 전압이 증가하는 과정에서 발생하는 충격파가 감소하는 과정에서 발생하는 충격파의 위치보다 항상 상류에 위치한다.

(4) 히스테리시스 현상으로 인해 초음속 풍동의 시동압력비와 작동압력비가 서로 다른 풍동압력비를 가진다. 이러한 현상을 적절히 제어한다면, 작동압력비를 줄여 초음속 풍동의 효율적인 운전이 가능하다.

Acknowledgments

본 연구는 교육과학기술부 한국연구재단(NRF)의 사업인 중견연구자지원사업 (No. NRF-2016R1A2B3016436)의 일환으로 수행되었으며 지원에 감사드립니다.

References

Lee, J.S., J.S. Kim, H.D., “The Effect of the Variation of Pressure Ratio on the Characteristics of Lateral Forces in an Over-Expanded Nozzle,”, Journal of the Korean Society of Propulsion Engineers, 14(6), p38-44, (2010).
Setoguchi, T., Matsuo, S., Alam, M.A., Nagao, J., and Kim, H.D., "Hysteretic Phenomenon of Shock Wave in a Supersonic Nozzle,”, Journal of Thermal Science, 19(6), p526-532, (2010). [https://doi.org/10.1007/s11630-010-0419-4]
Nam, J.S., and Kim, H.D., "Experimental Study on the Flow Hysteresis Phenomenon in a Supersonic Nozzle,”, The Korean Society of Mechanical Engineers, 16(2), p206-212, (2012). [https://doi.org/10.6108/kspe.2012.16.2.058]
Spalart, P., and Allmaras, S., "A One-equation Turbulence Model for Aerodynamic Flows.", 30th Aerospace Sciences Meeting and Exhibit, Reno, N.V., U.S.A., p439, Jan), (1992. [https://doi.org/10.2514/6.1992-439]
Akatsuka, J., and Nagai, S., "The Effect of Diffuser Geometry on the Starting Pressure Ratio of a Supersonic Wind Tunnel", 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Chicago, I.L., U.S.A., AIAA 2010-4344, Jun), (2010. [https://doi.org/10.2514/6.2010-4344]
“On the Design and Contruction of the 1m × 1m Supersonic Blow-down Wind Tunnel.”, Technical Report of National Aeronautical Laboratory, NAL-TR29, (1962).
入門朋子, 佐藤清, and 藤井孝藏, "ISAS 風洞における風洞始動時の衝撃荷重と流れ場.", 第38 回流体力学講演会論文集, p147-150, (2006).
“BAE SYSTEMS”, retrieved 20 Dec. 2016, from http://www.baesystems.com/ProductsServices/bae_prod_mas_wind_tunnel.html.
“ICAST(Information Center for Aerospace Science and Technology)”, retrieved 22 Dec. 2016, from http://www.icast.org.in/Resources/Dwttfi1.pdf.
Watanabe, M., Iijima, H., Sato, M., Nagai, S., Nishijima, H., Kimura, T., and Itabashi, Y., "A Measurement of Turbulent Boundary Layer Thickness at the JAXA 1m × 1m Supersonic Wind Tunnel,”, JAXA-SP-04-013, (2005).