음향가진된 횡단류 유동장 내 액체제트의 분무특성
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 횡단류 공기유동에 수직으로 분사되는 액체제트의 분열거리와 액주궤적에 대한 음향가진의 영향을 살펴보았다. 이를 위해 단공 원형노즐 분사기를 이용하여 동일한 횡단류 공기속도에서 분사압력과 음향가진의 크기를 변화시켜가며 수류실험을 수행하였다. 또한 음향가진 주파수 기준 12개의 위상각에서 분무 이미지를 얻어 위상각 변화에 따른 영향을 확인하였다. 실험결과 분열길이는 비가진 상태에 비해 음향가진 상태에서 전반적으로 감소하였지만 위상각에 따른 변화는 발견되지 않았다. 본 실험 범위 내에서 음향가진은 수직분사 액체제트의 액주궤적에 거의 영향을 주지 못하였다.
Abstract
This study investigated the acoustic forcing effects on the liquid column breakup length and the trajectory of liquid jets in crossflows. Cold-flow tests with a single hole circular nozzle injector were carried out by changing the injection pressure and acoustic forcing amplitude. Additionally, spray images were obtained at 12 phase angles to investigate the influence of the phage angle. The results revealed that the liquid column breakup lengths generally decreased under the acoustic forcing conditions, in comparison to those under the non-acoustic forcing conditions. However, they were not affected by the variation in the phase angles. On the contrary, it was found that the acoustic forcing hardly influenced the liquid column trajectories.
Keywords:
Liquid Jet in Crossflow, Acoustic Forcing, Liquid Column Breakup Length, Liquid Column Trajectory키워드:
수직분사 액체제트, 음향가진, 분열길이, 액주궤적1. 서 론
고속의 횡단류 유동에 수직으로 분사되는 액체제트의 분무방식은 램제트 엔진, 스크램제트 엔진 및 가스터빈 엔진과 같은 연소기에 많이 활용된다. 이러한 연소기에서 연소 효율과 안정성은 액체연료의 분무특성에 의해 크게 영향을 받기 때문에, 액체 미립화 조건과 이와 관련된 물리적인 현상에 대하여 이해하는 것이 중요하다. 따라서 분열길이, 액주궤적, 분무분포, 액적 크기와 같은 분무특성에 대해 많은 실험 및 수치해석적 연구가 수행되고 있다.
일반적으로 수직분사 액체제트의 분무형상은 액주(liquid column), 액사(ligament), 액적(droplet)으로 나누어진다[1]. 공력학적 항력에 의하여 분사된 액체제트의 액주 표면에 액주파가 형성되며, 하류로 가면서 더욱 증폭되어 결국 액주가 덩어리진 액사로 분열되는 미립화 현상이 나타나게 된다. 이러한 전반적인 분열과정을 액주분열(column breakup)이라 한다[2]. 이외에도 액주 자체의 난류 소용돌이에 의해 난류 파동이 발달하여 액적이 액주 표면으로부터 직접 분리되어 떨어지는 표면분열(surface breakup)이 발생하기도 한다[3,4].
분열 이전의 액주궤적과 분열길이는 분무의 분포에 큰 영향을 준다. 따라서 이에 대한 실험적 연구는 이미 많은 연구자들에 의하여 수행되어 왔다. Schetz와 Padhye는[5] 최대 침투 높이를 노즐 지름(d)의 약 6.25배로 정의했으며, 액체/기체 운동량 플럭스 비의 함수로 표현하였다. Inamura 등[6]은 접촉식 니들 프로브를 이용하여 분열길이를 측정하였으며, 분열길이 xb/d는 3 ~ 3.5 범위에 있다고 주장하였다. Ahn 등[7]은 더 나아가 캐비테이션과 수력튀김 현상이 분열 길이에 어떠한 영향을 미치는지 관찰하였으며, Wu 등[3]의 데이터와 비슷한 분열길이인 xb/d = 8로 수렴하는 결과를 제시하였다.
횡단류 유동에서 가진 수직분사에 대한 연구는 주로 액체연료[8,9,10]나 기체연료[11,12]에 섭동을 주는 방법이 사용되었다. Johari 등[8]은 변조분사 시스템을 구성하여 듀티 사이클과 주파수에 따른 수직분사 실험을 진행하였으며, 평면 레이저유도 형광기법(PLLIF)을 이용하여 펄스된 제트의 침투나 희석 그리고 구조적 특성들을 연구하였다. Eroglu 등[9]도 레이저유도 형광기법을 사용하여 액주 구조와 와류 형태를 연구하였으며, 높은 레이놀즈수에서 제트의 침투는 70%까지 상승하는 반면 최적화 주파수 범위에서의 화염길이는 50%로 감소하는 결과를 발표하였다. 또한 Omar 등[10]은 액추에이터를 이용하여 액체제트에 가진을 주는 방법을 사용하였다. 기체연료 수직분사의 경우 M‘Closkey 등[11]은 가진되는 기체제트의 동적특성을 연구하여 향상된 제어시스템을 개발하고자 하였다. 또한 Shapiro 등[12]은 개방형 루프 제어를 통하여 주파수 변화에 따른 기체제트의 혼합특성에 대하여 연구하였다.
램제트 엔진이나 가스터빈 엔진과 같은 덤프 연소기에서 연소불안정이 일어나게 되면 공기유입구에서 큰 압력섭동이 발생되어 횡단류 유동에 영향을 주게 된다. 하지만 횡방향 공기유동의 섭동에 따른 수직분사 액체제트에 대해서는 상대적으로 최근에서야 연구들이 수행되었고 많은 연구결과가 발표되지 않은 상황이다[13,14]. 따라서 본 연구에서는 횡단류 유동장 내 음향가진이 수직분사 액체제트의 분무특성(액주궤적, 분열길이)에 어떠한 영향을 주는지 살펴보고자 하였다.
2. 실험방법 및 실험조건
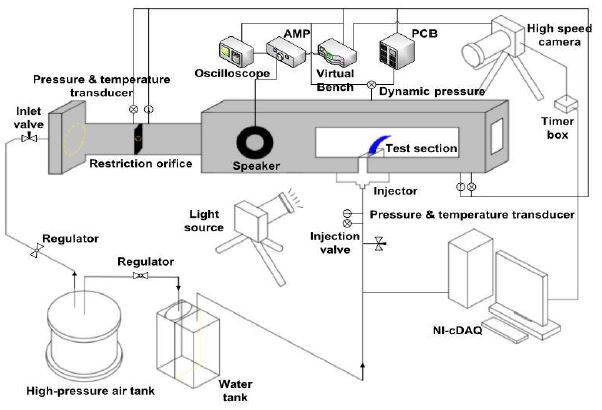
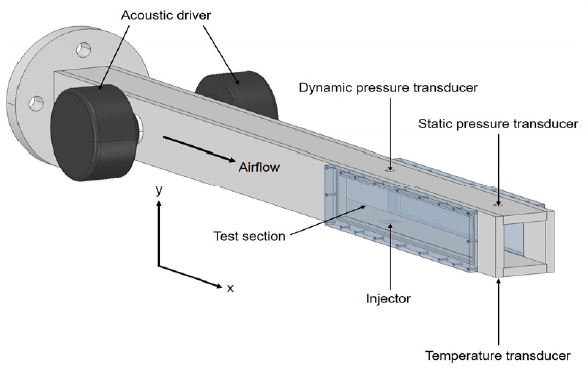
Fig. 1은 본 연구에 사용된 실험장치를 나타낸 도식도이며, Fig. 2에 test section의 상세도를 3D 모델링으로 나타내었다. 횡단류 유동으로는 공기가 수직분사 액체로는 물이 사용되었다. 초킹 오리피스와 레귤레이터를 이용하여 고압 실린더에 압축된 공기를 일정한 유량으로 실험장치에 공급하였으며, 추가적인 레귤레이터를 이용하여 분사기에 공급되는 물의 압력을 조절하였다. Test section의 높이와 너비는 각각 50 mm이며, 가시화를 위해 test section 전/후단에 길이 300 mm의 아크릴 창을 설치하였다. Test section 내 공기와 분사기 매니폴드에서 물의 압력 및 온도를 측정하기 위해 압력센서와 K-type 열전대를 사용하였다. 음향가진을 주기 위해 분사기 500 mm 전단에 75 W 음향가진기(acoustic driver) 2개를 대칭으로 배치하였다. 분사기는 test section의 하단에, 압력섭동 측정을 위한 동압센서(PCB, 101A05)는 분사기 위치의 상단에 flush-mount되도록 설치하였다. 동압센서의 신호는 PCB signal conditioner(482A16)를 통해 100배 증폭되어 기록되었다. 본 실험에서는 d = 0.5 mm, L/d = 10인 원형 오리피스 분사기를 사용하였다. 실험장치 및 분사기에 대해서는 기존 참고문헌[15,16]에 보다 자세히 설명되어 있다.
분무가시화 실험에는 고속카메라(최대 1632 × 1200 pixels)와 2개의 광원장치(Polarion, PS-X1)를 이용하였다. 음향가진 및 압력섭동과 고속카메라의 동기화를 위해 함수발생기(NI, VirtualBench)를 사용하였다. 함수발생기는 사인파와 디지털 트리거 신호를 발생하게 되는데, 사인파는 앰프(Inkel, AX5505)를 거쳐 증폭된 후 음향가진기에 전송되고, 트리거 신호는 고속카메라에 전달되어 카메라를 동기화하게 한다. 실제적으로 앰프, 음향가진기, 음향가진기와 분사기 사이의 거리 등으로 인해 함수발생기에서 발생한 신호와 동압센서에서 측정한 위상은 다르게 된다. 따라서 동압센서에서 측정한 신호와 고속카메라의 트리거 신호를 측정한 후 실제 촬용된 분무 이미지의 위상을 재분석하였다. 실험 시 측정된 압력, 온도, 동압신호, 트리거 신호는 모두 NI-cDAQ에 저장되었다.
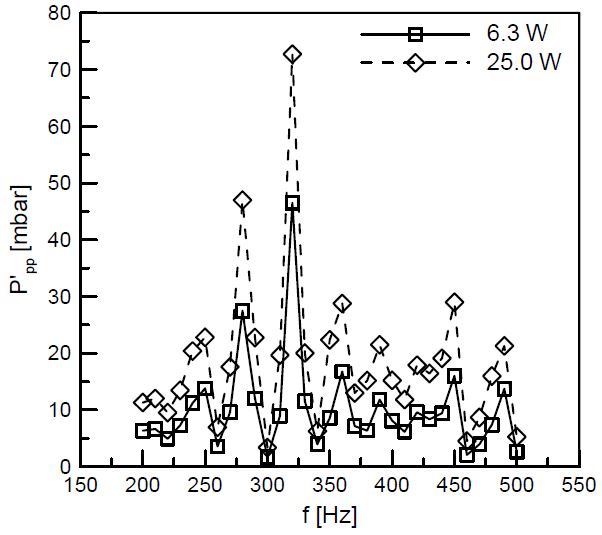
본 연구에서의 실험조건을 Table 1에 정리하였다. 공기속도 및 물의 분사압력은 기존 연구[15]와 동일하게 유지하였다. 가진 주파수를 결정하기 위해 음향가진기의 주파수 한계(150 ~ 5,000 Hz)와 덤프 연소기의 일반적인 고주파 연소불안정 범위를 고려하여 200 ~ 500 Hz 영역에서 음향실험을 수행하였다. 음향가진기의 출력을 6.3 W와 25.0 W로 고정시킨 상태에서 10 Hz 씩 주파수를 증가시켜가며 압력섭동 값을 측정하였다. 이에 대한 결과를 Fig. 3에 나타내었으며, 320 Hz에서 가장 큰 압력섭동 값을 나타내었다. 따라서 이 주파수에서 동압센서의 압력섭동 값을 peak-to-peak 기준 10 mbar부터 60 mbar까지 크기를 변화시켜가며 음향가진 크기에 따른 분무특성을 확인하였다. 또한 각 위상각에 따른 영향을 살펴보기 위해 카메라의 프레임 속도를 3,840 Hz로 설정하여, 총 12개의 위상각에서 각각 50장의 이미지를 촬영하였다. 프레임 속도 3,840 Hz에서 카메라의 최대 해상도는 480 × 600 pixels이었으며, 순간적인 분무 이미지를 얻기 위해 노출시간은 카메라의 최소 설정 값인 2 ㎲로 고정하였다. 평면파에서 압력섭동과 유동섭동은 P′ = ρcu′(여기에서 ρ: 공기의 밀도, c: 공기의 음속)의 관계식을 갖으며, 계측 데이터들로부터 유동섭동을 계산하여 평균유속에 대한 비(u’pp/U)를 Table 1에 정리하였다[17].
3. 실험결과
3.1 액체제트의 유량계수
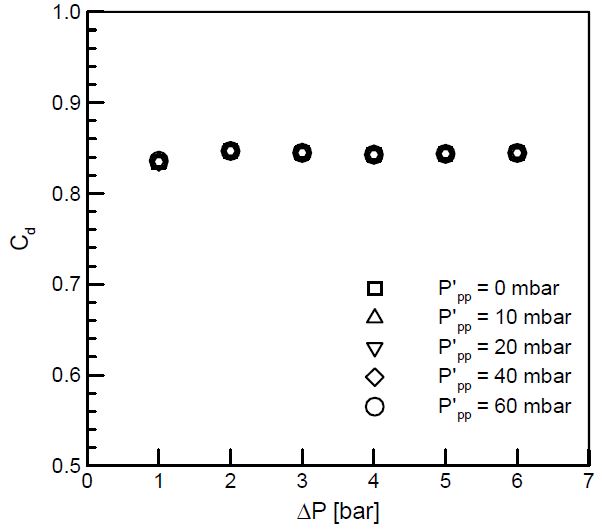
분사압력에 따른 유량특성을 분석하기 위해 Eq. 1을 사용하여 유량계수 값을 구하고, 결과들을 Fig. 4에 도시하였다.
| (1) |
유량계수는 음향가진이나 가진의 크기에 상관없이 각 분사압력에서 거의 일정한 값을 나타냈다. 분사압력에 따라 유량계수가 약간씩 달라지긴 하지만 변동폭이 매우 작고 4 bar 이상에서는 감소하지 않는 것으로 미루어, 본 실험 범위내에서 캐비테이션이나 수력튀김 현상이 나타나지 않는 것을 확인할 수 있었다[15]. 유량계수 측정값을 이용하여 분사되는 액체제트의 속도를 구하였으며, 이후 액체/기체 모멘텀 플럭스 비(q)를 계산하여 분열길이와 액주궤적 데이터를 분석하는데 사용하였다.
3.2 액체제트의 분열길이
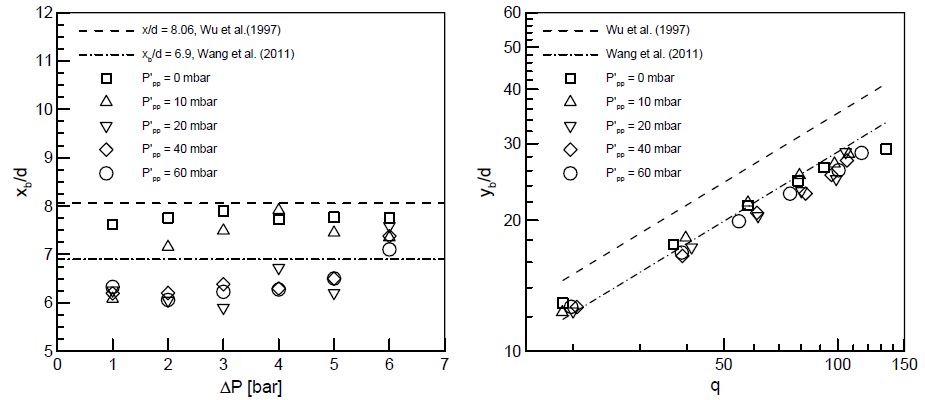
액주의 분열길이는 다량의 액적이 형성되기 시작하는 위치일 뿐만 아니라 수치해석에 있어서 유체와 입자 해석의 경계가 되기 때문에 중요한 분무특성 중 하나로 여겨진다. 비가진 상태와 가진 상태에서의 분열길이(xb, yb)를 각각 구하여 압력섭동 크기와 분사압력에 따라 이를 Fig. 5에 정리하였다. 분열길이 측정은 기존 연구들[7,15]과 동일한 알고리즘을 사용하였다. 이미지의 강도 값(intensity)을 바탕으로 분무 이미지를 이진화한 후, 오리피스 출구 직경에 비하여 분무된 액주가 연속적이지 않는 영역 즉, 분무가 끊어지는 영역을 분열지점으로 정의하였다. MATLAB 프로그랩 기반의 in-house code를 이용하여 데이터를 분석한 결과 xb의 표준편차는 평균적으로 0.96으로 나타났다. Fig. 5의 분열길이는 비가진 상태의 경우 600장의 분무 이미지에서 구한 평균 분열길이를 나타내며, 가진 상태의 경우 각 위상별로 50장씩 촬영한 분무 이미지에서 구한 분열길이를 평균한 후 다시 위상평균한 값을 나타낸다. 비가진 상태의 경우 실험압력 범위 내에서 분열길이는 선행연구 데이터[4,18,19]와 유사한 결과를 나타내었다. 하지만 20 mbar 이상의 가진 상태에서 x축 분열길이는 비가진 상태에 비해 상당히 줄어드는 현상을 발견할 수 있었다. P‘pp = 10 mbar의 경우 ΔP = 1 bar에서는 분열길이가 감소하지만, 분사압력이 증가함에 따라 분열길이의 감소가 줄어들어 4 bar 이상에서는 비가진 상태와 큰 차이를 보이지 않았다. P‘pp가 20 mbar 이상의 경우 압력섭동의 크기 증가는 분열길이 감소에 더 이상 영향을 주지 않는 것으로 판단되나, 전반적으로 분사압력이 증가할수록 분열길이의 감소는 줄어드는 결과를 나타내었다. 음향가진에 따른 x축 분열길이 감소에 따라 y축 분열길이도 또한 비가진 상태에 비해 줄어드는 것을 확인할 수 있었다.
이러한 분열길이의 감소는 공기유동 내 압력섭동과 액주표면 액주파의 상호작용에 의한 것으로 생각된다. 앞에서 언급하였듯이 공기역학적 힘에 의해 액주 표면에 생성되는 액주파는 하류로 가면서 더욱 증폭되게 된다. 일정값 이상의 음향가진이 액주와 만나게 되면서 액주파의 증폭을 더욱 촉진시켜 분열길이를 감소시키며, 또한 분사압력이 증가할수록 액체의 모멘텀이 증가하여 압력섭동의 영향을 덜 받는 것으로 판단된다.
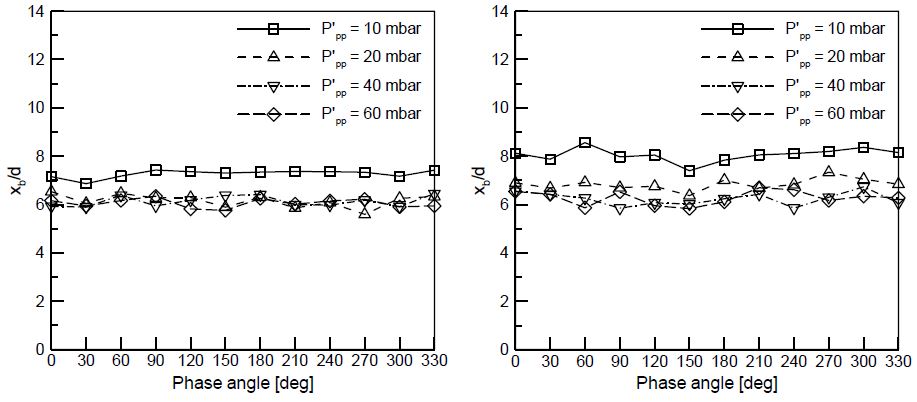
분사압력 2 bar, 4 bar 조건에서 위상각에 따른 분열길이의 변화를 Fig. 6에 나타내었다. 이 때 위상각 0도는 동압센서에서 측정한 압력섭동사인파의 시작점을 의미한다. Fig. 5에서와 같이 P‘pp가 20 mbar 이상에서는 P‘pp = 10 mbar에 비해 모든 위상에서 분열길이가 감소하는 것을 확인할 수 있지만 위상각에 따른 분열길이의 주기적인 변화는 발견할 수가 없었다. 분열길이와 액체의 속도를 고려할 때 분사시점부터 분열까지 대략 1 ms의 시간이 소요되는데, 가진 주파수가 320 Hz였기 때문에 액주는 대략 110도의 위상을 겪게 된다. 따라서 각 위상에서의 분열길이를 측정하였지만 액주 자체는 어느 정도 위상 평균된 영향을 받기 때문에 본 실험 범위에서 위상에 따른 분열길이의 영향은 발견되지 않는 것으로 생각된다.
3.3 액체제트의 액주궤적
수직분사 액체제트의 궤적은 분무분포에 영향을 주기 때문에 상당히 오랜 동안 실험적으로 연구되고 있다. 기존 연구들에 따르면 분열 이전 액주궤적은 모멘텀 플럭스 비(q)와 분사기 오리피스 지름(d)의 함수로 표현된다고 알려져 있다[19,20]. 본 연구에서는 액주의 위쪽 궤적(yu)뿐 아니라 위쪽 궤적과 아래쪽 궤적의 중심 궤적(yc)을 측정하여 액주궤적을 분석하였다. 분열 이후에는 궤적 데이터가 심하게 흩어지는 관계로 분열길이 이전의 유효한 데이터만을 사용하였다. 아래 식들은 비가진 상태에서 측정한 액주 궤적을 선형회귀분석을 통해 도출한 결과이다.
| (2) |
| (3) |
Fig. 7은 Eq. 2, 3과 함께 본 실험 데이터를 선행 연구들[4,7,20]의 경험식들에 대입하여 얻은 결과를 나타낸 그래프이다. 기존 연구들과 사용한 실험장치, 실험조건, 궤적측정 방법 등이 다르기 때문에 약간의 차이는 있지만, 액주의 위쪽 궤적과 중심 궤적 모두 상당히 일치함을 확인할 수 있었다.
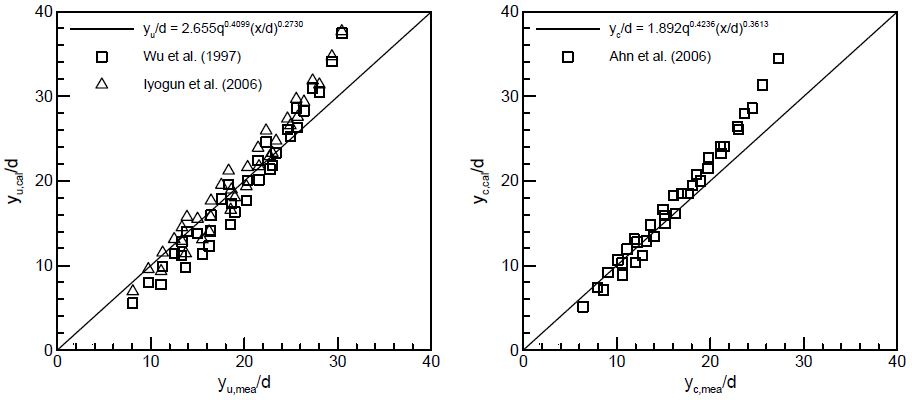
Liquid column trajectories normalized by orifice diameter without acoustic forcing (from left to right: upper boundary and centerline).
이를 바탕으로 비가진 상태와 가진 상태에서의 액주궤적을 비교한 데이터를 Fig. 8, 9에 정리하였다. Fig. 8의 데이터는 각 압력섭동에서 위상별 액주궤적의 값들을 모두 평균한 값을 나타내며, Fig. 9의 데이터는 P‘pp = 60 mbar의 압력섭동에서 각 위상별 액주궤적의 값들을 나타낸다. Fig. 10의 분무 이미지에서도 확인할 수 있듯이, 가진 상태의 액주궤적들이 압력섭동의 크기나 위상각에 상관없이 비가진 상태의 경험식들과 정확히 일치하는 것으로 미루어 압력섭동이 액주궤적에는 영향을 미치지 않는 것으로 판단된다. 이는 음향가진이 액주 표면에 영향을 주더라도 오리피스 출구로부터 분무되는 액주는 고유의 수직 모멘텀을 보존하고 있기 때문에 본 실험에서의 압력섭동 정도로는 공기나 액체의 모멘텀에 큰 영향을 미치지 못했기 때문으로 생각된다.
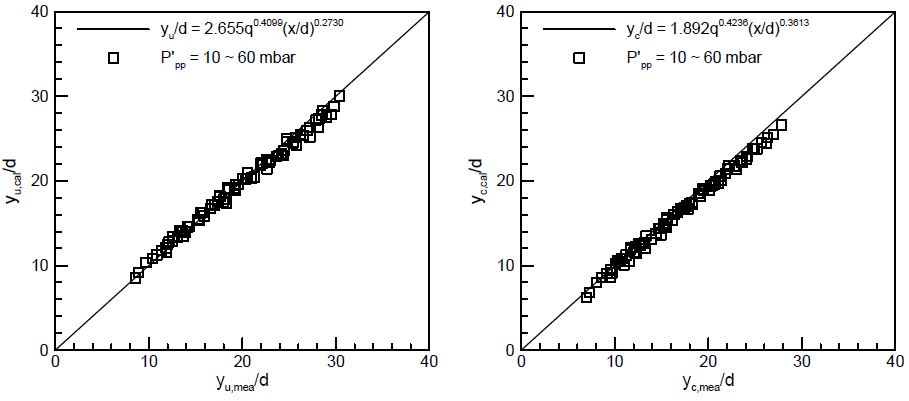
Liquid column trajectories normalized by the orifice diameter with acoustic forcing (from left to right: upper boundary and centerline).
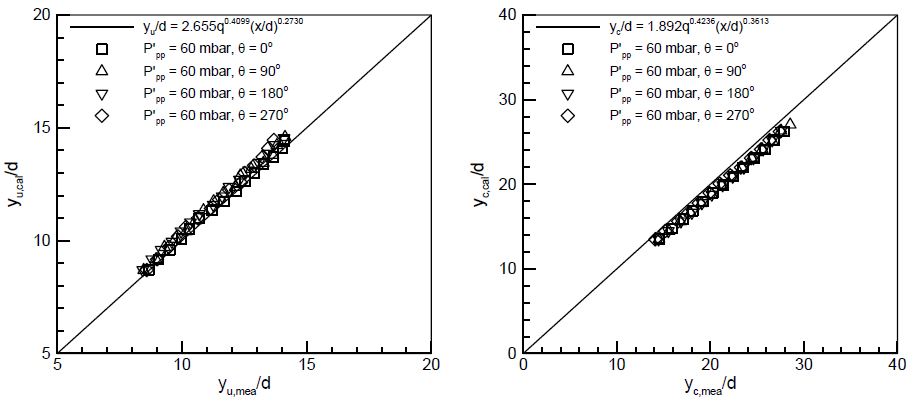
Liquid column trajectories with acoustic forcing as a function of the phase angle(θ) (from left to right: upper boundary at ΔP = 1 bar and centerline at ΔP = 6 bar).
4. 결 론
덤프 연소기에서 연소불안정이 일어나게 되면 공기 유입구에 압력섭동(속도섭동)이 발생하여 횡단류 유동 및 수직분사 액체제트에 영향을 주게 된다. 본 연구에서는 이를 모사하기 위해 음향발생기를 이용하여 횡단류 공기유동에 음향가진을 준 상태에서 수직분사 액체제트의 분무특성(분열길이, 액주궤적)에 대한 실험을 수행하였다.
비가진 조건에 비해 음향가진 조건에서 액주의 분열길이는 전반적으로 감소하였다. 압력섭동의 크기에 따라 분열길이 감소는 영향을 받았지만, P‘pp = 20 mbar 이상에서는 큰 변화가 발생하지 않았다. 분사압력 증가에 따라 분열길이 감소는 줄어드는 경향을 나타내었다. 또한 위상각에 따른 분열길이의 변화를 살펴보았지만 분열길이의 주기적인 변동은 발견되지 않았다.
액주궤적의 경우 비가진 조건에서 액주 위쪽 궤적과 중심 궤적을 구하여 선행연구들과 비교를 수행하였다. 하지만 액주궤적은 분열길이와는 다르게 음향가진에 따른 압력섭동의 크기나 위상각에 영향을 받지 않는다는 것을 확인하였다.
본 연구에서의 실험들은 실제 연소불안정 시의 압력섭동에 비해 매우 작은 섭동 영역에서 수행되었기 때문에 보다 큰 압력섭동에서의 추가 실험이 필요하다. 하지만 본 실험 범위에서도 분열 길이의 감소는 확인되었으며, 이러한 분열길이의 감소는 연소불안정 시 발생하는 덤프 연소기에서의 화염의 위치 변화에도 영향을 주는 것으로 예상할 수 있다. 현재 후속 연구를 위해 300 W의 음향발생기 및 앰프를 구매하여 실험을 준비 중이며, 큰 압력섭동 조건에서 가진 주파수를 낮추어 위상각에 따른 영향을 다시 살펴볼 예정이다.
Nomenclature
| A : | orifice area |
| Cd : | discharge coefficient |
| d : | orifice diameter |
| f : | acoustic forcing frequency |
| L : | orifice length |
| : | mass flow rate |
| P‘pp : | peak-to-peak value of the pressure fluctuations |
| q : | liquid/air momentum flux ratio |
| U : | air velocity |
| u’pp : | peak-to-peak value of the air velocity fluctuations |
| x : | distance from the orifice exit center in the airstream direction |
| xb : | breakup length in the x-direction |
| y : | distance from the orifice exit in the direction perpendicular to the airstream |
| yb : | breakup length in the y-direction |
| yc : | distance to the liquid column centerline |
| yu : | distance to the liquid column upper boundary |
| ΔP : | injection pressure drop |
| θ : | phase angle |
| ρf : | fluid density |
Acknowledgments
본 논문은 미래창조과학부의 재원으로 한국연구재단의 지원(NRF-2015M1A3A3A02011346, NRF-2017R1A1A1A05001237)을 받아서 수행되었으며, 이에 감사드립니다.
References
- Chen, T.H., Smith, C.R., Schommer, D.G., and Nejad, A.S., "Multi-Zone Behavior of Transverse Liquid Jet in High-Speed Flow", 31st Aerospace Sciences Meeting, Reno, N.V., U.S.A., AIAA 1993-0453, Feb. 1993.
-
Thomas, R.H., and Schetz, J.A., “Distribution Across the Plume of Transverse Liquid and Slurry Jets in Supersonic Airflow,“, AIAA Journal, 23(12), p1892-1901, (1985).
[https://doi.org/10.2514/3.9193]

-
Wu, P.K., Kirkendall, K.A., Fuller, R.P., and Nejad, A.S., "Breakup Processes of Liquid Jets in Subsonic Crossflows", Journal of Propulsion and Power, 13(1), p64-73, (1997).
[https://doi.org/10.2514/2.5151]

-
Wu, P.K., Miranda, R.F., and Faeth, G.M., "Effects of Initial Flow Conditions on Primary Breakup of Nonturbulent and Turbulent Round Liquid Jets", Atomization and Sprays, 5(2), p175-196, (1995).
[https://doi.org/10.1615/atomizspr.v5.i2.40]

-
Schetz, J.A., and Padhye, A., "Penetration and Breakup of Liquids in Subsonic Airstream", AIAA Journal, 15(10), p1385-1390, (1977).
[https://doi.org/10.2514/3.60805]

-
Inamura, T., Nagai, N., Watanabe, T., and Yatsuyanagi, N., “Disintegration of Liquid and Slurry Jets Traversing Subsonic Airstreams,”, 3rd World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Honolulu, H.I., U.S.A., Oct. 1993.
[https://doi.org/10.1016/0894-1777(93)90273-l]

-
Ahn, K., Kim, J., and Yoon, Y., "Effects of Orifice Internal Flow on Transverse Injection into Subsonic Crossflows: Cavitation and Hydraulic Flip", Atomization and Sprays, 16(1), p15-34, (2006).
[https://doi.org/10.1615/atomizspr.v16.i1.20]

-
Johari, H., Pacheco-Tougas, M., and Hermanson, J.C., "Penetration and Mixing of Fully Modulated Turbulent Jets in Crossflow", AIAA Journal, 37(7), p842-850, (1999).
[https://doi.org/10.2514/2.7532]

-
Eroglu, A., and Breidenthal, R.E., "Structure, Penetration, and Mixing of Pulsed Jets in Crossflow", AIAA Journal, 39(3), p417-423, (2001).
[https://doi.org/10.2514/2.1351]

-
Elshamy, O.M., Tambe, S.B., Cai, J., and Jeng, S.M., "Excited Liquid Jets in Subsonic Crossflow", 45th Aerospace Sciences Meeting and Exhibit, Reno., N.V., U.S.A., AIAA 2007-1340, Feb. 2007.
[https://doi.org/10.2514/6.2007-1340]

- M'Closkey, R.T., King, J.M., Cortelezzi, L., and Karagozian, A.R., "The Actively Controlled Jet in Crossflow", Journal of Fluid Mechanics, 452, p325-335, (2002).
-
Shapiro, S.R., King, J.M., M'Closkey, R.T., and Karagozian, A.R., "Optimization of Controlled Jets in Crossflow", AIAA Journal, 44(6), p1292-1298, (2006).
[https://doi.org/10.2514/1.19457]

- Proscia, W., “Modulation of a Liquid-Fuel Jet in an Unsteady Cross-Flow,”, ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, L.A., U.S.A., Jun. 2001.
-
Song, J., Ramasubramanian, C., and Lee, J. G., “Response of Liquid Jet to Modulated Crossflow,“, Atomization and Sprays, 24(2), p129-154, (2014).
[https://doi.org/10.1615/atomizspr.2013008071]

-
Song, Y., Hwang, D., and Ahn, K., "Effect of Orifice Geometry on Spray Characteristics of Liquid Jet in Crossflow", 55th Aerospace Sciences Meeting, Grapevine, T.X., U.S.A., AIAA 2017-1961, Jan. 2017.
[https://doi.org/10.2514/6.2017-1961]

- Song, Y., Hwang, D., and Ahn, K., “Effect of Orifice Geometry on Flow Characteristics of Liquid Jet from Single Hole Nozzle,”, Journal of the Korean Society of Propulsion Engineers, 21(5), p19-28, (2017).
- Dowling, A.P., and Williams, J.E.F., Sound and Sources of Sound, John Wiley & Sons Inc., New York, N.Y., U.S.A., p15-21, (1983).
-
Wang, Q., Mondragon, U.M., Brown, C.T., and McDonell, V.G., "Characterization of Trajectory, Break Point, and Break Point Dynamics of a Plain Liquid Jet in a Crossflow", Atomization and Sprays, 21(3), p203-219, (2011).
[https://doi.org/10.1615/atomizspr.2011002848]

-
No, S.Y., "A Review on Empirical Correlations for Jet/Spray Trajectory of Liquid Jet in Uniform Cross Flow", International Journal of Spray and Combustion Dynamics, 7(4), p283-314, (2015).
[https://doi.org/10.1260/1756-8277.7.4.283]

-
Iyogun, C.O., Birouk, M., and Popplewell, N., “Trajectory of Water Jet Exposed to Low Subsonic Cross-flow,”, Atomization and Sprays, 16(8), p963-980, (2006).
[https://doi.org/10.1615/atomizspr.v16.i8.70]