DACS 추진기관의 핀틀 구동장치 고장을 허용하는 추력 분배기법 연구

2.1 시스템 구성

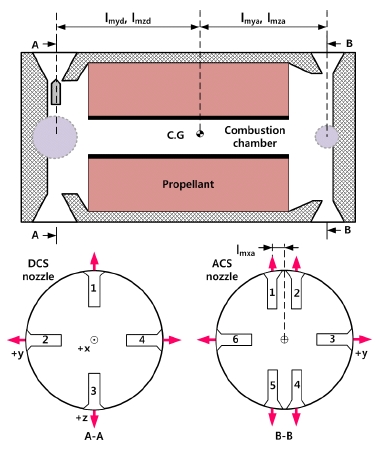
연구의 대상이 되는 추진기관의 구조도는 Fig. 1과 같다. 그림과 같이 연소 면적이 일정한 End burning 타입의 추진기관이며, 하나의 연소실에 대하여 DCS 4개, ACS 6개로 총 10개의 핀틀-노즐 구조체가 장착되어 있다[7].

시스템의 위치를 제어하기 위한 DCS 노즐에서는 ACS 노즐에 비해 상대적으로 큰 추력이 발생하며, 자세를 제어하기 위한 ACS 노즐은 모든 축 방향의 요구 모멘트를 만족시키기 위하여 DCS 노즐보다 2개 더 많은 6개의 노즐로 구성된다.

Fig. 1.

Configuration of propulsion system[7].

Fig. 1과 같이 좌표축이 정의된 시스템에서 x축 방향으로의 힘을 제외한 각 축 방향으로의 힘(F_y, F_z) 및 모멘트(M_x, M_y, M_z)를 정리하면 Eq. 1~5와 같다.

이 때 DCS 및 ACS 각각의 i번째 노즐에서 발생하는 추력을 각각 T_di, T_ai라고 하였으며, k축 방향의 모멘트에 대한 모멘트 암의 길이를 각각 l_mkd, l_mka라고 표현하였다.

위 식에서 좌변에 해당하는 시스템 전체의 힘과 모멘트 벡터를 T_b, 각 노즐에서 발생하는 추력을 T_n이라고 하면 Eq. 1~5를 다음과 같이 Eq. 6으로 정리할 수 있다.

이 때 T_n2b는 각 노즐에서 발생한 추력 벡터를 시스템의 추력 및 모멘트로 변환하는 행렬이다.

2.2 시스템 모델링

추진기관의 내탄도 시스템을 모델링하기 위하여 먼저 Robert의 연소식을 이용하면 Eq. 7과 같이 연소 속도, r_b를 표현할 수 있다.

위 식에서 η_rb는 보정계수, A_b는 연소면적이며, a와 n은 추진제의 특성에 따라 결정되는 연소속도 상수 및 지수이다. 이렇게 결정된 r_b와 질유량 보전법칙을 이용하여 내탄도 시스템을 Eq. 8, 9와 같이 모델링 할 수 있다.

위 식에서 P_c, V_c는 각각 연소실 내부 압력 및 부피이며, A_{t, tot}는 개별 노즐 목 면적의 총 합, ρ_p는 추진제 밀도, T_c는 화염 온도, η_d는 초킹 보정계수, C_d는 유량계수를 각각 의미한다.

2.3 제어 구조

DACS 추진기관의 역할은 시스템에서 요구되는 추력 및 모멘트를 만족시키는 것이며, 이를 위해서는 적당한 수준의 압력 제어 및 각 노즐의 추력 분배가 이루어져야 한다. 추력 분배에 앞서 각 노즐에서 발생하는 추력, F는 Eq. 10과 같이 정의할 수 있다.

이 때 η_f는 추력 보정계수, A_e는 노즐의 출구 면적을 의미하며, P_e 및 P_a는 각각 노즐 출구면에서의 압력 및 대기압을 의미한다. Eq. 10과 같이 정의된 식에서 추력 계수, C_f는 다음의 Eq. 11과 같이 정의된다.

이 때 ϵ은 노즐의 출구 면적과 노즐 목 면적의 비로 다음과 같이 정의된다.

일반적으로 연소관 내부 압력인 P_c는 P_e및 P_a보다 매우 크므로(P_c ≫ P_e, P_a), Eq. 11은 다음과 같이 간단하게 정리할 수 있다.

즉 일반적인 경우C_f는 Eq. 13과 같이 상수로 가정할 수 있으며, 본 논문에서도 이러한 가정을 적용하였다.

다음으로 Eq. 6에 표현된 T_n은 Eq. 14와 같이 정의할 수 있다.

이 때 A_ti는 각 노즐의 목 면적 벡터이다.

위 식에서 알 수 있듯이, 각 노즐에서 발생하는 추력은 노즐 목 면적뿐만 아니라 연소실 압력에 의해서 결정된다. 즉 단순히 추력 요구를 만족시키기 위해서 노즐 목 면적을 변화시킬 경우, 연소실 압력의 변화가 발생하므로 정확한 추력을 발생시킬 수 없게 된다. 따라서 추력 분배 기법의 단순화를 위해서는 추력 발생에 의해 연소실 압력의 변화가 없어야 하며, 이는 추력 분배기법에 의해 발생하는 노즐 목 면적 변화의 합이 0이 되어야 함을 의미한다.

이를 식으로 표현하면 다음과 같다. 먼저 각 노즐에 요구되는 노즐 목 면적 명령, A_ti,cmd는 Eq. 15와 같이 연소실 압력 명령을 만족시키기 위한 A_ti,prs와 추력 명령을 만족 시키기 위한 ∆A_ti,thr의 합으로 표현할 수 있다.

위 식에서 ∆A_ti,thr는 Eq. 16과 같은 요구 조건을 만족시켜야 한다[7].

2.4 압력 제어

연소실 압력 제어기는 단순한 제어기를 설계하여 적용하였으며, 제어해야 하는 총 노즐 목 면적 명령은 Eq. 17과 같다.

이 때 e_prs는 연소실 압력의 제어 오차, A_t0는 초기 노즐 목 면적의 합을 의미하며, e_prs는 다음과 같이 정의된다.

압력 제어기에 의해서 결정된 총 노즐 목 면적 명령(A_{tot, prs})을 개별 노즐 목 면적 명령(A_ti,prs)으로 분배하기 위해서 Eq. 19와 같이 압력 가중벡터, W_p를 이용하여 계산하였다[7].

위 식에서 $$ W_p^{*}$$는 가중벡터 W_p의 의사 역행렬을 L¹ norm으로 정규화 한 값이다.

이 때 노즐이 총 10개 이므로 W_p는 W_p∈R^10×1을 만족하는 가중벡터이다. 또한 Eq. 19와 같이 압력 제어를 위한 노즐 목 면적을 분배할 때 이로 인한 추력 및 모멘트를 발생시키지 않아야 하므로, W_p의 가중치 중 DCS 및 ACS에 해당하는 가중치는 서로 동일한 값을 가져야 한다[7].

3.1 추력 분배기법

압력 제어기법에 의해서 압력이 일정한 수준으로 유지되고 있다면, Eq. 16과 같은 요구 조건을 만족시키는 ∆A_ti,thr 만큼 각 노즐에 변화를 주어, 압력을 일정하게 유지하면서 요구되는 추력 명령(T_br)을 만족시킬 수 있다. 이 때 위 압력 제어기법에 의해 결정된 DCS 및 ACS 노즐의 A_ti,prs값이 서로 같으므로 T_br은 Eq. 21과 같이 표현할 수 있다.

이 때 W_t는 W_t∈R^10×10을 만족하는 대각행렬이며, 추력 요구를 만족시키기 위해 각 노즐로 분배되는 노즐 목 면적에 변화를 주는 가중행렬이다.

따라서 Eq. 16과 Eq. 21을 만족하면서, 벡터 ∆A_ti,thr의 크기가 최소가 되도록 최적화 수식을 정리하면 Eq. 22와 같고, 그 해는 Eq. 23과 같다. 기존의 연구와는 달리 압력 제어를 위해 노즐 목 면적 분배 기법에 사용한 가중벡터 W_p와 같이, 추력 분배기법에도 가중행렬 W_t를 사용하여 사용자의 의도 및 시스템의 특성에 따라 노즐별 분배되는 목 면적을 변화시킬 수 있도록 하였다.

위 식에서 F_{br A}, T_n2bA는 각각 Eq. 16을 만족시키기 위해 증대된 벡터 및 행렬이며, 다음과 같이 정의할 수 있다.

3.2 능동적 가중행렬 변환

추력 요구를 만족시키기 위해 Eq. 23에 의해서 분배된 노즐 목 면적 ∆A_ti,thr는 가중행렬 W_t의 대각 변수들을 변화시킴으로써, 해당 변수와 대응되는 노즐에 분배되는 노즐 목 면적을 증가 또는 감소시킬 수 있다. 따라서 이를 이용하면, 실시간으로 노즐 목 면적의 응답을 알 수 있고, 이로 인하여 노즐 목 면적 제어의 오차가 계산된다면 이를 가중행렬에 적용하여 노즐 목 면적 오차가 증가할수록 분배되는 면적을 감소시킴으로써, 요구되는 추력 및 모멘트를 더욱 효율적으로 만족시킬 수 있을 것이다.

먼저 노즐 목 면적의 오차, e_nzl을 Eq. 26과 같이 정의하였다.

이러한 오차를 정규화하기 위하여 각 노즐의 오차와 노즐 목 면적 오차의 최대값의 비율(Ratio)로 구성된 벡터 e_nzlR을 Eq. 27과 같이 정의하였다.

이 때 e_d,max, e_a,max는 각각 DCS와 ACS 노즐 목 면적 오차의 최대값으로, 다음과 같이 각각 DCS 또는 ACS 노즐 목 면적의 최대값과 최소값의 차이로 정의할 수 있다.

Eq. 23을 살펴보면 ∆A_ti,thr를 계산하기 위한 가중행렬 W_t는 역행렬로 곱해져 있는 것을 알 수 있다. 즉 가중행렬을 구성하는 가중치의 값이 증가할수록, 해당 가중치에 대응되는 노즐에 분배되는 면적 ∆A_ti,thr은 반대로 감소하게 될 것이다. 이러한 특성을 이용하면 Eq. 27에 의해 계산된 오차 비율의 크기가 클수록 이에 대응되는 노즐의 가중치를 마찬가지로 증가시킴으로써, 오차가 크게 발생한 노즐에 분배되는 면적을 줄이는 개선된(Modified) 가중행렬 W_tM을 정의하여야 할 것이다. W_tM은 Eq. 30과 같이 정의하였다.

위 식에서 K_wt는 상수이며 가중행렬 변환 이득을 의미한다.

이를 이용하여 최종적으로 Eq. 31의 식을 이용하여 추력 및 모멘트 요구를 만족시키기 위한 노즐 목 면적 분배량을 계산할 수 있다.

이 때 $$ W_{tM}^{*}$$은 가중행렬 W_tM을 L² norm으로 정규화 한 값으로 Eq. 32와 같이 계산된다.

4.1 DCS 노즐 고장조건

개선된 가중행렬의 영향을 살펴보기 위하여 임의로 노즐이 고장난 비정상적인 상황을 모의하였다. 특정 노즐(DCS 2번)이 고장, 즉 노즐 목 면적 명령이 인가되어도 전혀 움직이지 않는 상황을 설정하고 시뮬레이션을 수행하였으며, 노즐 목 면적 오차는 계산할 수 있다고 가정하였다.

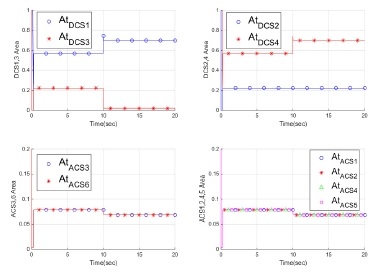
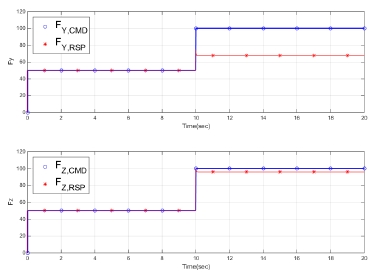
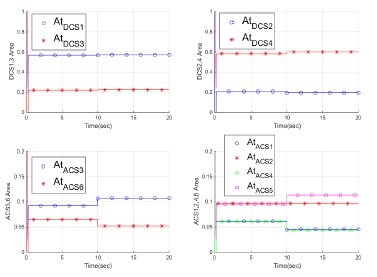
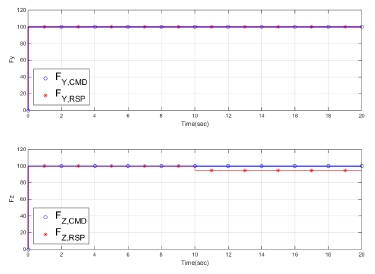
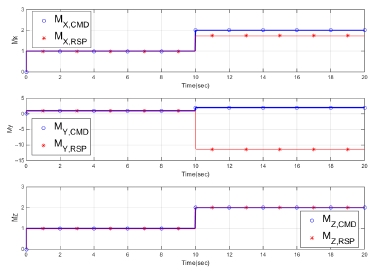
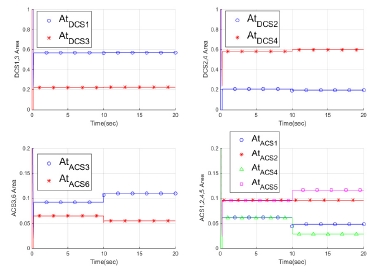
먼저 시뮬레이션 시간 5초에 DCS 2번 노즐에 고장이 발생하여 노즐이 움직이지 않고, 10초에 추력 명령이 변하였다고 모의하였다. 이 때 가중행렬 W_tM을 적용하지 않고 단위행렬을 적용하면, Fig. 2와 같이 고장으로 인하여 명령을 추종하지 못한 2번 노즐 목 면적(A_t,DCS2)은 정지해있게 된다. 이에 반하여 다른 노즐 목 면적은 변경된 추력 명령을 추종하기 위하여 고장이 발생하지 않았을 경우 계획된 명령 분배 위치로 이동하였다. 노즐 목 면적의 값은 특정 값으로 정규화하여 표기하였다. 이러한 노즐 고장으로 인한 추력 및 모멘트의 추종 결과는 Fig. 3, 4와 같다. 10초 이후에 변경된 추력 명령에 대하여 고장이 발생하지 않은 z축 방향의 추력(F_z)과 모멘트(M_z)는 명령을 추종하지만, y축 방향의 추력은 노즐 목 면적이 명령을 추종하지 못한 만큼 오차가 발생하게 된다. 추력 및 모멘트의 값 역시 특정 값으로 정규화하여 표기하였다.

Fig. 2.

Nozzle area for DCS2 failure (Wt=E).

Fig. 3.

Thrust for DCS2 failure (Wt=E).

Fig. 4.

Moment for DCS2 failure (Wt=E).

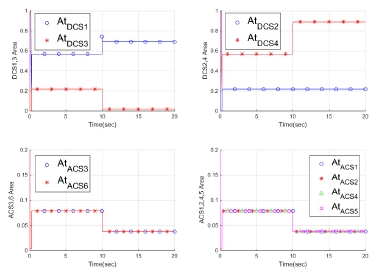
동일한 고장모의 조건에서 가중행렬 W_tM을 적용하면 다음과 같다. 먼저 Fig. 5의 노즐 목 면적을 살펴보면 고정된 DCS 2번 노즐에서 감소해야 할 추력을 보상하기 위하여 이와 대응되는 DCS 4번 노즐의 면적이 Fig. 2와 비교하여 상대적으로 크게 증가함을 알 수 있다.

또한 DCS 4번 노즐의 변화량이 증가하였으므로, 압력을 동일한 수준으로 유지하기 위하여 ACS 노즐의 변화 역시 큰 것을 확인할 수 있다.

Fig. 5.

Nozzle area for DCS2 failure (Wt=WtM).

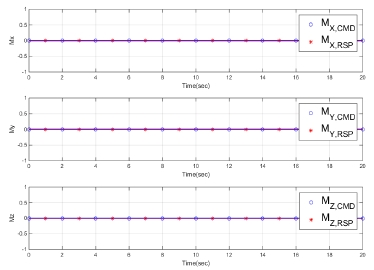
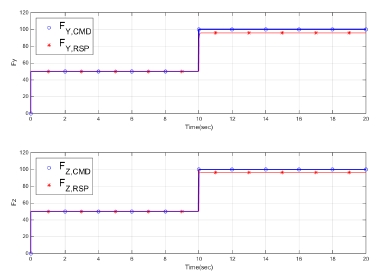
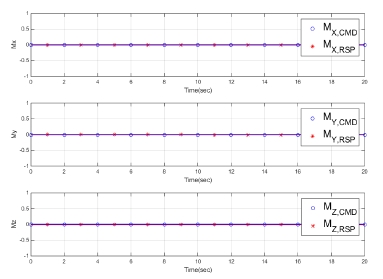
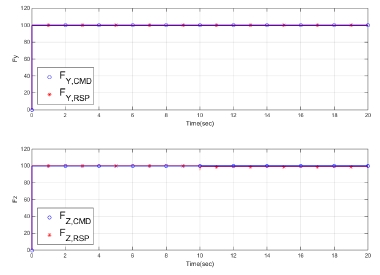
Fig. 6, 7과 같이 나타난 추력 및 모멘트 결과 역시 명령을 잘 추종함을 알 수 있다. 모멘트의 오차는 수치 계산으로 인한 결과이며, 특히 F_y의 경우 DCS 2번 노즐이 고정되면 개선된 가중행렬 W_tM을 사용하여 DCS 2번 노즐에 분배된 면적을 최소화하고, 그 결과 오차가 상당히 줄어든 것을 확인할 수 있다. 이에 대한 정량적인 비교는 Table 1에서 확인할 수 있으며, 오차가 급격하게 감소하였음을 알 수 있다.

Fig. 6.

Thrust for DCS2 failure (Wt=WtM).

Fig. 7.

Moment for DCS2 failure (Wt=WtM).

Table 1.

Y-axis Thrust Error Comparison.

4.2 ACS 노즐 고장조건

ACS 고장모의는 DCS와 유사하게 시뮬레이션 시간 5초에 ACS 2번 노즐이 고장으로 인하여 정지되었고, 10초에 모멘트 명령이 변화되었다고 모의하였다. 먼저 가중행렬을 W_tM이 아닌 단위행렬로 정의하면 그 결과는 Fig. 8~10과 같다. 4.1의 시뮬레이션 결과와 유사하게 10초를 기점으로 ACS 2번 노즐 목 면적(A_t,ACS2)을 제외한 나머지 노즐의 목 면적이 증가 또는 감소하는 것을 확인할 수 있다.

Fig. 8.

Nozzle area for ACS2 failure (Wt=E).

Fig. 9.

Thrust for ACS2 failure (Wt=E).

Fig. 10.

Moment for ACS2 failure (Wt=E).

또한 고장 발생 시점(5초)에서는 추력 및 모멘트 요구 변화가 없으므로 고장 발생 여부와 관계없이 목표 추력 및 모멘트를 만족시키며, 10초에 모멘트 명령이 증가하면 고장의 영향을 받지 않는 M_z는 응답이 명령을 정확하게 추종하지만, M_x 및 M_y는 명령 대비 오차가 발생하였다. 아울러 ACS 2번 노즐의 영향을 받는 Z축 방향 추력(F_z)에도 오차가 발생하였다.

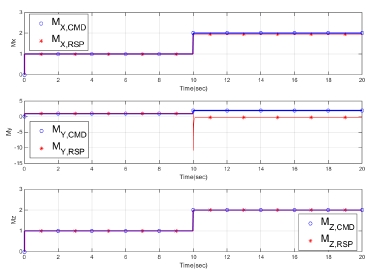
다음으로 능동 가중행렬(W_tM)을 적용한 시뮬레이션 결과는 Fig. 11~13과 같다. 먼저 Fig. 11의 노즐 목 면적을 살펴보면 고정된 ACS 2번 노즐에서 증가해야 할 추력이 보상되어야 한다. 이를 위해서 이에 대응되는 ACS 4번 노즐의 면적이 Fig. 8과 비교하여 상대적으로 크게 감소함을 알 수 있다.

Fig. 11.

Nozzle area for ACS2 failure (Wt=WtM).

Fig. 12.

Thrust for ACS2 failure (Wt=WtM).

Fig. 13.

Moment for DCS2 failure (Wt=WtM).

Fig. 12, 13을 살펴보면 오차가 발생한 방향의 추력 및 모멘트의 오차가 감소하였음을 확인할 수 있다.

다만 M_x와 비교하여 M_y의 경우 동일 노즐 목 면적 오차에 대하여 모멘트 오차가 상대적으로 큰 것을 확인할 수 있는데, 이는 ACS 노즐이 가지는 x 축에 대한 모멘트 암의 길이(l_mxa)가 y 축에 대한 모멘트 암의 길이(l_mya)보다 짧으므로 노즐에서 발생하는 추력 변화에 대한 모멘트의 변화량이 상대적으로 작기 때문이다. 추력 및 모멘트에 대한 명령 추종특성의 정량적 개선 효과는 Table 2, 3에서 확인할 수 있다.

Table 2.

Z-axis Thrust Error Comparison.

Table 3.

X, Y-axis Moment Error Comparison.