예혼합실을 갖는 연소-노즐 시스템의 음향장 해석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문은 “예혼합실+노즐+연소실”의 3단으로 구성된 예혼합 가스터빈 연소기의 열음향모델을 제시한다. 음향장의 동적특성은 화염섭동을 입력으로 화염면에서의 속도를 출력으로 하는 음향전달함수로 표현되었다. 음향전달함수의 극점들을 분석함으로서 음향장의 공진주파수는 각 단 사이의 면적비, 그리고 음향파가 각 단을 왕복 운동하는 3개 주파수들의 조합으로 주어짐을 보였다. 극점을 나타내는 함수의 형태를 분석하여 3단 연소기의 여러 파라미터가 변함에 따라서 공진주파수가 어떻게 변하는가에 대하여 해석적으로 분석하였고 문헌의 실험결과와 일치함을 확인하였다.
Abstract
This paper deals with an acoustic model for a lean premixed gas turbine combustor composed of three stages: premixing chamber, nozzle and flame tube. Our model is given as an acoustic transfer function whose input is a heat release rate perturbation and output is a velocity perturbation at a flame location. We have shown that the resonance frequencies are functions of three round-trip frequencies of acoustic wave in each stage, and area ratios between stages. By analyzing poles of the acoustic transfer function, we could characterize resonant frequencies and their dependency on various system parameters of a combustor. It was found that our analytic findings match with existing numerical and experimental results in literature.
Keywords:
Lean Premixed Combustion, Combustion Instability, Acoustic Transfer Function, Linear Thermoacoustic Model키워드:
희박 예혼합 연소, 연소불안정, 음향전달함수, 선형 열음향모델1. 서 론
현재 많은 연소 시스템에서는 시스템의 열효율 저하를 최소화하면서 연소온도를 낮추어 질소산화물의 배출량을 감소시키기 위하여 희박 예혼합 연소를 채택하고 있다. 희박 예혼합 연소 시스템은 공기와 연료를 연소실 이전 공간에서 완전히 혼합하여 얻은 균일한 혼합기를 연소실에 공급한다. 이때 당량비(equivalence ratio)를 희박 가연 한계(lean blow out)로 유지하기 위해 연소에 사용되는 연료의 양이 감소하므로 연소 온도가 낮아져 질소산화물의 배출양이 감소하는 효과를 얻게 된다.
하지만 희박 예혼합 가스터빈 연소기에서는 연소불안정(combustion instability)의 발생 가능성이 있다. 희박 예혼합 연소에서는 당량비(equivalence ratio)가 희박 가연 한계의 운전조건에서 이루어지기 때문에 화염은 미세한 음향장의 압력/속도 섭동에도 쉽게 반응하여 열발생율의 섭동을 야기한다. 열발생율의 섭동은 반대로 연소기 내부 음향장의 압력/속도 교란을 만들어 낸다. 이러한 두 가지 메커니즘이 서로 상승효과를 일으키는 경우에 연소실 내부의 압력진동의 크기가 점차 커지게 된다[1-5]. 이러한 압력 진동이 시스템의 내성 한계점 이상에 도달하면 연소기 부품을 손상시킬 수 있고 최악의 경우 압축기 및 터빈을 포함한 전체 시스템의 변형 또는 파괴로 이어질 수 있다.
연소불안정성 현상은 연소기 음향장의 동적인 특성과 연소기의 열발생 특성의 상호 결합으로 발생하기 때문에 연소기의 음향 특성에 대한 완전한 이해는 연소불안정 현상을 예측함에 있어서 필수적이다.
저자들의 이전 연구[2-4]에서는 선형 열음향 해석 모델을 개발하고 검증하기 위하여 연소 시스템을 “노즐 + 연소실”과 같이 가장 단순한 2단 덕트 형상으로 가정하고, 연소불안정 현상을 예측하는 방법을 제안하였다. 그러나 실제 많은 희박 예혼합 시스템 연구[6-8]에서는 노즐의 상류에 예혼합실을 두어 “예혼합실 + 노즐 + 연소실”의 3단 구조를 구성하고, 예혼합실에서의 유동, 연료-공기 혼합 및 열음향 특성이 전체 시스템의 안정성에 미치는 영향을 보고하였다. 특히, Schuller 등[7]의 연구에서는 이러한 예혼합실에서의 음향 경계 조건이 실제 시스템 전체의 열음향 문제에 큰 영향을 미치는 것으로 나타났다.
본 연구에서는 이전 연구(“노즐+연소기”의 2단 구조)에서 개발된 연소기의 음향 모델을 보다 복잡한 형태의 3단 덕트 연소기에 적용하기 위하여 확장하였다. 또한 연소기의 음향 모델을 나타내는 음향전달함수(Acoustic Transfer Function, ATF)의 분석으로부터 음향장의 공진주파수(resonance frequency)를 구하고, 이를 실험 결과와 비교 및 분석한다.
2. 열음향 모델
음향장의 동적 특성은 열발생 섭동에 의하여 발생하는 시스템의 유동 속도/압력 섭동의 관계로서 파악할 수 있으며 이를 기존의 연구[4]에서는 음향전달함수로 표현하였다.
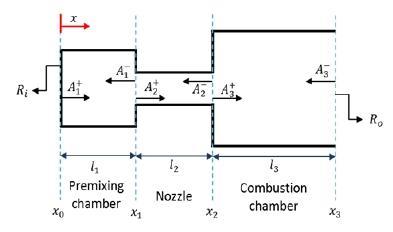
Fig. 1은 본 연구에서 해석 대상으로 선정한 “예혼합실+노즐+연소실”의 3단 구조 시스템의 대략적인 구성을 나타낸다. Fig. 1에서 면적 변화가 있는 두 지점 x = xi (i = 1,2)에서 질량은 보존되지만 운동량(momentum)은 감소 혹은 증가한다. 또한 x = x2 의 전후에서는 연소에너지만큼 에너지가 증가한다[4-5]. 이러한 관계로부터 면적변화가 있는 두 지점 x = xi (i = 1,2)에서 아래의 지배방정식들을 얻는다.
| (1) |
| (2) |
| (3) |
여기서 ρ, u, S, p는 차례대로 밀도, 속도, 면적, 압력을 나타내며 상하첨자 i, i + 1는 x = xi 지점 의 직전/직후를 의미한다.
또한 평균속도를 무시하고 음향장을 1차원으로 모델링하면 압력과 속도 섭동은 다음과 같이 표현할 수 있다 (i = 1,2,3)
| (4) |
| (5) |
| (6) |
여기서 Ai+(x, t), Ai-(x, t) (i = 1,2,3)는 음향장의 파동함수이며 (상첨자 ±는 각각 상류방향, 하류방향) , ci는 평균 밀도와 음속을 나타낸다.
Eqs. 4-6에서 공간좌표 값을 x ∈ {x1, x2}로 선택하고 시간좌표에 라플라스변환을 적용한 후에 Eqs. 1-3의 섭동형에 대입하면 6개의 (라플라스 변환된) 미지함수 에 관한 4개의 조건식을 얻는다. 여기에 입출구 x ∈ {x0, x3}에서의 2개 경계조건을 결합하면 6개의 등식을 얻는다. 이로부터 열섭동 을 입력으로 화염면에서의 속도 섭동 을 출력으로 하는 아래의 음향전달함수를 얻을 수 있다.
| (7) |
여기서
| (8) |
| (9) |
| (10) |
이며, α ≡ S2/S1, β ≡ S3/S2, 반사계수(reflection coefficient)는 아래와 같이 정의되었다.
| (11) |
또한 Eqs. 8-10에 등장하는 상수 δi (i = 1,2,3)는 아래 Eq. 12와 같이 정의되고, 이는 음향파가 각 단의 입구와 출구 사이에서 왕복을 하는데 필요한 소요시간을 의미한다.
| (12) |
본 논문에서는 δi와 1/δi을 각각 각 단에서의 “왕복운동주기(turn around period)”와 “왕복운동주파수(turn around frequency)”로 정의하였다.
또한, 개발된 모델의 검증을 위하여 Schuller[7] 및 Silva[8] 등의 실험 결과와 동일한 입출구 음향 조건을 적용하여, 예혼합실의 입구(x0)는 음향학적으로 닫힌 조건(rigid wall), 연소실의 출구(x3)는 열린 조건(open)으로 구성하였다.
3. 음향 특성 분석
연소기의 공진주파수는 Eq. 7에 주어진 음향 전달함수의 극점(pole)으로부터 얻을 수 있다. 여기서 극점이란 전달함수의 분모 부분이 영이 되는 복소수 들의 집합
| (13) |
을 의미한다. 하지만 Eq. 13의 방정식을 해석적으로 풀기에는 너무 복잡하므로 아래 조건
| (14) |
이 성립한다고 가정하고 ∆ 대신에 아래와 같은 근사적인 극점들의 집합을 구한다.
| (15) |
대부분의 연소기의 경우, 노즐과 연소실의 면적비가 β≫1이고 c3 ≥ c2이므로 위의 조건 (Eq. 14)을 대략적으로 만족한다. 특히 연소장의 경우에 c3 > c2이므로 비연소장(c3 = c2)에 비하여 위의 가정은 더 잘 만족하게 된다. Eq. 10에 의하여 모든 극점 s∈∆app은 아래의 두 가지 등식
| (16) |
| (17) |
중에서 하나를 만족함을 알 수 있다.
Fig. 1에서 소개하였듯이, 예혼합실 입구를 음향학적으로 닫힌 조건(rigid wall), 반대로 연소실 출구에서의 경계 조건을 열린(open) 경계면으로 가정하였기 때문에 해석 대상의 입출구 반사계수는 다음과 같다.
| (18) |
반사계수가 Ro = -1이면 Eq. 16을 만족하는 극점은 δ3s = π(1+2k) j, j2 := -1 (k = 0,1,2,⋯)을 만족한다. 따라서 s = jw = j2πf로부터 공진주파수는
| (19) |
로 주어진다. 이 공진 주파수는 연소기의 왕복운동주기 δ3(즉, 연소기의 길이와 음속)에만 의존할 뿐 예혼합실과 노즐의 왕복운동주기 δ1, δ2나 면적비 α, β에는 의존하지 않는 점은 주목할 만하다.
두 번째 조건(Eq. 17)을 만족하는 극점은 Ri = 1인 경우이므로 아래 식
| (20) |
을 만족한다. Eq. 20의 엄밀해(exact solution)는 구하기 어렵지만 테일러급수(Taylor series)를 적용하여 아래의 근사해
| (21) |
를 구할 수 있다(부록참조).
Eq. 21에 주어진 (근사적인) 공진주파수는 예혼합실과 노즐의 왕복운동주기 δ1, δ2 와 두단 사이의 면적비 α의 함수로 주어지며 노즐/연소실 사이의 면적비 β, 그리고 연소실의 왕복운동주기 δ2와는 무관하다.
Eq. 21의 물리적인 타당성을 확인하기 위해 면적비가 α = 1이라고 (즉, 예혼합실과 노즐이 분리되지 않고 하나의 단으로 합쳐져 있다고) 가정해 보자. 이 경우 주파수는
| (22) |
가 되어 예혼합실과 노즐을 병합한 전체 길이에 대응하는 새로운 왕복운동주파수가 되므로 이는 물리적인 직관에 부합한다.
δ1, δ2가 고정되어 있을 때 (1+α) / α는 구간 α∈ [0,1]에서 단조 감소하는 함수이므로 Eq. 21의 공진주파수는 의 비율로 단조 증가하는 함수이다. 다시 말해서 예혼합실과 노즐 사이의 면적비가 감소할수록 (노즐의 단면적이 예혼합실의 단면적에 비하여 상대적으로 작아질수록) 공진주파수는 계속 감소하여 α = 0 일 때 f = 0이 되고, 반대로 면적비가 증가하면 공진주파수도 함께 증가하여 α = 1 일 때 Eq. 22에 주어진 주파수에 도달한다.
이번에는 α와 δ2가 고정되어 있다고 가정하고 δ1 ≥ 0을 변수로 생각하자. 이 경우 Eq. 21의 제곱근 내부의 항은 δ1 ≥ 0의 이차함수이므로 공진주파수는 δ1 ≥ 0 일 때 최대크기 f = 1/ (πδ2)를 갖고 δ1 > 0이 증가할 때 1/δ1의 비율로 (즉 1/l1의 비율로) 단조 감소한다. 바꾸어 말하면 면적비 α∈ [0,1]와 노즐의 길이가 일정한 상황에서 예혼합실이 없을 때 (l1 = 0) 최대 크기의 공진주파수를 가지며 예혼합실의 길이가 길어질수록 공진주파수는 계속해서 작아짐을 알 수 있다. 이 사실은 예혼합실과 노즐을 서로 바꾸어도 그대로 성립하는데 이는 Eq. 21의 분모에서 δ1, δ2가 상호 대칭적이기 때문이다.
Eq. 21에 주어진 주파수는 예혼합실과 노즐의 왕복운동주파수에 비하여 상당히 낮은 주파수라는 점은 매우 흥미로운 사실이다. 일례로 1/δ1 = 1/δ2 = 2000 Hz, α = 0.1의 경우에 Eq. 21의 주파수는 f ≈ 177 Hz로서 왕복 운동주파수 2000 Hz의 약 8.9%에 불과하다. 사실 3단 연소기에서 왕복운동 주파수들보다 매우 낮은 저주파 공진점이 있다는 것은 여러 문헌에서 수치해석이나 실험으로 알려져 왔다[7]. 본 논문에서는 그 공진주파수에 대한 이론적인 분석과 간단한 계산 공식(Eq. 21)을 제시하였다.
4. 결과 및 고찰
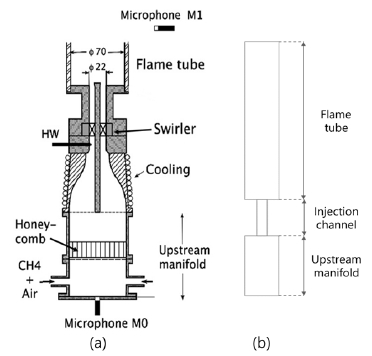
본 장에서는 앞에서 분석한 공진주파수의 특성을 실험결과와 비교하였다. Fig. 2에 보인 연소기는 예혼합실(upstream manifold), 노즐(유동 유입구, injection channel) 그리고 연소실(combustion chamber)로 구성되고, 참고문헌 [7,8]의 연구에서 소개되었다.
참고문헌[7]에서 실험에 사용된 연소기의 예혼합실의 길이는 0.100, 0.164, 0.228 m의 3가지로, 연소실의 길이는 0.100, 0.200, 0.400 m의 3 단계로 변경할 수 있다. 하지만 실제 예혼합실과 노즐의 단면적은 Fig. 2(a)와 같이 완만하게 변하여 앞의 Fig. 1에서 3단으로 모델링한 것과 차이가 있다. 이러한 차이점을 보정하기 위하여 문헌[8]에서는 예혼합실의 길이를 0.125, 0.189, 0.253 m로 수정하는 것을 제안하였고 이를 본 연구에서는 채택하였다. 그리고 Eq. 18의 경계 조건을 선택하였고 냉간 조건(cold condition)하에서 해석하였다(). 이 경우 Eq. 7에서 정의된 음향전달함수의 극점은 전달함수에 대응하는 제차미분방정식(homogeneous differential equation)의 특성방정식(characteristic equation)의 근이다. 다른 해석 조건은 Table 1에 요약되었다.
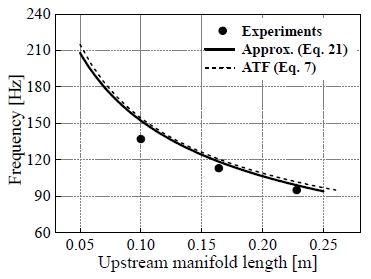
Fig. 3은 연소실 길이가 0.1 m일 때 예혼합실의 길이 변화에 따른 첫 번째 공진주파수를 나타내고 있다. 그래프에서 원형 도형은 실험값, 실선은 Eq. 21의 근사적인 계산식, 점선은 음향전달함수 (Eq. 7)의 극점을 수치적으로 계산한 값이다. 근사해와 전달함수로부터 얻은 해석결과는 매우 유사하지만 실험값과는 다소 차이가 있다. 근사식의 결과가 수치해석의 경우보다 실험값에 더 근접하지만 이는 단순히 근사식이 더 작은 공진주파수를 주었기 때문이다. 실험결과와의 차이는 연소기의 형상을 모델링 할 때 있어서 노즐입구의 면적 변화 형상을 적절하게 고려하지 못했기 때문으로 사료된다.
또한 앞장에서 근사식 Eq. 21로부터 예혼합실의 길이가 증가할 때 공진주파수는 1/l1의 비율로 감소할 것을 예측하였는데 Fig. 3은 이를 잘 반영하고 있다.
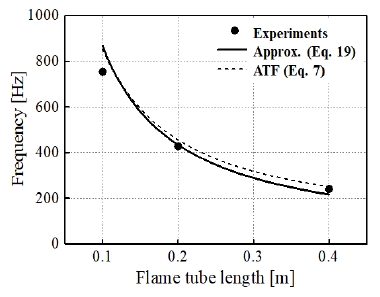
Fig. 4의 결과는 예혼합실의 길이가 0.125 m이고 노즐 길이가 0.117 m일 때 (δ1, δ2 가 일정할 때) 연소실의 길이에 대한 공진주파수 변화를 보여준다. 원형 도형은 실험값, 실선은 Eq. 19의 근사해, 점선은 음향전달함수(Eq. 7)로부터 얻은 결과인데 이들 3개 값들이 유사함을 알 수 있다. 공진주파수는 1/l3의 비율로 감소하고 있는데 이는 앞장에서 Eq. 19로부터 예측한 바와 일치한다.
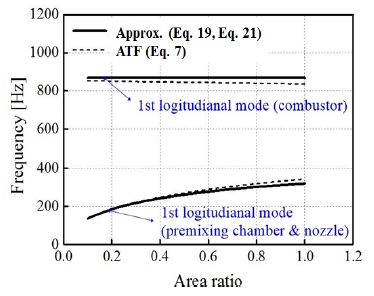
Fig. 5는 예혼합실/노즐/연소실의 길이가 주어졌을 때 (즉, δ1, δ2, δ3 가 일정할 때) 예혼합실과 노즐 사이의 면적비 α에 따른 첫 번째와 두 번째 공진 주파수의 변화를 나타낸다. 실선은 Eq. 19와 Eq. 21의 근사해에서 주어진 값이며 점선은 음향전달함수(Eq. 7)로부터 얻은 결과이다. 두 값은 전체적으로 유사하지만 일부 오차가 있는데 이 오차는 전술한대로 연소가 진행되는 경우에는 더 작을 것으로 기대할 수 있다.
또한 앞 장에서 면적비가 증가하면 첫 번째 공진주파수는 의 비율로 단조 증가하지만 두 번째 공진주파수는 면적비와 무관하게 일정한 것을 예측하였는데 Fig. 5의 곡선들은 이 경향을 보여주고 있다.
5. 결 론
본 연구에서는 “예혼합실+노즐+연소실”의 3단으로 구성되는 연소기의 열음향 모델을 개발하고 음향장의 특성을 분석하였다. 음향장의 동적 특성을 음향전달함수로 표현하였고 전달함수의 극점을 해석적으로 구하여 연소기 파라미터의 변화에 따르는 공진주파수의 특성을 분석하였다. 첫 번째 공진주파수의 경우 예혼합실과 노즐의 길이와 두 요소 사이의 면적비가 주된 결정인자이며, 두 번째 공진주파수는 연소실의 길이에 주로 의존하는 것으로 나타났다. 또한 시스템 파라미터로부터 첫 번째 공진주파수를 구하는 간단한 계산식을 제시하였다. 이론적인 결과를 문헌에 있는 실험결과와 비교한 결과 우리의 접근 방법으로 연소기 음향특성을 잘 예측할 수 있는 것으로 확인되었다. 추후 화염전달함수와 결합하여 3단 연소기 시스템의 연소불안정 문제에 대한 분석을 진행할 계획이다.
Nomenclature
| A : | Complex amplitude of pressure |
| c : | Speed of sound |
| l : | Length |
| M : | Mach number |
| p : | Pressure |
| q : | Heat release |
| R : | Reflection coefficient |
| S : | Area |
| s : | Laplace variable |
| u : | Velocity |
| α, β : | Area ratio |
| γ : | Specific heat ratio |
| δ : | Turn around period |
| ρ : | Density |
| ω : | Angular frequency |
| ' : | Perturbation |
| ㅡ : | Mean value |
| + : | Upstream direction |
| - : | Downstream direction |
Acknowledgments
이 논문은 산업통상자원부 항공우주부품기술개발사업(과제번호 : 10067074) 및 2015년도 정부(교육부)의 재원으로 한국연구재단의 기초연구 사업(NRF-2015R1D1A1A01058410)의 지원을 받아 수행된 연구 결과임.
References
-
Kim, K.T., and Santavicca, D., “Linear Stability Analysis of Acoustically Driven Pressure Oscillations in a Lean Premixed Gas Turbine Combustor“, Journal of Mechanical Science and Technology, 23(12), p3436-3447, (2009).
[https://doi.org/10.1007/s12206-009-0924-0]

-
Kim, D.S., and Kim, K.T., “Thermoacoustic Analysis Model for Combustion Instability Prediction – Part 1 : Linear Instability Analysis”, Journal of the Korean Society of Propulsion Engineers, 16(6), p32-40, (2012).
[https://doi.org/10.6108/kspe.2012.16.6.032]

-
Kim, J.A., and Kim, D.S., “Combustion Instability Prediction Using 1D Thermoacoustic Model in a Gas Turbine Combustor”, Journal of ILASS-Korea, 20(4), p241-246, (2015).
[https://doi.org/10.15435/jilasskr.2015.20.4.241]

-
Kim, J.A., Yoon, M.G., and Kim, D.S., “Combustion Stability Analysis Using Feedback Transfer Function”, Journal of the Korean Society of Combustion, 21(3), p24-31, (2016).
[https://doi.org/10.15231/jksc.2016.21.3.024]

-
Lieuwen, T.C., and Yang, V., Combustion Instabilities in Gas Turbine Engines, AIAA, Reston, V.A., U.S.A., (2005).
[https://doi.org/10.2514/4.866807]

-
Palies, P., Durox, D., Schuller, T., and Candel, S., “Nonlinear Combustion Instability Analysis Based on the Flame Describing Function Applied to Turbulent Premixed Swirling Flames“, Combustion and Flame, 158(10), p1980-1991, (2011).
[https://doi.org/10.1016/j.combustflame.2011.02.012]

-
Schuller, T., Durox, D., Palies, P., and Candel, S., “Acoustic Decoupling of Longitudinal Modes in Generic Combustion Systems“, Combustion and Flame, 159(5), p1921-1931, (2012).
[https://doi.org/10.1016/j.combustflame.2012.01.010]

-
Silva, C.F., Nicoud, F., Schuller, T., Durox, D., and Candel, S., “Combining a Helmholtz Solver with the Flame Describing Function to Assess Combustion Instability in a Premixed Swirled Combustor“, Combustion and Flame, 160(9), p1743-1754, (2013).
[https://doi.org/10.1016/j.combustflame.2013.03.020]