오리피스 형상에 따른 단공노즐 액체제트의 유동특성
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 원형 노즐과 타원형 노즐을 이용하여 공동현상과 수력튀김 현상이 유동특성에 어떠한 영향을 미치는지 파악하고자 하였다. 이를 위해 오리피스 길이 대 직경비(L/d)와 타원형 노즐의 종횡비(a/b)가 서로 다른 분사기들을 제작하여 분무실험을 수행하였다. 분사압력 증가에 따라 공동현상이 발생할 경우 유량계수가 서서히 감소하였으나 수력튀김 영역에서는 유량계수가 급격히 떨어진 후 일정한 값을 유지함을 확인하였다. 하지만 타원형 노즐에서 장축지름(a)과 단축지름(b) 대비 오리피스 길이의 비인 L/b가 8 이상, L/a가 8 이하인 경우, 유량계수 및 액체제트 형상은 기존의 원형 노즐과는 상당히 다른 결과를 나타내었다. 정상유동 상태인 경우 타원형 노즐에서 분사된 액주는 원형 노즐과는 달리 하류로 가면서 장축에서는 분무각이 감소하였으며 단축에서는 분무각이 커지는 모습을 보였다.
Abstract
Effects of cavitation and hydraulic flip in circular and elliptical nozzles on the flow characteristics have been studied. Spray tests were conducted using injectors with different ratios of an orifice length(L) to a diameter(d) and of a major axis diameter(a) to a minor axis diameter(b). With the increment of an injection pressure drop, discharge coefficients slightly decreased in cavitation flows, and those suddenly dropped and were almost constant in hydraulic flip flows. For elliptical nozzles with L/b > 8 and L/a < 8, discharge coefficients and flow patterns showed different results from those in previous circular nozzles. When a flow in the elliptical nozzle was under steady condition, as the liquid column went downstream from the nozzle, its spray angle a little decreased in the plane of a major axis and increased in the plane of a minor axis.
Keywords:
Circular Nozzle, Elliptical Nozzle, Cavitation, Hydraulic Flip, Discharge Coefficient키워드:
원형노즐, 타원형 노즐, 공동현상, 수력튀김, 유량계수1. 서 론
노즐 내부에서 발생하는 공동현상은 미립화 특성에 중요한 영향을 미치는 것으로 알려져 있다. 공동현상은 유동이 각진 모서리의 구조를 갖는 오리피스로 유입되면서 생성된다. 오리피스 입구에서는 유량에 영향을 미치지 않는 재순환 영역이 존재하게 되므로, 이로 인해 오리피스 면적보다 더 좁은 유효 면적에서 유동이 흐르게 되어 유체의 속도가 증가하게 된다. 유속이 증가하면 유체의 정압은 낮아지고, 이때 유체의 정압이 포화 수증기압 이하까지 떨어지면 기포가 성장하게 된다[1].
공동현상이 발생하면 오리피스 출구에서 액체제트는 불안정한 모습을 보이며, 하류로 갈수록 미립화가 진행되어 원래 형태의 모양이 부서지게 된다. 분사압력이 증가할수록 이러한 경향은 두드러지지만, 수력튀김이 발생하게 되면 이와는 다른 현상이 나타난다. 수력튀김의 경우 분사압력이 증가하면서 공동현상 기포가 오리피스 출구까지 발달하게 되는데, 이로 인해 오리피스 내부 및 외부와의 압력 균형이 깨지게 된다. 이 때문에 외부 기체가 오리피스 내부로 유입되면서 내부 유동과 오리피스 벽면이 분리되는 수력튀김 현상이 나타나게 된다[2,3].
최근에는 단공노즐의 미립화 특성을 향상시키기 위해 오리피스 형상을 기존의 원형이 아닌 삼각형이나 타원형 등으로 제작하여 연구되고 있다. Yunyi 등[4]은 타원형 노즐을 이용하여 연료 미립화에 관한 연구를 수행하여, 타원의 단축에서 분무각의 형태가 커지는 모습과는 반대로 장축에서는 분무각이 감소하는 축교차 현상을 발견하였다. Kasyap 등[5]은 타원형 노즐 출구로부터 액체제트의 프로파일과 분열길이의 변화를 관찰하였다. 타원형 노즐의 축교차 현상은 오리피스의 종횡비와 액체의 점성에 의해 많은 영향을 받으며, 액체제트 분열을 촉진시키는 것을 발견하였다. Hong 등[6,7]과 Ku 등[8]은 원형 노즐과 타원형 노즐의 내/외부 유동에 대해 실험과 해석프로그램을 이용하여 연구하였다. 타원형 노즐의 경우 동일 분사 조건에 있어 더 작은 액적이 형성되며, 분사된 연료와 주위공기와의 혼합효과가 향상된다는 결과를 발표하였다.
액체제트가 횡방향 공기 유동에 수직으로 분사될 때 1차 분열의 주원인이 내부 유동에 의한 오리피스에서의 교란이며, 분사기 오리피스 입구에서 일어나는 공동현상이 빠른 미립화 진행의 주된 요소라는 사실이 알려져 있다[9,10]. 또한 공동현상은 분무 특성뿐 아니라 유량계수에도 영향을 미친다고 보고되었다[11]. 이러한 이유에서 아음속 기체에 수직 분사되는 액체제트의 노즐 내부에서 발생되는 유동 현상에 관한 연구가 활발히 수행되었다. Ahn 등[12]과 Song 등[13]은 공동현상과 수력튀김 현상이 액주 분열과정에 어떠한 영향을 미치는지 관찰하고, 각 현상들에 대하여 유효지름, 유효속도 등의 개념을 제안하였다. 또한 PLLIF 기법을 이용하여 액적 영역의 분무구조에 있어 공동현상과 수력튀김 현상이 어떠한 영향을 주는지 연구하였다.
이전의 선행연구 결과들[14,15]을 종합해보면 원형 노즐에서의 횡방향 수직분사 연구들은 활발히 수행되었으나, 아직까지 타원형 노즐에서의 액체 미립화 연구들은 부족한 상황이다. 따라서 타원형 노즐에서의 오리피스 형상 및 내부 유동특성에 따른 횡방향 수직분사 실험들이 진행되고 있으며[16], 본 논문은 이를 위한 선행연구 결과로써 대기조건으로 분사되는 액체제트의 오리피스 형상, 노즐 길이, 분사압력에 따른 유동특성에 대하여 살펴보았다.
2. 실험방법
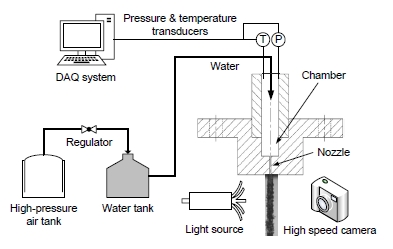
Fig. 1은 유량계수 측정 및 유동 가시화를 위한 실험장치를 나타낸다. 고압 압축기로 압축된 공기와 레귤레이터를 이용하여 물을 일정 압력으로 분사기에 공급하였다. 실험 시 분사기 챔버 내 물의 압력과 온도 측정을 위해 압력센서와 K-type 열전대를 사용하였다. 측정된 데이터는 100 Hz의 샘플링 속도로 NI-cDAQ를 이용하여 저장하였다. 유량계수 측정실험은 각 조건 당 60초씩 수행되었으며, 2회 반복하였다. 실험 시 분사기로 공급된 유량조건 중 일부분이 보유한 터빈 유량계들의 측정범위를 벗어나, 60초 동안 직접 물을 받아 전자저울(정밀도 2 g)로 측정하여 유량을 계산하였다. 유동 가시화를 위해 2개의 광원장치(Polarion, PS-X1)와 고속카메라(Vision Research, Phantom v9.1)를 이용하여, 분사기 출구로부터 분무되는 액체제트의 이미지를 촬영하였다. 분사기 오리피스의 직경이 작기 때문에 이미지 확대를 위해 매크로 렌즈를 사용하였다. 순간의 이미지를 촬영하기 위해 노출시간은 카메라의 설정 최소값인 2 ㎲로 하였으며, 각 분사압력 조건마다 1,000 fps로 40장의 이미지를 기록하였다.
실험에 사용한 분사기의 오리피스 형상 및 대표적인 사진을 Fig. 2에 나타내었다. 원으로 표시된 부분을 보면 왼쪽은 원형 노즐을, 오른쪽은 타원형 노즐을 갖고 있음을 알 수 있다. 분사기는 원형 노즐을 갖는 2개와 타원형 노즐을 갖는 6개가 제작되었으며, 오리피스 입구는 곡률 없이 각지게 설계되었다. 오리피스는 슈퍼드릴 천공 후 와이어 방전가공을 통해 그 단면 형상을 가공하였다.
각 분사기의 오리피스 형상, 크기, 길이를 Table 1에 정리하였다. 분사기 모델에서 “C”, “E”는 각각 원형 오리피스, 타원형 오리피스를 나타내며, 그 다음 숫자는 오리피스 단면의 종횡비(a/b)를, 마지막 숫자는 오리피스 길이 대 오리피스 지름(타원일 경우 단축지름) 비(L/d 혹은 L/b)를 의미한다. 기존의 결과들[17]에 의하면, 각진 모서리를 갖는 오리피스에서 L/d > 8에서는 공동현상이, L/d ≤ 8에서는 수력튀김이 현상이 나타난다고 알려져 있다. 본 연구에서는 원형 노즐의 경우 L/d가 5, 10을 갖도록 설계하였으며, 타원형 노즐의 경우 단축기준으로 L/b가 5, 10, 장축기준으로 L/a가 10을 갖도록 설계하였다. 유량계수 측정 및 유동 가시화는 분사압력을 1 bar에서 10 bar까지 1 bar씩 증가시키며 측정하였고, 실험은 각 조건에서 2회씩 반복 수행되었다.
3. 결과 및 고찰
3.1 액체제트의 유량계수 특성
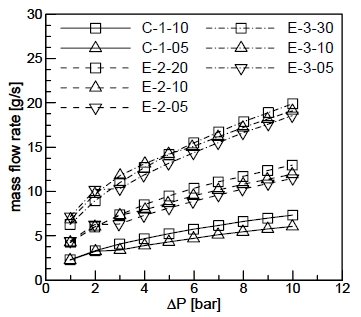
분사압력에 따른 질량유량 결과를 Fig. 3에 도시하였다. 오리피스의 형상이나 길이에 상관없이 압력이 증가함에 따라 질량유량은 전반적으로 증가하였으나, 동일 오리피스 형상에서 오리피스 길이가 가장 작은 분사기들의 경우 압력이 2 bar에서 3 bar로 높아질 때는 유량이 정체되는 현상이 나타났다. 또한 동일 오리피스 형상, 동일 압력 조건에서 압력이 대략 5 bar 이상으로 커지게 되면 오리피스의 길이가 클수록 질량유량도 커지는 결과를 갖게 되었다.
분사기의 압력차-유량 측정 결과를 분석하기 위해 Eq. 1과 같은 식을 사용하여 유량계수 값을 구하고, 결과들을 Fig. 4에 오리피스의 종횡비별로 나타내었다.
| (1) |
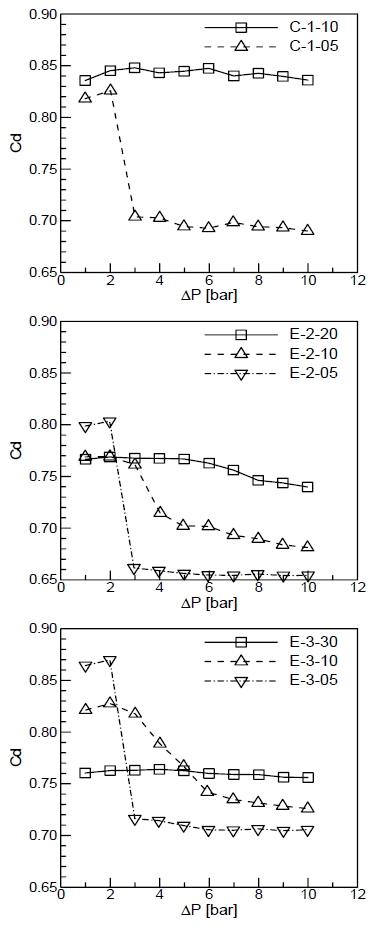
동일 오리피스 형상에서 오리피스의 길이가 가장 긴 C-1-10, E-2-20, E-3-30 분사기의 경우, 유량계수는 분사압력 6 bar 전까지는 약간 증가하거나 일정한 값을 보이다가, 6 bar 이후에서는 약간씩 감소하고 있다. 이는 오리피스 입구가 각진 모서리 형상을 갖기 때문에 6 bar 이후 공동현상이 발생한 것으로 예측할 수 있다. 하지만 유량계수가 매우 서서히 떨어지고 있는 점 그리고 다음 절에서의 유동 이미지 결과로부터, 기포가 오리피스 입구에서 발생한 후 오리피스 내부에서 다시 분열되어 노즐 출구까지는 전달되지 못한 것으로 생각된다[8,12].
L/b가 8 이상 그리고 L/a가 8 이하인 E-2-10, E-3-10 분사기의 경우, 유량계수가 압력 3 ~ 5 bar에서 급격히 줄어들다가 그 이후에도 지속적으로 감소하는 현상을 나타내었다. 공동현상이 발달하게 되면 과도한 기포가 발생하여 이상 유체의 평균 밀도가 낮아지고, 결국 액상 유체의 유입량을 감소시켜 유량계수를 감소시킨 것으로 생각된다[18]. 또한 이들 분사기의 경우는 장축 평면에서는 수력튀김이 단축 평면에서는 공동현상이 생성되어 원형 노즐에서는 나타나지 않는 결과를 갖는 것으로 판단된다.
동일 오리피스 형상에서 오리피스 길이가 가장 짧은 C-1-05, E-2-05, E-3-05 분사기의 경우 오리피스의 길이가 짧기 때문에 벽면에 의한 마찰 손실이 상대적으로 작아 분사압력이 낮은 조건에서는 유량계수가 다른 분사기에 비해 크게 나타난다. 하지만 압력이 3 bar 이상이 되면 압력 회복에 의한 캐비티의 소멸 및 재부착이 이루어지는 지점이 오리피스 출구에 점점 가까워지다가, 결국엔 압력 역구배에 의해 외부 공기가 오리피스 내로 유입되어 분무되는 제트의 단면적이 줄어드는 수력튀김 현상이 일어난다. 수력튀김이 발생하게 되면, 공기로 둘러싸인 유로로 인하여 유량계수가 낮아져 일정하게 된다. 좀 더 자세한 분석은 다음 절에 유동 이미지들과 함께 설명되어 있다.
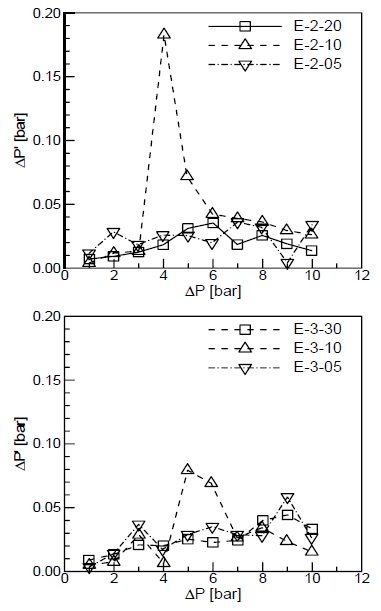
분사압력 데이터를 분석하는 과정에서 독특한 현상을 발견하여 Fig. 5에 정리하였다. 앞에서 언급하였듯이 60초 동안 유량을 측정하였으며, 이때 분사기 매니폴드 압력을 100 Hz로 측정하였다. 결국 6,000개의 분사압력 데이터의 표준편차를 구해보았는데, Fig. 5와 같이 L/b가 8 이상 그리고 L/a가 8 이하인 E-2-10 분사기의 경우 압력 4, 5 bar에서, E-3-10 분사기의 경우 압력 5, 6 bar에서 분사압력의 섭동이 다른 경우에 비해 상당히 큰 것을 확인할 수 있었다. 이 현상은 장축 평면에서 공동현상과 수력튀김 현상이 불안정하게 공존하면서 발생하는 것으로 생각된다. 하지만 압력이 더 커지게 되면 장축 평면에서는 완전히 수력튀김 현상이, 단축 평면에서는 공동현상이 발달되어 더 이상 이런 현상이 관측되지는 않는 것으로 예측된다.
3.2 액체제트의 유동특성
원형 노즐에서 분사된 액체제트 사진을 Fig. 6에 나타내었다. 공동현상이 일어나면 액체제트가 급격히 불안정해지는 반면 수력튀김이 일어나면 액체제트의 표면이 부드러워지며 지름이 정상유동 때보다 작아지게 되는데, 이러한 특성들을 통하여 공동현상 및 수력튀김 발생 여부를 확인하였다[12,13]. L/d가 10인 C-1-10 분사기의 경우 압력이 증가함에 따라 유속도 빨라지고 난류강도도 커지기 때문에 액체제트의 표면에 불규칙적으로 강한 섭동이 발생하여 제트 표면에 변형이 일어나게 된다. 이로 인해 고속 카메라를 통하여 순간적인 이미지를 촬영할 때 광원의 굴절이 발생하고 이미지에 음영이 생겨 투명도가 감소하게 된다. 하지만 압력 7, 9 bar에서도 공동현상으로 인한 유동의 흔들림은 관찰되지 않았다. 압력 7 bar 이상에서 유량계수가 서서히 감소하는 현상으로 미루어 공동현상이 오리피스 입구에서 발생하지만 기포가 출구까지 전달되지는 않는 것으로 생각된다. L/d가 5인 C-1-5 분사기의 경우 압력 3 bar 이상에서 수력튀김 발생하여 압력이 증가함에도 불구하고 상당히 투명한 액체제트를 나타내며 액주의 지름도 작게 보인다. Fig. 6에 제시하지는 않았지만 압력 2 bar에서는 공동현상이나 수력튀김이 없는 정상유동이 진행되었다.

Liquid column images from the circular nozzles (from top to bottom: C-1-10, C-1-05, from left to right: ΔP = 1, 3, 5, 7, 9 bar).
종횡비 3을 갖는 타원형 노즐에서 분사된 장축 평면에서의 액체제트 사진을 Fig. 7에 나타내었다. 분사압력 1 bar에서는 오리피스 길이에 상관없이 액주가 하류로 진행할수록 너비가 줄어드는 현상이 발견되었다. L/b, L/a가 모두 8 이상인 E-3-30 분사기의 경우 C-1-10 분사기와 유사한 경향을 나타내었다. 압력이 증가함에 따라 액체제트의 투명도가 감소하였으며, 하류로 갈수록 너비가 줄어드는 현상도 점차 사라짐을 확인하였다.

Liquid column images in the major axis’ plain from the elliptical nozzles (from top to bottom: E-3-30, E-3-10, E-3-5, from left to right: ΔP = 1, 3, 5, 7, 9 bar).
L/b, L/a가 모두 8 이하인 E-3-05 분사기의 경우 Fig. 7에 나타내진 않았지만 분사압력 2 bar에서 공동현상이 나타났으며, 3 bar이상에서는 수력튀김이 발생하였다. 4 bar 이상에서는 가운데 액주 사이에 날개처럼 옆면에 액막이 발견되는데 이는 종횡비가 큰 관계로 장축 평면과 단축 평면 사이에서 수력튀김 현상으로 오리피스 입구에서 떨어진 액체의 일부분이 장축 평면에서 떨어진 액주를 감싸는 현상으로 생각된다. 종횡비가 2인 E-2-05 분사기에서는 이런 현상의 관찰되지 않았다. L/b가 8 이상, L/a가 8 이하인 E-3-10 분사기의 경우 3 bar에서부터 공동현상이 나타났다. 장축 평면에서의 분무 이미지를 살펴보면 4, 5 bar에서 이보다 높은 압력 보다 훨씬 더 단면이 커진 현상을 나타내는데, 이는 장축 평면에서 공동현상이 수력튀김으로 완전히 발달하지 못했기 때문으로 생각된다. 사진을 살펴보면 매우 거칠긴 하지만 수력튀김에서와 같이 가운데 액주 사이에 날개와 같은 액막이 존재하고 있다. 6 bar 이상에서는 장축 평면에서 수력튀김이 단축 평면에서는 공동현상이 발생하여 5 bar에 비해 표면의 섭동이 작아진 것으로 예측된다.
종횡비 2를 갖는 타원형 노즐에서 분사된 단축 평면에서의 액체제트 사진을 Fig. 8에 나타내었다. 분사압력 1 bar에서는 오리피스 길이에 상관없이 액주가 하류로 진행할수록 너비가 커지는 현상이 발견되었다. L/b, L/a가 모두 8 이상인 E-2-20 분사기의 경우 압력이 증가함에 따라 액체제트의 투명도가 감소하였으며, 8 bar 이상에서는 기포가 외부까지 진행되어 섭동이 매우 큰 것으로 생각된다.

Liquid column images in the minor axis’ plain from the elliptical nozzles (from top to bottom: E-2-20, E-2-10, E-2-5, from left to right: ΔP = 1, 3, 5, 7, 9 bar).
L/b, L/a가 모두 8 이하인 E-2-05 분사기의 경우도 분사압력 2 bar에서 공동현상이 나타났으며, 3 bar 이상에서는 수력튀김이 발생하였다. 높은 압력에서도 액체제트의 너비가 하류로 갈수록 커지는 현상이 나타났으며, 상당히 매끈한 면을 갖고 있었다. L/b가 8 이상, L/a가 8 이하인 E-2-10 분사기의 경우 3 bar에서부터 공동현상이 나타나며, 액주분열 전 액주표면에서 떨어진 작은 액적들도 관찰된다.
타원형 노즐에서 유동이 정상상태일 때 장축 평면에서는 액주의 너비가 감소하고, 단축 평면에서는 액주의 너비가 증가하고 있다. 이와 같은 메커니즘은 축교차 현상으로 설명을 할 수 있는데[5], Fig. 9에 이에 관한 현상을 나타내었다. 타원형 노즐의 경우 원형의 모습으로 회복하려는 표면장력과 원형의 단면모양을 타원형으로 다시 바꾸려 하는 관성력이 액주제트에 작용함으로써 주기적인 축교차 현상을 지닌 분무 모습을 나타나게 된다.
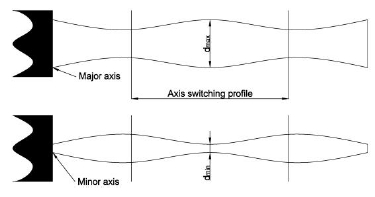
Schematic of an elliptical liquid jet spray from an elliptical orifice in major axis and minor axis[5].
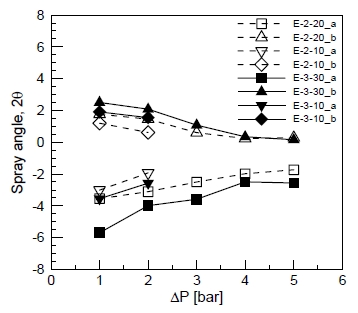
공동현상이나 수력튀김이 없는 타원형 노즐에서의 정상유동 상태에서 장축 평면과 단축 평면에서 분사압력에 따른 분무각의 변화를 Fig. 10에 도시하였다. 분무각 측정은 액주의 표면을 MATLAB 이미지 처리기법을 이용하여 분리한 후, 노즐 출구로부터 축방향으로 1.4 ㎜ 간격씩 7.0 ㎜까지 좌측, 우측 각각 5개의 측정 포인트를 연결하는 선을 구함으로써 계산되었다. 각 조건별로 40장의 이미지에서 데이터를 구하여 평균하였다. 분무각 0도를 기준으로 양수는 분무각이 커지는 경우, 음수는 분무각이 작아지는 경우를 의미한다. 동일한 분사압력에서 종횡비가 큰 경우 분무각의 감소율이나 증가율이 컸으며, 분사압력이 증가함에 따라 축교차 현상은 줄어드는 것을 확인하였다. 또한 같은 종횡비 조건에서는 L/d가 큰 경우 분무각의 감소율이나 증가율이 증가하였다. 이러한 현상은 유체의 표면장력, 노즐 출구에서의 액체의 속도성분, 그리고 난류강도에 의한 영향으로 설명될 수 있다. 종횡비가 클수록 표면장력에 의해 빠르게 액체제트의 단면이 원형으로 바뀌려고 하지만 L/d가 작은 경우 반경방향의 속도성분이 존재하여 이를 방해하며 분사압력이 증가할수록 액체제트의 난류강도가 증가하여 상대적으로 표면장력의 영향이 줄어드는 것으로 설명될 수 있다.
4. 결 론
본 연구에서는 오리피스 길이가 다른 원형 노즐과 타원형 노즐을 이용하여, 공동현상과 수력튀김 현상이 유동특성에 어떠한 영향을 주는지 살펴보았다. 유량계수는 노즐의 형상에 상관없이 공동현상이 발달되면 유량계수가 전반적으로 감소하며, 수력튀김이 발생하면 급격히 감소 후 일정해지는 현상을 나타내었다. 하지만 E-2-05, E-3-05 분사기의 경우 분사압력 2 bar의 액체제트 사진에서는 공동현상이 관찰되지만 유량계수에서는 이를 사전에 예측하지 못하였다. 결국 유량계수 결과만으로 공동현상의 발생 유무를 판단하는 것은 오차의 가능성을 내포하고 있음을 알 수 있었다.
L/b, L/a 모두 8 이하인 타원형 노즐의 경우 분사압력 3 bar 이상에서 수력튀김 현상이 발생하며, 종횡비가 큰 3인 경우는 수력튀김으로 생성된 액주를 날개처럼 감싸는 액막이 형성됨을 관찰할 수 있었다. L/b가 8 이상, L/a가 8 이하인 타원형 노즐의 경우 분사압력 3 bar 이상에서 액체제트의 표면이 매우 불안정한 공동현상이 나타났다. 장축 평면에서는 수력튀김이 발생하려 하지만, 단축 평면에서 발생하는 공동현상으로 결국 원형 노즐의 공동현상과 유사한 현상을 나타냄을 확인하였다. 특히, 특정 압력 조건에서 공동현상과 수력튀김 현상이 불안정하게 발달하는 히스테리시스 영역이 있다고 판단된다.
타원형 노즐에서 유동이 정상상태인 경우 장축 평면에서는 분무각이 줄여들고, 단축 평면에서는 분무각이 커지는 현상이 나타났다. 동일한 분사압력에서 종횡비가 큰 경우 분무각의 감소율이나 증가율이 컸으며, 분사압력이 증가함에 따라 축교차 현상은 줄어드는 것을 확인하였다.
Nomenclature
| A : | orifice area |
| AR : | aspect ratio, a/b |
| a : | major diameter of elliptical orifice |
| b : | minor diameter of elliptical orifice |
| Cd : | discharge coefficient |
| d : | diameter of circular orifice |
| L : | orifice length |
| : | mass flow rate |
| ΔP : | injection gauge pressure |
| ΔP’ : | standard deviation of injection pressure |
| 2θ : | spray angle |
| ρf : | fluid density |
Acknowledgments
본 논문은 미래창조과학부의 재원으로 한국연구재단의 지원(NRF-2017R1A1A1A05001237, NRF-2015M1A3A3A02011346)을 받아서 수행되었으며, 이에 감사드립니다.
References
-
Schmidt, D.P., and Corradini, M.L., “Analytical Prediction of the Exit Flow of Cavitation Orifices”, Atomization and Sprays, 7(6), p603-616, (1997).
[https://doi.org/10.1615/atomizspr.v7.i6.30]

- Soteriou, C., Andrews, R., and Smith, M., “Direct Injection Diesel Sprays and the Effect of Cavitation and Hydraulic Flip on Atomization,” SAE Technical Paper 950080, (1995).
- Soteriou, C., Andrews, R., and Smith, M., “Further Studies of Cavitation and Atomization in Diesel Injection,” SAE Technical Paper 1999-01-1486, (1999).
- Yunyi, G., Changwen, L., Yezhou, H., and Zhijun, P., “An Experimental Study on Droplet Size Characteristics and Air Entrainment of Elliptic Sprays,” SAE Technical Paper 982546, (1998).
-
Kasyap, T.V., Sivakumar, D., and Raghunandan, B.N., “Flow and Breakup Characteristics of Elliptical Liquid Jets”, International Journal of Multiphase Flow, 35(1), p8-19, (2009).
[https://doi.org/10.1016/j.ijmultiphaseflow.2008.09.002]

-
Hong, J., Ku, K., Kim, S., and Lee, C., “Effect of Cavitation in Circular Nozzle and Elliptical Nozzles on the Spray Characteristic”, Atomization and Sprays, 20(10), p877-886, (2010).
[https://doi.org/10.1615/atomizspr.v20.i10.40]

-
Hong, J., Ku, K., and Lee, C., “Numerical Simulation of the Cavitating Flow in an Elliptical Nozzle”, Atomization and Sprays, 21(3), p237-248, (2011).
[https://doi.org/10.1615/atomizspr.2011003127]

-
Ku, K., Hong, J., and Lee, C., “Effect of Internal Flow Structure in Circular and Elliptical Nozzles on Spray Characteristics”, Atomization and Sprays, 21(8), p655-672, (2011).
[https://doi.org/10.1615/atomizspr.2012004192]

-
Wu, P.K., Miranda, R.F., and Faeth, G.M., “Effects of Initial Flow Conditions on Primary Breakup of Nonturbulent and Turbulent Round Liquid Jets”, Atomization and Sprays, 5(2), p175-196, (1995).
[https://doi.org/10.1615/atomizspr.v5.i2.40]

-
Tamaki, N., Shimizu, M., Nishida, K., and Hiroyasu, H., “Effects of Cavitiation and Internal Flow on Atomiztation of a Liquid Jet”, Atomization and Sprays, 8(2), p179-197, (1998).
[https://doi.org/10.1615/atomizspr.v8.i2.30]

- Lefebvre, A.H., Atomization and Sprays, Hemisphere Publishing Corporation, Bristol, P.A., U.S.A., (1989).
-
Ahn, K., Kim, J., and Yoon, Y., “Effects of Orifice Internal Flow on Transverse Injection into Subsonic Crossflows: Cavitation and Hydraulic Flip”, Atomization and Sprays, 16(1), p15-34, (2006).
[https://doi.org/10.1615/atomizspr.v16.i1.20]

-
Song, J., Ahn, K., Kim, M.K., and Yoon, Y., “Effects of Orifice Internal Flow on Liquid Jets in Subsonic Crossflows”, Journal of Propulsion and Power, 27(3), p608-619, (2011).
[https://doi.org/10.2514/1.b34011]

-
No, S.Y., “Empirical Correlations for Breakup Length of Liquid Jet in Uniform Cross Flow - A Review”, Journal of ILASS-Korea, 18(1), p35-43, (2013).
[https://doi.org/10.15435/jilasskr.2013.18.1.035]

-
No, S.Y., “A Review on Empirical Correlations for Jet/Spray Trajectory of Liquid Jet in Uniform Cross Flow”, International Journal of Spray and Combustion Dynamics, 7(4), p283-314, (2015).
[https://doi.org/10.1260/1756-8277.7.4.283]

- Song, Y., and Ahn, K., “Effect of Orifice Geometry on Spray Characteristics of Liquid Jet into Subsonic Crossflows”, Annual Conference of ILASS-Korea, Jeju, Korea, p47, Oct.), (2016.
- Vennard, J.K., Elementary Fluid Mechanics, John Wiley & Sons Inc, New York, N.Y., U.S.A., (1961).
-
Nurick, W.H., “Orifice Cavitation and Its Effects on Spray Mixing”, Journal of Fluid Engineering, 98(4), p681-687, (1976).
[https://doi.org/10.1115/1.3448452]