알루미늄 입자가 다량 함유된 고폭약의 데토네이션 특성에 대한 수치적 연구

1. 서 론

본 연구는 데토네이션을 통한 고온 고압 환경 내에서 알루미늄 입자의 후연소(Afterburn)를 다루고 있다. 반응성 금속 입자들(주로 알루미늄과 마그네슘)은 총 발열 에너지의 증강을 위해서 고폭약 내에 자주 추가되곤 한다.

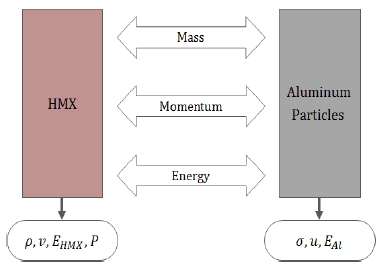
금속 입자들은 고폭약 혹은 주변 공기 내에서 반응하여 폭풍압에 기여하거나 두 번째 폭풍파 속도 증가에 기여한다. 알루미늄 입자 연소에 대한 연구는 수 십년간 광범위하게 이루어졌으며, 이를 수치 해석하기 위하여, 라그랑지안 해석을 사용하거나 오일러리안 해석을 적용한 이상 모델(Two-phase model)의 연구가 제안되었다. 여기서, 이상 모델은 공기역학적 지배방정식을 기초로, 유체 내 희석된 입자들의 거동을 기존의 라그랑지안 해석 대신 오일러리안 해석을 위해서 Nigmatulin에 의해 고안되었다[1]. 이 모델은 Fig. 1과 같이 두 상(기체와 고체입자) 간의 상호 작용을 다루며, 상호 작용하는 물리량들(질량, 운동량, 에너지)은 Khasainov et al.에 의하여 현상학적 모델로 제안되었다[2].

Fig. 1.

Structure of the heterogeneous solid explosive mixture model with Al particles.

이상 모델의 대표 연구자들로는 F. Zhang, A.L. Kuhl, 그리고 A.V. Fedorov가 있으며, 각각 다른 알루미늄 입자의 연소모델을 사용한다. A.V. Fedorov[3]는 아레니우스 형태의 연소모델을 조합하여 사용하였으며, A.L. Kuhl[4-5]의 경우에는 Khasainov의 모델을 동일하게 사용하였다. 기존 Khasainov의 연소모델은 실험식을 기반으로 모델링되었다. 또한 알루미늄 입자의 점화는 적정 점화온도를 기점으로 on/off 하는 형태이며, 일반적으로 점화온도는 녹는점인 932 K 이상 온도를 사용한다. 반면, F. Zhang[6-7]은 알루미늄 입자의 점화온도에서 연소를 on/off 하지 않고, 아레니우스 형태의 반응모델과 확산 모델을 조합한 혼형 모델(hybrid model)을 제안하였다.

본 연구에서는 Nigmatulin이 제안한 이상 모델을 기초로 Khasainov와 Veyssiere에 의해 제안된 KV 상호작용 모델(interaction model)을 사용하여, 고폭약 내에서 입자들의 후연소를 모사하고 데토네이션 속도를 실험 결과와 비교 검증하였다.

폭약의 데토네이션 특성을 확인하기 위해 흔히 사용되는 Thermochemical Computer Code인 Cheetah는 Wood-Kirkwood (WK) 반응모델을 사용한다. 이 모델은 고폭약에 대하여 빠른 반응 모델과 알루미늄에 대하여 간단한 표면적을 고려하는 제한된 반응속도를 사용하여, 평형 상태에서의 데토네이션을 계산한다. WK 반응모델에서 알루미늄은 H₂O의 출현에 따라 점화지연을 모델링하였으며, 반응 후 알루미늄 산화물인 산화알루미늄(Al₂O₃)을 고체로서 취급한다. 또한 고폭약 산화물과의 운동량-에너지 교환 그리고 알루미늄 입자 크기에 대한 영향을 고려하지 않는다. 하지만, 실제 알루미늄 산화물은 고온 환경 내에서 고체나 기화 상태로 있을 수 있으며, 폭약 반응영역 내 알루미늄은 입자의 크기에 따라서 큰 입자의 경우 비반응성 물질의 경향성을, 작은 입자의 경우에는 반응성 입자의 경향성을 띄게 된다.

2. 수치적 모델

본 연구에서는 공간 차분과 시간 차분을 위해 3차 Convex ENO 기법과 3차 Runge-Kutta (RK) 기법을 각각 사용하였다. 그리고 이상 모델은 아래의 수치적 가정을 바탕으로 이종 매질 내에서 기체와 고체 입자들은 분리하였다.

• 1. 기체매질 내 고체 입자들의 부피는 무시한다.
• 2. 고체입자간의 상호 작용은 무시한다.
• 3. 기체상과 분포된 고체입자상 모두 각 공간 내에 연속체로서 취급한다.
• 4. 분포된 고체입자들의 공간은 매질의 압력과 음속을 무시한다.

이러한 가정들로서 알루미늄 입자들을 오일러리안 해석으로 가능하게 한다. 그에 따라서, 각 입자의 자세한 연소는 모델링 할 수 없지만, 각각의 입자를 연속체로서 취급하면서 분포된 입자밀도로서 연소현상을 모사할 수 있다.

2.3 알루미늄 입자가 다량 함유된 고폭약의 초기 값

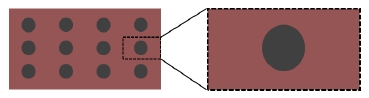
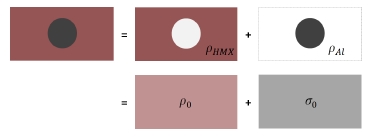
이상 모델은 폭약 공간 내에 고체 입자의 부피를 고려하지 않기 때문에 Fig. 2와 같이 폭약 공간 위에 고체 입자를 위한 가상공간이 존재한다고 생각할 수 있다. 그에 따라 모델 내에서 입자가 사라진 자리를 비어있는 공간이 아닌 연속체로서 폭약을 취급하기 때문에 Fig. 3과 같이 폭약의 밀도는 실제 순수 폭약의 밀도보다 희석된 밀도를 갖게 된다. 마찬가지로 가상공간 내에서 알루미늄 입자들 또한 연속체로 취급되어 희석된 밀도로 채워진다.

Fig. 2.

Assumption of uniform distribution.

Fig. 3.

Initialization of each diluted density of HMX and aluminum.

$\[ V_a{\rho }_{Al}:\left(V_t-V_a\right){\rho }_{HMX}=a : \left(1-a\right) \]$

(15)

$\[ {\rho }_0=\left(V_t-V_a\right){\rho }_{HMX}/V_t \mathrm{o}\mathrm{r} {\sigma }_0 = V_a{\rho }_{Al}/V_t \]$

(16)

각 공간 내 희석된 밀도는 Eq. 15-16과 같이 간단한 식으로 계산되는데, 이는 이미 알고 있는 값(전체 고폭약에 대한 알루미늄의 질량비(a)와 순수 알루미늄의 밀도(ρ_Al) 그리고 순수 고폭약의 밀도(ρ_HMX))과 더불어 전체 고폭약에 대한 알루미늄 입자가 차지하는 부피비(V_a)에 의하여 결정된다.

2.4 고폭약 반응 모델과 상태방정식(EOS)

본 연구에서 고려하는 HMX는 그 성분이 비슷한 PBX 9501 (95% HMX/ 5% Estane, BDNPA/F)을 채택하였으며, 고폭약의 반응 모델과 상태방정식은 아래의 Eq. 17-19와 같은 I&G 모델과 JWL EOS를 사용하였다. 반응모델과 EOS의 미정상수는 각각 Table 1과 Table 2에 기재하였다[8].

$\[ {\dot{w}}_H=I{\left(1-⋋\right)}^b {\left(\eta -a\right)}^x+G_1{\left(1-⋋\right)}^c{⋋}^d{P}^y G_1{\left(1-⋋\right)}^c{⋋}^d{P}^y+G_2{\left(1-⋋\right)}^e{⋋}^g{P}^z \]$

(17)

$\[ ;\mathrm{ }\eta =\frac{\rho }{{\rho }_0}-1 , V=\frac{\rho }{{\rho }_0} \]$

$\[ P_{unreacted}={A_0\left(1-\frac{w_0}{R_{01}V}\right)e}^{-R_{01}V}+{B_0\left(1-\frac{w_0}{R_{02}V}\right)e}^{-R_{02}V}+w_0\frac{E}{V} \]$

(18)

$\[ P_{reacted}={A_1\left(1-\frac{w_1}{R_{11}V}\right)e}^{-R_{11}V}+{B_1\left(1-\frac{w_1}{R_{12}V}\right)e}^{-R_{12}V}+w_1\frac{E}{V} \]$

(19)

Table 1.

I&G model parameters[8].

Table 2.

JWL EOS parameters[8].

물질의 상태량(압력, 내부에너지, 밀도)은 Eq. 20-22와 같이 표준 혼합물 법칙(standard mixture rule)을 적용하여 도출하였다.

$\[ P_{tot}=\left(1-⋋\right) P_{unreacted}+{⋋P}_{reacted} \]$

(20)

$\[ e_{tot}=\left(1-⋋\right) e_{unreacted}+{⋋e}_{reacted} \]$

(21)

$\[ {\nu }_{tot}=\left(1-⋋\right) {\nu }_{unreacted}+{⋋\nu }_{reacted} \]$

(22)

3. 결과 및 논의

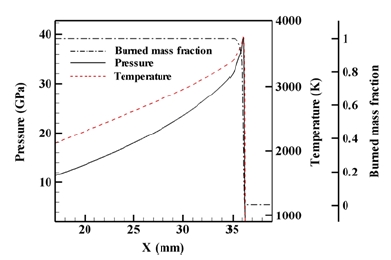
본 연구에서는 실험 조건과 동일한 알루미늄 입자를 함유하는 HMX에 대하여 20 mm의 지름과 100 mm 길이를 갖는 confined rate stick에 대하여 수치 해석을 수행하였다. Confiner의 재료는 구리이며 두께는 2 mm이다. 계산공간은 Fig. 4와 같이 초기에 세 물질로서 분할되었으며, 안쪽부터 고폭약, 구리 그리고 빈 공간(void)이다. 각 두 구성 요소간 경계는 level set 기법을 사용하여 분할하며, 경계면은 zero level set으로서 실선으로 나타나 있다. Fig. 5는 알루미늄 입자가 포함되지 않은 순수 고폭약이 지름 방향으로 무한하다고 가정할 경우의 rate stick 계산결과로서 압력선도와 온도선도, 그리고 연소된 질량 분율(burned mass fraction)을 보여준다. Table 3에는 Fig. 5의 수치해석 결과를 이용하여 순수 고폭약 데토네이션의 본 노이만 스파이크 압력(von Neumann spike pressure, P_ZND), CJ (Chapman-Jouguet)상태 압력(P_CJ), 온도(T_CJ) 그리고 반응 영역 길이 (reaction zone length, X_R)를 보여주며, 실험값과 Cheetah결과와 비교하여 수치해석에서 도출된 값들이 잘 모사함을 확인하였다.

Table 3.

ZND & CJ condition of PBX 9501.

수치해석에서, HMX의 밀도(ρ_HMX)는 1.808 g/cm3을 사용하였으며, 알루미늄 입자의 크기는 3가지 경우 (0.5, 7, 15 μm)를 다루었다. 또한 알루미늄의 함유량은 5-25%에 대하여 각각 수행하였다. 알루미늄 입자를 함유하는 HMX의 데토네이션 속도는 첨가된 알루미늄 입자의 함유량과 평균 입자 크기에 따라 결정된다는 가정 하에 일련의 계산을 수행하였다.

Fig. 4.

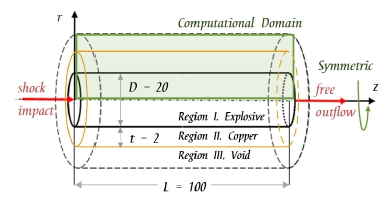
Computational domain of a 2-D cylindrical rate stick tests: 2mm-copper confined rate stick (D = 20 mm, L = 100 mm).

Fig. 5.

Structure of detonation wave representing the reaction zone of PBX 9501 at t = 2.5 ㎲.

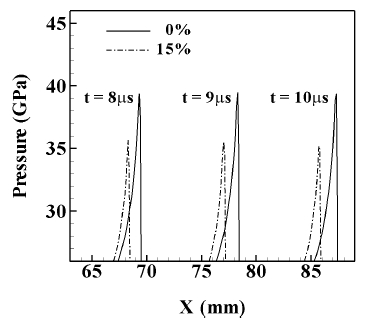
알루미늄 입자를 함유함에 따라서 데토네이션 속도 및 본 노이만 스파이크 압력 변화는 Fig. 6을 통하여 확인할 수 있으며, 실선은 순수 HMX를 사용한 rate stick의 결과이고 점선은 7 μm의 알루미늄 입자가 15% 함유된 고폭약의 결과이다. 각 스파이크 압력은 동일 시간에서 측정되었으며, 데토네이션 속도가 8823 m/s에서 8631.63 m/s로 감소하고 본 노이만 스파이크 압력은 39.1 GPa에서 35.71 GPa로 감소하였음을 확인할 수 있다.

Fig. 6.

Detonation velocity decreased by aluminizing 15% with particle diameter 7 μm.

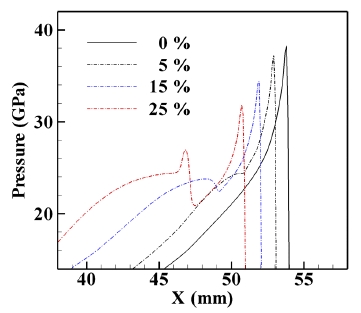
수치해석 결과로서, Fig. 7은 입자크기 7 μm의 알루미늄 함유량 증가에 따른 압력 선도를 보여주며, 알루미늄 입자 연소에 의한 두 번째 스파이크 압력 선도를 확인할 수 있다. 이러한 현상은 Gogulya. et al.[12]의 실험결과에서도 나타나며, 이상 모델을 적용한 수치 해석으로 이중 데토네이션(double front detonation) 압력선도 현상모사가 가능함을 확인 할 수 있다.

Fig. 7.

Detonation velocity decreased by aluminizing with particle diameter 7μm at t = 6㎲.

알루미늄 입자를 함유하는 고폭약의 데토네이션 속도 변화에 대한 수치 해석 결과와 Gogulya et. al.[12]의 실험 결과 비교는 Fig. 8을 통해 확인할 수 있으며, 추가로 Cheetah의 결과와도 비교하였다. 실험은 알루미늄 입자 함유량을 세 가지 (5, 15, 25%)를 다뤘으며, 이상 모델과 Cheetah는 10, 20%의 함유량을 추가하여 다섯 가지 함유량에 대하여 계산을 수행하였다.

Fig. 8에서 보이듯, 알루미늄 함유량의 증가에 따라 데토네이션 전파속도 감소 현상을 확인할 수 있다. 또한 동일 알루미늄 함유량일 경우, 알루미늄 입자의 크기가 작을수록 데토네이션 전파속도가 느려진다. 그리고 알루미늄 입자의 크기가 작을 때, 함유량이 증가함에 따라 데토네이션 속도의 감소율이 증가함을 확인할 수 있는데, 예로서 알루미늄 입자크기가 상대적으로 클 경우 (7 μm)와 작을 경우(0.5 μm)에서 데토네이션 속도와 속도 감소율이 많은 차이를 보인다.

Fig. 8.

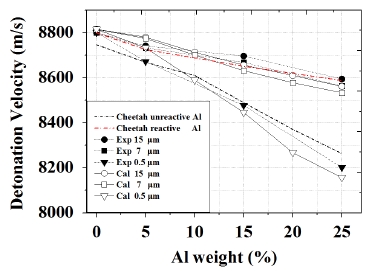
Detonation velocity versus Al content in HMX based formulations : experiments[12], Two-phase model simulation.

이는, 알루미늄 입자 하나가 동일 유동장 내에서 크기가 작을 경우, 큰 입자보다 입자의 가속도가 높기 때문이다. 따라서 동일 유동장 내에서 동일 질량의 알루미늄 입자들은 입자의 크기가 작아짐에 따라서 유동장 내의 운동량 감소를 가중시키게 되며, 그에 따라 데토네이션 전파 속도는 입자 크기가 작아질수록 줄어든다.

Cheetah를 사용한 결과에서 반응성 알루미늄 입자를 함유하는 폭약의 데토네이션 속도는 입자 크기가 작은 0.5 ㎛ 실험과 비교적 비슷한 결과를 보였으며, 비반응성 알루미늄 입자를 함유하는 폭약의 데토네이션 속도는 입자 크기가 큰 7 μm와 15 μm의 결과와 비슷한 결과를 보였다. Cheetah는 반응성 알루미늄 입자를 함유하는 고폭약에 대하여 WK 반응모델을 사용한다[13]. 알루미늄 반응모델은 Gogulya et al.의 실험데이터에 전체적인 경향성에 맞도록 모델링되었다[14].

이 실험은 0.5~150 μm의 알루미늄 입자를 함유한 HMX 폭약을 사용한 실험이며, 모델링 과정에서 알루미늄 입자 크기의 영향은 고려되지 않았다. 또한 알루미늄 입자와 고폭약 산화물과의 운동량, 에너지 교환에 대한 영향을 고려하지 않는다. 그렇기에 Cheetah의 결과는 알루미늄 함유량에 따른 전체적 경향성만 보여주며, 알루미늄 입자 크기에 따른 데토네이션 결과는 내놓지 못한다.

반면, 이상 모델을 사용한 수치 해석결과의 데토네이션 속도는 알루미늄 함유량과 입자의 크기에 대하여 전체적으로 실험 결과를 따라감을 알 수 있다. 실험결과와 이상 모델의 수치해석결과의 오차는 5%의 낮은 알루미늄 입자의 함유량에서 대략 0.6%로 비교적 높았으며, 나머지는 대략 0.4%내의 오차로 확인되었다.

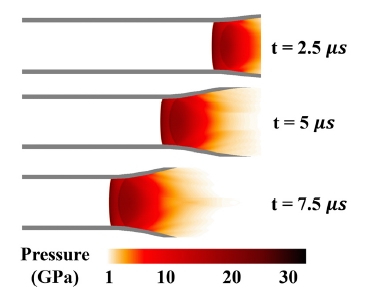
이차원 원통좌표계에서의 데토네이션 전파 형상은 Fig. 9와 같은 압력장으로 나타낼 수 있으며, 데토네이션 전파 속도, 8533 m/s는 Gogulya et al.[12]에 의해 수행된 실험값, 8560 m/s을 잘 모사하였다.

Fig. 9.

Pressure contours of 25% aluminized HMX confined rate stick simulation with aluminum particle diameter 7 ㎛.

4. 결 론

기존의 알루미늄 입자가 함유된 고폭약에 대한 연구는 단일 알루미늄 입자의 크기와 단일 함유량에 대하여 반응식을 모델링 하였으며, 이 방식은 알루미늄 입자의 크기와 함유량에 따라서 각기 새롭게 모델링되어야 했다.

하지만, 이상 모델을 적용함으로서 이러한 번거로운 반응모델링의 제한을 없앨 수 있으며, 하나의 순수 고폭약 반응모델을 이용하여 다양한 알루미늄 입자크기와 함유량에 따른 고폭약의 모델링을 할 수 있다. 또한 이를 바탕으로 데토네이션 성능을 정량적으로 계산할 수 있다. 이는, 고폭약 제작 전에 알루미늄 입자의 함유량과 직경에 따른 고폭약의 성능(폭속/압력/온도 등)을 사전에 예측함으로써 추후 고폭약 제작 관련 연구에 활용될 수 있을 것이다.

Acknowledgments

본 연구는 서울대학교 차세대 우주추진 연구센터와 연계된 미래창조과학부의 재원으로 한국연구재단의 지원을 받아 수행한 선도연구센터지원사업(NRF-2013R1A5A1073861)과 2016년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(2016R1A6A3A11932827)의 연구 결과입니다.

References

• Nigmatulin, R.I., “Dynamics of multiphase media,”, Hemisphere Pub. Corp, New York, N.Y., U.S.A., (1991).
• Veyssiere, B., and Khasainov, B., “A model for steady,plane, double-front detonations (DFD) in gaseous explosive mixtures with aluminum particles in suspension”, Combustion and Flame, 85(1), p241-253, (1991). [https://doi.org/10.1016/0010-2180(91)90191-d]
• Fedorove, A.V., and Kratovaa, Y.V., “Calculation of Detonation Wave Propa -gation in a Gas Suspension of Aluminum and Inert Particles”, Combustion, Explosion, and Shock Waves, 49(3), p335-47, (2013).
• Kuhl, A.L., Khasainov, B., and Bell, J., “Two-Phase Model of Combustion in Explosions”, 37th Int. Conference of ICT Energetic Materials: Insensitivity, Ageing, Monitoring, Karlsruhe, Germany, UCRLPROC-222284, Jun.), (2006.
• Kuhl, A.L., Bell, J.B., and Beckner, V.E., “Heterogeneous Continuum Model of Aluminum Particle Combustion in Explosions”, Combustion, Explosion, and Shock Waves,, 46(4), p433-48, (2010). [https://doi.org/10.1007/s10573-010-0058-9]
• Zhang, F., “Detonation in Reactive Solid Particle–Gas Flow”, Journal of Propulsion and Power, 22(6), p1289-1309, (2006). [https://doi.org/10.2514/1.18210]
• Zhang, F., and Gerrard, K., “Reaction Mechanism of Aluminum-Particle–Air Detonation”, Journal of Propulsion and Power, 25(4), p845-858, (2009). [https://doi.org/10.2514/1.41707]
• Tarver, C.M., , “Ignition and Growth Reactive Flow Modeling of Recent HMX/TATB Detonation Experiments”, 19th Biennial APS Conference on Shock Compression of Condensed Matter, Tampa, F.L., U.S.A., LLNL-PROC-675475, Jun.), (2015.
• Tarver, C.M., “Detonation Reaction Zones in Condensed Explosives”, 14th APS Conference on Shock Compression of Condensed Matter, Baltimore, M.D., U.S.A., UCRL-CONF-213704, Jul.-Aug.), (2005. [https://doi.org/10.1063/1.2263497]
• Howard, W.M., Fried, L.E., and Souers, P.C., “Kinetic Modeling of Non-Ideal Explosives with Cheetah”, Proceedings of the 1 Ith International Detonation Symposium, Snowmass, C.O., U.S.A., UCRL-CONF-127965, Aug.-Sep.), (1998.
• Loboiko, B.G., and Lubyatinsky, S.N., “Reaction Zones of Detonating Solid Explosives”, Combustion, Explosion, and Shock Waves, 36(6), p716-733, (2000).
• Gogulya, M.F., Makhov, M.N., Dolgoborodov, A.Y., Brazhnikov, M.A., Arkhipov, V.I., and Shchetinin, V.G., “Mechanical sensitivity and detonation parameters of aluminized explosives”, Combustion, Explosion, and Shock Waves, 40(4), p445-457, (2004). [https://doi.org/10.1023/b:cesw.0000033568.39812.2c]
• Howard, W.M., Fried, L.E., and Souers, P.C., “Modeling of non-ideal aluminized explosives”, 11th APS Conference on Shock Compression of Condensed Matter, Snowbird, U.T., U.S.A., UCRL-JC-132717, Jun.), (1999.
• Gogulya, M.F., Dolgoborodov, A.Y., Brazhnikov, M.A., and Baudin, G., “Detonation Waves in HMX/Al Mixtures-Pressure and Temperature Measurements”, Proceedings of the 1 lth International Detonation Symposium, Snowmass, C.O., U.S.A., p979-988, Aug.-Sep.), (1998.