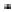다성분 입자계를 적용한 압축형 복합화약의 숔감도특성 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
압축형 복합화약에서는 압축 시 화약입자들의 재배열 및 변형으로 인하여 화약입자들의 압착화가 이루어지게 된다. 만약 깨지기 쉬운 화약입자들이 입자들의 최대 무질서밀집충진율보다 높아질 때까지 압축되면 큰 입자들은 깨짐으로써 빈 공간을 채울 수 밖에 없다. 본 연구에서는 다성분 입자계를 적용하여 압축 시 화약입자들의 손상을 막음으로써 둔감하면서도 고도로 충진된 압축형 복합화약을 얻고자 하였으며 실험결과, 2성분 입자계보다 3성분 입자계에서 더 고밀도이면서도 둔감한 숔감도를 갖는 압축형 복합화약을 얻을 수 있었다.
Abstract
In pressable polymer bonded explosives (PBXs), densification occurs due to rearrangement and deformation of explosive particles during pressing. If brittle explosives are compressed till particle fraction become higher than theoretical random close packing fraction (RCPF), bigger particles should be fractured to fill the void. In this study, multi-modal particle system was introduced for the decrease in possibility of particle fracture during compression expecting decrease in shock sensitivity of highly filled pressable PBX. The experimental results showed the trimodal particle system had low sensitivity with high density, compared to bimodal particle system.
Keywords:
Particle System, Shock Sensitivity, Pressable Plastic Bonded Explosives, Particle Packing, Theoretical Maximum Density키워드:
입자계, 숔감도, 압축형 복합화약, 입자충진, 이론최대밀도1. 서 론
대부분의 분자화약은 상온에서 고체입자로 존재하기 때문에 분자화약 자체만으로는 특정한 형태로 탄체 또는 탄두에 충전될 수 없다. 따라서 화약에 성형성을 부여하기 위해서는 결합제를 사용할 수밖에 없으며 그럼으로써 화약은 단일성분이 아니라 분자화약입자와 결합제 등 2종 이상의 다양한 성분들이 혼합되었다는 의미로 복합화약으로 불리게 된다. 복합화약의 결합제로 흔히 사용되는 고분자물질은 성형성 부여라는 기본 역할 외에도 외부충격을 흡수하여 화약의 감도를 둔감하게 하고 각 성분들의 균일혼화를 통하여 폭발특성을 정밀하게 조절할 수 있게 해주는 장점을 지니고 있다. 이러한 고분자 결합제가 적용된 복합화약을 PBXs (Plastic Bonded Explosives)라 칭한다.
일반적으로 화약의 폭발성능이 우수할수록 감도가 민감해지는 경향을 나타내는데, 실제 무기체계의 목표물 파괴력 증대와 운용 안전성 확보를 고려하면 화약 관련 과학기술자들이 추구해야할 목표는 높은 폭발성능과 둔감성을 동시에 갖는 화약을 개발하는 것으로서 이는 실로 두 마리 토끼를 쫓는 일과 같이 매우 어려운 일이다. 화약을 둔감화시키기 위한 방법으로는 크게 3가지로 집약된다. 첫째는 둔감한 분자화약의 개발이다. 실례로 둔감한 분자화약으로 알려진 NTO는 범용적으로 사용되는 RDX 분자화약에 비하여 충격에 수십배 둔감하며 이를 적용한 복합화약 역시 매우 둔감하게 된다. 둘째는 분자화약 결정입자 내부 결함(internal defect), 공동(cavity, pore)의 극소화이다. 이는 공동과 같은 결함이 있을 경우 이것이 열점(hot spot)이 되기 때문이다[1-3]. 열점은 그 크기, 온도 및 지속시간이 상호의존적으로 작용함으로써 최종적으로 실제 화약이 반응하도록 하는 임계열점(critical hot spot)이 되는데 Bowden, Yoffe 등은 임계열점의 조건으로 0.1∼10 μm의 크기, 700 K 이상의 온도 그리고 10-5∼10-3 s의 지속시간을 제안하였다[1].
이러한 열점의 주 생성 메커니즘으로 제시되는 것 중 대표적인 것이 앞서 언급한 공동에 포집되어 있는 기체종의 단열압축이다. 이상기체의 단열압축과정은 Eq. 1과 같이 쓸 수 있는데
| (1) |
이를 최종온도 Tf에 대하여 정리하면 Eq. 2와 같다.
| (2) |
내부에 공동을 갖는 화약이 있다고 가정해보자. 그 공동안의 기체종은 밀폐된 공간 안에 있는 것이고 숔은 매우 순간적인 자극이기 때문에 공동안의 기체는 단열압축된다고 볼 수 있다. 예를 들어 반응임계압력이 5 kbar인 화약이 있다고 할 때, 화약이 300 K(Ti), 1 bar(Pi)에서 1 kbar (Pf)의 숔을 받게 되면, 이상기체의 γ는 5/3이므로 이를 Eq. 2에 대입하면 Tf = 약 4700 K가 된다. 이렇듯 열점의 존재로 인하여 매우 높은 온도까지 가열됨으로써 반응임계압력인 5 kbar가 아닌 1 kbar에서도 그 화약은 반응할 수 있게 되는 것이고 결과적으로 민감한 감도를 갖게 된다. 따라서 이러한 공동의 크기나 그 분율을 극소화하는 것이 중요하다. 셋째는 충격 흡수력이 우수한 고분자 결합제의 개발이다. 앞에서 언급한 바와 같이 고분자결합제는 치수안정성을 부여해줄 뿐 아니라 외부의 충격(열적, 기계적)을 흡수하여 화약입자를 보호하는 역할을 하기 때문이다.
앞에서 열거한 복합화약의 둔감화 방안 외에 복합화약 제조과정 중에 화약입자를 손상시키지 않는 것도 매우 중요하다. 제조공정상 외력에 의하여 화약입자가 깨어지고 새로이 생성된 파단면이 결합제에 피복되지 않은 상태로 존재한다면 이 역시 열점이 될 수 있기 때문이다.
여러 유형의 복합화약 중에서 압축형 복합화약(pressable PBXs)은 빠른 폭발속도특성을 갖기 위하여 입상 분자화약의 함량비(부피분율 90%수준)가 가장 크기 때문에 일반 혼합공정으로는 제조가 불가하고 화약입자를 고분자 결합제로 피복한 후 이를 높은 압력으로 압축하여 일정 형태로 성형하는 공정을 거친다. 여기서 압축공정은 높은 압력 하에서 일부 화약입자들이 깨어질 수 있는 가능성을 내포한다. 화약입자가 깨어진 파단면은 결함이 되어 결국 복합화약을 민감하게 하는 요인이 된다. 따라서 압축형 복합화약에 있어서 화약입자를 큰 손상없이 압착(compaction)하기 위해서는 입자계(particle system)와 입자충진(particle packing)에 대한 연구가 필요하다.
2. 입자계와 충진율
하나의 크기만을 갖는 입자로만 구성된 단일성분 입자계(monomodal particle system)에서는 이론적으로 최대충진율(maximum packing fraction, φ)을 얻을 수 있는 충진구조는 면심입방(Face centered Close Packing, FCP) 또는 육방계(Hexagonal Close Packing, HCP)형태이며 충진율은 약 74%로서 하나의 크기를 갖는 입자로는 최대 74% 수준의 부피를 채울 수 있게 된다. 이외에도 체심입방형태의 경우는 약 68%, 단순입방형태는 약 52% 수준으로 단일크기의 입자계로는 FCP 또는 HCP가 최대의 충진율 값을 갖는다[4].
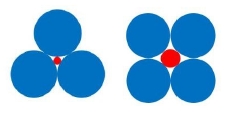
그러나 자연계에서 입자들은 FCP 또는 HCP와 같이 질서정연하게 충진하기 보다는 무질서 밀집충진(RCP)을 하며 단일성분 입자계의 무질서밀집충진율(RCPF)은 약 63~64%수준으로 밝혀져 있다[5-9].(본 연구에서는 63.4%로 선택하였음) 만약, 큰 입자 사이에 작은 입자를 채울 수 있다면 RCP 충진율은 64%보다 훨씬 증가될 수 있는데 이때 큰 입자와 작은 입자간의 크기 비가 7 이상일 경우 작은 입자는 큰 입자 사이에 생긴 빈 공간들을 수월하게 채우게 됨으로써 충진율이 향상되고 (Fig. 1 및 Fig. 2) 반대로 입자간의 크기 비가 7 이하일 경우 충진효율은 급격히 감소한다고 알려져 있다[10].
Liu. S나 McGeary. R.K 등 역시 실험 및 모사를 통하여 큰 입자와 작은 입자로 이루어진 2성분 입자계에서 두 입자의 크기 비에 따른 충진율을 보고한 바 있으며 이들은 2성분 입자계에서 크기 비가 1일 때 가장 낮은 충진율을 갖고 점차 크기 비가 커질수록 충진율이 증가하며 10에서 거의 최대 충진율에 도달할 수 있음을 보였다[9,11]. 따라서 입자계에서 충진율은 큰 입자와 작은 입자의 크기비의 함수이며 작은 입자는 충분히 작아야하고 그 작은 입자들이 적절한 부피함량으로 존재해야 높은 충진율을 가지게 됨을 알 수 있다.
A와 B로 구성된 2성분 입자계(bimodal particle system)를 생각해보자. B는 A사이에 생긴 빈 공간을 적절히 채울 수 있을 만큼 충분히 작으므로 A와 B, 각각이 독립적으로 RCP가 된다고 보면 A가 RCP가 되어 채운 나머지 공간을 B가 RCP로 독립적으로 채우는 것이므로 Table 2의 bimodal system과 같이 계산할 수 있으며 단일성분입자계에 비하여 훨씬 높은 충진율을 가질 수 있다. 마찬가지로 3성분 입자계나 4성분 입자계가 되면 이론적으로는 95%이상의 충진율을 가질 수 있게 된다. 또한, 입자들이 점유한 총 부피 내에서 각 크기에 해당하는 입자들의 점유부피 비를 Table 3에 나타내었는데 높은 충진율을 갖기 위해서는 상대적으로 작은 입자들이 적절한 부피함량으로 존재해야 함을 알 수 있다. 결과적으로 다성분 입자계로 갈수록 그 계의 밀도를 증가시킬 수 있다는 사실을 알 수 있다.

Volume fraction and ratio of each particle in the volume occupied by all particles (particle size: A>B>C>D).
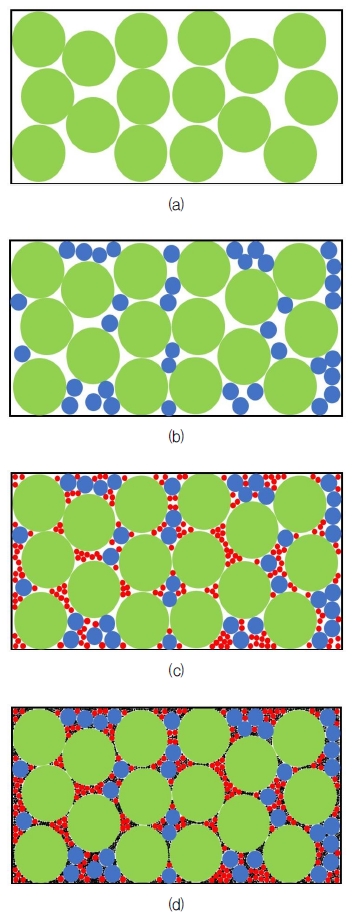
Schematic diagrams of particle systems with random close packing (a: monomodal, b: bimodal, c: trimodal, d: tetramodal).
입자의 구형도(sphericity)도 충진율에 영향을 미치게 되는데 구형도(Ψ)란 실제 입자(real particle)의 표면적(SP)에 대한 실제 입자와 같은 부피를 갖는 이상적인 구형입자(ideal sphere)의 표면적(SS)의 비를 말한다.
Ψ = surface of ideal sphere / surface of real particle
(where VS = VP)
= SS / SP
SS = surface of ideal sphere
SP = surface of real particle
VS = volume of ideal sphere
VP = volume of real particle
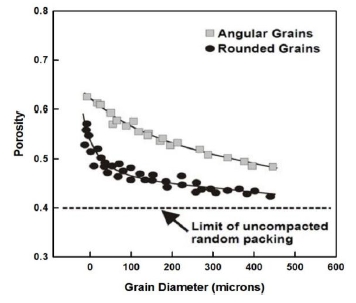
같은 부피라 할 때 완벽한 구형입자보다 다양한 모양을 가질 수 있는 실제 입자의 표면적이 항상 더 크게 되므로(Fig. 4) 실제 입자의 구형도는 항상 1보다 작은 값을 갖는다. 이 구형도가 중요한 이유는 구형도에 따라 충진율이 달라지기 때문인데 Fig. 5에서 볼 수 있듯이 구형도가 1인 완전 구형입자에 비하여 특정모양을 갖는 입자들의 경우 충진율이 감소하는 것을 볼 수 있다. 이는 충진이 잘 이루어지지 않고 공극(porosity)이 많이 존재한다는 것을 의미하며 실제 우리가 접하게 되는 충전재들은 대부분 1의 구형도 값을 가지지 못한다.
상술한 입자계와 구형도는 결과적으로는 압축형 복합화약의 감도에 큰 영향을 미치기 때문에 중요한 고려대상이 된다. 예를 들어 2성분 입자계로 구성하여 충전재의 부피함량이 90%가 되도록 압축형 복합화약을 설계한 상황을 가정해보자. 2성분 입자계는 상술한대로 이론 최대충진율이 87%로써 이마저도 입자들이 완전구형임을 가정했을 때의 충진율이고 실제로는 금속, 분자화약 등의 충전재들이 완전 구형이 아니기 때문에 2성분입자계로 RCP로써 채울 수 있는 부피는 87%에도 미치지 못할 것이다. 이런 상황에서 압축형 복합화약 압착분말을 압축하게 되면 현 상태의 입자계로는 설계 시 의도한 부피를 채우는 것이 불가능하므로 상대적으로 큰 화약입자들이 파괴, 손상됨으로써 본래보다 더 다성분의 입자계가 되어 그 부피를 채울 수 밖에 없을 것이다. 따라서 이 과정에서 결합제로 피복되지 않은 새로운 화약면이 생성되고 이 부분이 숔(shock), 충격(impact) 등의 외부자극에 노출될 때 열점의 근원으로 작용하여 결국 제조된 압축형 복합화약이 민감한 감도(sensitivity)를 갖게 하는 원인이 된다.
이와 더불어 입자계 선택이 적절하지 않음으로써 최적의 충진이 이루어지지 않으면 이는 압축형 복합화약 내부에 공극이 더 존재한다는 것을 의미하는데 이 공극 역시 서론에서 언급한 바와 같이 숔감도를 민감하게 하는 원인이 된다.
입자충진이론은 완전한 구형입자를 가정하기 때문에 실제 화약을 비롯한 충전재들의 충진을 완벽하게 설명하긴 어렵다. 그러나 입자충진이론을 바탕으로 압축형 복합화약 내의 충전재들이 차지하는 부피함량을 고려하여 적절한 입자계를 선택하는 것은 전술한 바와 같이 압축 시 화약입자의 파괴 및 손상을 최소화하고 최종 제품의 공극을 줄일 수 있기 때문에 압축형 복합화약의 숔감도를 개선하는데 있어서 반드시 필요하다.
따라서 본 연구에서는 이러한 입자충진이론을 바탕으로 입자계 조절을 통하여 최적의 충진 및 압축 시 입자들의 손상을 막음으로써 최종 압축형 복합화약의 숔감도를 개선하고자 하였다.
3. 실 험
3.1 원료
고체입자로서 ㈜한화 제품의 RDX 분자화약을 크기별로 5, 30, 250, 450 ㎛의 4종류를 사용하였고 ㈜창성제품의 30 ㎛크기의 알루미늄 분말을 사용하였다. 결합제 성분중 가소제로서 ㈜애경의 DOA (Dioctyl Adipate)를 사용하였고 고분자 결합제로서 아크릴계 고무인 Hytemp (Zeon chemicals)를 사용하였다. 이외에 유기용매로서 EA (Ethyl Acetate), EDC (Ethylene Dichloride), IPA (Isopropyl Alcohol) (Samchun chemicals)을 추가 정제없이 그대로 사용하였다.
3.2 압축형 복합화약의 제조 및 압축성형
압축형 복합화약은 금속을 원료로 사용하지 않는 PBX-1과 금속을 원료로 사용한 PBX-2를 제조하였으며 그 조성을 Table 4에 원료들의 부피함량으로 나타내었다. 이후 제조된 압축형 복합화약 압착분말은 압축성형을 거쳐 사용하였다.
3.3 특성분석
밀도는 시험화약당 압축성형된 펠렛 25개의 무게, 직경 및 높이를 측정하여 최종적으로 실제밀도 값을 얻었으며 이를 이론최대밀도(TMD)와 비교하여 다성분입자계 적용이 밀도에 미치는 영향을 파악하고자 하였다.
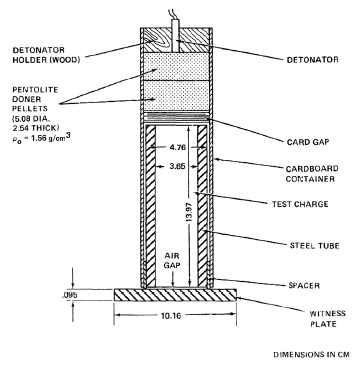
화약에 있어서 가장 중요한 특성인 숔감도는 미국에서 개발된 가장 널리 사용되는 숔감도시험인 LSGT (Large Scale Gap Test)를 통하여 분석하였다[14]. Fig. 6에서 볼 수 있듯이 숔압력원(donor explosives)으로는 pentolite 50/50을, card gap으로는 PMMA (Poly Methylmethacrylate)를, detonator는 비전기식뇌관 NONEL을 사용하여 제조된 시험화약(약 250 g)을 기폭함으로써 반응여부를 결정하고 그 결과를 시험에 사용된 PMMA의 gap 두께(또는 PMMA 카드 장수 또는 숔압력)로 얻으며 카드장수가 적다는 것은 그만큼 시험화약이 숔 압력원에 의해 기폭되기 어렵고 기폭에 필요한 숔압력값도 커야 한다는 것을 말하며 시험화약이 숔에 둔감하다는 것을 의미한다. 반응여부는 증거판에 구멍이 생길 경우를 go(또는 +), 생기지 않는 경우를 no-go(또는 -))로 하여 시험화약당 총 12회 시험하여 +와 –사이의 수렴값을 찾음으로써 최종적으로는 50%의 확률로 폭굉(detonation)되는 시험화약의 숔압을 얻는다. 그 후, 숔감도에 영향을 주는 인자인 입자속도(particle velocity), 숔(shock)의 속도 및 숔의 압력의 불확도로부터 최종적으로 합성측정불확도를 추정하여 위의 얻은 숔압에 대하여 보정해주는 값으로 표시해준다.(숔압력값±불확도추정값으로 표시) 이 때, 신뢰수준은 약 95%, k=2이었다.
각 입자계에 따라 압축형 복합화약의 압축성형과정에서의 입자들의 원형유지정도 및 파괴 정도가 다를 것이라 판단되었으므로 이를 확인하기 위하여 압축성형된 펠렛을 EDC 용매(RDX는 용해되지 않으나 결합제는 용해시킬 수 있음)를 사용하여 RDX만을 추출하여 이를 SEM (FE-SEM, 모델명: QUANTA 650, 제조사: FEI)을 통해 원형유지정도를 확인하였다.
기계적 물성은 Instron사의 UTM-3369 압축시험기를 통하여 압축형 복합화약 펠렛(직경 10 mm, 높이 10 mm)을 압축하면서 압축강도, 압축변형률 및 영률을 측정하였고 시험조건은 압축속도는 약 10 mm/min, 온도 25℃ 및 습도는 50%였으며 결과는 3개 시료의 평균을 취하여 얻었다.
4. 결 과
4.1 밀도
Table 5에 PBX-1 제조에 사용된 RDX 입자의 크기 비, 해당입자들의 부피 비 및 밀도를 나타내었다. 3성분 입자계의 경우는 서론에서 언급한 대로 입자들의 크기 비가 최소 7이상, 그리고 10에 가까울수록 충진에 효율적이므로 이를 최대한 반영하였으며 2성분 및 3성분 입자계에서 각각 0.0004, 0.0003의 표준편차를 갖는 균일한 밀도의 PBX-1 펠렛을 제조하였다. 이 때, 2성분 입자계 (TMD 대비 약 98.35%)에 비하여 3성분 입자계의 밀도가 TMD 대비 약 98.96%로 밀도가 더 증가하였다. Table 6에는 PBX-2의 입자크기 비, 부피 비 및 밀도측정결과를 제시하였는데 이 역시 2성분 및 3성분 입자계에서 각각 0.0003, 0.0005의 표준편차를 갖는 균일한 밀도의 PBX-2 펠렛을 제조하였다. PBX-1과 마찬가지로 2성분 입자계(TMD 대비 약 98.23%)에 비하여 3성분 입자계(TMD 대비 약 98.85%)에서 더 높은 밀도를 갖는 것을 확인할 수 있었다. 이러한 밀도의 차이는 3성분 입자계에 존재하는 가장 작은 입자의 존재로 인하여 생긴 것으로 가장 큰 입자와 중간 크기의 입자가 미처 채우지 못한 작은 공간을 가장 작은 입자가 채워줌으로써 미세하게나마 충진율이 향상되었고 이것이 결국 밀도향상으로 이어진 것으로 보인다. 이러한 밀도상승은 열점의 근원 중 하나인 화약 내부의 공극이 줄어들었음을 의미하며 3성분 입자계가 2성분 입자계에 비하여 좀 더 둔감한 숔감도를 가질 것이라 예상할 수 있다. Table 4에서 알 수 있듯이 PBX-1의 충전재함량은 전체의 약 89%, PBX-2는 약 90%에 달한다. 따라서 이러한 높은 충전재 함량을 갖는 경우에는 그 부피를 채우기 위하여 3성분 입자계를 사용하는 것이 바람직하다는 것을 알 수 있다.
4.2 숔감도
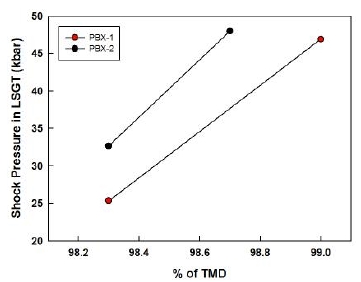
제조된 압축형 복합화약이 숔과 같은 갑작스러운 자극 하에 놓이게 되었을 때 구성입자계에 따라 화약입자들의 훼손된 정도와 공극이 차지하는 비율도 다르기 때문에 다른 숔감도 특성을 보일 것이며 상술한대로 3성분 입자계에서 PBX-1 및 PBX-2 모두 밀도가 2성분 입자계에 비해 높았으므로 감소한 공극률로 인하여 더 둔감한 숔감도를 가질 것이 쉽게 예상되었다. Table 7에 수록된 바와 같이 2성분 입자계 PBX-1을 기폭시키기 위한 LSGT 숔압력은 25 kbar 수준인 반면, 3성분 입자계의 숔압력은 훨씬 큰 46 kbar으로 나타남으로써 2성분 입자계에 비하여 3성분 입자계를 적용한 PBX-1의 숔감도가 80% 이상 둔감해진 것을 확인할 수 있다. PBX-2의 경우에도 2성분 입자계에 비하여 3성분 입자계의 숔압력이 크게 증가함으로써 (Table 8) 숔감도가 매우 둔감함을 알 수 있다. 측정불확도 추정값을 고려하여도 2성분 입자계와 3성분 입자계간 확연한 숔감도 차이가 나는 것을 볼 때 3성분 입자계가 확실히 숔에 둔감함을 알 수 있다. Fig. 7은 PBX-1 및 PBX-2의 밀도에 따른 숔감도를 도시한 것으로 이를 보면, 3성분 입자계를 적용하여 충진율을 향상시킴으로서 밀도가 증가됨과 동시에 열점의 근원인 공극을 감소시켜 숔에 둔감해지는 것을 알 수 있다.
4.3 RDX 입자의 변형
일반적으로 압축형 복합화약에서는 고압 하에서 화약이 압착되므로 어느 정도의 파괴는 불가피하다. 그러나 앞에서 보았듯이 3성분 입자계와 2성분 입자계에서 크게 차이가 나지 않는 밀도에 비하여 숔감도는 확연히 둔감해지는 것으로 미루어 볼 때, 3성분 입자계에서 화약입자들의 손상정도가 2성분 입자계에 비하여 훨씬 적을 것으로 예상되었다. 이에 따라 압축성형된 펠렛을 EDC로 RDX만을 추출하여 RDX 입자들의 원형유지정도를 확인하고자 하였다. Fig. 9는 2성분 입자계로 만들어진 PBX-1에서 추출된 RDX 입자를 보여주고 있는데 평균입경 250 μm의 RDX를 사용하였음에도 불구하고 scale bar인 200 μm에 준하는 크기의 RDX마저도 보이지 않는 것을 확인할 수 있다. 반면, 3성분 입자계로 만들어진 경우는 Fig. 8에서 볼 수 있듯이 전체적으로 큰 RDX입자들도 비교적 덜 파괴되어 있음을 확인할 수 있으며 이로 인하여 더 둔감한 숔감도를 가지는 것으로 판단된다. 따라서 충전재들의 부피함량이 90% 정도로 매우 높은 경우에는 3성분 입자계를 사용하는 것이 바람직하다는 것을 알 수 있다.
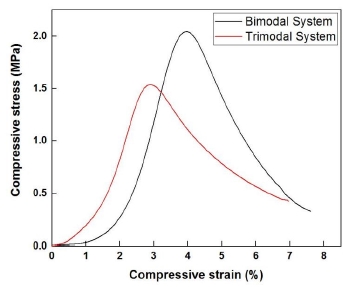
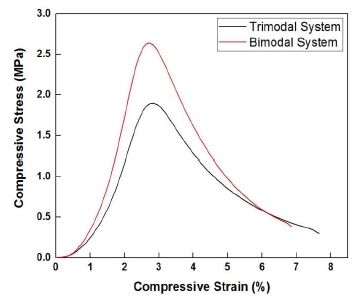
4.4 기계적 물성
제조된 압축형 복합화약 압착분말을 성형하여 얻은 펠렛을 3회의 압축시험을 통하여 압축강도 및 변형률, 영률을 측정한 후, 평균을 취하여 PBX-1과 PBX-2의 응력-변형률곡선을 Fig. 10과 Fig. 11에, 그리고 평균 최대응력, 평균 최대변형률 및 평균 최대영률을 Table 9에 나타내었다. 이를 보면 물성측면에서는 3성분 입자계가 2성분 입자계에 비하여 큰 장점이 없는 것으로 나타나는데 일반적으로 기계적 힘을 받을 때 물질 내부의 미시/거시구조에서 가장 약한 부분이 먼저 끊어지거나 파괴되므로 3성분 입자계의 경우 미세입자 사용으로 인하여 더 복잡한 미세구조 및 더 많은 입자-결합제간의 계면이 존재하게 되고 이것이 가장 약한 부분이 더 많이 생기게 함으로써 기계적 물성에 좋지 않은 영향을 미친 것으로 보인다.
5. 결 론
본 연구에서는 입자계 조절을 통하여 압축 시 입자들의 손상을 방지하고 고밀도의 압축형 복합화약을 제조함으로써 숔감도를 둔감화시키고자 하였다. 이론적으로 완전구형입자의 3성분 입자계에서의 크기별 입자의 점유부피 비는 약 7.4 : 2.7 : 1이므로 최대한 이를 반영하여 본 실험에서는 입자들의 점유부피 비가 약 11 : 4 : 1 (PBX-1) 또는 12 : 4 : 1 (PBX-2)가 되도록 입자계를 구성하였으며 그 결과 3성분 입자계에서 좀 더 밀도가 향상됨을 확인할 수 있었고 입자충진이론이 금속을 포함하거나 하지 않는 모든 경우의 압축형 복합화약에도 충분히 적용될 수 있음을 알 수 있었다. 또한, 밀도향상과 동시에 숔감도가 확연히 둔감해진 것을 확인할 수 있었는데 이는 밀도가 향상됨으로써 열점의 근원 중 하나인 공극이 줄어들었기 때문인 것으로 보인다. 뿐만 아니라 SEM을 통해 분석한 결과, 3성분 입자계에서의 화약입자들의 원형유지정도가 훨씬 양호함을 확인하였으며 이로 인해 3성분 입자계에서 훨씬 둔감한 숔감도를 가지는 것으로 판단된다. 한편, 기계적 특성에서는 3성분 입자계가 특별히 장점을 갖는다고 보기 어려웠고 오히려 더 좋지 않은 기계적 물성을 보였는데, 이는 3성분 입자계에서 2성분 입자계보다 더 많은 충전재-결합제의 계면이 존재하게 되기 때문인 것으로 보인다. 즉, 시편이 기계적 힘에 노출될 때 물질 내부의 가장 약한 부분이 먼저 끊어지거나 파괴되는데 3성분 입자계의 경우 미세입자 사용으로 인하여 더 복잡한 미세구조 및 더 많은 입자-결합제간의 계면이 존재하게 되고 이러한 계면이 가장 약한 부분으로 작용하므로 결과적으로 3성분 입자계에서 더 낮은 압축강도를 보이는 것으로 판단된다.
Nomenclature
| PBXs : | plastic bonded explosives |
| RCP : | random close packing |
| RCPF : | random close packing fraction |
| RDX : | research department explosive |
| TMD : | theoretical maximum density |
| Ψ : | sphericity |
Acknowledgments
논문작성 및 시험에 도움을 주신 이근득 박사님께 감사드립니다.
References
-
Field, J.E., “Hot Spot Ignition Mechanisms for Explosives”, Accounts of Chemical Research, 25(11), p489-496, (1992).
[https://doi.org/10.1021/ar00023a002]

-
Belmas, R., and Plotard, J.P., “Physical Origin of Hot Spots in Pressed Explosive Compositions”, Journal De Physicque IV Colloque, 5(C4), pC4-61-C4-87, (1995).
[https://doi.org/10.1051/jp4:1995406]

- Frey, R.B., “Cavity Collapse in Energetic Materials,” US ARMY BRL-TR-2748, (1986).
- William, D.C.JR., Materials Science and Engineering an Introduction, 7th ed, John Wiley & Sons Inc, New York, N.Y., U.S.A, (2007).
-
Torquato, S., Truskett, T.M., and Debenedetti, P.G., “Is Random Close Packing of Spheres Well Defined?”, Physical Review Letters, 84(10), p2064-2067, (2000).
[https://doi.org/10.1103/physrevlett.84.2064]

-
Kamien, R.D., and Liu., A.J., “Why is Random Close Packing Reproducible?”, Physical Review Letters, 99(15), p155501-1-155501-4, (2007).
[https://doi.org/10.1103/physrevlett.99.155501]

-
Radin, C., “Random Close Packing of Granular Matter”, Journal of Statistical Physics, 131(4), p567-573, (2008).
[https://doi.org/10.1007/s10955-008-9523-1]

-
Scott, G.D., and Kilgour, D.M., “The Density of Random Close Packing of Spheres”, British Journal of Applied Physics, 2(2), p863-866, (1969).
[https://doi.org/10.1088/0022-3727/2/6/311]

-
McGeary, R.K., “Mechanical Packing of Spherical Particles”, Journal of American Ceramic Society, 44(10), p513-522, (1961).
[https://doi.org/10.1111/j.1151-2916.1961.tb13716.x]

-
Fiske, T.J., Railkar, S.B., and Kalyon, D.M., “Effects of Segregation on the Packing of Spherical and Nonspherical Particles”, Powder Technology, 81(1), p57-64, (1994).
[https://doi.org/10.1016/0032-5910(94)02862-1]

-
Liu, S., and Ha, Z., “Prediction of Random Packing Limit for Multimodal Particle Mixtures”, Powder Technology, 126(3), p283-296, (2002).
[https://doi.org/10.1016/s0032-5910(02)00075-x]

- Hofmann, H., and Bowen, P., “Powder Technology from Landslides and Concrete to Avalanches and Chocolate”, World Wide Web location http://ltp.epfl.files/content/sites/ltp/files/shared/Teaching/Master/06-PowderTech-02.pdf/ (2015).
- Glover, P.W.J., Petrophysics MSc Course Notes, Imperial College, London Boroughs, U.K., (2008).
- Donna, P., “Gap Tests and How They Grow,” US NAVY AD-P005-315, (1986).