다상 유동모델과 동적 격자계를 활용한 가스-스팀 발사체계의 열유동과 탄의 운동성능 해석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 수치모사를 통해 탄의 사출관 내부의 열 ⦁ 유체역학적 분석과 탄의 운동성능 해석을 수행하였다. 동적 격자(dynamic grid)를 사용한 해석영역에서 계산이 진행되었고 증발이 완료된 물을 냉각제로 사용하였다. 고온의 공기와 냉각제간의 상호작용 및 유동장을 해석하기 위해, Realizable k-ε 난류 모델과 VOF (Volume Of Fluid) 모델을 선정하고 냉각제 유량변이에 따른 수치 해석을 진행하였다. 해석결과, 사출관의 압력은 냉각제의 유무에 따라 큰 차이를 보였고, 냉각제량에 따라서도 각각의 차이를 보였다. 탄의 속도와 가속도의 변이는 압력에 종속하여 나타났다.
Abstract
In this study, an analysis of the thermo-fluid dynamic and missile-motion performance was carried out through a numerical simulation inside the missile canister. Calculation was made in an analytical volume using dynamic grid and evaporated water was used as a coolant. To analyze the interaction among the hot gas, coolant, and mixture flow, Realizable k-ε turbulence and VOF (Volume Of Fluid) model were chosen and a parametric study was performed with the change of coolant flow rate. As a result of the analysis, pressure of the canister showed a large difference depending on the presence or absence of the coolant, and also showed a dependancy on the amount of coolant. Velocity and acceleration were dependent on the canister pressure.
Keywords:
Gas-steam Ejection, Ejection Canister, Multi-phase Flow, Volume Of Fluid, VOF, Dynamic Grid키워드:
가스 스팀 발사, 사출관, 다상유동, 동적 격자1. 서 론
탄을 발사관 밖으로 사출시키기 위한 방법은 로켓모터 추진력의 일부를 사출에 사용하는 부스터 발사방식(hot launch)과 별도의 동력원을 이용하는 사출발사방식(cold launch)으로 크게 구분된다. 각각의 발사방식은 장단점이 존재하여 유도탄 발사 플랫폼의 상황에 맞춰 적절한 발사방식을 채택한다.
이 중 사출발사는 부스터의 에너지가 아닌 별도 에너지원의 필요로 인한 추가적인 장치 때문에 구조가 복잡해지는 단점이 있으나, 발사초기, 탄의 발사관 이탈에 소모되는 추진기관의 에너지를 절감할 수 있어 그로 인한 유도탄 사거리 증가의 장점을 갖는다. 또한 로켓모터의 화염이 발생하는 부스터 발사방식에 비해 사출발사방식은 부스터의 화염이 없어 발사 플랫폼 및 유도탄의 생존성을 증대시킬 수 있다.
사출발사방식에 쓰이는 별도의 동력원으로는 고체추진제 가스발생기를 주로 사용한다. 그러나 가스발생기에서 생성되는 고온의 가스가 사출관의 벽면과 미사일의 꼬리부에 직접적으로 영향을 미쳐 손상이나 변형을 유발할 수 있어, 사출관과 미사일 아랫부분의 닫힌 공간으로 고온 가스가 도달하기 전에 냉각물질을 혼합시켜 주는 가스-스팀 사출발사방법(gas-steam eject launch method)이 최근에 이르러 효과적인 대안으로 떠오르고 있다.
Edquist와 Romine[1]은 가스-스팀 사출발사방식 연구를 위해 이상기체와 실제 혼합가스 상태를 가정하고 열손실이 포함된 모델을 구현하여 해석을 수행하고, 실제 미사일 사출 실험 데이터와 비교분석하였다. 그리고 10년 후 소형 대륙간 탄도미사일과 잠수함 발사 탄도미사일의 연구개발을 위해 가스 다이나믹 모델을 개발하여, 실제 peacekeeper 탄도미사일 발사 데이터, 소형 대륙간 탄도미사일의 실험 데이터와 비교분석하였다[2]. Edquist의 연구는 실제 실험과 미사일 발사 데이터를 통한 검증으로 신뢰도가 높아 가스-스팀 사출발사와 관련된 많은 연구에서 인용되고 있다. 이러한 높은 정확도의 해석모델은 직접적인 실험을 대신하여 물리현상을 예측할 수 있어 체계개발의 비용을 줄일 수 있는 장점이 있다.
최근에는 상용 CFD 소프트웨어의 발전으로 이를 이용한 가스-스팀 사출발사의 수치해석 연구가 수행되어 오고 있다. Liu와 Xi[3]는 상용 소프트웨어인 Fluent를 사용하여, 3상 유동모델과 동적격자(dynamic grid)로 수치해석모델을 수립한 뒤 사출관의 압력과 탄의 속도, 가속도 등을 실험 데이터와 비교분석하였는데, 상용프로그램으로도 상당히 실험에 근접한 해석결과를 나타낼 수 있음을 알 수 있다.
국내에서도 가스-스팀 사출발사에 대한 연구가 수행된 바 있다. Byun[4]은 Edquist와 마찬가지로 열손실 모델을 적용하여, 발사장치 내부의 열역학적 거동과 유도탄의 동적거동에 대하여 물리적인 모델을 수립하였다. Baek과 Yim[5]은 가스발생기용 저 연소속도 HTPB/AP계 고체추진제의 조성에서 냉각제인 Oxamide와 Melamine이 추진제의 연소특성에 미치는 효과를 고찰하였다. 국내의 경우 추진제와 냉각제의 상호작용에 관한 연구는 지속적으로 수행되고 있는 반면, 추가적인 해석모델 연구와 더불어 연구실 스케일의 실험은 아직 수행된 바 없다.
이번 연구에 앞서 저자들은 적절한 수치해석 방법과 해석모델 채택을 위해 탄이 움직이지 않는 상황을 가정하고 수치해석을 진행한 바 있다[6]. 이전 해석 이래 본 연구에서는 실험 설비구축 이전에 설계관련 데이터를 확보하기 위해, Fluent를 활용하여 다상 유동모델과 동적격자로 해석모델을 수립하여 수치모사하고 그 결과를 고찰하기로 한다.
2. 수치해석 방법
2.1 다상 유동 모델과 지배방정식
본 해석에서는 다상 유동 해석 모델로서 고정된 격자계(fixed Eulerian mesh)에 대해 표면 추적 기법을 사용하여 2개 이상의 상에 대한 경계면 분포를 해석하는 VOF (Volume Of Fluid) 모델을 사용하였다. 해석 시간 증분(Δt)의 제약을 피하고자 음함수(implicit) VOF 모델을 사용하였고, 계면을 구분하기 위한 interface scheme은 compressive 기법을 채택하였다.
VOF 모델의 질량보존식, 운동량 보존식은 다음의 Eq. 1, Eq. 2로 나타낸다. 본 VOF 모델에서 서로 다른 상 사이에서의 질량전달 현상은 고려되지 않기 때문에 질량보존식은 기존의 단상유동모델의 식과 동일하다. 또한 하나의 운동 방정식을 모든 상에서 공유하므로 운동량 보존식도 동일하다.
| (1) |
| (2) |
다상유동모델은 아래의 Eq. 3과 같은 체적분율식이 추가되어 각 상에 대한 구분을 수행한다. 계산의 효율성을 위해 기본상(primary-phase)의 체적분율은 2차상(secondary-phase)에 대한 체적 분율을 먼저 구한 뒤 Eq. 4를 이용하여 구한다. Eq. 4는 모든 상에 대한 체적분율의 합이 1인 것을 나타낸다. 각 식에서 α는 체적분율, 하첨자 q는 상(phase)의 식별인수, n은 고려중인 전체상의 수를 나타낸다.
| (3) |
| (4) |
에너지보존식 Eq. 5에서 에너지는 질량평균식 Eq. 6으로 다루어진다. 에너지 보존식은 운동량 보존식과 마찬가지로 각 상에서 공유된다.
| (5) |
| (6) |
2.2 난류 모델
Realizable k-ε 모델은 난류운동에너지 k와 난류운동에너지 소산율 ε을 풀어 난류유동장을 모사하는 Standard k-ε 난류 모델을 유체의 변형율과 회전율, 와도(vorticity)의 요동(fluctuation)을 고려하여 변형한 모델이다. 이 모델은 Standard k-ε, RNG k-ε 모델에 비해 실제에 근접한 난류유동을 모사한다고 알려져 있다[7]. 본 연구에서는 사출관 형상으로 인해 사출관 바닥면에서 복잡한 유동이 형성 되므로 유체의 변형과 회전을 고려하여 보다 정확한 난류유동을 모사할 수 있는 Realizable k-ε 모델을 사용하였다.
2.3 사출관의 형상과 격자
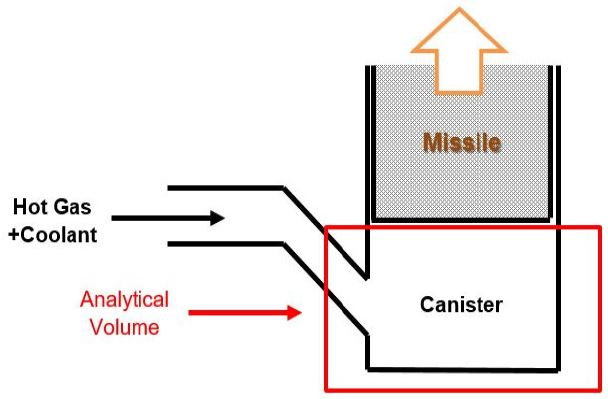
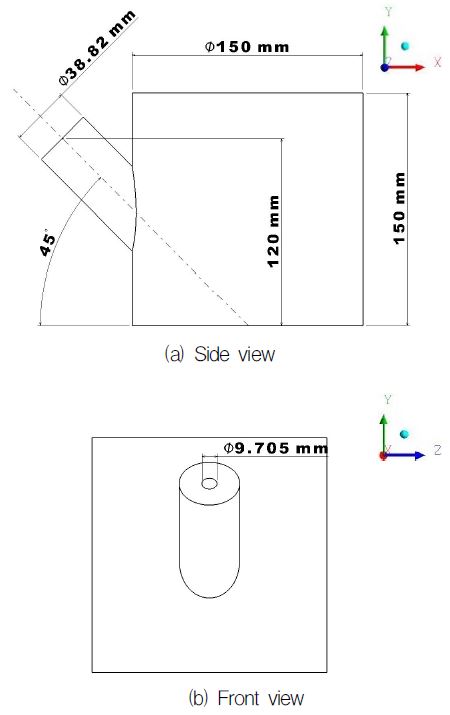
Fig. 1은 가스-스팀 사출발사 방법의 개략도와 해석 영역을 나타낸다. 본 해석에서 고려하는 축소형 모델 사출관은 직경 150 mm, 높이 150 mm의 원통형 구조이고, 유체가 사출관의 하부 중심을 향하도록 45° 기울어진 주입구가 형성되어 있으며, 주입구 직경은 향후 차원해석을 고려하여 사출관 원통 둘레의 1/6에 해당하는 부채꼴의 현과 동일한 길이인 38.82 mm로 Fig. 2(a)에 그 형상을 자세히 나타내었다. 또한, 주입구 직경의 1/4에 해당하는 지름 9.705 mm의 냉각제 입구를 추가하여, 공기(air)와 냉각제 수증기(water-vapor)가 함께 사출관 내부로 분사되도록 하였다.
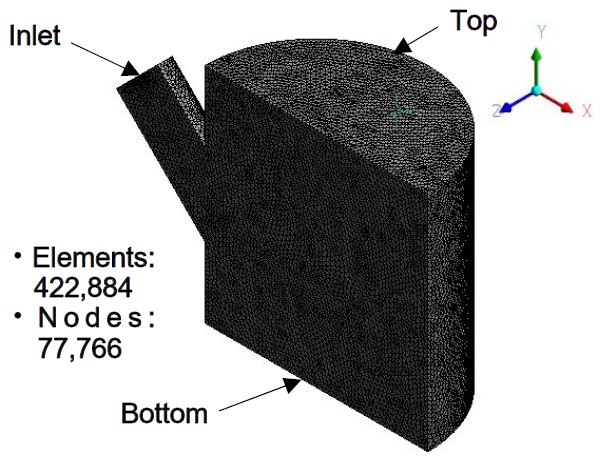
계산을 위한 격자점 생성은 ANSYS mesh editor를 이용하였다. 사출관은 X-Y 좌표면 기준으로 좌우대칭의 형상이므로, 계산의 효율성을 위해 절반의 geometry만 사용하여 격자점을 생성하고 대칭 절단면을 symmetric boundary condition으로 설정하였다. 경사진 주입구에 의해 형성되는 난류유동을 정확하게 모사하기 위해 tetrahedral 격자를 생성하였는데, Fig. 3에 보이는 계산영역 격자계는 약 423,000개 요소와 78,000개의 격자점으로 구성되어있다.
2.4 동적 격자계(dynamic grid system)
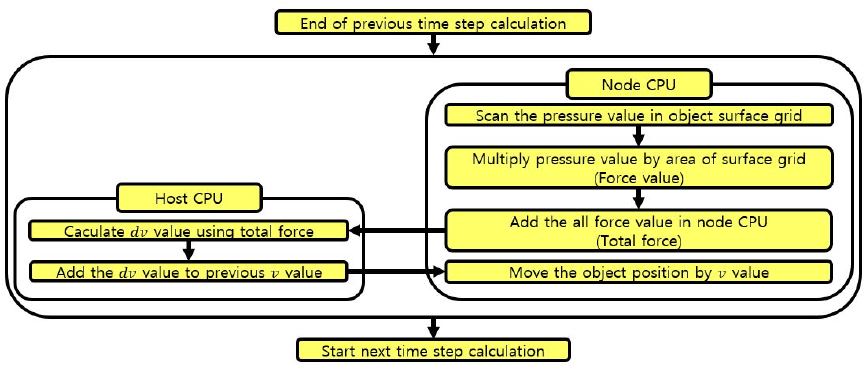
사출관 하부에서 생성되는 압력이 탄의 중량을 극복하고 탄을 움직일 수 있을 때, 사출관 하부 공간의 부피가 증가하기 시작한다. 이는 계산영역이 고정되어있지 않고 확대되는 것을 의미하며 이러한 현상을 모사하기 위해 동적 격자계 설정이 필요하다. 계산영역의 상부경계면을 위로 이동시키는 것으로 탄의 상승을 표현하고 상부 경계면의 속도와 가속도를 계산함으로써 탄의 운동을 예측할 수 있다. 하지만 사출관 하부의 압력에 연동하여 탄의 운동이 변화하므로, 이를 모사하는 별도의 계산 절차(routine)가 필요하다. Fluent는 다중 CPU를 사용하여 계산할 때 Host CPU와 Node CPU를 두고 계산을 진행하는데, 계산영역을 Node CPU 개수만큼 분할한 다음 각각 분할된 영역(partition)에서 연산을 수행한 후 Host CPU가 Node CPU에서 연산된 수치를 모두 통합하여 필요한 값을 도출하게 된다. Fig. 4는 동적 격자계를 이용하면서 탄의 운동을 결정하는 알고리즘을 나타낸다. 과정을 살펴보면, 먼저 이전 time step의 계산이 완료된 후, Node CPU에서 위치를 이동시킬 오브젝트(계산영역의 상부면)의 표면격자에 저장된 압력 값을 모두 참조한 후 각각 해당격자의 넓이를 곱한 뒤 모두 합하여 force를 구한다. 그리고 분할된 영역의 force들을 전부 더하여 total force를 구한 뒤 Host CPU에 전달한다.
| (7) |
| (8) |
Eq. 7은 탄의 속도증분에 대한 식으로, Host CPU는 Eq. 8을 이용, 속도를 현행화(update)하여 Node CPU에 전달하고, Node CPU는 경계면 오브젝트를 속도값에 맞춰 이동시킨다.
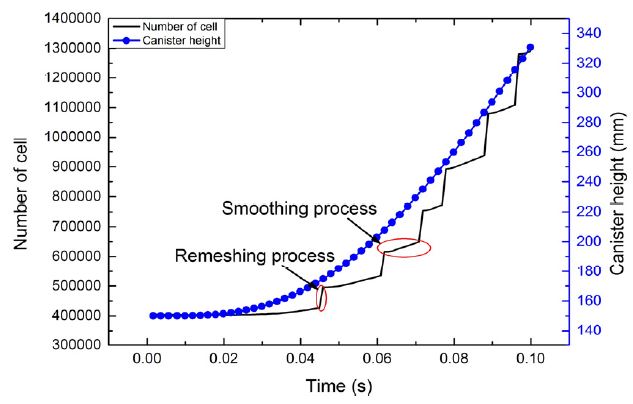
상부면의 이동으로 격자가 변형하면서 smoothing과 remeshing 작업을 수행하게 되는데, Fig. 5는 전술한 작업의 특징을 설명하기 위해 단상유동의 계산과정에서 사출관의 격자수와 높이의 변화를 나타낸 그래프이다. Smoothing은 격자점을 생성 및 재배치하여 제한적으로 격자를 refine 시키는 작업으로서 Fig. 5에서 나타나듯 약간의 격자수 변화가 존재한다. Remeshing은 smoothing만으로 더 이상 격자품질을 유지할 수 없을 때, 전면적으로 격자를 분할하여 재생성시킴으로써 격자품질을 높이는 작업으로, 급격한 격자수 증대를 가져온다.
2.5 해석 방법
해석을 위해 Intel사의 E5-2680 v3 CPU 2개 (CPU당 12개 코어)로 계산을 수행하였다. 상용 소프트웨어인 Fluent를 사용하였으며 압력 기반의 PISO (Pressure Implicit with Splitting of Operator) 해석 알고리즘을 사용하였다. 운동량, 난류 스칼라 값, 에너지 방정식들의 경우 각각 2차 상류차분식의 공간이산화 기법을 사용하였고, 구배 보간법은 셀 기반 최소제곱법, 시간적분 기법은 1차 정확도의 음함수 시간적분법을 사용하였다.
3. 해석 조건
입구를 통하여 1200 K인 고온의 공기와 냉각제 역할을 하는 373.15 K의 수증기를 각각 분사하여 사출관 내부의 수증기의 분포, 압력과 온도의 변화 그리고 그에 따른 탄의 운동성능 변화 등을 해석하였다. 수증기의 경우 주입구 부분에서 증발이 완료된 상태를 가정하여 온도를 설정하였고, 발사체의 운동성능 해석을 위해 탄의 무게를 80 kg으로 가정, 9.81 m/s2의 중력 가속도를 적용하고 외부 대기압을 1 atm으로 설정하였다.
냉각제가 없는 단상(single-phase)유동의 경우(only air)와 냉각제가 있는 이상유동(two-phase)의 경우(air/water-vapor)에서 해석을 진행하였으며, 냉각제의 유량은 공기 유량(0.03 kg/s)대비 5%, 10%, 15%로 설정하여 각각 계산을 수행하였다. Table 1은 상기한 조건들과 초기조건을 정리하고 있다. 모든 계산은 비정상(unsteady) 상태조건으로 이루어졌으며 시간 증분은 1×10-6~1×10-5 s로 최종시간 0.1 s까지 해석을 수행하였다. 수렴기준은 에너지방정식의 경우 10-6 이하, 연속방정식과 운동량방적식, 난류에너지 및 소산율방정식의 경우 10-3 이하의 잔차값으로 설정하였고, 매 시간고정 내부 반복 계산(internal iteration at fixed time step)에서 60 iteration 전후로 수렴하는 것을 확인하였다.
4. 수치해석 결과
압력은 사출관에서 발사되는 탄의 운동성능을 결정하는 중요한 변수로 사출관 하부공간의 온도, 부피와 상호작용하면서 변화한다. Dynamic grid와 연계해서 이러한 상호작용을 계산할 수 있었으며, 사출관 내부의 물리거동을 확인할 수 있는 의미있는 압력데이터를 확보할 수 있었다.
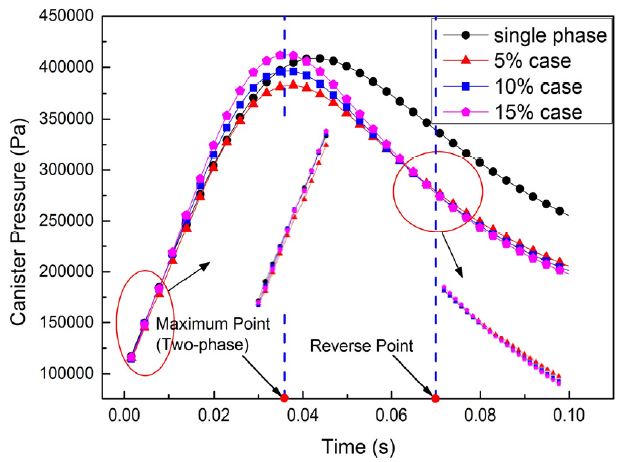
Fig. 6은 전체 계산시간(t = 0.1 s)동안의 압력 변화를 도시하는 그래프이다. 단상유동의 경우와 이상유동의 경우의 압력변이가 확연한 차이를 보이며, 이상유동 사이에서도 냉각제량 증가에 따른 압력의 차이가 나타난다. 이전의 연구[6]에서, 탄이 움직이지 않아 밀폐, 고정된 경우, 냉각제 첨가에 의한 총 질량유량(air + water-vapor) 증가의 영향으로 인해 공간상의 압력과 온도는 이상유동의 경우가 단상유동의 경우보다 크게 증가하는 것을 확인하였다. 본 해석에서는 보다 복잡한 현상이 발생하는데, Fig. 6에서 이상유동은 단상유동보다 더욱 짧은 시간(약 0.036 s)에 최대값에 도달하고, 냉각제의 질량유량이 클수록 압력의 최대값은 더 높다. 또 이상유동의 경우 압력이 최대값 도달 직후 빠르게 감소하면서 단상유동의 그것보다 현격히 낮아지게 되고. 또한 특정 시점(약 0.07 s)이후 이전의 압력 경향이 역전되어 냉각제의 질량유량이 클수록 압력이 더 낮아지는 모습까지 보인다. 경계(혹은 사출관 체적)가 변하지 않는 경우와는 크게 다른 위와 같은 현상은 Fig. 7을 통해 설명할 수 있다. 즉, 탄이 이동하면서 이동 경계를 갖는 사출관에 가스와 함께 냉각제가 유입됨에 따라, 사출관 내부에는 압력증가에 기여하는 냉각제 질량전달 기구와 냉각으로 인한 온도감소를 통하여 압력저하에 기여하는 열전달 기구, 그리고 탄의 움직임으로 발생하는 사출관내 체적의 증가로 압력저하에 기여하는 이동경계 기구 등이 혼재한다. 따라서 사출관 내 압력은 이들 세 가지의 기구들이 서로 경쟁적으로 영향을 주고받으며 비선형적으로 형성되고 변화한다.
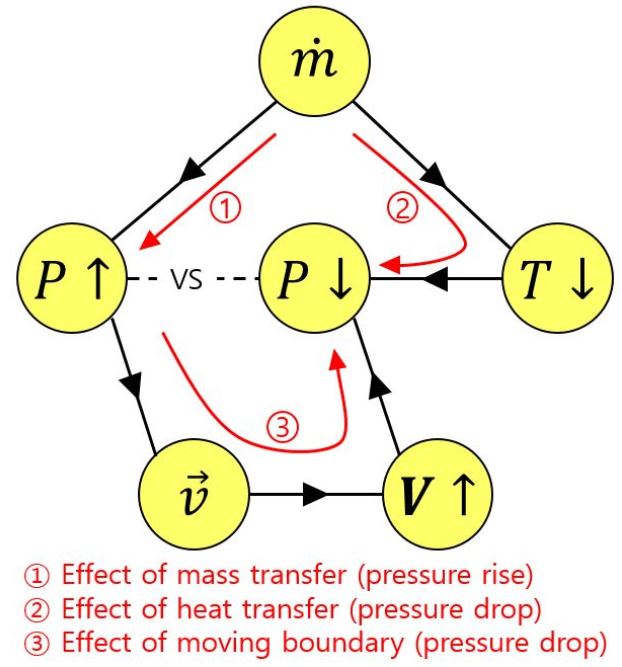
Competitive mechanism affecting the thermodynamic properties change in a canister with moving boundary.
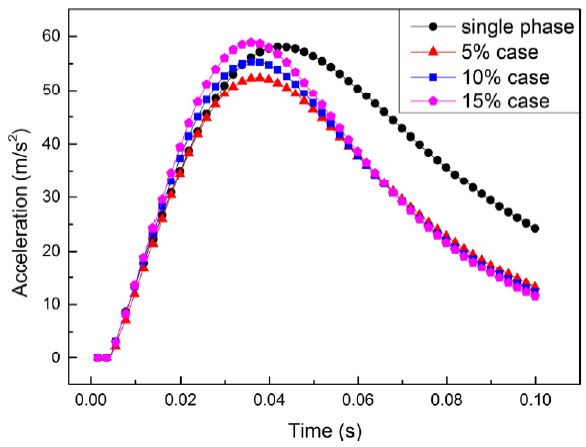
탄의 하부면 넓이와 질량은 변하지 않고 사출관 하부에서 가해지는 압력만 변화하므로 탄의 가속도선도는 사출관의 압력선도와 동일한 형태로 나타난다. Fig. 8은 탄의 가속도를 나타내고 사출관 작동초기의 탄이 움직이기 시작할 때까지의 짧은 기간을 제외하고는 Fig. 6과 유사한 경향을 보인다. 단상유동의 경우 최대가속도 값은 58 m/s2로 나타나고 이상유동 5%, 10%, 15% case의 경우 각각 52 m/s2, 55 m/s2, 59 m/s2의 최대가속도에 도달한다.
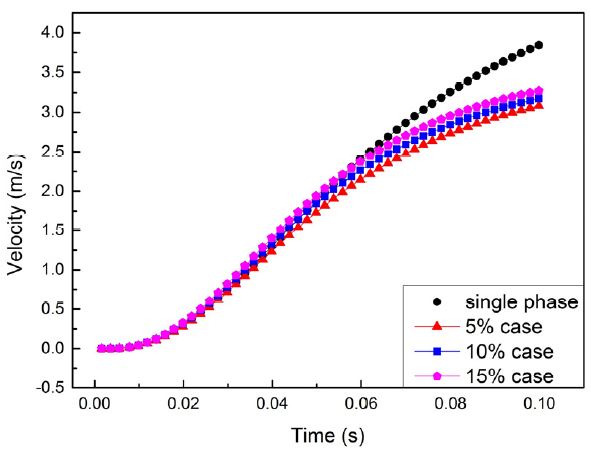
Fig. 9는 탄의 속도를 나타내는 그래프로서 Fig. 8의 가속도 그래프와 연관되어 있다. Fig. 8에서 가속도가 최대값에 도달한 직후 급격히 감소하므로 속도는 가파르게 증가하다가 시간이 지날수록 기울기가 감소하게 된다. 압력과 가속도는 약 0.07 s 이후 냉각제의 질량유량이 클수록 값이 더 낮아지므로, 0.1 s 이상 해석을 진행할 경우 종국에는 속도값이 역전될 수 있음을 예측할 수 있다.
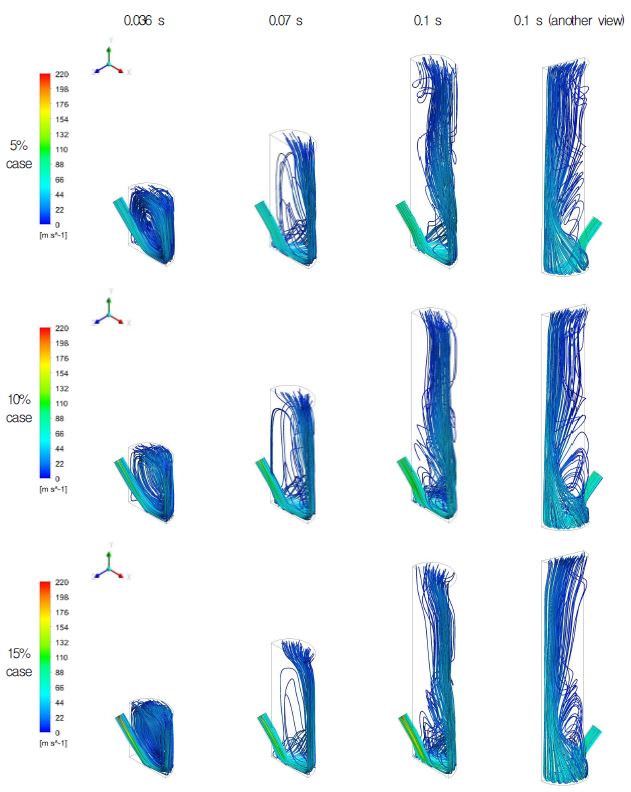
사출관 내부의 냉각제와 온도의 분포는 내부에서 형성되는 유동과 밀접한 연관이 있다. Fig. 10은 압력과 가속도가 최대값에 도달하는 0.036 s에서의 유선과 냉각제량의 영향이 역전되는 0.07 s에서의 유선을 냉각제의 유량증가에 따라 isometric view로 나타내었으며 속력에 따라 유선의 색상에 차이를 두었다. 5%, 10% 15% case에서 냉각제는 각각 최대 117 m/s, 147 m/s, 220 m/s의 속력으로 입구에서 나와 고온의 air와 섞이면서 유동을 형성하는데, 0.036 s에서는 이전 연구[6]와 비슷하게 사출관 전체를 아우르는 순환유동이 생성됨을 확인할 수 있다. 0.07 s에서는 탄의 이동으로 사출관의 부피가 상당히 증가하면서 유동의 흐름이 다르게 나타난다. 주입구로부터 나온 유동은 사출관 바닥면 중앙에 도달한 뒤 방사형으로 퍼지게 된다. 대부분의 유동은 +X 방향의 끝에 있는 사출관 벽면을 따라 수직으로 상승하게 된다. 하지만 일부의 유동은 +X축과 Z축 사이의 방향으로 향하게 되는데, 전술한 유동을 주유동, 후술한 유동을 확산유동이라 할 때, 확산유동은 둥그런 원통의 형상을 띄고 있는 벽면을 따라 주유동과 다시 만나면서 사출관내 유동장을 형성하게 된다. Fig. 10은 또한, 0.1 s에서의 유선도 냉각제의 유량증가에 따라 isometric view를 서로 반대의 위치에서 별도의 view로 나타내고 있다. 그림에서는 위쪽 경계면의 이동과 함께 사출관 부피가 커지면서 유발되는 국소적 압력의 차이와 원통형상의 영향을 받아 초기에 형성되어있던 아래쪽의 순환유동이 사출관 길이 방향으로 신장되어(stretched) 나선형태의 유선을 동반하는 유동구조를 보이고 있다.
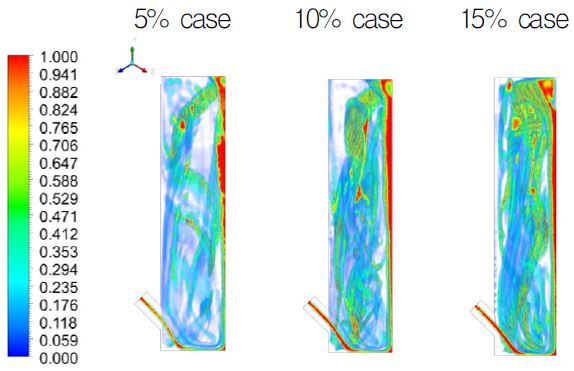
순환유동의 신장으로 만들어지는 나선모양의 유동은 냉각제의 분포에 직접적인 영향을 미친다. Fig. 11에서는 사출관 내부의 냉각제 분포를 확인하기 위해서 volume rendering 기법을 이용하여 0.1 s에서 5%, 10%, 15% case의 냉각제를 각각 표현하고 체적분율에 따라 색상에 차이를 두었다. Fig. 11을 보면 대부분의 냉각제가 우측 끝의 벽면을 타고 올라가 상부에 도달하게 되지만 일부의 냉각제는 나선모양으로 사출관 전체에 퍼지면서 상부에 도달하게 된다. 또한, 냉각제의 질량유량이 증가하면서 계산영역의 상부면(탄의 하부면)에 도달하는 냉각제의 양 또한 증가하는 양상을 보이는데, 이는 유입되는 냉각제의 속도가 증가하면서 탄의 이동보다 빠른 속도로 상부면에 도달하여 냉각제가 누적되는데 기인하는 것으로 판단된다.
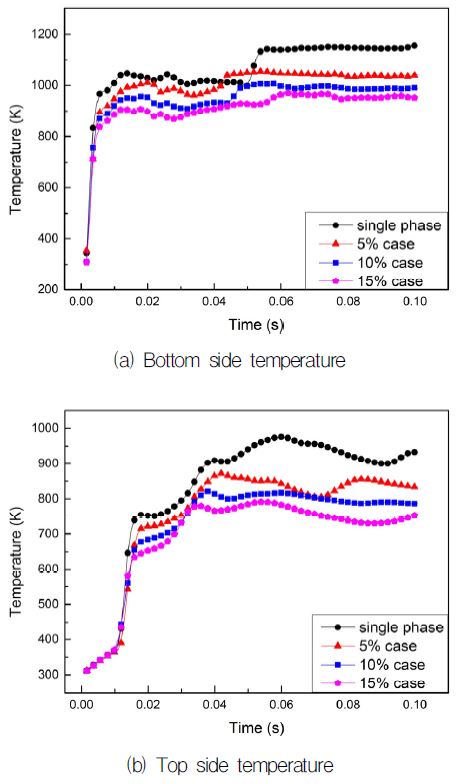
가스-스팀 발사방법의 주 목적은 냉각제로 고온 가스의 온도를 낮춰 탄과 사출관의 열손상을 방지하는데 있으므로, 사출관내 온도분포는 가스-스팀 발사방법 효율의 척도가 되는 중요한 변수이다. 사출관의 하부면은 주입구에서 나온 가스-스팀의 혼합기체가 처음 맞닿는 부분이므로 가장 높은 온도 분포를 보여 사출관의 열손상에 가장 민감한 부분이고, 계산영역의 상부면은 탄의 하부면을 나타내므로 탄에 대한 열손상 가능성을 알 수 있는 부분으로, Fig. 12는 계산영역의 상부면과 사출관의 하부면의 평균온도를 나타내고 있다. 이전 연구[6]에서는 사출관 전체를 아우르는 순환유동으로 인해 사출관 하부면의 초기온도값이 요동(fluctuation)을 나타내는 것을 확인한 바 있다. 탄의 이동을 모사한 본 해석에서는 Fig. 12(a)에서 나타나듯이 초기에 아주 미약한 요동을 보이고 이후에는 균일한 온도를 나타낸다. 이는 탄의 이동과 함께 하부면 근처에서 순환유동의 강도가 약해지기 때문으로 이전 해석과 차이를 보이는 부분이다. 계산영역 상부면의 온도분포를 나타내는 Fig. 12(b)에서는 파장이긴 요동이 나타나는데, 이는 Fig. 7에서 기술하였듯이 혼합기체의 질량전달, 냉각제의 열전달, 사출관 체적의 증가 등이 열역학 상태량(p, m, V, T)에 경쟁적으로 서로 영향을 주고받으며 발생하는 비선형적 현상으로 판단된다. 이전 해석에서는 밀폐, 고정된 영역에서의 계산으로 인해 냉각제량이 증가할수록 오히려 냉각제가 없는 경우 보다 온도가 높아지는 현상을 보였는데, 본 해석에서는 Fig. 12에서 보듯 냉각제량에 비례한 온도 감소 효과를 나타내었다. 다만 이상유동의 최대압력값 도달 시간이 단상유동보다 빠르고, 상부면 온도의 요동효과로 인해 냉각제량에 비례하지 않는 온도값이 잠시 나타나긴 하지만 0.1 s에 가까워질수록 냉각제량 증가에 따른 냉각효과가 확실히 나타내는 것을 확인할 수 있다.
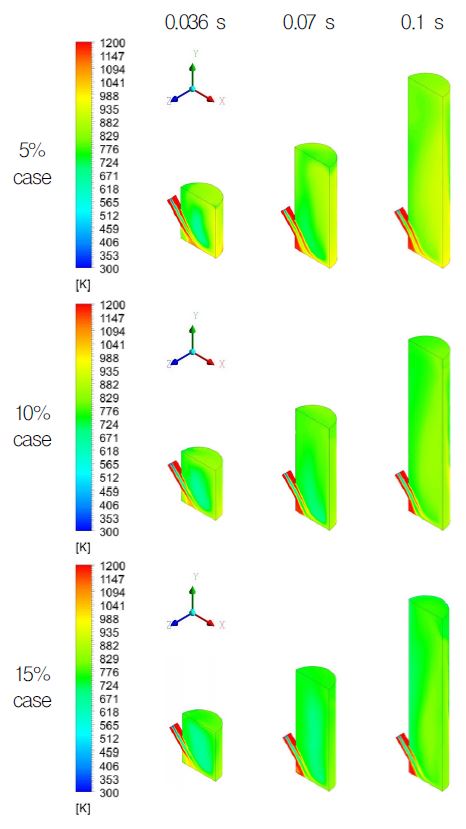
Fig. 13은 좌측에서부터 시간변화에 따라 0.036 s, 0.07 s, 0.1 s에 해당하고, 종방향으로는 냉각제 유량 증가에 따라 5%, 10%, 15%에 해당하는 사출관 내부의 온도분포를 isometric view로 나타내었고 이를 통해 유선과 온도분포의 상관관계를 확인할 수 있다. 5% case의 0.036 s, 0.07 s에서는 X-Y 평면 관점 기준 우측의 벽면부분에서 사출관 중심부에 비해 높은 온도 분포를 보이는데 이는 고온 혼합기체의 주유동이 벽면을 따라 흐르기 때문이다. 0.1 s에서는 나선유동으로 인해 이전 시점보다는 다소 공간적으로 균등하게 온도분포가 나타난다. 10%, 15% case에서는 냉각제 유량 증가에 따라, 상기한 온도차이가 줄어들고 전체적으로 온도분포가 균등하게 이루어지는 것을 확인할 수 있다. X-Y 평면 관점에서 좌측 하단부분의 온도 분포를 보면, 주입구에서 나오는 고온의 혼합기체로 인해 온도가 바깥으로 전파되지 않고 와류유동 영역에 갇혀있는 상태를 보인다. 결과적으로 사출관 하단의 구석부분에서는 고온상태를 계속 유지하여 냉각효과를 기대할 수 없게 된다. 이는 실제 설계에 있어서 반드시 고려해야 할 사항으로 판단된다.
5. 결 론
가스-스팀 발사체계 개발을 위한 사출관 실험 설비구축에 앞서 설계관련 기초데이터를 확보하기 위해, Realizable k-ε 난류 모델과 VOF 모델, 동적격자계를 사용하여 단상유동과 이상유동 해석을 수행하였고 사출관 내부에서 형성되는 유동과 압력변화, 탄의 가속도 및 속도의 변화, 냉각제의 거동 등을 분석하였다.
해석결과, 압력은 이상유동이 단상유동에 비해 빠르게 최대압력값에 도달한 뒤 급격히 줄어들어 종국에는 단상유동보다 낮은 압력값이 나타났다. 또한 이상유동끼리 비교하였을 때, 총 질량유량의 영향이 지배적으로 작용하여 냉각제량이 클수록 압력이 높았으나, 0.07 s 이후에는 냉각제량이 증가할수록 압력이 낮아지는 모습을 보였다. 탄의 가속도는 사출관내 압력에 종속적이므로 가속도의 변이선도는 압력의 그것과 같았고, 속도는 단상유동일 경우 가장 크게 나타나고 이상유동의 경우 냉각제의 질량유량이 클수록 높은 값을 보였다. 유동은 유입구에서 혼합기체가 나와 방사형으로 퍼진 이후 경계면의 이동으로 인한 체적증가와 사출관 형상에 기인하는 복잡한 흐름으로 나선모양의 상승유동을 형성하는 것을 확인할 수 있었다. 냉각제는 그러한 나선유동을 따라 사출관 전체에 분포되는 모습을 보였다. 온도는 체적이 변하는 사출관내에서 질량전달 및 열전달의 경쟁적 기구(competitive mechanism in mass and heat transfer)에 기인하는 비선형성으로 인하여 냉각제량에 비례하는 온도감소효과가 나타나지 않는 구간이 존재하였으나, 0.1 s에 가까워질수록 냉각제에 비례한 확실한 냉각효과를 보였다. 또한 공간상으로는 주유동의 흐름을 따라 열전달이 이루어짐을 관찰할 수 있었고, 사출관 하부의 와류유동 영역에서 온도가 감소하지 않는 부분을 발견할 수 있었다.
본 연구를 통해 Dynamic grid 활용 기법을 확립하고, 향후 추가적인 수치해석 또는 사출관 실험설비 구축에 필요한 기초데이터를 확보할 수 있었다. 그러나 증발과정에 대한 모델링을 생략하였기 때문에 향후 실제에 가까운 열전달 해석을 위해 증발효과를 추가한 해석모델을 개발하고 그에 대한 심도있는 수치계산을 진행할 필요가 있다.
Nomenclature
| E : | energy |
| Eq : | energy of phase |
| F : | force |
| : | gravity vector |
| k : | thermal conductivity |
| keff : | effective thermal conductivity |
| m : | mass |
| i,air : | inlet air mass flow rate |
| i,vapor : | inlet vapor mass flow rate |
| n : | total number of phase |
| p : | pressure |
| t : | time |
| t0 : | initial time |
| T : | temperature |
| Ti,air : | inlet air temperature |
| Ti,vapor : | inlet vapor temperature |
| v : | velocity |
| vt : | velocity at current time |
| vt-Δt : | velocity at previous time |
| : | velocity vector |
| : | velocity vector of phase |
| : | symmetric velocity vector |
| V : | volume |
| α : | volume fraction |
| αq : | volume fraction of phase |
| Δt : | time difference |
| μ : | friction coefficient |
| ρ : | density |
| ρq : | density of phase |
Acknowledgments
이 연구는 국방과학연구소(ADD-14-01-08-11)의 지원을 받아 수행된 연구임.
References
- Edquist, C.T., and Romine, G.L., “Canister Gas Dynamics of Gas Generator Launched Missiles”, 16th Joint Propulsion Conference, Hartford, C.T., U.S.A., AIAA 1980-1186 Jun. 1980.
- Edquist, C.T., “Prediction of the Launch Pulse for Gas Generator Launched Missiles”, 24th Joint Propulsion Conference, Boston, M.A., U.S.A., AIAA 1988-3290 Jun. 1988.
-
Liu, Y., and Xi, A., “An Interior Trajectory Simulation of the Gas-steam Missile Ejection”, Journal of Computers, 8(5), p1321-1326, (2013).
[https://doi.org/10.4304/jcp.8.5.1321-1326]

- Byun, J.R., “Analytical Study on the Launching System with gas Generator”, Journal of the Korean Society of Propulsion Engineers, 5(3), p52-59, (2001).
- Baek, G.H., and Yim, Y.J., “Coolant Effect on Gas Generator Propellant”, Journal of the Korean Society of Propulsion Engineers, 9(2), p1-8, (2005).
-
Kim, H.M., Bae, S.H., Park, C.H., Jeon, H.S., and Kim, J.S., “Thermo-fluid Dynamic Analysis through a Numerical Simulation of Canister”, Journal of the Korean Society of Propulsion Engineers, 21(1), p72-83, (2017).
[https://doi.org/10.6108/kspe.2017.21.1.072]

- ANSYS, Inc., ANSYS FLUENT 14.5 Theory Guide, (2012).