FOD로 인한 로터블레이드 파손이 천음속 축류압축기의 유동 특성에 미치는 영향에 대한 수치적 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
FOD(Foreign Object Debris)는 외부에서 유입되는 물질 중, 엔진 부품을 크게 파손시킬 수 있는 물질을 의미한다. FOD는 크기와 재질이 다양하고, 충돌 조건을 특정하기가 힘들다. 그러므로 본 연구에서는 NASA Stage37 축류압축기 모델을 2가지 가정을 통해 FOD에 의한 파손 형상을 특정화하여 모든 로터블레이드가 동일하게 파손된 압축기의 전산해석을 진행하였다. 결과적으로, FOD에 의해 파손된 압축기는 질량 유량, 전압력비, 최대효율이 감소하였다. 블레이드의 파손은 로터 앞전 궁형충격파를 발생시키고 스테이터 후류의 박리영역이 넓어지게 하며, 서지에 빠르게 도달하도록 유도한다.
Abstract
Foreign Object Debris(FOD) refers to a material that may damage engine parts. FODs vary in size and material, and collision conditions cannot be specified. Therefore, in this research, the NASA Stage37 axial compressor FOD damaged model was specified through two assumptions, and CFD was conducted. The axial compressor damaged by FOD decreases mass flow rate, total pressure ratio, and maximum efficiency. The breakage of the blade induces a bow shock wave in front of the rotor, widens the area of stator trailing edge separation, and it promotes a compressor to reach surge point more quickly.
Keywords:
Axial compressor, Foreign Object Debris(FOD), Computational Fluid Dynamics, Performance Curve키워드:
축류압축기, 전산 해석, 성능 곡선1. 서 론
터보제트 엔진은 외부의 공기를 압축하여 연소시킨 후 노즐을 통해 분사하는 형태로 프로펠러를 이용한 항공기 엔진에 비해 더 높은 속도를 낼 수 있는 장점이 있다. 하지만 이러한 구조상의 문제로 외부 물질 유입에 의한 결함에 취약하며, 작동환경에 영향을 많이 받는다. 외부 물질에 의한 피해는 조류 충돌(Bird Strike)에 의한 블레이드 변형 결함, 블레이드를 마모시키는 erosion, 유분에 점착되어 부품 표면에 가루가 쌓이게 되는 fouling, 부품을 직접적으로 파손시키는 FOD(Foreign Object Debris) 등이 있다.
조류 충돌은 최근 김기하 등[1]이 터보팬 엔진 블레이드의 비선형 조류 충돌 해석 이후 팬 블레이드 파손과 변형 정도, 진동안정성에 대해 연구한 사례가 있다. Erosion과 fouling은 엔진이 특정 환경에 오래 노출된 경우에 발생하며, 변형 정도가 크지 않아 Tabakoff[2]의 입자 추적(particle tracking)과 같은 방법을 통해 파손 형상을 예측할 수 있다. 또한, Chen[3]과 Aldi[4]의 연구와 같이 압축기 표면 거칠기를 수정하는 방법 등의 특정 방법을 통해 유동해석을 진행한 선행 연구 사례가 다수 존재한다.
FOD에 의한 파손은 사례가 가장 많을 뿐 아니라 대형 사고로 이어질 확률이 매우 높으므로 FOD에 의한 엔진파손에 의한 사고 진단과 대처는 중요하다. Hussin[5]은 Aircraft Transport Safety Board(ATSB)가 조사한 자료에서 FOD에 의한 엔진 손상 중, 항공기 운항에 영향을 크게 주진 않더라도 회항하거나 이륙이 제한되는 경우가 약 80%이라는 점을 지적하였다. 그러므로 FOD로 인한 엔진의 손상은 승객의 안전사고와 항공기 운항의 기계적 결함에 의한 손실만 야기하는 것이 아니라 항공사들의 경제적인 피해 원인 중 하나로 작용한다.
FOD는 그 위험성으로 인해 오랜 기간 다양한 분야에서의 선행 연구사례가 존재한다. 신동진 등[6]은 FOD의 인적요인 사례를 조사하고, 인적요인에 의한 FOD 발생을 줄이기 위한 방안을 제시하였다. 강명수 등[7]은 축류압축기 블레이드가 외부 물질에 의해 파손되었을 때 터빈 부품에 미치는 2차적인 손상이 열 차폐 성능을 저하시키는 점을 지적하고 실제 사례 등을 소개하였다. Witek 등[8]은 FOD로 인하여 V형태로 파손된 블레이드를 실험을 통해 파손된 부분이 공명을 야기하여 파손 부위가 블레이드 내부에 추가적 균열을 유발하는 것을 확인하였다. Marandi 등[9]은 FOD로 인하여 앞전이 파손된 블레이드의 구조적인 분석을 진행하여 파손 정도에 따른 부품의 응력이 집중되는 곳의 위치를 특정하였다. Xu 등[10]은 외부로부터 유입되는 물체의 충돌각도와 속력에 따라 티타늄으로 제작된 블레이드가 파손되는 형태를 구조해석과 실험을 통해 제시하였다. Li 등[11]은 블레이드의 앞전이 FOD와 충돌하여 변형이 일어났을 경우 유동의 변화와 진동이 어떻게 발생하는지 수치적 계산을 통해 확인하였다.
FOD는 그 종류와 관계없이 흡기가 존재하는 엔진에 가장 높은 비율로 충돌하며, 충돌 시 엔진에 치명적인 피해를 초래한다[5]. 하지만 FOD로 인한 엔진파손은 충돌 조건과 외부 물질의 재질이 정해져 있지 않으므로 파손 위치와 형상을 특정하기가 쉽지 않다. 이러한 이유로 선행 연구는 이미 파손된 블레이드의 구조적인 해석을 진행하거나, 위와 같은 FOD 유입 조건 중 하나를 지정하여 실험적으로 파손 형태를 조사하는 것이 일반적이며 공력 성능을 해석한 연구 사례는 부족하다.
본 연구에서는 FOD에 의해 파손된 로터 블레이드의 형상을 몇 가지 가정으로 특정하여 다양한 크기의 파손이 축류압축기 유동 특성에 어떠한 영향을 미치는지 살펴보고, 이로 인해 발생하는 성능 변화 정도를 알아보기 위해 수치적 방법을 이용해 연구를 수행하였다.
2. 전산 해석
2.1 압축기 모델 선정
본 연구에서는 FOD에 의한 로터의 파손이 스테이터 유로(Passage)에 어떤 변화를 가져오는지 확인하기 위해 NASA Stage 37 [12] 모델을 선정하였다. Stage 37은 하나의 로터와 하나의 스테이터로 구성된 1단 축류압축기로서 NASA에서 다단 압축기의 첫 단에 사용하기 위하여 설계되었다. Stage 37은 축류압축기 중 형상이 공개되어 오랜 기간 다양한 연구에서 이용되어 왔으며 본 연구에서는 Stage 37을 전산해석을 위한 기준 모델로 선정하였다. Fig. 1은 Stage 37의 자오면(Meridional line)을 나타낸 것이다. 전산해석을 수행하기 위한 압축기 3차원 모델의 설계조건을 Table 1에 정리하였다. Stage 37은 천음속 축류압축기로 블레이드 팁에서의 속도는 마하수 1이상의 값을 가지며, 17186 rpm의 회전속도를 가진다. 36개의 로터 블레이드와 46개의 스테이터 블레이드로 구성되어 있으며 설계압축비는 2.05, 효율은 0.842이다. 해당 조건을 바탕으로 제작한 NASA Stage 37의 3차원 모델을 Fig. 2에 나타내었다. 전산해석은 상용 전산해석 프로그램 CFX 18.0을 이용하였다. 작동유체는 이상기체(Ideal gas air)로 가정하고, 난류모델은 k-ε standard, 난류강도는 5%의 조건으로 하였다. 또한, 1단 압축기를 지나는 유동의 온도는 큰 폭으로 변화하지 않으므로 밀도와 점성은 대기압을 기준으로 고정된 값을 사용하였다.
2.2 격자 의존도 테스트
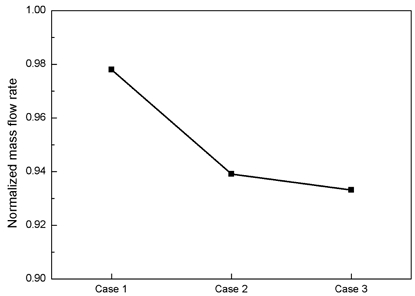
전산해석을 진행하기에 앞서, Stage 37의 3차원 모델의 격자 의존도 테스트를 진행하였다. 난류 모델은 k-ε standard 모델을 채택하였으며 격자는 30 < y+ < 300의 벽법칙 조건을 만족하도록 생성하였다. 격자를 약 70만개씩 증가시키며 case 1, case 2, case 3의 3가지로 나누어 격자의존도 테스트를 진행하였다. Table 2에 case별 격자 개수를 나타내었다. 각각의 격자를 이용한 전산해석을 진행하고 서지점(Surge point)에서의 무차원 질량유량(Normalized mass flow rate)을 비교하였다. 무차원 질량유량()의 관계식은 아래 Eq. 1에 나타내었다.
| (1) |
서지점(Surge point)에서의 질량유량은 case 1에서 0.978, case 2에서 0.939 case 3에서 0.933값을 얻었다. Fig. 3는 서지점에서의 질량유량을 격자수 별로 비교한 그래프를 나타낸 것이다. 질량유량은 case 1과 case 2의 오차가 약 4.15%로 1%보다 큰 값을 보였고, case 2와 case 3의 오차는 약 0.64%으로 1% 이하의 오차를 보였다. Fig. 3의 결과 비교에서 볼 수 있듯이, case 2 수준의 격자를 채택하여 성능해석을 진행하여도 해석 결과 오차가 미미한 수준이므로 이후 계산에서는 약 146만개의 수준의 격자수를 기준으로 모델링하였다.
2.3 검증(Validation)
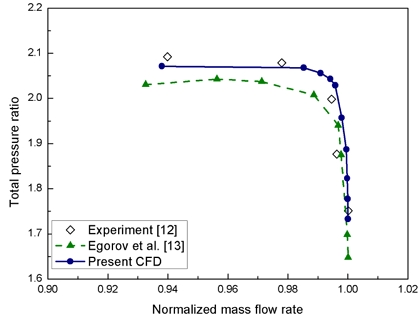
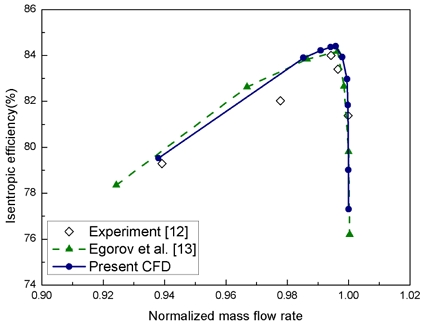
본 연구에서는 수치 검증을 위해 NASA의 실험데이터[12]와 Egorov[13]의 전산해석 결과를 참고하여 성능 계산을 진행하였다. Fig. 4와 Fig. 5는 각각 질량유량에 대한 전압력비(PR)와 등엔트로피 효율(η)을 Stage 37의 실험데이터[12] 및 Egorov의 전산해석 결과[13]와 본 연구의 전산해석 결과를 함께 비교하여 나타낸 그래프이다.
질량유량에 대한 전압력비를 나타낸 Fig. 4에서 본 연구의 전산해석 결과는 Egorov[13]의 전산해석 결과에 비해 질량유량 전 구간에서의 전압력비와 서지점에서의 질량유량 값이 NASA의 실험값[12]에 좀 더 가까운 결과를 보인다. Fig. 5는 질량유량 대 등엔트로피 효율 그래프를 나타낸 것으로, 본 연구에서 수행한 Stage 37 검증 결과는 실험값[12] 및 참고문헌의 전산해석 결과[13]와 매우 유사한 결과를 얻었다. 사용된 전압력비(PR)와 등엔트로피 효율(η)의 관계식을 Eq. 2와 Eq. 3에 나타내었다.
| (2) |
| (3) |
2.4 파손 모델
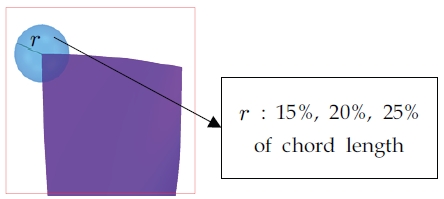
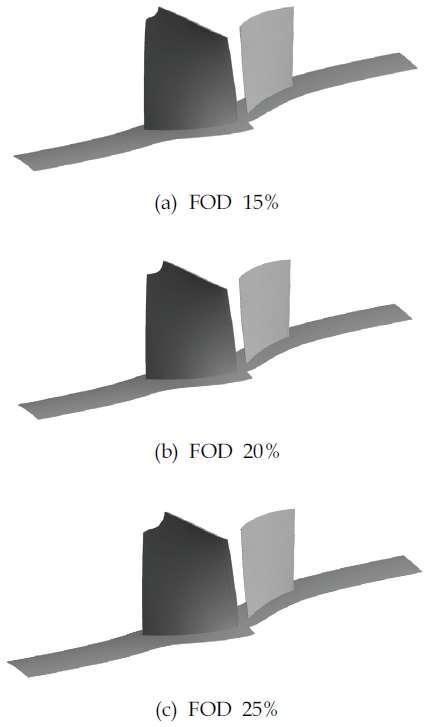
FOD에 의한 손상은 그 파손형상을 정확하게 결정하는 것이 불가능하므로 파손모델을 결정하기 위한 몇 가지 가정이 필요하다. 파손 형상을 결정하기 위하여 Xu[9]와 Duo[14]의 실험 결과를 참고하였다. 외부로부터 유입된 물질은 압축기의 블레이드 앞전에 충돌하는 경우가 많다는 점과[14], FOD가 350 m/s 이상의 속도로 블레이드 앞전과 충돌하였을 경우 손상부위가 충돌물체와 동일한 형상으로 완전히 뜯겨 나간다는 점[9]을 참고하여 파손형상을 결정하였다. 또한 외부로부터 유입된 FOD가 가장 먼저 충돌하는 로터에만 손실이 일어났을 경우를 고려하였다. 압축기로 외부물질이 유입되었을 경우 고속으로 회전하는 블레이드의 특성상 FOD와 충돌 시 여러 개가 손상되며[6], 본 계산에 적용할 방식의 특성상 일부의 블레이드에 손상모델을 적용하기가 어려운 문제로 인해 로터 블레이드 전체에 동일한 손상이 일어난 경우로 가정하였다. 이러한 조건으로 FOD에 의해 손상된 압축기의 모델은 구형물체가 블레이드와 충돌하여 앞전 팁이 손상된 형태로 결정하였으며, Fig. 6에 그 파손형상을 나타내었다. 구형물체의 반지름은 로터 중간 단면 코드길이의 15%, 20%, 25% 크기로 가정하여 3가지 파손모델을 선정하였다. 스테이터의 형상과 격자생성 조건은 모든 파손모델에서 동일하다. 위와 같은 조건으로 제작된 모델의 전체적인 형상을 Fig. 7에 나타내었다.
3. 결과 및 고찰
3.1 성능변화
결함이 없는 압축기와 FOD로 인해 파손된 압축기의 전산해석은 앞서 수행한 검증(Validation)과정과 동일한 경계조건으로 진행하였다.
해석에 사용된 작동유체는 이상기체 공기(Ideal air)이며, 그 물성치를 Table 3에 정리하였다. 기준값(Reference value)으로는 대기압인 101.325 kPa, 288.15 K 조건을 부여하였다.
축류압축기의 공력성능을 판단하기 위해서 질량유량 대 전압력비 그래프와 질량유량 대 등엔트로피 효율 그래프를 Fig. 8과 Fig. 9에 각각 나타내었다. Fig. 8은 x축이 보정된 질량유량(Corrected mass flow rate)이며, y축은 전압력비를 나타낸 성능 그래프이다. Eq. 4에 보정된 질량유량() 관계식을 나타내었다.
| (4) |
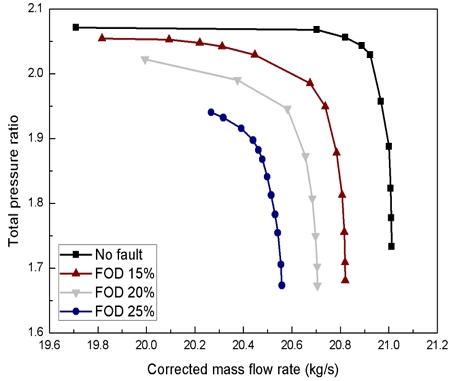
Fig. 8로부터 파손모델은 결함이 없는 정상모델(No fault model)과 비교해서 질량유량과 전압력비 모두 감소하고, 손상도가 클수록 서지(Surge)에 빠르게 도달함을 확인할 수 있다. 최대 압력비를 가지는 서지점에서의 보정 질량유량값은 정상모델에서 19.71 kg/s이며, 파손모델은 FOD 15%, 20% 25%이 각각 19.82 kg/s, 19.99 kg/s, 20.27 kg/s의 값을 가진다. 전압력비는 정상모델이 2.074, 파손모델이 FOD 15%, 20% 25% 순서로 2.054, 2.023, 1.940의 값을 가진다. 위에서 언급한 바와 같이 FOD로 파손된 압축기는 결함이 없는 정상모델에 비해 빠르게 서지에 도달하게 되기 때문에 이 현상 또한 서지점의 압축비 감소와 질량유량 증가에 영향을 미치는 것을 확인할 수 있다.
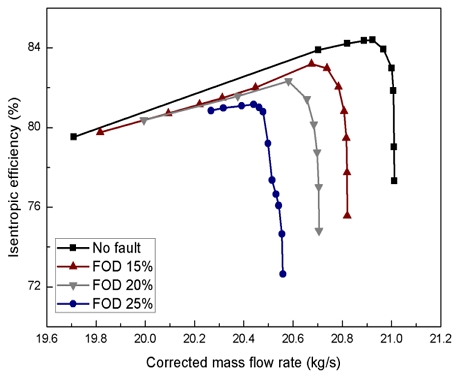
Fig. 9는 질량유량 대 등엔트로피 효율을 나타내는 그래프로, 파손 정도에 따라 최대 효율이 감소한다. 결함이 없거나 작을수록 서지가 더 낮은 질량유량에서 일어나므로, 최대 효율점과 서지점에서의 효율 차이는 파손정도가 작아질수록 더 커지는 것을 볼 수 있다.
Table 4에는 최대 등엔트로피 효율을 가지는 지점에서의 정상모델 및 파손모델의 등엔트로피 효율, 질량유량, 전압력비 값을 비교하였다.
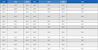
Isentropic efficiency, corrected mass flow rate and total pressure ratio at the highest isentropic efficiency point.
최대 등엔트로피 효율은 정상모델에서 84.40%를 나타내었고 FOD 15%, 20%, 25% 파손모델에서 정상모델과는 각각 1.42%, 2.44%, 3.84%의 차이를 보였다. 이때의 보정 질량유량은 정상모델이 20.92 kg/s로, FOD 15%, 20%, 25% 파손모델이 정상모델과 각각 1.15%, 1.63%, 2.29%의 차이를 보였다. 압축비는 정상모델이 2.029의 값을 가지며 파손모델은 정상모델과 비교하여 각각 2.17%, 4.09%, 6.51% 더 낮은 값을 보여 다른 성능과 비교할 때 압축비가 비교적 더 큰 폭으로 감소하는 것을 확인 할 수 있다.
3.2 유동변화
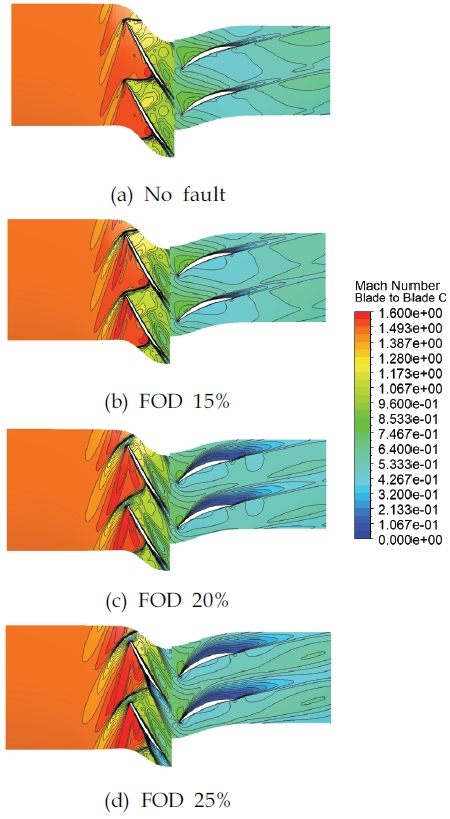
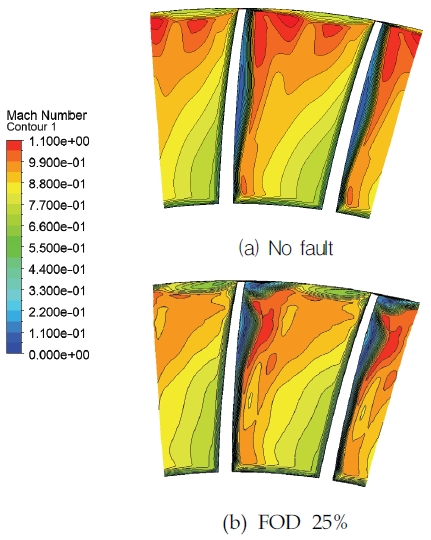
Span 95%에서의 상대 마하수 분포를 Fig. 10에 나타내었다. Fig. 8의 성능곡선을 통하여 FOD로 인해 파손된 블레이드는 같은 압축비에 도달하지 못하는 경우가 있으므로 FOD 25% 파손모델 서지점의 경계조건과 동일한 출구 정압조건에서 4가지 모두 비교하였다. 결함이 없는 정상 압축기모델과 FOD 파손모델간의 큰 차이 중 하나로 파손이 일어나지 않은 블레이드는 빠른 속도로 회전하면서 경사충격파가 생기는 반면, FOD 파손모델의 블레이드는 형상변화로 인해 궁형충격파가 형성된다. 파손 정도가 클수록 앞전의 형상은 상대적으로 두꺼운 블레이드의 중심부로 이동하게 되어 궁형충격파는 앞전으로부터 더 멀리 떨어진 곳에 생성되는 것을 확인 할 수 있다. 이러한 변화는 궁형충격파로 인해 블레이드와 충격파 사이에 유속이 급락하여 마하수가 1 이하로 내려가는 영역이 넓어지는 원인이 된다. 파손정도에 따른 유동 변화를 비교하기 위해 Fig. 10(a)∼Fig. 10(d)를 살펴보면, FOD 15% 파손모델의 마하수 분포에서 스테이터에 나타나는 박리 및 후류영역이 파손 모델 중에서 가장 좁으며 로터 흡입면의 충격파 영향을 가장 적게 받는다. 하지만 결함이 없는 모델과 비교하였을 때 앞전 충격파에 의해 속도가 저하되는 영역이 상대적으로 더 크며, 충격파가 인접한 블레이드의 흡입면에 충돌하는 위치도 차이를 보인다. 로터 블레이드 사이의 속도가 저하되는 영역은 파손 정도가 커질수록 넓어진다. 이와 같은 유동 변화가 로터와 스테이터 뒷쪽 박리영역을 넓히는 원인으로 작용하여 압축비가 감소한다.
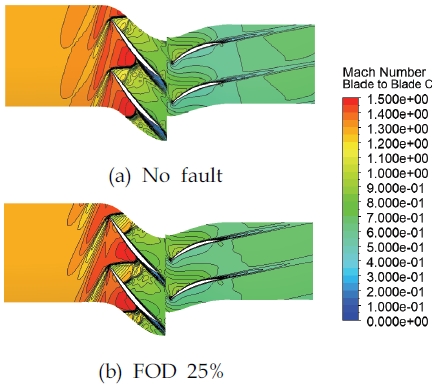
Fig. 11은 결함이 없는 모델과 FOD 25% 모델의 span 50%에서의 상대 마하수 분포를 나타낸 것이다. 앞서 언급한 바와 같이 해당 위치의 블레이드 단면 형상차이는 없으므로 두 경우 모두 앞전에서 경사충격파가 발생한다. 결함이 없는 모델의 경우에 로터 후류의 박리영역이 FOD 25%의 박리영역에 비해 상대적으로 넓게 나타나고 있고, FOD 25% 모델에서는 경사충격파 뒤로 블레이드 압력면에 국부적으로 생성되는 수직충격파가 더 강하게 발생하고 있다. 로터 블레이드에서 발생하는 경사 충격파와 국부적인 수직 충격파의 강도 및 구조와, 충격파에 의한 박리가 발생하는 위치 및 크기가 FOD 파손에 의해 달라지는 것을 볼 수 있다.
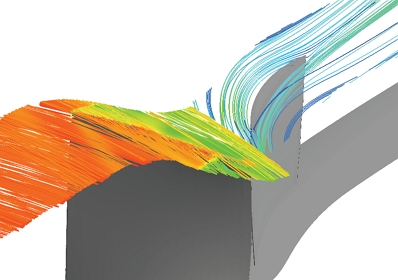
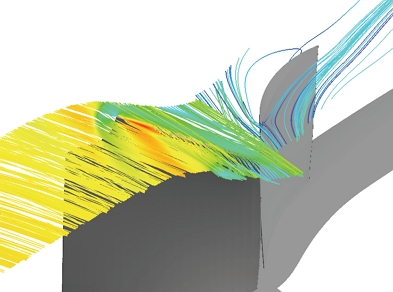
Fig. 12와 Fig. 13은 파손된 영역에 의해 유동의 방향이 어떻게 변화하는지 확인하기 위해 블레이드 팁 주위의 유선을 나타낸 것이다. 로터 앞전 팁에서부터 생성된 누설 와류는 인접한 블레이드 뒷전 압력면 방향으로 흘러가게 된다. 파손모델에서는 상대적으로 앞전이 뒤로 위치하게 되고, 캠버라인이 유동의 흐름과 만나는 각도가 달라진다. 앞전에서 생성되는 와류는 팽창파로 인해 가속된 유동과 만나 더욱 빠르게 회전하며 흐르게 되고, 로터 블레이드 뒤쪽으로 넓은 박리영역을 생성한다.
로터 박리영역의 확장은 뒤쪽에 위치한 스테이터에도 넓은 박리영역을 만드는 원인이 된다.
Fig. 14는 정상모델과 FOD 25% 파손모델의 로터블레이드 코드 70% 지점에서 유로의 마하수 분포를 나타낸 것이다. Fig. 14(b)에서 파손되지 않은 블레이드 주위 유동과 달리 팁 부근의 넓은 박리영역이 관찰되며, 흡입면에서 발생하는 박리영역이 스팬방향으로 상승하였다. 회전하는 압축기는 팁의 속도가 가장 빠르므로 Fig. 14(a)와 같이 팁 주위 유동의 속도가 가장 빨라야 하지만, Fig. 14(b)의 파손된 압축기는 팁 주위 와류 생성으로 인해 속도저하가 일어나고 span 70% 지점에서 가장 유속이 빠르다.
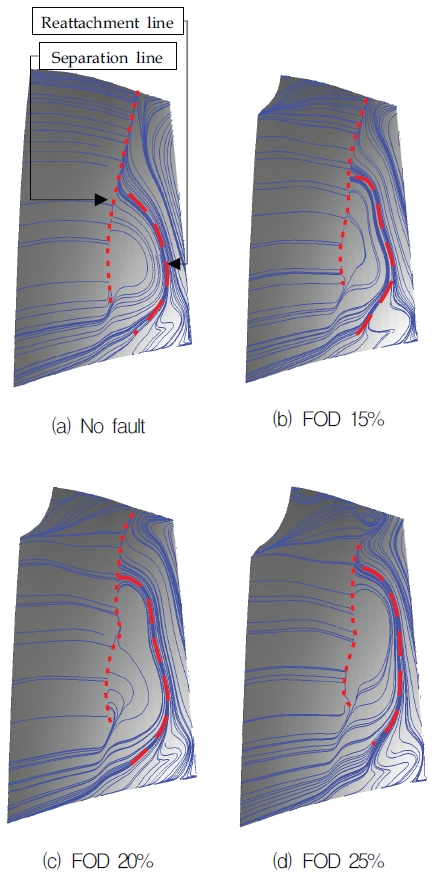
Fig. 15는 정상모델과 FOD로 인하여 파손된 로터블레이드 표면의 유선을 나타낸 것이다. Dinh[15]은 높은 전압력비에서는 블레이드 표면에 선명한 박리선(Separation line)과 재부착선(Reattachment line)을 확인 할 수 있다고 설명하였다. 압축기의 높은 전압력비에서 박리선과 재부착선을 비교하기 위해 FOD 25% 파손모델의 서지점과 같은 출구조건에서 4가지 블레이드 표면 유선을 비교하였다. 결함이 없는 블레이드의 표면 유선은 Fig. 15(a)와 같이 매끄러운 곡선 형태의 박리선과 재부착선이 분포하고 있다. 하지만, Fig 15(d)의 FOD 25% 파손모델의 표면 유선분포에서는 팁으로부터 파손된 기점까지 박리선이 명확하게 나타나지 않는다. 전압력비의 차이가 크게 나지 않는 FOD 15%의 파손모델에서도 로터 주위 유동은 블레이드 전체에 영향을 받아 박리선이 매끄러운 곡선이 아닌 불규칙 적인 곡선을 그리며 생성된다. FOD 25% 파손모델에서는, 팁 부근의 박리선이 관찰되지만, 와류와 만나 그 경계가 불확실해진다. 또한, 블레이드의 파손이 커지면 재부착선이 팁쪽으로 넓게 퍼지고, 팁 주위 박리선은 블레이드 뒷전으로 밀려나게 된다. 이런 변화는 Fig. 15(c)와 Fig. 15(d)에서 명확하게 확인 가능하다. 파손이 없는 모델의 재부착선과 다르게, 파손모델의 재부착선이 팁 쪽으로 넓게 퍼지게 되면서 블레이드 주위 박리영역이 확인된다. Fig. 15(d)에서 팁 주위 와류가 생기는 영역이 블레이드 앞전의 파손된 영역으로부터 흘러온 유동과 팁 누설와류와 만남으로써 생성된다는 점도 확인이 가능하다.
4. 결 론
본 연구에서는 전산해석을 통하여 천음속 1단 축류압축기가 FOD에 의해 파손된 경우의 유동변화를 확인하기 위해 상용 유동해석 프로그램인 CFX 18.0을 이용하여 1단 축류압축기인 NASA Stage 37을 대상으로 전산해석을 진행하였다. FOD와 로터블레이드 충돌에 의한 파손은 형상을 특정하기가 쉽지 않으므로 2가지 가정을 적용하였다. 계산방식에 따른 문제로 인해 파손이 모든 로터블레이드에 적용된 것으로 가정하여 파손형상을 결정하고 파손정도에 따른 3가지 파손모델에 대해 성능해석을 수행하였다.
FOD에 의해 파손된 압축기는 성능곡선에서 질량유량과 전압력비 모두 감소하고, 서지에 빠르게 도달하게 된다. 또한 효율 곡선에서는 최대 효율점이 파손이 커질수록 하락하며, 서지점에 가까워질수록 결함이 없는 경우와 FOD 파손모델의 효율차는 줄어들었다. Span 95%는 유동의 흐름이 파손영역에 직접적인 영향을 받는 구간으로, FOD 파손모델에서는 파손이 없는 블레이드가 경사충격파가 생기는 것과 다르게 궁형충격파가 형성되어 유동의 변화가 크게 나타난다. 파손 크기에 따라 앞전의 위치가 상대적으로 뒤로 이동하게 되고 형상도 변화하므로 궁형충격파의 생성 위치와 크기가 달라진다. 또한 충격파의 변화는 파손에 의한 블레이드 형상이 바뀐 앞전으로부터 다른 방향과 속도의 와류를 형성하고 유동의 방향을 바꾸게 된다. 유동방향의 변화는 파손부위에 직접적인 영향을 받는 팁 주위 뿐 아니라 블레이드 전체에 적용된다. 로터에서의 유동변화는 스테이터 유동 입사각에도 영향을 크게 미치며 스테이터 후류에 넓은 박리영역을 유도하여 전체적인 성능감소를 유도한다.
본 연구에서는 앞전 팁의 파손이 모든 로터에 적용된 것으로 가정하고 전산해석을 진행하였다. FOD가 축류압축기로 유입되더라도 실제로는 모든 압축기 블레이드에 파손을 주지는 못하므로 실제 상황에서 파손된 압축기의 성능감소보다 전산해석 결과에서의 성능감소 폭이 더 클 것으로 예상된다. 그리고 파손을 5%간격으로 늘려가며 FOD 15%부터 25%까지 3개의 case를 전산해석만을 진행 하였으나, 정상모델과 FOD 15%은 파손이 코드길이 15%의 차이가 나지만 파손모델과의 서지점에 도달하는 압축비의 차이가 20%, 25% 파손모델과의 차이보다 더 적다. 또한 질량유랑 감소량이 FOD 15%, 20% 의 0.1 kg/s 보다 FOD 20%, 25%에서 0.14 kg/s으로 그 차이가 더 크며, FOD 15%와 20%의 최대 효율점의 차이가 0.86%, FOD 20%와 25%의 차이는 1.16%로, 블레이드 파손정도가 일정하게 커지더라도 성능감소는 더욱 가속될 것임을 예상 할 수 있다. 또한 충분한 압축비가 달성되기 전에 블레이드 주위 유동변화로 인해 서지점에 비교적 빠르게 도달하기 때문에 압축비를 충분히 확보하지 못하여, 해당 크기의 파손은 작동중인 압축기 성능에 큰 영향을 미칠 것으로 예상된다.
Nomenclature
| PR : | Total pressure ratio |
| P01 : | Inlet total pressure |
| P03 : | Outlet total pressure |
| T01 : | Inlet total temperature |
| T03 : | Outlet total temperature |
| : | Normalized mass flow rate |
| : | Corrected mass flow rate |
| : | Maximum mass flow rate |
| γ : | Specific heat ratio |
| η : | Isentropic efficiency |
| m : | Molar mass |
| Cp : | Specific heat capacity |
| κ : | Thermal conductivity |
| μ : | Dynamic viscosity |
References
-
Kim, K.H., Kim, D.H., Choi, J.G., Kim, S.J. and Kim, Y.I., “Nonlinear Bird Strike Analysis of Turbofan Engine Blade Based on MIL-E-5007D Specification,” Journal of the Korean Society of Propulsion Engineers, vol. 27, No. 5, pp. 52-64, 2023.
[https://doi.org/10.6108/KSPE.2023.27.5.052]

-
Tabakoff, W., “Compressor erosion and Performance deterioration,” Journal of Fluids Engineering, ASME, vol. 109, pp. 297-306, 1987.
[https://doi.org/10.1115/1.3242664]

-
Chen, S.W., Shi, H., Zhang, C., Wang, S.T. and Wang, Z.Q., “Study on numerical simulation of fouling in compressor rotor,” International Journal of Turbo & Jet-Engines, vol. 29(3), pp. 179-188, 2012.
[https://doi.org/10.1515/tjj-2012-0026]

-
Aldi, N., Morini, M., Pinelli, M., Spina, P.R., Suman, A. and Venturini, M., “Performance evaluation of nonuniformly fouled axial compressor stages by means of computational fluid dynamics analyses,” Journal of turbomachinery, vol. 136, 2014.
[https://doi.org/10.1115/1.4025227]

-
Hussin, R., Ismail, N. and Mustapa, S. “A study of foreign object damage(FOD) and prevention method at the airport and aircraft maintenance area,” Innovation in Aerospace Engineering and Technology, vol. 152, 2016.
[https://doi.org/10.1088/1757-899X/152/1/012038]

- Shin, D.J. and Kim, C.Y., “Study on FOD prevention improvement for the application of the human factors,” The Korean Society for Aviation and Aeronautics, pp. 144-147, 2015.
- Kang, M.S., Yun, W.N. and Kim, K.Y., “Effects of the Damaged Axial-flow Compressor Blade on the Gas Turbine Components,” Korean Society for Power System Engineering, vol. 11(3), pp. 53-58, 2007.
-
Witek, L., Bednarz, A. and Stachowicz, F., “Fatigue analysis of compressor blade with simulated foreign object damage,” Engineering Failure Analysis, Elsevier, vol. 58(1), pp. 229-237, 2015.
[https://doi.org/10.1016/j.engfailanal.2015.09.002]

-
Marandi, S.M., Rahmani, K. and Tajdari, M., “Foreign object damage on the leading edge of gas turbine blades,” Aerospace Science and Technology, Elsevier, vol. 33(1), pp. 65-75, 2014.
[https://doi.org/10.1016/j.ast.2014.01.001]

-
Xu, Y., Chang, L., Shu, C., Chen, X. and Li, P., “Foreign object damage performance and constitutive modelling of titanium alloy blade,” International Journal of Aerospace Engineering, Hindawi, vol. 2020, 2020.
[https://doi.org/10.1155/2020/2739131]

-
Li, Y.L. and Sayma, A.I., “Computational fluid dynamics simulations of blade damage effect on the performance of a transonic axial compressor near stall,” Institution of Mechanical Engineers, vol. 229(12), pp. 1-19, 2014.
[https://doi.org/10.1177/0954406214553828]

- Reid, L. and Moore, R.D., “Design and overall performance of four highly loaded, high-speed inlet stages for an advanced high-pressure-ratio core compressor,” NASA TP-1337, 1978.
-
Egorov, I., Butukli, T., Popov, G., Goriachkin, E., Novikova, Y. and Volkov, A., “Experimental compressor multidisciplinary optimization using different parameterization schemes,” MATEC Web of Conferences, vol. 220, 2018.
[https://doi.org/10.1051/matecconf/201822003005]

-
Duo, P., Pianka, C. and Golowin, A., “Simulated foreign object damage on blade aerofoils: real damage investigation,” ASME Turbo Expo 2008: Turbomachinery Technical Conference and Exposition, 2008.
[https://doi.org/10.1115/GT2008-50371]

-
Dinh, C.T., Ma, S.B. and Kim, K.Y., “Effects of a circumferential feed-back channel on aerodynamic performance of a single-stage transonic axial compressor,” ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, 2017.
[https://doi.org/10.1115/GT2017-63536]