스플릿라인 TVC 시스템을 적용한 핀틀 추력조절 노즐의 유동해석 및 추력 성능 예측
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 스플릿라인 TVC를 적용한 핀틀 추력조절 노즐에 대한 유동해석을 수행하고 추력 성능을 예측하였다. 해석 결과로 도출된 추력계수를 시험결과와 비교하여 수치해석 결과를 검증하였으며, 동일한 수치해석 기법을 적용하여 주요 성능 변수인 운용고도, 핀틀 스트로크 위치, TVC 각도에 따른 1/10 크기의 노즐의 유동특성을 확인하였다. TVC 각도가 증가할수록 추력손실이 발생하였고, 핀틀 스트로크 위치에 따라 AF의 경향성이 달랐다. 해석결과를 기반으로 반응표면법을 적용하여 추력계수에 대한 관계식을 도출하였고, 해석 결과와 평균 1.2% 수준의 근소한 차이를 가지는 추력 성능 모델을 생성하였다.
Abstract
In this study, analysis of the flow characteristics of pintle-controlled nozzle with split-line TVC system and the thrust performance prediction was performed. The numerical computation was verified by comparing the thrust coefficient derived from the analysis results with the experimental data. By applying the same numerical analysis technique, the flow characteristics of nozzle were confirmed according to operating altitude, pintle stroke position and TVC angle with the 1/10 scale. As the TVC angle increased, thrust loss occurred and the tendency of AF was different depending on the position of the pintle stroke. Based on the analysis results, the relation of thrust coefficient was derived by applying the response surface methods. The thrust performance model with a slight difference of 1.2% on average from the analysis result was generated.
Keywords:
Thrust Vectoring Control, Pintle-Controllde Nozzle, Solid Rocket Motor, Response Surface Method, Cf키워드:
추력방향제어, 핀틀 구동 노즐, 고체로켓모터, 반응표면법, 추력계수1. 서 론
추력조절이 가능한 고체 로켓모터는 즉각적으로 발사가능하고, 액체 로켓엔진에 비해 비교적 구조가 간단하다는 고체 추진기관의 장점을 그대로 유지하는 동시에 미사일 운용능력을 기존보다 확대할 수 있다는 강점을 가진다. 국외에서는 1950년대부터 고체 추진로켓에 적용가능한 추력조절 기술에 대한 연구가 수행되었으며, 핀틀을 사용하여 노즐 목 면적을 조절하는 기술이 1980년대 본격적으로 연구되었다[1].
노즐 목 면적 조절 범위와 추진제 압력지수가 클수록 추력 조절비를 늘릴 수 있으며, 급격한 핀틀 구동을 통해 연소실 내부 압력을 강하시킴으로써 추진제 소화를 가능하게한 실험적 연구가 수행되었다[2]. 또한, 핀틀 추력조절 추진기관에 추력방향제어 기술을 연동하여 방향 전환 조절능력을 향상시키는 연구를 수행한 바 있다[3].
국내에서도 추력조절기술에 대한 연구가 활발히 수행되고 있다. 핀틀을 활용하여 정밀한 추력제어를 위한 단축, 다축 핀틀에 대한 성능 연구 및 핀틀과 노즐에 대한 연소실 압력 거동특성 연구 등이 수행되었다[4,5]. 또한 다양한 핀틀 형상에 대한 유동해석과 공압시험을 수행한 바 있다[6,7]. 미사일 운용능력 확대 및 고기동성 확보를 위해서는 추력조절과 추력방향 제어가 동반되어야 하며, 이에 관한 상호 영향성 분석이 요구된다.
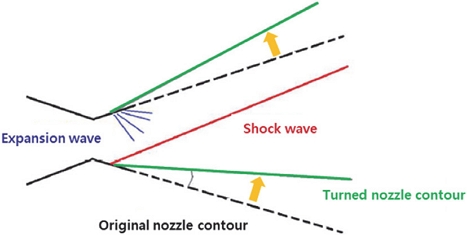
추력방향 제어 방식은 방향을 다각도로 바꿀 수 있는 로테이팅 방식과 힌지를 사용한 노즐 방식 또는 스플릿라인 노즐을 통한 충격파를 발생시키는 방식 등이 활용되고 있다. 본 연구에서는 핀틀을 사용하여 추력제어와 동시에 사용가능한 추력방향 제어 구동 방식으로 Fig. 1과 같은 초음속 스플릿라인 TVC 노즐을 채택하였다. 배기가스 유동을 꺾기 위해 노즐 확대부를 움직여 추력 방향전환을 수행하는 스플릿라인 추력방향제어 방식은 핀틀 위치에 따른 유동 흐름 변화에 대한 민감도, 추력방향전환, 중량 등의 관점에서 핀틀구동 노즐과 가장 잘 호환된다고 평가되고 있다[8]. 일반적인 스플릿라인 TVC 노즐의 경우 TVC 각도가 적을수록 TVC 효과가 증가하는 경향이 있으며, 이는 스플릿라인에서 꺾이면서 발생하는 하류의 성능손실이 각도가 커질수록 증가하는 것에 기인한다[9].
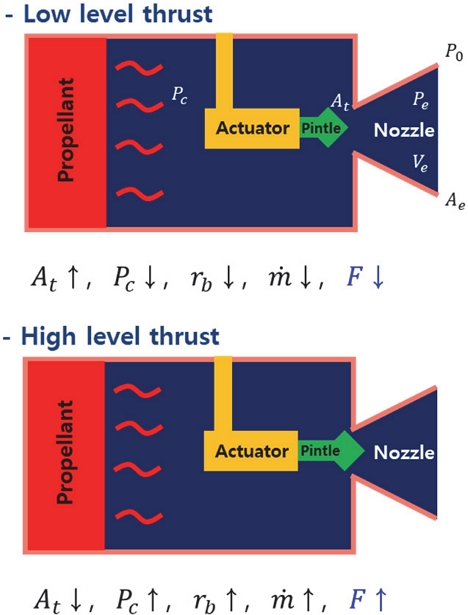
핀틀을 통한 추력제어의 주요 원리는 Fig. 2와 같다. 핀틀은 노즐 목과 멀어지는 방향으로 이동할 경우 노즐 목 면적은 증가하고 연소실 내부의 압력이 줄어들게 된다. 이에 따라 추진제 연소속도가 감소하며, 노즐로 빠져나가는 유량이 적어져 추력이 감소한다. 반대로 핀틀 목면적을 작게 만들 경우 연소실 내부 압력이 증가하여 유량이 많아져 추력이 증가된다. 핀틀 노즐은 특히 핀틀 경사면의 형상에 따라 핀틀의 끝단 충격파의 발생위치가 달라지며 이로 인하여 핀틀 형상에 따라 유동박리 발생 위치와 크기에 큰 차이가 난다는 특징이 있다[10].
본 논문에서는 추력방향제어에 있어서 핀틀 스트로크의 위치와 TVC의 각도, 작동압력에 따른 노즐의 유동을 수치해석을 통해 분석하였으며, 각 변수에 의한 추력계수를 반응표면법을 도입하여 성능예측 모델을 생성하였다. 고체로켓 추진기관에서 본 논문에 사용된 핀틀과 스플릿라인 TVC 기술로 추력크기와 방향제어를 동시에 적용한 사례는 국내에서는 전무하며, 국외에서도 실험수행에 관한 내용만 기술되고 있다[2,3]. 또한 국외 실험 논문을 통해서는 핀틀 구동과 TVC 유동 관계의 특성을 확인하기는 한계가 있었으며, 본 논문을 통해 유동 특성을 파악하고자 하였다.
2. 수치해석 기법과 검증
2.1 수치해석 모델 선정
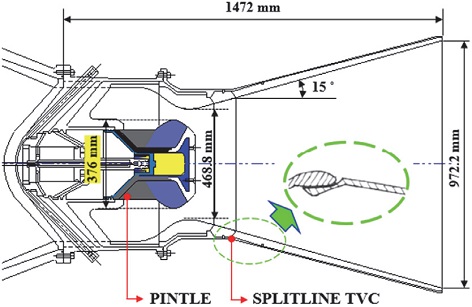
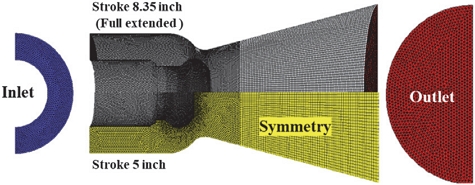
수치해석 모델은 D. C. Sayles의 논문에 기술된 운용고도조건에서의 핀틀구동 및 소화시험을 수행한 모델로 선정하였다[3]. Fig. 3은 모델의 개략도와 크기를 보여준다. 노즐목 전단에 위치한 핀틀을 통해 추력 크기를 조절하고 노즐 확대부에 위치한 스플릿라인 TVC로 추력방향 조절이 가능하다. 해당모델의 형상정보, 고도시험 데이터, 핀틀 위치에 따른 목면적 정보를 사용하여 시험데이터와 해석을 비교하여 검증하도록 하였다. Full Scale의 노즐 내부해석과 10% 크기의 노즐 내외부 해석을 수행하였으며, 고도, 핀틀 위치, 스플릿라인 TVC 각도에 따른 유동조건을 비교하도록 하였다.
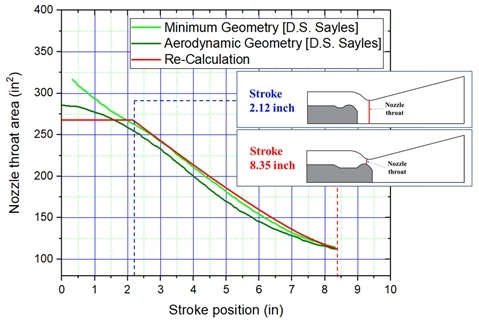
핀틀 스트로크 위치정보를 얻기 위하여 스트로크 위치 대비 기하학적 노즐 목 면적을 D. C. Sayles 논문에서 제시된 면적과 대비하여 역계산하는 방법으로 확인하였다. Fig. 4는 논문에서 제시된 스트로크 위치별 기하학적 노즐 목 면적 및 공력학적 노즐 목 면적과, 기하학적 노즐 목 면적과 맞도록 핀틀 위치를 설정하고 역 계산한 노즐 목 면적의 값이 제시되어 있다.
역 계산한 노즐 목 면적의 경우 핀틀 스트로크 위치 2.12 inch 부근에서 수렴되어 더 증가하지 않는데, 이는 스트로크의 위치가 줄어들면서 노즐 목 면적이 커지다가 이후에는 일반적인 추진기관의 노즐목 위치에서 목 면적이 생성되기 때문이다. 이를 검증하기 위하여 Eq. 1과 같이 내부 연소압을 역계산하였으며 이를 사용하여 유동해석을 수행하였다. 연소면적은 최대인장(최소 노즐목면적) 시험 데이터에서 역계산하여 획득하였고, 최소추력(최대 노즐목면적)을 내는 핀틀 스트로크 2.12 inch와 0 inch 지점의 유동해석을 수행하였다.
| (1) |
2.2 수치해석 검증
수치해석에는 범용 프로그램인 ANSYS FLUENT를 사용하였다. Fig. 3의 도면 정보를 사용하여 3차원 형상정보를 생성하였으며, 비정렬 격자로 구성하였다. 핀틀 스트로크 위치는 8.35 inch(최대 인장상태)와 5 inch, 2.12 inch, 0 inch로 총 4가지 조건에서 노즐 내부 유동해석을 수행하였다.
Fig. 5와 같이 작동압력을 Pressure inlet 조건으로 입력하였으며, 노즐 출구를 Pressure outlet 조건으로 설정하였다. 핀틀 노즐의 형상으로 인해 유동박리특성을 동반한 복잡한 난류 유동의 특성이 발생하며 이를 고려하기 위하여 SST k-omega 모델을 사용하였다. Flux type은 AUSM 기법을 사용하였으며, 공간차분법은 upwind scheme을 적용하였다. 유동해석 조건은 Density-Based typed이며, 70년대 사용하던 HTPB계열의 추진제 물성을 가정하였다. 입력변수 조건은 Table 1과 같다.
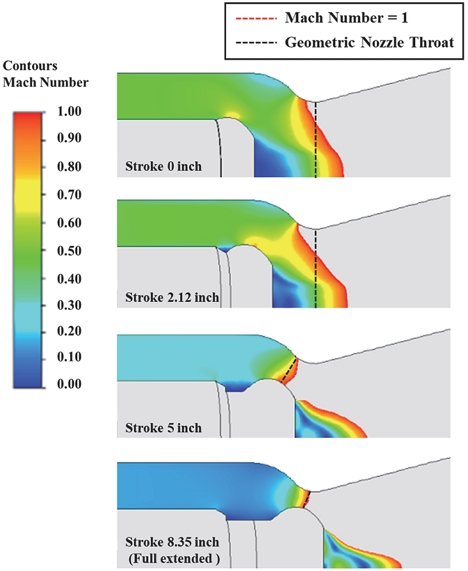
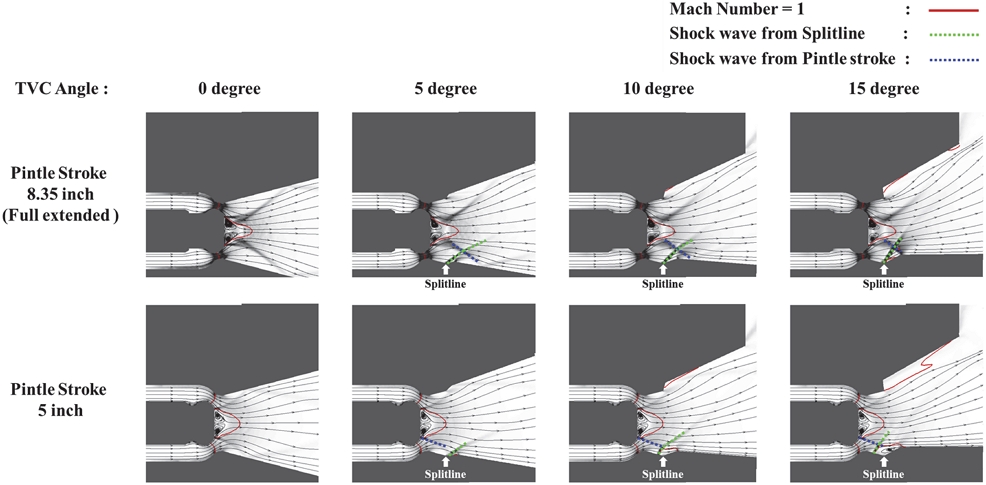
핀틀 스트로크 위치에 따른 노즐 목 형성 위치를 검증하기 위하여 스트로크 위치별 마하 1이 되는 지점을 Fig. 6에 나타내었다. 스트로크 위치가 0 inch와 2.12 inch 일 때, 모두 일반적인 추진기관의 노즐 목 위치에서 마하 1이 형성되는 것을 확인할 수 있다. 이는 핀틀 스트로크가 최대인장에서 최소 지점으로 움직이면서 노즐 목 면적을 증가시키는데, 2.12 inch 위치에서부터는 목 면적의 크기가 핀틀 경사면에서 생기는 면적보다 노즐 자체의 목면적이 작아지기 때문이다. 스트로크 위치 5 inch와 8.35 inch 모두 기하학적으로 계산한 노즐 목의 위치가 마하 1의 위치와 근접함을 확인하였다.
| (2) |
| (3) |
D. C. Sayles의 고도시험으로부터 핀틀 스트로크 위치 8.35 inch(최대인장)와 5 inch 조건의 데이터를 획득하였으며, 유동해석 결과로 추력계수를 계산하여 비교한 결과를 Table 2에 제시하였다. 추력계수는 Eq. 2로부터 도출할 수 있다. 추력은 노즐 출구에서의 평균 속도와 질량유량 그리고 압력을 사용하여 계산하였다. 계산식은 Eq. 3과 같으며 모멘텀 항과 압력에 대한 항으로 나눠진다. 시험데이터는 핀틀 구동에 따라서 노즐목면적과 연소실 압력이 위상차를 가지고 있기에 정상상태를 가정한 현 해석과는 다소 차이를 보일 수 있으며 추진제 물성 또한 가정된 값이지만 해석 결과 추력계수가 오차 1% 내로 유사하게 계산되었음을 확인하였다.
3. 결과 및 논의
핀틀구동과 추력방향제어를 동시에 수행할 수 있는 추진기관의 성능을 분석하기 위하여 운용고도, 핀틀 스트로크 위치, TVC 각도에 따른 유동 특성을 확인하고자 하였다. 수치해석을 통해 각 변수에 대한 추력계수 및 추력편향각도 값을 획득하고, 회귀함수를 통해 각 변수에 따른 추력 성능에 대한 영향성을 파악하고자 한다.
3.1 수치해석
스플릿라인 TVC 노즐을 적용한 핀틀 추진기관의 유동특성을 분석하기 위해 Table 3과 같이 주요성능인자와 그 값을 설정하였다. 추진기관의 운용고도(0, 5, 10, 15, 20 km), 핀틀 스트로크 위치(8.35, 5 inch) 및 추력방향제어 각도(0, 5, 10, 15°)를 주요 성능 인자로 선정하였다.
주요인자는 3가지로 추후 회귀함수를 획득하기 위하여 총 40가지 해석을 수행하였다. 고도에 따라 외기 압력조건이 달라지며, 핀틀 스트로크 위치에 따라 연소실 내부 압력 조건이 바뀐다. 또한, 추력방향제어 각도는 스플릿라인 TVC 형상을 개략적으로 모사하여 적용하였다.
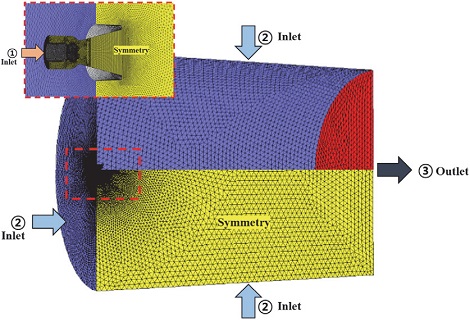
노즐 출구면 경계조건에 대한 영향성을 최소화하기 위하여 노즐후류 영역을 계산하였으며, 해석시간을 줄이기 위하여 10% 크기의 해석을 수행하였다. 노즐 후류에 출구반경 R을 기준으로 길이 45R x 반경 15R의 원통형 도메인을 설정하였으며, 경계조건을 입력하였다. 격자는 Fig. 7과 같이 구성하였으며, 격자수는 약 65만개이다. 해석 유체는 검증 시 사용한 가스물성치를 사용하였다.
1/10 Scale 해석에 대한 검증은 Full-Scale 해석과 동일한 조건에서 검증을 수행하였다. Scale에 따른 추력계수 편차는 1% 내외이며, 모두 시험과 유사한 결과를 보였다[Table 2]. 이 방식을 통해 스플릿라인 TVC가 적용된 핀틀 추진기관의 유동 특성을 분석하였다.
Fig. 8은 고도 20 km에서 핀틀 스트로크 위치 및 스플릿라인 TVC 각도에 따른 유동구조를 나타낸 것이다. Contour는 밀도구배를 나타내며 붉은색 line은 노즐 마하수가 1이 되는 지점을 표시한 것이다. 핀틀 위치에 따라서 노즐 목의 위치와 면적이 다른 것을 확인할 수 있는데 이는 핀틀 위치에 따라 연소실 압력이 달라져 노즐 출구에서 속도분포와 유량이 바뀌어 추력의 모멘텀 항에 영향을 주기 때문이다.
Contours of the density gradient for the nozzle according to the TVC angle and pintle stroke position at 20 km of altitude.
Fig. 9와 같이 핀틀이 최대 인장상태(8.35 inch)일 때, 연소실 압력이 높고 노즐 팽창비(노즐출구면적/노즐목면적)가 커지기 때문에 저압구간의 핀틀 위치(5 inch)에 있을 때보다 추력계수가 높은 것을 확인할 수 있다. 추력계수는 Eq. 4와 같이 x방향과 y방향의 추력합으로 계산하였다.
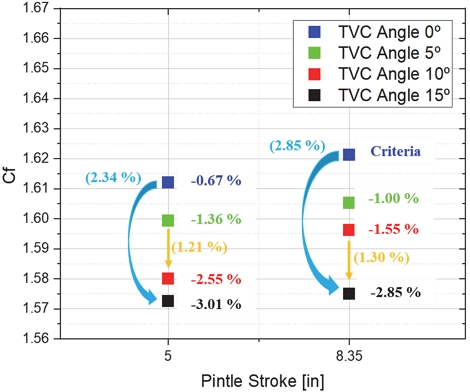
TVC 각도 5° 간에 따라 약 0.5∼1.3%의 손실이 발생하였으며, 특히 최대인장 스트로크 위치(8.35 inch)에서는 10°에서 15°로 꺾어질 때, 5 inch 스트로크 위치에서는 5°에서 10°로 넘어갈 때 손실이 1.2% 이상 발생하였다. 즉, 핀틀 스트로크의 위치가 최대인장 위치(8.35 inch)에서 5 inch 위치보다 TVC 각도를 더 크게 틀어도 추력손실 폭이 적은 것으로 보인다. 하지만 각 핀틀 위치에서 0°에서 최대 추력편향 각도(15°)만큼 각도를 틀 때 최대인장 스트로크 위치에서의 추력 손실이 약 2.85%로 5 inch 위치에서 2.34%보다 0.5%가량 컸다. 즉, 압력이 높을 때 일정한 각도까지는 연소실 내부 압력이 높을 때가 TVC 각도 제어에 있어 유리하지만, 그 이상의 각도 편향에서는 압력이 높을수록 손실 총량이 커진다는 것을 확인하였다.
| (4) |
| (5) |
| (6) |
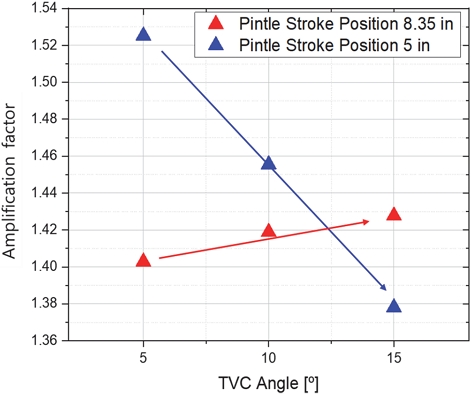
Fig. 10은 핀틀 스트로크 위치에 따른 목표추력각 대비 계산된 추력편향각의 비(AF)를 나타내고 있다. 추력편향각은 Eq. 5를 통해 구할 수 있으며, AF는 Eq. 6으로 구할 수 있다. 추력편향각에 사용된 축 방향 속도는 노즐 출구면에서의 평균 속도값이다. 모든 구간에서 목표추력각 대비 40% 이상의 추력편향각이 발생하였으며, 이는 스플릿라인 TVC 시스템이 노즐이 꺾인 윗 구간에서는 팽창파가 생기고 스플릿라인이 있는 아랫 구간에서 충격파가 발생하여 두 가지 현상의 결과로 유동이 목표한 각도보다 크게 꺾임으로서 발생하는 현상이다. 일반적으로 스플릿라인 노즐의 AF 값은 1.25 – 1.7 수준이며[9], 본 연구에서 계산된 AF 값이 타당한 수준임을 확인하였다.
최대인장 스트로크 위치에서는 각도가 높아질수록 AF 값은 증가하였으나, 5 inch 위치에서는 반대로 낮아지는 것을 확인할 수 있다. 이는 Fig. 8에서 볼 수 있듯이 최대인장 스트로크 위치에서는 연소실 내부 압력이 높아 스플릿라인 전단에서 박리가 발생하지 않고, 의도한 위치에서 충격파를 발생시켜 박리된 유동의 간섭없이 각도를 편향시킬 수 있기 때문으로 보인다. 또한 핀틀 구조물에 의해 발생된 핀틀 뒷단의 유동박리가 이 충격파의 방향에 크게 영향을 주지 않고 있음을 확인할 수 있다.
하지만 스트로크 5 inch 위치에서는 TVC 각도 10˚, 15˚ 만큼 꺾일 때, 노즐이 꺾인 지점의 후단에서 박리가 발생하여 스플릿라인 전단에서 충격파가 발생하는 것을 확인할 수 있다. 또한 이 충격파가 핀틀 후단 유동에 영향을 받아 충격파가 반대방향으로 꺾이는 것을 확인할 수 있다. 즉, 5 inch 스트로크 위치에서는 의도된 위치에서 충격파가 발생하지 않고, 핀틀에 의한 후류유동과 만나 유동이 반대로 꺾이는 현상이 발생하여 AF 값이 낮아진 것으로 판단된다.
Fig. 11은 핀틀 스트로크 최대인장 위치(8.35 inch)에서 고도별 TVC 각도에 따른 마하수 Contour를 나타내고 있다. TVC 각도가 5°일 경우에는 Sea Level 대기조건에서만 노즐내부 유동에서 박리가 발생하지만, 각도 10°에서는 고도 5 km, 15°에서는 고도 10 km에서도 내부박리가 발생하는 것을 확인할 수 있다.
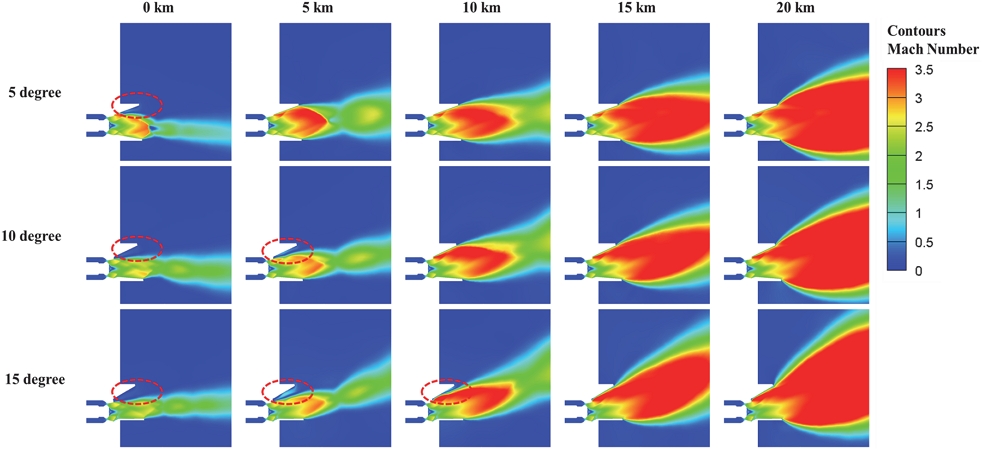
Contours of the mach number for the nozzle flow according to the altitude and TVC angle at full extended pintle stroke position(8.35 inch).
현재 적용된 추진기관 노즐이 고고도 노즐로 대기조건에서는 압력비가 부족하여 유동 박리가 발생할 수 있지만, 고도가 높아지면 자연스럽게 압력비가 회복된다. 그러나 스플릿라인 TVC에 의해 각도가 발생하면서 각도가 꺾어지는 방향으로 팽창비가 커지면서 박리가 발생된 것으로 보인다.
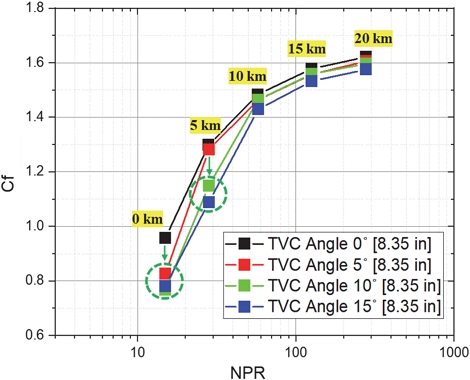
Fig. 12는 핀틀 스트로크 최대인장 위치에서 고도별 TVC 각도 조건에 따른 추력계수 그래프이다. 고도가 낮아질수록 추력계수가 낮아지며 특히 고도 5 km에서 TVC 각도 10°, 15° 조건과 고도 0 km에서 TVC 각도 5°, 10°, 15° 조건이 TVC 0°의 추력계수 경향성에서 벗어나 훨씬 못미치는 것을 확인할 수 있는데 이는 Fig. 11에 나타나는 내부유동 박리 영향성 때문으로 보인다.
3.2 회귀분석 수행
반응표면법(Response Surface Method)을 통해 유동해석 결과를 각 주요성능인자들에 대한 관계식으로 만들도록 하였다. 반응면을 구성하기 위해서 세가지 주요인자인 운용고도, 스트로크 위치, TVC 각도를 정해진 실험점을 대상으로 유동해석을 수행하여 그 특성을 확인하였다. 근사 반응함수를 생성함으로써 주요 인자들과 추력계수와의 관계를 정의하고, 다른 조건의 성능을 확인할 수 있도록 하였다. 반응함수는 이차 다항식모델을 사용하도록 하였으며 회귀 변수는 다음과 같이 정의하였다.
| (7) |
설계변수들의 선형항 , 제곱항 , 그리고 상호 작용 항 등 모두 9개의 변수로 이루어진 방정식을 생성하도록 하였다. 목적함수는 아래와 같이 추력계수에 대한 값으로 정의하였다. 결과적으로 추정된 반응표면은 다음과 같다.
| (8) |
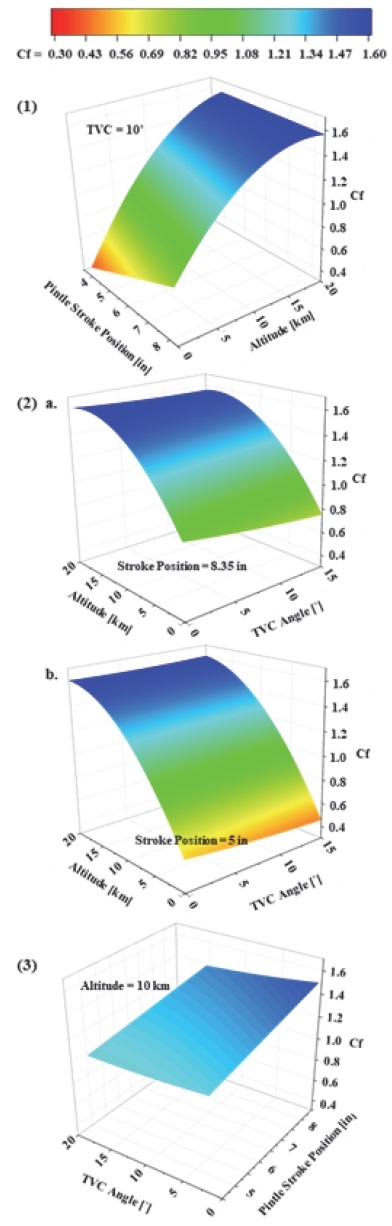
Fig. 13에 세 가지 주요 인자의 모든 작용항에 대해서 Eq. 8이 나타내는 반응표면을 보여주고 있다. 각각의 그래프에서 (1) TVC 10°, (2) a. 핀틀 스트로크 위치 8.35 inch, b. 핀틀 스트로크 위치 5 inch, (3) 고도 10 km로 고정된 상태이다. (1)의 그래프에서 볼 수 있듯이 고도에 따른 추력계수 값이 가장 급격하게 변하는 것을 볼 수 있으며, (2)의 핀틀 스트로크 5 inch 일 때가 8.35 inch 일 때보다 고도에 따른 영향이 큰 것을 확인할 수 있다. 또한 TVC 각도에 따라 최대인장 스트로크 위치에서의 각도에 따른 추력계수가 5 inch 위치에서보다는 영향을 더 크게 받고 있음을 알 수 있다. (3) 그래프로부터 핀틀 스트로크 위치에 따른 추력계수의 크기 변화 영향성은 크지 않지만, 최대인장 스트로크에서 더 큰 추력계수를 가지는 것을 확인할 수 있다. 스트로크 위치에 대해서는 검증된 두 조건(8.35, 5 inch)에 대해서만 해석이 수행되었기 때문에 핀틀 위치에 따른 내부 압력 데이터를 분석하여 추가적인 해석이 필요할 것으로 판단된다.
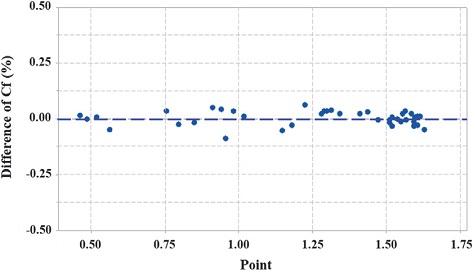
Fig. 14는 Eq. 7에 의한 반응표면 모델에서 얻어진 추력계수 값과 해석을 통해 얻은 값의 상대적인 차이를 보여준다. 수치해석 결과와 반응표면 모델 결과의 편차는 약 0.09%로 두 결과가 잘 일치함을 확인할 수 있다.
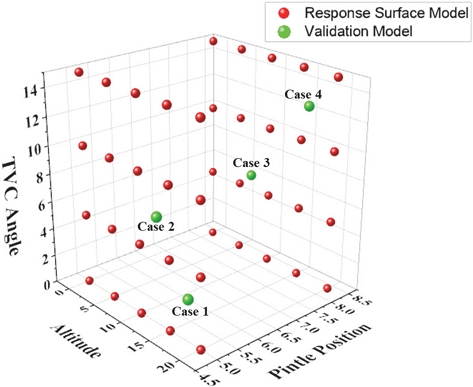
반응표면에 사용된 수치해석 결과 외에 임의 조건의 수치해석을 통해 반응표면 모델과 비교하여 검증하도록 하였다. Fig. 15과 같이 반응표면에 사용한 모델과 다른 임의의 해석조건들을 표시하였다. 검증에 사용된 모델은 총 네 가지로 그 결과를 Table 4에 나타내었다. 평균 1.19%의 오차율을 가지고 있으며 최대 2.28%로 반응표면 모델의 신뢰성이 있음을 확인할 수 있었다.
4. 결 론
본 논문에서는 핀틀 추력조절 노즐과 스플릿라인 TVC 시스템을 적용한 추진기관의 성능을 분석하고 성능예측 모델을 생성하였다. 이를 위해 실제 시험데이터와 해석을 통해 계산된 추력계수를 비교하여 검증하였으며, 이후 수치해석을 통해 운용고도, 핀틀 스트로크 위치, TVC 각도에 따른 추력계수 및 추력방향제어 효율 값을 획득하였다. 추력방향 각도가 5°씩 커질수록 0.5∼1.3%의 손실이 발생하였고, 최대인장 스트로크 위치에서는 각도 증가에 따라 AF의 경향이 높아졌지만 5 inch 위치에서는 반대로 낮아짐을 확인하였다. 그리고 저고도로 갈수록 TVC 각도가 커지게 되는 경우, 팽창에 필요한 압력비가 부족하여 쉽게 박리가 되는 것을 확인할 수 있었다. 수치해석 유동특성 결과를 사용하여 근사 반응함수를 생성하였으며, 주요 인자들과 추력계수와의 관계를 정의하여 반응표면을 생성하였다. 모델에 사용된 해석 결과와의 편차는 약 0.09%이며, 임의의 해석 조건과의 편차는 평균 1.19%로 반응표면 모델에 대한 신뢰성을 확인하였다. 본 연구결과로 핀틀을 통한 추력조절과 동시에 스플릿라인 TVC 기능을 가진 추진기관 노즐에 대한 성능 특성을 분석하고, 추력예측 모델을 생성하였으며, 이후 연구단계인 형상설계 및 성능모델에 적용가능한 방법론을 정립하였다.
Nomenclature
| Ab : | Burning area |
| Ae : | Nozzle exit area |
| At : | Nozzle throat area |
| AF : | Amplification factor |
| a : | Burning rate constant |
| CD : | Discharge coefficient |
| CF : | Thrust coefficient |
| F : | Thrust |
| : | Mass flow rate |
| n : | Burning rate |
| NPR : | Nozzle pressure ratio |
| Pa : | Ambient pressure |
| Pc : | Chamber pressure |
| RS : | Response surface model |
| TVC : | Thrust vectoring control |
| Ve : | Exit velocity |
| Ve,x : | Exit velocity of x direction |
| Ve,y : | Exit velocity of y direction |
| ηD : | Discharge correction factor |
| ηrb : | Burning rate correction factor |
| δresult : | Angle of thrust result |
| δobject : | Angle of Mechanical object |
| ρp : | Propellant density |
Acknowledgments
이 논문은 2022년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임.This work was supported by Agency for Defense Developement(ADD) - Grant Funded by Defense Acquisition Program Administraion (DAPA)
References
- Nijanthan, M., Vignesh, S., Hemasai, N.D., Pavithra M. and Sanalkumar V.R., “Conceptual Design and Shape Optimization of a Pintle Nozzle for Controllable Thrust Propulsion and Steering,” AIAA Propulsion and Energy Forum, Atlanta, GA, AIAA 2017-4870, July 2017.
-
Sayles, D.C., “Development of Test Motors for Advanced Controllable Propellants,” Journal of Spacecraft and Rocket, Vol. 12, No. 3, pp. 174-178, 1975.
[https://doi.org/10.2514/3.56962]

-
Sayles, D.C. and Levinsky, C.T., “Advanced Pintle-Controlled Motor with Thrust Vector Control,” SAE Transactions 710619-710867, Vol. 80, Section 4, pp. 2557-2564, 1971.
[https://doi.org/10.4271/710763]

- Ha, D.S. and Lim, S.T., “Research Trends in Propulsion Technology for Divert and Attitude Control System,” 2017 KSPE Spring Conference, Busan, Korea, pp. 353-357, May 2017.
- Jeong, K.Y., Heo, J.Y., Sung, H.G., Yang, J.S. and Ha, D.S., “Thrust Characteristics of Through-type Pintle Nozzles with Large Scale Seperation Flow,” 2014 KSPE Spring Conference, Busan, Korea, pp. 32-38, May 2014.
-
Kim, J.J., Oh, S.J., Heo, J.Y. and Lee, D.H., “Analysis of the Flow Characteristics of Plug Nozzle for Cold Air Test with Pintle Shape and Operating Pressure,” Journal of the Korean Society of Propulsion Engineers, Vol. 23, No. 3, pp. 28-34, 2019.
[https://doi.org/10.6108/KSPE.2019.23.3.028]

- Kim, J.J., “Analysis of the Characteristics of an Aerospike Pintle Nozzle in terms of Stroke and Operating Pressure,” Journal of Aerospace System Engineering, Vol. 14, No. 4, pp. 1-9, 2020.
- Ervin, W.D. and Kums, C.H., “Altitude Test of the Aerojet Modified Heavyweight Full-Scale Controllable Solid-Propellant Rocket Motor(CSRM-4),” AEDC-TR-73-189, 1973.
- Ravnan, S., “Advantage of a Supersonic Split line nozzle over a submerged movable nozzle,“ Delft University of Technology, Nederland, Mar. 2021.
- Park, H.J., Kim, L.N., Heo, J.Y., Sung, H.G. and Yang, J.S., “Numerical Study on Dynamic Characteristics of Pintle Nozzle for Variant Thrust,” 2011 KSPE Autumn Conference, Busan, Korea, pp. 213-217, Nov. 2011.