유전 알고리즘을 이용한 Finocyl 그레인 형상 최적 설계 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
기존 Finocyl 그레인 형상 설계는 임의의 형상을 가정하고 Burn-back 해석을 통해 요구조건 만족 여부 확인, 형상 수정의 과정을 반복한다. 이와 같은 설계는 작업자의 설계 피로도를 높이고, 역량에 따라 설계 완성도가 상이한 문제를 가지고 있다. 이에 본 연구는 기존 설계의 문제를 해결하기 위해 Burn-back 자동화 해석 프로그램에 유전 알고리즘을 적용한 최적 설계 방법을 개발하였다. 안정적인 탐색을 위해 가변형 Offset, 작도 불능 형상 변수 제어 기법을 개발하고, 중립형 및 이중추력형 면적 선도 형상을 설계하여 성능을 검증하였다.
Abstract
Existing Finocyl grain designs assume configurations and repeat the process of configuration modification and confirmation of the requirements through burn-back analysis. Such a design increases the design fatigue of workers and has a problem of different design completeness depending on capabilities. Therefore, this study devised an optimal design method that applied genetic algorithms to the Burn-back automation analysis program to solve the problem of existing design. For stable search, variable-offset and non-drawable configuration control techniques were developed. The program performance was verified through the searching neutral and double thrust grains.
Keywords:
Solid Rocket Motor, Solid Propellant, Genetic Algorithm, Optimum Design키워드:
고체 로켓 모터, 고체 추진제, 유전 알고리즘, 최적 설계1. 서 론
고체 로켓 모터는 군사 안보, 우주 추력기, 분리장치, 긴급 구조 등 다양한 분야에서 활용 되고 있다[1]. 최근에는 한⋅미 미사일지침이 종료됨에 따라, 군사용, 우주 발사체용 고체 로켓 모터에 대한 연구가 활발히 수행되고 있다. 고체 로켓 모터는 모터 케이스, 내열재, 고체 추진제, 노즐 등으로 구성되는데, 이 중 고체 추진제 그레인의 형상은 고케 로켓 모터의 성능을 결정하는 중요한 요소이다.
고체 로켓 모터가 점화되면, 케이스 내 그레인 표면으로 화염이 착화된다. 그레인 표면의 화염에 의해 연소가스가 발생하고 노즐을 통해 분사되어 추력을 발생시킨다. 이 때 추진제에서 생성되는 질유량은 그레인의 연소면적과 비례하여 발생한다. 따라서 고체 로켓 모터의 추력, 압력을 예측하기 위해선 그레인 형상의 Burn-back 해석이 필수이다. Burn-back 해석은 추진제 그레인의 연소에 따른 기하학적 그레인의 형상 변화를 도출하는 과정으로 주로 이론적(Analytical), 수치적(Numerical), 작도(Drafting) 세 가지 방법을 통해 진행되며, 그레인의 형상이 복잡한 경우에는 일반적으로 작도를 이용한 방법를 사용하여 해석한다.
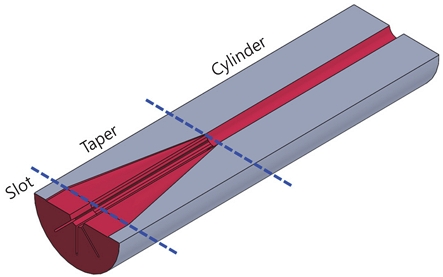
연소면적 선도는 추력 변화 양상에 따라 저감형, 중립형, 점증형, 이중추력형 등으로 구분된다. 임무에 따라 요구되는 선도는 다양하지만, 일반적으로 추력 크기가 일정한 중립형 면적 선도가 많이 선호되며 운용 임무에 따라 이중추력형 면적 선도가 요구되는 경우도 있다. 본 연구에서 대상으로 하는 Finocyl 형상은 높은 충진율을 가지며 중립형 면적 선도를 구현하는 것이 용이해 널리 활용되는 형상이다. 또한 일부 연구에서 특정한 설계 및 제작 조건에 따라 이중추력형 면적 선도도 발생 시킬 수 있는 것으로 보고된 바 있다[3]. 하지만 Finocyl 형상은 Fig. 1에 보이는 것과 같이, Cylinder-Taper-Slot 구간으로 구성된 복잡한 형상으로, 변수에 따른 면적 선도 변화 경향성을 파악하기 어렵고 형상 변수가 매우 많아 체계적인 분석의 사례가 많지 않다. 이로 인해 Finocyl 형상 설계는 주로 설계자의 경험에 의존하여 반복 설계를 통해 진행된다[2]. 이러한 기존의 설계 방식은 설계 피로도가 높고 설계자의 역량에 따라 설계 완성도가 상이한 문제가 있다.
이와 같은 문제를 해결하기 위해 최근 최적화 기법을 적용한 해외 사례가 일부 있으나 관련 연구는 많지 않다. 보고된 연구에서는 그레인 형상을 단순화한 후 이론적 Burn-back 해석을 수행하거나 수치적 방법에 최적화 기법을 적용해 중립형 Finocyl 형상을 탐색하는 것이 가능함을 보였다[4,5]. 하지만 기존 연구들의 경우 최적화 결과가 미흡하거나 중립형 형상을 탐색하는 것이 가능함을 보이는 정도에 그쳤으며, 구체적인 최적화 설계 기법을 제공하고 있지 않다. 이에 본 연구에서는 유전 알고리즘을 이용한 최적화 기법을 통해 중립형 및 이중추력형 면적 선도를 갖는 Finocyl 그레인의 형상 변수를 안정적으로 탐색할 수 있는 방안을 제시하고자 하였다.
2. Burn-back 자동화 해석
2.1 Finocyl 형상
Fig. 1은 대표적인 Finocyl 그레인 형상으로, 빨간색 내부 면이 연소가 이루어지는 면에 해당한다. 본 연구에서는 최적화 설계를 위해 설계 제한조건으로서 그레인 직경과 길이를 120 mm, 450 mm로 임의 설정하였다.
2.2 Burn-back 자동화 해석 프로그램
Burn-back 해석에서 일반적으로 연소면 변화는 연소면으로부터 수직하게 일정 길이만큼 이동하는 것으로 가정한다. 작도형 Burn-back 해석은 주로 CAD 프로그램의 내장기능인 Offset을 이용하여 연소를 묘사한다. Offset 기능은 작도 형상을 설정한 길이만큼 평행이동하여 확장, 축소시키는 기능이며 연소면 이동의 가정을 정확히 묘사한다. 또한 CAD 프로그램은 선택 면에 대한 면적정보를 제공한다. 따라서 CAD 프로그램을 이용하여 작도형 Burn-back 해석을 진행하면 초기 형상을 작도하여 연소면적을 획득한 후, Offset 하고 다시 연소면적을 획득하는 과정을 자동으로 반복하도록 할 수 있다.
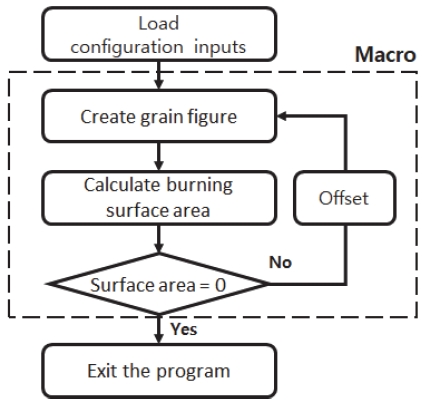
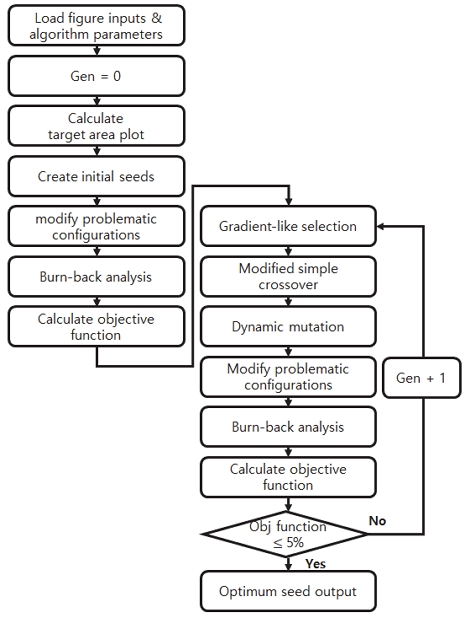
본 연구에서 Burn-back 해석은 선행 연구로 개발⋅검증한 Burn-back 자동화 해석 프로그램을 사용하였다. 앞서 언급한 자동화 해석 프로그램은 그레인 형상을 Input으로 획득해, 초기 형상 작도, Offset, 면적 획득의 과정을 그레인 형상이 모두 삭제될 때까지 반복하여 연소면적 선도를 획득한다. 이와 같은 일련의 과정은 Fig. 2에 제시하였다.
2.3 가변형 Offset
Burn-back 해석에서 Offset 간격을 조밀하게 설정하면, 작도해야하는 케이스가 많아져 해석 시간이 증가하게 된다. 반대로 Offset 간격을 너무 크게 하면 해석 정확도가 떨어지는 문제점이 있다. 따라서 본 연구에 맞도록 Offset 간격을 유연하게 설정할 수 있는 가변형 Offset을 고안하여 적용하였다.
연소면적 선도에서 급격한 면적 변화는 작도 형상의 급격한 부피 변화로 확인할 수 있다. 본 연구에는 CAD 프로그램이 제공하는 부피 정보를 통해 면적 변화량을 예측하고 면적 변화량에 따라 Offset 간격이 조절되도록 하였다. 면적 변화량이 큰 구간은 Offset 간격을 작게, 면적 변화량이 적은 구간은 큰 Offset 간격으로 Burn-back 해석을 진행하도록 설계했다.
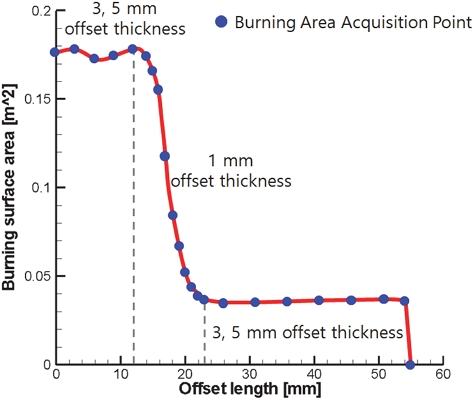
Fig. 3은 이중추력 형상을 설계하는데 있어 가변형 offset을 적용한 결과의 예로, Booster, Sustainer 구간 사이 Transition 구간이 1 mm Offset 간격으로, 나머지 구간은 3 mm 및 5 mm Offset 간격으로 해석되었다. 이를 통해 연소면적 획득 횟수를 줄여 Burn-back 해석 소요 시간을 절감할 수 있도록 하였다.
3. 최적 설계 기법
3.1 유전 알고리즘
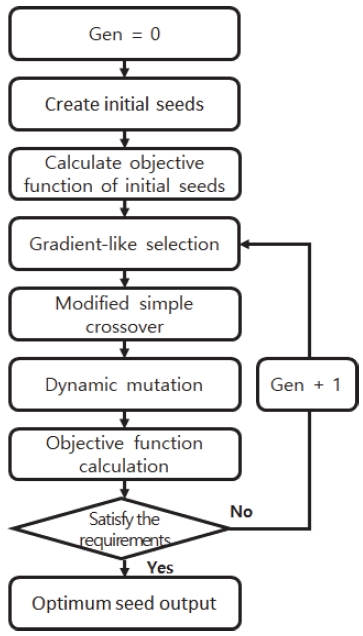
유전 알고리즘은 자연선택과 유전자 법칙을 모사해 정해진 탐색 장 내에서 전역 해를 탐색하는 최적화 기법이며, 다 변수 탐색에 유리해 본 연구의 최적화 기법으로 적합하다고 판단했다[6,7]. 또한 제한된 시간 내에 탐색 능력을 증가시키기 위해 재생성 연산자, 수정 단순 교배, 동적 돌연변이, 엘리트 전략 기법을 적용했다. 탐색 변수는 Finocyl 형상 변수로 설정하여 요구 연소면적 선도와 최소 오차를 갖는 형상을 찾도록 설계하였다. Fig. 4와 같이 유전 알고리즘을 구성하였으며, 그레인 Burn-back 자동화 해석 프로그램을 내장하여 목적 함수를 계산했다.
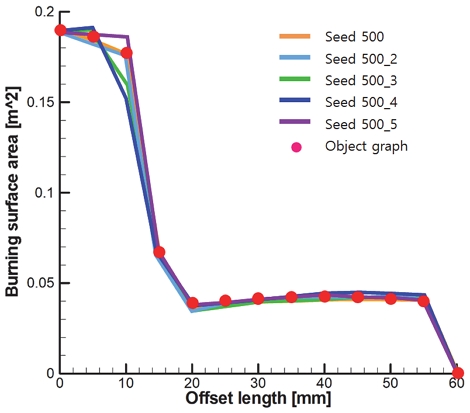
유전 알고리즘 파라미터는 예비 탐색을 통해 적절한 탐색 소요시간과 탐색 정확도를 고려하여 선정했다. Seed 수 500개, 교배 확률 80%, 돌연변이 확률 33%로 설정했다. 탐색 세대수는 목적함수가 일정 기준을 만족할 때까지 탐색을 반복하도록 설정했다. Fig. 5는 해당 조건을 적용한 결과의 예로서, 특정 연소면적 선도의 형상을 찾도록 5회 반복 탐색한 결과이다. 반복 탐색 결과, 5% 내외 편차의 결과를 탐색하였으며, 이에 적용한 파라미터가 적절한 것으로 판단된다.
3.2 탐색 변수
본 연구는 Finocyl의 형상 변수를 탐색 변수로 설정했으며 탐색하지 않아도 될 형상 변수와 탐색할 필요가 있는 형상 변수를 판별하였다. 추진제 그레인의 전체 길이와 외경은 그레인 외형의 크기를 결정하므로, 그레인 형상 설계 이전에 결정되는 제한 조건으로 간주하였다. 또한 추진제 종류가 선정되고 임무에 따라 연소 시간이 결정되면, Web 길이도 결정되어 설계 제한조건이 된다. 본 연구에서 탐색하는 Finocyl의 Web 길이는 추진제 그레인 외경과 내부 Port 직경으로 결정되므로, 추진제 그레인의 길이, 외경, 내부 port의 직경은 탐색하지 않는 변수로 분류하고 임의의 값으로 설정하였다.
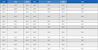
그 외, Finocyl 형상 변수는 다음 Table 2에서 제시한 범위를 탐색하도록 설정하였다. Table 2에서 제시한 탐색 변수는 아래와 같은 의미를 가진다.
- - Front length : Cylinder 형상의 구간 길이
- - Back length : Slot 형상의 구간 길이
- - Slot No. : Slot 가지의 개수
- - Slot 내부 반지름(Inner radius) : Slot 형상의 내부 반지름
- - Slot branch length : 중심점에서부터 Slot 가지 끝까지의 길이
- - Slot width : Slot 가지 두께의 1/2 길이
Fig. 6에 각각의 형상 변수가 갖는 형상적 의미를 그림으로 제시하였다. 제시된 바와 같이, 전체 형상 변수는 탐색 및 비탐색 변수로 구분된다.
3.3 목적 함수
요구 연소면적 선도 설정
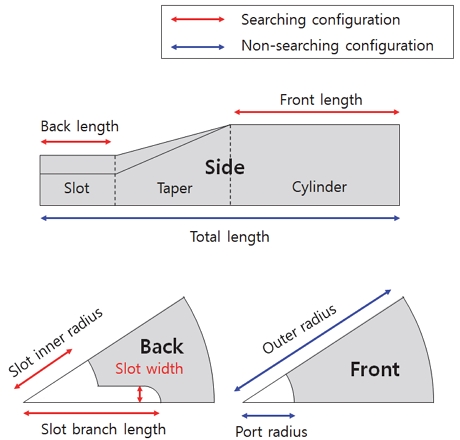
본 연구에서는 요구 연소면적 선도를 입력하면 가장 유사한 면적 선도를 갖는 그레인 형상을 찾도록 설계했다. 본래 연소면적 선도는 특정 임무에 따라 결정되고 그레인 형상은 요구되는 연소면적 선도를 만족하도록 도출된다. 그러나 본 연구에서는 특정 목표를 만족하는 설계형상을 도출하는 것보다는 그레인 형상 설계에 있어 적절한 최적화 설계 기법을 개발하는 것을 연구 목표로 하고 있어, 임무를 특정하지 않고 충진율을 도입하여 요구 연소면적 선도를 도출했다. 충진율은 연소실 부피 대비 그레인이 차지하는 부피의 비율로, 충진율에 의한 추진제의 부피는 총 연소면적 선도의 적분 값과 동일한 개념을 갖는다. 따라서 충진율이 결정되면 총 연소면적 선도의 적분 값이 결정될 수 있고 이를 만족하는 중립형 또는 이중추력형의 원하는 연소면적 선도를 도출할 수 있다. Fig. 4는 충진율의 개념과 그레인의 최적 형상 설계를 대상으로 하는 요구 연소면적 선도를 도출한 결과를 나타낸다. 충진율은 Finocyl 형상을 고려하여 임의로 80%로 설정했다.
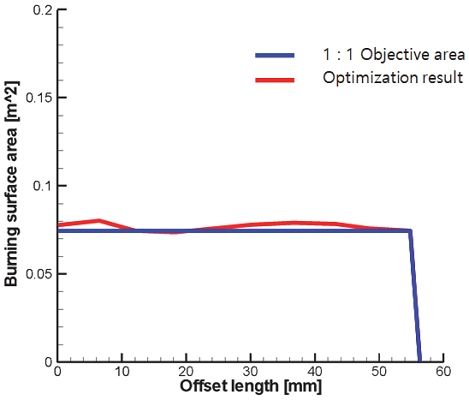
이에 따라 중립형 선도의 경우는 Fig. 7(a)와 같이 Web 길이 55 mm를 만족하는 요구 연소면적이 도출된다. 이중추력형의 경우는 Booster 구간과 Sustainer 구간의 비를 요구하는 추력비 또는 면적비에 따라 설정하여 도출한다. Fig. 7(b)의 경우는 면적비 5 : 1의 선도를 도출하는 예를 나타낸다.
목적 함수 설정
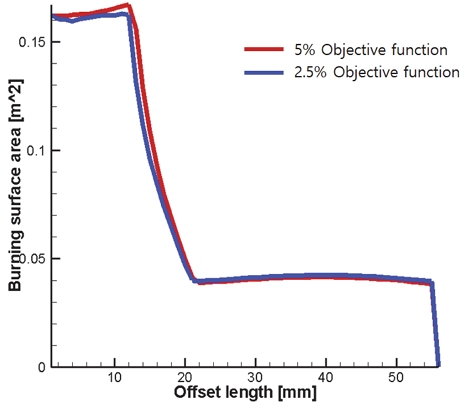
유전 알고리즘을 사용할 때, 사용자의 의도에 맞는 탐색을 수행하기 위해선 적절한 목적 함수를 설정하는 것이 중요하다. 본 연구에서는 목적 함수를 Eq. 1과 같이, 요구 연소면적을 목표로 하고 Seed에 따라 입력된 그레인 형상의 연소면적과의 평균 오차로 설정했다. Seed에 입력된 형상은 Burn-back 자동화 해석 프로그램을 통해 연소면적을 획득하게 되는데, 앞서 언급한 가변형 Offset 간격에 따라 연소면적을 획득한다. 1 mm(Transition), 3 mm, 5 mm(Booster, Sustainer) 간격으로 입력된 연소면적 데이터를 다시 1 mm Offset 간격으로 Interpolation을 수행한다. 이후 전체 Offset 구간을 1 mm 간격으로, 요구 연소면적과의 평균 오차를 목적함수로 계산한다. 계산된 목적함수가 특정 기준 이하인 경우 탐색을 종료하도록 설정 했으며 목적함수 기준 2.5%와 5% 이하의 경우를 비교했다. 아래 Fig. 8은 각각 목적함수가 2.5%, 5% 이하일 때 탐색을 종료토록 한 4 : 1 면적비를 탐색결과이다. 목적함수 5% 기준은 약 20세대 동안 반복 탐색한 반면, 2.5%는 37세대를 반복하여 탐색했다. 본 연구는 최적 설계 방법에 대한 연구이므로 목적함수 5% 이하를 도달할 때까지 탐색을 진행하면 탐색을 종료하고 설계 요구조건을 달성한 것으로 간주했다.
| (1) |
3.4 작도 불능 형상 변수 제어
Seed 교배 및 돌연변이를 통해 생성된 형상 변수는 기하학적 작도 가능 여부를 고려하지 않기 때문에 작도가 불가능한 형상이 발생할 수 있다. 작도 불가능한 형상 변수를 가진 불량 Seed는 전체 Seed 수 500개 중 적지 않은 부분을 차지하여 탐색 성능을 떨어트리는 주요 원인이 된다. 따라서 본 연구에서는 작도 불가능한 Seed를 판별하여, 작도가 가능한 형상으로 수정하는 기능을 적용하였다.
비정상 그레인 길이 조합
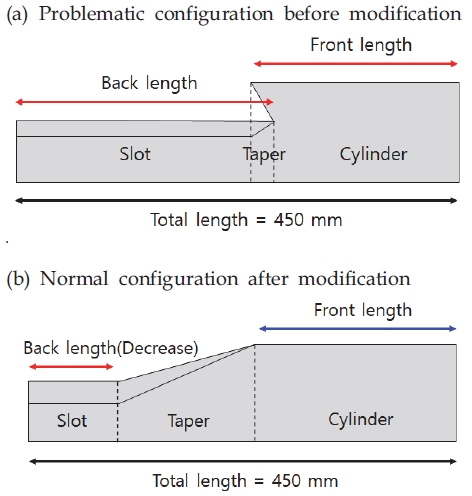
Cylinder 구간 길이(Front length)와 Slot 구간 길이(Back length)의 합이 그레인 전체 길이 450 mm를 넘는 경우, 해당 형상은 작도가 불가능한 형상이다. 이와 같은 경우 랜덤 함수를 이용하여 두 구간 중 하나의 구간 길이를 선택한 뒤, 작도가 가능한 길이 중 랜덤으로 형상 변수를 수정하도록 하였다. Fig. 9는 작도가 불가능한 형상을 제어한 예시로, Cylinder 구간이 선택되어 작도 가능한 길이로 수정되었다.
비정상 Slot 두께(width)
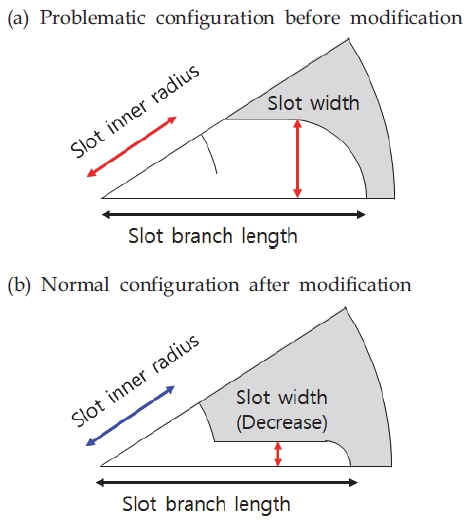
Slot 두께 두꺼운 형상에서 일부, Slot 내부 반지름(Inner radius)를 넘어서는 경우가 발생한다. 이 때 Slot 두께를 랜덤한 두께로 감소시켜 정상적인 형상으로 변경되도록 하였다. Fig. 10은 비정상적으로 두꺼운 Slot 두께를 감소시켜 작도 가능한 형상으로 제어한 예를 나타낸다.
비정상 Slot branch 길이
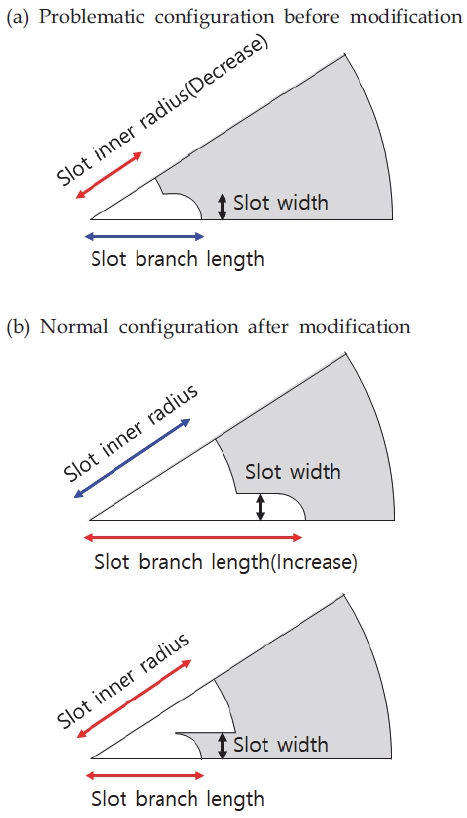
Slot의 Branch와 내부 반지름의 길이 관계에 따라 비정상 형상이 작도될 수 있다. Slot branch 길이가 내부 반지름보다 짧게 되면 Slot branch가 내부 반지름 안으로 매몰된 비정상 형상이 작도된다. 이와 같은 경우 랜덤으로 Slot branch 또는 내부 반지름을 선택하고 Slot branch가 선택되면 랜덤 값으로 증가, 내부 반지름이 선택되면 랜덤 값으로 감소시켜 정상적인 형상이 유도되도록 하였다. Fig. 11은 앞서 언급한 매몰된 형상과 Slot branch 또는 내부 반지름을 조절하여 수정한 예를 나타낸다.
작도 불능 형상 변수를 제어함으로써 초기 Seed 500개 중 불량 Seed를 약 420개를 모두 제어하여 정상 형상으로 수정했다. 이로 인해 작도 가능한 정상 Seed만 탐색할 수 있도록 하였고, 결과적으로, 적은 Seed 수(500개)로 탐색해도 편차 5% 내외의 결과를 획득할 수 있었다.
4. 최적 설계 결과
4.1 최적 설계 프로그램
본 연구에서는 Burn-back 자동화 해석 프로그램에 유전 알고리즘을 적용하여 최적 설계 프로그램을 개발했다. Fig. 12는 최적화 설계 절차를 나타낸다. 설계 형상은 대표적인 중립형 그레인 형상인 Finocyl을 채택했다. 유전 알고리즘의 목적 함수는 요구 연소면적과 평균 오차로 설정해 최솟값 탐색을 수행했다. 또한 소요시간을 단축시키기 위해 가변형 Offset, 작도가 불가능한 형상에 대해서는 변수 제어를 통해 적은 Seed로 우수한 결과를 획득할 수 있도록 최적화 프로그램을 구성했다.
4.2 중립형, 이중추력형 형상 탐색
본 최적 설계 프로그램의 탐색 능력을 확인하기 위해 1∼5 : 1의 면적비를 갖는 중립형 및 이중추력형 연소면적 선도를 가진 그레인 형상을 탐색했다.
Fig. 13과 Table 3에서 확인할 수 있듯이, 중립형 형상 탐색결과 모든 Offset 지점에서 요구 연소면적과의 오차가 4% 이하였다. 본 탐색에선 450 mm 길이의 그레인에 충진율을 80%을 가정하여 탐색했지만, 설계자 조건에 맞는 그레인 길이와 충진율을 고려하여 요구 면적 선도를 수정하면, 설계자가 원하는 크기의 중립형 연소면적을 가진 형상도 충분히 탐색할 수 있을 것으로 예상된다.
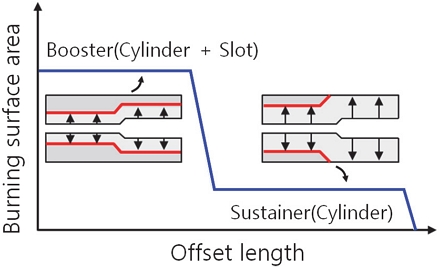
일반적으로 이중추력형 선도는 Sustainer 구간에서 end burning 형태의 추진제 형상을 이용하지만, 경우에 따라서는 추력 요구 조건이나 추진제 연소속도 조건에 따라 Finocyl 형상의 그레인으로도 구현이 가능하다. 탐색으로 획득한 Finocyl 그레인을 통해 이중추력형 연소면 형상에 대한 경향성을 파악했다. Fig. 14에 Finocyl 그레인에서 발생되는 이중추력형 연소면이 형성되는 과정을 도식화하였다. Booster 구간에서는 Slot 구간과 Cylinder 구간이 모두 존재해 높은 연소면적을 발생시키며, Sustainer 구간은 Slot 구간은 모두 연소되어 남은 Cylinder 형상이 연소하며 낮은 연소면적을 발생시킨다. 이 사이, Slot 형상이 사라지는 과정에서 Transition 구간이 형성된다.
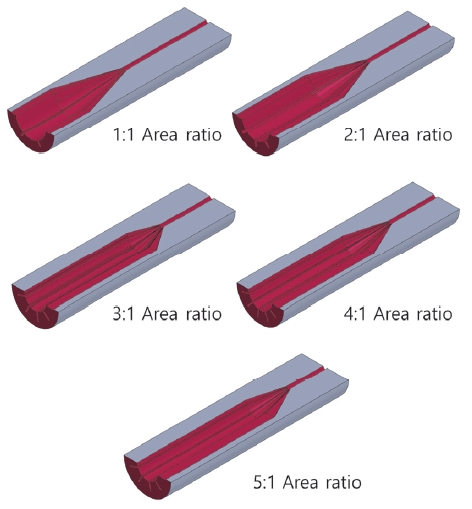
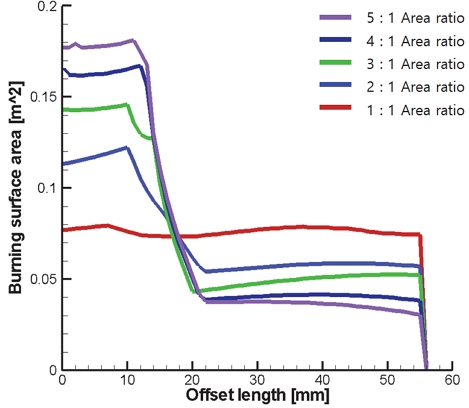
Fig. 15에 1∼5 : 1의 면적비를 갖도록 탐색된 초기 추진제 그레인의 형상을 제시하였다.
면적비가 높아질수록 Sustainer 연소면적이 낮아지게 되는데, 이는 설계 제한 조건으로 추진제 그레인이 동일한 길이와 부피에서 요구 연소면적 선도를 산출했기 때문이다. 높은 면적비가 요구되면 Sustainer 연소면적이 감소되도록, Sustainer 구간에서 연소되는 Cylinder 구간의 길이가 감소하게 된다. 반대로 높은 Booster 구간 요구 연소면적이 커져 Slot 구간의 길이가 길어짐을 확인할 수 있다. 따라서 Finocyl 그레인의 전체 길이를 증가시키고 Slot 구간 길이를 조절하여 Cylinder 구간 길이를 확보하면, 설계자가 원하는 면적비의 이중추력형 그레인 형상을 획득할 수 있을 것으로 예상된다.
5. 결 론
본 연구에서는 Burn-back 자동화 해석프로그램에 유전 알고리즘을 적용하여 Finocyl 형상에 대한 최적 설계 프로그램을 개발하였다. 안정적인 탐색을 위해 가변형 Offset, 작도 불능 형상 변수 제어 기법을 개발했다. 1∼5 : 1 중립형 및 이중추력형 형상을 탐색하여 성능을 확인하였고, 요구조건을 만족하는 형상을 획득했다. 설계된 형상을 분석하여 중립형 형상뿐만 아니라, 사용자가 원하는 면적비의 형상도 충분히 설계가 가능함을 확인했다. 본 연구를 통해, 설계자 경험의 영역이었던 그레인 형상 설계에 기계학습을 적용하여 요구 조건을 만족하는 그레인 형상 설계 방법을 제시하였다. 이는 다양한 요구 추력 프로파일을 만족하는 그레인 형상 설계에 도움이 될 것으로 기대된다.
Acknowledgments
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NO. 2021R1A2C1095356).
References
-
Oh, S.H., Kim, Y.C., Cha, S.W. and Roh, T.S., “Study of Hybrid Optimization Technique for Grain Optimum Design,” International Journal of Aeronautical and Space Sciences, Vol. 18, No. 4, pp. 780-787, 2017.
[https://doi.org/10.5139/IJASS.2017.18.4.780]

-
Park, C.W., Roh, T.S., Lee, H.J. and Jung, E.H., “Analysis of Burn-back Tendency on the Finocyl Grain,” Journal of the Korean Society of Propulsion Engineers, Vol. 25, No. 2, pp. 55-65, 2021.
[https://doi.org/10.6108/KSPE.2021.25.2.055]

-
Lee, D.H., Yoon, M.W. and Hwan, K.S., “Development of the Dual-Thrust Rocket Motor,” Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 32, No. 9, pp. 130-135, 2004.
[https://doi.org/10.5139/JKSAS.2004.32.9.130]

-
Khurram Nisar, Liang Guozhu and Qasim Zeeshan, “A Hybrid Optimization Approach for SRM FINOCYL Grain Design,” Chinese Journal of Aeronautics, Vol. 21, No. 6, pp. 481-487, 2008.
[https://doi.org/10.1016/S1000-9361(08)60164-8]

-
Saeed Mesgari, Mehrdad Bazazzadeh and Alireza Mostofizadeh, “Finocyl Grain Design Using the Genetic Algorithm in Combination with Adaptive Basis Function Construction,” International Journal of Aerospace Engineering, Vol. 2019, 2019.
[https://doi.org/10.1155/2019/3060173]

-
Kim, S.M., Young, M.C., Roh, T.S. and Choi, D.W., “A Study on Diagnostics of Single Performance Deterioration of Aircraft Gas-Turbine Engine Using Genetic Algorithms,” Journal of The Korean Society Aeronautical and Space Sciences, Vol. 35, No. 3, pp. 238-247, 2007.
[https://doi.org/10.5139/JKSAS.2007.35.3.238]

- Jin, K.K., Genetic Algorithms and Their Applications, 1st ed., Kyowoo Inc., Seoul, S.E.L., Korea, Cp. 5, 2002.