공통격벽 추진제 탱크 구조의 좌굴 Knockdown Factor 도출 연구

2.1 임계 좌굴 하중 수식화

균일한 압축 하중이 작용하는 실린더(perfect shell)의 고전 선형 좌굴 응력은 다음과 같다.

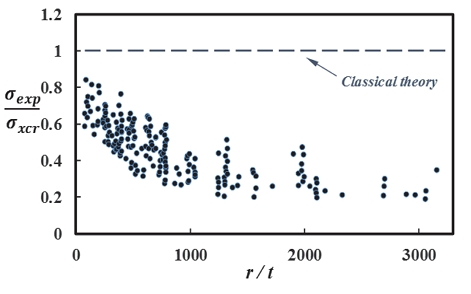
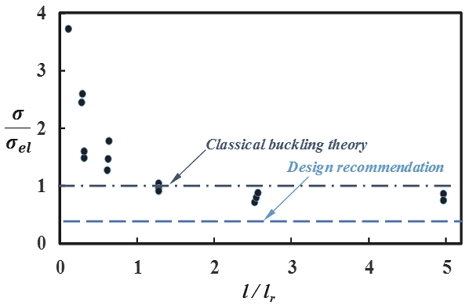
초기 결함이 없는 완전한 실린더의 전역 좌굴 응력인 Eq. 1의 값은 Fig. 1에서 보이듯이 실험값보다 높은 값을 가지며 실험값과의 비가 두께비에 따라 감소하는 경향을 보인다. Fig. 2에서는 실린더 길이에 대한 좌굴 영향을 보이고 있는데 참조길이$$ \left(l_r=4\sqrt{rt}\right)$$에 대한 비가 1보다 작은 즉 실린더 길이가 아주 짧은 경우를 제외하고는 길이에 의한 좌굴 영향은 없으며 Fig. 1과 같이 이론값은 실험값보다 높은 값을 보인다. 이처럼 선형 좌굴 해석값과 좌굴 시험값의 차이를 발생시키는 인자는 초기결함으로 이는 실린더 구조의 좌굴 하중을 감소시킨다. 따라서 실린더 구조 설계 시에는 Eq. 2와 같이 초기 결함에 따른 좌굴 하중의 감소 비율이 반영되어야 하고 이를 knockdown factor로 정의한다.

Fig. 1

Early tests with axially loaded cylinder shells[7].

Fig. 2

Experimental resistance of shells with r/t=400 versus the length of the shell[8].

초기 결함은 구조물에 기하 비선형성으로 반영되는데 초기 결함 구조의 임계좌굴하중을 다음과 같이 수식으로 확인할 수 있다. 단, 구조거동은 선형으로 가정한다.

구조물이 평형을 유지하고 있는 임의의 상태는 기본 상태이고, 섭동하중(perturbation load) Δp를 가한 상태를 섭동상태라 정의한다. 섭동하중에 의해 발생하는 응력 변화와 변위 변화를 각각 Δσ, Δu라고 하면 구조물은 선형거동을 하므로 섭동하중 λΔp에 의해 발생하는 변화는 λΔσ, λΔu이다. 이때의 평형방정식은 다음과 같다.

여기서 T_ij는 1차 Piola-Kirchhoff 응력을 나타내고, $$ \overline{t_j}$$는 공칭 트랙션(nominal traction), n_i는 법선벡터를 나타낸다. 위 식에 가상변위(virtual displacement) w_j를 적용하면 다음과 같이 약화식(weak form)으로 표현된다.

이 식을 비율형태(rate form)로 바꾸면 다음과 같다.

현재 상태를 기본 상태로 놓으면 1차 Piola-Kirchhoff 응력은 다음과 같이 나타난다.

여기서 L_ik는 속도구배텐서(velocity gradient tensor)를 나타낸다. 그리고 Kirchhoff 응력의 Truesdell 비율은 다음과 같으므로

이를 이용하여 1차 Piola-Kirchhoff 응력을 다음과 같이 나타난다.

또한, Truesdell 비율은 응력의 객관미분(objective rate)이므로 다음과 같이 구성방정식을 이룰 수 있다.

여기서 C_ijkl은 계수텐서(modulus tensor)이고, D_kl은 변형률 비율텐서(rate of deformation tensor)이다. 공칭 트랙션의 비율은 변형구배텐서(deformation gradient tensor) F_mn의 비율로 다음과 같이 표현된다.

여기서 Nanson 공식을 적용하면 진 트랙션(true traction) $$ \overline{p_i}$$으로 표현될 수 있다.

정리하면 Eq. 6은 다음과 같이 나타난다.

임계점에 대해 두 번째와 세 번째 항을 λ로 묶어 표현하고 유한요소로 근사한 가상변위 w_j와 속도 벡터 v_i를 이용하여 표시하면 다음과 같다.

여기서 [K_B]는 Eq. 13의 첫 번째 항에서의 강성행렬로 정적해석에서 사용하는 강성행렬과 같은 행렬이다. [K_Δ]는 Eq. 13의 두 번째와 세 번째의 행렬로 기하 비선형(geometric non-linearity)에 기인되는 항으로 기하 강성 행렬(geometric stress matrix)이다.

Eq. 14에서 보이는 것처럼 좌굴하중은 고유치 문제로 나타날 수 있으며 첫 번째 고유치에 하중을 곱한 값이 임계좌굴하중이 되며, 첫 번째 고유모드가 좌굴 모드가 된다.

2.2 해석 조건 및 선형 해석 결과

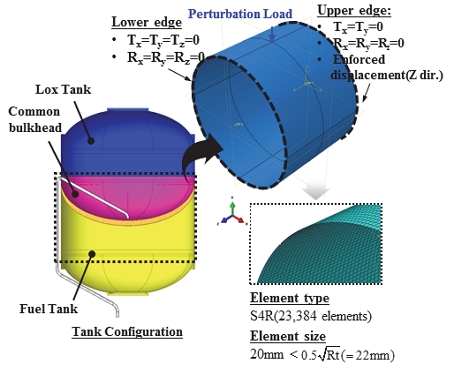
본 연구에서 고려한 공통격벽 추진제 탱크의 실린더는 Fig. 3과 같이 별도의 보강재가 없는 원통형 구조이며 해석에 사용된 유한요소모델 및 해석조건 등을 나타내었다. 유한요소모델은 쉘 요소 중 S4R 요소를 이용하였고 좌굴 하중의 정확성을 위해 실린더 길이 방향으로 요소길이가 $$ 0.5\sqrt{Rt}$$이하[9]가 되도록 구성하여 총 요소 수는 23,384 개이다.

Fig. 3

Configuration and FE model of the cylinder.

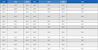
실린더 소재는 알루미늄-리튬 합금으로 재료 물성치와 형상정보는 Table 1과 Table 2에 각각 나타내었다.

Table 1.

Material of the cylinder.

Table 2.

Geometry of the cylinder.

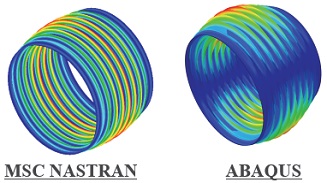
추진제 탱크 실린더의 선형 좌굴 값은 Eq. 15를 통해 계산되며 이는 Table 3에서 유한요소 해석 결과와 비교하여 보여주고 있다. 비선형 좌굴 해석에 적용되는 ABAQUS 모델을 검증하기 위해 선형 좌굴 해석은 MSC.NASTRAN과 ABAQUS를 이용하여 각각 수행되었다. 그 결과 해석 코드별 각 좌굴 하중 값은 거의 동일하며 이론값과 차이가 1% 미만으로 선형 좌굴 하중 및 해석 모델을 검증할 수 있었다. 또한, Eq. 15의 이론값에서 식별되지 않는 좌굴모드를 Fig. 4와 같이 유한요소 해석 결과를 통해 확인할 수 있는데, 해석 코드별 좌굴 모드 형상이 상당히 유사하여 선형 좌굴 해석 결과를 검증할 수 있었다.

Table 3.

Verification of linear buckling analysis.

Fig. 4

Comparison for linear buckling mode shape.

앞에서 계산된 실린더 선형 좌굴 하중은 실제 좌굴 하중값과 차이가 발생되므로 설계 좌굴 하중은 Eq. 2의 knockdown factor(ρ)를 적용하여 Eq. 16과 같이 도출해야 한다.

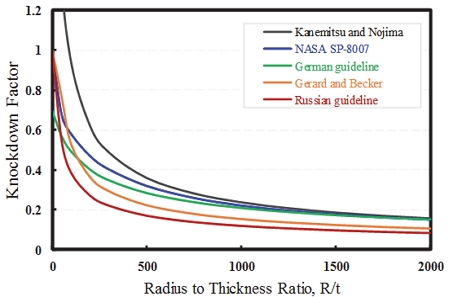
기존에 NASA 등 에서 정립한 knockdown factor(ρ)[1,10-13]는 Fig. 5에서 같이 두께비에 따라 그 값을 보이고 있으며, 본 연구의 구조 대상인 실린더의 knockdown factor 값은 Table 4에서 확인할 수 있다. 그 결과 실린더의 knockdown factor는 방법 별로 0.173에서 0.358로 분포하여 knockdown factor 선정에 대한 고찰이 필요하며 최소값 적용 시 상당히 보수적인 설계가 진행되어 신규 좌굴 설계 기준 마련이 요구된다.

Fig. 5

Comparison for knockdown factor.

Table 4.

Comparison for knockdown factor.

3.1 해석모델 구성

본 연구에서는 공통격벽 추진제 탱크의 적절한 설계 기준을 마련하기 위해 ABAQUS를 이용한 비선형 좌굴 해석을 수행하였다. 해석은 Table 5와 같이 EU 규격인 EN 1993 1-6[5]에서 제시하는 해석 중 앞에서 수행한 선형좌굴해석(LBA) 뿐만 아니라 기하 비선형 해석(GNA), 초기 결함 기하 비선형 해석(GNIA)과 초기 결함 기하/재료 비선형 해석(GMNIA)을 수행하였다. 초기 결함은 구조물에 기하 비선형성을 초래하는데 이를 구현하기 위해 ABAQUS에서는 정적 해석의 변위, 선형 좌굴 모드의 중첩 그리고 불안전성값을 직접 지정하는 방식을 적용할 수 있다. 본 연구에서는 각각의 방식을 적용하여 초기 결함이 구현된 모델을 구성하였다.

Table 5.

Type of analysis for shell buckling.

실린더의 좌굴 거동 확인을 위해 ABAQUS의 Newton-Raphson기법과 변위 제어 방법을 주로 적용하였다. 실린더 양 끝단 중 한 부분은 6개 자유도를 구속하고, 나머지 끝단 부분에는 Z방향으로 강제변위를 인가하고 이외 자유도는 구속하였다. 또한 stabilize방법을 사용하여 국부적 좌굴이 발생하는 부분에 대해 변형률 에너지를 다른 부분으로 전달하거나 감소시키도록 가상 감쇠(artificial damping)를 도입함으로써 특정부분에 불안정성이 집중적으로 발생시키는 것을 완화하고 구조물 형상이 변형이 유발되기 쉬운 방향으로 유도하여 수렴성을 증가시킨다.

3.2 섭동하중 인가 모델(SPLA)

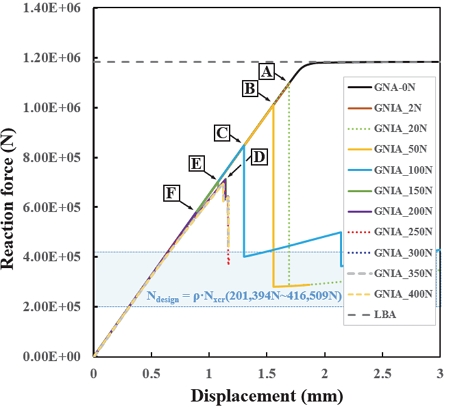
정적 해석 변위로 초기 결함을 구현하는 기법을 이용하기 위해 실린더 측면에 일정의 섭동하중을 인가하고 비선형 정적 해석을 수행 후 변형 형상에 대해 비선형 좌굴 해석을 수행하는 섭동하중 인가 해석 모델을 구성하였다. Fig. 6은 선형좌굴해석(LBA), 기하 비선형 해석(GNA),그리고 섭동하중 인가 모델을 이용한 초기 결함 기하 비선형 해석(GNIA)의 결과를 강제변위에 따른 반력 즉 임계 좌굴 하중으로 보여주고 있다. 섭동하중은 2 N에서 400 N까지 달리하였다.

Fig. 6

Linear and nonlinear buckling analysis result.

기하 비선형 해석(GNA)은 선형좌굴해석(LBA)과 동일하게 구조물을 perfect shell로 정의하나 선형 해석과 달리 큰 변형의 비선형 효과를 고려함과 동시에 그 결과가 다음 과정에 영향을 주는 것으로 해석 결과 임계 좌굴 하중값은 선형좌굴해석(LBA)과 유사하고 거동에서 비선형성이 보인다. 초기 결함 기하 비선형 해석(GNIA)은 섭동하중 증가에 따라 임계 좌굴 하중이 감소하지만 150 N이상에서는 약 700 kN으로 수렴하고 있다. 임계 좌굴 하중은 초기 결함이 있는 모델 즉 섭동하중이 작용하는 경우에 대해서만 감소 경향을 보이며 선형 임계 좌굴 하중에 비해 상당히 작은 2 N 섭동하중 인가에도 유의미한 감소를 보이고 있다.

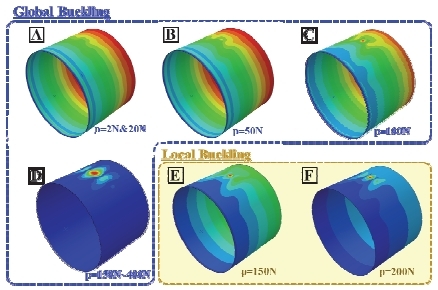
Fig. 7에서는 좌굴모드를 확인할 수 있는데, 섭동하중이 150 N 미만인 A, B, C는 Fig. 4의 선형 좌굴 모드와 유사한 형상의 전역 좌굴이 보이는 반면 150 N 이상의 D에서는 섭동하중 작용부에서 발생한 전역 좌굴 모드로 좌굴 모드가 상이함을 확인할 수 있다. 그리고 좌굴 하중이 수렴되는 섭동하중 150 N과 200 N의 E, F에서는 국부 좌굴이 발생하는데 국부 좌굴 하중 값은 섭동하중이 클수록 낮은 값을 가진다. 섭동하중이 더 커지면 국부 좌굴은 발생하지 않는다.

Fig. 7

Buckling mode shape for nonlinear buckling analysis.

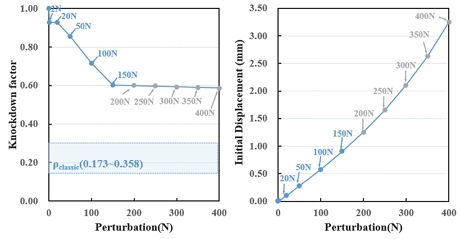
Fig. 8은 섭동하중 증가에 따른 knockdown factor와 초기 변위값을 보이는데, knockdown factor는 섭동하증이 증가할수록 감소하다가 0.6으로 수렴하는 반면 초기 변위는 섭동하중이 증가할수록 지속적으로 증가하여 초기 결함이 점점 커지는 것이 잘 모사되고 있음을 확인 할 수 있다. 이를 통해 일정 크기 이상에서는 좌굴의 영향성이 발생하지 않는 임계 초기 결함 크기가 존재하며, 임계 초기 결함에서는 구조물의 전역 좌굴 모드 형상이 구조 전체에서 결함부로 변경되고 국부 좌굴도 발생됨을 알 수 있었다. 그리고 섭동하중 인가 모델의 knockdown factor는 기존 좌굴 설계 기준인 Table 4의 값 중 최대값인 0.358보다 높은 값을 가지어 경량화가 실현되는 신규 좌굴 설계 기준을 제시한다.

Fig. 8

Knockdown factor and initial displacement according to perturbation load.

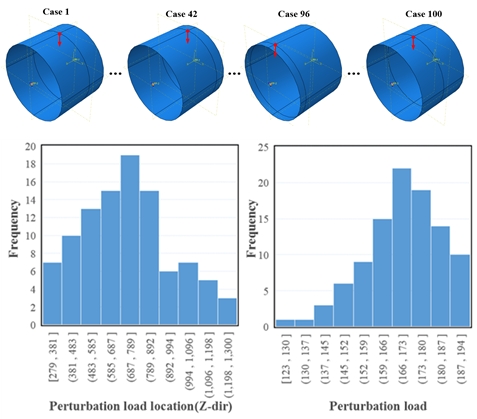
섭동하중 크기 뿐 아니라 작용점 즉 초기 결함 크기와 위치에 따른 조합조건과 좌굴하중의 상관관계를 확인하기 위해 Fig. 9와 같이 몬테카를로 방법을 적용하여 섭동하중의 크기와 위치를 달리한 해석 조건 100가지를 구성하고 해석을 수행하였다. 단, 가상 감쇠는 적용하지 않고 국부 좌굴과 전역 좌굴의 구분 없이 첫 좌굴 모드의 하중을 임계 좌굴 하중으로 간주하였다.

Fig. 9

Histogram of perturbation location and values generated for Monte-Carlo-Method.

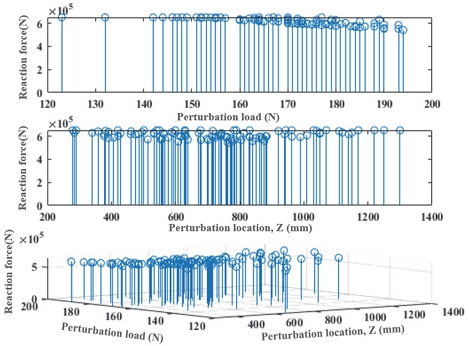
해석 결과 Fig. 10에서와 같이 섭동하중이 증가함에 따라 임계 좌굴 하중은 소폭 감소하는데 이는 국부 좌굴의 영향으로 임계 섭동하중인 150 N에서 200 N사이에서 발생하는 국부 좌굴은 섭동하중이 증가할수록 낮은 좌굴 하중 값에서 나타나 임계 좌굴 하중도 감소하는 경향으로 나타나는 것으로 확인된다.

Fig. 10

Results for the buckling load according to Monte-Carlo-Method.

그리고 실린더 중앙부인 700 mm 주위에는 다른 부위에 비해 낮은 임계 좌굴 하중 결과가 분포하고 있는데, 그 값이 최대값 대비 20% 낮은 값을 가지어 초기 결함 위치에 따른 좌굴 영향성이 존재함을 확인할 수 있었다. 최종적으로 몬테카를로 모델의 평균 knockdown factor는 0.519로 앞선 결과와 유사하게 기존 좌굴 설계 기준의 최대값인 0.358보다 높은 값이 도출되었다.

3.3 선형 좌굴 모드 중첩 모델

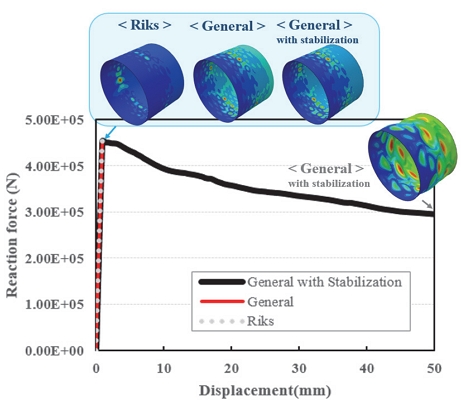
본 연구에서는 선형 좌굴 모드를 이용한 초기 결함 모델을 적용하기 위해 Riks, Newton-Rap son 그리고 Newton-Rapson(stabilize방법) 해석 기법을 각기 적용하고 그 해석 결과를 Fig. 11에 정리하였다.

Fig. 11

Results for the buckling load with a linear superposition of buckling eigenmodes.

Riks는 좌굴현상과 같이 snap-back이 발생하는 거동에 적합한 해석 기법으로 구조물의 변형률에너지(strain energy)를 보존하며 해석을 수행한다.

그 결과 세 기법 모두 거의 동일한 임계 좌굴 하중 값이 도출되며 좌굴 모드도 유사하여 선형 좌굴 모드를 이용한 결함 모델의 좌굴 평가 시 해석 기법에 따른 영향성은 없는 것으로 확인하였다. 단, 기법에 따라 후좌굴 거동에서 차이를 보이고 있으나 본 과제는 knockdown factor 도출이 주요하여 이후 해석에서는 수렴이 빠른 Newton-Rapson 해석 기법을 적용하였다.

선형 좌굴 모드 중첩 기법에는 여러 선형 좌굴 모드를 조합하여 사용하는 방법[14] 또는 첫 번째 모드 사용 방법[15]이 제안되며 Eurocode 3[16]에서는 첫 번째 좌굴 모드와 scale factor 1.0 적용을 추천한다.

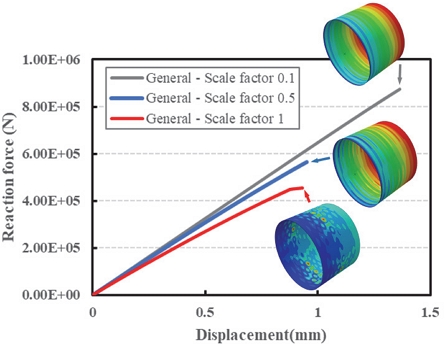
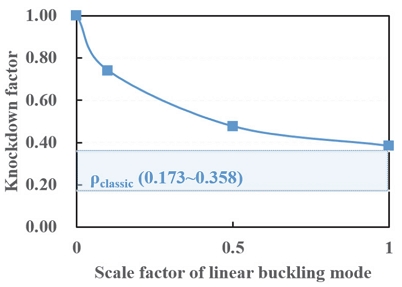
본 과제에서는 첫 번째 선형 좌굴 모드를 이용하였으며, scale factor는 0.1, 0.5 그리고 1.0으로 각기 달리 적용하여 해석을 수행하고 그 결과를 Fig. 12와 Fig. 13에 정리하였다.

Fig. 12

Results for the buckling load according to buckling eigenmodes scale factor.

Fig. 13

Knockdown factor according to buckling eigenmodes scale factor.

해석 결과 scale factor가 커질수록 임계 좌굴 하중 값은 점점 감소하여 scale factor 1.0 적용 조건에서 knockdown factor는 0.383으로 최소값을 보이나 기존 좌굴 설계 기준의 최대값인 0.358보다 소폭 높은 값을 가진다. 해석 모델의 평균 knockdown factor는 0.533으로 도출된다.

좌굴 모드는 scale factor 0.1, 0.5의 경우 Fig. 4의 선형 좌굴 모드와 유사한 형상의 전역 모드가 나타나나 scale factor 1.0의 경우 국부 모드와 전역 모드가 혼재된 형상을 보이고 있어 scale factor 적용 값에 따라 좌굴 모드의 차이가 있음을 확인하였다.

3.4 국부 강성 감소 모델

본 연구에서는 초기 결함을 구현하기 위해 불안전성값을 직접 지정하는 방식의 일환으로 구조물의 국부 강성을 감소시키는 LRSM(Localized Reduced Stiffness Model)을 사용하였다. 이 방법은 Croll[17]이 제안한 것으로 얇은 쉘 구조의 좌굴 하중 하한값을 결정하기 위해 사용된다.

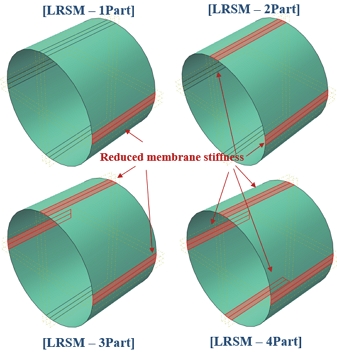
Croll의 의하면 초기결함은 쉘의 멤브레인(membrane)에너지를 약화시키므로 멤브레인 에너지를 제외한 해석을 통하여 좌굴 하중의 하한값을 도출할 수 있다고 한다. Fig. 14는 본 과제에서 적용한 LRSM으로 용접이 예상되는 부분을 1부분에서 4부분까지 확장하여 모델을 구성하고 해당 부분의 ABD 강성 행렬 중 멤브레인 강성에 해당하는 A 행렬을 0.1, 0.05, 0.01, 0.005 로 각각 감소시키어 해석을 수행하고 그 영향성을 확인하였다. 실린더 제작 시 발생되는 용접부는 제작방법과 허용오차에 따라 형상 차이를 유발할 수 있으며 좌굴 하중에도 영향을 미치므로 용접부 형상과 오차를 고려한 reduction factor를 적용하는 좌굴평가식이 이용되기도 한다[8].

Fig. 14

Localized reduced stiffness model due to weld lines.

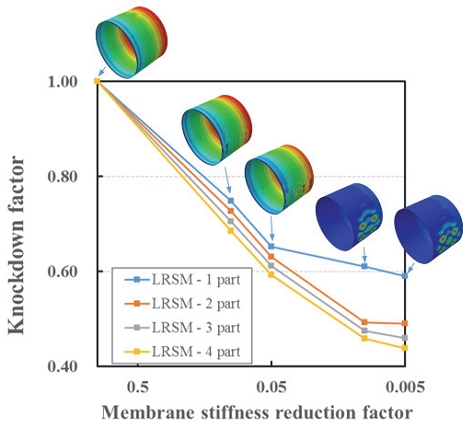
해석 결과 멤브레인 강성 감소 영역이 증가할수록 knockdown factor는 감소하며, 강성 감소 계수 0.1에서 0.005로 작아질수록 knockdown factor도 감소하다 수렴하는 경향을 Fig. 15에서 확인할 수 있다. 좌굴 하중의 하한값은 네 부분의 멤브레인 강성이 0.5%까지 감소한 조건(LRSM-4part)의 knockdown factor 0.44로 도출하였다.

Fig. 15

Knockdown factor according to localized reduced stiffness model.

3.5 재료 비선형 모델

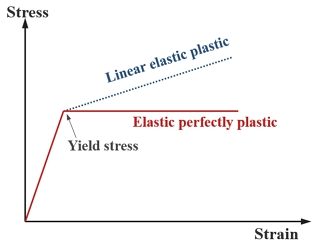
마지막으로 본 연구에서는 추진제 탱크 실린더 구조의 좌굴 설계를 위해 Fig. 16과 같이 재료를 탄-완전소성체(Elastic perfectly plastic)로 가정한 초기 결함 기하/재료 비선형 해석(GMNIA)을 수행하였다.

Fig. 16

Stress-strain curve for GMNIA.

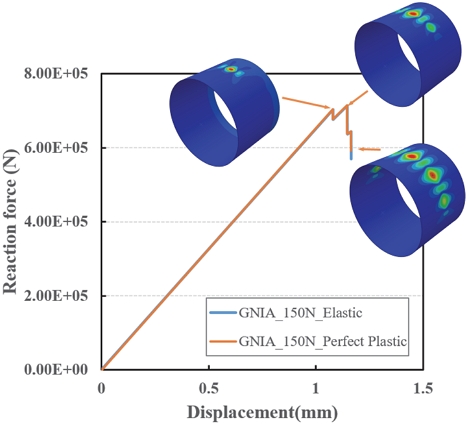
앞서 초기 결함 비선형 모델(GNIA) 중 임계 섭동하중인 150 N이 인가되는 모델에 탄-완전소성을 적용하여 해석한 결과, Fig. 17에서 보이듯이 탄성 모델의 좌굴하중 및 거동과 동일하게 나타남을 알 수 있다. 따라서 본 연구 대상인 실린더 구조 형상에서는 재료 비선형에 대한 영향성은 없는 것으로 판단된다.

Fig. 17

Results for the buckling load with a linear superposition of buckling eigenmodes.

3.6 해석 결과 비교

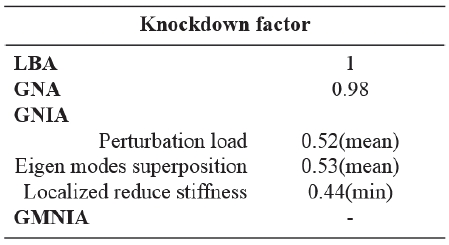
본 연구에서 도출된 실린더 구조의 다양한 해석 모델에 대한 좌굴 knockdown factor의 비교 결과를 Table 6에 나타내었다. 기하학적 비선형 해석(GNA)은 선형해석(LBA)과 거의 차이가 없으나 초기 결함이 반영된 해석(GNIA)에서는 좌굴 하중이 감소되어 모델별로 0.44에서 0.53으로 유사한 수준의 knockdown factor가 도출되었다. 본 연구에서 도출된 knockdown factor는 발사체 구조 설계에 주로 적용되는 기존의 NASA 설계 기준(0.321)보다 최소 37%에서 최대 65%만큼 높은 값을 보인다. Wagner[18]의 돔 구조 좌굴 연구에 의하면 LRSM 해석 결과는 실험값 보다 약간 보수적인 knockdown factor를 도출하여 새로운 좌굴 설계 기준으로 적합하다고 제시하고 있다. 따라서 본 과제에서의 초기 결함 기하 비선형 해석(GNIA) 결과 중 LRSM의 결과인 0.44의 knockdown factor를 신규 실린더 구조 설계 기준으로 적용 가능하다고 판단된다. 그리고 신규 knockdown factor 0.44 적용 시 기존 설계 기준(0.321)보다 중량은 15% 감소하여 경량 설계가 이루어짐을 확인하였다.

Table 6.

Comparison of knockdown factor.