Finocyl 그레인의 Burn-back 경향성 분석

2.1 Finocyl 형상

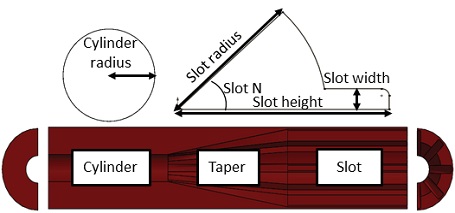
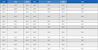
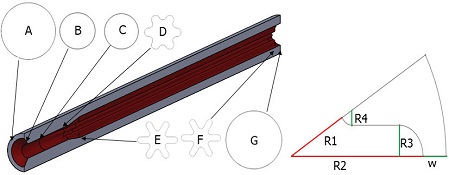
Fig. 1은 Finocyl 그레인의 대표적인 형상을 나타낸다. 일반적으로 Finocyl 형상은 실린더, 테이퍼, 슬롯으로 구성된다. Table 1은 Finocyl 그레인의 형상 변수를 정의하였다. 본 연구에서는 형상 변수가 연소면적선도에 미치는 영향을 파악 하는 것을 목적으로 하고 있으므로, 추진제 그레인의 외부 직경을 고정하고 형상의 길이를 포함한 다른 형상 변수들을 변경하는 것으로 설정하였다. 본 연구에서 적용된 추진제 그레인의 외경은 전술급 유도무기 직경을 감안하여 임의로 120 mm로 설정하였다. 이후 모든 변수는 설계 및 제작 가능한 영역을 고려하여 변화시킬 수 있도록 설정하였다. 변수 설정에 있어서는 상호 종속적인 관계를 고려하였다. 예를 들어, 실린더 길이, 테이퍼 길이, 슬롯 길이는 전장길이가 고정되어 있으므로 서로 종속적인 관계를 가진다. 따라서 한 개의 변수를 고정시키고 나머지 한 개의 변수를 조절하면 자동적으로 남은 한 개의 변수도 결정된다.

Fig. 1

Finocyl grain configuration.

Table 1.

Variables of Finocyl grain.

2.2 해석방법

앞서 언급한 바와 같이, 연소면적선도를 구하는 과정을 Burn-back 해석이라 한다. Burn-back 해석은 수행방법에 따라 수치적(Numerical), 이론적(Analytical), 제도(Drafting) 방법으로 구분된다. 수치적 방법의 경우 해석이 정확하며 3차원의 복합적 형상을 해석할 수 있으나 해석시간이 오래 걸리며 격자크기에 따라 오차가 발생한다는 단점이 있다[6,8,9]. 이론적 방법은 기하학 해석에 근거하므로 해석값이 정확하며 계산시간이 빠르지만 매우 복잡한 형상을 갖는 그레인의 경우 해석이 어려워 해석 가능한 형상이 제한적이다[10,11]. 제도방법은 CAD프로그램을 이용하는 방법으로 해석이 정확하고 다양한 형상을 해석할 수 있다. 하지만 연소형상의 변화 과정을 반복적으로 모델링하고 연소면적을 기록하는 과정에서 상당한 피로감을 느끼며 수동 처리의 경우 시간이 매우 오래 걸리는 단점을 갖는다. 이에 본 연구에서는 다양한 형상 변수에 대해 설계 가능한 영역에서 변수에 따른 해석을 빠르고 용이하게 수행하기 위해 제도 방법의 자동화 프로그램을 개발하여 적용하였다.

자동화 제도(Drafting) 기법

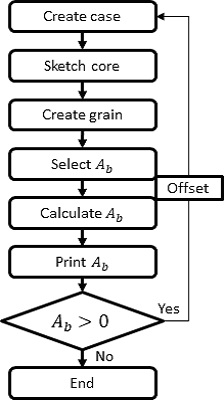
제도 기법을 이용한 Burn-back 해석은 CAD 프로그램에 내재되어 있는 offset 기능을 사용한다. Offset 기능을 사용하면 기존 스케치형상이 입력한 길이만큼 수직방향으로 증가한다. 실제 추진제가 연소할 경우 각각의 연소면에 수직한 방향으로 연소가 진행되는 것으로 가정하므로 연소환경을 모사하기에 적합한 방법이다. CAD 프로그램을 이용한 구체적인 해석방법은 Fig. 3에 명시된 순서로 진행된다. 첫 번째로 추진제에 해당하는 외형을 생성한다. 다음으로 그레인 코어를 스케치하여 그레인 형상을 완성한다. 마지막으로 연소하는 면의 면적을 계산하여 기록한다. 이후 offset 길이를 늘려가며 같은 과정을 반복수행 한다.

본 연구에서 사용한 CAD 프로그램은 내부적으로 API(Application Programming Interface) 기능과 매크로를 제공한다. API는 Microsoft 기반 언어인 Visual Basic 으로 구성되어 있다. 본 연구는 API 기능을 활용하여 Burn-back 해석의 전 과정을 코드로 구성하여 자동화 하였다. 하지만 API는 내부적으로 Spread sheet를 제공하지 않기 때문에 후처리를 통하여 연소면적을 계산하였다.

Fig. 2

Flow chart of Burn-back analysis.

2.3 주요 연소현상 모사방법

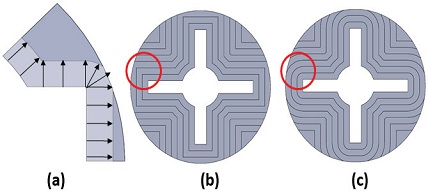
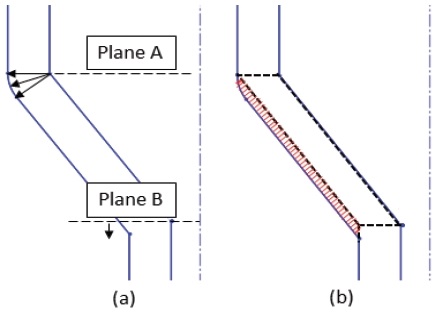
Offset을 통해 연소과정을 모사할 경우 직각 형상을 갖는 그레인 형상의 경우 오류가 발생한다. 그레인 형상의 직각 부분은 실제 연소 시 Fig. 3(a)처럼 연소가 진행되는 것으로 모사할 수 있다. 하지만 offset 기능을 사용할 경우 Fig. 3(b)와 같이 round effect가 재현되지 않아 오차의 원인이 된다.

Fig. 3

Round effect for burn-back process.

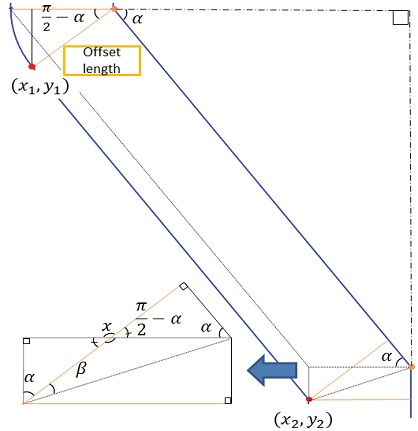
선행연구[3]의 경우, 초기 형상에 직각 영역을 작은 원형으로 대처하여 관련 문제를 해결하였다. 본 연구에서는 초기 형상에서의 정확도를 향상시키기 위해 첫 offset 이후, Offset 길이만큼 원형으로 대처하여 해석이 진행될 수 있도록 설정하였다. Finocyl과 같은 복합형상은 실린더와 슬롯의 중간 Taper 영역에서도 round effect가 발생할 수 있다. Fig. 4는 형상의 Taper 구간에서 발생할 수 있는 round effect를 도식화하였다. 평면A구간은 연소가 진행됨에 따라 round effect가 발생하며 평면B구간은 round effect가 발생하지 않지만 평면의 위치가 아래로 내려온다. offset 기능만을 이용할 경우 iteration이 진행될 때마다 기존평면A, B에 스케치를 생성하게 된다. 하지만 실제연소과정은 Fig. 4(a)와 같이 일어난다. 기존평면에 스케치를 하는 경우와 실제연소과정을 비교하면 Fig. 4(b)의 빗금 친 부분과 같은 연소면적의 차이가 발생하게 된다. 이를 해결하기 위해 Fig. 5처럼 기하학적 관계를 분석하여 두 지점의 좌표를 구하였으며 이를 이용하여 새로운 평면을 만들어 정확도를 향상시켰다.

Fig. 4

Drafting error for the tapered configuration.

Fig. 5

Schematic of geometric relationships.

2.4 자동화 프로그램 성능 검증

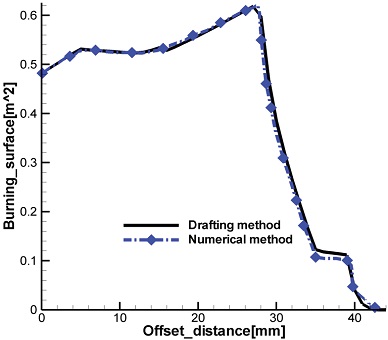
본 연구에서 구성한 프로그램을 검증하기 위해 복잡한 구성요소로 복합되어 있는 NAWC no.6 그레인 형상을 선정하였다. NAWC no.6는 총 7곳에서 형상의 변화가 발생하며 구체적인 형상변수는 Table 2에 나타내었다. 기존 참고문헌[12,13]에서 수치적 방법을 이용하여 해석한 결과와 본 연구에서 구성한 자동화 프로그램을 이용하여 도출한 결과를 Fig. 7에 나타내었다. 해석결과 offset distance 34 mm 이후 구간에서 미세한 차이가 관찰되는데, 이는 수치적 기법의 수치적 오차에 의한 것으로 분석되며 두 방법 간 오차는 1.7%로 나타났다. 이상의 검증 결과에 따라 개발한 제도 기법의 자동화 프로그램은 복잡한 3차원 형상에 대한 정밀한 Burn-back 해석이 가능할 것으로 판단된다.

Table 2.

NAWC no.6 variables.

Fig. 6

NAWC no.6 grain configuration.

Fig. 7

Comparison of burn-back results.

3.1 Finocyl 형상 경향성 분석

Finocyl형상의 형상변수 중 슬롯의 개수(Slot N), 슬롯 영역의 길이, 슬롯 폭(Slot width), 슬롯 높이(Slot height), 슬롯 반경(Slot radius), 실린더 반경(Cylinder radius)에 대하여 경향성 분석을 수행하였다. 경향성 분석 진행 시, 설계 변수와 연관 변수를 제외하면 나머지 변수들은 비교를 위해서 고정되어야 한다. 이에 기본 변수 값은 Table 3에 명시하였다. 예를 들어, 슬롯의 개수에 따른 연소면적선도의 변화를 관찰할 때 Slot N을 제외한 나머지 변수는 Table 3에 제시된 값에 해당한다. 해석 결과의 이해를 돕고자 각 분석결과 그래프 내에 변수값에 해당하는 부분을 그림으로 표시하여 제시하였다.

Table 3.

Variables of Finocyl grain.

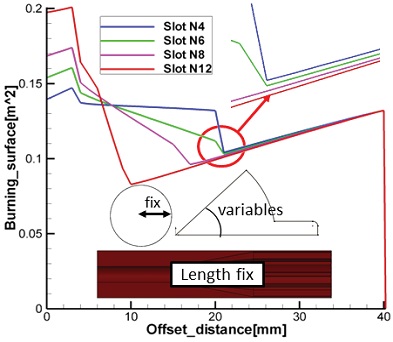
슬롯 개수

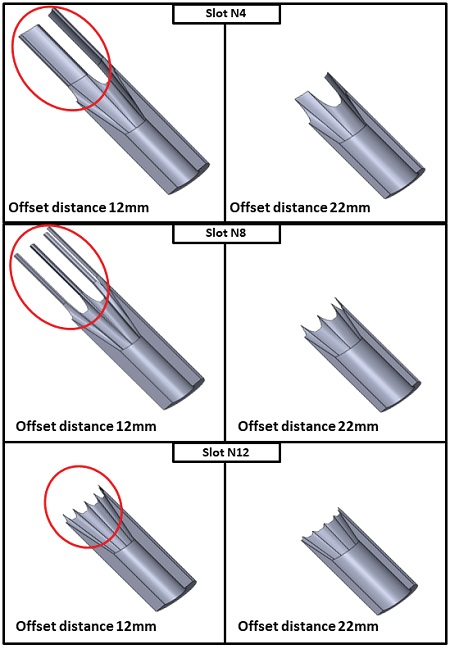
형상의 길이를 각각 200 mm로 설정하고 슬롯 개수를 변화시키며 해석한 결과를 Fig. 8에 나타내었다. 해석결과 슬롯 개수가 증가할수록 최대 연소면적과 최소연소면적의 차이가 증가하며, 초기 연소면적은 증가하였으나 이후의 연소면적이 급격히 감소하였으며 슬롯 개수에 따라 개형이 꺾이는 구간이 상이하였다. 슬롯 개수 4개, 6개의 경우 offset distance 22 mm일 때 개형이 꺾이는 구간이 발생하였으나 슬롯 개수 8개, 12개의 경우 offset distance 22 mm 이전에 개형이 꺾이는 구간이 나타났다. 이와 같은 차이를 분석하기 위해 offset distance 12 mm, 22 mm일 때의 슬롯 개수에 따른 연소형상을 Fig. 9에 나타내었다. Offset distance 12 mm의 경우 슬롯 개수 12개일 때의 연소형상은 다른 형상과 다르게 슬롯 형상이 모두 연소되어 연소면적이 가장작음을 확인하였다. Offset distance 22 mm의 경우 슬롯 개수에 관계없이 슬롯 형상이 모두 연소되고 테이퍼와 실린더 형상만 남게 되어 면적차이가 미미함을 알 수 있다. Fig. 9의 결과를 토대로 슬롯 형상의 존재유무에 따라 그래프의 개형이 꺾이는 구간이 발생함을 확인하였다. 이에 본 연구는 슬롯 형상이 모두 연소하는 구간을 천이구간이라 정의하였으며 Fig. 8의 결과로부터 본 연구에서 사용한 Finocyl 형상을 이용하여 중립형 연소면적선도를 나타낼 경우 슬롯 개수는 6개에서 8개가 유리한 것으로 판단된다.

Fig. 8

Burning surface area with slot N.

Fig. 9

Burning surface configuration with slot N.

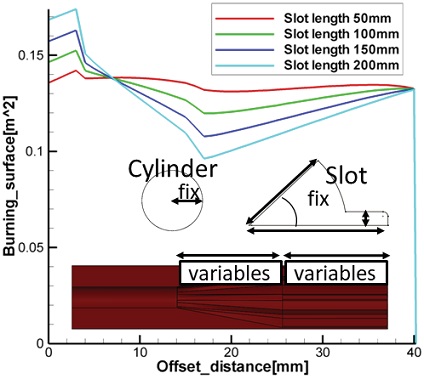
슬롯 길이

앞서 언급한 바와 같이 형상의 길이는 서로 종속적이기 때문에 실린더 길이를 350 mm로 고정하고 슬롯 길이 변화에 따른 경향성 분석 결과를 Fig. 10에 나타내었다. 경향성 분석결과 슬롯 길이가 길어질수록 초기연소면적이 증가하고 천이구간 이전의 연소면적이 감소한다. 천이구간 이후 테이퍼형상과 실린더 형상의 연소가 지배적이지만 슬롯 형상이 길어지면 테이퍼 형상이 줄어들게 되므로, 두 형상 중 실린더 형상의 연소가 지배적이게 되어 실린더 형상의 연소 특성인 점증형 선도가 나타난다. 따라서, 실린더 길이가 짧을수록 중립형 연소면적선도를 발생시키는 것이 유리하였으며, 슬롯 길이 50 mm, 실린더 길이 350 mm의 경우 중립형 연소면적선도에 가까움을 확인하였다.

Fig. 10

Burning surface area with slot length.

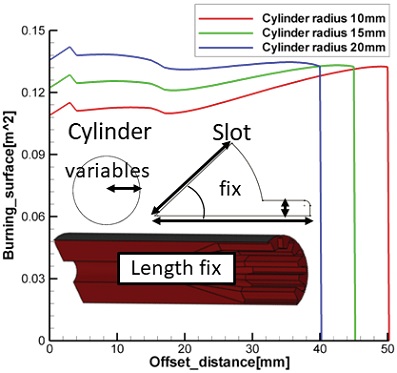
실린더 반경

실린더 반경의 변수변화에 따른 경향성을 분석하여 Fig. 11에 나타내었다. 경향성 분석결과 실린더 반경이 증가할수록 초기 연소면적이 증가하였다. 이는 실린더 반경이 증가하여 실린더 형상과 테이퍼 형상의 연소면적이 증가하기 때문이다. 따라서 초기 연소면적이 작을 경우 실린더 직경을 늘려야 중립형 연소면적선도를 나타내기에 유리하다.

Fig. 11

Burning surface area with cylinder radius.

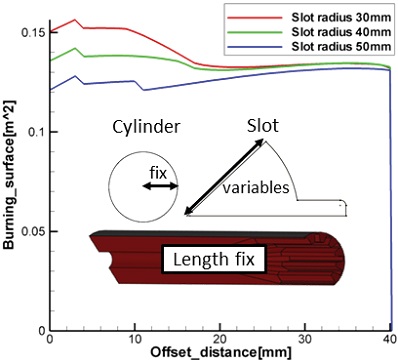
슬롯 반경

슬롯 반경의 변수변화에 따른 경향성을 분석하여 Fig. 12에 나타내었다. 경향성 분석결과 슬롯 반경이 커질수록 초기연소면적과 천이구간 이전의 연소면적선도가 전반적으로 감소하였다. 앞서 실린더 반경 증가 결과와 상이한 결과를 보이는데 이는 슬롯 형상의 연소면적은 슬롯 그레인의 여러 가지 형상 변수에 의한 복합작용으로 이루어지기 때문이다. 실린더 반경과 슬롯 반경 분석결과를 종합하면 실린더 반경 20 mm, 슬롯 반경 40 mm 일 경우 중립형 연소면적선도에 가장 근접하였다. 위 결과를 통해 중립형 연소면적선도를 내기 위해선 실린더와 슬롯의 반경비가 1:2 정도일 때 중립형 연소면적선도를 내기 유리하다고 판단된다.

Fig. 12

Burning surface area with slot radius.

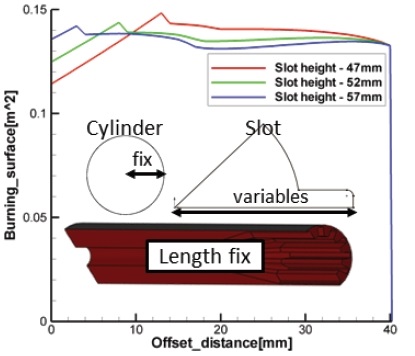
슬롯 높이

슬롯 높이의 변수변화에 따른 경향성을 분석하여 Fig. 13에 나타내었다. 경향성 분석결과 슬롯 높이가 짧을수록 슬롯 형상과 테이퍼 형상의 연소면적이 작아져 초기 연소면적은 줄어들며 테이퍼 형상의 연소가 후반부에 진행되므로 천이구간 이후 전반적인 연소면적이 증가하였다. 또한 슬롯 그레인은 web 길이가 0이 될 때까지 연소면적이 증가하고 이후에 연소면적이 감소하는 특성이 있다. 이러한 연소 특성 때문에 슬롯 높이가 길수록 중립형 연소면적선도에 가까움을 알 수 있다.

Fig. 13

Burning surface area with slot height.

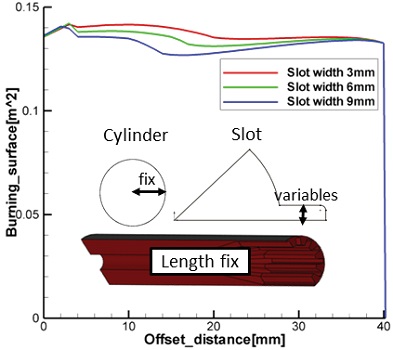
슬롯 폭

슬롯 폭 변수 변화에 따른 경향성을 분석하여 Fig. 14에 나타내었다. 경향성 분석 결과 슬롯 폭이 커질수록 전반적인 연소면적이 감소하며 다른 변수들과 달리 초기연소면적은 거의 변하지 않았다. 이를 통해 슬롯 폭은 중립형 연소면적선도에 큰 영향을 끼치지 않음을 알 수 있다.

Fig. 14

Burning surface area with slot width.

L/D (길이 직경비)

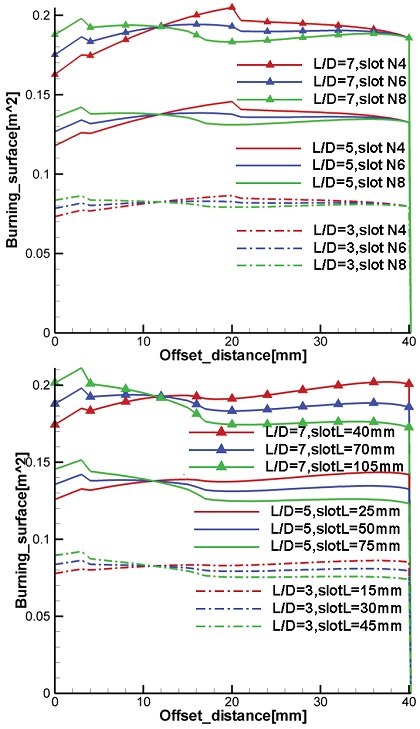
L/D의 경향성을 슬롯 개수와 슬롯 길이에 변화를 주어 해석한 결과를 Fig. 15에 나타내었다. 동일 직경에 대해 길이를 변경하는 경우, 실린더 길이, 테이퍼 길이, 슬롯 길이의 비율을 동일하게 설정하여 계산하였다. 해석결과 슬롯 개수와 슬롯 길이에 의한 경향성은 L/D에 무관하게 일정함을 확인하였다. 또한 L/D가 증가할수록 연소면적이 일정하게 증가하였으며 L/D = 3, 5, 7에서 중립형 선도를 나타내는 슬롯과 실린더 길이를 Table 4에 명시하였으며, 슬롯과 실린더 길의 비가 일정한 것으로 나타났다.

Fig. 15

Burning surface area with L/D.

Table 4.

Variables by L/D of Finocyl grain.

중립형 선도를 위한 형상 조건 요약

경향성 분석결과 본 연구에서 사용한 Finocyl 형상에 대한 중립형 연소면적선도를 만족하기 위해서는 슬롯 개수는 6∼8개, 슬롯 높이는 외경보다 작은 범위에서 가능한 클수록 바람직하다. 실린더 반경과 슬롯 반경의 비율이 1:2, 실린더 길이와 슬롯 길이의 비율이 1:7일 때 중립형 연소면적을 나타내었다. 해석에 사용한 추진제 반경 60 mm와 전장길이 600 mm를 더하여 길이비를 확장할 경우, 실린더 반경과 슬롯 반경, 추진제 반경의 비율은 1:2:3이며 실린더 길이와 슬롯 길이, 추진제 전장길이의 비율은 7:1:12로 도출되었다.

3.2 평균 연소면적 계산

Fig. 15의 L/D 변화에 따른 연소면적 그래프를 살펴보면 슬롯 길이와 실린더 길이의 비율이 고정된 경우, L/D가 증가할 때 일정하게 연소면적이 증가하는 것을 확인하였다. 위 결과를 토대로 L, D와 평균 연소면적간의 일정한 관계가 있음을 유추할 수 있다. 이는 Eq. 1과 같이 간단히 선형관계로 표현되며, L, D, 평균 연소면적을 Table 5에 명시하였다. Table 5에 명시한 변수 사이의 관계를 분석하여 얻은 α(평균 연소면적상수)값의 타당성을 검증하기 위해 L/D= 4, 5, 6, 8, 10에 대해 검증을 수행하고 그 결과를 Table 6에 제시하였다. D가 기존과 동일한 경우 슬롯의 형상변수는 모두 동일하게 사용하였으며, D가 다른 경우, 앞서 언급한 반경의 비율로 실린더와 슬롯의 반경을 설정하였다. D에 따라 슬롯의 형상이 달라지므로, 슬롯 폭과 슬롯 높이를 결정해야 하는데 언급한 두 가지 형상 변수는 경향성 분석결과를 토대로 슬롯 높이는 추진제 반경과 유사하게 설정하였으며 슬롯 폭은 큰 영향이 없으므로 기하학적으로 타당한 값으로 설정하였다. 비교 결과 Eq. 1을 이용하여 구한 평균연소면적이 Burn-back해석을 통해 구한 평균연소면적과 거의 일치함을 확인하였다. 본 연구결과를 바탕으로 Eq. 1과 계수를 사용하면 개념설계 단계에서 추진제 그레인의 직경 혹은 전장길이가 결정되어 있을 경우 중립형 연소면적 선도를 나타내는 다른 형상 변수를 알아낼 수 있으며 내탄도 해석 없이 평균연소면적을 빠르게 도출할 수 있다.

Table 5.

Burning surface area results of L/D.

Table 6.

Verification results of average burning surface equation.

3.3 민감도 분석

경향성 분석결과를 토대로 Finocyl 형상의 네 가지 변수의 중립형 연소면적선도에 대한 민감도 분석을 진행하였다. 경향성 분석과 마찬가지로 각 변수에 대한 민감도 분석을 진행할 때 고정되는 값이 존재하며 이는 Table 3에 명시하였다. 민감도 분석을 진행할 경우 같은 물리적 차원이거나 비교를 위해 무차원화 하는 것이 필요하다[14]. 본 연구에서 사용한 변수는 차원이 다르므로 무차원화 시키는 과정이 필요하여 표준편차의 정의를 이용하였으며 이를 Eq. (2)-(5)를 통해 무차원화 하였다. X_i는 offset 길이별 연소면적, μ는 평균연소면적, m은 연소종료 시점까지 생성된 데이터 개수, V(X)는 분산이며 σ는 표준편차이다. 표준편차와 민감도 분석 결과를 Table 7과 8에 나타내었다. 슬롯 반경 변화율 50%의 경우 슬롯 반경은 슬롯 높이 보다 클 수 없기 때문에 수행하지 않았다. 중립형 선도를 만족하는 일반적인 정의가 제시된 바 없지만, 편의상 본 연구에서는 평균 연소면적으로부터 벗어난 연소면적의 표준편차가 0.17 이하인 경우로 정의하였다.

Table 7.

Standard deviation with variables.

Table 8.

Sensitivity analysis results with variables.

민감도 분석 결과 변수가 증가할수록 민감도는 증가하였으나 변수가 작아질 경우 민감도가 항상 증가하는 것은 아닌 것으로 나타났다. 이는 경향성 분석 결과에서 확인할 수 있듯이 슬롯 폭은 중립형 연소면적선도에 큰 영향을 끼치지 않으며 슬롯 길이는 작을수록 좋기 때문이다. 또한 슬롯 폭의 경우 변화율이 바뀌어도 민감도가 20%를 넘지 않으므로 네 가지 변수 중 가장 낮은 민감도를 가진다고 할 수 있다. 슬롯 길이의 경우 -25% 변화율에서 두 번째로 높은 민감도를 보이지만 전체적인 양상을 볼 때 슬롯 폭 다음으로 민감도가 낮다. 슬롯 개수, 슬롯 반경과 실린더 반경은 변수의 증감에 관계없이 변화율이 커질수록 민감도가 증가하였다. 슬롯 반경은 변화율이 감소할 경우 가장 민감하게 변하였으며 변화율이 증가하는 경우 실린더 반경이 가장 민감하게 변하였다. 변화율에 따른 세 가지 변수의 민감도는 다르지만 제작 가능한 영역을 고려하였을 때 슬롯반경, 실린더 반경, 슬롯 개수, 슬롯 길이, 슬롯 폭 순으로 중립형 연소면적선도에 민감하게 작용하는 것을 알 수 있다.