넓은 비행영역을 고려한 2D 스크램제트 흡입구 설계 방법
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
넓은 비행영역에서 스크램제트 엔진의 운용을 위해, 비행 조건의 변화에도 안정적인 성능을 나타내는 흡입구의 설계가 중요하다. 본 연구에서는 마하수 4∼6, 받음각 -6도∼6도의 넓은 비행영역에서 안정적인 성능을 얻기 위한 2D 고정형 흡입구의 설계 방법에 대한 연구를 수행하였다. 설계 방법 및 설계 주안점에 대해 제시한 후, 넓은 비행영역에서 높은 전압력 회복율과 유량 포획율을 갖는 흡입구를 설계함에 있어 가장 중요한 설계요소인 초기 압축각도와 비행 마하수 설계점에 따른 성능예측 및 분석을 수행하였다. 분석 결과를 바탕으로 넓은 비행영역에서 안정적인 성능을 나타내기 위한 두 가지 주요 설계요소의 선정기준을 제시하였다.
Abstract
For the operation of the scramjet engine in the wide flight range, the design of the inlet must show stable performance in various flight conditions. In this study, the design methods of a 2D fixed inlet for stable performance in wide flight ranges of Mach number 4 to 6 and angle -6° to 6°, is performed. After proposing the design method and design focus, performance prediction and analysis were performed by various initial compression angles and design Mach numbers, which are essential design factors in total pressure recovery and inlet capture area ratio in the wide flight range. Based on the analysis results, we present the selection criteria for the two main design elements to represent stable performance in the wide flight range.
Keywords:
2D Mixed Compression Inlet, Wide Flight Range, Total Pressure Recovery, Capture Area Ratio키워드:
2D 혼합 압축형 흡입구, 넓은 비행영역, 전압력 회복, 포획면적 비1. 서 론
스크램제트 엔진의 구성요소 중 흡입구는 연소실에 적정한 수준의 압력과 유량의 공기를 공급하는 구성요소로서, 스크램제트 엔진 전체의 효율에 영향을 주는 중요한 구성요소이다[1]. 스크램제트 엔진 흡입구는 압축면의 형상에 따라 2D 흡입구와 3D 흡입구로 구분할 수 있다. 그 중 2D 흡입구는 3D 흡입구에 비해 설계 및 제작이 용이하다는 장점이 있으며, 미국의 마하수 5.1 비행에 성공한 X-51A에도 적용된 바 있다.
스크램제트 엔진 흡입구는 충격파에 의해 공기를 압축하므로, 마하수 또는 받음각이 변화할 경우 충격파 각도의 변화로 흡입구의 성능이 설계점에서의 성능에 비해 크게 저하될 수 있다.
탈설계점에서의 충격파 각도 변화로 인한 흡입구 성능저하를 방지하기 위해, 가변 카울을 적용하여 충격파의 위치나 충격파 각도를 재배치하여 흡입구 성능을 개선하기 위한 연구들이 수행되었다[2-4]. 2D 흡입구에 가변 카울을 적용함으로써 비행조건의 변화에 따른 흡입구 성능저하 문제를 개선할 수 있으나, 흡입구 구조가 복잡해지는 문제와 극초음속 비행 중 형상을 변화시키는 것에 대한 기술적인 문제가 발생할 수 있다. 따라서 스크램제트 엔진 흡입구를 설계함에 있어 넓은 영역의 마하수와 넓은 영역의 받음각 조건에서 별도의 가변장치 없이, 흡입구 자체 형상으로 고른 성능을 나타내는 흡입구의 설계가 중요하다.
Torrez 등은 탈설계점에서 전압력 회복성능이 크게 저하되는 문제를 개선하기 위해, 모든 비행영역에서 첫 번째 충격파가 카울보다 전방에 위치하도록 흡입구를 설계하는 방법을 제시하였다[5]. 기존의 흡입구와 설계를 개선한 흡입구의 전압력 회복성능을 비교한 결과, 설계를 개선한 흡입구가 비행 조건이 변화하여도 고른 성능을 나타나는 결과를 보였다. 그러나 모든 비행영역에서 첫 번째 충격파를 카울보다 전방에 위치시켰으므로, 기존의 흡입구보다 유량포획 면적이 저하되는 문제가 발생할 수 있다.
그 외에도 다양한 비행범위에서 고른 성능을 나타내는 흡입구 설계의 중요성에 대한 언급은 되었으나[6-8], 넓은 비행영역을 고려한 2D 고정형 흡입구의 설계 방법이나 설계 주안점에 대해 분석한 연구는 찾아보기 힘들다. 전압력 회복성능과 유량 포획면적 성능은 흡입구의 가장 중요한 성능지수로서, 일반적으로 순항조건에서 이 두 가지 성능을 극대화하는 방향으로 설계 연구가 수행되었다. 이 경우 Torrez가 지적한 바와 같이 탈설계점에서의 급격한 성능저하로 인해 흡입구 운용범위가 제한되는 문제가 발생할 수 있다[5].
본 연구에서는 기존의 연구에서 수행된 흡입구 설계방법과는 다른 접근 방법을 바탕으로, 넓은 비행영역에서 좋은 성능을 나타내는 2D 고정형 흡입구 압축각도를 설계하기 위한 설계 주안점과 이를 바탕으로한 설계 방법을 제시하고자 하였다. 초기 설계단계에서는 수많은 흡입구 설계안에 대한 빠른 분석이 요구된다. 따라서 간단한 성능예측 방법을 바탕으로 여러 흡입구 설계안의 다양한 비행조건에 대한 성능예측 결과를 빠르게 산출할 수 있도록 성능예측 코드를 구축하여 연구를 수행하였다. 구축된 코드의 예시 흡입구 모델에 대한 결과와 전산해석 결과와의 비교를 통해 성능해석 코드에 대한 검증을 수행하였다. 검증된 코드를 바탕으로 초기 설계단계에서 넓은 비행영역에서 높은 전압력 회복율과 유량 포획율을 갖는 흡입구를 설계함에 있어 가장 중요한 설계요소인 초기 압축각도와 비행 마하수 설계점에 따른 성능예측 및 분석을 수행하고, 이를 바탕으로 두 가지 주요 설계요소에 대한 선정기준을 제시하고자 하였다.
2. 2D 흡입구 설계 및 성능해석 방법
본 연구에서는 분석 및 서술의 용이성을 위해, 다양한 흡입구의 종류 중 혼합 압축형 흡입구를 기준형상으로 선정하였다. 혼합 압축형 흡입구는 외부 압축형 흡입구의 조파항력 문제와 내부 압축형 흡입구의 불시동 문제를 보완한 흡입구로[7], 여러 연구에서 채택된 형상이다[2-5].
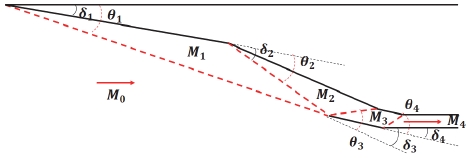
Fig. 1은 2D 혼합 압축형 흡입구의 개념도를 나타낸 그림이다. 그림에서 나타난 바와 같이 2개의 외부 충격파와 2개의 내부 충격파를 이용하여 공기를 압축한다. 흡입구 항력감소 측면에서 연소실 유입유동의 방향과 자유 유동의 방향이 동일한 형상을 나타내고 있다.
2.1 2D 혼합 압축형 흡입구 설계 방법
스크램제트 엔진 흡입구는 압축 면에서 발생하는 충격파를 이용하여 공기를 압축하므로, 흡입구 압축면의 압축각도가 주요 설계인자라 할 수 있다. 일반적으로 흡입구 압축각도는 모든 충격파의 세기를 동일하게 설계함으로써, 최대의 흡입구 전압력 회복성능을 얻을 수 있는 것으로 알려져 있다[8]. Oswatitsch 기법은 여러 흡입구 설계에 대한 연구에서 적용되었다[5,9,10].
그 중 Torrez 등은 Oswatitsch 기법을 적용하여 단일 설계점에 대해 전압력 회복성능을 최대화할 경우 탈설계점에서 전압력 회복성능이 크게 저하되는 결과를 확인하였다[5]. 비행조건의 변화에 대한 흡입구 유량 포획면적 성능 및 항력감소 측면에서, Zhang은 흡입구 외부 압축각도의 총합과 첫 번째 압축각도가 작을수록 유리하다는 사실을 확인하였다[6].
그러나 작은 초기 압축각도 값을 설정하여 모든 충격파 세기를 동일하게 설계할 경우, 초기 압축각도에 따라 연소기 요구 압력을 만족하지 못하는 문제가 발생할 수 있다. 따라서 본 연구에서는 기존의 Oswatitsch 기법을 이용하여 모든 충격파의 세기가 동일한 압축각도를 설계하는 방법이 아닌, 고정된 초기 압축각도에 대해 연소기 요구 압력을 충족하는 압축각도를 설계하는 방법을 적용하였다. Fig. 1은 본 연구에서 채택한 혼합 압축형 흡입구의 개념도를 나타낸 그림이다. Fig. 1의 개념도에 나타난 바와 같이 연소실 유입유동의 방향이 자유 유동의 방향과 동일하므로, 아래의 관계식을 만족하여야 한다. 이때 δ1∼δ4는 첫 번째에서 네 번째 압축각도를 의미한다.
| (1) |
Eq. 1에서 초기 압축각도 δ1은 고정되고 δ4는 종단 충격파를 지난 유동의 방향이 자유 유동의 방향과 동일한 방향을 갖는 조건을 만족시키는 각도이므로 δ1 ~ δ3에 의해 결정된다. 따라서 설계변수는 두 번째와 세 번째 압축각도인 δ2와 δ3이다. 또한 흡입구는 연소실에 적정한 수준의 압력의 유동을 공급해야 하므로, 네 번째 충격파 이후의 정압력이 설계요구 압력조건을 만족하도록 설계해야 한다. Smart의 연구에 의하면 흡입구가 연소기에 공급해야하는 압력 수준은 연소기의 스케일에 따라 달라지지만, 일반적인 스케일의 스크램제트 연소기일 경우 50 kPa 이상의 압력이 요구된다는 결과를 보고한 바 있다[11]. 본 연구에서는 margin을 두어 설계 압력조건을 동일하게 70 kPa로 설정하여 설계를 수행하였다. 주어진 조건에서 최적의 전압력 회복성능을 얻기 위해, 내부 압축구간인 세 번째와 네 번째 충격파의 세기가 동일하도록 하였다. 최종적으로 흡입구 압축각도 설계는 위의 모든 조건들을 만족하는 δ2와 δ3를 찾는 방식으로 진행되었다.
2.2 2D 혼합 압축형 흡입구 성능예측 방법
2D 스크램제트 엔진 흡입구는 압축 면에서 발생하는 충격파의 각도에 따라, 경사충격파 관계식을 이용하여 충격파 이후의 전압력 회복성능 및 압축 비율 등을 계산할 수 있다. 흡입구 설계초기 단계에서 다양한 비행조건에 대한 빠른 성능 분석을 위해 1D 문제로 가정하였으며, 점성 및 난류효과는 고려하지 않았다. 경사충격파 이후의 전압력 회복성능은 아래의 Eq. 2에 의해 계산된다.
| (2) |
또한 받음각 조건이 음의 값을 가질 경우 첫 번째 압축 면에서 팽창파가 발생할 수 있다. 팽창파에 대한 효과를 고려하기 위해 아래의 Eq. 3에 정리된 Prandtl Meyer 함수를 이용하였다.
| (3) |
다음으로 흡입구 포획면적 성능은 흡입구 카울 좌표에서의 유선추적을 통해 예측한다. 2D 흡입구의 형상은 설계된 압축각도와 흡입구 목 면적, 충격파 각도간의 기하학적 관계식을 이용하여 도출할 수 있다. 본 연구에서는 분석의 용이성을 위해 목 면적은 40 mm로 통일하였으며, 설계점에서 최대의 공기유량을 포집할 수 있도록 shock on lip 조건을 만족하는 흡입구 형상을 도출하여 유선추적을 진행하였다.
2.3 2D 혼합 압축형 흡입구 성능해석 코드 검증
앞 절에서 소개한 2D 혼합 압축형 흡입구 설계 방법과 성능예측 방법을 적용한 흡입구 설계 코드와 성능해석 코드를 작성하였다. 본격적인 흡입구 분석에 앞서, 예시 모델로서 본 연구진이 설계한 바 있는 SC01-A 흡입구 모델에 대한 흡입구 성능예측 코드 결과와 전산해석 결과를 비교하여 코드를 검증하고자 하였다.
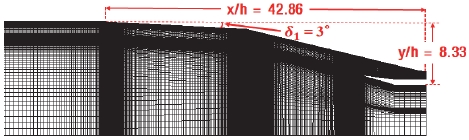
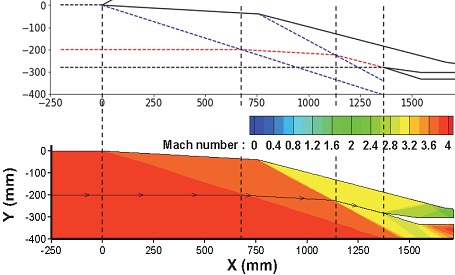
Fig. 2는 SC01-A 흡입구 모델의 격자계와 형상정보를 나타낸 그림이다. 그림의 x/h와 y/h 값은 각각 전체 길이(x)와 높이(y)를 흡입구 목 면적(h)으로 나눈 값이다. SC01-A 흡입구 모델은 앞 절의 설계 방법과 동일한 방법을 이용하여 설계된 흡입구 모델로, 초기 압축각도 3˚이며 흡입구 출구 압력 70 kPa을 만족하도록 하였다.
전산해석은 2D Navier-Stokes 방정식을 해석하기 위해 Density-based solver를 사용하였으며, Flux scheme은 Roe-FDS scheme을 사용하였다. 코드 결과와의 비교를 위해 inviscid 해석을 수행하였으며, Table 1에 SC01-A 흡입구 모델의 설계점과 비행조건을 정리하였다.
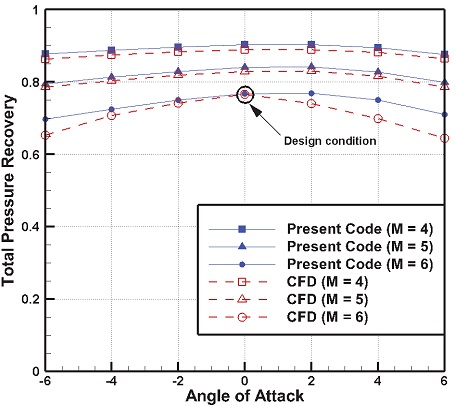
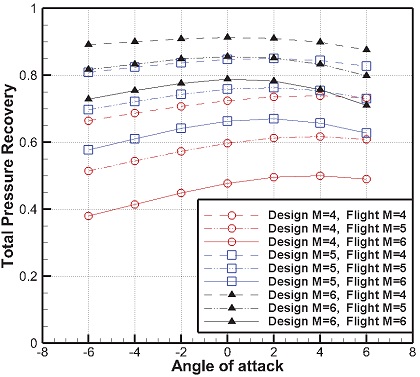
Fig. 3는 SC01-A 흡입구 모델의 전압력 회복성능에 대한 성능해석 코드 결과와 전산해석 결과를 비교한 그림이다. 전산해석 결과의 경우 흡입구 출구 면에서의 Area weighted average 값으로 나타내었다. 그림에서 나타난 바와 같이 앞 절에서 소개한 흡입구 성능예측 방법을 이용한 성능해석 코드가 설계점에서 전압력 회복 성능을 정확하게 예측하고 있음을 확인할 수 있다. 그러나 탈설계점의 일부영역에서는 전압력 회복성능 예측에 오차가 발생했음을 알 수 있다.
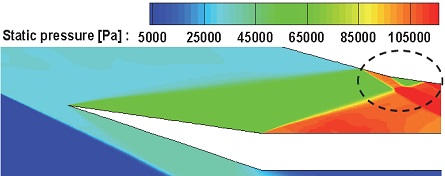
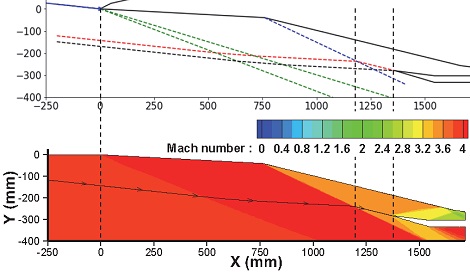
오차의 원인에 대한 분석을 위해 Fig. 4에 마하 6, 받음각 6˚ 조건에 대한 흡입구 내부 압축영역의 압력분포를 나타내었다. 그림의 표시된 영역에서 나타난 바와 같이 흡입구 카울에서 발생한 세 번째 충격파가 흡입구 벽면에서 반사되어 네 번째 충격파와 간섭을 일으키고 있음을 확인할 수 있다. 이를 통해 성능예측에 대한 오차의 원인은 반사 충격파의 강도와 간섭영역 차이는 있겠으나, 카울에서 발생한 충격파의 반사 충격파와 네 번째 충격파와의 간섭에 따른 추가적인 전압력 손실에 의한 것임을 알 수 있다. 그러나 간단한 방법을 이용하여 성능을 예측했음에도, 모든 비행영역에 대해 전반적인 수치와 경향성을 잘 예측하고 있으므로 성능예측 및 분석에는 큰 무리가 없을 것으로 판단하였다.
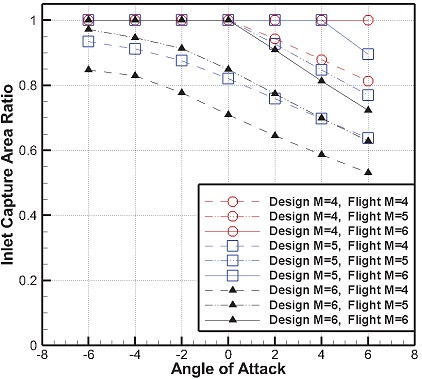
Fig. 5와 Fig. 6는 흡입구 유량 포획면적 성능예측을 위한 성능해석 코드 상에서의 흡입구 카울에서의 유선추적 결과와 전산해석 상에서의 유선 추적결과를 나타낸 그림이다. 탈설계점에서 첫 번째 압축 면에서 충격파가 발생한 경우와 팽창파가 발생한 경우에 대한 유선추적 결과를 전산해석 결과와 비교 및 검증하고자 하였다. 비교를 위해 성능해석 코드 결과와 전산해석 결과를 동일한 scale로 나타내었다.
Streamline tracing results for Mach 4 and AOA –6˚, predicted result(up) and numerical result (down).
Fig. 5는 마하수 4, 받음각 0˚ 조건에 대한 유선추적 결과를 나타낸 그림이다. 성능해석 코드결과에서 검정색 점선은 최대 유량 포획면적을 의미하며, 붉은색 점선은 카울 좌표로부터 유선추적을 통해 예측한 흡입구 포획면적을 의미한다. 파란색 점선은 경사 충격파를 나타낸 그림이다. 그림에서 나타난 바와 같이 자유 마하수가 설계점의 마하수보다 낮으므로 충격파 각도가 상승하여 흡입 유량의 손실이 발생하고 있음을 확인할 수 있다. 전산해석 결과에서 나타난 유선추적 결과와 성능해석 코드 상에서 계산한 유선추적 결과가 동일한 결과를 나타내어 이를 잘 예측하고 있음을 확인할 수 있다.
Fig. 6는 마하수 4, 받음각 -6˚ 조건에 대한 유선추적 결과를 나타낸 그림이다. 성능해석 코드 결과에서 팽창파 영역은 초록색 점선으로 표시되었다. 그림에서 나타난 바와 같이 전산해석 결과에서 팽창파 구조의 경우 육안으로 식별이 어렵다. 그러나 두 번째 충격파 구조 및 유선추적 선에 대한 전산해석 결과와 성능해석 코드 상의 붉은색 점선으로 표시된 유선추적 결과를 비교했을 때, 흡입유량에 대한 유선추적이 제대로 예측되고 있음을 확인할 수 있다.
유선추적 결과를 바탕으로 계산한 마하수 4∼6 범위에 대한 흡입구 포획면적 성능해석 결과와 전산해석 결과를 Table 2에 정리하였다. 표에 나타난 바와 같이 포획면적 성능에 대한 성능해석 코드 결과와 전산해석 결과가 거의 일치하고 있음을 확인할 수 있다.
3. 2D 혼합 압축형 흡입구의 성능해석 결과 분석
전산해석 결과와의 비교를 통해 코드에 대한 검증이 완료되었다고 판단되어, 성능해석 코드를 이용하여 넓은 비행영역에 대한 여러 흡입구 설계 case의 성능해석을 수행하고자 하였다. 흡입구의 가장 중요한 성능지수인 전압력 회복율과 유량 포획 면적비는 비행 마하수와 받음각 조건 등 비행 조건에 많은 영향을 받는다. 넓은 비행영역에서 이 두 가지 성능지수가 안정적인 성능을 나타낼 수 있도록 흡입구를 설계 하는 것이 중요하며, 이를 위한 가장 중요한 설계요소는 흡입구 초기 압축각도와 비행 마하수 설계점이다. 따라서 본 절에서는 초기 압축각도와 비행 마하수 설계점에 따른 여러 흡입구 case에 대한 성능예측 및 분석을 수행하여, 이를 바탕으로 넓은 비행영역에서 높은 전압력 회복율과 유량 포획율을 갖는 흡입구를 설계하기 위한 두 설계요소의 선정기준을 제시하고자 하였다.
3.1 초기 압축각도에 따른 흡입구 성능해석 결과 분석
앞서 소개한 두 가지 흡입구 주요 설계요소 중, 초기 압축각도 값의 변화에 따른 흡입구 성능해석 결과에 대한 분석을 수행하여 넓은 비행영역에 대한 흡입구 설계 시 적정한 초기 압축각도 범위를 확인해보고자 하였다. 흡입구 초기 압축각도 0.5˚부터 10˚ 범위에 대해 0.5˚ 간격으로 총 20가지 case의 흡입구를 설계하여 성능분석을 수행하였다. 설계점은 고도 23 km, 마하수 6, 받음각 0˚ 조건으로 선정하였다. 설계 결과 모든 case에 대해 전체 압축각도는 26.6˚∼27.8˚ 수준을 나타냈다. 성능해석을 수행한 비행 영역은 각 흡입구 설계 case에 대해 마하수 범위 4∼6, 받음각 범위 –6˚∼6˚이다. 흡입구 초기 압축각도에 따른 흡입구 전압력 회복성능 및 포획면적 성능을 분석한 결과 일정한 경향성이 나타남을 확인하였다. 본 논문에서는 지면 관계상 주요설계 case인 초기 압축각도 0.5˚, 3.5˚, 6˚, 10˚ case에 대한 흡입구 성능해석 결과를 다루었다.
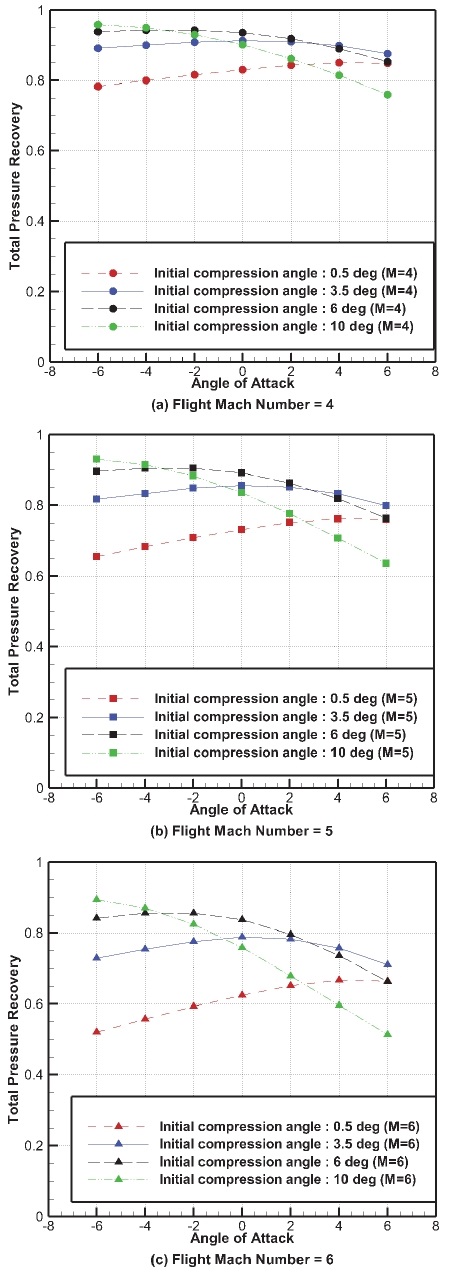
Fig. 7은 마하수 4∼6, 받음각 –6˚∼6˚ 범위에 대한 초기 압축각도 0.5˚, 3.5˚, 6˚, 10˚ case의 전압력 회복성능 예측 결과를 나타낸 그림이다. 그림에서 나타난 바와 같이 모든 마하수 영역에서 설계 받음각인 0˚ 조건의 경우 초기 압축각도가 증가할수록 전압력 회복율이 높아지며, 초기 압축각도 6˚ case에서 가장 높은 값을 나타냈다. 6˚ case를 기점으로 초기 압축각도가 증가할수록 전압력 회복율이 감소하는 경향을 보였다. 이에 대한 원인을 분석하기 위해, 마하수 6, 받음각 0˚ 조건에서 각 충격파 이후의 전압력 회복율에 대한 표준편차 값을 계산하여 비교하였다.
마하수 6, 받음각 0˚ 조건에서 표준편차 값을 비교한 결과, 초기 압축각도 6˚ case에서 각 충격파 이후의 전압력 회복율에 대한 표준편차 값이 약 0.02로 가장 낮은 값을 보였다. 초기 압축각도 3.5˚ case의 경우 각 충격파 이후 전압력 회복율에 대한 표준편차 값이 약 0.07, 10˚ case의 경우 0.09, 0.5˚ case의 경우 0.16으로 가장 높은 값을 나타냈다. 이는 초기 압축각도 6˚ case가 다른 흡입구 case들에 비해 4개의 충격파 세기가 상대적으로 고르게 분포하여 전압력 회복성능이 높게 나타났음을 의미한다. 추가적으로 초기 압축각도 0.5˚ case의 경우 상대적으로 낮은 전압력 회복성능을 나타내고 있다. 이는 흡입구에 4개의 충격파를 배치하였으나, 과도하게 작은 초기 압축각도로 인해 3개의 충격파에 의해 공기를 압축하는 것과 비슷한 효과가 적용되어 각 충격파의 세기가 다른 흡입구 case들에 비해 강한 것이 원인으로 판단된다.
Fig. 7(a)∼(c)에 나타난 바와 같이 모든 마하수 영역에서 각 흡입구 case 별로 서로 다른 특정 받음각에서 전압력 회복성능이 높게 나타나고 있음을 확인할 수 있다. 이를 분석하기 위해 서로 다른 초기 압축각도 case에서 가장 높은 전압력 회복성능을 나타내는 조건에 대해 분석하였다. 서로 다른 초기 압축각도 case에 대해 가장 높은 전압력 회복성능을 나타내는 조건은 0.5˚ case의 경우 받음각 4˚, 3.5˚ case의 경우 받음각 0˚, 6˚ case의 경우 받음각 –2˚ 조건이었으며 10˚ case의 경우 받음각 –6˚ 조건에서 전압력 회복성능이 가장 높은 값을 나타냈다.
나열한 조건들에서 주목할 점은 모든 흡입구 case의 모든 마하수 영역의 전압력 회복성능 결과에서, 첫 번째 압축면에 대한 turning angle(초기 압축각도+받음각)이 3.5˚∼4.5˚ 범위의 조건에서 전압력 회복 성능이 최대가 되고, 이 조건과 차이가 많이 날수록 전압력 회복 성능이 하락하는 점이다. 이러한 현상의 원인을 파악하기 위해 각 충격파 이후 전압력 회복율에 대한 표준편차 값을 분석한 결과, 초기 압축각도와 받음각의 합이 3.5˚∼4.5˚ 범위의 조건에서 전압력 회복율에 대한 표준편차 값이 가장 낮은 결과를 보였다. 이는 해당 조건에서 각 충격파의 세기가 가장 고르게 분포하여 전압력 회복성능이 높게 나타났음을 의미한다. 이와 달리 각 흡입구 case에서 받음각 조건이 초기 압축각도와 받음각의 합이 3.5˚∼4.5˚가 되는 조건과 차이가 많이 날수록 각 충격파 이후의 전압력 회복율에 대한 표준편차 값도 증가하였다. 이는 각 충격파의 세기가 고르지 못하고 특정 압축면에서 강한 충격파가 발생한 것이 원인으로 볼 수 있다. 이와 같은 사실을 바탕으로 초기 압축각도 3.5˚ case의 경우 받음각 0˚에서 초기 압축각도와 받음각의 합이 3.5˚∼4.5˚ 범위의 조건을 만족하므로, 다른 흡입구 case에 비해 상대적으로 받음각 변화에 따른 전압력 회복율의 변화가 적은 것으로 판단된다.
제시된 흡입구 case에 대한 성능평가를 위해, 전압력 회복성능에 대한 정량적인 비교를 수행하였다. 넓은 비행영역에서 좋은 성능을 갖는 흡입구 설계의 관점에서 전체 비행영역에서 마하수와 받음각 변화를 고려한 정량적인 분석을 위해, 마하수와 받음각에 따른 가중치를 부여하였다. 전압력 회복율의 분석에 있어 고 마하수 영역에서의 전압력손실이 크므로 좀 더 높은 가중치를 두어 마하수 4, 5, 6일 때 각각 0.2, 0.3, 0.5의 가중치를 부여하였다. 받음각의 경우 넓은 비행영역에서 좋은 성능을 갖는 흡입구 설계를 위해, 고 받음각 영역에서의 성능에 좀 더 높은 가중치를 부여하였다. 7개의 받음각 조건에 대해 받음각 0˚ 조건의 경우 0.1의 가중치를 부여하고, 0˚를 기준으로 받음각의 절대값이 2˚, 4˚, 6˚로 증가할수록 각각 0.125, 0.15, 0.175의 가중치를 부여하였다. 마하수와 받음각의 변화에 따른 가중치를 부여하여 초기 압축각도에 따른 전체 비행 영역에 대한 전압력 회복율의 평균 성능을 계산한 결과, 초기 압축각도 6˚ case가 0.837로 가장 높은 결과를 나타냈으며, 다음은 초기 압축각도 3.5˚ case로 0.805, 10˚ case가 0.783, 0.5˚ case가 0.685 순으로 나타났다.
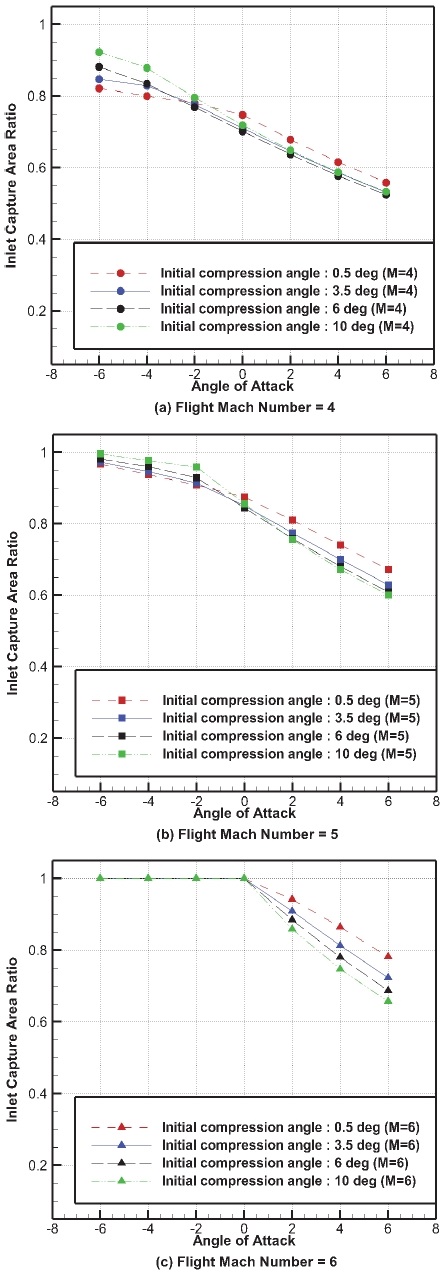
Fig. 8은 마하수 4∼6, 받음각 –6˚∼6˚ 범위에 대한 초기 압축각도 0.5˚, 3.5˚, 6˚, 10˚ case의 흡입구 유량 포획 면적비 성능을 나타낸 그림이다. 그림에서 나타난 바와 같이 각 흡입구 case에서 받음각이 양의 방향으로 증가할수록, 마하수가 낮을수록 유량 포획면적비가 감소하는 모습을 확인할 수 있다. 이는 받음각이 양의 방향으로 증가하는 경우 첫 번째 압축각도가 증가하는 것과 동일한 효과를 나타내므로 첫 번째 경사충격파 각도가 설계점에서의 경사충격파 각도보다 증가하며, 첫 번째 충격파 이후 마하수가 설계점에서의 첫 번째 충격파 이후 마하수보다 감소하게 된다. 동일한 압축각도에 대해 마하수가 감소할수록 θ-β-M relation에 의해 경사충격파 각도가 증가하므로 두 번째 충격파의 각도도 증가하게 된다. 이로 인해 유량 유출면적이 증가하여 유량 포획면적비가 감소한 것으로 볼 수 있다. 각 흡입구 case에서 받음각이 음의 방향으로 증가할 경우 유량 포획 면적비가 증가하는 결과를 나타냈으며, 이는 받음각이 양의 방향으로 증가한 경우와 반대의 현상이 발생한 것이 원인으로 볼 수 있다.
각 흡입구 case의 유량 포획 면적비에 대한 성능평가를 수행하였다. 넓은 비행영역에서 좋은 성능을 갖는 흡입구 설계의 관점에서 전체 비행영역에서 마하수와 받음각 변화를 고려한 정량적인 분석을 위해, 마하수와 받음각에 따른 가중치를 부여하였다. 설계점을 기준으로 성능저하가 발생하는 양의 방향의 고 받음각 영역과 저 마하수 영역에 더 높은 가중치를 부여하였다. 받음각 0˚ 이하의 조건에서는 0.1의 가중치를 부여하였으며, 받음각이 2˚, 4˚, 6˚로 증가할수록 각각 0.15, 0.2, 0.25의 가중치를 부여하였다. 마하수 조건의 경우 마하수 4, 5, 6일 때 각각 0.5, 0.3, 0.2의 가중치를 부여하였다. 전체 비행영역에서 마하수와 받음각에 따른 가중치를 부여하여 초기 압축각도에 따른 전체 비행영역에 대한 유량 포획 면적비의 평균 성능을 계산한 결과, 초기 압축각도 0.5˚ case가 0.763으로 가장 높은 결과를 나타냈다. 다음으로 높은 결과는 초기 압축각도 3.5˚ case로 0.742, 10˚ case가 0.741, 6˚ case가 0.735 순이었다.
Fig. 7과 Fig. 8의 결과를 종합해보면 마하수 4∼6 범위와 받음각 –6˚∼6˚ 범위에서 전압력 회복율 측면에서는 초기 압축각도 6˚ case가 가장 우수한 성능을 보였으며, 초기 압축각도 3.5˚ case가 다음으로 높은 성능을 나타냈다. 유량 포획 면적비 측면에서는 초기 압축각도 0.5˚ case가 가장 높은 성능을 나타냈으며, 초기 압축각도 3.5˚ case가 다음으로 높은 성능을 나타냈다. 흡입구의 가장 중요한 성능 지수인 전압력 회복율과 유량 포획 면적비에 대해 각 흡입구 case의 성능을 분석하였다. 두 성능 지수의 결과를 모두 고려하여 전체적으로 높은 흡입구 전압력 회복율이 요구될 경우 초기 압축각도는 6˚가 적절할 것으로 판단되며, 받음각 4˚ 이상의 고 받음각 영역에서의 전압력 회복율과 전반적으로 높은 유량 포획면적비가 요구될 경우 초기 압축각도가 3.5˚가 적절할 것으로 판단된다.
3.2 비행 마하수 설계점에 따른 흡입구 성능해석 결과 분석
일반적으로 흡입구 설계점을 결정할 때 고 마하수 영역에서 전압력 손실이 크므로, 전체 비행 영역을 기준으로 고 마하수에서 전압력 회복성능이 최대가 되도록 설계를 진행한다. 본 절에서는 비행 마하수 설계점 선정이 흡입구 성능에 미치는 영향을 분석하여 비행 마하수 설계점에 대한 선정 기준을 제시하고자 하였다. 흡입구 초기 압축각도는 앞 절에서 좋은 성능을 나타냈던 초기 압축각도 3.5˚와 6˚ 중 3.5˚로 고정한 후 고도 23 km 조건에서 비행 마하수 설계점을 4, 5, 6으로 변경하여 3가지 흡입구에 대한 기초설계를 진행하였다.
Fig. 9는 초기 압축각도 3.5˚일 때 비행 마하수 설계점을 변경해가며 설계한 흡입구의 마하수 4∼6, 받음각 범위 –6˚∼6˚에 대한 전압력 성능해석 결과이다. 그림의 붉은색 데이터는 비행 마하수 설계점을 주어진 마하수 범위에서 저 마하수인 4로 설정하여 흡입구를 설계하였을 때의 결과이며, 검정색 데이터는 고 마하수인 6을 기준으로 흡입구를 설계하였을 경우의 결과이다. 그림의 붉은색 데이터 결과에서 나타난 바와 같이 모든 비행영역에 대하여 비행 마하수 설계점이 낮을수록 전압력 회복성능도 낮게 나타나는 것으로 확인되었다. 동일한 대기조건에서 비행 마하수 설계점이 낮은 경우 비행 마하수 설계점이 높은 경우에 비해 압축면에서 발생하는 충격파의 세기가 약하다. 따라서 충격파에 의한 압축비가 낮으므로 비행 마하수 설계점이 높을 때보다 더 큰 압축각도를 사용해야 연소기 요구 압력을 충족시킬 수 있다. 초기 압축각도 3.5˚, 비행 마하수 설계점이 6인 경우 첫 번째 압축 면에 의한 압축비가 약 1.646이다. 이에 비해 초기 압축각도 3.5˚, 비행 마하수 설계점이 4인 경우 첫 번째 압축 면에 의한 압축비는 약 1.408이다. 따라서 초기 압축각도는 고정하였으므로 비행 마하수 설계점이 낮을수록 나머지 흡입구 압축각도가 증가하며, 증가된 압축각도에 의해 전압력 손실이 증가한 것이 전압력 회복성능이 낮게 나타나는 원인으로 볼 수 있다. 이를 바탕으로 비행 마하수 설계점이 높은 경우 저 마하수를 기준으로 설계했을 때보다 상대적으로 각 압축 면에서의 압축각도가 작은 값을 갖게 되므로, 검정색으로 표시된 바와 같이 전압력 회복성능이 높게 나타나는 것을 알 수 있다. 파란색으로 표시된 중간 마하수에 대한 설계 흡입구의 경우 앞의 두 흡입구와 비교했을 때 전체적으로 중간 값을 나타내고 있음을 확인할 수 있다.
Fig. 10은 비행 마하수 설계점에 따른 마하수 4∼6, 받음각 범위 –6˚∼6˚에 대한 포획면적 성능해석 결과이다. Fig. 9과 마찬가지로 붉은색 데이터는 비행 마하수 설계점을 저 마하수로 설정하여 흡입구를 설계하였을 때의 결과이며, 검정색 데이터는 고 마하수를 기준으로 흡입구를 설계하였을 경우의 결과이다. 그림에서 나타난 바와 같이 전압력 회복성능 결과와는 다르게 설계점을 저 마하수로 선정하여 설계했을 경우 고 마하수로 선정하여 설계했을 경우보다 모든 비행영역에서 포획면적 성능이 높게 나타나는 것을 확인하였다. 경사충격파 관계(θ-β-M relation)에서 동일한 압축각도에 대해 마하수가 증가할수록 충격파 각도는 감소한다. 제시된 3가지 흡입구 case들은 모두 비행 마하수 설계점에서 shock on lip 조건을 만족하도록 기본형상을 도출하였다. 따라서 비행 마하수 설계점을 저 마하수로 선정하였을 경우 비행 마하수 설계점보다 높은 마하수 영역에서 충격파 각도가 감소하므로 충격파가 흡입구 안쪽으로 위치하게 되어 Fig. 10에 나타난 바와 같이 대부분의 비행조건에서 유량 포획면적비가 1을 만족하게 된다. 고 마하수를 기준으로 설계한 경우 마하수가 감소하거나 받음각이 증가할수록 충격파 각도가 증가하므로 포획면적비가 감소하는 모습을 확인할 수 있다. 비행 마하수 설계점을 중간 마하수 기준으로 선정한 경우, 앞서 언급한 이유와 같은 이유로 비행 마하수 설계점보다 낮은 영역에서는 포획면적비가 감소하고, 비행 마하수 설계점보다 높은 영역에서는 포획면적비가 증가하는 결과를 나타냈다.
Fig. 9과 Fig. 10의 결과를 근거로 종합하면 다음과 같다. 흡입구 설계 시 주어진 임무 비행범위를 바탕으로 비행 마하수 설계점을 선정함에 있어 저 마하수를 기준으로 흡입구를 설계할 경우 전압력 회복 성능은 고 마하수를 기준으로 흡입구를 설계했을 때보다 부족한 성능을 보이지만, 유량 포획성능 측면에서 우수한 성능을 보였다. 반대로 고 마하수를 기준으로 설계할 경우 전압력 회복성능 측면에서 유리하며, 포획면적 성능은 저 마하수 영역에서 낮은 결과를 나타냈다. 따라서 임무 비행궤적에 따라 요구되는 흡입유량 범위 또는 전압력 회복성능을 고려하여 비행 마하수 설계점을 선정하는 것이 바람직할 것으로 판단된다.
4. 결 론
본 연구에서는 넓은 비행영역에서 전압력 회복율과 유량 포획면적비 측면에서 높은 성능을 나타내는 2D 고정형 흡입구를 설계함에 있어 순항조건 위주의 설계 시 놓칠 수 있는 설계 주안점을 제시하였으며, 주요 설계요소인 초기 압축각도와 비행 마하수 설계점에 따른 성능예측 및 분석을 수행하여 이에 대한 선정기준을 제시하였다. 성능예측의 경우 초기 설계단계에서 여러 흡입구 설계안의 다양한 마하수 및 받음각 범위에 대한 빠른 분석이 요구되므로, 간단한 관계식들을 이용한 성능예측 코드를 구성하여 예시 흡입구 모델에 대한 전산해석 결과와의 비교를 통해 검증을 수행하였다. 검증된 코드를 바탕으로 초기 설계단계에서 넓은 비행영역에서 높은 전압력 회복율과 유량 포획율을 갖는 흡입구를 설계함에 있어 가장 중요한 설계요소인 초기 압축각도와 비행 마하수 설계점에 따른 성능예측 결과에 대한 정량적인 분석을 수행하였다.
초기 압축각도와 비행 마하수 설계점에 따른 성능에 대한 분석결과, 마하수 4∼6 범위와 받음각 –6˚∼6˚ 범위에서 초기 압축각도의 경우 전체적으로 높은 흡입구 전압력 회복율이 요구될 경우 초기 압축각도는 6˚가 적절할 것으로 판단하였으며, 받음각 4˚ 이상의 고 받음각 영역에서의 전압력 회복율과 전반적으로 높은 유량 포획면적비가 요구될 경우 초기 압축각도가 3.5˚가 적절할 것으로 판단하였다. 비행 마하수 설계점 선정의 경우 유량 포획성능 측면에서는 저 마하수를 기준으로 설계하는 것이 유리하지만, 전압력 회복성능 측면에서는 고 마하수를 기준으로 설계하는 것이 유리한 것으로 확인되었다. 따라서 비행 마하수 설계점의 경우 비행임무에 따라 요구되는 흡입 유량 또는 전압력 회복성능을 고려하여 선정해야함을 확인하였다.
Nomenclature
| M : | Mach number |
| p : | Pressure |
| δ : | Wedge angle(compression angle) |
| θ : | Shock angle |
| υ : | Prandtl-Meyer expansion angle |
| γ : | Specific heat ratio |
subscripts
| i : | Before shock value |
| i+1 : | After shock value |
| t : | Total value |
Acknowledgments
본 연구는 스크램제트 복합추진시스템 특화연구실 과제(과제코드 : 16-106-501-035)의 지원을 받아 수행하였으며, 이에 감사드립니다.
References
-
Murthy, S.N.B. and Curran, E.T., “Scramjet Propulsion,” Progress in Astronautics and Aeronautics, Vol. 189, pp. 447-511, 2001.
[https://doi.org/10.2514/4.866609]

-
Dou, L., Gao, J., Zong, Q. and Ding, Z., “Modeling and Switching Control of Air-Breathing Hypersonic Vehicle with Variable Geometry Inlet,” Journal of the Franklin Institute, Vol. 355, Issue 15, pp. 6904-6926, 2018.
[https://doi.org/10.1016/j.jfranklin.2018.07.007]

-
Dalle, D.J., Torrez, S.M. and Driscoll, J.F., “Performance Analysis of Variable-Geometry Scramjet Inlets Using a Low-Order Model,” 47th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference & Exhibit, San Diego, U.S.A., AIAA 2011-5756, August 2011.
[https://doi.org/10.2514/6.2011-5756]

- Kim, J.W. and Kwon, O.J., “Numerical Investigation on Performance Characteristics of Supersonic Intake at Various Angles of Attack,” 2015 Korean Society for Aeronautical & Space Sciences Fall Conference, pp. 66-69, Nov. 2015.
-
Torrez, S.M., Driscoll, J.F., Dalle, D.J. and Fotia, M.L., “Preliminary Design Methodology for Hypersonic Engine Flowpaths,” 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, AIAA 2009-7289, Oct. 2009.
[https://doi.org/10.2514/6.2009-7289]

-
Zhang, K., “Hypersonic Curved Compression Inlet and Its Inverse Design,” Advanced Topics in Science and Technology in China, Vol. 56, Springer, Singapore, pp. 281-325, 2020.
[https://doi.org/10.1007/978-981-15-0727-4]

-
Heiser, W.H., Pratt, D.T., Daley, D.H. and Mehta, U.B., Hypersonic Airbreathing Propulsion, AIAA Education Series, American Institute of Aeronautics and Astronautics, Inc., Washington D.C, U.S.A., Ch. 5, 1994.
[https://doi.org/10.2514/4.470356]

- Oswatitsch, K., “Pressure Recovery for Missiles with Reaction Propulsion at High Supersonic Speeds(the Efficiency of Shock Diffusers),” NACA TM 1140, 1947.
-
Smart, M.K., “Optimization of Two-Dimensional Scramjet Inlets,” Journal of Aircraft, Vol. 36, No. 2, pp. 430-433, 1999.
[https://doi.org/10.2514/2.2448]

-
Raj, N.O.P. and Venkatasubbaiaha, K., “A New Approach for the Design of Hypersonic Scramjet Inlets,” Physics of Fluids, Vol. 24, Issue. 8, pp. 1-15, 2012.
[https://doi.org/10.1063/1.4748130]

-
Smart, M.K., “How Much Compression Should a Scramjet Inlet Do?,” AIAA Journal, Vol. 50, No. 3, pp. 610-619, 2012.
[https://doi.org/10.2514/1.J051281]