분리형 로터리엔진 사이클 해석

1. 서 론

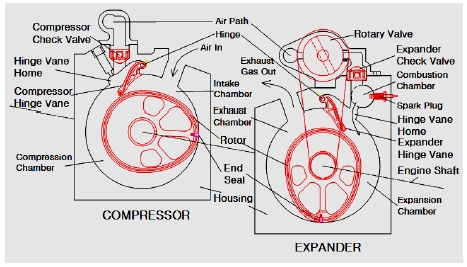
Compressor와 Expander로 구성된 Separate Type Rotary Engine(SRE)[1,2](Fig. 1 참조)의 열역학적 성능 계산 방법은 저자에 의해 이미 발표된 바 있다{3}. 본 논문은 기존 SRE의 성능 향상을 위해 압축공기를 냉각할 때 그 영향을 분석할 수 있도록 계산 방법을 보완한 것이다.

Fig. 1

SRE structure.

SRE는 압축기와 팽창기가 별도로 구비되어 있다. 압축기에서 압축된 공기는 체크밸브를 통해 공기 공기통로에 잠시 머물다 연소실로 통하는 로터리밸브가 열리면서 연소실로 유입된다. 피스톤엔진의 경우 흡입된 공기는 피스톤이 상사점으로 이동함에 따라 밀폐된 공간에서 점진적으로 압축되는데 반해 SRE에서는 로터가 회전하면서 먼저 압축기 내에서 공기가 압축되다가 압축기 공기압이 공기통로 공기압보다 커질 때 팽창기 힌지베인이 연소실을 밀폐함과 동시에 압축기 체크밸브와 로터리밸브가 열려 압축기 공기와 공기통로 공기 그리고 연소실 잔여가스가 혼합되고 이후 로터의 회전이 계속되면서 혼합된 공기가 합쳐진 체적 내에서 압축된다. 이렇게 연소실로 공급되는 압축공기는 피스톤엔진에서와 달리 2단계의 과정을 거쳐 압축되므로 엔진 성능 분석을 위해서는 각 단계에서 공기의 열역학적 거동이 함께 해석되어야 한다.

2. SRE 기본 사이클 해석

신개념 로터리엔진은 동일한 부피에서 공기 흡입, 압축, 연소 및 팽창, 배기하는 일반 엔진과 달라 왕복동 피스톤엔진이나 반켈 로터리엔진과 동일한 방법으로 열역학적 성능을 계산할 수 없다. 이 엔진에 적합한 성능계산 방법을 찾아야 하는데 이를 위해서는 먼저 엔진 작동 메카니즘 분석이 필요하다.

2.1 엔진 내 작동유체 이동 메카니즘

압축기(Compressor)에서는 로터(Rotor)가 회전하면서 확장되는 흡기실(Intake Chamber)로 흡입구를 통해 공기가 유입되고 축소되는 압축실(Compression Chamber)에서는 공기가 압축되어 압축기 체크밸브(Compressor Check Valve)를 통해 공기통로에 저장된다(Fig. 2 압축기 참조). 이때 인젝터로 연료를 공기통로에 분사하여 연료가 공기통로에서 공기와 혼합된 상태로 존재한다.

Fig. 2

SRE operation mechanism.

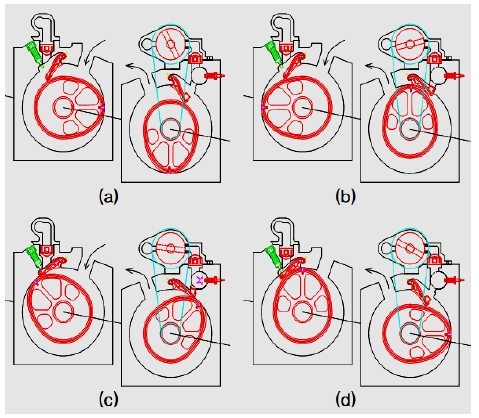
팽창기(Expander)에서는 연소가스 압력으로 엔진 축(Engine Shaft)을 회전시키는 동력을 발생하면서 힌지베인의 캠 역할도 하는 팽창기 로터가 특정 회전 위치에서 힌지베인을 밀어 올려 연소실(Combustion Chamber)을 밀폐된 공간으로 닫을 때 로터에 풀리로 연동된 로터리밸브(Rotary Valve)가 공기통로를 열어 공기통로의 압축된 연료 혼합공기가 연소실로 유입된다(Fig. 2(b), (c) 팽창기 힌지베인 및 로터리밸브 거동 참조). 혼합공기의 연소실 유입이 완료되는 시점에서 점화장치(Spark Plug)로 혼합공기를 폭발시켜 고온 고압의 연소가스를 만들고, 로터 회전이 진행되면서 힌지베인이 연소실을 열 때 연소가스가 팽창실(Expansion Chamber)로 배출되면서 로터를 회전시켜 동력을 발생시킨다(Fig. 2(c), (d) 팽창기 연소실, 힌지베인 참조).

2.2 SRE 기본 사이클 해석

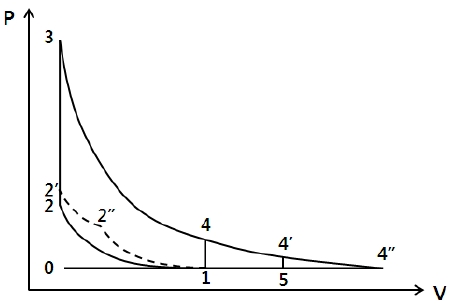
정적연소(Constant volume combustion)를 하는 일반적인 피스톤 내연기관에서 공기와 연소가스의 열역학적 거동을 Fig. 3과 같이 P-V 선도로 나타낼 수 있으며, 선도상에서 움직이는 경로에 따라 Otto Cycle(0-1-2-3-4-1-0), Atkinson Cycle (0-1-2-3-4"-0) 및 Over-expanded Cycle (0-1-2-3 -4'-5-0)등으로 분류된다.

Fig. 3

Cycle P-V Diagram.

팽창비가 압축비보다 크도록 설계된 SRE는 Over-expanded Cycle로 작동되지만 압축기와 팽창기 사이에 공기통로가 있고 압축실과 공기통로 사이에 체크밸브, 공기통로와 연소실 사이에 로터리밸브와 체크밸브가 설치되어 이들 밸브의 개폐에 따라 P-V 선도에서 피스톤엔진과 다르게 거동하며 0-1-2“-2‘-3-4’-5-0 경로를 따른다.

보다 정확한 사이클 해석을 위해서는 사이클의 각 단계마다 작동유체의 열역학적 상태 분석이 필요하다. 분석에 필요한 열역학적 관계식은 교과서로 널리 사용되는 내연기관 전문서적{4}을 참고하였고, 동작유체는 이상기체 법칙을 만족하며 비열은 온도에 관계없이 일정하다고 가정하였다.

2.2.1 압축기 체크밸브 열리기 전 압축실 공기

체크밸브가 열리기 전 압축실은 하우징, 로터, 힌지베인 및 체크밸브에 의해 밀폐된 공간이다. 압축실 최대 체적는 로터 엔드실(End Seal)이 흡입구를 막 통과할 때의 체적이며 이는 피스톤엔진의 행정체적에 해당한다.

피스톤엔진에서는 피스톤이 위로 올라감에 따라 연소실이 포함된 실린더 내 체적이 감소하면서 공기가 압축되고 피스톤이 상사점에 도달할 때 실린더 내 모든 공기가 연소실에 압축되지만 SRE에서는 연소실이 포함되지 않은 압축실 체적 안에서만 공기가 압축되다가 압축실 공기의 압력이 공기통로 압력보다 커지는 순간 체크밸브가 열리면서 압축실과 공기통로가 연결되고, 그 이후부터는 로터 회전이 지속되는 동안 압축실과 공기통로 공기가 동시에 압축된다. 따라서 체크밸브가 열리기 전까지는 압축실 체적이 연소실을 포함하는 피스톤엔진의 그것보다 작으며 이는 Fig. 3의 1-2‘’선도와 같이 SRE 압축실 압력 급상승의 원인이 된다.

체크밸브가 열리기 직전 Fig. 3의 2“위치에서 압축기 압력과 온도는 아래와 같다.

$\[ Pc{2}^{\text{'}\text{'}}=P1{\left(\frac{Vc1}{Vc{2}^{\text{'}\text{'}}}\right)}^{\gamma } \]$

(1)

$\[ Tc{2}^{\text{'}\text{'}}=T1{\left(\frac{Vc1}{Vc{2}^{\text{'}\text{'}}}\right)}^{\left(\gamma -1\right)} \]$

(2)

Fig. 3의 SRE 압축선도 1-2‘’-2‘의 부피(V)는 피스톤엔진과 비교를 위해 압축실과 연소실을 합한 것을 표시한다. V1은 압축기 로터가 압축을 시작하는 위치에서 압축실 체적 Vc1(Fig. 3의 1 위치에서 compression chamber의 volume)과 연소실 체적 Vb를 합한 체적이다. 즉 V1 = Vc1 + Vb가 된다. 또, V2"는 압축기 로터가 회전하면서 압축실 압력이 공기통로 압력보다 커져 압축실과 공기통로 사이의 체크밸브가 열리는 시점에서 압축실 체적 Vc2"와 연소실 체적 Vb를 합한 부피이다. V2" = Vc2" + Vb 이다. 압축이 완료되어 압축실의 체적이 없어지는 2’ 위치에서 압축공기 제적 V2'는 Vb가 된다.

2.2.2 로터리밸브가 열린 후 공기통로와 연소실 혼합공기

팽창기 로터가 회전하면서 힌지베인을 위로 밀어 올리면 연소실과 팽창실이 분리되어 폐쇄공간의 연소실이 형성되고, 동시에 엔진 축과 연동되어 회전하는 로터리밸브가 열려 공기통로와 연소실이 열린 공간으로 합쳐지면서 공기통로의 압축공기가 연소실로 유입되어 연소실의 잔류 연소가스와 혼합된다. 로터리밸브가 열리는 위치를 2“로 설정하면 혼합된 기체의 압력과 온도는 Eq. 3, 4와 같다.

$\[ Papb{2}^{\text{'}\text{'}}=\frac{Pap{2}^{\text{'}}Vap+P5Vb}{Vap+Vb} \]$

(3)

$\[ Tapb{2}^{\text{'}\text{'}}=\frac{Tap{2}^{\text{'}}T5\left(Pap{2}^{\text{'}}Vap+P5Vb\right)}{Pap{2}^{\text{'}}VapT5+P5VbTap2\text{'}} \]$

(4)

Eq. 3, 4에서,

P5 : 혼합직전 연소실 압력(=대기압)
Pap2' : 혼합직전 공기통로 압력(=P2')
T5 : 혼합직전 연소실 온도
Tap2' : 혼합직전 공기통로 온도(=T2‘)

2.2.3 압축실, 공기통로 및 연소실이 동시에 합쳐질 때 혼합공기

로터리밸브가 열려 공기통로와 연소실이 합쳐지면 압력이 낮은 연소실 영향으로 혼합공기의 압력은 혼합전 공기통로의 압력보다 낮아진다. 압축기 로터와 팽창기 로터의 상대적인 설치 각도에 따라 로터리밸브가 열릴 때 압축실의 공기압이 공기통로와 연소실 혼합공기 압력보다 높으면 압축기 체크밸브가 열릴 것이고 그렇지 않으면 로터 회전이 조금 더 진전된 후 열릴 것이다. 본 연구에서는 로터리밸브가 열릴 때 압축실과 공기통로를 연결해주는 체크밸브가 동시에 열리도록 두 로터 사이의 설치 각도가 적절히 설정된 경우에 대한 사이클 해석을 기술한다.

로터리밸브가 열려 공기통로와 연소실이 합쳐질 때 혼합공기의 압력과 온도는 Eq. 3, 4와 같다. 압축기 로터가 회전하여 압축실의 압력이 Papb2''보다 커지면 압축기 체크밸브가 열려 압축실과 공기통로 및 연소실이 모두 합쳐진 하나의 열린 공간이 되며 이때 Fig. 3의 2“위치에서 혼합된 공기의 압력과 온도는 Eq. 6, 7과 같다,

$\[ Pc{2}^{\text{'}\text{'}}=Papb2\text{'}\text{'} \]$

(5)

$\[ P{2}^{\text{'}\text{'}}=Pc2\text{'}\text{'} \]$

(6)

$\[ T2=\frac{Tc{2}^{\text{'}\text{'}}Tapb2\text{'}\text{'}\left(Pc{2}^{\text{'}\text{'}}Vc{2}^{\text{'}\text{'}}+Papb2\text{'}\text{'}\left(Vap+Vb\right)\right)}{Pc{2}^{\text{'}\text{'}}Vc{2}^{\text{'}\text{'}}Tapb{2}^{\text{'}\text{'}}+Papb{2}^{\text{'}\text{'}}\left(Vap+Vb\right)Tc2\text{'}\text{'}} \]$

(7)

2.2.4 압축 완료 후 연소실 압축공기

압축실, 공기통로 및 연소실이 합쳐진 후에도 로터가 더 회전하여 압축실 공기가 모두 공기통로와 연소실로 유입될 때까지 혼합기는 계속 압축된다. 압축이 완료된 2‘위치에서 공기통로와 연소실의 압력과 온도는,

$\[ P{2}^{\text{'}}=P2\text{'}\text{'}{\left(\frac{Vc{2}^{\text{'}\text{'}}+Vap+Vb}{Vap+Vb}\right)}^{\gamma } \]$

(8)

$\[ T{2}^{\text{'}}=T2\text{'}\text{'}{\left(\frac{Vc{2}^{\text{'}\text{'}}+Vap+Vb}{Vap+Vb}\right)}^{\left(\gamma -1\right)} \]$

(9)

혼합된 상태에서 Pap2'와 Tap2'는 각각 P2'와 T2'와 같다.

$\[ Pap{2}^{\text{'}}=P2\text{'} \]$

(10)

$\[ Tap{2}^{\text{'}}=T2\text{'} \]$

(11)

2.2.4' 공기통로 공기 냉각시 온도 압력

공기통로는 압축기에서 압축된 고온의 공기가 연소실로 유입되기 전에 일정 시간(로터 약 1/2회전 소요시간) 머무는 곳으로 부피에 비해 표면적이 커 내부 공기의 냉각에 용이한 구조를 갖고 있다. 압축공기를 냉각하여 얻는 이점은 공기 밀도는 유지하면서 압력이 낮아져 압력에 소요되는 동력을 줄일 수 있고, 연소실 온도를 동일하게 유지할 때 연료를 더 분사시켜 출력을 향상시킬 수 있다는 것이다.

냉각을 통해 공기통로 압축공기의 압력을 △P 만큼 낮춘다면 냉각 후 공기통로 압축공기 압력과 온도는

$\[ Pap{2}^{\text{'}}=P{2}^{\text{'}}-\text{Δ}P \]$

(10’)

$\[ Tap{2}^{\text{'}}=T{2}^{\text{'}}\left(Pap{2}^{\text{'}}/P2\text{'}\right) \]$

(11‘)

2.2.5 연소실 폭발압 및 온도

연소실 온도는 연료 공급량에 비례한다. 연소실 온도는 연소실 냉각, 연소실 소재 등에 따라 최대값이 제한 될 수 있으므로 엔진 개발자가 적절히 정한다. 3위치에서,

$\[ T3=Tmax \]$

(12)

$\[ P3=P2\text{'}\frac{T3}{T2\text{'}} \]$

(13)

2.2.6 연소가스 팽창 완료 후 압력 및 온도

연소실 폭발 후 고온, 고압의 연소가스는 팽창실에서 로터를 회전시켜 동력을 생산하고 팽창하게 된다. 팽창이 완료된 4‘위치에서,

$\[ P{4}^{\text{'}}=P3{\left(\frac{1}{Er}\right)}^{\gamma } \]$

(14)

$\[ T{4}^{\text{'}}=T3{\left(\frac{1}{Er}\right)}^{\left(\gamma -1\right)} \]$

(15)

여기서 Er은 팽창비이며 Eq. 19로 정의된다.

2.2.7 연소가스 배기 완료 후 연소실 공기압 및 온도

T5와 P5는 연소실에서 연소가스의 배기행정이 완료되어 대기압으로 팽창한 후의 온도와 압력을 나타낸다. P5는 대기압과 같으나 T5는 아래 Eq. 16과 같다.

$\[ T5=T4\text{'}{\left(\frac{P5}{P{4}^{\text{'}}}\right)}^{\left(\gamma -1\right)/\gamma } \]$

(16)

2.3 SRE 열역학적 효율 계산

SRE 엔진의 열역학적 효율은 Eq. 17로 계산 할 수 있다.

$\[ {\eta }_{SRE}=1-\frac{\left(T{2}^{\text{'}}-Tap2\text{'}\right)*Vap/Vb+T4\text{'}-T1}{T3-T2\text{'}} \]$

(17)

공기통로에서 압축공기의 냉각이 없으면 위 식은 Otto cycle 이론 효율식과 같은 형태를 갖는다.

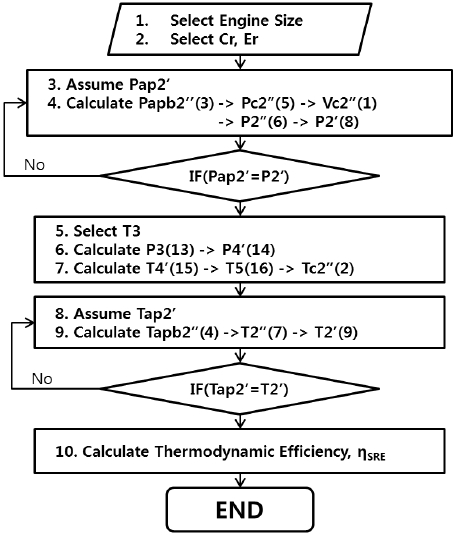
Eq. 17의 T2', Tap2', T3, T4'를 구하기 위해 2.2절에 기술된 각 단계에서 작동 유체의 열역학적 특성을 모두 알아내야 하는데 이를 위해 미지수 16개의 연립 다차방정식을 풀어야 한다. 해석적인 방법으로 실제 해(exact solution)을 구하는 것이 가능하다 하더라도 매우 번거로울 것이어서 본 논문에서는 컴퓨터를 이용한 근사해를 계산하였으며 적용한 알고리즘은 Fig. 4와 같다. 공기통로에서 압축공기의 냉각이 이루어 진다면 Eq. 3과 4에서 Pap2'와 Tap2'를 적용할 때 Eq. 10' 및 11‘의 값을 적용하면 된다.

Fig. 4

SRE Cycle Analysis Algorithm.

이상적인 Otto Cycle 엔진의 열역학적 효율은 압축전 엔진 실린더가 대기온도의 공기로만 채워진다는 가정하에 아래 Eq. 18로 계산할 수 있다. 그러나 엔진으로 들어오는 외부 공기는 연소실에 남아있는 전 사이클의 연소가스와 섞여서 압축되므로 열효율은 Eq. 18로 계산한 것보다 다소 낮아진다. 본 논문에서 더 상세한 계산 방법은 기술하지 않겠지만 SRE 열역학적 효율을 계산한 것과 유사한 방법으로 연소실에 남아있는 이전 사이클의 연소가스의 영향을 고려하여 Otto Cycle의 열역학적 효율을 계산하면 Eq. 18로 계산한 값보다 약 1%정도 낮게 나오는 것을 알 수 있다(Table 1 Residual gas effect reflected참조).

$\[ {\eta }_{Otto}=1-\frac{1}{C{r}^{\left(\gamma -1\right)}} \]$

(18)

Table 1

Cycle Comparison between Otto and SRE.

3. Otto Cycle과 SRE Cycle 비교

팽창비가 압축비보다 큰 Over-expanded Cycle을 만들면 엔진 열효율을 높일 수 있다. 팽창실 최대 체적을 Ve4‘ 로 표시하면 압축비 Cr과 팽창비 Er은 다음 식으로 계산된다.

여기서,

Cr : 압축비
Er : 팽창비
Ve4‘ : 팽창실 최대 체적

Fig. 5는 압축비 및 팽창비가 10인 Otto Cycle과 압축비 10, 팽창비 11.2인 SRE Over Expanded Cycle을 비교한 것이다. 두 엔진의 배기량을 동일하게 하고 SRE 연소실 최고온도를 3,600℃로 설정하였으며 SRE과 동일 양의 연료를 공급받는 Otto Cycle을 분석하였다. SRE 압축공기는 Otto Cycle과 비교하여 동일한 압축비에서 1-2“-2‘-2-1 면적에 해당하는 만큼 압축 일을 추가로 더 흡수하여 Otto Cycle의 압축공기보다 온도와 압력이 높아진다. Fig. 6은 공기통로 체적이 연소실 체적의 0.1배인 경우(a)와 5배인 극단적인 경우(b)를 비교한 것인데 압축을 완료하기 위해 압축기가 Otto Cycle에 비해 추가로 수행하는 일의 크기에 큰 차이가 있음을 알 수 있다.

Fig. 5

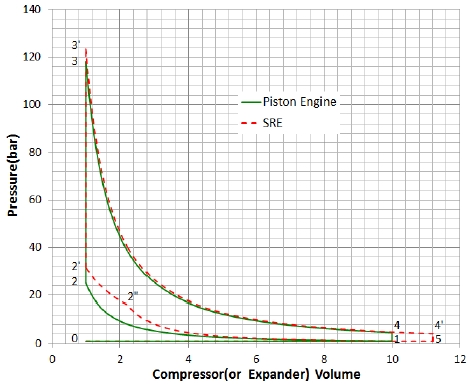
Characteristics of the SRE P-V Diagram where SRE air path size is same with the combustion chamber and quantity of fuel supply are same for both SRE and Otto cycles.

Fig. 6

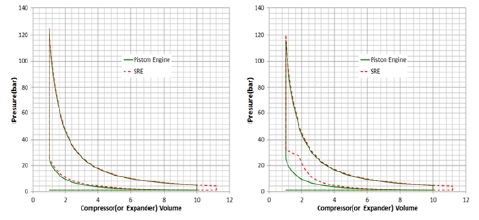
Comparison of Work required for different air path sizes. (a) air path size = combustion chamber×0.1, (b) air path size = combustion chamber×5.0.

Table 1은 같은 배기량에 연소실 최고온도를 3600℃로 설정한 Otto Cycle과 SRE Cycle을 비교한 것이다. 추가적인 압축 일로 인하여 SRE의 열효율이 Otto Cycle에 비해 저하되지만 압축공기압 P2'가 Otto Cycle 압축공기압 P2보다 높아져 엔진효율의 향상을 가져오므로 추가 압축일의 일부는 회수된다고 볼 수 있다. 또, Over Expanded Cycle SRE는 Fig. 5의 4-4‘-5-1-4에 해당하는 동력을 더 얻을 수 있으므로 이를 감안한 전체 Cycle의 열효율 저하는 동일 압축비의 Otto Cycle에 비해, Air Pass 체적에 따라 0 ~ 2% 정도로 제한된다.

압축기에서 압축되어 공기통로에 들어간 압축공기는 연소실로 공급되기 전 로터가 약 180도 회전하는 시간동안 대기한다. 공기통로로 들어오고, 일정시간 대기하다 연소실로 공급되는 동안 압축공기는 냉각이 되며, 이렇게 냉각된 공기는 연소실 초기온도(T2')를 낮추어 동일한 연소실 최고온도를 유지하면서 연료를 더 많이 연소할 수 있게 하므로 엔진의 출력을 증가시키는 역할을 한다(Table 2 참조). 여기서 압축공기의 냉각으로 열손실이 발생하므로 열효율의 저하가 있으나(최대 약 0.2%) 그 양은 출력 증가(최대 약 7%)와 비교해 매우 작으므로 냉각핀 설치 등 적극적인 냉각방법을 적용하여 엔진의 출력을 높이는 설계가 바람직하다.

Table 2

SRE performances with no heat loss except air pass cooling effect(for given fixed T3 and air pass volume equivalent to combustion chamber).

4. 결 론

팽창비가 압축비보다 큰 Over Expanded SRE 사이클 해석을 위해 작동유체의 흐름을 따라 Cycle의 주요 부위에서 열역학적 분석을 수행한 결과 다음과 같은 결과를 얻었다.

1) SRE는 일반 내연기관과 달리 공기 압축과정이 두 단계로 구성되어 P_V 선도에서 압축선도가 두 개의 곡선으로 나타나며, 그 결과 압축에 소요되는 일량이 늘어나 엔진의 효율을 떨어뜨리지만 압축기와 팽창기가 분리된 구조상 손쉽게 구현이 가능한 Over Expanded Cycle을 적용함으로써 확보되는 효율 증가분이 있어 결과적으로 Otto cycle과 거의 동일한 수준의 엔진 효율을 얻을 수 있다.

2) 공기통로의 압축공기를 냉각함으로써 연소실 최대 온도를 유지하면서 더 많은 연료를 분사시킬 수 있어 추가적인 열 손실 대비 큰 출력 향상을 얻을 수 있다.

본 논문에서 확인된 바와 같이 SRE는 Otto Cycle 왕복동 피스톤엔진에 비해 열역학적 효율의 저하가 크게 없으면서(최대 2%) 동일 출력에서 크기와 무게를 대폭 줄일 수 있는 장점이 있어 드론이나 무인기와 같은 소형 항공기로부터 이륜차, 하이브리드 자동차, 발전기 등 다양한 분야에서 기존 피스톤엔진을 대체할 것으로 기대된다.

Acknowledgments

[이 논문은 한국추진공학회 2018년도 추계학술대회(2018. 12. 19-21, 웨스틴 조선호텔 부산) 발표논문을 심사하여 수정·보완한 것임.]

본 연구는 국방과학연구소 민군협력진흥원의 지원으로 수행되었으며, 이에 감사드립니다.

References

• Ki, D.J., and Choi, H.J., 'New Rotary Engine with separate Compressor and Expander', Journal of the Korean Society of Propulsion Engineers, 21(4), p71-78, (2017).
• Ki, D.J., “Separate-type Rotary Engine”, US9212603, 15), Dec., (2015.
• Ki, D.J., 'Thermodynamic Performance Analysis of the Separate Type Rotary Engine', 2017 Asia-Pacific International Symposium on Aerospace Technology, Seoul, Korea, C7-3, Oct.), (2017.
• Ganesan, V., Internal Combustion Engines, 2nd ed., Tata McGraw Hill, New Delhi, India, (2003).