가이드 베인을 부착한 핀-휜 유동에서 가이드 베인 위치와 입사각에 따른 전열 및 유동 특성에 관한 수치적 연구
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 핀-휜이 있는 유로에 위치와 유동 입사각이 다른 가이드 베인을 부착하여 전열 성능 및 압력 강하 특성 변화를 분석하였다. 레이놀즈수가 1400일 때 가이드 베인의 위치와 입사각에 따른 전열 성능과 유동 특성을 수치해석으로 확인하였고, 핀-휜 만 있는 해석 결과와 비교하였다. 수치해석을 수행한 결과, Case 1의 입사각 0°일 경우에 전열 성능이 최대가 되고 핀-휜 만 있는 유로에 비해 약 5% 향상되었다. Case 2의 입사각 10°일 경우에 압력 손실이 최소가 되고 약 1.9% 감소하였다.
Abstract
In this study, a guide vane with varying positions and incidence angles was adopted to a pin-fin channel to analyze the change in thermal performance and pressure loss characteristics. A numerical analysis was conducted to investigate the effect of incidence angles and positions on heat transfer and flow characteristics at Re =1400. The results of it were compared those of a pin-fin channel without a guide vane. In case 1 when the incidence angle is 0°, the heat transfer performance is maximized and improved by approximately 5% when compared to the pin-fin channel without the guide vane. In case 2 when the incidence angle is 10°, the pressure loss is minimized and decreased by approximately 1.9% when compared to the pin-fin channel without the guide vane.
Keywords:
Pin-fin, Heat exchanger, Guide vane, Incidence angle키워드:
핀-휜, 열교환기, 가이드 베인, 입사각1. 서 론
핀-휜 열교환 장치는 에어컨, 냉장고, 자동차 및 항공 분야 등 다양한 분야에서 사용되고 있다. 이러한 분야에서 전열 성능과 압력 손실의 비율은 에너지 소비 효율과 직결되는 요소이기 때문에 전열 성능을 향상시키고 압력 손실을 개선시키는 것은 매우 중요한 과제이다. 소형 열교환 장치의 전열 성능과 압력손실의 비율을 증가시키기 위해 핀-휜 유로에 전열 성능을 향상하고 압력손실을 개선하는 장치를 부착하는 연구는 활발하게 진행되어왔다.
Torii 등[1]은 핀과 같은 높이의 종횡비가 2인 델타 윙렛 형태의 와류 발생기를 정배열의 핀-휜 유로에 부착하였으며, 실험을 통해 와류 발생기가 부착된 핀-휜 유로에서 전열 성능이 향상되고 압력손실이 개선되는 것을 확인하였다. Song 등[2]은 굽혀진 델타 윙렛 형태의 와류 발생기를 엇갈린 배열의 핀-휜 유로에 부착하여 실험을 통해 전열 성능과 압력손실의 변화를 연구하였다.
Gong 등[3]은 펀칭 된 휘어진 사각 와류 발생기를 엇갈린 배열의 핀-휜 유로에 부착하여 전열 성능 개선을 위한 수치적 연구를 수행하였다. Sinha 등[4]은 채널 높이의 절반인 직사각형 와류 발생기를 핀-휜 열교환기에 부착하였다. 이들은 정배열과 엇갈린 배열에서 와류 발생기의 상대적인 위치를 변경하였고, 각 변수가 열전달과 유동 특성에 미치는 영향을 수치적으로 연구하였다.
Salviano 등[5]은 종횡비 2의 델타 윙릿(Delta winglet)형태의 와류 발생기를 엇갈린 배열의 핀-휜 유로에 부착시켰고, 와류 발생기의 회전각, 받음각 그리고 위치를 최적화 기법인 DO(Direct Optimization)와 RSM(Response Surface Methodology)를 사용하여 최적화를 통해 전열 성능, 압력 강하와 그 두 성능의 비율에 대한 최적의 각도와 위치를 찾는 수치적 연구를 수행하였다. 또한 두 레이놀즈수 영역에서 SIMPLEX 방법으로 와류 발생기의 형상, 위치, 회전각과 받음각을 최적화하는 수치적 연구를 진행하였다. 이 연구는 정배열, 엇갈린 배열 두 가지의 핀-휜 유로를 기반으로 수치해석을 진행하였다[6]. 다른 최적화 연구로, Jang 등[7]은 핀 뒤에 블록 타입의 와류 발생기를 장착하여 엇갈린 배열의 핀-휜 유로에서의 전열 특성을 확인한 것이 있다. 이들은 여러 레이놀즈 영역에서 스팬 각도와 와류 발생기의 유동 방향 위치에 대해 최적화 연구를 수행하였다.
와류 발생기를 핀-휜 유로에 부착하였을 경우 박리 지연 효과가 발생하여 핀의 박리 영역이 줄어든다. 이로 인하여 압력 손실이 줄어들고 전열 성능이 향상된다[5,6]. 가이드 베인의 경우 직접적으로 유동 방향을 바꾸어 박리 지연을 발생시키고 박리 영역이 줄어드는 효과를 얻을 수 있다. 그러므로 본 논문에서는 엇갈린 배열의 핀-휜 유로에서 핀 후류 박리 영역을 제어하기 위해 가이드 베인을 부착하였으며, 이에 따른 전열 성능과 유동 특성의 변화를 확인하였다. 또한 가이드 베인의 형상 변수가 전열 성능과 유동에 미치는 영향을 확인하기 위해 가이드 베인 앞전(Leading edge) 위치와 유동 입사각을 변경하였다. 선정한 형상 변수에 따른 전열 성능과 유동 특성의 변화를 수치적 기법을 통하여 연구하였다.
2. 수치해석 방법
2.1 지배방정식
유로에 흐르는 유동은 정상상태라고 가정하며, 유로 내부의 유동은 비압축성 유동으로 가정하였다. 그러므로 연속 방정식은 Eq. 1과 같이 나타낼 수 있다. 운동량 보존 방정식은 비압축성 유체로 가정하였기 때문에 밀도가 미분항 밖으로 나간 Eq. 2와 같이 나타낼 수 있다. 에너지 방정식은 Eq. 3과 같다.
| (1) |
| (2) |
| (3) |
핀-휜에 가이드 베인을 부착할 때 가이드 베인의 전열 성능과 압력 강하 정도를 평가하기 위해 Eq. 4에 나타낸 Colburn factor(j)와 Eq. 5에 나타낸 Friction factor(f)를 이용하였다.
| (4) |
| (5) |
수치해석은 Ansys사의 CFX를 이용하였다. 핀 후류의 난류를 모사하기 위해 난류 모델은 Salviano 등[5,6]이 핀-휜 유동 연구에 이용하였던 k-w SST(Shear Stress Transport)를 사용하였다.
2.2 해석형상 및 계산조건
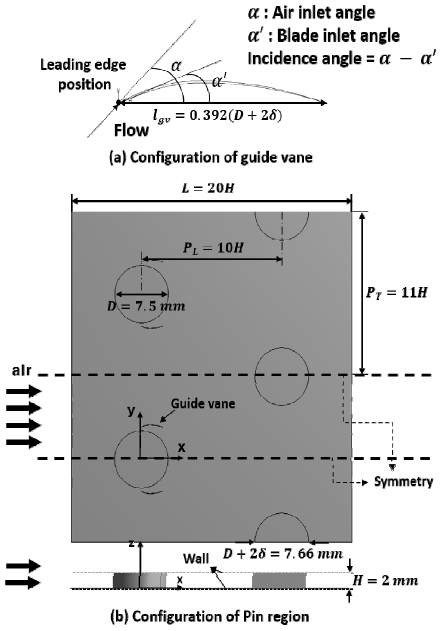
가이드 베인을 부착하였을 경우 형상은 Fig. 1과 같다. 가이드 베인의 형상과 입사각 정의를 위쪽에 나타냈으며, 아래에는 핀 구간을 나타내었다. 핀의 열(row) 개수는 2개이며, 가이드 베인은 첫 번째 열의 핀 부근에 부착하였다. x축 방향으로 유동이 진행하며, y는 수직 배열 방향, z는 핀의 높이 방향을 나타낸다. 해석 형상의 핀 구간 높이(H)는 2 mm이고 핀 구간의 길이(L)는 20H 이다. 핀은 2개의 열을 엇갈리게 배치하였으며, 핀의 수평 피치(PL)는 10H 이며, 핀의 수직 피치(PT)는 11H 이다.
핀의 지름(D)은 7.50 mm 이고, 핀의 두께(δ)는 0.08 mm 이다. 그러므로 수치해석에 사용한 핀의 지름(D+2δ)은 7.66 mm 이다.
가이드 베인의 길이(lgv)는 0.392(D+2δ)이며, 가이드 베인으로 인해 유동 각도의 변화 폭이 크도록 길이를 기준으로 최대 캠버는 9.5%로 하였고, 캠버 포지션은 40% 그리고 가이드 베인의 두께로 인해 발생하는 압력 손실을 줄이기 위해 두께는 1%인 익형을 사용하였다. 가이드 베인의 높이(hgv)는 H이다.
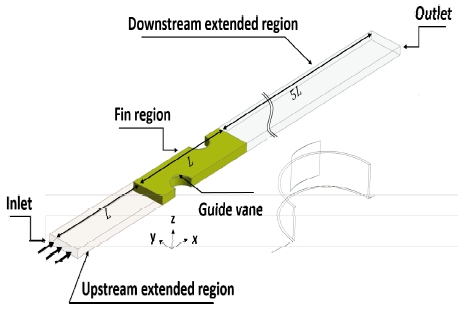
수치해석을 진행한 전체 핀-휜 유로는 Fig. 2와 같다. 각각 상류 구간, 핀 구간 그리고 하류 구간으로 나누었다. Fig. 2의 노란색 부분은 핀과 가이드 베인이 있는 핀 구간이다. 상류의 확장된 유동 구간은 핀 구간과 동일한 길이(L)로 만들었다. 후류의 확장된 유동 구간은 빠져나가는 유동에서 역류(Reverse flow)가 발생하는 것을 방지하기 위해 핀 구간의 5배 길이(5L)로 만들었다. 상류와 하류 구간의 윗면과 아랫면은 경계층이 발달하지 않고 유동이 들어오고 나가는 핀 외부의 환경과 z 방향으로 적층된 핀-휜 유로를 모사하기 위해 주기조건을 주었다. 상류 구간, 핀 구간 그리고 하류 구간의 옆면에 모두 대칭 조건을 사용하였다. 핀 구간의 윗벽, 아랫벽과 가이드 베인에 점착 조건(No-slip condition)을 주었고, 300 K의 일정 온도가 유지되는 벽면 조건을 이용하였다.
입구의 유동은 레이놀즈수 1400으로 균일한 유동이 유로 내부로 들어오며, 사용한 레이놀즈수의 정의는 아래의 Eq. 6과 같다. 이때 입구 유동의 온도는 340 K이다. 비압축성 유동으로 가정하고 계산을 진행하였기 때문에 밀도는 변하지 않는 조건을 사용하였다. 출구는 대기압과 동일한 압력조건을 주었다.
| (6) |
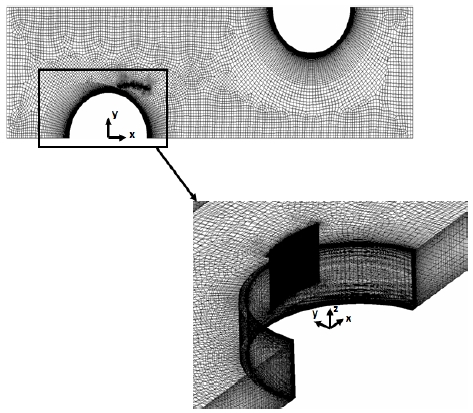
Fig. 3에 핀 구간의 격자 구성을 나타내었다. k-w SST 난류 모델을 사용하였기 때문에 모든 벽면 근처에 격자를 밀집시켜 y+가 1보다 낮은 값을 가지도록 핀 구간의 격자를 구성하였다. 가이드 베인의 위치와 각도가 바뀌어도 총 격자 개수는 약 193만 개 수준을 유지하도록 격자를 구성하였다.
2.3 격자 의존도 확인 및 계산 검증
수치 해석에 사용한 격자계 검증을 위해 격자수를 변경해 가며 격자 의존도를 확인하였다. 이 때 격자 의존도 확인 형상은 엇갈린 배열의 핀-휜 유로에 가이드 베인이 부착되어진 것이다. 핀 구간의 전체 Colburn factor와 Friction factor를 비교하여 격자 의존도 테스트를 진행하였다.
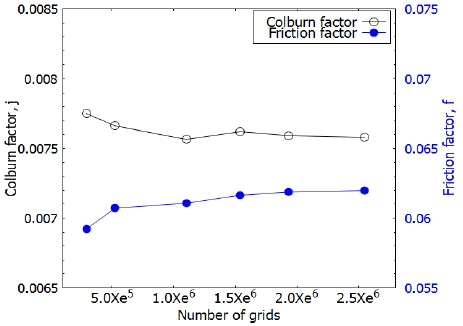
격자 수가 다른 가이드 베인이 부착된 핀-휜 유로의 수치해석 결과는 Fig. 4에 나타내었다. 격자 의존도 확인 결과 약 193만 개의 격자 이후로는 핀 구간 전체의 Colburn factor와 Friction factor의 변화량이 1% 미만으로 나타났다. 그러므로 본 연구에서는 193만 개 수준의 격자를 이용하여 수치해석을 진행하였다.
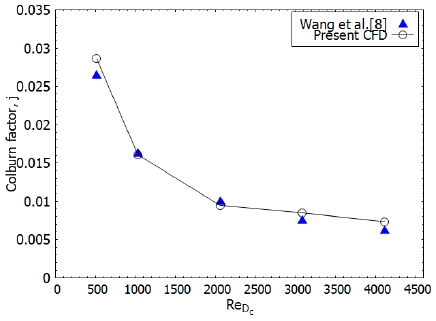
본 연구의 신뢰도를 얻기 위해 Wang 등[8]이 제안한 핀-휜 열교환기에서 레이놀즈수에 따른 Colburn factor 상관식과 전산 해석 결과를 비교하여 검증하였다. 아래의 Eq. 7은 검증에 사용한 Wang의 상관식이다. 이 때 사용한 레이놀즈수의 정의는 아래의 Eq. 8과 같다. Fig. 5에서 Wang의 상관식과 본 연구의 수치해석이 유사한 경향을 나타내는 것을 확인할 수 있다.
| (7) |
| (8) |
3. 결과 및 논의
핀-휜 배열에 x 방향으로 위치를 변경해가며 가이드 베인을 부착하였고 각 위치에서 입사각을 바꾸어 가며 수치해석을 진행하였다. 첫 번째 핀의 중심을 기준으로 전, 후로 위치를 변경하였다. 각 Case의 위치와 유동 입사각은 Table 1에 정리하였다. 위치는 핀의 실제 직경(D+2δ)로 나누어 무차원화 하였으며, x 방향에 대해서만 가이드 베인의 위치를 변경하였기 때문에 y 방향의 좌표는 모두 같다. 각 위치에서 입사각을 변경해가며 각 Case의 Colburn factor와 Friction factor를 핀-휜 만 있는 유로의 Colburn factor(j0)와 Friction factor(f0)로 나누어준 값인 Colburn factor ratio(j/j0)와 Friction factor ratio(f/f0)를 계산하여 그래프에 도시하였다.
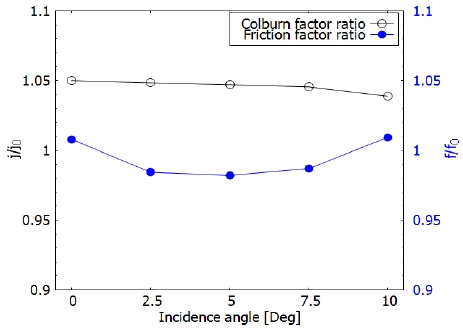
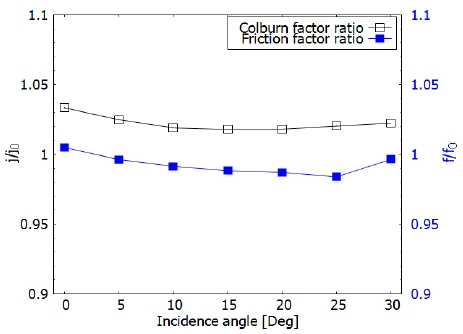
Fig. 6은 Case 1의 Colburn factor ratio와 Friction factor ratio를 입사각에 따라 나타낸 그래프이다. 입사각이 0°에서 5°까지 증가함에 따라 Friction factor ratio는 줄어드는 경향을 보였고, 5° 이후에는 다시 증가하는 경향을 보인다. Case 1에 대한 수치해석 결과 중 가장 Friction factor가 가장 낮은 경우는 입사각이 5°일 경우이다. 이 경우 핀-휜 만 있는 유로에 비해 약 1.8% 감소하는 것을 확인할 수 있었다. Case 1은 입사각이 증가함에 따라 Colburn factor ratio는 비슷하지만 조금씩 감소하며, 7.5°에서 10°로 입사각이 증가하면 이전보다 큰 폭으로 감소한다. 입사각이 0°일 때 수치해석 결과 중 가장 높은 Colburn factor를 가지며, 이는 핀-휜 만 있는 유로에 비해 약 5% 증가한 수치이다.
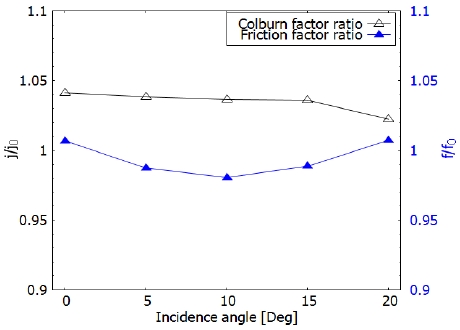
Fig. 7은 Case 2에 대한 Colburn factor ratio와 Friction factor ratio를 입사각에 따라 도시한 것이다. 0°에서 10°까지는 입사각이 증가함에 따라 Friction factor ratio가 감소하는 경향을 보였고, 10° 이후는 다시 증가하는 추이를 보였다. Case 2에 대한 수치해석 결과 중 10°에서 Friction factor가 가장 낮았고, 이는 핀-휜 만 있는 유로에 비해 약 1.9% 감소된 값이다. Colburn factor ratio는 입사각에 따라 비슷하지만 조금씩 감소하고, 15°에서 20°로 입사각이 증가하면서 이전보다 큰 폭으로 감소하였다. Colburn factor가 가장 높은 입사각은 0°이며, 이 때 값은 핀-휜 만 있는 유로에 비해 4.1% 증가한 것이다.
Fig. 8은 Case 3에 대한 Colburn factor ratio와 Friction factor ratio를 입사각에 따라 도시한 것이다. Friction factor ratio는 입사각이 25°가 될 때까지 감소하고 25°이후 증가하는 것을 확인할 수 있다. 입사각이 25°에서 가장 낮은 Friction factor 값이 나타났고, 이는 핀-휜 만 있는 유로에 비해 약 1.6% 감소한 값이다. Colburn factor ratio의 경우에는 0°에서 15°까지 소폭 감소하는 경향을 보이고, 15°이후에는 소폭 증가하는 값을 가지는 것을 확인할 수 있다. Colburn factor는 0°에서 가장 높았고, 이는 핀-휜 만 있는 유로에 비해 약 3.3% 증가한 값이다.
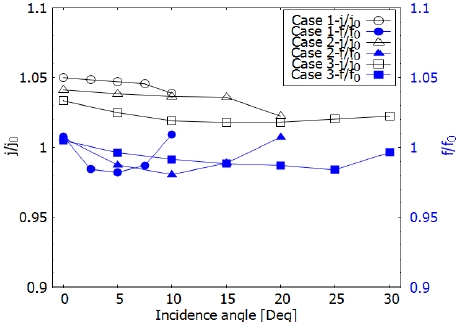
Fig. 9에 모든 Case의 Colburn factor ratio와 Friction factor ratio를 도시하였다. Colburn factor ratio는 Case 1에서 Case 3로 위치가 바뀔수록 최댓값이 감소하며 전반적인 값도 감소하는 경향을 보인다. 입사각에 대해서 유사한 값을 가지는 경향을 보이고 일정 입사각 이후 감소하거나(Case 1, Case 2), 감소하다가 일정 입사각 이후 증가하는 추이를 보인다(Case 3).
Friction factor ratio의 경우 세 Case 모두 최솟값은 유사하였다. 또한, 입사각이 증가함에 따라 Friction factor ratio는 감소하고 일정 입사각 이후 다시 증가하는 추이를 보였다. 이는 입사각이 일정 입사각보다 증가하게 되면 가이드 베인 박리 영역이 커져서 이 박리 영역이 가이드 베인을 통해 감소시킨 핀 후류 영역보다 크게 형성되기 때문이다.
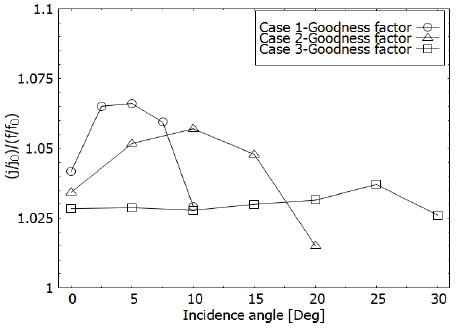
Fig. 10에 성능을 비교할 수 있게 Goodness factor를 나타내었다. 이는 Colburn factor ratio와 Friction factor ratio의 비로 나타내어지는 지수로, 성능 지표를 확인할 수 있는 무차원수이다.
Fig. 10에서 Case 1에서 입사각이 5° 일 경우 가장 높은 Goodness factor를 가지는 것을 확인할 수 있다. Case 1과 Case 2는 입사각이 증가 함에 따라 급격하게 증가했다가 각각 5° 와 10° 이후 급격하게 감소하는 경향을 보인다. Case 3은 입사각이 증가하면서 점진적으로 Goodness factor가 커지며, 25° 이후 급격하게 감소한다.
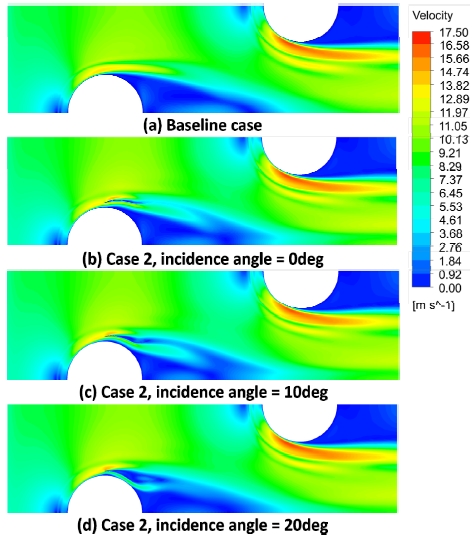
Fig. 11에 가이드 베인의 입사각에 따라 박리 영역의 변화를 명확하게 확인할 수 있는 위치인 z/H = 0.125에서의 속도 분포를 나타내었다. Fig. 11의 (a)~(d)는 핀-휜 만 있는 경우, Case 2의 입사각 0°, 10°와 20°인 경우의 속도분포를 나타낸 것이다. (a)~ (d)는 핀의 앞부분과 유동이 만나서 정체 점(Stagnation point)이 발생하여 속도가 느려지는 지점이 생성된다. 핀의 후류에서 박리 영역이 발생한다. 첫 번째 핀의 영향으로 유동이 가속이 되어 두 번째 핀에서 속도가 높아진다. (b)와 (c)의 첫 번째 핀 후류의 박리 영역은 (a)에 비해 감소되었다. 하지만 (b)나 (c)보다 입사각이 큰 (d)의 경우 가이드 베인 후방의 박리 영역이 커져서 이 영역과 핀의 후류 박리 영역이 만나 (a)와 유사한 크기의 박리 영역을 만들어 내는 것을 확인할 수 있다.
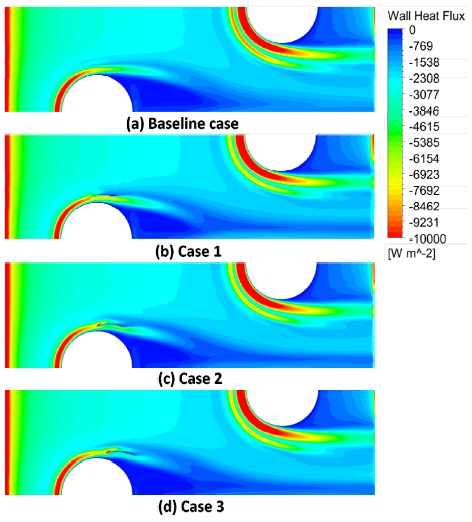
Fig. 12는 각 Case에서 가장 Colburn factor가 높았을 때의 열 유속을 핀 구간 아래 벽면에서 나타낸 것이다. (a)는 핀-휜 유로만 있을 때의 열 유속분포 그림이고 (b)~(d)는 Case 1~Case 3 경우의 가이드 베인 입사각이 0°일 때 열 유속분포 그림이다.
Fig. 12의 열 유속 분포 그림을 통해 핀 후류의 박리 영역에서는 열 유속이 매우 낮은 것을 확인할 수 있다. (a)~(d)는 상류에서 흐르던 유동이 핀 구간의 위, 아래 벽면과 만나 상류 부근의 열 유속이 급격하게 증가하는 것을 확인할 수 있다. 또한 핀 주위에서 생성된 말굽 와류로 인하여 열 유속이 높아진다. Fig. 12 (b)~(d)에서는 가이드 베인이 유동 방향을 바꾸어 핀 후류의 박리 영역을 줄여주기 때문에 (a)에 비해서 핀 후류의 박리 영역에서 열 유속이 매우 낮은 영역의 크기가 줄어든다. 이로 인해 전열 성능이 향상되는 것을 볼 수 있다. 특히 (b)의 첫 번째 핀 후류의 박리 영역이 (a)의 박리 영역에 비해 많이 줄어드는 것을 확인할 수 있다.
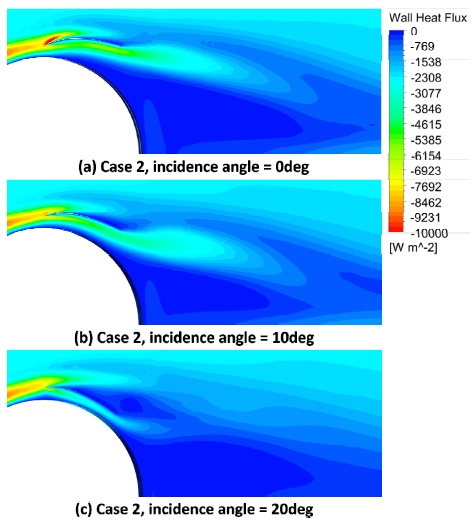
Fig. 13은 Case 2의 열 유속분포를 가이드 베인 근처에서 확대하여 그림으로 나타낸 것이다. (a)~(c)는 Case 2에서 가이드 베인의 입사각이 0°, 10° 그리고 20°일 경우이다. (a)는 (b)에 비해서 핀 후류의 박리 영역이 크지만, 가이드 베인의 박리 영역은 작은 것을 알 수 있다. 또한 (a)의 가이드 베인 앞전에서 열 유속이 증가하는 것을 확인할 수 있다. (a)에서 (b)와 (c)로 입사각이 증가함에 따라 이 현상이 줄어드는 것을 확인할 수 있다. (c)의 경우 가이드 베인에서 박리 영역이 커져서 핀 후류의 박리 영역과 합쳐지기 때문에 전열 성능이 하락하는 것을 확인할 수 있다.
4. 결 론
본 연구에서는 수치해석을 이용하여 엇갈린 배열의 핀-휜 유로와 동일 유로의 첫 번째 핀 주위에 가이드 베인을 부착하였다. 이 때 전열 성능 및 유동 특성을 가이드 베인의 위치와 입사각에 따라 비교하였다. 연구의 결론은 아래와 같다.
- 1. Case 1의 입사각이 0°일 경우 Colburn factor가 핀-휜 만 있는 유로에 비해 5% 증가하였고, 이 증가 수치는 연구에서 진행한 수치해석 결과 중 가장 높은 값이다. Case 2와 Case 3에서도 입사각이 0°일 때 가장 높은 Colburn factor가 나왔고, 핀-휜 만 있는 유로에 비해 4.1%, 3.3% 증가하였다.
- 2. Friction factor는 각 위치에서 입사각이 각각 5°, 10°, 25°일 경우 핀-휜 만 있는 유로에 비해 각각 1.8%, 1.9%, 1.6% 감소하는 것을 확인하였다.
- 3. 가이드 베인은 유동의 방향을 바꾸어 핀 후류의 박리 영역을 감소시킨다. 이로 인해 벽면에서 전열 성능이 향상된다.
Nomenclature
| A0 : | total flow area(m2) |
| Am : | minimum free flow area (m2) |
| uin : | velocity at inlet (m/s) |
| f : | friction factor |
| j : | Colburn factor |
| Pr : | Prandtl number |
| Re : | Reynolds number |
| L : | fin region length (mm) |
| H : | pin height (mm) |
| D : | pin diameter (mm) |
| δ : | pin thickness (mm) |
| hgv : | guide vane height (mm) |
| lgv : | guide vane length (mm) |
| PL : | longitudinal pitch (mm) |
| PT : | transverse pitch (mm) |
| cp : | specific heat coefficient (J/kgK) |
| Δp : | pressure drop (Pa) |
| h : | heat transfer coefficient (W/m2K) |
| ρ : | density (kg/m3) |
| μ : | dynamic viscosity (kg/ms) |
Acknowledgments
이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
-
Torii, K., Kwak, K.M., and Nishino, K., "Heat transfer enhancement accompanying pressure-loss reduction with winglet-type vortex generators for fin-tube heat exchangers", International Journal of Heat and Mass Transfer, 45(18), p3795-3801, (2002).
[https://doi.org/10.1016/s0017-9310(02)00080-7]

-
Song, K., Xi, Z., Su, M., Wang, L., Wu, X., and Wang, L., "Effect of geometric size of curved delta winglet vortex generators and tube pitch on heat transfer characteristics of fin-tube heat exchanger", Experimental Thermal and Fluid Science, 82, p8-18, (2017).
[https://doi.org/10.1016/j.expthermflusci.2016.11.002]

-
Gong, B., Wang, L.B., and Lin, Z.M., "Heat transfer characteristics of a circular tube bank fin heat exchanger with fins punched curve rectangular vortex generators in the wake regions of the tubes", Applied Thermal Engineering, 75, p224-238, (2015).
[https://doi.org/10.1016/j.applthermaleng.2014.09.043]

-
Sinha, A., Chattopadhyay, H., Iyengar, A. K., and Biswas, G., "Enhancement of heat transfer in a fin-tube heat exchanger using rectangular winglet type vortex generators", International Journal of Heat and Mass Transfer, 101, p667-681, (2016).
[https://doi.org/10.1016/j.ijheatmasstransfer.2016.05.032]

-
Salviano, L.O., Dezan, D.J., and Yanagihara, J.I., "Optimization of winglet- type vortex generator positions and angles in plate-fin compact heat exchanger: Response Surface Methodology and Direct Optimization", International Journal of Heat and Mass Transfer, 82, p373-387, (2015).
[https://doi.org/10.1016/j.ijheatmasstransfer.2014.10.072]

-
Salviano, L.O., Dezan, D.J., and Yanagihara, J.I., "Thermal-hydraulic performance optimization of inline and staggered fin-tube compact heat exchangers applying longitudinal vortex generators", Applied Thermal Engineering, 95, p311-329, (2016).
[https://doi.org/10.1016/j.applthermaleng.2015.11.069]

-
Jang, J.Y., Hsu, L.F., and Leu, J.S., "Optimization of the span angle and location of vortex generators in a plate-fin and tube heat exchanger", International Journal of Heat and Mass Transfer, 67, p432-444, (2013).
[https://doi.org/10.1016/j.ijheatmasstransfer.2013.08.028]

-
Wang, C.C., Chi, K.Y., and Chang, C.J., "Heat transfer and friction characteristics of plain fin-and-tube heat exchangers, part II: Correlation", International Journal of Heat and mass transfer, 43(15), p2693-2700, (2000).
[https://doi.org/10.1016/s0017-9310(99)00333-6]