공압시험용 플러그 노즐의 핀틀 형상 및 작동압력에 따른 유동 특성 분석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
공압시험용 플러그 노즐 구동에 따른 추력제어, 핀틀 형상 및 작동압력에 따른 유동특성 분석을 수행하였다. 이를 위해 시험에서의 유동구조와 추력계수를 비교함으로써 수치해석의 타당성을 확인하였다. 이후 각 노즐형상이 설계의도지점에 노즐목이 형성됨과 원뿔형 노즐에 대하여 핀틀 구동만으로 1:8의 추력제어가 가능함을 확인하였다. 마지막으로 고도보정 효과가 뛰어난 에어로 스파이크 노즐일지라도, 너무 낮은 NPR에 맞춰 설계된 경우, 부족팽창 조건에서 불리할 가능성을 확인하였다.
Abstract
The thrust control calculation according to the operation of plug nozzle for cold air test and the analysis of the flow characteristics of the pintle shape and operation pressure are performed. The numerical computation was verified by comparing the flow structure and the coefficient of thrust with the experimental data. It was confirmed that the nozzle throat was formed at the design position on each pintle shape, and thrust control up to 1:8 was achieved only by the stroke change. Finally, although the aerospike nozzle is autonomous, it is unfavorable in the under_expansion condition, if it is designed for a very low nozzle pressure ratio.
Keywords:
Pintle, Conical Nozzle, Aerospike Nozzle, Thrust Control, Coefficient of Thrust키워드:
핀틀, 원뿔형 노즐, 에어로 스파이크 노즐, 추력제어, 추력계수1. 서 론
군사용 유도무기의 대부분을 차지하는 고체 추진기관의 경우, 액체 추진기관과 다르게 실시간으로 추력의 크기를 조절하여 에너지를 효율적으로 사용하기 위해서는 추가적인 장치가 요구된다. 이에 다중 펄스 추진기관, 핀틀 추진기관의 유동특성 및 동적특성에 대한 연구가 수행되었다[1,2].
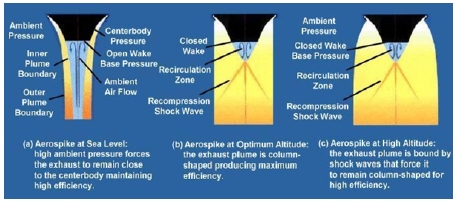
기존의 핀틀 추진기관 연구는 수축-확산 노즐을 이용하고 있는데, 수축-확산 노즐의 경우 고도에 따른 배압 변화에 따라 성능 차이가 발생하는 단점이 있다. 반면에 에어로 스파이크 노즐은 기존 노즐과 다르게 Fig. 1과 같이 고도 보상 효과로 인해, 고도와 상관없이 상대적으로 일정한 효율을 낼 수 있어 국내외적으로 연구 및 시험개발이 수행되었다[4-8].
종합적으로 이와 같이 외벽이 존재하지 않는 핀틀 추진기관을 설계하게 된다면, 추력제어가 가능하면서 다양한 고도에서 효율적으로 운용할 수 있게 된다. 지상연소시험에 앞서서 공압시험을 준비하는 과정으로써, 본 연구에서는 핀틀 형상 및 작동압력에 따른 유동 특성과 스트로크에 따른 정적 추력에 대한 기초연구를 수행하였다.
2. 수치해석 검증
2.1 수치해석 모델 선정
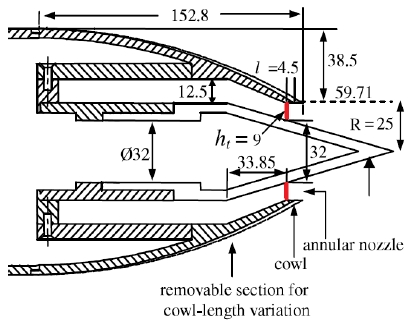
공압시험의 핀틀 형상 결정에 참고할 수 있도록, 유동해석 및 추력 값을 검증하고자 하였다. Fig 2와 같이 원뿔형 플러그 노즐로 구성되어 단순하고, 상세한 수치가 제공되어 있는 S. B. Verma의 40%로 잘린 원뿔형 노즐을 검증 모델로 선정하였다[7]. 원뿔형 노즐의 경사보다 덮개의 경사각이 크기 때문에, Fig 2의 붉은 선으로 표시한 지점에 노즐목이 형성된다. 해당 모델을 통해 Nozzle Pressure Ratio (NPR)에 따른 추력계수를 실험값과 비교하였다.
2.2 해석조건
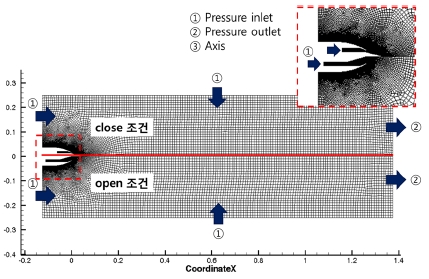
유동해석 검증을 위하여 범용 유동해석 프로그램인 FLUENT를 사용하였다. Fig. 2의 형상 정보를 사용하여, 비정렬 격자로 구성하였다. 노즐 출구 반경 R을 기준으로 가로 120R X 세로 20R로 도메인을 설정하였으며, 외기는 pressure outlet 조건을 주었다. Fig. 2의 챔버 내부의 수직 경계를 Pressure inlet 조건으로 작동압력을 입력하였다. 유동해석 조건은 density-based typed, transient, 2D axisymmetric이며, 난류모델로 k-omega SST를 사용하였다. 해석유체는 이상기체로 가정한 공기이며, 입력변수는 Table 1과 같다.
2.3 검증결과
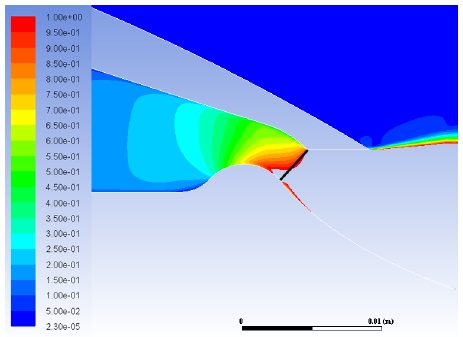
40%로 잘린 원뿔형 노즐의 NPR 2.57 조건에서의 유동장 결과는 Fig. 3과 같다. 해석결과는 과팽창 조건에 해당하며, 제트 경계와 유동박리가 일어나는 유동구조가 시험결과와 유사함을 확인하였다. 또한 아래 식으로 추력계수를 계산하여 비교하였다.
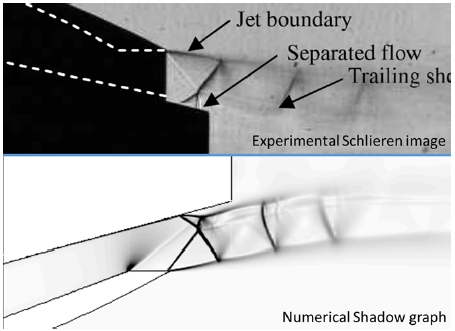
Flow structure for 40% conical nozzle at NPR 2.57: (top) experimental schlieren image[7]; (bottom) numerical shadow graph.
| (1) |
이상팽창(Pe = Pa) 조건의 추력계수는 각 NPR 조건에 맞춰 아래 식을 사용하였다.
| (2) |
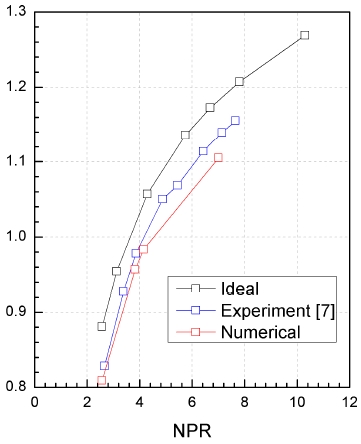
유동해석으로 다음의 식을 사용하여 추력을 계산하여 추력 계수를 비교한 결과 Fig. 4와 같이 일정한 gamma 값으로 인한 오차가 존재하지만 NPR 변화에 따른 추력계수 경향이 동일함을 확인하고 본 연구를 진행하였다.
| (3) |
3. 본 론
3.1 핀틀 노즐 설계
원뿔형 노즐의 경우, 검증 모델을 스케일 다운하여 사용하였다. 에어로 스파이크 노즐의 경우, 아래와 같은 Prandtl-Meyer 팽창파 공식을 만족하도록 설계되었다.
| (4) |
원뿔형 노즐과 다르게 에어로 스파이크 노즐은 이상팽창 조건을 만족하기 위해 노즐목이 특정 각도를 가지게 된다. 유동의 연속성을 위해 상류 영역은 에어로 스파이크 노즐과 접하도록, 노즐 중심축 반경을 감소시켜 경량화 및 구동 하중 제어를 위해 볼록한 형상으로 설계하였다. 이에 위쪽에 위치한 덮개(cowl)의 형상도 함께 수정하여, 2차원 단면적이 Fig. 5에서와 같은 위치에 위치하도록 설계하였다. 유동해석 전에 핀틀 노즐과 덮개의 임의의 점들에서의 2차원 단면적을 계산하여, 최솟값이 설계된 위치에서의 단면적인지를 확인하였다.
3.2 격자구성 및 해석조건
설계된 원뿔형, 에어로 스파이크 형상을 바탕으로 비정렬 격자를 구성하였다. Fig. 6과 같이 노즐 출구 반경 R을 기준으로 가로 120R X 세로 20R로 도메인을 구성하고, 경계조건을 입력하였다. 유동해석 조건은 density-based typed, transient, 2D axisymmetric이며, 난류 모델로 k-omega SST를 사용하였다. 해석 유체는 이상기체 비연소 가스로, 추후 지상연소시험에서 사용할 임의의 물성치를 사용하였다.
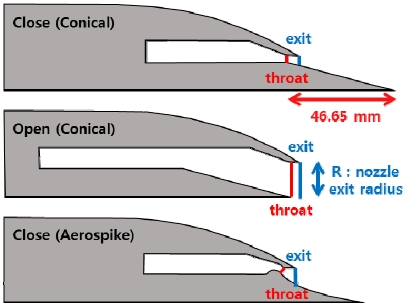
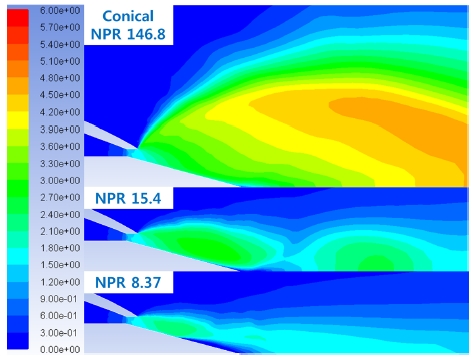
입력 변수는 Table 2와 같으며, 원뿔형 노즐의 경우 Stroke에 따라 Close, Open 조건으로 나뉜다. Close 조건을 stroke 0 mm로 설정하였으며, 노즐목에서 끝단까지의 거리 46.65 mm 만큼을 내부로 집어넣은 경우가 Open 조건이다. Stroke는 연소실 최대 압력과 순항이 가능한 최소 추력에 의해 제한된다. 압력 조건의 경우 사전 성능 설계를 기반으로 계산된 최대압력 2,158 psi(Close 조건)와 최소압력 123 psi(Open 조건)를 사용하였다. 또한 원뿔형, 에어로 스파이크 노즐의 Close 조건에 대해 작동압력을 달리하여 NPR을 변화시켰다. NPR 146.8은 부족팽창 조건, 15.4는 이상팽창 조건, 8.37은 과팽창 조건에 해당한다. 이상팽창의 NPR은 유동이 수평으로 나오는 상황으로 덮개 출구 높이를 반경으로 노즐 출구 면적으로 설정하고, 면적-마하수 관계를 이용하여 계산하였다.
3.3 해석결과
먼저 Conical, Spike 핀틀 형상에 대하여, 설계상으로 의도한 위치에 노즐목 조건이 형성되었는지를 확인하였다. 사용한 연소가스 물성치로 결정된 유출계수(discharge coefficient)로 유효노즐목면적을 계산하였다.
| (5) |
Table 3과 같이 원뿔형의 경우 유효 노즐목 면적이 설계된 값과 거의 일치하며, 작동압력에 따라 상대적으로 변화가 없음을 확인하였다. 반면에 에어로 스파이크의 경우, Fig. 7과 같이 작동압력 변화에 따라 왜곡되는 현상을 나타냈다. 이는 노즐목을 기준으로 상류 형상이 직선으로 구성된 원뿔형의 경우와 다른 상류 형상의 영향을 받기 때문으로 생각된다.
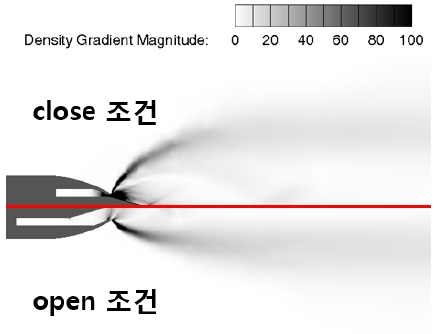
다음으로 Fig. 8은 원뿔형 노즐에 대하여 Stroke를 변화시킨 Close, Open 조건의 밀도구배장을 나타내고 있다. 각각의 노즐목에 대하여 부족팽창 조건에 해당하여 제트 경계가 퍼지는 모습을 확인할 수 있다. 또한 사전에 유동해석으로 검증된 추력 계산식을 사용한 결과, Close 조건에서 최대 추력 1,252 lbf, Open 조건에서 최소 추력 153 lbf로 핀틀의 구동만으로도 1:8.2의 추력제어 가능성을 보여주었다.
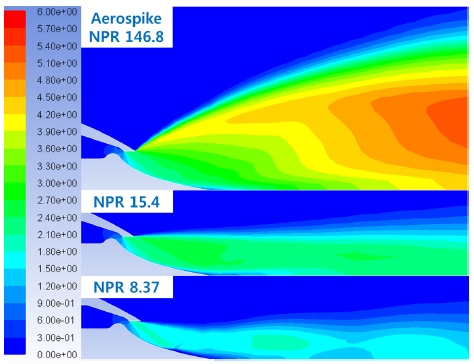
마지막으로 Close 조건에서 핀틀 형상 및 작동압력 조건 변화에 따른 유동특성과 추력계수를 살펴보았다. Fig. 9와 Fig. 10은 NPR에 따른 원뿔형, 에어로 스파이크 노즐의 유동특성을 보여주고 있다. 에어로 스파이크 노즐은 이상팽창 NPR에서 덮개 출구를 기준으로 수평으로 유동이 진행하는 반면에 원뿔형 노즐의 경우 이상팽창 조건에서 유동장이 왜곡되고, 노즐 끝단 직전에 유동박리가 일어나는 것을 확인할 수 있다. 과팽창 조건에서는 원뿔형과 에어로 스파이크 노즐 모두 유동박리와 충격파가 발생하였다.
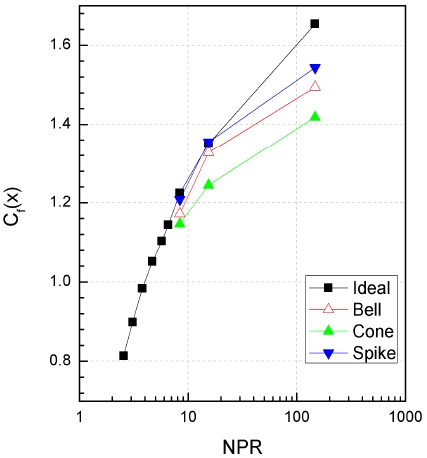
Fig. 11은 플러그 노즐 형상에 따른 추력계수를 이상팽창 조건 및 bell 노즐과 비교하고 있다. 각 노즐의 형상은 NPR 15.4 조건에서 이상팽창 하도록 설계되어있다. 각 NPR에서 이상팽창 추력계수는 앞선 공식으로 계산하였으며, bell 노즐의 경우 확산반각 15도를 기준으로 동일한 연소가스 물성치, 노즐목, 노즐출구 반경을 사용하여 이론적인 추력계수를 얻었다. 마지막으로 원뿔형, 에어로 스파이크 노즐의 추력계수 또한 검증에 사용된 공식을 통하여 획득하였다. 추력계수 비교 결과, 원뿔형 노즐은 과팽창, 이상팽창, 부족팽창 모든 경우에 대해서 bell 노즐보다 효율이 떨어짐을 확인할 수 있었다. 이는 원뿔형 노즐이 bell 노즐에 비해 반경방향으로 손실되는 비율이 상대적으로 높기 때문이다. 에어로 스파이크 노즐은 모든 조건에서 최고의 효율을 보여주었지만, 부족팽창 조건에서 상대적으로 고도보상효과가 약해짐을 확인할 수 있었다. 낮은 NPR에 맞춰 설계되었기 때문에, 핀틀 헤드의 길이가 해당 압력조건에서 배기가스(plume)를 충분한 팽창 및 가속시키기에 부족했기 때문이다. 따라서 정적 추력계수 비교결과에 한해서는 실제 추진기관의 작동 고도 중 높은 NPR에 맞춰서 형상을 최적화시키는 방향이 바람직할 것으로 생각된다.
4. 결 론
공압시험용 플러그 노즐의 스트로크 변화에 따른 정적 추력 특성, 핀틀 형상과 작동압력에 따른 유동특성과 추력계수에 대한 분석을 수행하였다. 이를 위해 실제 시험결과와 유동특성 및 추력계수를 비교함으로써 수치해석 및 추력 계산방법을 검증하였다. 이후 수치해석을 통해 원뿔형 노즐과 Prandtl-Meyer 팽창파 조건을 만족하는 에어로 스파이크 노즐의 설계점에 노즐목이 생성되는지 직접 확인하였다. 또한 원뿔형 노즐에 대해서 핀틀 구동만으로 1:8의 추력제어가 가능함을 확인하였다. 마지막으로 Close 조건에 대해 핀틀 형상 및 작동압력에 따른 유동특성 및 추력계수를 분석하여, 너무 낮은 NPR에 맞춰 설계된 에어로 스파이크 노즐의 경우 부족팽창 조건에서 불리할 수 있음을 알 수 있었다. 추가적인 동적 추력 특성 분석이 필요하지만 본 연구결과로 공압시험 형상 최적화 방안을 제시함으로써, 효율적인 에어로 스파이크 핀틀 추진기관 설계 및 제작에 기여할 것으로 기대된다.
Acknowledgments
[이 논문은 한국추진공학회 2018년도 추계학술대회(2018.12.19-21, 웨스틴 조선호텔 부산) 발표논문을 심사하여 수정·보완한 것임.]
References
- Kim, J.K., Lee, J.H., and Chang, H.B., “Computation Investigation of Pintle Nozzle Flow”, Journal of the Korean Society of Propulsion Engineers, 13(3), p35-41, (2009).
-
Jin, J., Ha, D.S., and Oh, S., “Experimental Study and Performance Analysis of the Solid Rocket Motor with Pintle Nozzle”, Journal of the Korean Society of Propulsion Engineers, 18(5), p19-28, (2014).
[https://doi.org/10.6108/kspe.2014.18.5.019]

- “Aerospike Engine”, retrieved 26 Nov. 2018, from http://www.aerospaceweb.org/design/aerospike/.
-
Ruf, J.H., and McConnaughey, P.K., “The Plume Physics Behind Aerospike Nozzle Altitude Compensation and Slipstream Effect”, 33rd Joint Propulsion Conference & Exhibit, Seattle, Washington, U.S.A., AIAA Paper No. 97-3217, July), (1997.
[https://doi.org/10.2514/6.1997-3218]

-
Besnard, E., Chen, H.H., Mueller, T., and Garvey, J., “Design, Manufacturing and Test of a Plug Nozzle Rocket Engine”, 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, Indiana, U.S.A., AIAA-02-4038, July), (2002.
[https://doi.org/10.2514/6.2002-4038]

-
Bui, T.T., Murray, J.E., Rogers, C.E., Bartel, S., Cesaroni, A., and Dennett, M., “Flight Research of an Aerospike Nozzle using High Power Solid Rockets”, 41th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, Arizona, U.S.A., AIAA-2005-3797, July), (2005.
[https://doi.org/10.2514/6.2005-3797]

-
Verma, S.B., “Performance Characteristics of an Annular Conical Aerospike Nozzle with Freestream Effect”, Journal of Propulsion and Power, 25(3), p783-791, (2009).
[https://doi.org/10.2514/1.40302]

-
Nair, P.P., Suryan, A., and Kim, H.D., “Computational Study of Performance Characteristics for Truncated Conical Aerospike Nozzles”, Journal of Thermal Science, 26(6), p483-489, (2017).
[https://doi.org/10.1007/s11630-017-0965-0]