가변추력을 위한 기체주입식 와류형 분사기의 분무특성
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
액체로켓엔진에서의 추력조절을 위해 기체주입식 가변추력 방법에 대한 기초적인 연구를 수행하였다. 기체주입식 가변추력은 간단한 구조로 추력을 조절할 수 있을 뿐만 아니라 밀도 감소에 비례하여 증가된 분사차압에 의해 미립화 성능 증가라는 장점을 갖는다. 본 연구에서는 기체주입식 와류형 분사기를 이용하여 액체 질량유량과 기체주입량의 변화에 따른 분무 불안정, 분무형상, 분무각, 분열길이와 같은 분무특성을 살펴보았다.
Abstract
A fundamental study on a gas injection variable thrust method for thrust throttling in a liquid rocket engine was conducted. The gas injection variable thrust has the advantage of not only being able to control the thrust with a simple structure but it also increases the atomization performance through the injection pressure drop that increases in direct proportion to the density reduction. In this study, spray characteristics such as spray instability, spray pattern, spray angle, and breakup length based on changes in the liquid mass flow rate and amount of injected gas were investigated using effervescent swirl injectors.
Keywords:
Variable Thrust, Gas Injection, Effervescent Swirl Injector, Two Phase Flow, Liquid Rocket Engine키워드:
가변추력, 기체주입, 기체주입식 와류형 분사기, 이상유동, 액체로켓엔진1. 서 론
엔진의 가변추력은 우주발사체의 최적 궤도를 유지하거나, 달, 화성 등의 착륙선에 필수적으로 요구된다. 노즐에서 배출되는 연소가스의 압력이 이상적으로 팽창하여 외부 압력과 동일하다면, 엔진의 추력은 추진제의 질량유량에 비례하게 된다. 따라서 가변추력은 일반적으로 연소기에 공급되는 추진제의 질량유량을 조절함으로써 이루어진다[1,2].
분사기 출구 오리피스 면적이 일정하고 액체 추진제가 공급될 경우, 분사차압(injection pressure drop)은 감소되는 질량유량 비의 제곱에 비례하여 낮아진다. 분사차압이 연소실 압력 대비 대략 15% 이하로 감소되면 미립화 성능의 저하뿐 아니라 저주파 연소불안정에 취약해지게 된다[3-5]. 가변추력에서의 이러한 문제점을 해결하기 위해 고 압력강하 분사기, 이중 매니폴드 분사기, 핀틀 분사기, 기체주입 등 다양한 방법들이 연구되어 왔다[3-5].
기체주입을 이용한 가변추력은 헬륨이나 질소와 같은 불활성 기체를 액체 추진제 내로 공급하여, 액체 추진제와 가변추력용 기체의 이상유동(two phase flow)을 형성한다. 액체 추진제 내로 기체가 주입됨에 따라 전체 밀도는 낮아지게 되고, 동일 추진제 유량 조건에서 밀도가 감소된 만큼 분사기 차압이 증가하게 된다. 기체주입을 이용한 가변추력은 구조가 간단하고 미립화 성능을 증가시킬 수 있는 장점이 있다. 하지만 주입되는 기체의 양에 따라 유동특성이 변화하며, 이는 분무 불안정으로 이어질 수 있는 단점이 있다[3-6].
가변추력을 위한 기체주입은 미국 Apollo 프로그램 당시 NASA 및 민간 기업에서 진행되었던 만큼 많은 자료가 공개되어 있지 않다. Morrell[6]은 가변추력용 기체로 헬륨을 사용하여 추력을 조절할 수 있음을 증명하였다. 열적 평형 하에서 등온 기체유동과 단열 기체유동을 가정하여 2가지 모델을 제시하였으며, 공급되는 기체와 액체의 압력차가 6 psi 내로 유지되어야 안정적인 분무가 가능하다고 보고하였다. 또한 기체주입을 통하여 미립화 성능이 개선되어, 추진제의 질량유량이 감소하여도 연소효율에는 영향을 주지 않는 것을 확인하였다. 이외 약간의 공개된 자료에서는 가변추력에 초점이 맞추어져 분무특성에 관한 연구는 찾기가 어려운 상황이다[7-11].
최근 가스터빈, 스크램제트 엔진 등에서 기체주입은 가변추력 목적이 아닌 미립화 성능 개선의 해결책으로 주로 이용된다. 주입된 기체는 기포 형태로 액체 연료와 같이 분사기 출구 오리피스에서 분사되며, 이러한 기포들은 기포 내 압력과 주위 압력차에 의해 급격히 팽창하게 된다. 이러한 현상을 기포 파열(bubble bursting)이라 하며, 이로 인해 분열길이가 감소하고 액체를 작은 액적으로 분열할 수 있게 된다[12].
Chen과 Lefebvre[13]는 기체주입식 분사기를 이용하여 주위 압력(ambient pressure)과 분사차압에 따른 SMD(Sauter mean diameter)의 변화를 살펴보았다. 그들은 주위 압력이 증가하면 SMD는 최댓값으로 증가한 후 감소하는 것을 확인하였으며, 액체 유량이 줄더라도 기체주입량을 늘려 분사차압을 동일하게 유지시키는 경우 SMD가 감소한다고 보고하였다. Ghaffar 등[14]은 기체주입식 와류형 분사기에서 분열길이 변화에 대한 연구를 수행하였다. 주입된 기체가 기포로 액체와 함께 분사됨으로써 기포 파열이 발생하고, 따라서 GLR(gas-liquid mass flow rate ratio)이 증가할수록 분열길이가 감소하였다.
기체주입식 분사기는 단공노즐을 사용한 연구가 대부분이다[13,15-17]. 이외 기체주입식 와류형 분사기에 대한 약간의 연구는 선회기(swirler)를 장착한 분사기에 대해서만 진행되었다[14,18-19]. 따라서 본 연구에서는 접선홀을 갖는 기체주입식 와류형 분사기에서 가변추력 시 액체 질량유량과 GLR이 변화함에 따라 분무특성의 변화를 살펴보고자 하였다.
2. 실험장치 및 조건
2.1 실험장치
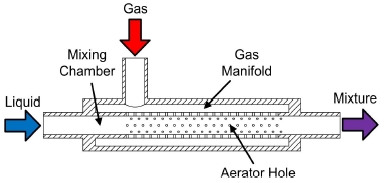
Fig. 1은 기체-액체 혼합물을 형성하기 위해 사용된 에어레이터(aerator)이다. 에어레이터는 기체가 혼합실(mixing chamber) 외부에서 내부로 공급되는 방식으로 설계하였다. 액체는 에어레이터 중심의 1/4 inch 튜브로 공급되며, 가변추력용 기체는 1/2 inch 튜브의 기체 매니폴드에서 에어레이터 홀을 통하여 혼합실로 공급된다. 에어레이터 홀은 0.5 mm 직경으로 한 열에 4개씩 드릴로 가공되었으며, 서로의 간섭을 최소화하기 위해 1 mm 간격으로 45°씩 회전하여 40열을 갖도록 설계하였다. 따라서 에어레이터는 총 160개의 홀을 갖는다. 에어레이터의 총 길이는 95 mm이며, 에어레이터 홀의 마지막 열은 에어레이터 출구에서 25 mm 떨어진 곳에 위치한다.
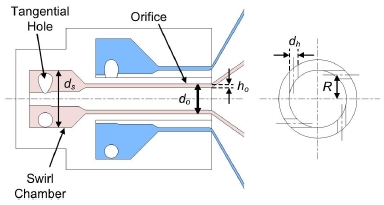
본 연구에서 사용된 분사기는 산화제로 N2O4, 연료로 MMH(monomethylhydrazine)를 사용하는 정격추력 420 N 추력기를 위해 제작된 동축 와류형 분사기이다. 분사기는 Fig. 2에서와 같이 내/외부 접선홀을 갖는 닫힘형(closed-type) 와류형 분사기로 구성되어 있다. 분사기에 대한 자세한 사항은 참고문헌[20]에 정리되어 있다.
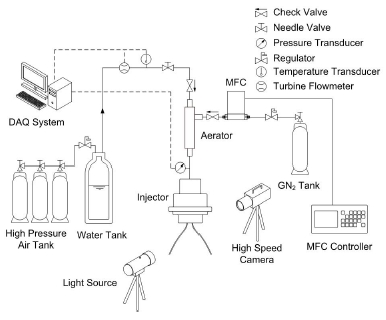
Fig. 3은 수류시험장치의 개략도이다. 본 연구에서는 모사 추진제로 물을, 가변추력용 기체로 질소를 이용하였다. 물탱크를 고압공기로 가압하여 물을 공급하였으며, 물의 유량과 압력을 측정하기 위해 유량계(Kometer, KTP-500)를 에어레이터 전단에, 압력계(Sensys, PSH model)를 분사기 전단에 설치하였다. 물의 질량유량은 니들 밸브로, 기체질소의 질량유량은 MFC(MKP, VIC-D220)를 이용하여 조절하였다. 기체질소와물의 밀도를 얻기 위해 공급라인에 K-type 열전대를 설치하여 온도를 측정하였다. 본 연구에서 분사차압은 분사기 전단의 압력과 대기압의 차로 계산하였으며, Fig. 3에서와 같이 액체/기체가 혼합된 이후의 분사기 차압을 의미한다. 유량, 압력, 온도 데이터는 NI cDAQ를 통하여, 각 실험마다 1 kHz의 샘플링 속도로 1초 동안 기록하였다. 또한 분무 이미지 획득을 위해 고속카메라(Vision Research, Phantom v9.1)와 제논 광원(Polarion, PS-NP1)을 사용하였으며, 1000 fps의 속도로 100장의 사진을 촬영하였다. 이때 카메라의 노출시간은 2 μs이었다.
2.2 실험조건
정격추력이 420 N일 때 정격추력 대비 가변추력 비(TR, thrust ratio)를 10%에서 50%까지 설정하였다. 정격조건에서 안쪽 분사기는 MMH를 50.82 g/s로, 바깥쪽 분사기는 N2O4를 83.86 g/s로 분사한다. 실제 추진제 대신 물을 이용하였기 때문에 동일한 분사차압을 맞추기 위해서는 실제 추진제와 물의 밀도비를 고려해 주어야 한다. 분사기의 유량계수가 일정하다는 가정 하에 물의 질량유량은 모사 추진제의 질량유량에 물/실제 추진제 밀도비의 제곱근을 곱하여 구할 수 있다. 따라서 정격조건에서 안쪽 분사기의 질량유량을 54.36 g/s, 바깥쪽 분사기의 질량유량을 69.82 g/s로 설정하였다.
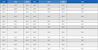
설정된 물의 질량유량을 기준으로 GLR을 0.0%에서 1.0%까지 변화시키며 실험을 진행하였다. 사용된 MFC가 제공할 수 있는 유량 범위 한계로 인하여 안쪽 분사기의 경우 TR 40%일 때 GLR이 1.0%, TR 50%일 때 GLR이 0.8, 0.9, 1%인 조건을 제외하였으며, 바깥쪽 분사기의 경우 TR 30%일 때 GLR이 1.0%, TR 40%일 때 GLR이 0.8, 0.9, 1.0%, TR 50%일 때 GLR이 0.6, 0.7 0.8, 0.9, 1.0%인 경우를 제외하였다. 자세한 실험조건은 Table 1에 정리하였다. 여기서 은 물의 질량유량을 나타낸다.
3. 이상유동 모델
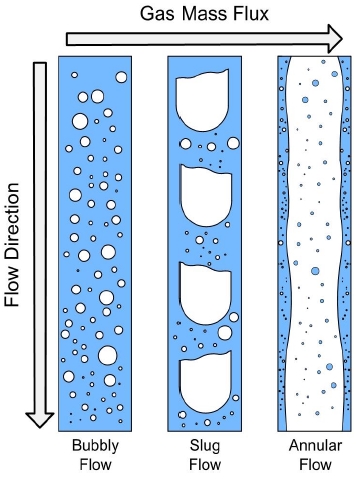
에어레이터 내에서 기체와 액체는 서로 혼합되며 기체-액체 혼합물을 형성한다. 이때 기체는 액체 내에서 기포로 존재하며, 이러한 기포의 형태에 따라 이상유동 유형을 정의한다[12]. Fig. 4는 기체 질량 플럭스에 따른 이상유동 유형을 나타낸다. 기체 질량 플럭스가 낮아 주입된 기체가 작은 기포의 형태로 존재할 때, 이를 기포유동(bubbly flow)이라 정의한다. 기체 질량 플럭스가 증가하면 이러한 기포들은 서로 병합하여 성장하며, 기포의 크기가 혼합실 직경과 유사한 크기로 성장하여 슬러그를 형성하게 되면 슬러그유동(slug flow)으로 천이된다. 기체 질량 플럭스가 더욱 증가하게 되면, 액체는 혼합실 벽면을 따라 액막의 형태로 흐르게 되며 혼합실 중심에 기체층이 형성된다. 이러한 유동을 환상유동(annular flow)이라 한다. 기포유동과 환상유동에서는 안정적인 유동이 가능하지만, 슬러그유동에서는 기체와 액체가 교대로 움직이며 압력섭동을 발생시키기 때문에 유동이 불안정해진다. 이는 분무가 연속적이지 않은 서징(surging)을 야기하게 된다[6,12].
기체-액체 혼합물의 밀도는 이상유동 유형에 따라 다양한 이상유동 모델을 통하여 표현될 수 있다. 일반적으로 혼합물의 밀도는 다음과 같은 식으로 나타낸다[12,21].
| (1) |
여기서 ρm, ρg, ρl, α는 각각 혼합물의 밀도, 기체의 밀도, 액체의 밀도, 기공도이다. 다시 기공도(void fraction)는 건도(기체의 질량유량/혼합물의 질량유량, ), 기체-액체 밀도비, 슬립비(S, slip ratio)로 표현할 수 있다[21].
| (2) |
다양한 이상유동 모델에서의 차이는 슬립비에서 나타난다. 슬립비는 기체 속도(ug)와 액체 속도(ul)의 비로 정의하는데, 기체와 액체가 동일한 속도로 움직이는 것을 가정하는 균질유동 모델(homogeneous flow model)이 대표적이다[12,21]. 하지만 실제 이상유동에서 기체와 액체는 서로 다른 속도를 가지며 움직인다. 따라서 슬립비는 1 이상의 값을 갖게 된다.
Chisholm[22]은 환상유동일 때, 모멘텀 플럭스가 최소가 된다는 가정으로 다음과 같은 슬립비를 제안하였다.
| (3) |
| (4) |
| (5) |
여기서 Mm, Mg, Ml은 각각 혼합물의 모멘텀 플럭스, 기체의 모멘텀 플럭스, 액체의 모멘텀 플럭스이다. 기포유동은 매우 작은 기공도를 갖는다. 따라서 Chisholm[22]은 추가적으로 기공도가 충분히 작다면 기체는 액체의 속도를 따라가게 되어 다음과 같이 표현할 수 있다고 가정하였다.
| (6) |
| (7) |
| (8) |
여기서 ρh는 균질유동에서 혼합물의 밀도이다.
본 연구 전에 수행된 선행연구[20]에서 몇 가지 이상유동 모델을 해석적/실험적으로 검증하였으며, Chisholm[22]이 제안한 Eq. 8의 슬립비로 구한 분사차압이 실험결과와 가장 정확하게 일치하는 결과를 얻었다. 본 연구에서는 매우 낮은 GLR에서 기포유동을 형성시키는 것을 목표로 하였기 때문에, Eq. 8의 슬립비로 얻어지는 이상유동 모델을 적용하여 결과를 분석하였다.
4. 실험결과
4.1 분무 불안정
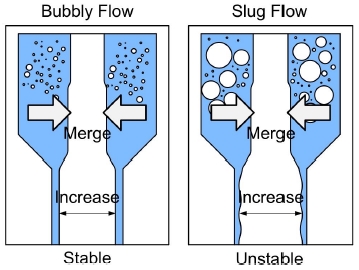
추진제 내로 공급된 기포들은 유로가 축소하거나 모서리 및 다른 구조물이 있는 경우 서로 병합하게 된다. 그리고 주입되는 기체의 양이 증가하거나 유로 내 체류기간이 증가할 경우에도 서로 병합한다. 이러한 기포들의 병합은 유동을 천이시킨다. 와류형 분사기에서 주입된 기포는 분사기 중심에 존재하는 공기층과 합쳐져 공기층의 직경을 증가시키는 역할을 한다는 연구결과가 있다[20]. Fig. 5와 같이 기포유동에서 기포들은 매우 작은 크기를 가지고 있고 크기의 편차가 크지 않기 때문에 안정적으로 공기층 내로 병합될 수 있지만, 슬러그유동에서는 기포의 크기가 상당히 크고 크기의 편차가 높기 때문에 안정적으로 공기층과 병합하지 못할 것이다. 또한 단공노즐 분사기와 달리 와류형 분사기에서는 작은 크기의 접선홀을 통해 기포들이 와류실로 들어가기 때문에, 크기가 큰 기포가 있게 되면 분무가 불안정해질 수 있다.
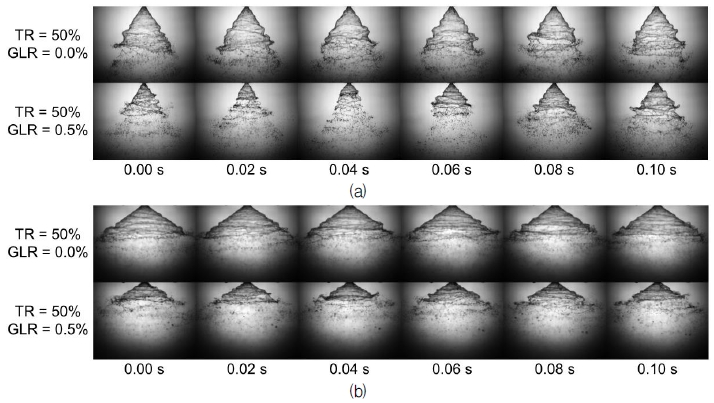
이를 확인하고자 Fig. 6에 TR = 50%, GLR = 0.0%, 0.5%일 때, 시간 변화에 따른 분무 이미지를 나타내었다. 안쪽 분사기와 바깥쪽 분사기 모두 GLR이 0.0%인 경우에는 안정적인 분무가 가능하지만, GLR이 0.5%로 증가하면 안쪽 분사기에서 분무 불안정이 나타났다. 이러한 분무 불안정은 불규칙하게 발생하였다. 반면 바깥쪽 분사기는 GLR이 0.5%로 증가하여도 분무가 불안정해지지 않음을 확인할 수 있었다. TR에 따라 약간씩 다르긴 하지만, 안쪽 분사기는 GLR이 0.4%, 바깥쪽 분사기는 GLR이 0.6% 정도부터 분무 불안정이 발생하였다. 이는 바깥족 분사기가 상대적으로 큰 유로를 갖고 있기 때문으로 판단된다. 하지만 이러한 분무 불안정은 에어레이터 설계에 영향을 받을 수 있다. 또한 실제 연소조건에서는 외부 압력이 대기압 보다 높기 때문에, 보다 정량적인 분석을 위해서는 다양한 기체주입 방법을 이용한 고압챔버에서의 분무실험이 추가적으로 필요하다.
4.2 분무형상
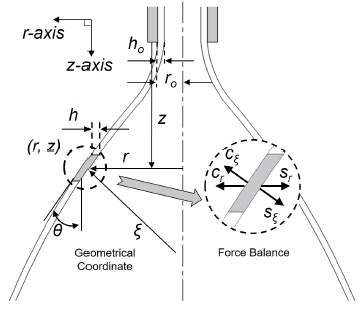
와류형 분사기의 분무형상은 Fig. 7과 같이 접선방향 속도에 의한 원심력과 표면장력을 이용한 힘의 평형으로 나타낼 수 있다. 접선방향 모멘텀은 분무를 중공원추(hollow cone) 형상으로 발달시키는 역할을 하며, 표면장력은 분무를 수렴시키는 역할을 한다[23].
| (9) |
여기서 σ, ξ, r, θ, h, w는 각각 표면장력, 곡률반경, 분사기 중심에서 분무까지의 반경, 분무에서의 분무각, 분무에서의 액막 두께, 분무에서의 접선방향 속도이다. Eq. 9에서 중력 효과와 점성, 액막 안팎의 압력차는 무시되었다. 중력에 대한 영향은 매우 미미하며, 분무가 중공원추 형상으로 완전히 발달하게 되면 액막 안팎의 압력차는 무시할 수 있을 정도로 작다.
접선방향 속도는 각 운동량 보존에 의하여 wr = woro로 표현할 수 있으며, 출구 오리피스에서의 접선방향 속도는 Horvay와 Leuckel[24]이 제시한 경험식을 통해 계산할 수 있다.
| (10) |
여기서 Mo, Mi는 분사기 출구 및 접선홀에서의 각 운동량이며, Re는 접선홀에서 유체의 레이놀즈수이다. K는 와류형 분사기 형상계수이며, 다음 식으로 얻어진다.
| (11) |
여기서 Ah는 접선홀의 전체 단면적, R은 접선홀 중심부터 분사기 중심까지의 거리, n은 접선홀 개수, rh는 접선홀 직경이다. 축방향 속도는 다음과 같은 질량보존 식으로 결정할 수 있다. 축방향 속도(u0)는 분무가 진행됨에 따른 변화가 거의 없기 때문에 일정한 값으로 가정하였다.
| (12) |
본 연구에서 사용된 분사기가 닫힘형 와류형 분사기이므로, 초기 액막 두께(h0)는 Suyary와 Lefebvre[25]가 제시한 경험식(Eq. 13)을 이용하였다.
| (13) |
분무가 진행됨에 따라 변화하는 액막 두께는 Eq. 12를 이용하여 계산할 수 있다. Eq. 9의 모든 변수는 r의 함수로 나타낼 수 있으며, 따라서 상미분 방정식을 계산함으로써 분무형상을 구할 수 있다[26].
Fig. 8은 안쪽 와류형 분사기에서 TR과 GLR에 따라 계산된 분무형상과 측정된 분무 이미지를 나타낸다. TR이 10%, 20%인 경우에는 접선방향 속도가 작아 원심력보다 표면장력의 영향이 커지게 되어, 분무가 완벽한 중공원추 형상을 갖지 않으며 수렴하게 된다. 이러한 조건에서는 계산된 분무형상이 초기 분무 이후로는 실제 분무 이미지보다 더 큰 것을 알 수 있다. 이는 액체 시트(liquid sheet)의 수렴에 의하여 시트 안쪽의 압력이 대기압보다 낮기 때문이다. 액체 시트 안팎의 압력차를 고려하여 계산하게 되면 이러한 차이는 줄어들 것이다. TR이 30%, 40%인 경우에는 실제 분무 이미지와 계산된 분무형상이 매우 잘 일치한다. 또한 GLR이 증가함에 따라 분무가 조금씩 더 발달 혹은 확장되며 분열길이가 짧아지는 것을 확인할 수 있다.

Comparison between the measured spray image and the calculated spray pattern for the inner swirl injector.
Fig. 9는 바깥쪽 와류형 분사기에서 계산된 분무형상과 측정된 분무 이미지를 나타낸다. TR이 10%인 경우는 분무가 형성되지 않아 결과에서 제외하였다. TR = 20%, GLR = 0.0%인 경우 양파모양의 분무가 형성되었다. TR이 30-50%인 조건에서는 중공원추 형상의 분무가 형성되었으며, 모든 조건에서 GLR이 증가함에 따라 분무가 약간씩 팽창되며 분열길이가 감소하는 것을 알 수 있다. 하지만 안쪽 분사기에 비해 바깥쪽 분사기는 접선방향 속도가 크기 때문에 낮은 TR에서도 분무가 충분히 발달하여 GLR 증가에 따른 영향은 상대적으로 적었다.

Comparison between the measured spray image and the calculated spray pattern for the outer swirl injector.
와류형 분사기에서 분무각은 접선방향 속도와 축방향 속도의 비로 나타낼 수 있다[27]. 액체 질량유량과 GLR이 증가함에 따라 두 속도 성분이 증가하여 분무가 발달하게 된다. 분무의 발달은 분무각 증가로 이어지게 된다. 안쪽 분사기 GLR 0.0%에서, TR이 10%에서 20%로 증가할 때 분무각의 증가가 TR이 40%에서 50%로 증가할 때의 분무각 증가보다 더 컸다. 이처럼 와류형 분사기에서 분무가 중공원추 형상으로 발달되지 않았을 경우 액체 유량이 증가함에 따라 분무각이 크게 증가하지만, 분무가 중공원추 형상으로 발달하게 되면 액체 유량의 영향은 크게 줄고 분무각은 거의 일정한 값으로 수렴하게 된다. 동일한 TR 조건에서 GLR이 증가함에 따라서도 분무가 더욱 발달하게 된다. 이러한 분무 발달 효과는 낮은 TR(작은 액체 유량)에서 크게 나타났으며, 어느 이상의 TR(큰 액체 유량)에서는 분무각에 큰 영향을 주지 못하였다[19].
4.3 분열길이
Fig. 8과 Fig. 9에서 살펴보았듯이, TR과 GLR에 따라 액체 시트의 분열길이는 변하였다. 와류형 분사기에서 분열길이는 분무각을 따라 분열길이를 측정하는 방법과 수직으로 분열길이를 측정하는 방법으로 나뉜다. 액체로켓엔진의 경우 수직방향 분열길이가 화염의 축방향 위치에 큰 영향을 주기 때문에, 본 연구에서 분열길이(Lvb)는 분사기 출구 오리피스 중심에서 첫 번째 액사(ligament)가 발생하는 지점까지의 수직거리로 정의하였다.
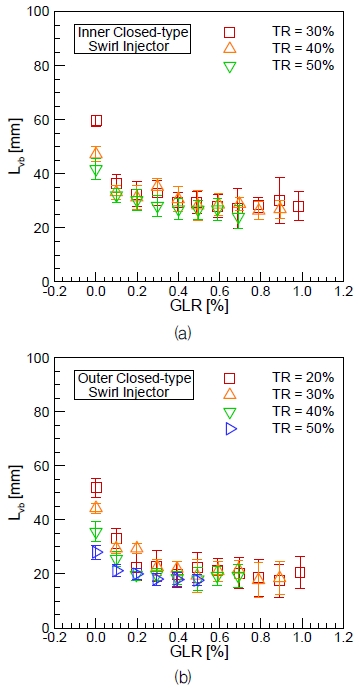
Fig. 10에 각 조건별 액체 시트의 평균 분열길이 및 표준변차를 나타내었다. 이를 위해 각 실험 조건마다 20장의 분무 이미지를 분석하였다. 안쪽 분사기에서 TR이 10%, 20%, 바깥쪽 분사기에서 TR이 10%인 조건은 GLR이 0.0%일 때 중공원추 형상의 분무가 형성되지 않고 액체 시트끼리의 충돌에 의한 분열이 발생하여 결과에서 제외하였다. 동일한 GLR 조건에서는 액체 질량유량이 증가함에 따라 분열길이가 감소하였으며, 액체 질량유량이 동일한 경우 GLR이 증가함에 따라 분열길이는 감소하였다. 낮은 GLR에서는 GLR이 증가함에 따라 분열길이가 빠르게 감소하였지만 GLR 0.4% 이상에서는 GLR이 증가하여도 분열길이는 거의 변화가 없었다. 이는 주입되는 기체의 양을 증가시켜도 분열길이 감소효과에는 한계가 있음을 의미한다. 또한 앞에서 살펴보았듯이 대략 GLR 0.6% 이상에서는 분무 불안정으로 인해 분열길이의 표준편차가 커지는 것을 확인할 수 있다.
와류형 분사기에서 액체 시트의 분열은 액체 시트 표면에서 발생한 표면파가 임계진폭까지 성장하면 발생한다. GLR과 액체 질량유량이 증가함에 따라 액막 두께가 얇아지고 축방향 속도는 증가하게 된다. 이러한 영향에 의하여 표면파가 빠르게 임계진폭까지 성장할 수 있으며, 빠른 분열이 가능해진다.
5. 결 론
액체로켓엔진 추력조절을 위한 기체주입 가변추력 시 와류형 분사기에서 분무특성 변화에 대한 연구를 수행하였다. 기체-액체 혼합물을 형성하기 위해 에어레이터를 제작하여 사용하였으며, TR과 GLR를 변수로 수류실험을 진행하였다.
GLR이 어느 한계 이상으로 증가함에 따라 분무 불안정이 발생하였다. 향후 고압챔버에서의 추가적인 실험을 통해 외부 압력의 영향을 살펴보아야 하겠지만, GLR을 증가하여 혼합물의 밀도를 낮추는 방법은 분무 불안정으로 인해 어느 한계를 갖게 될 것으로 예상된다.
원심력과 표면장력의 힘의 평형을 이용하여 분무형상을 계산하였다. 이때 기포유동에서의 혼합물 밀도를 계산하기 위해 Chisholm[22]이 제시한 이상유동 모델을 사용하였다. 계산된 분무형상은 분무가 중공원추 형상으로 발달된 경우 실제 분무 이미지와 매우 일치하는 것을 확인할 수 있었다. 이를 통해 이상유동에서 TR 및 GLR에 따른 분무형상 및 분무각의 변화를 해석적으로 예측할 수 있음을 알 수 있었다.
기체주입식 와류형 분사기에서 분열길이는 액체 질량유량과 GLR이 증가함에 따라 감소하였다. 낮은 GLR에서는 GLR 증가에 따라 분열길이 변화가 큰 반면, 일정 GLR 이상에서는 GLR 증가에 따른 분열길이 변화가 크지 않았다.
Acknowledgments
본 논문은 과학기술정보통신부의 재원으로 한국연구재단의 지원(NRF-2017R1A1A1A05001237, NRF-2018M1A3A3A02065683) 및 서울대학교 차세대 우주추진 연구센터와 연계된 선도연구센터지원사업(NRF-2013R1A5A1073861)의 연구결과입니다. 이에 감사드립니다.
References
-
Huzel, D.K., and Huang, D.H., Modern Engineering for Design of Liquid-propellant Rocket Engines, 2nd ed., AIAA, Washington D.C., U.S.A., (1992).
[https://doi.org/10.2514/4.866197]

- Sutton, G.P., Rocket Propulsion Elements, 6th ed., John Wiley & Sons Inc., New York, N.Y., U.S.A., (1992).
-
Casiano, M.J., Hulka, J.R., and Yang, V., “Liquid-propellant Rocket Engine Throttling: A Comprehensive Review“, Journal of Propulsion and Power, 26(5), p897-923, (2010).
[https://doi.org/10.2514/1.49791]

- Tomazic, W.A., “Rocket-engine Throttling“, NACA RM E55J20, (1995).
-
Dressler, G.A., “Summary of Deep Throttling Rocket Engines with Emphasis on Apollo LMDE“, 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Sacramento, C.A., U.S.A., AIAA 2006-5220, Jul.), (2006.
[https://doi.org/10.2514/6.2006-5220]

- Morrell, G., “Rocket Thrust Variation with Foamed Liquid Propellant“, NACA RM E56K27, (1957).
- Conrad, W., Hannum, N.P., and Bloomer, H.E., “Photographic Study of Liquid-oxygen Boiling and Gas Injection in the Injector of a Chugging Rocket Engine“, NASA TM X948, (1989).
- Mitchell, J.P., “Technical Report No. 2 of Advanced Throttling Concepts Study“, PWA FR 1045, (1964).
- Mitchell, J.P., “Technical Report No. 3 of Advanced Throttling Concepts Study“, PWA FR 1108, (1964).
- Mitchell, J.P., “Final Report No. 2 of Advanced Throttling Concepts Study“, PWA FR 1279, (1964).
-
Rivard, J.G., “New Techniques for Throttleable Bipropellant Rocket Engines“, Propulsion Joint Specialist Conference, Springs, C.O., U.S.A., AIAA Paper 1965-560, Jun.), (1965.
[https://doi.org/10.2514/6.1965-560]

- Sovani, S.D., Sojka, P.E., and Lefebvre, A.H., “Effervescent Atomization“, Progress in Energy and Combustion Science, 27(4), p483-521, (2001).
-
Chen, S.K., Lefebvre, A.H., and Rollbuhler, J., “Influence of Ambient Air Pressure on Effervescent Atomization“, Journal of Propulsion and Power, 9(1), p10-15, (1993).
[https://doi.org/10.2514/3.11479]

-
Ghaffar, Z.A., Kasolang, S., Hamid, A.H.A., Ow, C.S., and Roseley, N.R.N., “Design, Development and Performance Evaluation of New Swirl Effervescent Injector“, Jurnal Teknologi, 75(1), p19-25, (2015).
[https://doi.org/10.11113/jt.v75.2813]

-
Whitlow, J.D., and Lefebvre, A.H., “Effervescent Atomizer Operation and Spray Characteristics“, Atomization and Sprays, 3(2), p137-155, (1993).
[https://doi.org/10.1615/atomizspr.v3.i2.20]

-
Lefebvre, A.H., Wang, X.F., and Martin, C.A., “Spray Characteristics of Aerated-Liquid Pressure Atomizers“, Journal of Propulsion and Power, 4(4), p293-298, (1988).
[https://doi.org/10.2514/3.23066]

-
Huang, X., Wang, X., and Liao, G., “Visualization of Two Phase Flow inside an Effervescent Atomizer“, Journal of Visualization, 11(4), p299-308, (2008).
[https://doi.org/10.1007/bf03182198]

- Karnawat, J., and Kushari, A., “Controlled Spray Pattern Factor using a Twin-Fluid Swirl Atomizer“, Experiments in Fluid, 41(4), p649-663, (2006).
- Jedelsky, J., Otahal, J., and Jicha, M., “Effervescent Atomizer for Atomization of Suspensions Containing Large Particle“, 22nd European Conference on Liquid Atomization and Spray Systems, Como Lake, Italy, Sep.), (2008.
- Lee, W., Yoon, Y., and Ahn, K., “A Study on the Thrust Throttling Using Gas Injection in Swirl Injectors“, Journal of ILASS-Korea, 23(4), p159-168, (2018).
- Michaelides, E.E., Crowe, C.T., and Schwarzkopf, J.D., Multiphase Flow Handbook, 2nd ed., CRC Press, New York, N.Y., U.S.A., (2016).
-
Chisholm, D., “Two-phase Flow in Heat Exchangers and Pipelines“, Heat Transfer Engineering, 6(2), p48-57, (1985).
[https://doi.org/10.1080/01457638508939624]

-
Kim, D., Im, J., Koh, H., and Yoon, Y., “Effect of Ambient Gas Density on Spray Characteristics of Swirling Liquid Sheets“, Journal of Propulsion and Power, 23(5), p603-610, (2007).
[https://doi.org/10.2514/1.20161]

- Horvay, M., and Leuckel, W., “Experimental and Theoretical Investigation of Swirl Nozzles for Pressure-jet Atomization“, German Chemical Engineering, 9(5), p276-283, (1986).
- Suyary, M., and Lefebvre, A.H., “Film Thickness Measurements in a Simplex Swirl Atomizer”, Journal of Propulsion and Power, 2(6), p528-533, (1986).
-
Sivakumar, D., and Raghunandan, B.N., “Converging Swirling Liquid Jets from Pressure Swirl Atomizers: Effect of Inner Air Pressure“, Physics of Fluids, 14(12), p4389-4398, (2002).
[https://doi.org/10.1063/1.1518694]

-
Kang, Z., Wang, Z., Li, Q., and Cheng, P., “Review on Pressure Swirl Injector in Liquid Rocket Engine“, Acta Astronautica, 145, p174-198, (2018).
[https://doi.org/10.1016/j.actaastro.2017.12.038]