수소발생기의 일차원 모델링
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 수소발생기에 대한 일차원 모델링을 수행하였다. 본 연구에서 고려하고 있는 수소발생기에서 알칼리용액은 위로부터 건조한 알루미늄 파우더로 공급되며, 알칼리용액이 아래방향으로 진행함에 따라 알루미늄과 반응하여 수소가 발생한다. 수소기체와 알칼리용액에 대한 화학종보존방정식과 기체-액체-고체 혼합물에 대한 에너지보존방정식을 고려하였으며, 기체의 상승속도와 액체의 하강속도는 이론적인 접근법을 이용하여 고려하였다. 개발된 프로그램은 수소발생량 및 수소포집기압력과 비교하여 검증한다. 또한, 개발된 프로그램은 농도, 부피분율, 온도 등 반응대의 내부 물성변화를 성공적으로 예측하였으며, 이는 혁신적인 수소발생기의 설계에 많은 도움을 줄 수 있을 것으로 사료된다.
Abstract
This paper presents the one-dimensional model of a hydrogen generator, where the alkali solution was supplied from the top to the dry aluminum powders. Hydrogen was produced as the solution moved downward and reacted with aluminum. The species conservation equations were considered for the hydrogen gas and alkali solution, while the energy conservation equation was applied to the gas-liquid-solid mixture as a single medium. The gas rising velocity and liquid penetration velocity were also included in the theoretical approach. The developed code was validated with the experimental data of the hydrogen production amount and collector pressure. Additionally, the model successfully predicted the various reactor properties, such as the concentrations, volume fractions, and temperatures, and is expected to help significantly in the design of a novel hydrogen generator.
Keywords:
Hydrogen Generator, Aluminium-Water Reaction, Alkali Solution, One-dimensional Analysis키워드:
수소발생기, 알루미늄-물 반응, 알칼리용액, 일차원해석1. 서 론
물 반응 금속(hydro-reactive metal)의 점화 및 연소는 군사적으로 수중 운동체(어뢰, 잠수함)의 추력발생시스템 또는 동력으로 활용이 가능하고, 산업적으로는 연소반응의 열을 이용하여 전력을 발생함과 동시에 부산물인 수소를 분리/포집하여 대체 에너지로 활용할 수 있는 중요한 기술이다[1,2].
다양한 수소발생 메커니즘 중 최근에는 고체금속과 물과의 반응, 그 중에서도 알루미늄/알루미늄합금과 물과의 반응이 주로 사용되며, 많은 연구들이 이루어져 왔다[3-10]. 하지만, 이론해석의 어려움으로 인하여 실험적인 연구들이 대부분이며, 이론적인 연구는 하나의 입자나 플레이트만을 고려한 경우에만 제한적으로 이루어져 왔다. Soler et al. [3] Al/Si 와 Al/Co 합금이 이산화탄소를 포함하지 않는 수소를 발생시킬 수 있음을 실험적으로 관찰하였으며, Rosenband and Gany [4]는 이러한 수소발생량을 정량화하였다. Chen et al. [5]는 알루미늄 및 알루미늄합금 입자들을 볼-밀링 방법으로 쉽게 제작이 가능함을 보였다. Jia et al. [6]은 수소생성량이 Ni/Al 합금비와 알칼리용액의 함량에 따라 변화함을 실험적으로 확인하였으며, Xu et al. [7]은 XRD, SEM, EDX, DSC 등의 엄밀한 측정방법과 열역학적 기법을 이용하여 수소생성 메커니즘을 관찰하였다. Yavov et al. [8]은 나노 또는 마이크로 단위의 알루미늄 입자들에 대한 알루미늄-물 반응에 의한 수소생성을 관찰하며, 크기가 작아질수록 많은 양의 수소가 생성됨을 관찰하였다. Hiraki et al. [9]은 단일 알루미늄입자와 물과의 반응을 감쇄코어(shrinking core)모델을 이용하여 해석하였으며, 실험결과와의 비교를 통하여 활성화에너지를 도출하였다. 최근에 Razavi-Tousi and Szpunar [10]은 전통적인 감쇄코어모델을 입자의 크기 효과와 수산화(AlOOH)층에서의 공극률 변화를 고려할 수 있도록 개선하였다.
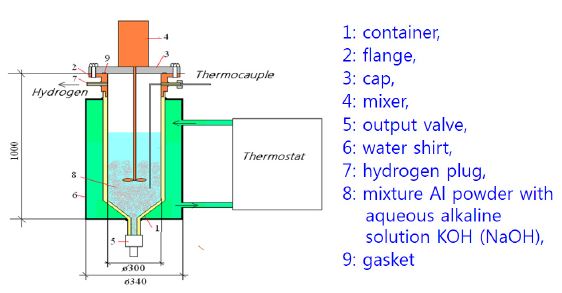
Fig. 1은 소형 수소발생기에 대한 일반적인 개략도이다. 알루미늄과 물 사이의 반응을 촉진하기 위하여 NaOH나 KOH 등이 첨가된 알칼리용액을 사용한다. 알루미늄 파우더는 초기에 수소 발생기의 아래 부분에 이미 공급되어 있으며, 알칼리용액이 위에서 분무형태로 유입됨에 따라 수소가 지속적으로 발생하고, 발생된 수소기체들은 위쪽의 수소포집부로 이동한다. 이러한 기술은 미국에서 이미 상용화된 기술이기는 하지만, 정확한 메커니즘, 장치의 구성 및 핵심기술 등은 아직 알려져 있지 않다. 이러한 수소발생기의 경우에는 단위시간 당 수소발생량이 가장 중요한 성능 지표임이 알려져 있다[11].
알루미늄입자 파우더와 알칼리용액과의 반응을 이용하는 수소발생기의 3차원 해석을 위해서는 고체-액체-기체 3상 유동과 열전달 및 화학반응에 의한 상변화 및 부피분율 변화 등이 동시에 일어나는 매우 복잡한 현상의 해석을 요구하며 현재까지는 수행된 적이 없고, 반응로 내의 물리현상 각각에 대한 현상론적인 모델도 아직은 존재하지 않는다.
이를 고려하여 본 연구에서는 3차원 해석 대신 단순화된 일차원 모델링을 수행하여 대표적인 성능지표인 수고발생량을 예측하고자 한다. 일차원 모델링에서는 반경방향의 물성치들의 구배를 무시하고 반응로의 높이에 따른 단면적의 변화 효과는 고려할 수 없지만, 반응로의 핵심 메커니즘인 알루미늄-알칼리용액 반응에 대한 엄정한 모델링 및 반응로 벽면을 통한 냉각, 그리고 발생한 수소기체의 상승운동과 알칼리용액의 하강운동 등 원래 시스템의 핵심 원리들은 여전히 포함한다. 본 연구를 통하여 수소발생량의 정확한 예측뿐만 아니라 수소발생기 내부의 다양한 물리적인 현상들에 대한 물리적인 이해 또한 향상시킬 수 있을 것으로 사료된다. 아울러, 개발된 프로그램을 이용하여 급격한 온도 상승이 나타나지 않도록 알칼리수용액의 적정공급량을 예측할 수 있다.
2. 소형 수소발생기 제작 및 수소발생량 측정
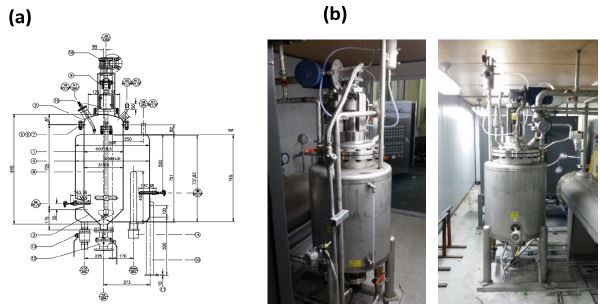
Fig. 2는 본 연구에서 개발된 프로그램을 검증을 수행한 실제 수소발생기를 보여주고 있다. 전체적으로 내부직경은 300 mm, 높이는 740 mm인 STS304로 만들어진 원통형의 형상을 가지며 내부용량은 약 52,500 cm3이다. 입자의 크기가 30 μm인 알루미늄 파우더가 수소발생 반응 전에 미리 수소발생기에 공급되어 있으며, 급격한 반응에 의해 발생기의 손상이 일어나는 것을 피하기 위하여 수소발생기 하부 경사진 영역에만 공급된다. 반응에 사용되는 NaOH 알칼리수용액은 외부의 알칼리용액 저장설비에서 3.7 kW의 용량을 가진 펌프를 통해 공급되며 발생기 내부에서는 120°의 분사각을 가지고 스파이럴 형태로 아래의 알루미늄 파우더를 향해 분사되며, 이로 인하여 알루미늄 파우더 반응대 단면적 전체에 골고루 일정하게 알칼리수용액이 공급된다고 생각할 수 있다. 발생된 수소기체는 발생기 위쪽의 배관설비를 통하여 외부의 수소포집장치로 이송되며 수소포집기의 입구에 계측장비를 설치하여 수소의 총발생량, 압력, 온도를 측정하였다.
3. 수소발생기 일차원 모델링
3.1 일차원 모델링 및 가정
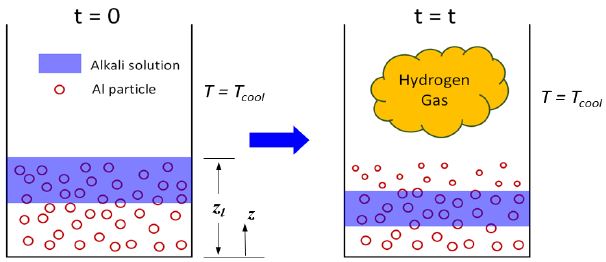
본 연구에서는 Fig. 2의 수소발생기의 물리적인 핵심들은 잃어버리지 않으면서 시스템을 Fig. 3에 주어진 바와 같이 일차원으로 단순화하여 모델링하였다. 이를 통하여 수소발생기 내부의 알루미늄 입자들의 크기가 NaOH 알칼리수용액이 침투하여 반응에 의해 감소하고, 알칼리수용액은 지속적으로 아래로 이동하면서 알루미늄과의 반응에 의해 소비되는 과정을 모사하고자 한다. 이를 위해 다음의 가정들이 일차원 모델링을 위해 사용되었다.
1. 알루미늄 입자들의 크기는 실험조건으로 반영하여 30 μm로 설정하였으며 움직이지 않는다.
2. 고체입자는 반응에 의하여 성분이 알루미늄에서 Al(OH)3로 변화할 뿐이며 입자의 크기는 변화하지 않는다.
3. 고체입자의 부피분율은 초기값으로 주어지며, ϕs = (4/3)π(dp/2)3np = (πnpdp3)/6 로 계산된다.
4. 시스템에 존재하는 모든 상들은 열적평형을 이루고 있다.
5. 알루미늄-물 화학반응에 의해 생성되는 기체에 의한 버블의 크기는 Tate 관계식[12]으로 계산한다. 본 관계식은 기체의 유량이 작다면 위식은 버블의 크기를 잘 예측할 수 있는 것으로 알려져 있으며, 본 연구와 비슷한 수소발생용량을 가지는 수소발생기의 현상론적 모델링에 적용된 적이 있다[2].
초기에 공급되는 알루미늄 입자들의 양이 정해지면 알루미늄 파우더의 겉보기밀도에 의하여 수소발생기 내부에 알루미늄 입자가 채워진 반응대(reaction bed)의 높이(z = zl)가 정해지며, 수치적인 해석은 이러한 반응대 영역 (0 < z < zl)에서만 행해진다. 일반적으로 수소발생기에서는 반응이 너무 과도하게 일어나는 것을 방지하기 위하여 알루미늄입자들이 반응기 하부의 경사진 부분만을 채울 정도로만 공급되는데, 본 연구에서는 일차원 모델을 사용하기 때문에 이러한 효과를 고려하기 위하여 경사진 부분에 대한 환산직경과 환산단면적을 계산하여 일차원 해석을 수행하였다. 수소발생기는 일정한 온도(T = Tcool)를 가진 냉각수로 냉각이 되고 있으며 이는 벽면에서의 대류열전달계수가 hext인 대류 열손실로 모델링하였다. 알루미늄-알칼리용액 반응에 의해 생성된 수소기체는 상부의 수소포집기로 유입된다.
3.2 알루미늄-알칼리용액 화학반응
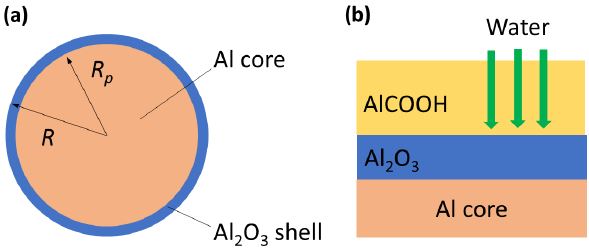
알칼리용액에 담긴 구형의 알루미늄입자는 초기에 Fig. 4(a)에 주어진 바와 같이 얇은 알루미늄 산화막으로 둘러싸여 있으며, 알루미늄-물 반응의 화학반응식은 다음과 같다[13].
| (1) |
하지만, Fig. 4(b)에 주어진 바와 같이 알루미늄-물 산화반응의 반응속도는 알루미늄-물 사이의 반응보다는 Al2O3 층과 AlOOH 층을 통한 확산현상에 의해서 결정되는 것으로 알려져 있다[13]. 본 연구에서는 이 점을 고려하여 수소생성률에 대한 활성화에너지를 AlOOH 층을 통한 확산현상에 대한 값인 17 kJ/mole을 사용하였다[13]. 본 연구에서 반응계수 kg는 다음의 식에 주어진 바와 같이 Arrhenius 형태로 표현된다.
| (2) |
위 식에서 Ag는 수소 생성에 대한 pre-exponential factor이며 단위는 [m/s]이다. 이 값은 알루미늄 입자의 packing 정도, 반응이 일어나는 알루미늄 입자들 사이의 상호작용 등이 전체적인 화학반응에 영향을 끼침을 고려하여 실험값과의 비교를 이용하여 결정하였다.
3.3 수소기체에 대한 화학종 방정식
본 연구에서 사용된 수소기체에 대한 화학종 방정식은 다음과 같다[14].
| (3) |
위 식에서 수소기체의 생성률 는 아래와 같이 주어진다[9,15].
| (4) |
또한, NaOH가 물에 잘 녹아있다고 생각할 수 있으며 이 경우, NaOH의 농도는 다음과 같이 표현할 수 있다.
| (5) |
위 식에서 r은 알칼리수용액의 농도와 NaOH 농도 사이의 비례상수이다. 따라서 Eq. 2는 다음과 같이 쓸 수 있다.
| (6) |
3.4 알칼리수용액에 대한 화학종전달방정식
수소기체에 대한 화학종전달방정식과 비슷하게 알칼리수용액에 대한 화학종전달 방정식은 다음과 같이 쓸 수 있다.
| (7) |
NaOH 수용액의 소모에 대한 pre-exponential factor, Al는 Al =- 2Ag로 계산되는데, 이는 화학 반응식 Eq. 1에 따르면, 물이 1몰 소모될 때 수소가 0.5 몰 생성되기 때문이다.
3.5 부피분율(volume fraction)
수소기체-알칼리수용액-고체입자 혼합물의 시스템 크기가 ΔV로 주어진 경우, 수소기체의 몰농도 Cg에 해당되는 기체부피 Vg는 이상기체에 대한 상태방정식으로부터 계산될 수 있다.
| (8) |
ΔV 중에 고체입자가 차지하는 부피는 다음과 같이 표현된다.
| (9) |
따라서 액체의 부피는 아래의 식으로 계산된다.
| (10) |
최종적으로, 각 상의 부피분율은 다음과 같이 계산할 수 있다.
| (11) |
| (12) |
| (13) |
위 식에서 ϕs,0는 고체입자들이 차지하고 있는 초기 부피분율이며, 고체입자들의 초기 부피 Vs,0로부터 다음과 같이 계산된다.
| (14) |
3.6 기체의 상승속도
입자들과 액체가 섞여 있는 매질을 통한 기체의 상승속도에 대한 일반적인 해석은 그 자체로 매우 복잡하고 어려운 문제이다. 따라서 본 연구에서는 고체 그레인 사이를 기체-액체 혼합물이 이동하는 상황에 대하여 Corapcioglu et al.[16]에 의해 제안된 이론적인 관계식을 사용하였다.
| (15) |
위 식에서
| (16) |
| (17) |
| (18) |
Corapcioglu et al.[16] 에 의한 모델은 액체로 차 있는 다공성 매질에서 기체버블의 상승운동에 대한 모델이며, 관성력, added mass 효과, 부력, 버블의 표면장력, 항력 사이의 평형으로부터 유도된 운동방정식으로부터 이론적으로 유도할 수 있다. Eq. 18은 본 연구에서 다루고 있는 시스템과 비슷하게 비드(bead)로 가득한 물을 통과하는 기체에 대한 실험결과[17]와 비교하여 검증된 바 있다.
3.7 액체의 하강속도
알칼리수용액의 반응대를 지나가는 속도는 압력강하에 대한 관계식은 Ergun 관계식[18]과 중력과의 평형 관계식으로부터 유도할 수 있으며, 유체의 속도 u0에 대한 방정식은 다음과 같다.
| (19) |
위 식에서 계산된 속도는 표면속도이며, 주어진 공극률을 이용하여 국소속도를 계산한다.
3.8 기체-액체-고체 혼합물에 대한 에너지보존방정식
기체-액체-고체 혼합물에 대한 에너지보존방정식은 다음과 같이 쓸 수 있다[14].
| (20) |
위 식에서 hext [kW/(m2․K)]은 Tcool의 온도를 가진 냉매로의 열손실에 대한 대류열전달계수이다. 그리고 a[m2․m-3]는 반응대의 단위부피에 대한 외부벽면적이다. 위의 에너지보존방정식은 생성률과 혼합물전도도에 대한 관계식을 적용하여 다음과 같이 간단하게 쓸 수 있다.
| (21) |
위에서 정리된 지배방정식들을 비선형성이 매우 심한 방정식으로 일반적인 유한차분 이산화로는 수렴이 잘 되지 않으므로 각 계산 노드에 대한 적분을 수행한 뒤 이산화를 수행하는 유한체적법을 사용하여 수치해석을 수행하였다. 비정상 해석을 위해서는 내재적인 접근법을 사용하였다.
4. 결과 및 토의
본 연구에서는 Fig. 2에 언급된 수소발생기의 실험에 사용된 다음의 운용조건을 입력값으로 사용하였다.
- ① 알루미늄입자 투입량: 3.6 kg
- ② 알칼리촉매(NaOH) 투입량: 1.29 kg
- ③ 물의 투입량: 10.8 kg
위의 조건을 사용한 경우 실험에서는 약 2시간 30분 동안 2,200 리터의 수소기체가 생성되었고 압력은 0.25 bar로 측정되었으며, 이는 약 50%의 수율에 해당된다. 수치해석에서는 알칼리 수용액이 3.7절에서 유도된 속도로 전체 시뮬레이션 동안 반응대에 유입된다고 가정하였으며, 총 시뮬레이션 시간은 이 속도에 의해 계산된 질량유량에 의해 주어진 물이 모두 투입될 때까지의 시간으로 설정하였다. 위의 운용조건의 경우 시뮬레이션 시간은 약 10,000 초에 이른다.
4.1 시간에 따른 수소반응기 출구기체의 물성치 변화
Fig. 5는 수소반응기에서 생성되는 수소기체 물성치의 시간에 따른 거동으로, Fig. 5(a)에 나타난 바와 같이 공급되는 물의 양은 시간에 관계없이 일정하다고 가정하였다. Fig. 5(b)는 생성되는 수소기체의 부피유량을 보여주고 있다. 반응이 일어남에 따라 입자의 성분이 알루미늄에서 산화알루미늄으로 변화하는데 수소생성반응의 초기단계에는 알루미늄 성분이 대부분이 입자가 물이 공급되는 반응대 표면에 다량 분포하므로 급격하게 수소가 방출되지만, 이러한 짧은 과도과정 이후 알칼리수용액이 알루미늄 파우더 층으로 일정한 비율로 침투하고 알루미늄-알칼리 수용액 반응에 의하여 발생하는 수소의 부피유량은 비교적 일정하게 유지된다. 그리고 시간이 지나감에 따라 알루미늄 입자의 크기가 감소함에 따라 발생하는 수소의 양은 감소한다. Fig. 5(c)는 발생하는 부피의 시간에 따른 축적량을 보여주며, Fig. 5(b)에서 관찰되는 짧은 순간의 과도과정은 전체적인 수소기체 축적량에 거의 영향을 끼치지 못하고 있음을 알 수 있다. 수채해석을 통해 계산된 수소의 총발생량은 약 2,200 리터이며, 이 값은 실험에서 측정된 값과 거의 일치한다. 이는 현재 프로그램에서 사용한 물의 AlOOH 층으로의 확산에 대한 활성화에너지를 이용한 접근이 타당함을 의미한다. 알루미늄-물반응에 수소생성에 대한 활성화에너지 값은 알루미늄 플레이트와 물 사이의 반응에 대해 알려진 68.4 kJ/mol 값이 일반적으로 사용되어 왔다[9]. 하지만, 본 연구에서는 이 값을 사용하면 수소발생량이 지나치게 낮게 관찰되었으며, 최근에 Yavor [13]에 의해 제안된 AlOOH층 확산 메커니즘에서의 확산현상 활성화에너지를 사용한 경우에만 수소발생량 측정값이 성공적으로 예측되었다. 따라서 본 연구에서는 AlOOH 확산현상의 활성화에너지 값인 17 kJ/mol을 사용하였다.
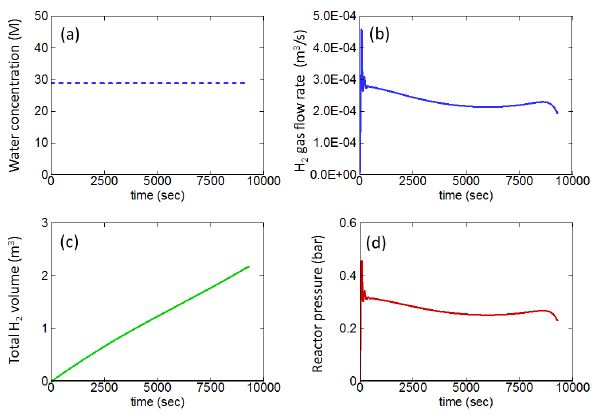
Time history of (a) water provided; (b) volume flow rate of hydrogen gas produced; (c) accumulated volume of hydrogen gas produced; (d) reactor pressure.
Fig. 5(d)는 반응대에서의 출구압력을 나타내고 있으며, 전체적으로 비교적 일정한 0.3 bar의 값이 유지된다. 실험에서는 수소포집기 입구에서 압력을 측정하여 약 0.25 bar의 값을 얻었는데, 수소반응기에서 발생된 수소가 배관을 통해 수소포집기에 들어가기까지 일정한 압력손실이 있을 수 있다는 점을 고려하면, 실험값과 계산값 사이의 20% 정도 차이는 비교적 받아 들여질만한 수준이라고 사료된다.
4.2 시간, 위치에 따른 알루미늄코어 크기 변화
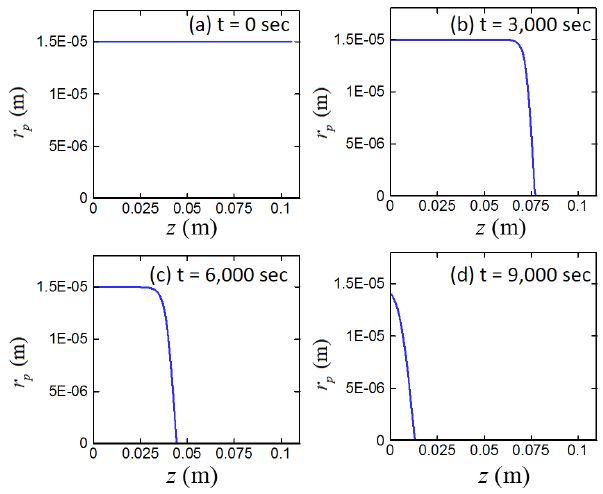
Fig. 6은 시간과 위치에 따른 알루미늄 코어의 크기변화를 보여준다. 이하 그림들에서 가로축은 반응대의 높이를 의미하며, 본 연구에서 고려하고 있는 바와 같이 알루미늄 파우더를 3.6 kg 투입한 경우 알루미늄 파우더의 겉보기 밀도와 반응대의 환산단면적에 의하여 약 zl = 10 cm의 값을 가지게 된다. 즉, 공급된 알루미늄 파우더의 질량에 비례하여 반응대의 높이가 증가한다. 반응이 전혀 일어나지 않은 알루미늄 입자의 초기직경은 1.5×10-5 m이며, 지속적으로 공급되는 알칼리수용액과의 반응을 통하여 알루미늄 코어는 크기가 지속적으로 감소하여 궁극적으로는 소멸한다. t = 9,000 sec 에 다다르면, 대부분의 입자의 알루미늄 코어는 반응을 통해 소멸하고, 남아 있는 입자들의 알루미늄 코어의 크기도 대부분 입자의 초기 크기보다 작다. 본 연구에서는 알루미늄 입자는 반응에 의하여 Al(OH)3로 변화할 뿐이며 입자의 크기는 변화하지 않는다고 가정하였다. 이로 인하여, 시스템의 공극율은 전체 시뮬레이션 시간동안 일정하다.
4.3 시간, 위치에 따른 수소기체 몰농도 변화
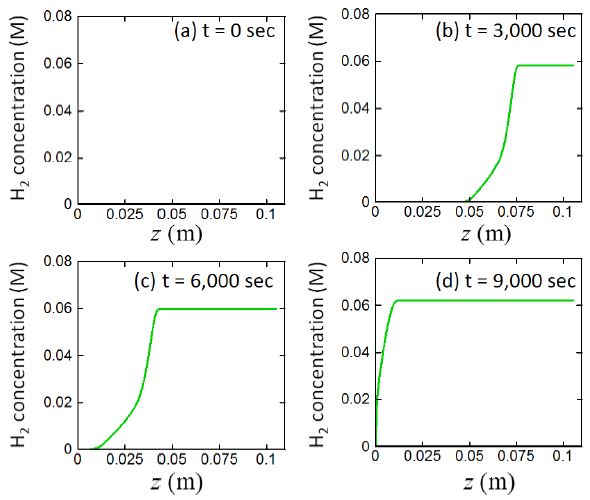
Fig. 7은 생성된 수소기체의 시간, 위치에 따른 변화이다. 앞의 그림에서 언급한 알루미늄 코어가 소모됨에 따라, 반응대 내부에서 수소기체가 형성되며 형성된 수소기체는 반응대를 지나 수소기체 포집기로 전달된다. 그래프에 보여지는 수소기체의 몰농도는 매우 작지만 이상기체의 상태방정식에 따라 계산되는 생성되는 부피는 충분히 크다. 이러한 수소기체 생성은 Fig. 8에서 나타난 알칼리수용액의 거동을 살펴보면 이해할 수 있다.
4.4 시간, 위치에 따른 알칼리수용액 몰농도 변화
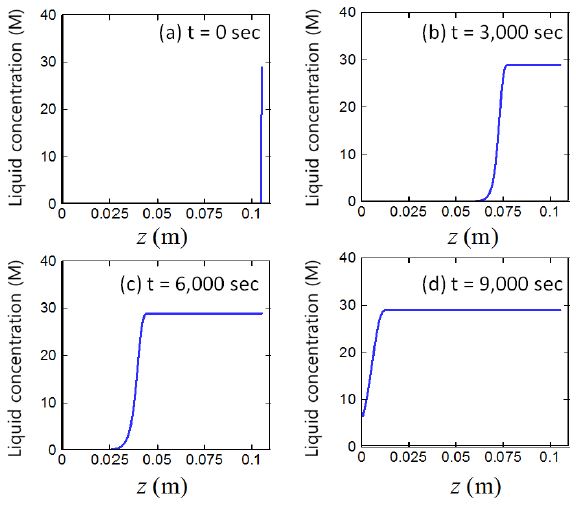
Fig. 8은 알칼리수용액의 시간과 위치에 따른 분포를 보여준다. 알칼리수용액은 지속적으로 공급되고 있다고 가정하였으므로 그림에서는 알칼리수용액이 서서히 아래쪽으로 투습됨을 보여준다. 약 t = 9,000 sec에는 알칼리수용액은 반응대바닥(z = 0)에 도달하며, 투습되는 동안 알루미늄 입자들과 반응한다. t = 6,000 sec에서 9,000 sec 로 바뀌면서, 그래프의 기울기의 미분값이 바뀌는데, 이는 t = 6,000 sec의 경우에는 알칼리 용액이 확산에 의해 투습되어 가면서 반응이 지속적으로 일어나는 상황이지만, t = 9,000 sec의 경우에는 아래 바닥면을 제외하고는 입자의 알루미늄 성분이 거의 소모되어 알칼리용액의 많은 부분이 바닥면 부분에 도달하여 그 지역에서 수소기체가 다량 발생하기 때문이다. 이러한 내용은 Fig. 6에서 나타난 바와 같이 알루미늄 코어의 변화로 나타난다. 각 시간단계에서 알칼리 수용액의 분포와 Fig. 7의 수소기체의 분포는 완전히 일치하지는 않는데, 이는 수소기체와 알칼리수용액의 확산이 서로 차이가 나기 때문이다. 수소기체의 경우에는 확산계수가 액상의 알칼리 수용액에 비하여 매우 크기 때문에 매우 적은 양의 알칼리수용액이 알루미늄 코어와 반응하여 생성된 수소기체가 알루미늄 입자층을 통해 급격하게 확산한다.
본 주어진 조건에서 반응대의 높이는 약 zl = 0.1 m 이고, 알칼리 수용이 바닥까지 내려가는데 약 9,000 초가 걸리며, 이는 알칼리수용액은 매우 dense한 porous 매질을 통과하는 상황으로 액체상의 속도가 매우 느리기 때문이며, 실험결과인 실험값인 2.5 시간(= 9,000 초)과 일치한다. 이러한 상황에 대한 모델링으로 널리 받아들여지고 있는 것이 Ergun 관계식[16]이며, 이 관계식에 따르면 물은 매우 천천히 아래 방향으로 이동한다.
4.5 시간, 위치에 따른 수소기체/알칼리수용액/입자 부피분율 변화
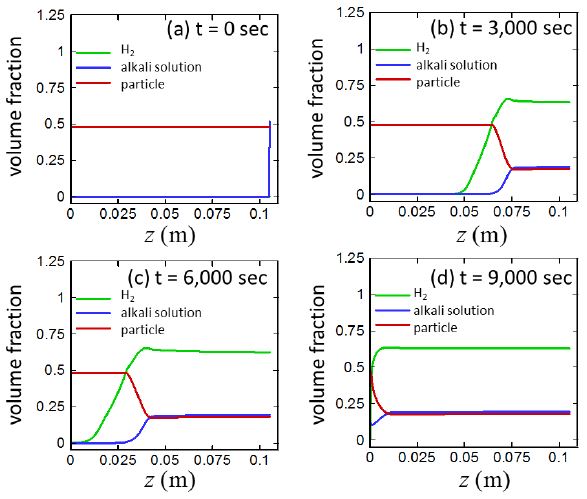
Fig. 9는 수소기체/알칼리수용액/입자 부피분율의 시간, 위치에 대한 변화를 보여준다. 위의 그림에서 부피분율은 고체/액체/기체 각 상(phase)을 기준으로 나타내었으며 고체상은 ‘particle’로 표시하였다. 본 연구의 가정에 의하면 입자는 알칼리수용액과의 반응 전에는 알루미늄이지만 반응 후에는 수산화알루미늄으로 변화하므로, ‘입자’라고 표시되지만, 반응 전후 의미하는 바는 다르다. 주어진 위치의 매질에서 알칼라 수용액이 존재하지 않는 경우에는 알루미늄입자 파우더의 빈공간에 공기가 들어있어, 알루미늄입자, 수소, 알칼리용액의 부피분율의 합은 1보다 적다. 예를 들어, z = 0인 위치에서는 아직 알칼리용액이 유입되지 않아 부피분율의 합이 1보다 적다. 또한, 수소기체의 경우에는 몰수가 적더라도 밀도가 작기 때문에 차지하는 부피는 크다. 따라서 수소기체가 발생하기만 하면 (t > 1,000 sec), 수소의 부피분율은 다른 알칼리수용액이나 입자의 부피분율과 비교하여 매우 크다.
가정에 의하여 입자상이 반응대 내부에서 차지하는 부피는 항상 일정하고 경계조건에 의하여 알칼리수용액의 농도는 수소발생부의 위쪽 경계에서 항상 일정하게 공급되기 때문에 그 부분에서의 부피분율은 항상 일정하다 또한 알칼리수용액이 지나간 지역에서는 생성된 수소기체, 고체입자, 알칼리수용액의 농도는 항상 일정하게 유지된다. 이미 앞의 그림에 대한 토의에서 언급된 바와 같이 아주 미세한 양의 알칼리수용액이 침투하더라도 알루미늄과의 반응에 의하여 수소기체가 형성되고 그 양은 몰수로는 매우 작을 수 있으나 기체라는 특성 때문에 부피분율은 매우 커진다. 이로 인하여, 그림에서 수소기체의 부피분율이 반응기의 바닥으로 다른 부피분율에 비하여 더욱 빠르게 전진하는 것처럼 나타난다.
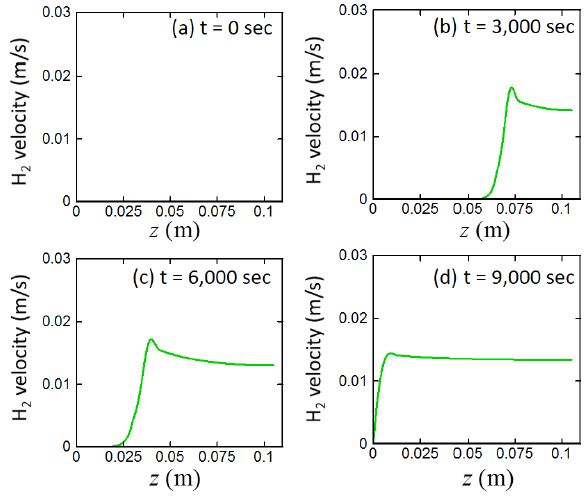
4.6 시간, 위치에 따른 발생한 수소기체 속도 변화
Fig. 10은 시간과 위치에 따른 수소기체의 속도변화를 보여준다. 수소기체의 속도는 수소가 발생하는 양이 증가함에 증가하지만, 수소기체가 더 이상 발생하지 않는 반응대 바깥 영역을 통과하는 속도는 일정하게 유지된다. 즉, 생성된 수소기체는 반응대 경계까지는 가속되지만, 반응대 경계를 지나면서 더 이상 수소기체를 가속할 수 있는 화학반응이 존재하지 않기 때문에 수소기체의 최대 속도는 반응대 경계에서 관찰된다.
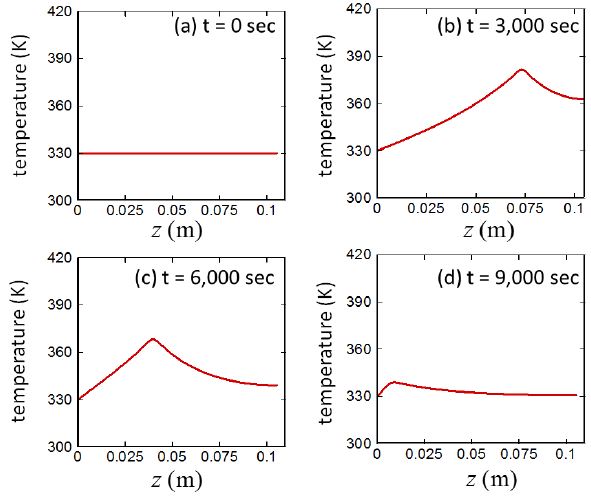
4.7 시간, 위치에 따른 수소기체/알칼리수용액/입자 혼합매질의 온도 변화
마지막으로 Fig. 11은 반응대 내의 수소기체/알칼리수용액/입자 혼합매질에서의 온도의 시간 및 위치에 따른 변화를 보여준다. 전체적으로 알루미늄-물 반응이 일어나면 온도가 증가하며, 최대 온도는 알칼리수용액이 존재하는 반응대의 위쪽 경계에서 관찰된다. 알칼리수용액이 존재하는 반응대 중 반응이 일어나고 있는 지역에서는 반응에 의한 반응열이 지속적으로 공급되지만, 알루미늄 코어가 모두 소모되어 더 이상의 반응이 일어나지 않는 반응대 내의 전달부에서는 전도에 의해서 반응부의 열이 외부로 전달되어 냉각된다. 또한 반응부의 열은 일정한 냉각수의 온도로 유지된다고 가정한 수소발생기의 바닥으로 빠져 나간다. 시간이 진행되어 가면서 초기에는 반응량의 증가에 따라 혼합매질 온도가 전체적으로 증가하지만, 시간이 더욱 진행되면 반응을 공급할 수 있는 알루미늄입자들의 양이 감소하면서 매질의 온도가 전체적으로 감소하여 반응의 후반부에는 매질의 상당부분 영역이 냉각수의 온도 (Tcool = 330 K)와 일치할 정도로 냉각이 이루어진다.
4.8 벽면열손실 효과
Fig. 12는 열손실이 존재하지 않는 경우 (hext = 0) 수소반응기에서 생성되는 수소기체 물성치의 시간에 따른 변화를 보여주고 있다. 벽면을 통한 열손실이 존재하는 경우 4.1절의 결과와 비교를 하면 열손실은 수소기체의 부피유량과 반응대출구 압력에 거의 영향을 끼치지 못하는 것을 확인할 수 있다. 이는 시간이 경과함에 따라 반응물인 알루미늄 입자들이 소모되더라도 열손실이 벽면으로 일어나지 않아 반응대 내부의 온도가 비교적 높게 유지되고 이로 인하여 알루미늄-물 사이의 화학반응이 활발하게 일어나고, 이에 따라 압력 또한 감소하지 않아서 벌어지는 현상으로 사료된다. 일정하게 유지되는 부피유량의 값은 4.1절의 Fig. 5(b)와 비교를 할 때 과도상태 후 초기에 관찰되는 최대값과 거의 일치한다 (Q ≈3×10-4 m3/s). 즉, 초기에 형성된 반응이 시뮬레이션이 끝날 때까지 유지됨을 의미한다. 따라서 Fig. 12(d)에 보여지는 바와 같이 반응대 출구압력 또한 줄어들지 않고 일정하게 유지된다.
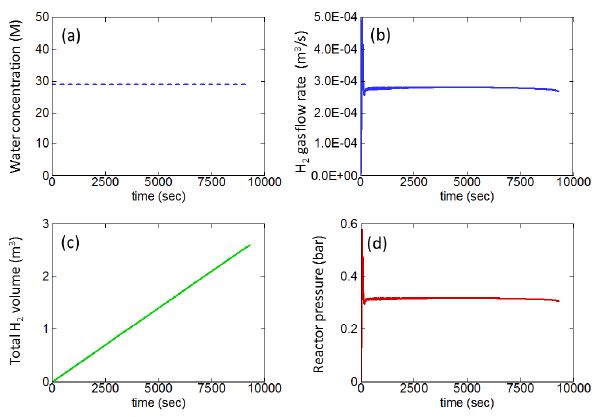
Time history of (a) water provided; (b) volume flow rate of hydrogen gas produced; (c) accumulated volume of hydrogen gas produced; (d) reactor pressure for the hydrogen reactor without heat loss.
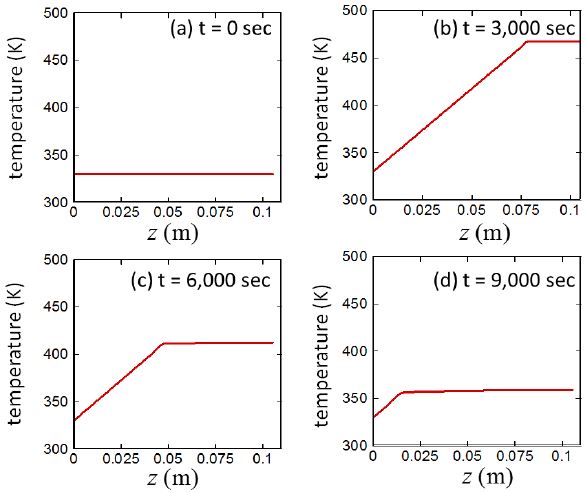
Fig. 13은 시간과 위치에 따른 수소기체-알칼리수용액-알루미늄입자 혼합매질의 온도 변화이다. 4.7절의 결과와 비교할 때 전체적으로 매질의 온도가 상승한 것을 확인할 수 있다. 하지만, 반응대의 위쪽 경계면을 중심으로 위쪽 경계면 위로는 고온의 온도가 일정하게 유지되지만, 반응대의 위쪽경계면 아래로는 혼합매질을 통한 바닥으로의 전도열전달 때문에 온도가 거의 선형적으로 변화한다. 반응이 활발하게 일어나는 t = 2,000 sec 그리고 t = 3,000 sec 의 온도분포를 살펴보면 최대온도가 Tmax = 480 K 즉, 200℃ 까지 상승한다.
5. 결 론
본 연구에서는 알루미늄-알칼리용액 반응을 이용하는 수소발생기의 성능을 해석할 수 있는 일차원 프로그램을 작성하고 작성된 프로그램을 이용하여 성능해석을 수행하였다. 개발된 프로그램은 수소기체와 알칼리용액에 대한 화학종보존 방정식과 기체-액체-고체 혼합물에 대한 에너지 보존방정식을 유한체적법을 이용하여 수치적인 해석을 수행한다. 그 결과 주어진 위치와 시간에서의 수소기체 및 알칼리용액의 농도 및 부피분율 그리고 기체-액체-고체 매질의 온도 등 반응대 내부의 물성치 뿐만 아니라, 생성되는 수소기체의 질량유량 및 총량 그리고 포집되는 수소기체의 압력 등의 성능물성치 또한 계산이 가능하다. 개발된 프로그램은 측정된 값들과 비교하여 검증하였다. 본 해석을 통해 얻어진 결론들을 요약하면 다음과 같다.
1. 본 연구에서 고려한 수소발생기의 일차원 모델링에서는 반경방향의 물성치들의 구배를 무시하고 반응로의 높이에 따른 단면적의 변화 효과 등은 고려할 수 없지만, 반응로의 핵심 메커니즘인 알루미늄파우더-알칼리용액에 대한 엄정한 모델링 및 반응로 벽면을 통한 냉각, 그리고 발생한 수소기체의 상승운동과 알칼리용액의 하강운동 등 수소발생기의 물리적인 중요한 핵심현상들을 여전히 포함하였으며, 수소발생량 실험결과와 견주어 모델링의 합리성을 확보하였다. 이는 수소발생기의 운용조건을 수소발생량을 기준으로 결정하는 과정의 실험과정을 전산해석으로의 대체를 가능하게 하여 수소발생기 개발과정을 단축할 수 있을 것으로 사료된다.
2. 일차원해석을 성공적으로 수행하기 위하여 pre-exponential factor, 반응대벽면을 통한 열전달계수를 조절파라미터(tuning parameter)로 도입하였으며, 측정된 총수소발생량 값과의 비교를 통해 결정하였다.
3. 본 연구를 통해 개발된 일차원 해석프로그램은 수소발생기의 핵심개념인 물의 침투현상 및 반응에 의한 알루미늄 입자의 소모를 성공적으로 모사하였다.
4. 반응로 주변을 통한 냉각이 없는 경우에는 반응로의 온도는 상당히 고온(본 연구의 일차원 모델의 경우에는 200℃)까지 상승할 수 있고 이는 반응로의 안정성에 문제점을 야기할 수 있으므로, 이를 억제하기 위한 벽면냉각이 요구된다.
5. 본 연구에서 고려한 운용조건에서는 수소의 발생량 및 이에 따른 압력은 초기의 급격한 과도과정을 제외한다면 전체 시뮬레이션 시간동안 비교적 일정한 값을 유지하였다.
Nomenclature
| Ci : | molar concentration (i = g, l, s) |
| Di : | diffusion coefficient (i = g, l, s) |
| dp : | particle diameter |
| E : | total energy |
| g : | gas phase (hydrogen gas) |
| l : | liquid phase (alkali solution) |
| np : | particle number density |
| p : | pressure |
| Qg : | Heat of formation of H2 gas |
| RU : | universal gas constant (= 8.20574587×10−5, m3·atm·K−1·mol−1). |
| rp : | particle radius |
| Sp : | particle surface area |
| s : | solid phase (particle) |
| T : | temperature |
| Tcool : | coolant temperature |
| t : | time |
| Vi : | volume (i = g, l, s) |
| z : | z-dimension |
| ϕi : | volume fraction (i = g, l, s) |
| λm : | thermal conductivity of mixture |
| σ : | surface tension |
| θ : | contact angle |
| : | reaction rate (i = g, l, s) |
Acknowledgments
본 연구는 세연 E&S의 지원에 의해서 수행되었습니다.
References
-
Risha, G.A., Son, S.F., Yetter, R.A., Yang, V., and Tappan, B.C., "Combustion of Nano-Aluminum and Liquid Water", Proceedings of the Combustion Institute, 31(2), p2029-2036, (2007).
[https://doi.org/10.1016/j.proci.2006.08.056]

-
Shmelev, V., Yang, H., and Yim, C., "Hydrogen Generation by Reaction of Molten Aluminum with Water Steam", International Journal of Hydrogen Energy, 41(33), p14562-14572, (2016).
[https://doi.org/10.1016/j.ijhydene.2016.05.277]

-
Soler, L., Macanas, J., Munoz, M., and Casado, J., "Aluminum and Aluminum Alloys as Sources of Hydrogen for Fuel Cell Applications", Journal of Power Sources, 169(1), p144-149, (2007).
[https://doi.org/10.1016/j.jpowsour.2007.01.080]

-
Elitzur, S., Rosenband, V., and Gany, A., "Study of Hydrogen Production and Storage Based on Aluminum–Water Reaction", International Journal of Hydrogen Energy, 39(12), p6328-6334, (2014).
[https://doi.org/10.1016/j.ijhydene.2014.02.037]

-
Chen, X., Zhao, Z., Liu, X., Hao, M., Chen, A., and Tang, Z., "Hydrogen Generation by the Hydrolysis Reaction of Ball-Milled Aluminium–Lithium Alloys", Journal of Power Sources, 254, p345-352, (2014).
[https://doi.org/10.1016/j.jpowsour.2013.12.113]

-
Jia, Y., Shen, J., Meng, H., Dong, Y., Chai, Y., and Wang, N., "Hydrogen Generation Using a Ball-Milled Al/Ni/NaCl Mixture", Journal of Alloys and Compounds, 588, p259-264, (2014).
[https://doi.org/10.1016/j.jallcom.2013.11.058]

-
Xu, F., Sun, L., Lan, X., Chu, H., Sun, Y., Zhou, H., Li, F., Yang, L., Si, X., Zhang, J., Walter, S., and Gabelica, Z., "Mechanism of Fast Hydrogen Generation from Pure Water Using Al–SnCl2 and Bi-Doped Al– SnCl2 Composites", International Journal of Hydrogen Energy, 39(11), p5514-5521, (2014).
[https://doi.org/10.1016/j.ijhydene.2014.01.154]

-
Yavor, Y., Goroshin, S., Bergthorson, J.M., Frost, D.L., Stowe, R., and Ringuette, S., "Enhanced Hydrogen Generation from Aluminum–Water Reactions", International Journal of Hydrogen Energy, 38(35), p14992-15002, (2013).
[https://doi.org/10.1016/j.ijhydene.2013.09.070]

-
Hiraki, T., Takeuchi, M., Hisa, M., and Akiyama, T., "Hydrogen Production from Waste Aluminum at Different Temperatures, with LCA", Materials Transactions, 46(5), p1052-1057, (2005).
[https://doi.org/10.2320/matertrans.46.1052]

-
Razavi-Tousi, S.S., and Szpunar, J.A., "Modification of the Shrinking Core Model for Hydrogen Generation by Reaction of Aluminum Particles with Water", International Journal of Hydrogen Energy, 41(1), p87-93, (2016).
[https://doi.org/10.1016/j.ijhydene.2015.11.080]

-
Balaji, R., Senthil, N., Vasudevan, S., Ravichandran, S., Mohan, S., Sozhan, G., Madhu, S., Kennedy, J., Pushpavanam, S., and Pushpavanam, M., “Development and Performance Evaluation of Proton Exchange Membrane (PEM) based Hydrogen Generator for Portable Applications,“, International Journal of Hydrogen Energy, 36(2), p1399-1403, (2011).
[https://doi.org/10.1016/j.ijhydene.2010.10.072]

- Tate, T., "On the Magnitude of a Drop of Liquid Formed Under Different Circumstances", Philosophical Magazine Series 4, 27(181), p176-180, (1864).
-
Yavor, Y., "Aluminum-Water Reaction Mechanism – Modeling of the Different Reaction Stages", 14th International Energy Conversion Engineering Conference, Salt Lake City, U.T., U.S.A., AIAA 2016-5021, Jul), (2016.
[https://doi.org/10.2514/6.2016-5021]

- Kuo, K.K., Principles of Combustion, 2nd ed., Wiley-Interscience, New York, N.Y., U.S.A., Ch. 3, (2005).
- Hu, H., Qiao, M., Pei, Y., Fan, K., Li, H., Zong, B., and Zhang, X., "Kinetics of Hydrogen Evolution in Alkali Leaching of Rapidly Quenched Ni-Al Alloy", Applied Catalysis A: General, 252(1), p173-183, (2003).
-
Corapcioglu, M.Y., Cihan, A., and Drazenovic, M., "Rise Velocity of an Air Bubble in Porous Media: Theoretical Studies", Water Resources Research, 40(4), pW04214, (2004).
[https://doi.org/10.1029/2003wr002618]

-
Roosevelt, S.E., and Corapcioglu, M.Y., "Air bubble migration in a granular porous medium: Experimental studies", Water Resources Research, 34(5), p1131-1142, (1998).
[https://doi.org/10.1029/98wr00371]

-
Ergun, S., and Orning, A.A., "Fluid Flow through Randomly Packed Columns and Fluidized Beds", Industrial & Engineering Chemistry, 49(6), p1179-1184, (1949).
[https://doi.org/10.1021/ie50474a011]