다단 축류 터빈에서의 초킹 영역 탈설계 성능 해석을 위한 평균반경 해석법
Copyright ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
일반적으로 다단 축류 터빈은 높은 팽창비에서 유동 가속으로 인하여 특정 단에서 초킹 현상이 발생하게 된다. 입구 유량 경계조건을 사용하는 일반적인 평균반경해석법을 사용하는 경우 유량 변화없이 팽창비만 증가하게 되는 초킹 현상을 예측하는데 한계가 있다. 본 연구에서는 이러한 문제점을 해결하기 위해 초킹 영역에서의 성능을 예측하는 알고리즘을 제안하였다. 초킹 지점 이후에는 초킹이 발생하는 노즐 혹은 로터 출구 유동이 팽창하는 특성을 반영하여 고정된 유량 조건에서 팽창비가 변할 수 있도록 알고리즘을 구성하였다. 계산된 결과를 다단 축류 터빈 전산해석 결과 및 실험결과와 비교하여 신뢰성을 확인하였다.
Abstract
In general, the choking phenomenon occurs due to the flow acceleration of a turbine under high pressure-ratio. During choking, the total pressure ratio increases without any variation in the mass flow rate. It is difficult to predict choking characteristics by using conventional meanline analysis, which utilizes mass flow inlet boundary condition. In this study, an algorithm for predicting the choking point is developed to solve this problem. In addition, a performance estimation algorithm is presented to estimate the performance after choking, based on the flow behavior of flow expansion at the choked nozzle or rotor. The analysis results are compared with 3D CFD analysis and experimental data to validate this method.
Keywords:
Multi-stage, Axial Turbine, Choking, Meanline Analysis, Off-design Performance키워드:
다단, 축류 터빈, 초킹, 평균반경 해석법, 탈설계 성능1. 서 론
일반적으로 다단 축류 터빈은 하나의 독립된 구성품으로 구동되는 경우보다 압축기, 연소기, 터빈으로 구성된 가스터빈과 같이 하나의 시스템으로 운용되는 경우가 대부분이다. 가스터빈 시스템 성능 해석을 위해서는 구성품의 대표 성능 지표인 유량, 팽창비, 효율 등이 필요하다. 특히 설계점 이외인 탈설계 지점에서의 성능 해석을 위해서는 구성품의 대표 성능을 나타낼 수 있는 상관식이나 성능 선도가 필수적으로 요구된다.
가스터빈의 성능 선도를 도출하는 방법에는 크게 세 가지로 나뉜다. 첫 번째로는 기존의 유사한 성능 맵의 설계 지점과 적용하고자 하는 가스터빈 설계점과의 비를 이용하여 나머지 지점의 값들을 축척(scaling)하는 방법이 있다[1]. 두 번째로는 형상 정보를 바탕으로 수치적 방법을 이용하여 설계점 및 탈설계 지점에서의 구성품 성능을 예측하는 방법이 있다[2]. 마지막으로는 시험을 통해 설계된 구성품의 성능 선도를 도출할 수 있다. 첫 번째 방법인 축척의 경우에는 설계하고자 하는 가스터빈과 축척에 사용되는 구성품의 운용 조건이 유사한 경우 정확도가 높다. 하지만 구성품의 성능 특성은 엔진 회사의 고유한 자산이기 때문에 일반적으로 공개된 데이터를 찾기 어렵다. 세 번째 방법인 설계된 형상을 구성품 시험을 통해 도출하는 방법이 가장 정확한 성능 선도 도출 방법이지만, 설계 과정 중에서 도출하기 어렵고 비용이 많이 든다는 단점이 있다. 이려한 이유로 수치적인 방법을 이용하여 성능 선도를 도출하는 것이 가스터빈 설계과정에서 일반적인 방법이다.
수치해석적인 방법에도 1차원 평균반경(meanline analysis) 해석법, 2차원 관통 유동 해석법 (through flow analysis), 그리고 Navier-Stokes 방정식을 이용한 3차원 해석법이 있다. 1차원 평균반경 해석법의 경우, 상대적으로 적은 계산 시간과 경험식을 적용하여 예측 정확도를 높일 수 있다는 장점이 있기 때문에 설계과정에서 탈설계점 성능 선도를 도출하는데 많이 사용된다. 일반적인 터빈의 경우 높은 팽창비 영역에서 유동 가속으로 인하여 노즐 혹은 로터 목에서 마하수 1.0이 되는 초킹(choking) 현상이 발생한다. 초킹이 발생한 이후에는 유량의 변화 없이 팽창비만 증가하는 특성을 가지게 된다. 이러한 터빈 초킹 특성을 정확하게 예측하는 것이 탈설계점 성능 선도를 생성하는데 매우 중요하다. Glassman[3]은 축류 터빈 설계 프로그램을 개발하였다. 설계 과정중에 발생하는 초킹 지점을 정의하기 위해 유량과 평균반경 속도의 변화 비율을 이용하였다. 이 비율이 4배가 되면 초킹이 된 것으로 판단하고 설계 인자가 변하도록 프로그래밍하였다. Flagg[4]는 특정 지점의 전압과 정압의 비율이 지정된 한계치를 넘는 경우를 초킹 지점으로 판별하였다. Glassman[5]은 축류 터빈 탈설계 성능해석을 위한 프로그램을 개발하였으며, Flagg[4]가 적용한 방법을 이용하여 초킹 여부를 판별하였다. 초킹 지점 이후의 터빈 손실을 팽창비에 따라 감소하는 것으로 가정하고 효율을 계산하였다. Chen[6]은 Glassman[5]이 개발한 프로그램을 터빈 출구 안내익을 포함한 성능해석이 가능하도록 개선하는 연구를 수행하였다. 높은 부하를 가지는 4.5단과 3.5단 축류 터빈에 대한 검증을 수행하였다. Hendricks[7]는 단순한 터빈성능 선도를 사용하지 않고 1차원 터빈 성능해석 프로그램을 사이클 프로그램과 연계하여 가스터빈의 탈설계 성능 해석이 가능하도록 하는 연구를 수행하였다. 일반적으로 가스터빈 탈설계점 성능해석은 엔진 유량, 회전 수, 터빈 팽창비 등과 같은 여러 가지의 변수와 이에 상응하는 관계 식을 수치적인 방법을 통해 찾는 방식으로 진행된다[8]. 터빈에서의 팽창비 또한 가스터빈 탈설계 해를 찾기 위해 사용 되는 대표 변수이다. 터빈 프로그램을 사이클 해석 프로그램과 연계하여 해를 찾기 위해서는 초킹 영역에서의 터빈 성능을 예측하는 방법이 입구 유량을 바탕으로 하는 것이 아니라 입-출구 팽창비 바탕으로 해야 한다는 것을 의미한다. 입구 유량을 바탕으로 성능을 도출할 경우, 초킹영역과 같은 유량에 따른 팽창비 변화가 적은 곳에서는 해를 찾기 어렵기 때문이다. 이를 위해 Hendricks[7]는 터빈의 입구 조건으로는 전압력을, 출구 조건으로는 정압력을 사용하여 성능을 예측할 수 있도록 프로그램을 구성하였다. 설계과정에서 입구 전압과 목에서 마하수가 1.0이 되는 경우의 정압비를 한계 팽창비로 정의하였다. 설계점에서는 터빈 입구 전압과 출구의 정압 비율이 한계 팽창비를 넘는 경우를 초킹 지점으로 판별하였다. 탈설계점에서는 설계점에서 지정된 노즐 혹은 블레이드 목에서의 초킹 유량보다 큰 경우 초킹이라고 판별하였다. 하지만 이러한 경우에는 독립적인 터빈 탈설계 프로그램에서 적용하기 어렵다는 단점이 있다.
본 연구에서는 축류 터빈 탈설계 영역 성능해석을 위해 노즐 혹은 로터 출구 마하수를 바탕으로 초킹 지점을 예측할 수 있는 알고리즘을 제안하였다. 또한 초킹 이후의 영역에서는 유동이 팽창하는 현상을 반영하여 성능을 계산할 수 있도록 하였다. 유로내에 발생하는 손실들을 예측하기 위해 형상 손실 (profile loss), 이차 유동에 의한 손실 (secondary loss), 충격파에 의한 손실 (shock loss), 뒷전에서의 손실 (trailing edge loss), 팁 간극에 의한 손실 (tip clearance loss) 모델들을 고려하였다. 본 연구에서는 Tournier and El-Genk[9]의 연구에서 적용 및 검증된 손실 모델들을 사용하였다. 또한 구성된 모델을 3차원 전산해석 결과 및 시험 결과와 비교하여 검증을 수행하였다.
2. 터빈 해석 방법
2.1 1차원 평균 반경 해석법
1차원 평균 반경 해석법은 압축기와 터빈과 같은 터보기계의 설계초기 단계에서 유용하게 사용된다. 이러한 방법을 이용한 해석법의 장점은 3차원 해석법과 비교하여 상대적으로 적은 계산 시간으로 단단 및 다단을 가지는 터보기계에 대한 다양한 조건에서의 성능을 계산할 수 있다는 것이다.
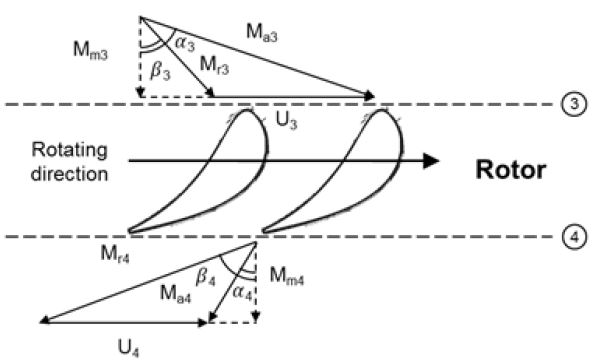
1차원 평균 반경 해석법은 중간 단면에서의 성능이 노즐과 로터 높이 방향으로의 성능을 대변하는 것으로 가정하고 성능해석을 수행한다. 노즐에서 단열조건이면 출구에서의 전온도는 입구에서의 전온도와 동일하다고 가정할 수 있다. 노즐 출구에서의 전압력은 유로에서 발생하는 전압력 손실로 인하여 줄어들게 되며 이는 손실모델을 이용하여 계산할 수 있다. 로터에서는 노즐과 같이 단열조건으로 가정하더라도 Fig. 1과 같이 회전성분이 존재하기 때문에 출구에서의 전온도가 입구에 비해서 감소하게 된다. 이는 각 운동량 보존법칙으로 계산할 수 있으며 관계식은 Eq. 1과 같다.
| (1) |
노즐 및 로터에서의 전압력 손실은 Eq. 2와 같이 손실 계수 Yt를 이용하여 계산할 수 있다.
| (2) |
터빈의 속도 삼각형을 계산하기 위해서는 노즐 및 로터 입구와 출구에서의 속도 크기, 방향이 필요하게 된다. 이는 각 입-출구 면에 전온도, 전압력, 유량, 유동 각도, 그리고 면적을 통해서 속도 크기와 방향을 계산할 수 있다. 노즐 및 로터 입구 면에서의 초기 마하수를 가정하고 이를 통해서 밀도를 계산한다. 이를 바탕으로 주어진 유량에서의 마하수를 다시 계산하게 되며, 계산된 마하수와 가정된 마하수의 차이가 10-4이하가 될 때까지 같은 과정을 반복한다.
노즐 및 로터 출구에서의 전압력은 유로에서 발생하는 손실에 의해서 일부 감소하게 되는데 이를 반영하기 위해서 초기에 마하수뿐만 아니라 출구 전압력 또한 가정하여 계산을 수행한다. 초기 가정된 출구 전압력을 이용하는 것 이외에는 마하수를 계산하는데 입구에서와 같은 계산과정을 거친다. 추가적으로, 가정된 마하수를 계산된 값으로 바꾸는 과정에서 가정된 출구 전압력 또한 손실 계수가 반영된 실제 전압력으로 다시 입력하게 된다.
2.2 손실 모델
터빈 유로내의 전압력 손실을 예측하기 위한 손실모델의 종류에는 여러 가지가 있으며 여러 손실인자들을 고려한 모델들을 중첩하여 전체손실을 계산하는 방법이 일반적이다. 본 연구에서는 터빈 유로내의 전압력 손실을 예측하기 위해 Tournier and El-Genk[9]이 제안한 손실모델조합을 적용하였다.
2.3 초킹 이전 영역에서의 성능 해석법
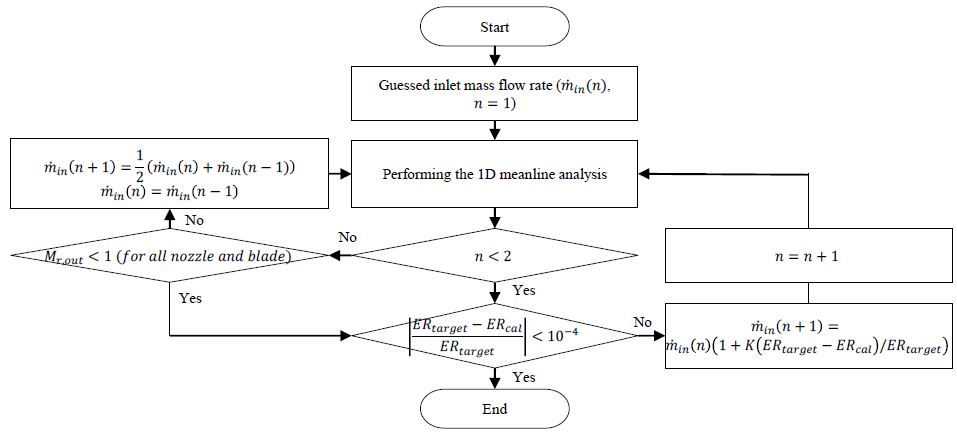
본 연구에서는 터빈 노즐 및 로터에서의 초킹지점을 판단하기 위한 알고리즘을 제안하였다. 터빈 성능 해석에 사용되는 입력 변수로는 입-출구 팽창비와 형상 변수 및 초기 입구 공기 유량이다. Fig. 2는 개발된 알고리즘을 나타낸 것이다. 우선 초기 입구 공기 유량으로 주어진 형상 변수와 1차원 평균반경 해석법을 이용하여 각 단별 및 전체 단의 성능해석을 수행한다. 이후 노즐 및 로터 출구의 마하수가 1.0보다 작은 경우에는 입구 공기 유량 변화시킨다. 만약 계산된 입-출구 팽창비가 목표값과 같아지는 경우에는 계산을 종료하게 되며, 목표값보다 작은 경우에는 입구 공기 유량을 증가시켜주게 된다. 공기유량을 증가시켜주는 경우에도 목표 팽창비와 계산된 팽창비와의 차이를 이용하여 다음 입구공기 유량의 정도를 산정한다. 출구 마하수가 1.0보다 큰 경우에는 초킹이 된 것으로 판단하고 유량을 변화시킨다. 이 때 정확한 초킹 지점을 판단하는 것이 중요하기 때문에 계산된 팽창비가 목표 팽창비보다 작은 조건에서 반복 계산과정에서 유량 변화의 정도가 10-4보다 작은 경우 초킹되는 지점으로 판단하였다. 이러한 방식은 Hendricks[7]의 방식과는 다르게 설계해석 과정 없이 형상 변수만으로 초킹 지점 예측이 가능하다.
2.4 초킹 이후 영역에서의 성능 해석법
초킹 이전 영역에서는 유량이 증가함에 따라 유속이 증가하여 터빈 전체 팽창비가 증가하지만 초킹 이후 조건에서는 이러한 과정을 이용할 수 없다. 일반적으로 특정 노즐 및 로터에서 초킹 되는 경우, 출구 압력이 더 낮아지기 위해서는 유동이 팽창하여 가속되어야 한다[7]. 이러한 특성을 이용하여 본 연구에서는 노즐 및 로터에서 초킹이 되는 경우 출구 유동 각도를 증가시켜 출구 압력이 감소되도록 하였다.
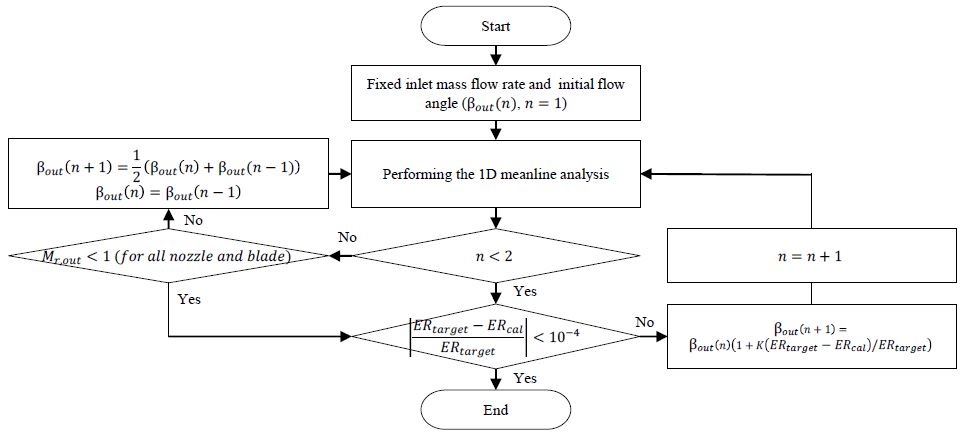
초킹 이후 영역에서의 목표 팽창비를 만족하는 조건을 찾기 위한 알고리즘을 Fig. 3에 나타내었다. 앞서 설명한 초킹 이전 영역 해석법을 통해 도출된 초킹 유량을 이용하여 초킹 이후에서는 유량을 고정하였다. 또한 초킹이라고 판단된 노즐 혹은 로터 출구의 유동 각도를 증가시키게 된다. 만약 계산된 팽창비가 목표 값보다 작은 경우에는 두 차이를 이용하여 다음 계산 과정에서의 유동 각도를 가정하게 된다. 또한 유동 각도를 증사키는 과정에서 하류 노즐 및 로터에서의 출구 마하수가 1.0이 넘는 경우, 출구 유동 각도를 변화시키는 지점을 바꾸게 된다. 이는 초킹이 발생하는 노즐 및 로터 상류에서는 입구 조건이 바뀌지 않은 한 유동 조건이 변하지 않기 때문이다.
3. 터빈 해석 결과
3.1 전산해석 결과와의 비교
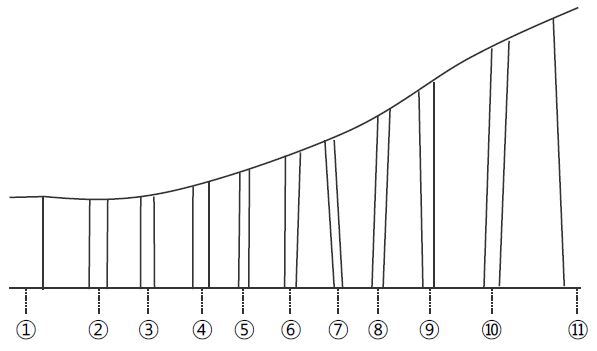
앞서 설명한 해석법의 검증을 위해 다단 축류 터빈의 3차원 전산해석 결과와 비교하였다. 난류모델은 k-ω SST이며, 노즐-로터의 경계면은 혼합면 기법(mixing plan)을 적용한 결과이다[10]. 격자 형태 및 전산해석에 대한 세부적인 설명은 박명환[10]의 연구에서 확인할 수 있다. 대상 터빈은 축류 5단 천음속 터빈이며, 각 로터의 Tip clearance는 각각 2% 이다. Fig. 4는 대상 터빈의 개념도와 비교를 위한 지점들을 나타낸 것이다.
Table 1은 3차원 전산해석 및 1차원 평균 반경해석법의 결과를 비교한 것이다. 참고 문헌들을 통해 수집된 경험식의 경우 도출된 형상 및 조건에 따라 정확도가 달라질 수 있다. Petrovic et al.[11]은 손실이 최소가 되는 입사각 및 출구 이탈각(deviation angle)의 경험식에 보정계수를 적용하여 해석 모델에 대한 정확도를 향상시켰다. 본 연구에서는 개발된 초킹 영역에서의 알고리즘을 검증하는 것을 목표로 한다. 이를 위해 주어진 팽창비에서 입구 유량을 노즐 및 로터출구 이탈각 경험식에 보정 계수를 적용하여 유량을 보정하였다.
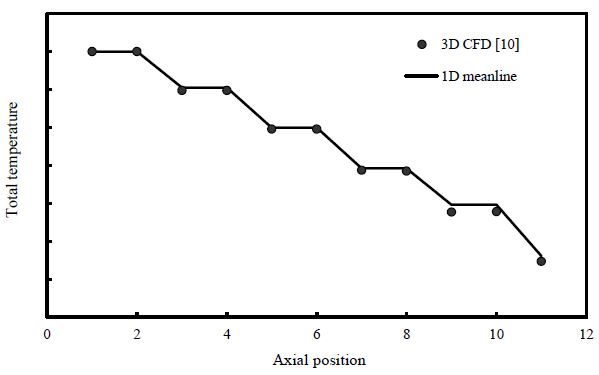
Fig. 5는 축방향 위치별 평균 전온도 결과를 비교한 것이다. 9번과 10번 위치에서 1차원 평균 반경 해석법이 상대적으로 전온도를 높게 예측하는 결과를 보이지만, 전반적으로 전온도가 축방향으로 감소하는 경향을 잘 예측하는 것을 볼 수 있다.
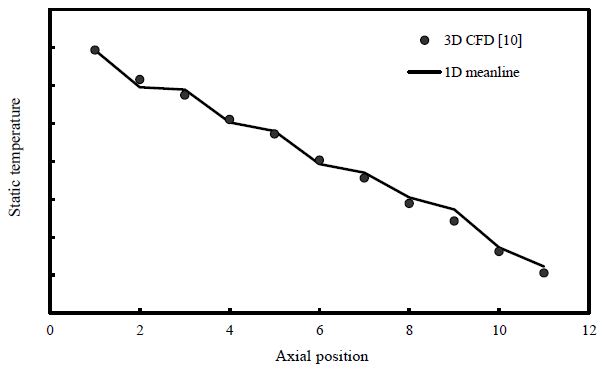
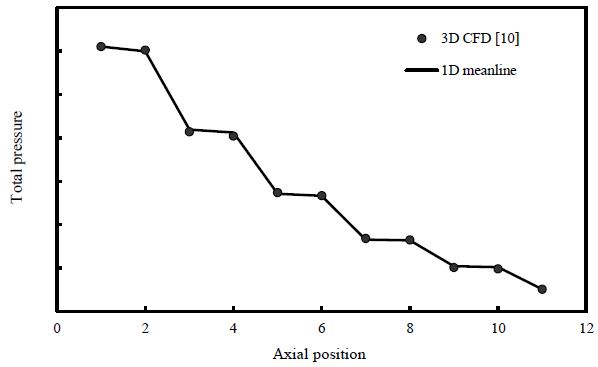
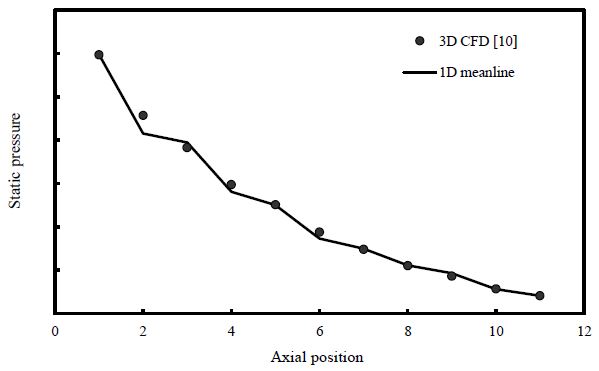
Fig. 6은 축방향 위치별 평균 정온도 결과를 나타낸 것이다. 1차원 평균 반경 해석법의 경우 중간 단면에서의 속도 성분이 높이 방향으로의 분포를 대변한다는 가정으로부터 도출된다. 하지만 3차원 전산해석의 경우 높이 방향으로의 속도 분포를 해석하기 때문에 두 결과가 일부 차이나는 것으로 판단된다. 또한 벽면에서의 경계층 발달로 인한 실제 유로 면적 감소 효과 및 복잡한 3차원 유동 현상으로 1차원 평균반경 해석법과 3차원 전산해석 결과와의 차이가 발생할 수 있다. 하지만 1차원 평균반경 해석법이 전반적으로 3차원 전산해석 결과의 경향을 잘 예측하는 것을 확인하였다. Fig. 7과 8은 전압 및 정압결과를 비교한 것이다. 앞서 설명한 온도 결과와 마찬가지로 전반적으로 압력이 축방향으로 감소하는 경향을 잘 예측하는 것을 볼 수 있다.
Table 2는 전압력 및 전온도 결과를 정량적으로 비교한 결과이다. 터빈 마지막 단 노즐 출구에서의 가장 큰 전압력 차이를, 마지막 단 노즐입구에서 가장 큰 전온도 차이를 보였다. 결과적으로 1차원 평균반경 해석법이 3차원 전산해석 결과와 비교하여 전압력과 전온도를 각각 최대 3.89% 및 2.23% 높게 예측하였다.
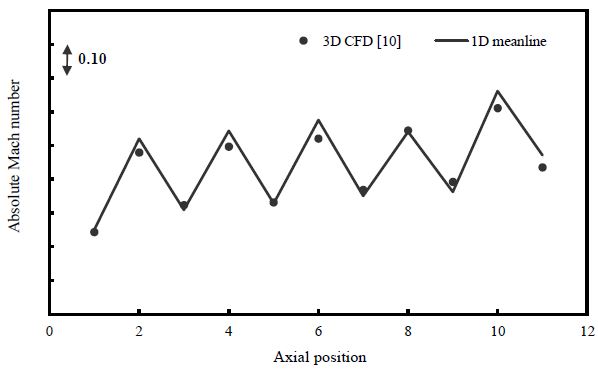
Fig. 9는 중간단면에서의 절대 마하수 분포를 비교한 결과이다. 노즐에서 가속이 되고 로터에서 팽창이 되는 결과를 확인할 수 있다. 노즐 출구 및 로터 입구에서 1차원 평균 반경해석법이 3차원 전산해석 결과와 비교하여 비교적 높은 마하수를 보인다. 이는 앞서 언급한 3차원 유동 및 손실 모델에 의한 영향인 것으로 판단된다. 또한 마지막단 노즐에서 초킹이 되어 출구 마하 수가 높게 나타나는 것을 확인할 수 있다.
3.2 실험 결과와의 비교
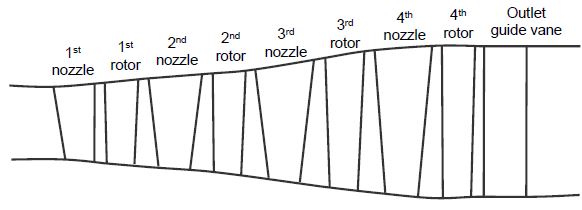
Fig. 10은 결과 비교를 위한 4단 축류 터빈의 개념도를 나타낸 것이다. 이 터빈의 경우 노즐 및 로터의 50% 높이 지점의 위치가 흐름 방향으로 변하지 않는 특징을 가진다. 대상 터빈에 대한 설계 및 실험 결과는 Evans and Hill[12]과 Walker and Tomas[13]의 연구에 각각 나타나있다.
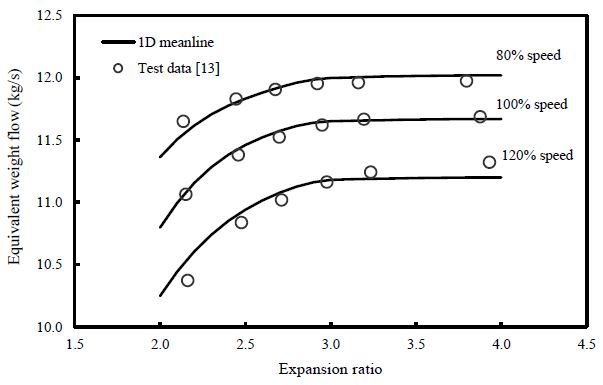
Fig. 11은 팽창비에 따른 보정 질량 유량(equivalent mass flow rate)결과를 회전 수 별로 나타낸 것이다. 결과적으로 1차원 평균 반경해석법 및 본 연구에서 제안한 알고리즘을 적용할 경우 초킹 지점 및 경향을 잘 예측하는 것을 확인할 수 있다. 120% 회전수 실험 결과의 경우, 높은 팽창비에서 유량이 일부 증가되는 것을 볼 수 있는데 이는 손실이 최소가 되는 입사각 및 출구 이탈각이 초킹된 이후 조건에서 유동 팽창에 영향을 받기 때문으로 보이며, 추가적인 경험식 개선이 필요할 것으로 판단된다.
4. 결 론
본 연구에서는 다단 축류 터빈의 초킹 지점 및 초킹 이후 성능을 평균반경해석법을 이용하여 예측할 수 있는 알고리즘을 제안하였다. 형상정보 및 입-출구 팽창비를 입력하여 계산이 수행되도록 구성하였다. 초킹 이전 영역에서는 목표팽창비를 만족하기 위한 유량 조건을 찾게 되며, 계산된 노즐 및 로터 출구 마하수를 이용하여 초킹 여부를 판별하도록 하였다. 초킹 이후 지점에서는 유량을 고정하고 초킹 이후 유동이 팽창되는 물리 현상을 반영하여 목표 팽창비를 찾을 수 있도록 하였다. 이렇게 구성된 알고리즘을 평균반경 해석법에 작용하였으며, 3차원 전산해석 결과 및 실험결과와의 비교를 통해 신뢰성을 확인하였다. 결과적으로 단별 성능 및 팽창비에 따른 입구 유량의 경향을 잘 예측하는 것을 확인하였다.
Nomenclature
| cp : | Specific heat |
| : | Mass flow rate |
| n : | Number of iteration |
| Ma : | Absolute Mach number |
| Mr : | Relative Mach number |
| Mm : | Mach number for Axial direction |
| P0 : | Total pressure |
| P : | Static pressure |
| ER : | Expansion ratio |
| T0 : | Total temperature |
| U : | Rotating speed |
| Vw : | Tangential velocity |
| Yt : | Total loss coefficient |
| α : | Absolute flow angle |
| β : | Relative flow angle |
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 2013101010170A)
References
-
Kong, C., Ki, J., and Kang, M., "A New Scaling Method for Component Maps of Gas Turbine Using System Identification", Journal of Engineering Gas Turbines Power, 125(4), p979-985, (2003).
[https://doi.org/10.1115/1.1610014]

- Steinke, R.J., "A Computer Code for Predicting Multistage Axial-Flow Compressor Performance by a Meanline Stage-Stacking Method", NASA TM-2020, (1982).
- Glassman, A.J., "Users Manual and Modeling Improvements for Axial Turbine Design and Performance Computer Code TD2-2", NASA CR-189118, (1992).
- Flagg, E.E., "Analytical Procedure and Computer Program for Determining the Off-Design Performance of Axial Flow Turbines", NASA CR-710, (1967).
- Glassman, A.J, "Modeling Improvements and Users Manual for Axial-Flow Turbine Off-Design Computer Code AXOD", NASA CR-195370, (1994).
- Chen, S.S, "Capability Extension to the Turbine Off-Design Computer Program AXOD With Applications to the Highly Loaded Fan-Drive Turbines", NASA TM-2011-217129, (2011).
-
Hendricks, E.S., "Meanline Analysis of Turbines with Choked Flow in the Object-Oriented Turbomachinery Analysis Code", 54th AIAA Aerospace Sciences Meeting, San Diego, C.A., U.S.A., AIAA 2016-0119, Jan. 2016.
[https://doi.org/10.2514/6.2016-0119]

- Sellers, J.F., and Daniele, C.J., "DYNGEN: A program for calculating steady-state and transient performance of turbojet and turbofan engines", NASA TN-7901, (1975).
-
Tournier, J.M., and El-Genk, M.S., "Axial Flow, Multi-Stage Turbine and Compressor Models", Energy Conversion and Management, 51(1), p16-29, (2010).
[https://doi.org/10.1016/j.enconman.2009.08.005]

- Bang, M.H., "Effect of combustor exit flow and endwall leakage flow on a multi-stage turbine system", Ms degree, School of Mechanical Engineering, Pusan National University, Pusan, Korea, (2015).
-
Petrovic, M.V., Wiedermann, A., and Banjac, M.B., "Development and Validation of a New Universal Through Flow Method for Axial Compressors.", Proceedings of ASME Turbo Expo 2009, Orlando, F.L., U.S.A., GT 2009-59938, Jun. 2009.
[https://doi.org/10.1115/gt2009-59938]

- Evans, D.C., and Hill, J.M., "Experimental Investigation of a 4.5-stage Turbine with Very High Stage Loading Factor I – Turbine Design", NASA CR-2140, (1973).
- Walket, N.D., and Tbomas, M.W., "Experimental Investigation of a 4.5-stage Turbine with Very High Stage Loading Factor II – Turbine Performance", NASA CR-2363, (1974).