POD와 DMD를 이용한 와류형 분사기의 극저온 질소 분무 동적 특성 분석
Copyright Ⓒ The Korean Society of Propulsion Engineers
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
초임계 환경에서 와류형 분사기의 극저온 질소 분무 동적 특성 분석을 위하여 3차원 LES 난류 모델을 적용하였다. 초임계 상태에서 질소의 상태량들을 정확하게 예측하기 위해 SRK 실기체 상태방정식을 사용하였고, 점성계수와 열전도도는 Chung의 고압 상태 혼합물에 대한 방정식, 그리고 확산 계수는 Fuller의 이론에 Takahashi의 보정식을 적용하였다. 질소 분무 결과, 분사기 내, 외부에서 유동장과 음향장 사이의 상호작용으로 복잡한 유동구조가 형성된다. 복잡한 유동 현상을 분석하기 위해 FFT, POD 그리고 DMD 기법을 적용하여 해석을 수행하였다. FFT 해석을 수행하여 분사기 내, 외부에서 나타나는 특정 주파수를 파악하였으며, POD와 DMD를 통해 각 주파수가 어떠한 유동 구조를 갖는지에 대한 연구를 수행하였다. 또한, DMD를 통해 각 주파수의 감쇠 계수를 파악하여 이를 실험 결과와 비교하였다.
Abstract
The cryogenic nitrogen spray of a swirl injector has been numerically investigated using three dimensional LES turbulence model to analyze the dynamic characteristics under supercritical condition. To predict the precise nitrogen properties under supercritical condition, SRK equation of state, Chung’s method for viscosity and thermal conductivity and Takahashi’s correlation based on Fuller’s theory for diffusion coefficient are implemented. The complex flow structures due to interaction between flow field and acoustic field are observed inside and outside the injector under supercritical condition. FFT, POD, and DMD techniques are employed to understand the coherent structures. By implementing the FFT, the dominant frequencies are identified inside and outside the injector. The coherent flow structures related to the dominant frequencies are visualized using the POD and DMD techniques. In addition, the DMD provides the damping coefficient which is related with the instability prediction.
Keywords:
Swirl Injector, Large Eddy Simulation(LES), Cryogenic Nitrogen, Dynamic Mode Decomposition(DMD)키워드:
와류형 분사기, 대와류모사, 극저온 질소, 동적 모드 분해1. 서 론
로켓의 성능과 효율을 향상하기 위해서, 연소실 온도와 압력을 상승시키는 연구가 주목받고 있다. 연소실 온도와 압력이 임계점 이상으로 상승하면 연소실 내부 유체는 초임계 상태가 된다. 초임계 상태에서는 밀도, 비열, 열전도도, 확산 특성 그리고 표면장력과 같은 열역학적 상태량이 기존의 액체와 기체와는 확연히 다른 거동을 보인다. 초임계 상태의 유체는 액체와 같이 높은 밀도를 가지면서 동시에 기체와 같이 활발한 확산 특성이 나타난다. 또한, 초임계 상태에 도달하게 되면 표면 장력이 영(zero)에 가까워진다. 이는 기존의 아임계 상태에서 기화가 ‘액주(liquid core) - 분해(break up) - 미립화(atomization) - 기화(vaporization)’ 순서로 일어나는 것과 달리 액주가 곧바로 기화가 되는 원인이 된다. 초임계 영역에서의 빠른 기화 현상은 추진제의 혼합에 유리하여 높은 효율을 갖는다. 그리고 초임계 상태에서는 에너지 밀도가 매우 높으므로 연소기에서의 작은 압력진동과 불안정한 열 방출이 결합하면 심각한 불안정성을 초래할 수 있다[1].
로켓의 분사기 또한 성능과 효율에 밀접한 관련이 있다. 분사기는 충돌형, 전단형과 와류형의 종류가 있다. 이 중 와류형 분사기는 충돌형과 전당형에 비해 추진제의 혼합이 균일하며 큰 질량유량에 대해서도 높은 혼합 효율을 갖고 쵸킹(choking)이나 공동현상(cavitation)에 덜 민감하다는 장점이 있다[2]. 또한, 제작 과정에서 발생하는 공차에 대해서도 영향을 덜 받는다.
본 연구에서는 초임계 환경에서 극저온 질소를 분무하는 와류형 분사기를 고려하였다. 작동 압력은 실험 데이터가 존재하는 50 bar로 설정하였다. 정확한 난류 유동 모사를 위해 동적 Smagorinsky 모델을 적용한 LES 난류 모델을 이용해 3차원 수치해석을 수행하였다. 수치해석 결과에서 나타나는 복잡한 유동장을 해석하기 위해 특정 위치에서의 음향특성을 파악할 수 있는 Fast Fourier Transform (FFT) 방법과 Proper Orthogonal Decomposition (POD) 그리고 Dynamic Mode Decomposition (DMD) 방법을 사용해 비교 분석하였다.
2. 이 론
2.1 지배방정식
본 연구에서는 복잡한 난류유동을 모사하기 위해 큰 와류는 직접 풀고, 격자보다 작은 와류는 모델링하는 방법을 사용하는 LES 난류 모델을 적용하였다. Favre-averaged된 질량, 운동량,
| (1) |
| (2) |
에너지 보존방정식이 사용되었으며 사용된 식은 다음과 같다[3].
| (3) |
미 완결 항인 SGS항은 다음과 같이 정의된다.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
SGS 모델은 대수적 모델의 단점[3,4]을 해결한 Germano[5]의 동적 Smagorinsky모델을 사용하였다.
2.2 열역학적 상태량 및 전달물성치
초임계 영역에서는 액체와 기체처럼 명확하게 상이 분리되지 않고 액체와 같이 높은 밀도를 가지며 동시에 기체와 같이 활발한 확산특성을 갖는다. 이러한 독특한 상태에서의 물성치를 예측하기 위하여 여러 상태방정식과 전달 물성치 방정식들이 제안되어 왔다. 고압환경에서 극저온 질소에 대한 열역학적 상태량과 전달물성치에 대한 연구결과를 바탕으로[6], Soave-Redlich-Kwong (SRK)[7] 상태방정식을 적용하였다. 점성계수와 열전도도는 Chung[8]이 제안한 고압 상태 혼합물에 대한 방정식을 적용하였으며 확산계수는 Fuller 이론에 Takahashi[9]가 제안한 고압 상태의 특징을 보정한 식을 적용하였다.
2.3 수치기법
본 연구에 사용된 in-house 코드는 보존 법칙을 정확하게 만족하는 유한 체적방법을 지배방정식에 적용한 코드이다. 속도가 매우 낮은 재순환 영역에서 수렴속도가 저하되는 것을 개선하고, 큰 폭으로 변하는 밀도로 인한 수치적 불안정을 개선하기 위해 예조건화 기법을 적용하였다[3, 10-12]. 공간에 대해서는 4차 중앙차분을, 시간에 대해서는 4차 Runge-Kutta 방법을 적용하였다. 또한, 계산을 효과적으로 수행하기 위해 MPI library를 사용하는 병렬기법을 적용하였다[13-15].
2.4 Dynamic Mode Decomposition (DMD)
POD 기법은 참고 문헌[15]을 참조하길 바라며 본 논문에서는 DMD 기법을 간략히 소개한다. DMD는 데이터 분해 기법으로 시간에 대한 실험 혹은 수치적 데이터에서 동적으로 관련된 유동 형상을 추출하는 방법이다[16]. 일반적인 j시간에서의 유동장 데이터를 각각 벡터 υj로 나타내면 N개의 시간에 대한 스냅사진을 다음과 같이 표현할 수 있다.
| (9) |
선형 근사가정을 사용하면 하나의 스냅사진에서 다음 시간의 스냅사진으로의 관계인 선형 사상 행렬 를 가정할 수 있으며 다음과 같이 나타낼 수 있다.
| (10) |
Eq. 10에 Singular Value Decomposition(SVD)방법을 적용하여 유도되는 최종식은 Eq. 11과 같다[17].
| (11) |
각 공진모드의 감쇠계수는 다음과 같은 식을 통해 구할 수 있다[17].
| (12) |
| (13) |
감쇠 계수가 음인 경우는 해당 주파수가 감쇠함을 뜻하고, 양인 경우에는 해당 주파수가 증폭됨을 의미한다.
3. 결 과
3.1 해석모델
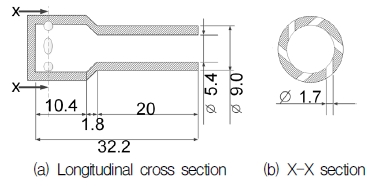
본 연구에서 사용된 극저온 와류형 분사기의 형상은 Fig. 1과 같다[18]. 6개의 포트에서 극저온의 질소가 접선 방향으로 유입되는 형상이며 중간에 면적이 작아지는 closed type이다. 형상에 대한 자세한 정보는 Table 1과 같다.
Schematic of a swirl injector in unit mm[18].
Injector geometry[18].
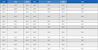
해석에 사용된 경계조건과 격자를 Fig. 2에 나타내었다. 각 블록은 30 × 40 × 30개의 격자를 갖고 있으며 총 111개의 블록으로 구성되어 있다. 작동조건은 Table 2에 나타내었다. 참고로 작동 유체인 질소의 임계압력과 온도는 34 bar와 126 K로, 질소주입 온도인 115 K에서는 액체(compressed liquid) 상태이다. 주입된 질소가 혼합과정으로 온도가 상승하여 천이임계(transcritical) 상태를 거치고 최종적으로 초임계 상태가 된다.
Schematics of computational domain and grid system.
Calculation condition.
입구 경계조건은 실험에서의 입구 조건과 일치하도록 5 bar의 차압 조건으로 설정하였다. 입구에 해당하는 격자의 압력과 5 bar와의 차압을 계산한 후 Bernoulli 식을 통해 속도를 도출하는 방법을 사용하였다. 즉, 입구에서 전압력을 55 bar로 고정한 압력조건이다. 계산된 속도에 난류 강도 10%의 Gaussian random number를 적용하여 난류효과를 적용하였다. 분사기 벽면은 단열조건을 적용하였으며, 출구 조건은 ambient 조건의 outflow로 설정하였고 Fig. 2의 빗금 친 부분이 이에 해당한다. 계산의 효율성을 증대시키기 위해 주입 포트를 따로 만들지 않고 주입 포트를 분사기에 투영시켰으며 이를 Fig. 2에 나타내었다.
3.2 해석 결과
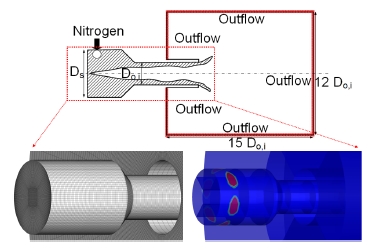
Fig. 3은 50 bar 조건에서 와류형 분사기의 순간적인 밀도장과 속도장을 나타낸 그림이며 분사기 내부와 외부에서 음향학적 영향을 관찰하기 위해 선정된 위치를 나타낸 그림이다. Fig. 3을 보면 6개의 포트에서 극저온의 질소가 접선방향으로 분사되며 원심력으로 인해 벽으로 붙는 현상이 관찰된다. 벽으로 붙은 질소는 얇은 액체 필름을 형성하며 동시에 중간 부분은 기상 코어가 생성된다. 액체 필름의 두께는 기상 코어와의 상호작용으로 축 방향과 접선 방향에 대해 모두 변한다. 액체 필름은 운동량 보존에 의해 수축부에서 속도가 증가하며 두께가 얇아진다. 얇아진 필름은 분사기에서 빠져나가며 일정한 분무각을 가지고 Kelvin-Helmholtz 종류의 불안정으로 인해 깨져나가며 기화한다. 필름이 분사기에서 빠져나갈 때 분사된 필름은 스월방향으로 팽창되어 중심부에서는 상대적으로 낮은 압력이 형성된다. 이로 인하여 분사기 후방에서 재순환 영역이 생성된다. 동시에 유동이 역류하는 현상이 관찰된다. 또한, 필름이 분사기를 빠져나간 직후에는 필름이 바깥 방향을 향해 퍼져나가다가 중심부의 저압으로 인해 점차 중심부로 다시 모이는 유동 구조도 관찰된다. 밀도장과 속도장의 형상을 통해 분사기 내, 외부에서 다양한 동적 현상이 혼재함을 알 수 있다. 따라서 이러한 복잡한 유동을 분석하기 위해 FFT, POD 그리고 DMD 방법을 적용하였다.
Instantaneous density and velocity contours and probe positions of a swirl injector.
분사기에서 나타나는 동적 거동을 분석하기 위해서, 특정 위치에서 시간에 따른 압력 섭동이 통계적 정상상태(statistically steady)에 도달한 후부터의 데이터를 해석에 사용하였다. Fig. 3의 위치별 FFT 결과로 나타난 주파수를 Fig. 4에 나타내었다. FFT 방법은 특정 위치에서 나타나는 주파수를 특별한 처리방법 없이 빠르게 파악할 수 있다. 분사기 가장 안쪽의 위치 1에서는 4.5 kHz와 8.92 kHz가 주로 관찰된다. 4.5 kHz는 분사기 가장 안쪽에서 최대 크기를 갖고 후방으로 전파될수록 그 크기가 점점 작아진다. 반면 8.92 kHz는 분사기 내부에서는 일정한 크기를 유지하다가 분사기 외부로 빠져나가면서 작아진다. 1.67 kHz와 3.25 kHz는 주로 액체 필름의 표면 따라서 분포하며 분사기 내부의 출구 위치와 분사기 후방 부분에서 관찰된다.
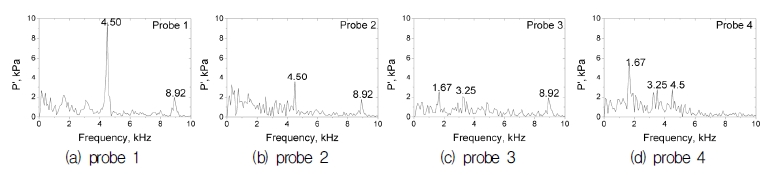
Power spectral densities of pressure fluctuations inside the injector at Prob. 1(a), Prob. 2(b), Prob. 3(c) and Prob. 4(d).
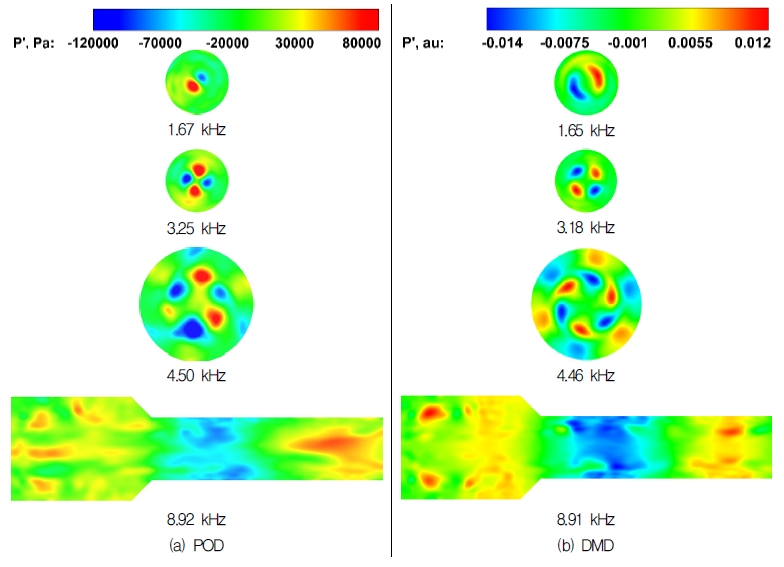
FFT 방법은 특정 위치에서의 정보만을 알 수 있으므로 분사기 내, 외부에서 어떠한 불안정과 관련된 음향장이 발생하는지 정확히 판단하기 힘들다. 서로 연관된 동적 구조를 파악하는 방법으로 주로 POD 기법와 DMD 기법이 연구되고 있다[15-17]. POD 기법은 스냅 사진으로부터 공간 관계에 대한 행렬을 대각선화 하여 에너지의 분포가 큰 유동구조를 찾는 방법이다. 하지만 해당 유동구조가 감쇠하는지 증폭되는지는 알 수 없다. 반면에 DMD기법은 스냅 사진을 시간에 대해 대각화하여, 해당 주파수의 증가, 감쇠도 알 수 있다는 장점이 있다. POD와 DMD의 비교를 위해 동일한 데이터를 사용하였다. 총 400개의 스냅사진을 사용했으며 각 스냅사진의 시간 간격은 50 μs이다. Fig. 5는 Fig. 4에서 나타난 여러 주파수에 해당하는 POD와 DMD 결과를 나타낸 그림이다. DMD 결과는 0.10 kHz의 저주파부터 10 kHz의 고주파까지 모든 영역에서의 수많은 주파수를 도출해낸다. 그중에서 관찰이 필요한 주파수를 POD 분석에서 특정화하는 방법을 사용하였다. 1.67 kHz, 3.25 kHz는 1T, 2T 모드에 해당하며, 4.50 kHz, 8.92 kHz는 3T, 5L 모드에 해당함을 알 수 있다[6]. Fig. 5에서 관찰할 수 있듯이 POD와 DMD의 음향구조 형태는 매우 유사하다. 반면 4.5 kHz와 같은 복잡한 구조에서는 DMD가 POD보다 음향구조 형태가 더욱 명확하다. 그리고 DMD의 주파수는 FFT와 POD에 비하여 약간 차이가 나는데, 이는 DMD가 평면 데이터를 기반으로 주파수를 추출하기 때문으로 판단된다. POD는 해당 모드에 대한 감쇠 계수를 알 수 없지만 DMD 기법을 통해 계산할 수 있으며 각 주파수에 대한 감쇠 계수를 Table 3에 나타내었다. 3.18 kHz를 제외한 주파수들은 감쇠 계수가 음수이기 때문에 시간이 지남에 따라 안정되어 가지만, 3.18 kHz는 감쇠 계수가 양수로 나타나 점차 증폭되어 감을 알 수 있다. 여기서 3.18 kHz는 실험에서[18] 나타나는 주파수인 3.1 kHz와 약 2.5%의 차이를 보인다.
Spatial distributions of oscillatory pressure field of POD and DMD.
Frequencies and damping coefficients.
4. 결 론
본 연구에서는 초임계 환경에서 극저온 질소를 분무하는 와류형 분사기에 대한 3차원 LES 수치 계산을 수행하였다. 초임계 환경에서 극저온 질소의 상태량들을 정확하게 모사하기 위해 SRK 상태방정식과 Chung의 방법, Takahashi의 관계식을 적용하였으며 동적 Smagorinsky모델을 사용하였다.
해석 결과, 분사기 내, 외부에서 유동장과 음향장 사이의 상호작용으로 복잡한 유동 형상이 관찰되었다. 정확한 분석을 위해 FFT, POD 그리고 DMD 기법을 사용하였다. FFT 방법을 통해 각 위치에서 1.67, 3.25, 4.50 그리고 8.92 kHz가 발생함을 확인하였다. FFT 방법은 단일 위치에서의 정보밖에 알 수 없으므로, 분사기 내부의 전반적인 유동 거동을 파악하기 위해 POD 기법과 DMD 기법을 사용하였다. DMD 기법은 매우 많은 주파수가 추출되기 때문에 POD를 수행하여 관찰할 주파수를 특정화하였다. 그 결과 1.67, 3.25, 4.50 그리고 8.92 kHz가 각각 1T, 2T, 3T 그리고 5L 모드임을 확인하였다. 특히 DMD 결과에서 3.18 kHz는 실험결과인 3.1 kHz와 약 2.5%의 차이를 보이며 감쇠 계수를 통해 점차 증폭되는 모드임을 파악하였다.
본 논문에서는 FFT, POD 그리고 DMD 방법을 각각의 장단점을 상호 보완하여 단일 와류형 분사기의 동적 거동을 파악하였다. 위와 같은 방법은 차후 연구할 연소를 동반한 동축 와류형 분사기의 경우에도 적용할 수 있을 것으로 기대된다.
Nomenclature
| Dij : | non-linearity of viscous stress term |
| E : | specific total energy |
| Ei : | I-th pseudo-eigenvector |
| Hi : | energy flux |
| Nstep : | number of time step |
| P : | period of acoustic oscillation |
| Qi : | heat flux |
| t : | time |
| T : | temperature |
| ui : | i-component velocity |
| ∆t : | time step |
| δij : | Kronecker delta |
| ⋋i : | I-th eigenvalue |
| ξi : | damping coefficient |
| ρ : | density |
| σi : | viscous work |
| τij : | viscous stress tensor |
| ㅡ : | time averaged |
| ~ : | Favre-averaged |
| sgs : | subgrid-scale |
Acknowledgments
본 연구는 서울대학교 차세대 우주추진 연구 센터와 연계된 미래창조과학부의 재원으로 한국연구재단의 선도연구센터 지원사업(NRF-2013R1A 5A1073861)과 산업통상자원부 주관 항공우주부품 기술개발 사업(10050539)의 지원을 받아 수행한 연구 결과입니다.
References
- Culick, F.E.C., and Yang, V., “Overview of Combustion Instabilities. In: liquid-propellant Rocket Engines”, AIAA, p3-37, (1995).
- Bazarov, V.G., Yang, V., and Puneesh, P., “Design and Dynamics of Jet and Swirl Injectors In: Liquid Rocket Thrust Chambers: Aspect of Modeling, Analysis, and Design”, Progress in Astronautics and Aeronautics, (2004).
-
Heo, J.Y., Hong, J.S., and Sung, H.G., “Effect of Dynamic SGS Model in a Kerosene-LOx Swirl Injector under Supercritical Condition“, International Journal of Aeronautical and Space Sciences, 16(2), p254-263, (2015).
[https://doi.org/10.5139/ijass.2015.16.2.254]
- Poinsot, T., and Veynante, D., Theoretical and Numerical Combustion, 2th ed, R.T. Edwards Inc, Philadelphia, P.A., U.S.A., (2005).
-
Germano, M., Piomelli, U., Moin, P., and Cabot, W., “A Dynamic Subgrid-scale Eddy Viscosity Model“, Physics of Fluid, 3(7), p1760-1765, (1991).
[https://doi.org/10.1063/1.857955]
-
Kang, J.S., Heo, J.Y., Sung, H.G., and Yoon, Y.B., “LES Investigation on The Cryogenic Nitrogen Injection of Swirl Injector Under Supercritical Environment“, Journal of the Korean Society for Aeronautical and Space Sciences, 44(4), p343-351, (2016).
[https://doi.org/10.5139/jksas.2016.44.4.343]
-
Soave, G., “Equilibrium Constants from a Modified Redlich-Kwong Equation of State“, Chemical Engineering Science, 27(6), p1197-1203, (1972).
[https://doi.org/10.1016/0009-2509(72)80096-4]
- Chung, T., Ajlan, M., Lee, L., and Starling, K., “Generallized Multi-Parameter Corresponding State Correlation for Ployatomic, Polar Fluid Transport Properties”, Industrial and Chemical Engineering Research, 27(4), p671-679, (1988).
- Takahashi, S., “Preparation of a Generalized Chart for the Diffusion Coefficients of Gases at High Pressures”, Journal of Chemical Engineering, 7, p417-420, (1974).
-
Sung, H.G., Yeom, H.W., Yoon, S.K., Kim, S.J., and Kim, J.G., “Investigation of Rocket Exhaust Diffusers for Altitude Simulation”, Journal of Propulsion and Power, 26(2), p240-247, (2010).
[https://doi.org/10.2514/1.46226]
-
Meng, H., and Yang, V., “A Unified Treatment of General Fluid Thermodynamics and its Application to a Preconditioning Scheme“, Journal of Computational Physics, 189(1), p277-304, (2003).
[https://doi.org/10.1016/s0021-9991(03)00211-0]
-
Kim, J.C., Yoo, K.H., and Sung, H.G., “Large-eddy Simulation and Acoustic Analysis of a Turbulent Flow Field in a Swirl-stabilized Combustor”, Journal of Mechanical Science and Technology, 25(10), p2703-2710, (2011).
[https://doi.org/10.1007/s12206-011-0741-0]
-
Kim, K.J., Heo, J.Y., and Sung, H.G., “Study on Thermophysical Property Characteristics of a 4 Species Kerosene Surrogate in a Swirl Injector at Supercritical Pressure Condition”, Journal of the Korean Society of Propulsion Engineers, 17(6), p45-58, (2013).
[https://doi.org/10.6108/kspe.2013.17.6.048]
- Yoo, K.H., Kim, J.C., and Sung, H.G., “Effects of Cooling Flow on the Flow Structure and Acoustic Oscillation in a Swirl-stabilized Combustor, Part I. Flow Characteristics”, Journal of Visualization, 16, p287-295, (2013).
-
Sung, H.G., Yoo, K.H., and Kim, J.C., “Effects of Cooling Flow on the Flow Structure and Acoustic Oscillation in a Swirl-stabilized Combustor, Part II. Acoustic Analysis”, Journal of Visualization, 17(1), p69-76, (2014).
[https://doi.org/10.1007/s12650-013-0193-y]
-
Schmid, P.J, “Application of the Dynamic Mode Decomposition to Experimental Data”, Experiments in Fluid, 50(4), p1123-1130, (2011).
[https://doi.org/10.1007/s00348-010-0911-3]
- Jourdain., G., Eriksson., L., Kim., S.H., and Sohn, C.H., “A Study on Quantification of Acoustic Amplification Using Dynamic Mode Decomposition Method”, 38th The Korea Society of Propulsioin Engineer Spring conference, Gumi, Korea, p364-366, Apr.), (2012.
-
Cho, S.H., Kim, H.S., Yoon, Y.B., and Sung, H.G., “Dynamic Characteristics of a Cryogenic Swirl Flow Under Supercritical Conditions”, Aerospace Science and Technology, 51, p162-170, (2016).
[https://doi.org/10.1016/j.ast.2016.02.008]